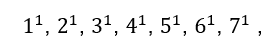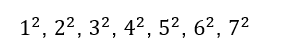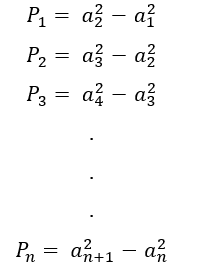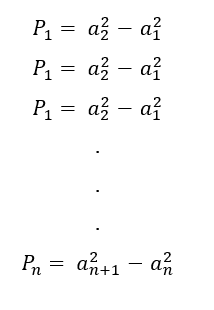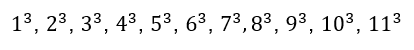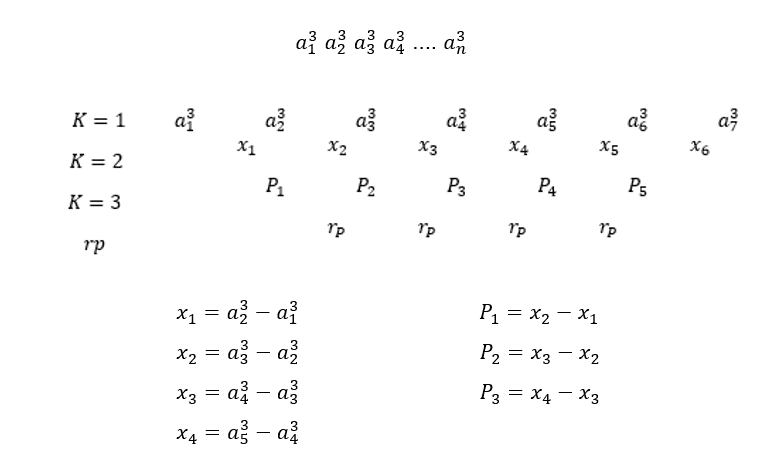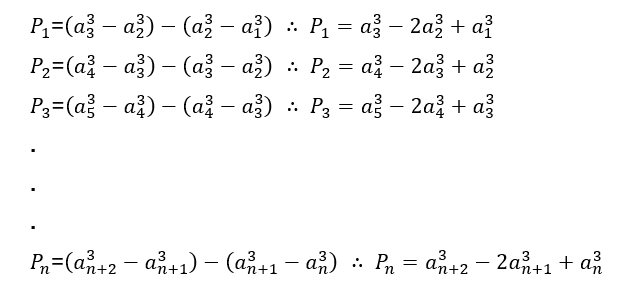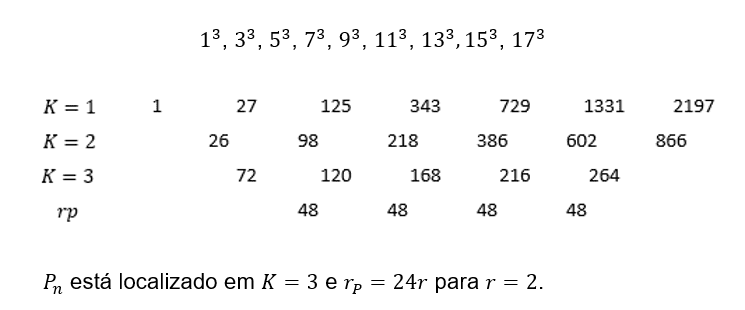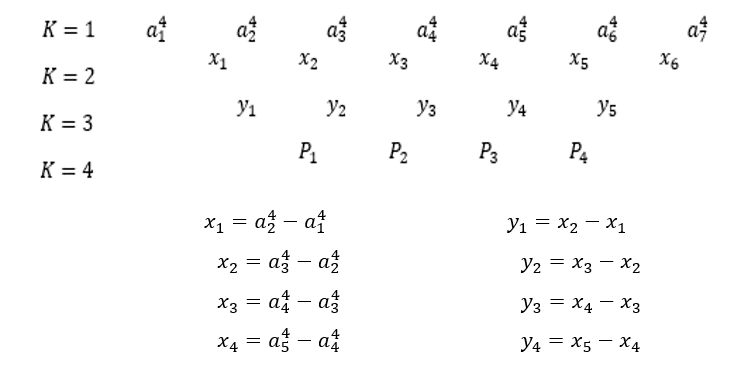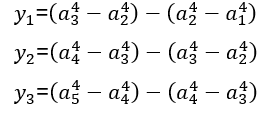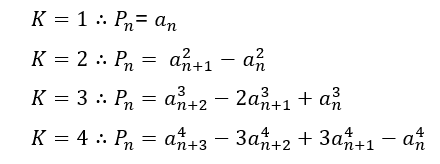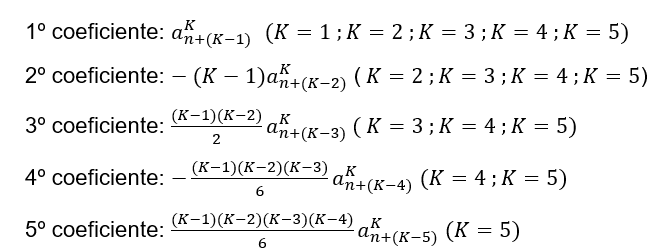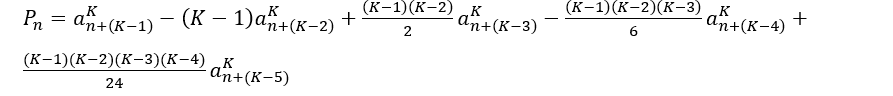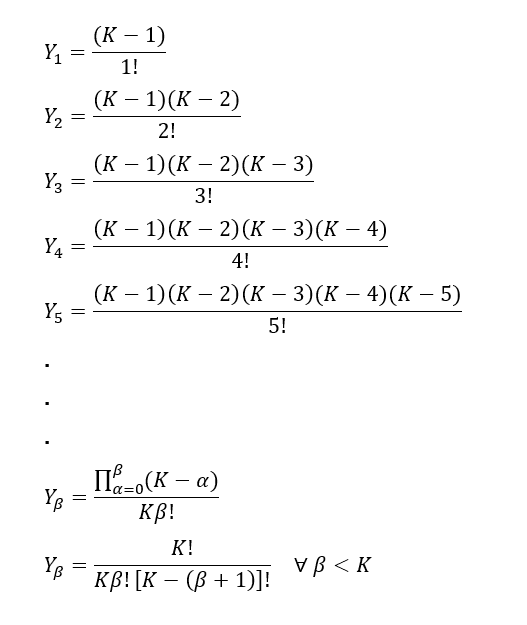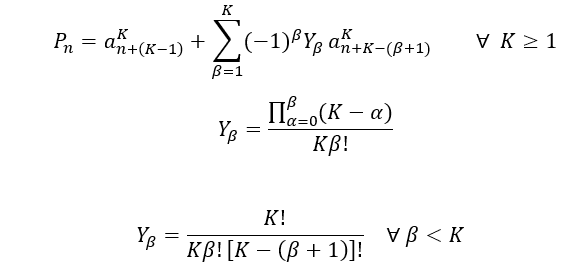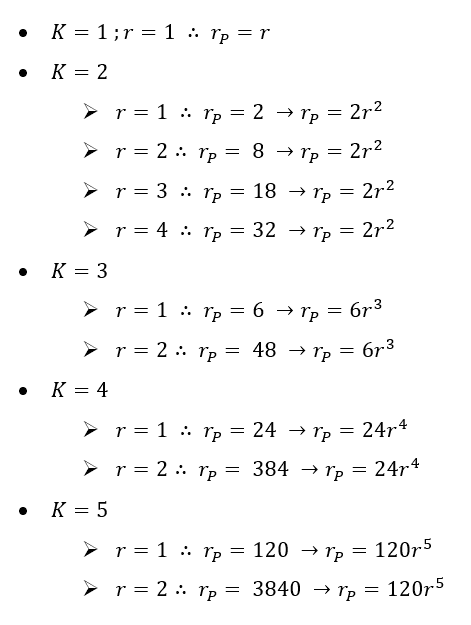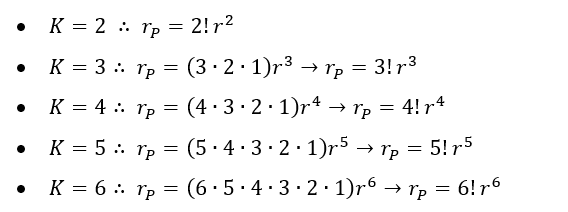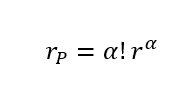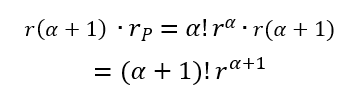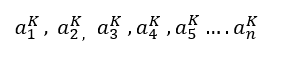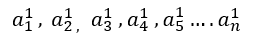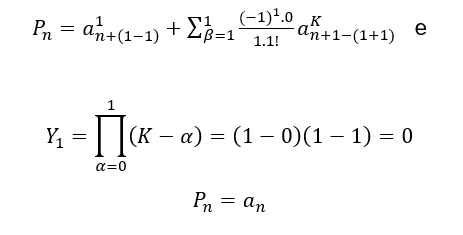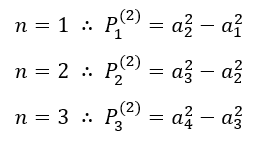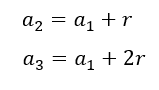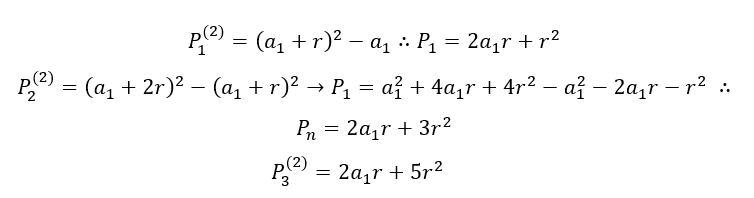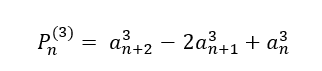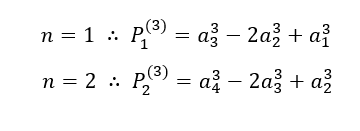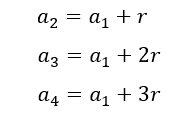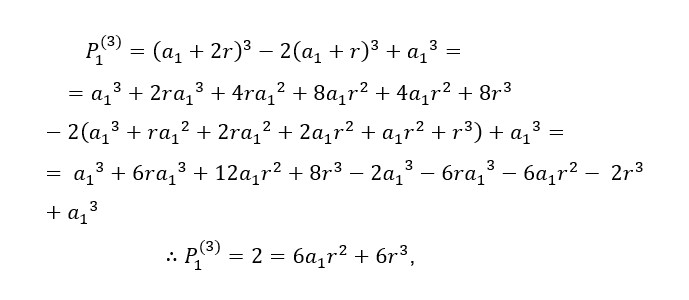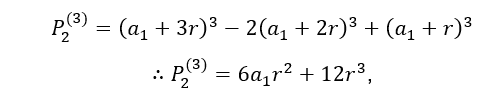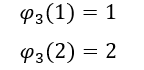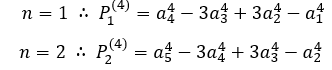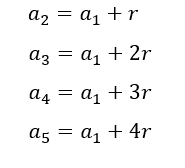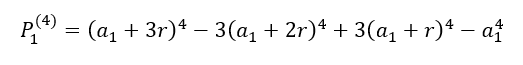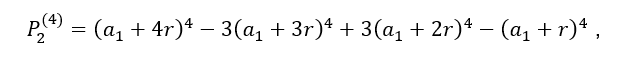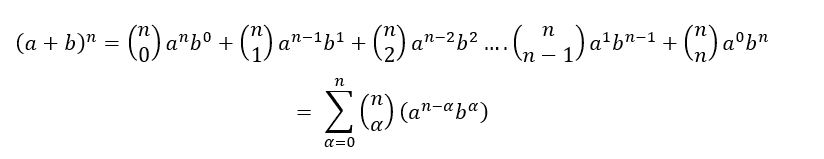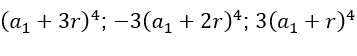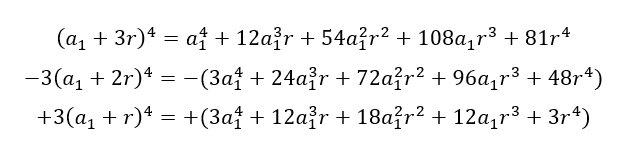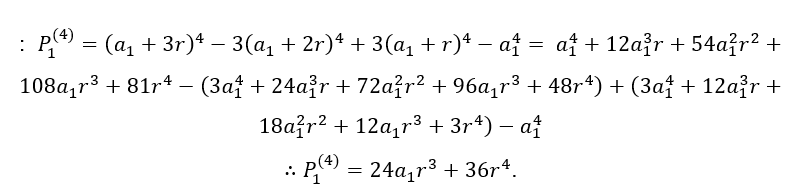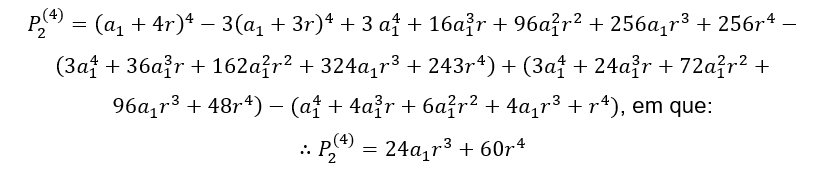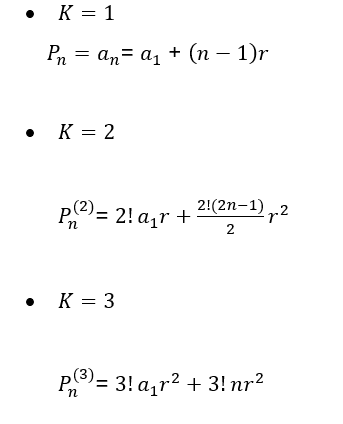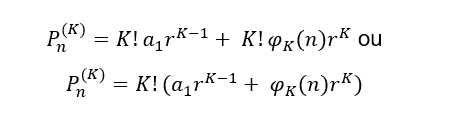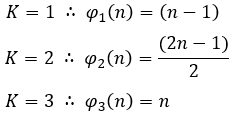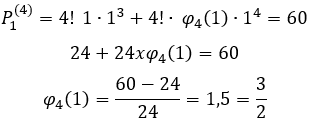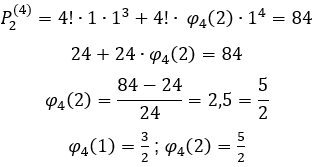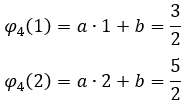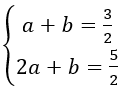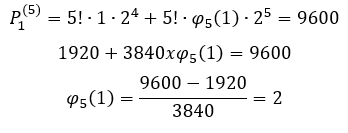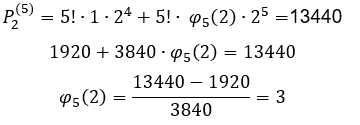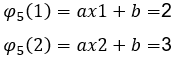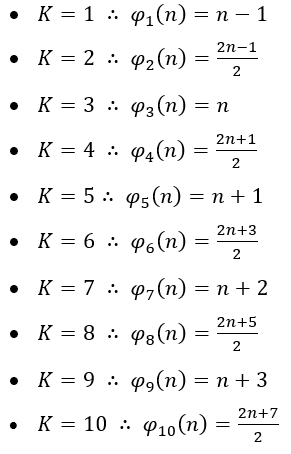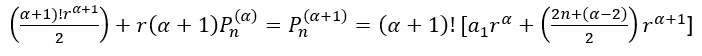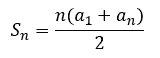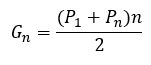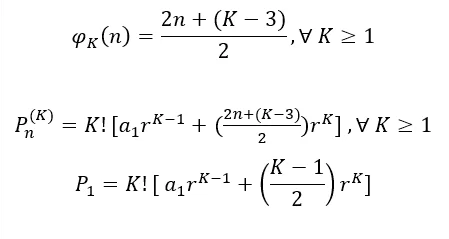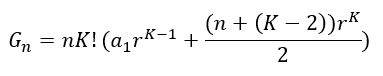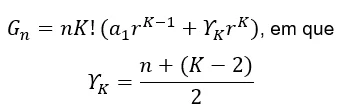ARTIGO ORIGINAL
CARNEIRO, Tiago Isaac dos Santos [1]
CARNEIRO, Tiago Isaac dos Santos. Progressão Aritmética de ordem superior: Progressão Aritmética gerada por uma sequência de termos do tipo aKn. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano. 07, Ed. 07, Vol. 06, pp. 63-91. Julho de 2022. ISSN: 2448-0959, Link de acesso: https://www.nucleodoconhecimento.com.br/matematica/ordem-superior , DOI: 10.32749/nucleodoconhecimento.com.br/matematica/ordem-superior
RESUMO
Atualmente o estudo da Progressão Aritmética de ordem superior é bastante limitado no quesito de uma formulação matemática mais simples. Alguns autores mencionam ordem superior, como uma equação polinomial de grau k. O objetivo deste trabalho é fazer um contraponto das definições apresentadas de outros trabalhos, através de uma fórmula matemática original que gera progressões aritméticas de qualquer ordem através das diferenças sucessivas de um termo ![]() pelo termo
pelo termo ![]() de cada linha, até que se obtenha uma sequência estacionaria na linha ou ordem k, chamada de progressão aritmética gerada de ordem superior.
de cada linha, até que se obtenha uma sequência estacionaria na linha ou ordem k, chamada de progressão aritmética gerada de ordem superior.
Palavras-chave: Progressão Aritmética, Formulação Matemática, Ordem Superior, Diferenças Sucessivas.
1. INTRODUÇÃO
Atualmente o estudo da Progressão Aritmética de ordem superior é bastante limitado no quesito de uma formulação matemática mais simples. Alguns autores mencionam ordem superior, como uma equação polinomial de grau k. O objetivo deste trabalho é fazer um contraponto das definições apresentadas de outros trabalhos, através de uma fórmula matemática original que gerem progressões aritméticas de qualquer ordem, através das diferenças sucessivas de um termo ![]() pelo termo
pelo termo ![]() de cada linha, até que se obtenha uma sequência estacionaria na linha ou ordem k, chamada de Progressão Aritmética gerada de ordem superior.
de cada linha, até que se obtenha uma sequência estacionaria na linha ou ordem k, chamada de Progressão Aritmética gerada de ordem superior.
Como diz Filho (2020), a formulação da Progressão teve grande contribuição do matemático Carl Friederich Gauss, quando o seu professor lhe pediu para somar os termos de 1 a 100, e este aos 7 anos de idade fez aplicando a fórmula da soma dos termos da PA.
De acordo com Diógenes e Lima (2020), a Progressão Aritmética de ordem k está relacionada com um polinômio de grau k. A definição de ordem segundo Nobre e Rocha (2018), é a aplicação do operador diferença entre os termos ![]() e
e ![]() , que resultará em linhas subsequentes, uma determinada sequência até chegar a uma ordem em que se obtenha uma sequência estacionária.
, que resultará em linhas subsequentes, uma determinada sequência até chegar a uma ordem em que se obtenha uma sequência estacionária.
2. PROGRESSÃO ARITMÉTICA GERADA POR UMA SEQUÊNCIA DE TERMOS DO TIPO 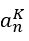
Os termos ![]() é a base geradora de uma Progressão Aritmética de ordem k, que também é uma Progressão Aritmética de ordem k=1. Os valores de k, que percorrem toda a sequência, é quem vai determinar em qual linha ou ordem está sendo gerada a nova Progressão Aritmética de razão
é a base geradora de uma Progressão Aritmética de ordem k, que também é uma Progressão Aritmética de ordem k=1. Os valores de k, que percorrem toda a sequência, é quem vai determinar em qual linha ou ordem está sendo gerada a nova Progressão Aritmética de razão ![]()
2.1 PA DE ORDEM K=1
2.1.1 EXEMPLO
Aplicando o operador diferença dos termos, tem-se: ![]() , ou seja
, ou seja ![]() , como K=1 define a ordem ou linha que está sendo gerada uma nova PA, logo a PA gerada é a mesma da geradora, e seu termo geral já é conhecido:
, como K=1 define a ordem ou linha que está sendo gerada uma nova PA, logo a PA gerada é a mesma da geradora, e seu termo geral já é conhecido:
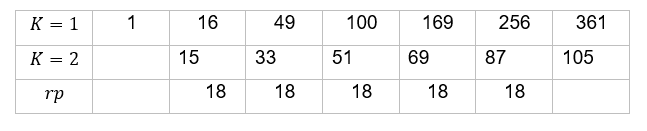
2.2 PA DE ORDEM K=2
2.2.1 EXEMPLO
Seja ![]() , como foi dito anteriormente segue o mesmo raciocínio para k=2.
, como foi dito anteriormente segue o mesmo raciocínio para k=2.
Aplicando o operador diferença de cada termo nas linhas k=1 e k=2 , obtém-se:
Note que a PA de razão ![]() é maior que r que é a razão da nova PA gerada na linha
é maior que r que é a razão da nova PA gerada na linha ![]() . A PA gerada será denotada por
. A PA gerada será denotada por ![]() . Note que
. Note que
![]() , o valor
, o valor ![]() para
para ![]() . Analisando a diferença dos termos de cada linha de sequência obteremos uma expressão geral de uma PA gerada de
. Analisando a diferença dos termos de cada linha de sequência obteremos uma expressão geral de uma PA gerada de ![]() , assim:
, assim:
Que é o termo geral da PA gerada ![]() .
.
Demonstração:
Seja uma PA em que seus termos têm um expoente ![]()
2.2.2 EXEMPLO
onde ![]() está localizado em
está localizado em ![]() que mais uma vez determina a ordem da PA gerada e
que mais uma vez determina a ordem da PA gerada e ![]() para
para ![]() .
.
2.2.3 EXEMPLO
Sejam, ![]() , obtém-se a sequência e a PA gerada:
, obtém-se a sequência e a PA gerada:
onde ![]() está localizado em
está localizado em ![]() tal que
tal que ![]()
2.3 PA DE ORDEM K=3
2.3.1 EXEMPLO
Demonstração
Seja uma PA em que seus termos têm o expoente K=3
Substituindo os valores em![]() , temos:
, temos:
2.3.2 EXEMPLO
Sejam ![]() , segue a sequência e a PA gerada.
, segue a sequência e a PA gerada.
2.4 PA DE ORDEM K=4
2.4.1 EXEMPLO
PA de razão ![]() , obtem-se a PA gerada.
, obtem-se a PA gerada.
Demonstração
Substituindo os valores em ![]() , temos:
, temos:
Substituindo os valores em ![]() , temos:
, temos:
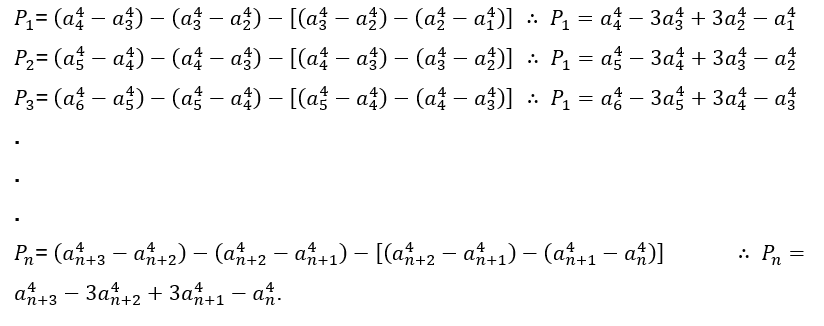 Para termos superiores segue o mesmo raciocínio.
Para termos superiores segue o mesmo raciocínio.
3. FÓRMULA GERAL DE UMA SEQUÊNCIA NUMÉRICA GERADA 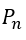 PARA K≥1
PARA K≥1
Reescrevendo as fórmulas de cada valor de ![]() dos exemplos anteriores:
dos exemplos anteriores:
Para se obter o padrão geral, basta observar os coeficientes para cada valor de ![]()
Ao somar todos os coeficientes acima, resulta em ![]() para o intervalo
para o intervalo
![]()
Essa fórmula é geral apenas no intervalo ![]() , para achar a fórmula
, para achar a fórmula ![]() para todos os valores de
para todos os valores de ![]() , isto é,
, isto é, ![]() , basta dar continuidade nos valores para
, basta dar continuidade nos valores para ![]() denota-se,
denota-se, ![]() como todos os coeficientes
como todos os coeficientes ![]() tal que
tal que ![]() , ou seja, segue todos os coeficientes de 1 até k:
, ou seja, segue todos os coeficientes de 1 até k:
Note também que os denominadores dos coeficientes podem ser escritos da seguinte forma:
1=1!
2=2!
6=3!
24=4!
Podemos reescrever a equação geral ![]() como:
como:
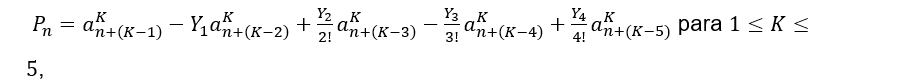
Observe também os sinais dos coeficientes alternam à medida que cresce o valor de ![]() , portanto a fórmula geral de
, portanto a fórmula geral de ![]() para
para ![]() , fica da seguinte forma:
, fica da seguinte forma:
3.1 RELAÇÃO ENTRE 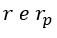
Pode-se também padronizar o valor da razão ![]() de uma PA gerada com a razão
de uma PA gerada com a razão ![]() de sua PA geradora, tomando como base os exemplos anteriores para cada valor de k tem-se:
de sua PA geradora, tomando como base os exemplos anteriores para cada valor de k tem-se:
A relação ![]() pode ser padronizada para qualquer valor de
pode ser padronizada para qualquer valor de ![]() , sendo:
, sendo:
Portanto analisando as relações ![]() dos diferentes valores de
dos diferentes valores de ![]() , tem-se a fórmula de geral de
, tem-se a fórmula de geral de ![]() :
:
![]() é chamado de razão de uma PA gerada.
é chamado de razão de uma PA gerada.
A demonstração da razão de uma PA gerada é feita pra indução finita.
Seja ![]() a razão da PA gerada tal que :
a razão da PA gerada tal que :
Tomemos para K =1 e substituindo na expressão acima obtém-se:
![]() , ou seja, é a própria razão da PA geradora.
, ou seja, é a própria razão da PA geradora.
Hipótese de indução: assumindo que ![]() é verdadeira para
é verdadeira para ![]() , tem-se:
, tem-se:
![]() Tese de indução: assumindo que
Tese de indução: assumindo que ![]() é verdadeira para
é verdadeira para ![]() , é o que segue:
, é o que segue:
Multiplicando os dois lados da igualdade por ![]() , obtem-se:
, obtem-se:
Como queríamos demonstrar ∎
3.2 FÓRMULA GERAL DA PA GERADA 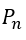 DE ORDEM K≥1 DO TIPO
DE ORDEM K≥1 DO TIPO 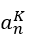
Para gerar uma Progressão Aritmética de ordem ![]() do tipo
do tipo ![]() tem que haver uma PA de razão
tem que haver uma PA de razão ![]() , em que seus termos sejam elevados ao grau ou potência
, em que seus termos sejam elevados ao grau ou potência ![]() .
.
Retomando os termos de uma PA elevado a um valor K:
Em que an é uma PA e ![]() é a ordem que se quer gerar a PA, para provar que isso é verdade toma-se como exemplo uma PA gerada para
é a ordem que se quer gerar a PA, para provar que isso é verdade toma-se como exemplo uma PA gerada para ![]()
PA gerada para ![]()
Utilizando a fórmula geral e calculando para ![]() temos:
temos:
Ou seja, a PA gerada é a própria PA inicial, observa-se que a fórmula da PA de ordem ![]() , já é conhecida como:
, já é conhecida como:
Observamos anteriormente que a fórmula geral de uma sequência gerada ![]() para
para ![]() é:
é: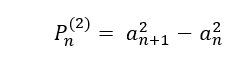
Substituindo os valores de ![]() na equação
na equação ![]() obtém-se a seguinte expressão:
obtém-se a seguinte expressão:
Nota-se que o primeiro termo de cada equação se repete, variando apenas as incógnitas do segundo termo, portanto para cada termo há uma variação de um valor ![]() do 2º termo, para achar o valor de
do 2º termo, para achar o valor de ![]() observa-se:
observa-se:
Idem ao raciocínio anterior para obter a fórmula geral de uma sequência gerada ![]() para
para ![]() é:
é:
Calcularemos os termos ![]() , para então estabelecermos o padrão para essa ordem.
, para então estabelecermos o padrão para essa ordem.
observe também que:
Substituindo os valores acima na equação ![]() tem-se a seguinte expressão:
tem-se a seguinte expressão:
Fazendo os mesmos cálculos para ![]() resulta:
resulta:
Há uma variação de um valor 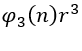 no 2º termo, para acharmos o valor de
no 2º termo, para acharmos o valor de ![]() :
:
Calcula-se os termos ![]() , para então estabelecer o padrão para esta ordem.
, para então estabelecer o padrão para esta ordem.
Observa-se também que:
Substituindo os valores acima na equação ![]() tem-se a seguinte expressão:
tem-se a seguinte expressão:
fazendo os mesmos cálculos para ![]() , temos:
, temos:
Utilizando o binômio de Newton para os termos:
Somando os todos os termos:
Seguindo o mesmo raciocínio para ![]() , tem-se:
, tem-se:
De acordo com os valores apresentados para as ordens
![]() observa-se que o primeiro termo sempre se repeti para qualquer ordem apresentada, havendo uma variação de um valor
observa-se que o primeiro termo sempre se repeti para qualquer ordem apresentada, havendo uma variação de um valor ![]() no 2ª termo apresentando os padrões anteriores para
no 2ª termo apresentando os padrões anteriores para ![]() , obtém-se uma formula Geral para
, obtém-se uma formula Geral para![]() , ou seja, basta analisar a expressão constante e a expressão variante, para então achar a formula de forma mais fácil para qualquer termo
, ou seja, basta analisar a expressão constante e a expressão variante, para então achar a formula de forma mais fácil para qualquer termo ![]() então:
então:
Ao analisar essas equações observa-se as expressões constantes e variantes, ou seja :
A Fórmula acima representa qualquer PA gerada para qualquer ordem ou valor![]() . Será possível calcular a expressão
. Será possível calcular a expressão ![]() que é uma função de n para cada valor de K:
que é uma função de n para cada valor de K:
Calcula-se agora ![]() para estabelecer a fórmula geral para
para estabelecer a fórmula geral para ![]() , para isso segue um exemplo:
, para isso segue um exemplo:
3.2.1 EXEMPLO
Seja uma PA em que ![]() , para acharmos uma PA de e
, para acharmos uma PA de e ![]() , basta elevarmos a potência cada termo o valor
, basta elevarmos a potência cada termo o valor ![]() , que fica:
, que fica:
Calcula-se o valor de ![]() através da expressão :
através da expressão :
Que vem da fórmula geral de qualquer sequência numérica gerada, procura-se achar o valor de ![]() para então substituir na fórmula da PA para
para então substituir na fórmula da PA para ![]() , para se achar a expressão
, para se achar a expressão ![]() :
:
Substituindo na fórmula ![]() ; tem-se:
; tem-se:
Calcula-se agora o valor de ![]() através da expressão:
através da expressão:
![]()
Que vem da fórmula geral de qualquer sequência numérica gerada, obtém-se agora o valor de ![]() para então substituir na fórmula da PA para
para então substituir na fórmula da PA para ![]() , para achar a expressão
, para achar a expressão ![]() :
:
Substituindo na fórmula ![]() ; temos:
; temos:
A expressão geral de uma função da reta é ![]() , que fica da seguinte forma:
, que fica da seguinte forma: ![]() , tendo os pontos para encontrar a equação:
, tendo os pontos para encontrar a equação:
Resolvendo o sistema temos os valores de ![]() , obtendo a expressão
, obtendo a expressão ![]() , tirando o m.m.c., obtém-se a seguinte expressão:
, tirando o m.m.c., obtém-se a seguinte expressão:
![]()
Essa é a expressão ![]() para a fórmula geral da PA
para a fórmula geral da PA ![]() .
.
Dessa forma obtém-se uma fórmula geral para qualquer PA gerada ![]() obedecendo, a seguinte formula Geral da PA gerada por uma PA inicial elevada a potência
obedecendo, a seguinte formula Geral da PA gerada por uma PA inicial elevada a potência ![]() , que o próprio
, que o próprio ![]() estabelece em qual ordem ou linha que está localizada a PA gerada.
estabelece em qual ordem ou linha que está localizada a PA gerada.
Sendo assim a fórmula geral da PA![]() é :
é :
3.2 EXEMPLO
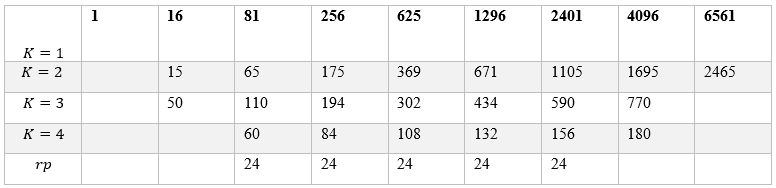
Seja uma PA gerada para ![]() , apresenta os valores calculados acima.
, apresenta os valores calculados acima.
Seja a PA gerada abaixo, obedecida pela fórmula da sequência gerada :
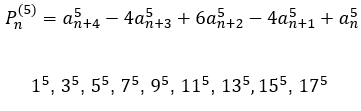
Substituindo o valor da PA na fórmula ![]() para achar a expressão
para achar a expressão ![]() tem-se:
tem-se:
Substituindo na fórmula ![]() , para achar a expressão
, para achar a expressão ![]() tem-se:
tem-se:
Para acharmos a expressão ![]() , basta calcular a fórmula da sequência numérica gerada e substituir na fórmula da PA gerada, a expressão
, basta calcular a fórmula da sequência numérica gerada e substituir na fórmula da PA gerada, a expressão![]() é uma função do 1º grau, bastando apenas de 2 pontos da reta para estabelecer a função geral, ou seja
é uma função do 1º grau, bastando apenas de 2 pontos da reta para estabelecer a função geral, ou seja
A expressão geral de uma função da reta é ![]() , que fica da seguinte forma:
, que fica da seguinte forma: ![]() , tendo os pontos para encontrar a equação:
, tendo os pontos para encontrar a equação:
(1;2) e (2;3)
Substituindo :
Resolvendo o sistema temos os valores de ![]() , obtendo a expressão
, obtendo a expressão ![]() , obtém-se a seguinte expressão:
, obtém-se a seguinte expressão:![]() Essa é a expressão φ para a fórmula geral da PA
Essa é a expressão φ para a fórmula geral da PA ![]() .
.
Observação: Para achar expressão ![]() para qualquer valor k segue o mesmo raciocínio das expressões anteriores.
para qualquer valor k segue o mesmo raciocínio das expressões anteriores.
Sendo assim cada função ![]() representa uma PA de ordem
representa uma PA de ordem ![]() diferente ou seja:
diferente ou seja:
A formula padrão φ para qualquer ordem ![]() observa-se os valores de
observa-se os valores de ![]() impares, ela é crescente e seu valor é sempre inteiro, enquanto os valores de
impares, ela é crescente e seu valor é sempre inteiro, enquanto os valores de ![]() pares , também é crescente , mas da forma racional, portanto a formula de
pares , também é crescente , mas da forma racional, portanto a formula de ![]() quando for ímpar no lado das constantes tem-se: -1,0,1,2,3…, enquanto par tem-se: -1/2, 0 , 1/2, 3/2, 5/2, 7/2 ,ou seja, múltiplos de 1/2.
quando for ímpar no lado das constantes tem-se: -1,0,1,2,3…, enquanto par tem-se: -1/2, 0 , 1/2, 3/2, 5/2, 7/2 ,ou seja, múltiplos de 1/2.
Se tirarmos a fração do termo n, observa-se que ela sempre somará com uma constante racional, logo a fórmula ![]() , é:
, é:
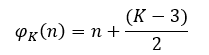 Efetuando o m.m.c. pode-se ainda escrever a equação da seguinte forma:
Efetuando o m.m.c. pode-se ainda escrever a equação da seguinte forma:
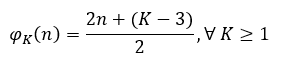 Substituindo na fórmula de
Substituindo na fórmula de ![]() Obtém-se:
Obtém-se: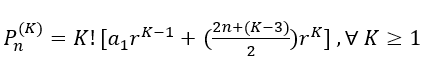
Essa é a fórmula completa de qualquer PA gerada a partir de uma PA inicial elevada a potência ![]() , que
, que ![]() é a ordem da PA gerada.
é a ordem da PA gerada.
3.2.1 – DEMONSTRAÇÃO DA FÓRMULA ![]() POR INDUÇÃO:
POR INDUÇÃO:
substituindo na expressão acima obtém-se:
![]() , que é uma PA de primeira ordem, ou a própria PA geradora.
, que é uma PA de primeira ordem, ou a própria PA geradora.
Hipótese de indução: assumindo que ![]() é verdadeira para
é verdadeira para![]() , temos:
, temos:
Tese de indução: assumindo que ![]() seja verdadeira para
seja verdadeira para ![]() é o que segue a demonstração:
é o que segue a demonstração:
Seja ![]() somando os dois lados da igualdade por
somando os dois lados da igualdade por 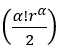 obtém-se:
obtém-se:
![]() , na parte direita da igualdade.
, na parte direita da igualdade.
Coloca-se o ![]() em evidência obtendo:
em evidência obtendo:
![]() , em seguida multiplica-se a equação nos dois lados da igualdade por
, em seguida multiplica-se a equação nos dois lados da igualdade por ![]() , tem-se:
, tem-se:
![]() , inserindo
, inserindo ![]() dentro do colchete obtém-se:
dentro do colchete obtém-se:
![]() , arrumando ainda mais a expressão fica:
, arrumando ainda mais a expressão fica:
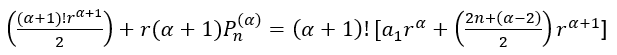 , essa igualdade é válida pois tanto no lado esquerdo como o direito da igualdade obtém-se:
, essa igualdade é válida pois tanto no lado esquerdo como o direito da igualdade obtém-se:
4 – SOMA DE UMA PROGRESSÃO ARITMÉTICA GERADA DE ORDEM K
Sabe-se que a fórmula geral da soma de uma PA é :
A fórmula geral para a soma de uma PA gerada em função apenas da razão r da sequência geradora do tipo ![]() , é determinada com base nos estudos citados anteriormente. Seja dado a soma da PA gerada denotada por
, é determinada com base nos estudos citados anteriormente. Seja dado a soma da PA gerada denotada por ![]() , ou seja, definida pela expressão abaixo:
, ou seja, definida pela expressão abaixo:
Observando a expressão demonstrada anteriormente:
Substituindo na equação ![]() obtém-se a seguinte expressão:
obtém-se a seguinte expressão:
Simplificando ainda mais a expressão obtém-se o termo geral da soma da PA gerada.
compactando ainda mais a expressão obtém-se:
A fórmula acima é chamada soma de termos de uma PA gerada a partir de uma PA de razão![]() elevado a um grau K.
elevado a um grau K.
4. CONSIDERAÇÕES FINAIS
De acordo com o trabalho a expressão matemática estabelece um padrão para todos os valores k de uma PA geradora, que tem como objetivo de gerar outra PA na linha K, e claro que a PA gerada continua sendo de grau único, ou seja, não se deve confundir ordem com grau, pois o mesmo está relacionado com potência ou expoente. No desenvolvimento deste trabalho foi possível obter uma fórmula matemática que geram progressões de uma determinada ordem k a partir de uma progressão base elevado ao grau k, este mesmo grau é que define, qual a ordem ou localização que a outra PA está sendo gerada.
REFERÊNCIAS
DIOGENES, R. J; LIMA, E. J. S. Progressões Aritméticas de Ordem Superior e Recorrências Lineares. Ciências Exatas e da Natureza, Mestrado Profissional em Matemática em Rede Nacional, Bento Goncalves, RS, v. 6, n. 1, p. 1-12, 3 jun. 2020. DOI: https://doi.org/10.35819/remat2020v6i1id3700. Disponível em: https://periodicos.ifrs.edu.br/index.php/REMAT/article/view/3700/2602. Acesso em: 27 de abr. 2020.
FILHO, S. F. R. Progressão Aritmética de Ordem Superior. 2020. 102 p. Dissertação (Mestrado em Matemática) – Centro de Ciências Exatas e tecnológicas, Universidade Federal do Maranhão, São Luís, 2020.
NOBRE, J. F. F ; ROCHA, R. A. Progressões Aritméticas de Ordem Superior. v. 5, n. 1, p. 35-48, jul./2018.
[1] Graduação em Matemática. ORCID: 0000-0002-2301-1496.
Enviado: Maio, 2022.
Aprovado: Julho, 2022.