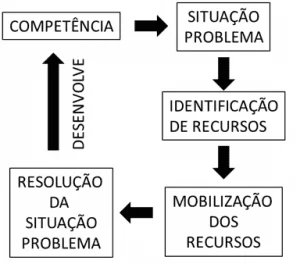
ORIGINAL ARTICLE
SCHWANTES, Vilson [1], XAVIER, Márcio Pizzete [2], SCHWANTES, Eloísa Bernardete Finkler [3], SCHWANTES, Daniel [4], JUNIOR, Affonso Celso Gonçalves [5], KRACKE, Elisa [6], JUNIOR, Élio Conradi [7]
SCHWANTES, Vilson. Et al. A reflection on the ethnomathematics of the bricklayer and the school mathematics. Revista Científica Multidisciplinar Núcleo do Conhecimento. 04 year, Ed. 07, Vol. 14, pp. 87-106. July 2019. ISSN: 2448-0959
1. SUMMARY
This article reflects on Ethnomathematics, analyzes interviews with a group of bricklayers and sellers of construction material from the municipalities of Mercedes and Marechal Cândido Rondon, PR. It seeks to know the mathematical knowledge used by these workers in the exercise of their professions and their possible relationship with the teaching of school mathematics. In the reports of the participants it seems that these knowledge are intimately linked to the socio-cultural environment, denoting a conception that the school is a privileged place where the mathematical knowledge is learned in an organized and systicated way. necessary for professional life. It is evident that there are challenges to be overcome by the school for its effective consolidation, so that the pedagogical practice of school education has connections with the socio-cultural world of the student.
Key words: ethnomathematics perspective, mathematical education, mathematical knowledge, classroom routine.
2. INTRODUCTION
The teaching of mathematics in Brazilian schools, over the last decades, has been predominantly traditional, without major pedagogical changes, except for a few exceptions. Within this perspective and reality it is perceived that little is used of the previous Sabres of the students, and even less is made relationships of the mathematical concepts taught with the life of the pupils outside the school environment. In this scenario it is still common to hear in the school environment expressions such as: “Teacher where I will use this in my life?”.
According to Santos (2016):
The lack of contextualization in the teaching of mathematics can lead to the discouragement of the discipline, resurrecting the traditional methods that conceptualize mathematics as a science that brought all things ready, as if it were a ready knowledge and Over. (p. 5)
In many Brazilian schools, it is still heard that the teaching of mathematics is distant and decontextualized from the reality experienced by students and citizens. For Demo (1996), the construction of knowledge begins from the knowledge incorporated by each individual in his sociocultural experience. For the author “All speak, communicate, use a basic vocabulary, manage concepts within common sense, have references of the reality in which they are inserted” (p. 32).
Although we are still experiencing such situations in our schools, there is a consensus that students entering the school bring in their luggage some knowledge, even if it is only within common sense. This includes the mathematical knowledge generated in the family and in the sectors of society, which is incorporated by the children and it is essential that the school knows it and considers it, building on the basis of these knowledges, the systate knowledge. For Pompey and Monteiro (2001), “Students learn in daily life, in their relationship with the world” (p. 62).
For Lopes (2014),
“Ideas and situations of a mathematical nature are present in the everyday things, in professional activities, in the practices of different cultures, in situations of counting, measurement and calculation, which are easily recognized as mathematics.” (p.5)
A teaching with the production of meanings about the context is as fundamental as the relationship with the real world, abstract and symbolic world. Starting from the cultural experience of each student, the meaning that he brings from his social and cultural experience, one can advance and understand other cultures, individuals and society. We shared with D’ambrosius (1993), when he postulated that it is fundamental to understand that when formal schooling begins, the child already has an ethnomathematics that allows him to face the interpretations of the systematic mathematics of the school.
This perspective, according to Marques (2001), represents and means:
Construction of new knowledge, based on previous knowledge; In fact, a reconstruction of them, in the sense of disassembly and recovery in a new way. The knowledge of each interlocutor-confidant, readers, authors summoned with their works, subjects of social practices to whom I heard, interviewed, blue-and my knowledge is merged and transformed, reformulated. In a very special way, my previous knowledge now configures others. That’s what we call learning. Why not research? (P. 26).
We share with Fiorentini (1995) by highlighting that in the ethnomathematics approach, the teaching-learning process has as its starting point the emphasis given to the problems that somehow has meaning for children. In this sense, the student-teacher relationship occurs in the context of intersubjectivity, where through dialogue, interlocution between subjects, exchange of experiences, both (re) construct knowledge by Problematization (mathematization) about common sense and knowledge Systate, constructing a new look at the context.
Although it is clear that the school needs to work on the systematic mathematical knowledge, we believe that an appreciation of the mathematical knowledge resulting from the students ‘ cultural relations can make the growth positively and psychologically Children’s income, as opposed to an initiation through techniques and rules to reach correct answers. This possibility can be glimpsed and concreted with the adoption by the mathematical educators of an ethno posture in teaching, because according to Pompey and Monteiro (2001), “Ethnomathematics seeks a transformation of the current relations of man with the World” (p. 148 ).
To act in the world today, it is necessary a new posture, a new paradigm, a theoretical review that has as central objective the Organization/reformulation/understanding of the theoretical and practical basis that permeate the pedagogical action of Educators (SILVA, 2012, p. 174 ).
For D’ambrósio (2001), Ethnomathematics can assist in the Constitution of the researcher teacher of his practice, arousing him to learn in a continuous way to be a teacher, according to current educational needs, transforming the classroom into an environment of knowledge exchange, rescuing historical-socially constructed knowledge of mankind.
School pedagogical projects lack adequacy to the new educational paradigm, centered on intersubjectivity and interlocution of the actors. A mathematical approach in this perspective transforms the classroom into an environment of exchange of knowledge by valuing individual differences, because the redemption of curiosity recovers the historical knowledge-socially built by man, along the History of mankind.
Reflections and discussions about the teaching of this discipline, also consists in verifying the expectations and social needs of mathematics taught in the school, according to the words of Demo (1996, p. 10), is “getting out of the beaten reproductive posture, marked Especially for the repeated class to repeat. ”
The new trends in education and mathematics education emphasize that the art of learning to teach involves not only knowing what to teach and knowing about teaching methods, but, above all, involves a knowledge about learning. We refer to the learning, both of the teacher, about the process itself and the results of his/her learning, and of a knowledge of the teacher in relation to the learning of his students. (SILVA, 2012, p.197).
Thus, teaching mathematics in the classroom, taking into account the previous knowledge and cultural diversity of the students can be an important strategy for a more meaningful and less traditional teaching of school mathematics, generating more interest and Students ‘ participation in the construction of mathematical knowledge.
We believe that a didactic-pedagogical posture that part of the knowledge that the student already has of his/her daily experience, provides educators with a (re) construction of the systate mathematical knowledge, both in the perception of the existence of several Mathematics in our midst, as well as the pursuit of a teaching that contemplates social expectations.
3. JUSTIING THE PRESENCE OF MATHEMATICS IN THE DAILY ACTIVITY OF THE MASON
When we perform at different times, the study sessions with the bricklayers, we seek to investigate dialogically with each professional, their opinions about mathematical questions of general character that permeate their daily toll.
Questioned about the use of mathematics in their work, the bricklayers were unanimous in stating that it is fundamental in exercising their profession. According to Oscar, “mainly at the beginning of a work, the plumb wire. With the plumb wire we make a mathematics not as complicated as that of the school and without formulas, complements the Mason. What we use most is reasoning, emphasizing. ”
Sérgio comments that he uses mathematics “to measure and calculate the amount of tiles, bricks, sometimes square meters. It’s calculations of tim[multiplicação]es, more[adição] and splitting. ” Alberto also says using mathematics “from the foundation of construction, to take out the square, through the Pythagorean theorem. On the roof to make the percentage of the water fall. I also use mathematics in the area measures “ends.
When we argued that they used a practical mathematics, Oscar was soon saying that in the exercise of a profession a “more practical and simple” mathematics is not used in the formulas taught in the school. We always try to simplify procedures. In a construction we will define the type of calculation you will use. We don’t waste much time on complicated calculations, everything is done in a more simplified way, he argues. ”
Instigated to better clarify the mathematics he uses and allows him to make calculations simplificately, Oscar reported that it is “a reasoning that is practically the day-to-day of the builder and involves especially measures. We care about them all day and, you need to be always attentive. ”
According to Breda, Lima and Guimarães (2011, p. 15):
I started to look at the proposal of Ethnomathematics as a possibility of differentiating the work that the teacher develops in schools, that is, the conteudist and meaningless practice can be replaced by a teacher oriented by a new look, that fosters The appreciation of the socio-cultural context of the educating, its processes of thought and its ways of understanding, explaining and exercising its practice in contemporary soc[…]iety an invitation to revisit its pedagogical practices and its effects or even look at its role, As a lecturer who deals with different perspectives of subject in the school context.
For the research, we consider it interesting to question where and how they learned this mathematics that uses the algorithms of operations, but it brings underlying a type of reasoning that allows the resolution of the problem situations they face daily. Sérgio says he learned “in the day-to-day, with the people I learned to work as a mason. I started out as a helper and learned until I arrived at this point of being autonomous. ”
The Mason Oscar, in his report, says he learned “in the primary course the basics, but a great percentage of what we use, learns from the work itself. As the problems are appearing, you will solve and learn in the day-to-day construction itself. ” According to Pompeu and Monteiro (2001), this posture reflects the adoption of the empirical conception, using mathematics to solve the most immediate problem situations that permeate the daily life of the Mason’s activity. The fundamental, in this perspective according to the authors, is to solve the practical problems faced in the daily toll of the profession.
Asked to say how he learned the necessary procedures to pursue this profession, Oscar reported that “at first he worked as an auxiliary and was observing how other people did. I think the person has to have interest and in time learns and perfects what he does, finding other ways to do the calculations. You can’t be standing still, you have to be curious within what you do, trying to pay maximum attention to perfecting and becoming ever more objective in the work you accomplish. ” According to D’ambrósio (2001) A behavior that reflects “the adventure of the human species in the search for knowledge and in the adoption of procedures” (p. 17).
“I was always very devoted to my father who was a bricklayer, I was very noser so I learned many things from him. Many things I also learned in day-to-day, but without the mathematics of the school it would be difficult to exercise my profession, for it helps a lot, “concludes Alberto. According to Marques (2000) “The learning processes are inevitably inserted into communicative and public communities in which men learn from each other and with one another” (p. 29).
Mathematics needs to be interpreted as a sociocultural-natural product of a people, according to Rosa Neto (2002, p. 7 and 19).
Mathematics was created and has been developed by man according to his needs. (…) Culture is a form of adaptation because it is a way of acting on the environment that was built along with it.
For Rosa Neto (2002), there is a significant relationship between mathematics and culture, both as a result of our adaptation according to our survival needs through the times, representing both, an empirical, systematic and Scientific.
Considering that the Masons participating in the research consider that the mathematics of which they use, in the practice of the profession, satisfies their professional needs and, due to the fact that they have been learned in their basic formation, in daily toll with other More experienced bricklayers, we consider it pertinent to ask if they believed that the mathematics of the school could improve the mathematics they use daily.
In the speeches, they demonstrated believing that the school is a place where in an organized and intentional way the systematization of knowledge seized within or outside its territorial boundaries is processed. Oscar stated: “I believe that the mathematics of the school would improve my calculations, and I could make things more easily by leaving school all the time. The mathematics taught in the school is valid and serves as a starting point, helping in what we do. Although we usually always choose to do the way you learned in everyday life. ” It appears in the Mason’s speech, according to Giardinetto (1999) that “access to systematic mathematical knowledge has been indispensable for the transformation of Everyday Life” (p. 7).
Through these enunciations, it is evident the presence of an understanding that is supported by the Reflections of Giardinetto (1999), emphasizing that in fact “the school knowledge exceeds the mode of thought present in everyday life from elements, germs Present in daily life and which are incorporated by school knowledge “(p. 50). According to the author, “The formation of every man goes far beyond what was determined by practical-utilitarian activities of everyday life” (p. 78).
For Sergio, “without the mathematics of the school, even the four basic operations would become difficult.” This shows, according to Giardinetto (1999) that “the very knowledge that each individual prepares for his/her daily life does not account to respond to the needs of his/her own daily life” (p. 7).
However, when asked about how he sees mathematics that is currently taught at school, Sergio postulated that it helps people and is necessary. He emphasized, however, that he has difficulty in opine with greater depth, “I don’t know the mathematics of the school. I only did until the fourth grade and my kids are still small, “he concludes.
According to Oscar, today’s school mathematics is “very complex and very complicated. There are many formulas and in the day-to-day you can not apply them, so little save the formulas in memory to do the calculations. It would be important to teach mathematics more conveniently, more in what you will use in your day-to-day in any sector. For my construction work, I think these school formulas have little relation to what I’m going to need every day. ”
Reflecting on the importance of relating the mathematical content with a real situation, Alberto comments: “It is true, as in the case of the Pythagorean theorem, years ago to remove the square of the house, we used the own square and was aligning until Get the right footage. Now, recently emerged for us the 3m; 4m and 5m which also leaves the house in the square. I learned at school that this is the Pythagorean theorem, I mean, by doing the 3m measure; 4m, the diagonal with 5m puts everything in the square “.
When being instigated on the mathematics taught currently at the school Alberto says that “she is very theoretical, should bring more the practical part. Working the practice, not only the theory, this would be very important for the child, helps in intellectual development. The child having the theoretical and the practical she will enter the smartest professional field, “concludes the bricklayer.
And his speech, Oscar still reports that in the exercise of his profession “many times we can solve certain calculations through other formulas simpler than those taught by the school”. Certainly for these cases, we should behave as they suggest Lins and Gimenez (1997), that is, “from what is most familiar” (p. 10). With this didactic posture, according to the authors, what would be learned in school, would not serve “only for school” (p. 17), because they would have a direct relationship with the sectors of daily activity.
By being instigated to talk about how they would like to be taught the mathematics of the school, Alberto readily says: “With practical examples, seeking applications in various professions: trade, bricklayers, carpenters, among others. Practical problems not to teach mathematics only through exercise resolution. These mathematical problems can make the student assimilate the theory and understand everything better, otherwise it is meaningless. I learned the Pythagorean theorem in school, but the teacher did not show for it to serve in the day-to-day, completes the bricklayer.
The enunciations of the Bricklayers show, according to the perspective of Lins (1994), in his studies on the theoretical model of semantic fields “that the same text, spoken with different justifications, constitutes different knowledge[8]” (p. 29).
To finalize the reflection we have proposed, we leave them at ease to say something more about mathematics taught in school and the mathematics they use in the exercise of their profession. Oscar returned to prioritize in his speech the importance of school mathematics, “The basics I learned in school and use today in my profession. The mathematics of the books you use today is more advanced and I particularly do not use much in my work, but it may be used in other areas and in other sectors.
The mathematics I learned at school, and my parents have learned to use a lot of memory. Today we use the formulas and the calculator. I even use neither calculator, I prefer to work with memory, although the calculator is much more practical. In my work, in many situations I need to define things with the capacity of memory, to capture things, to finalise. ”
According to Alberto the mathematics of the school “helps a lot. It was very good for me to study. The experience I had with my father was very important, but without school, it doesn’t. Solving everything in the scream doesn’t work. I think the mathematics of the school has a very big importance in my profession. The mathematics of the school helped me avoid many mistakes that I had committed before. All work done in construction is accomplished with some sort of mathematics. ”
According to D’ambrósio (2001), the Mason’s testimony shows that, “You are at least mistaken for the mathematical educator who does not realize that there is much more in his mission as an educator than teaching to make contins or solve equations and problems absolutely Artificial, even if it often has the appearance of being referring to real facts “(p. 46).
Regarding the importance dispensed to mathematics taught by the school, Oscar was emphatic, stating that “we cannot rule out the mathematics of the school because it teaches the principles of calculations and without them everything becomes complicated. It turns out that the mathematics of the school becomes complicated because of many formulas and this, for the bricklayer, brings a certain discontent among the students themselves.
For Rolim,
Thinking about the historical-cultural context in the process of teaching mathematics learning is to consider that “doing” involves more than rules and techniques; is to acknowledge that as a science, mathematics is itself a building of humanity (ROLIM, 2010, p. 43).
With disinterest the student escapes from mathematics, is terrified and this must have a relationship with the way she is taught. I don’t think I should talk much about this issue because I didn’t go to school too much. What I said is because of what I have followed in my children’s school life, trying to help them on some occasions, and I can say that I have not been able to solve most issues and problems because it is difficult to grasp the formulas that are used in school today. ”
The initial affirmation of the bricklayer gives the idea, according to Giardinetto (1999) that, “it is necessary to understand that knowledge in everyday life is a fragmented knowledge that manifests itself according to a conceptual logic that is proper to the demands of all daily lives. This is a conceptual logic that is appropriate to the practical-utilitarian objectives and responds effectively to the necessities of everyday life “(p. 6).
In the face of Oscar’s speech, ask him if he thought that often the teaching of mathematics was far from a real situation, to what he agreed to say: “Exactly, if I look at the mathematics I use in my work and the one that is in the books , 99% I do not use in day-to-day.
In this sense I think it is necessary to reflect on this issue and to check in the future on how to make modern mathematics more applied. ” According to Giardinetto (1999), it is about understanding the “school activity as a mediator of this relationship in order to rescue the indispensable role of the school for the formation of the individual, overcoming the superficial and immediate interpretations that They overvalue daily knowledge to the detriment of the appropriation of School knowledge “(p. 12).
According to Marques (2000) “Education in its various instances, especially in school, tends to standardize learning with a view to the production of the individual modeled by the current culture”. In view of this observation of the author, we tried to show that the mathematical knowledge exists and is used by the people of the community, but not in a unique and standardized way. Within this intersubjective scenario, we believe that only an ethno approach will provide the teaching of school mathematics the discursive debate about the knowledge in circulation in the various human activities, reconstructing both (p. 34).
Mathematics can, however, occupy knowledge and understandings that do not fit into the institutionalized structures by curricula and research programs. In this sense, it would be possible to highlight the mathematics present in the day to day of many professions. It is an integral part of technology, design and decision making, is in tables, diagrams and graphs. Simply browse a newspaper to find a lot of mathematics (SKOVSMOSE, 2014, p. 13-14).
The teaching mediation, according to the perspective of Vygotsky (2001) does not monopolize the discourse of the classroom, however, transforms it into an argumentative community of learning, where the role of both is relevant in the process of (re) Constitution of the learnings. In this perspective, the participation of students in the classroom and the participation of the sectors that compose the school community would be broadlisted, constantly creating a climate of cognitive debates between them, which reconstructs and renews the learning of both.
In the visits we made to three stores that resend construction material, it drew our attention, both the good service of the employees, as to the manifestations of concern of the managers, as to the shortage of training courses for the bricklayers on General-mode construction and ceramic coating in particular.
In one of the stores visited, as the central theme of the investigation reached the ears of the company’s leaders, we were first introduced to the civil engineer and him to the owner manager. In dialogue, we hear from them many anxieties and concerns. All the concerns were directed to the decontextualized treatment given to school mathematics, as well as the lack of its dominance by the bricklayers in general, in the exercise of their professions.
In their speeches, they report routine customer complaints related to the inaccuracy of the ceramic settlement, especially in cases where customers wish to do so, laying the ceramics diagonally-45 º with the wall. According to the testimonies, in this region of the state of Paraná, there is hardly a wall or floor in the plumb and square, which also compromises any ceramic settlement.
They credit part of this responsibility to school mathematics, which according to them, has served only to satisfy the routine activities of the school itself. In his speeches it appears, according to the understanding of Pompey and Monteiro (2001) that “we live a moment when the fragmentation of knowledge limits the understanding of reality, t[porque]he school organization persists in maintaining an analytical, Cartesian curricular system” ( P. 19). It is fundamental, therefore, that the teaching of school mathematics contextualizes the contents, relating them to the activities developed by the citizens in the various sectors of human activity.
In his critical argument, in relation to how the school currently teaches mathematics, the entrepreneur reports that recently a Lord – pit-drill, came several times in his shop asking to calculate how many cubic meters would have the well, which had just Drill. “The last time you were here,” says the entrepreneur, “he commented with me that for 20 years he had been a sawmill owner in the state of Santa Catarina. I asked him then, “comments the owner manager of the store,” if he knew how to Cubicar wood. To my surprise the pit puncher promptly replied “:” For sure, I bought and sold wood, needed to know how many cubic meters had each tora. ”
“I questioned the pit drill about the following”: “If w[relata o empresário]e put a round log inside this well, woul[circular]d you know how to calculate the cubic meters of the well?” ‘ Yes, there is easy, ‘ replied the man, and according to the entrepreneur, at this moment his face began to become ‘ red ‘ because he now managed to make the connection between the two situations.
During our prose, both the entrepreneur and the civil engineer accentuated the lack of interaction between the mathematics of the scientific community and the mathematics practiced in the various human activities, due to the mathematics classes being restricted to Formal scope.
Such situations show how the school mathematics is disconnected from the real situations experienced by the citizens daily. However, citizens know that they need this knowledge, but they have difficulties in making connections. These observations show, in the understanding of Pompey and Monteiro (2001) that “Today’s teachers have a great challenge: educated in a fragmented process, they will have to overcome the limits that this formation imposes on them and extrapolate the boundaries of Content viewed in a partial and a-historical way “(p. 15).
It is not about overvaluing formal or informal knowledge. The question that is presented, seeks to reflect on the effective possibilities of relating mathematics taught in schools with mathematical practices practiced in human activities. In doing so reflexively, we seek to find convergent points, because according to Pompey and Monteiro (2001), “If education occurs fundamentally in a relationship” with “the other, with the world, neither the other nor the world can be seen in a fragmented way” (p. 24).
All these perspectives clarify how important it is in the teaching of mathematics, the establishment of bonds of knowledge of the community with the knowledge of the school and vice versa. This dynamic provides a (re) construction of both knowledge. In theory, when working in this perspective, the school allows students to understand better and systematically what they do and why they proceed mathematically.
According to the understanding of Pompey and Monteiro (2001), “a meaningful educational process begins with the interaction of school and Community” (p. 55), whose relations can resignify the role of the school as a privileged place for exchanging experiences to Better understand the knowledge circulating in everyday life.
The adoption of a pedagogical practice that leaves the technicality and center the perspective of linking the world of life with the school world, can contribute to the minimization of the process of exclusion of a reflective critical mathematical knowledge about reality. According to D’ambrósio (1996), it means the adoption of a socio-interactionist posture, seeking a new educational paradigm replacing the already worn-out teaching-learning, based on the obsolete relationship of cause-effect.
We understand and share with Marques (2000) that no knowledge can be closed in its scope of action. It needs to be socialized, (re) constructing itself entirely in and by the communicative action established among the actors subjects. With and by the use of language, in an interactive-dialogical perspective, one can provide the (re) construction of both learnings, making the subjects singularized, not subjected to subjection.
That from this reflection the pedagogical practice in the classroom can be reoriented to the development of the full citizenship of the students. That, according to Pinheiro and Rosa (2016), the:
[…] Mathematics teachers immerse themselves in the cultural dynamics of students and use teaching and learning strategies that value the cultural dimension in the classroom, so that an inclusive mathematical education can be developed that could effectively Contribute to social transformation (p. 79).
A teaching with the focus of ethnomathematics, we believe to provide the students, conditions to interfere in reality through the knowledge produced historically, placing the student at the center of the educational process, as an active subject in the (re) construction of his Knowledge. This was evidenced in the speeches of the bricklayers, because from their work activity, they create processes of their own thoughts and strategies, with inspiration for their prior knowledge and learning acquired throughout their life history.
4. GOALS
4.1 To contribute from the reflection to the mathematics educator to adopt an investigative critical posture in relation to the teaching of mathematics, initiating his teaching activity through the establishment of bonds between daily mathematics and mathematics School 4.2 Contribute to the Constitution of the researcher teacher of his practice, arousing him/her to learn in a continuous way to be a teacher, according to current educational needs, transforming the classroom into an environment of exchange of knowledge, rescuing Historical knowledge-socially built by mankind; 4.3 Deepen the understanding of ethnomathematics, seeking to understand the role of the various cultural contexts in mathematical education, made possible by the approximation between mathematics and reality.
5. METHODOLOGY
We develop the work through different moments, namely: theoretical study on the theme Ethnomathematics, conversations with bricklayers and sellers of construction material stores. We investigate dialogically with each professional about the mathematical knowledge used in their activity. We seek to reflect pedagogically on possible connections between mathematics and reality in the possibility of establishing bonds between the mathematical knowledge used by bricklayers and school mathematics.
6. EXPECTED CONTRIBUTION
It is hoped that teaching mathematics in the classroom through the ethnographic a[9]pproach allows teachers and students to learn about the very cultural diversity of mathematics. That the results of this research help in the development of a methodology that contributes to the teaching of basic mathematics, with Ethnomathematics as a support for this understanding.
In the words of RAM one,
[…] Teaching mathematics in this conception will allow the student to link the concepts working in class to their daily experience, according to their natural, social and cultural environment. It is not about rejecting academic mathematics, but rather incorporating values that are experienced in group experiences, considering the historical-cultural bonds (CARNEIRO, 2012, p. 3).
Through the text produced, the result of readings and the study sessions, it aims to pedagogically, the Union of Theory and Practice for the (re) construction of systematised knowledge. It is also hoped that the reflections resulting from the reading of the text allow a new look at the reality and on the mathematical education, from the perspective of the production of knowledge from the daily practice and the establishment of possible connections between Mathematics and reality.
7. BIBLIOGRAPHICAL REFERENCES
BREDA, Adriana LIMA, Valderez Marina do Rosário e GUIMARÃES, Gleny Terezinha Duro. A utilização da Etnomatemática nos cursos de formação continuada de professores: implicações das relações de poder saber na produção de subjetividades. Curitiba. Novembro de 2011. Disponível em: http://educere.bruc.com.br/CD2011/pdf/4668 _ 2898.pdf. Acessado em: 20/08/2017.
CARNEIRO, K. T. A. Cultura Surda na aprendizagem matemática da sala de recurso do Instituto Felipe Smaldone: uma abordagem etnomatemática. Anais do 4º Congresso Brasileiro de Etnomatemática. Belém, PA: ICEm4, 2012.
D’AMBROSIO, Ubiratan. Etnomatemática – elo entre as tradições e a modernidade. Coleção Tendências em Educação Matemática, 1. Belo Horizonte: Autêntica, 2001, 112p.
——-. Etnomatemática: Arte ou técnica de explicar e conhecer. Editora Ática, Série Fundamentos, 2. edição, São Paulo, 1993.
——-. Educação Matemática: da teoria à prática. Editora Papirus (Coleção Perspectivas em Educação Matemática), Campinas – São Paulo, 1996.
DEMO, Pedro. Pesquisa e construção de conhecimento: Metodologia científica no caminho de Habermas. 3.ed. Rio de Janeiro: Tempo Brasileiro, 1996. 125p.
FIORENTINI, Dario. Alguns modos de ver e conceber o ensino da matemática no Brasil. In. Zetetiké. Campinas, São Paulo, ano 3, n.4,p.1-37, 1995.
GIARDINETTO, José Roberto Boettger. Matemática escolar e matemática da vida cotidiana. Coleção polêmicas do nosso tempo, autores associados, Campinas – São Paulo, 1999, 128p.
LOPES, Antônio José. Os saberes das crianças como ponto de partida para o trabalho pedagógico. In: BRASIL. Secretaria de Educação Básica. Diretoria de Apoio à Gestão Educacional. Pacto Nacional pela Alfabetização na Idade Certa: Apresentação / Ministério da Educação, Secretaria de Educação Básica, Diretoria de Apoio à Gestão Educacional. – Brasília: MEC, SEB, 2014.
LINS, R. C.; GIMENEZ, J. Perspectivas em Aritmética e Álgebra para o Século XXI. Série Perspectivas em Educação Matemática. SBEM. Campinas: Papirus Editora, 1997, 176p.
LINS, Rômulo Campos. O modelo teórico dos campos semânticos: uma análise epistemológica da álgebra e do pensamento algébrico. In: Dynamis, v.1, n.7, p. 29-39, abr/jun, Blumenau, 1994.
MARQUES, Mario Osorio. A aprendizagem na mediação social do aprendido e da docência. Ijuí, Editora UNIJUÍ, 2. edição, 2000, 144 p.
_______. Escrever é Preciso: o princípio da pesquisa. Ijuí, Editora UNIJUÍ, Coleção educação, 4. edição, 2001, 163p.
MONTEIRO, A.; POMBEU, G. Jr. A matemática e os temas transversais. Editora Moderna, São Paulo, 2001, 160p.
PINHEIRO, R. C.; ROSA, M. Uma perspectiva etnomatemática para o processo de ensino e aprendizagem de alunos Surdos. RPEM, v. 5, n. 9, p. 56-83, 2016.
ROSA NETO, R. Didática da matemática, São Paulo: Ática, 2002.
ROLIM, Carmem Lucia Artioli. Fórmulas de Silêncio: metodologias no processo de ensino da Matemática. In: SANTOS, Jocyléia Santana. ZAMBONI, Ernesta. Potencialidades Investigativas da Educação. Goiânia: Ed. da PUC Goiás, 2010.
SANTOS, Lijecson Souza dos. Contextualização Matemática Em Situação De Ensino E Aprendizagem No Eja. Disponível em: https://editorarealize.com.br/revistas/cintedi/trabalhos/TRABALHO_EV060_MD1_SA18_ID 492_23102016194610.pdf. 2016. Acesso em 11/11/2017, Hora: 22hrs e 38 min.
SILVA. Adelmo Carvalho da. et. al. Paradigmas Educacionais: Contribuições para o Ensino de Matemática. In. SILVA, Adelmo Carvalho. et al, Ensinar matemática: Formação, investigação e práticas docentes. Cuiabá, MT: DUFMT, 2012.
SKOVSMOSE, Ole. Um convite à educação matemática crítica. Tradução de Orlando de Andrade Figueiredo. Campinas: Papirus, 2014.
VYGOTSKY, Lev Seminovich. A construção do pensamento e da linguagem. Tradução: Paulo Bezerra, São Paulo, Martins Fontes, 2001, 496p.
8. Knowledge, in this perspective is understood as a belief-affirmation, along with a justification for belief-affirmation.
9. In this work used to designate the investigation of the conceptions, traditions, and mathematical practices of a social[pedreiros] group and the pedagogical work that can be developed in the perspective that the group interprets and codify their knowledge; Acquire the knowledge produced by academic mathematics, using, when confronted with contextualized situations, the one that seems more appropriate.
[1] Master in Science Education – Mathematics, UNIJUI – RS. Degree and Specialization in Science and Mathematics. Prof. Assistant of the CCA – Center for Agricultural Sciences, Campus of Marshal Cândido Rondon, UNIOESTE, PR – Brazil.
[2] Master in Sustainable Rural Development-UNIOESTE, Mathematics Specialist, Physics-UNIPAR, People Management and Special Education with emphasis on Multiple Disability-UNIASSELVI, Graduated in Mathematics with emphasis in Physics-UNIPAR.
[3] Specialization in Exact Science Teaching – Mathematics, Physics and Chemistry. UNIOESTE – State University of Western Paraná. Graduation: Science and Mathematics. UNIJUI, RS. Professor of the State Education Network of the State of Paraná.
[4] Professor of Plant Protection and Human Health at the Pontifical Catholic University of Chile, Department of Plant Sciences, he holds an interdisciplinary position shared between the Faculty of Agronomy and Ingeniería Forestal (FAIF), Faculty of Medicine and Faculty of Chemistry. Research Professor associated with the Study Group on Soils and Environment (GESOMA – UNIOESTE). Master in Agronomy from UNIOESTE, PhD in Agronomy from UNIOESTE (2013-2016) – Sandwich Period (CAPES Scholarship) from the University of Lisbon, at the Instituto Superior de Agronomia (ULisboa).
[5] Research Productivity Level 1C by CNPq in the area of Environmental Sciences with three Postdocs, UEM-PR (Brazil), University of Santiago de Compostela (Spain), UFG-GO (Brazil). He is currently an Associate Professor at UNIOESTE-PR and acts as a professor and researcher at the Center for Agrarian Sciences, teaching chemistry. Lecturer in the Master Program in Agricultural Sciences at UEM. He is currently ad hoc consultant to CNPq, CAPES and Fundação Araucária. Acts as volunteer environmental consultant with MP-SP and CONAMA-DF.
[6] Undergraduate student in agronomy-UNIOESTE-State University of the west of Paraná-undergraduate administration-Unip-Universidade Paulista.
[7] Master student in Agronomy (Plant Production) from the State University of Western Paraná (UNIOESTE). Agricultural Engineer graduated from UNIOESTE (2014-2018), acts as a researcher associated with the Study Group on Soils and Environment (GESOMA – UNIOESTE).
Submitted: June, 2019.
Approved: July, 2019.