ARTIGO ORIGINAL
XAVIER, Márcio Pizzete [1], SCHWANTES, Vilson [2], KRACKE, Elisa [3], GRAUNKE, Carla Kuhn [4], GONÇALVES JUNIOR, Affonso Celso [5], SCHWANTES, Eloísa Bernardete Finkler [6]
XAVIER, Márcio Pizzete. Et al. Reflexão sobre a constituição do pensamento algébrico. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano 06, Ed. 06, Vol. 11, pp. 129-153. Junho de 2021. ISSN: 2448-0959, Link de acesso: https://www.nucleodoconhecimento.com.br/educacao/constituicao-do-pensamento, DOI: 10.32749/nucleodoconhecimento.com.br/educacao/constituicao-do-pensamento
RESUMO
O ensino da álgebra, na maioria das vezes restringe-se a questões técnicas e operacionais, deixando de lado o desenvolvimento de conceitos e o pensamento algébrico. Os alunos geralmente apresentam dificuldades na aprendizagem da álgebra por terem dificuldades de significar sua linguagem, além de nem sempre perceberem que ela está presente na resolução de diversas situações-problemas do nosso cotidiano. Este artigo, resultado de reflexões teóricas que procuram entender a relação que existe entre pensamento e linguagem para a constituição do pensamento algébrico, traz uma reflexão que pretende minimizar tais dificuldades. A fundamentação pedagógica encontra motivação nos escritos de Lins (1994) e Vygotsky (2001). O estudo objetiva compreender o que permite um ser humano pensar algebricamente, procura clarificar a relação que existe entre pensamento e linguagem para uma efetiva organização, desenvolvimento e constituição deste pensamento. A partir do referencial teórico adotado acredita-se que sua constituição é possível, pela posse da linguagem significada, internalização dos significados produzidos na interlocução através da observação e comunicação das ideias matemáticas presentes em situações-problema.
Palavras-chave: Pensamento Algébrico, Linguagem, Produção de Significado, Generalização, Escrita Algébrica.
1. INTRODUÇÃO
A mente humana trabalha o tempo todo. Através dela é possível desenvolver habilidades de raciocínio que possibilitem ao ser humano equacionar e resolver problemas de natureza diversa. Neste sentido, por meio do pensamento podemos criar estratégias para controlar o gasto de energia elétrica em função da renda familiar, resolver problemas de relacionamento pessoal, minimizar dificuldades de aprendizagem, compreender as mudanças que ocorrem na nossa sociedade. É possível ainda desenvolver e aprimorar, por meio da linguagem, uma forma de pensamento que utiliza como ferramenta a matemática algébrica.
O ensino de álgebra nas últimas décadas, muito por conta da formação tecnicista da maioria dos docentes, tem se fundamentado na resolução metódica de exercícios, baseando-se na transmissão e memorização de regras e fórmulas. No entendimento de Demo (1996, p. 10) “[…] aulas copiadas para ensinar a copiar, na transmissão decorada […]”. Essa realidade, vivida por muitas escolas, configura a existência de um conhecimento imposto de métodos inquestionáveis. Nessa “[…] postura reprodutiva surrada […]” (DEMO, 1996, p. 10), o encaminhamento didático dos conteúdos caracterizou-se, como consequência, muito mais por dissensos do que consensos.
O que se percebe nas escolas não é somente, segundo Lins e Gimenez (1997), o ensino da álgebra tentando se justificar por si só. Há também que se considerar, de acordo com esses autores, que os conceitos propostos são desprovidos de contextualização. Postulam que de todas as formas de linguagem, as palavras possuem um papel fundamental e central para o desencadeamento do desenvolvimento do pensamento humano e algébrico. De acordo com Freitas (1995, p. 158), a álgebra para comunicar suas ideias, pode incorporar no processo ensino-aprendizagem, “[…] a linguagem como formadora do pensamento”.
De modo geral, no Brasil, existe um consenso estabelecido em relação à necessidade de se repensar o ensino da álgebra. Para Lins e Gimenez (1997, p. 105), “a visão dominante é a letrista”, que pode ajudar a entender a falta da produção de significados para a atividade algébrica nas escolas. Machado (1993), ao enfocar as diferentes formas de material concreto, incluindo situações-problema contextualizadas, para o ensino aprendizagem, ressalta uma dimensão que pode ser explorada no trabalho matemático, ou seja, trabalhar o programa de ensino recheando os conteúdos de significações.
Compartilhamos da opinião de Machado (1993), de que à medida que os alunos utilizam o texto matemático de forma interativa e comunicativa, os objetos matemáticos são “[…] apreendidos prenhes de significações e não como meras formas vazias, destinadas a interpretações posteriores” (p. 136).
É importante que professor e aluno, pela prática pedagógica, encontrem, segundo Demo (1996, p. 10) “[…] indicações concretas que facilitem o aprender a aprender e o saber pensar, na busca da […] qualidade educativa do homem, crítico e criativo, sujeito histórico capaz de definir seu espaço coletivamente”.
O caminho sugerido por Lins e Gimenez (1997) é a produção de significados para a linguagem. Essa produção sobre situações-problema, carregando linguística e matematicamente as palavras de significados permitiria, segundo Vygotsky (2001), a formação dos conceitos. Assim, à medida que os conceitos se formam, inicia-se o desenvolvimento do pensamento algébrico que pode ser expresso simbolicamente por meio da linguagem formal.
Os estudos realizados por Vygotsky mostram que a utilização de situações-problema para a produção do pensamento algébrico é condição necessária, porém, não suficiente. O autor nos mostra que diante de uma situação-problema em que se busca a produção do pensamento algébrico surge a necessidade do professor introduzir os meios, que são os conceitos, os quais, além de necessários, passam a ser significados durante a execução da tarefa e nas interações que ela proporciona.
Em situações de aprendizagem, o professor usa a linguagem para ensinar e aprender, e o aluno também aprende por meio da linguagem. Assim, em suas modalidades – oral e escrita – a linguagem é o elemento central do desenvolvimento do pensamento e da consciência humana (FARIAS; BORTOLANZA, 2015).
O pensamento algébrico perpassa pela linguagem, como um conhecimento resultante da experiência humana com o mundo cultural. Sua aprendizagem requer uma leitura de conteúdos de saber que circulam nos grupos sociais. Sua apropriação pela via dialógica, modifica os saberes prévios de crianças, adolescentes e de adultos. Cria capacidades, habilidades e competências para o enfrentamento de situações das mais diversas. Através dele o homem busca, permanentemente, reduzir situações-problema a expressões simbólicas concisas que explicitam de forma geral, porém, precisamente todo o funcionamento do contexto.
Acreditamos que o pensamento algébrico também perpassa por um processo natural de constituição, resultante da vida em sociedade, da produção cultural dos indivíduos, assim como ocorre quando o ser humano se apropria da linguagem. O domínio de sistemas de representação, regras que regem a abstração e a generalização, também perpassam pelo entendimento linguístico do texto. Uma leitura com entendimento textual pressupõe conhecimento da linguagem e do sistema de signos utilizados na matemática. Sem este conhecimento torna-se difícil a atribuição de significados às expressões algébricas.
O desenvolvimento da linguagem simbólica, além de representar uma maneira de comunicarmos falas, fatos e situações-problema, permite que escrevamos por meio de códigos a respeito de quantidades e formas. Quando desvelados, esses códigos trazem em seu bojo o papel de agentes facilitadores da comunicação do conhecimento matemático. No entanto, o uso dessa simbologia desprovida de compreensão, sem clarificar sua significação, favorece o efeito contrário, ou seja, torna-se um instrumento que dificulta o processo de aprendizagem da matemática. Devido a esta prática, no entendimento de Lins e Gimenez (1997, p. 9) “[…] hoje a álgebra escolar representa o mais severo corte (momento de seleção) da educação matemática escolar […]”.
De acordo com Vygotsky (2001), a linguagem precede o pensamento, sendo este um reflexo dela. O pensamento algébrico pode se manifestar através da linguagem, em situações-problema, em que as ideias algébricas podem estar presentes, ser percebidas e generalizadas. Essas situações-problema podem ser de natureza diversa, envolvendo atividades do nosso cotidiano, da física, geometria, aritmética, álgebra, química, biologia, astronomia, economia, agronomia, zootecnia, etc. Através dessas situações, pode-se observar um padrão comportamental, uma associação de ideias, uma sequência infinita, enfim, perceber a presença do pensamento algébrico e a possibilidade de sua constituição nas diferentes formas de linguagem.
O desenvolvimento do pensamento algébrico perpassa pela internalização das estruturas significadas da álgebra pela própria linguagem da álgebra, introduzidas pela posse da linguagem significada. É a produção de significados sobre o contexto de cada situação-problema que possibilita a representação dessa situação por meio de uma linguagem simbólica, estritamente algébrica. Na verdade, segundo Vygotsky (2001), o ponto fulcral se concentra na linguagem que, quando carregada de significados, se transforma em pensamento, o qual pode, nesse momento, ser expresso.
Para Vygotsky (2001), a imaginação é (re)construída pela experiência vivida e, a partir dela o aluno recria o real, tornando concretas em seu imaginário as fantasias humanas. Esta característica humana não pode e não deve ser negada aos alunos pela escola, antes, deve ser colocada a serviço da aprendizagem escolar.
O pensamento algébrico é uma forma de pensamento que pode comunicar ideias matemáticas presentes em qualquer área do conhecimento. O seu desenvolvimento no ser humano pode ocorrer por meio de atividades de aprendizagem que lhe permitem a percepção de regularidades em padrões e sequências, de aspectos que não variam em contrapartida com outros que variam. O uso natural da linguagem cotidiana para se chegar na linguagem algébrica formal, para expressar ou explicitar matematicamente a estrutura de situações-problema, contribui significativamente para o desenvolvimento desse pensamento (FIORENTINI; MIORIM e MIGUEL, 1993b).
O pensamento algébrico pode se manifestar também através de generalizações, na construção e manipulação de expressões [transformismo algébrico – Lins e Gimenez (1997)], no relacionamento entre grandezas e no estudo de formas distintas de resolução de determinados problemas. Além das situações de ensino já descritas e possíveis para um efetivo desenvolvimento e constituição do pensamento algébrico, de acordo com Vygotsky (1998), o jogo utilizado na forma de brinquedo também faz com que o aluno crie uma situação imaginária. Por isso, Vygotsky percebeu no contexto do jogo a presença de um sistema de signos que pode favorecer a generalização de acontecimentos da realidade vivida e que os mesmos são fundamentais para o desenvolvimento do pensamento algébrico.
Cabe ressaltar que segundo a Base Nacional Curricular Comum, BNCC (2016), as ideias de regularidade, de generalizações e de equivalências se constituem também em alicerces para o desenvolvimento de outras dimensões da álgebra, como a resolução de problemas de estrutura algébrica e a noção de função. Segundo relata a BNCC:
Os estudantes devem ser motivados a, em seu percurso escolar, questionar, formular, testa e validar hipóteses, buscar contraexemplos, modelar situações, verificar a adequação da resposta a um problema, desenvolver linguagens e, como consequência, construir formas de pensar que o levem a refletir e agir de maneira crítica sobre as questões com as quais ele se depara em seu cotidiano (BNCC,2016, p. 131).
Acreditamos que um trabalho pedagógico de matemática, utilizando-se metodologicamente situações-problema, pode-se perceber, segundo o referencial teórico adotado nesta pesquisa, que o que permite pensar algebricamente é a linguagem.
A linguagem deve ser utilizada na forma comunicativa, permitindo através do processo dialógico, a constituição do pensamento algébrico. Para a representação algébrica da situação-problema, o que permanece é a linguagem simbólica, sintetizando o pensamento.
2. DESENVOLVIMENTO
Para explicitar melhor a metodologia docente que acreditamos contribuir para o desenvolvimento e constituição do pensamento algébrico discente, seguem atividades, sobre as quais passaremos a refletir. Através da situação que segue e, observando-se atentamente da esquerda para a direita a quantidade de bolinhas representadas em cada posição da Figura 1, pode-se conduzir os alunos a uma reflexão sobre a regra matemática que permite calcular o número total de bolinhas para uma posição qualquer da sequência.
Figura 1: Sequências de bolinhas que apresentam algum tipo de regularidade na repetição de seus elementos.
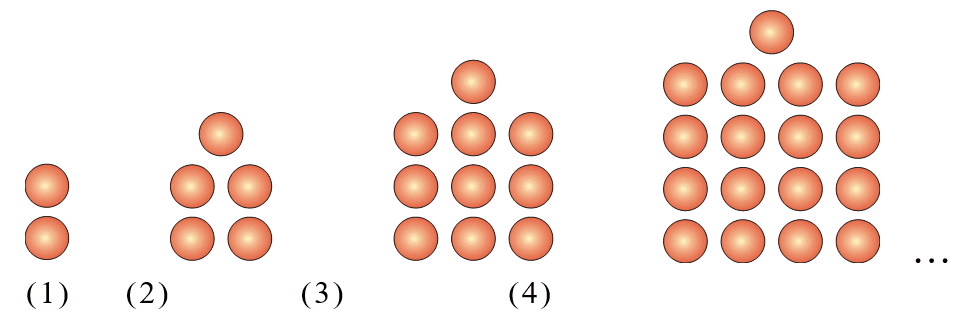
Para isso, após a observação, sugere-se o início do diálogo sobre a quantidade de bolinhas existentes em cada uma das posições da figura, numa tentativa de compreender dialogicamente alguma regularidade presente. Também é fundamental que os alunos sejam estimulados a desenhar a próxima figura da sequência dizendo, em seguida, de quantas bolinhas ela é formada.
A continuidade da conversação sobre a sequência, na intenção dos alunos dizerem quantas bolinhas teremos na 6ª posição, depois na 7ª posição etc. é fundamental. A ideia básica é que os alunos consigam, após a elaboração de conjecturas, representar cada figura da sequência através de uma operação matemática, iniciando pela primeira posição. Este tipo de atividade pode ser caracterizado como algébrica porque resolvendo-a os alunos são estimulados a partir do uso natural da linguagem cotidiana a um pensamento generalizante que, por sua vez, pode ser escrito simbolicamente através de uma expressão algébrica.
Vygotsky (2001), alerta que o pensamento generalizado se inicia a partir da significação dos signos produzida nas interações da ação pedagógica. Portanto, são os significados produzidos para os conceitos algébricos, nas interações produzidas nesta ação, que permitem o pensamento algébrico.
Após expressarem cada posição da sequência, através de uma operação matemática, os alunos têm condições de escrever em palavras o comportamento dessa sequência. A partir desse estágio, abrem-se caminhos para a elaboração de uma expressão matemática na forma algébrica para representar a situação-problema. Pode-se expressar então, para esta situação, o pensamento algébrico por meio de uma linguagem estritamente simbólico-formal para obter-se o número total de bolinhas para uma posição qualquer. Neste sentido, após a elaboração de um modelo matemático é interessante que se explore o número total de bolinhas da posição 50, 100, 300, etc.
Ao realizar este tipo de atividade, acreditamos que os alunos sejam conduzidos na direção do que Lins e Gimenez (1997, p. 137) consideram que seja atividade algébrica, ou seja, “A atividade algébrica consiste no processo de produção de significado para a álgebra” (itálico dos autores).
Atividades desse tipo permitem ao aluno a familiarização com sequências que envolvem a percepção de regularidades com formas, números e símbolos. Possibilitam também perceber e utilizar a linguagem cotidiana em suas diferentes expressões: Oral, visual e escrita, enfatizando a sua importância na elucidação dessas situações-problema. Tais atividades podem ajudar a capacitar o aluno, tanto na comunicação da regra de uma sequência pela linguagem cotidiana quanto para estabelecer uma relação geral que mostre a existência de uma correspondência entre a posição do elemento na sequência e a forma que o elemento apresenta na posição que ocupa.
Deste modo, acreditamos que a formação do pensamento algébrico discente pode se constituir a partir da elaboração de uma forma de pensar generalizante, utilizando-se a linguagem cotidiana. Atividades orientadas na forma de situações-problema e, por meio da linguagem, contribuem na iniciação do desenvolvimento do pensamento algébrico.
Situações de caráter numérico e geométrico podem ser problematizadas para explorar aspectos que variam e que não variam, desenvolvendo-se o pensamento algébrico por meio de um processo que vai das palavras utilizadas no cotidiano [linguagem cotidiana] à álgebra [linguagem formal]. A elaboração de conjecturas perpassa o processo de validação do pensamento algébrico, podendo este ser expresso simbolicamente a partir das práticas discursivas.
O desenvolvimento do pensamento algébrico propicia a elucidação genérica de problemas diversos, inclusive de atividades lúdicas como já sugerimos. Sua apropriação requer uma (re)construção continuada do pensamento durante a fase estudantil, perpassando o ensino fundamental e médio, avançando para níveis que permitem generalizar problemas cada vez mais complexos.
Compartilhamos com Lins e Gimenez (1997), quando sugerem que esse desenvolvimento é possível em séries anteriores ao 6º ano do ensino fundamental. Para isso pode-se explorar situações-problema, nas quais este pensamento se manifesta, podendo ser expresso com ou sem a necessidade de uma linguagem simbólica. É importante na iniciação ao ensino da linguagem algébrica que a produção de significados seja trabalhada sobre contextos que possam propiciar ao aluno oportunidades para relacionar observações do mundo real a representações. Também é importante que essa produção possa levá-lo a adquirir competências para desenvolver o pensamento algébrico por meio da linguagem algébrica.
Para Vygotsky (1998, 154), “[…] a linguagem escrita adquire o caráter de simbolismo […]”. Expressá-la através de uma linguagem simbólica, que utiliza letras, pode ser desenvolvido a partir de atividades, como as que seguem, as quais consideramos um estágio importante na busca de um pensar que leva o aluno a generalizar situações. A sequência de figuras geométricas representadas a seguir, Figura 2, da esquerda para a direita, pode, além de exercitar, constituir as funções psicológicos superiores, desenvolver as estruturas cognitivas do aluno.
Através do desenvolvimento dessas sequências repetidas, o aluno pode encontrar um modelo matemático que retrate o pensamento desse contexto sequencial, tendo como suporte a observação e a produção de significados sobre a linguagem. O pensamento matemático expresso na linguagem representa uma forma generalizada através da qual lhe seja possível saber, por exemplo, qual das figuras estará numa posição qualquer.
Figura 2: Sequência de figuras geométricas que apresentam algum tipo de regularidade na repetição de seus elementos.

À medida que o aluno produz significados sobre uma situação-problema ele vai desenvolvendo o pensamento e começa a perceber que a matemática não é uma ciência pronta e acabada, constituída apenas de fórmulas e leis que não se justificam. A observação e a análise de sequências [numéricas, simbólicas, geométricas,…] permitem o reconhecimento de padrões e a produção de significados sobre a linguagem, facilitam a associação de ideias e as generalizações que, por sua vez, também favorecem o surgimento do espírito crítico e o desenvolvimento da capacidade intelectual de pensar.
As autoras Vale e Pimentel, em seu trabalho com padrões ressaltam que:
Muito do insucesso em matemática deve-se ao facto de os alunos recorrerem apenas à memorização e não à compreensão. O primeiro passo para aprender a pensar matematicamente é aprender a descobrir padrões e estabelecer conexões. A procura de padrões deve constituir o núcleo das aulas em todos os temas, já que eles surgem nas fórmulas que descobrimos, nas formas que investigamos e nas experiências que fazemos. (VALE; PIMENTEL, 2011, p.1)
A álgebra perde seu caráter social se ensinada aos alunos como um conjunto de símbolos, letras e números sem vida, sem significação e sem vínculo com a realidade. Expressões algébricas descontextualizadas [expressões por expressões] são expressões sem significação. A escola precisa considerar o aluno como um ser pensante e criativo em permanente transformação. Como um ser capaz de criar e recriar suas próprias perspectivas, com capacidade de interligar a matemática da vida e a matemática da escola.
Para Mestre e Oliveira (2011), uma generalização “é uma afirmação sobre um conjunto de dados matemáticos” (p. 4). Compartilhamos do entendimento de Lins e Gimenez (1997, p. 137) a respeito do que seja álgebra, ou seja, considera que “A álgebra consiste em [sic] um conjunto de afirmações para as quais é possível produzir significado em termos de números e operações aritméticas, possivelmente envolvendo igualdade ou desigualdade” (itálico dos autores).
O que ocorre com frequência nas escolas é que não há uma construção da linguagem algébrica. Ela é apresentada como pronta e acabada. Não se caminha a partir de uma situação-problema, seguida da produção de significados sobre seu contexto e, não se busca por meio do uso natural da linguagem cotidiana uma aproximação com a linguagem simbólica. Esta, por sua vez, mostra-se como um obstáculo cognitivo na aprendizagem da álgebra, por não ser significada. Os alunos apresentam dificuldades na construção de estruturas algébricas que caracterizam uma situação-problema, ou seja, apresentam deficiências para representar expressões na linguagem algébrica, por não terem conseguido significar essa linguagem.
O fundamental para o desenvolvimento do pensamento algébrico na iniciação ao estudo da álgebra é propiciar condições, por meio da linguagem, nas atividades de aprendizagem, para que o aluno consiga entender e expressar, em última instância, a generalização da situação-problema. Essas condições permitem que ele elabore e manipule as expressões, relacione-as com representações numéricas, geométricas e algébricas de forma a compreender a resolução dos problemas.
O estabelecimento de relações associativas entre os objetos, para a produção de complexos no desenvolvimento das potencialidades individuais do aluno e a consequente apropriação dos signos permite, segundo Vygotsky (2001), a elaboração e o desenvolvimento de sua forma própria de pensar. Em um cenário intersubjetivo, o aluno pode usar a linguagem para fundamentar a construção de seu pensamento algébrico através da mediação linguística com o outro. O que precisa acontecer, na ação pedagógica é que o aluno formule o pensamento sobre uma situação-problema pela significação dos conceitos.
A exploração de sequências repetidas, como as sugeridas anteriormente, pode contribuir tanto no desenvolvimento quanto na apropriação do pensamento algébrico. Através dessas situações-problema, a linguagem algébrica surge da produção de significados para cada contexto, desenvolvendo-se gradativamente, até ser internalizada, momento em que se inicia sua apropriação.
Na pesquisa desenvolvida por Carmo (2014), o autor ressalta a importância do uso de padrões e sequências com algum tipo de repetição para introduzir a linguagem algébrica no ensino fundamental, enfatiza o quanto estas atividades podem trazer benefícios na aprendizagem da escrita algébrica, porém,
[…] este tipo de atividade está sendo pouco utilizada para a introdução da linguagem algébrica, embora várias pesquisas e documentos oficiais mostrem o potencial desse tipo de atividade para a iniciação do estudo da álgebra (CARMO, 2014, p. 103).
No entendimento de Coxford e Shulte (1995), o problema mais complicado enfrentado na resolução de problemas de natureza algébrica reside na não apropriação da linguagem matemática por parte do aluno. Ressaltam que,
[…] à medida que as ações concretas são assimiladas a criança torna-se capaz de reexecutar as ações concretas anteriores […] depois de desenvolvimentos intelectuais posteriores, ela se torna capaz de reproduzir essas ações por meio de símbolos e operações abstratas (COXFORD e SHULTE, 1995, p. 80).
À semelhança da produção de significados para as palavras do cotidiano, pode-se postular que, de acordo com Vygotsky (2001), enquanto as palavras usadas no ensino da álgebra não tiverem significado, além de encontrarmos enormes dificuldades de compreensão dos conceitos algébricos, pouco ou quase nada conseguiremos evoluir. Em suas pesquisas, o autor mostrou que o pensamento humano tem origem nas palavras e à medida que o aluno se desenvolve ele amplia essa significação pelo uso contínuo da linguagem, o que faz sua forma de pensar evoluir, modificando seu pensamento anterior.
No que tange ao processo ensino-aprendizagem, Vygotsky (2001) chama a atenção para as relações existentes entre os sistemas de signos criados pelos indivíduos. Tais relações se constituem em um instrumento através do qual o ser humano pode intervir no meio circundante para compreender melhor, resolver problemas das matemáticas e de outras áreas do conhecimento.
Concordamos com Fiorentini; Miorim e Miguel (1993b) em relação ao que também procuramos clarificar com Vygotsky (2001), quando aqueles autores afirmam que as interações sociais são determinantes para o desenvolvimento do pensamento no ser humano. Assim, os significados para a álgebra podem ser explorados a partir do contexto, pelo uso da linguagem. O pensamento algébrico pode ser desenvolvido por meio de situações didáticas especificas para esse fim, partindo-se tanto da linguagem cotidiana quanto das linguagens aritmética, geométrica e algébrica.
Lins e Gimenez (1997) propõem uma (re)leitura da atividade algébrica, imbricada com a aritmética, a geométrica e outros campos do conhecimento. Atentam para a possibilidade de se explorar pontos de convergência entre as matemáticas praticadas na vida cotidiana e na escola, ressaltando a importância da produção de significados pelo aluno, o que, creio, pode contribuir significativamente para a formação de cidadãos autônomos, reflexivos e críticos.
Os autores ainda observam que compete à escola (re)organizar os conceitos matemáticos presentes nas atividades cotidianas, pois “[…] são parte do processo de organização da atividade humana” (LINS e GIMENEZ, 1997, p. 23). Assim, acreditamos que, ao trabalhar sua sistematização, o aluno não só se apropriará dos conceitos científicos, como compreenderá a matemática sob outra perspectiva, desenvolvendo o pensamento algébrico por meio da produção de significados sobre atividades contextualizadas.
Na dimensão semântica, o pensamento algébrico reflete a compreensão dos sentidos atribuídos ao conceito algébrico e sua relação com a realidade vivida. A aprendizagem desse conceito é percebida pelo uso que o aluno faz do tema estudado, empregando suas próprias palavras no estabelecimento de relações com outros temas e na elaboração de generalizações.
O pensamento algébrico teria pouco sentido se tivesse que se sustentar apenas pela atividade algébrica. Sua presença e manifestação extrapolam o campo da matemática dita algébrica. Assim como a aritmética não pode se restringir e ser validada como campo da matemática que trata apenas de regras e números, o pensamento algébrico também não diz respeito somente a atividades da álgebra.
Os pensamentos algébrico e aritmético têm sustentação em suas linguagens específicas, cujos signos foram socialmente construídos e apresentam significados diferentes em contextos distintos. Esses pensamentos, segundo Vygotsky (2001), só poderão ser desenvolvidos quando os significados produzidos nas interlocuções forem internalizados já que, nessa perspectiva, as capacidades intelectuais dos sujeitos são desenvolvidas num processo contínuo pela linguagem significada.
De acordo com Vygotsky (2001), o pensamento algébrico, manifesto pela linguagem, pode possibilitar ao aluno a produção de significados, quando esse refletir sobre situações-problema, em geral. Uma postura reflexiva sobre o que está aprendendo pode favorecer o crescimento pessoal e do grupo de estudo e, por conseguinte, de suas aprendizagens. Nas palavras do autor, “[…] ensina-se à criança o que ela não tem diante dos olhos, o que vai além dos limites da sua experiência atual e da eventual experiência imediata” (VYGOTSKY, 2001, p. 268).
A internalização das significações sobre situações-problema, através da linguagem, possibilita a apropriação do pensamento algébrico. As funções psicológicas superiores permitem o pensamento generalizante, a capacidade de generalizar fatos e situações-problema, o que perpassa por um entendimento da linguagem, capacitando os sujeitos a (re)inventar soluções para as questões que se apresentam cotidianamente.
Esse olhar, voltado para a produção do conhecimento algébrico a partir de uma perspectiva dialógica, sugere ao educador outra dinâmica de trabalho pedagógico, mais reflexiva e crítica sobre sua prática. Possibilita ao educador perceber que suas aulas de álgebra podem, no âmbito da própria escola, representar uma alavanca para compreender a realidade circundante. E considera o processo de (re)construção do conhecimento como social, histórico e contextualizado, no qual a interlocução é indispensável.
2.1 APROPRIAÇÃO DA LINGUAGEM E DESENVOLVIMENTO DO PENSAMENTO ALGÉBRICO
Acreditamos que a interlocução docente, competente na organização e execução da prática pedagógica e as reflexões dialógicas sobre cada situação-problema podem permitir uma nova leitura da atividade algébrica, alavancando, por conseguinte, todo o processo ensino-aprendizagem da álgebra para uma compreensão da realidade circundante.
Esta reflexão nos leva à percepção de que a linguagem algébrica está presente nas relações estabelecidas entre a linguagem cotidiana, os símbolos, os números, as operações aritméticas e em situações diversas da atividade humana. Traz subjacente que o pensamento algébrico se manifesta a partir da produção de significados sobre tais situações e este fato exige dos educadores uma atenção especial para a linguagem e suas diferentes formas de manifestação.
No livro Perspectivas em aritmética e álgebra para o século XXI, Lins e Gimenez (1997, p. 124) relatam uma situação-problema envolvendo dois tanques iguais, assim enunciada: “Para encher o tanque da esquerda são precisas mais 9 baldes. Para encher o da direita, são precisos mais 5 baldes. O que você pode falar sobre essa situação?”.
Através desta situação os autores levaram os alunos a pensar e a falar sobre o que viam, exercitando suas capacidades de visualizar e imaginar significados e justificações[7], representando estas pela linguagem cotidiana e simbólica. Em seguida os alunos, conduzidos pelos autores, expressaram através da linguagem algébrica, transformações diretas de expressões, com base em propriedades da igualdade em relação às operações aritméticas.
Neste contexto, segundo os autores, “[…] os alunos são requisitados a produzir duas justificações: uma em relação ao núcleo dos tanques e outra em relação a [sic] transformação direta de alguma crença-afirmação já estabelecida” (LINS e GIMENEZ, 1997, p. 129).
Nessa atividade os autores conduziram os alunos a expressarem o pensamento algébrico por meio de uma linguagem formal que representasse a totalidade da situação-problema. Esta, ao ser escrita matematicamente, ganhou um caráter conciso e universal.
O desenvolvimento do pensamento algébrico torna-se possível pela introdução da linguagem simbólica, num processo que se inicia pela significação da linguagem cotidiana, perpassando pela observação, discussão e significação de cada situação-problema. Decorre de uma interlocução dialógica reflexiva do ato de ler e significar a linguagem expressa no texto matemático.
O pensamento, expresso simbolicamente pela linguagem, reflete o nível de conhecimento consolidado. Ambos, pensamento e linguagem, tornam-se fundamentais para a compreensão do mundo e na comunicação das ideias matemáticas. Para Lorenzato e Vila (1993), o indivíduo que pensa algebricamente é aquele que consegue atribuir às palavras presentes em um contexto uma interpretação semântica, sendo capaz de compreender as ideias contidas no texto ou as usadas verbalmente.
A situação-problema que segue objetiva reforçar nossa postura didática, sugerida nesta reflexão, ou seja, a ênfase para a importância da produção de significados sobre cada situação-problema trabalhada com a classe.
Quem já não comentou em algum momento de sua vida com os alunos que, normalmente em festas de caráter familiar – casamentos, aniversários, batizados, etc, quando estão presentes, parentes próximos e distantes, a falta de lugares nas mesas em função de alguém ter feito a junção delas para facilitar a comunicação das pessoas, fez com que o número de assentos ficasse reduzido.
com a junção das mesas todos os convidados ficaram mais próximos para se comunicarem, porém, este fato pode gerar um desconforto para os organizadores da festa. Queremos dizer, poderão faltar mesas, caso muitas delas forem encostadas [conforme figura que segue] para a conversação familiar citada. E agora? A álgebra, o pensamento algébrico pode dar alguma contribuição para tranquilizar os organizadores da festa? Ou você acha que essa situação, tão comum nessas festividades, não tem nada a ver com a matemática?
Observe atentamente, da esquerda para a direita, a quantidade de mesas representadas em cada situação da Figura 3, bem como o número de lugares que cada uma das mesas acomoda.
Figura 3: Sequência com mesas e cadeiras que apresentam algum tipo de regularidade.
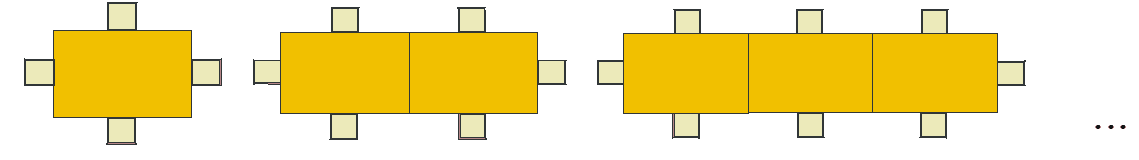
Vocês acreditam que se pode construir um modelo matemático que forneça o número de lugares, cadeiras, para determinado número de mesas agrupadas, enfileiradas sequencialmente? Sabemos que os organizadores da festa podem, dado o número de convidados e mesas disponíveis, construir um modelo matemático que era capaz de informar o número ![]() de lugares, caso enfileirássemos
de lugares, caso enfileirássemos ![]() mesas dessa sequência.
mesas dessa sequência.
A expressão ![]() , através de um raciocínio matemático, pelo qual se precisa produzir significados para cada termo da expressão, pode de forma organizada calcular o número de convidados com assento. Observe que para qualquer número de mesas sempre teremos 2 lugares nos lados extremos. Esse valor 2 é o coeficiente da expressão algébrica. Observe também que para cada mesa acrescida na sequência aumentam 2 lugares, que são considerados como constantes e devem ser somados, para determinar o número total de
, através de um raciocínio matemático, pelo qual se precisa produzir significados para cada termo da expressão, pode de forma organizada calcular o número de convidados com assento. Observe que para qualquer número de mesas sempre teremos 2 lugares nos lados extremos. Esse valor 2 é o coeficiente da expressão algébrica. Observe também que para cada mesa acrescida na sequência aumentam 2 lugares, que são considerados como constantes e devem ser somados, para determinar o número total de ![]() lugares da sequência.
lugares da sequência.
Para o caso específico desta situação-problema, a livre conversação, os depoimentos sobre o que cada aluno pode perceber ao observar o número de lugares, representados na 1ª, 2ª, 3ª, 4ª, 5ª posições da sequência, relacionados com o número de mesas, são tão importantes quanto os questionamentos e suas justificações. Todos esses procedimentos geram e amadurecem um pensar generalizante que, antes de ser expresso na linguagem simbólica, perpassa pelo entendimento linguístico e por um raciocínio indutivo.
Após explicitarem seus procedimentos de várias formas, os alunos devem ser questionados e conduzidos dialogicamente a elaborar uma expressão algébrica que diga quantos lugares [cadeiras] teremos nessa sequência quando forem juntadas mesas. Desenhar algumas posições subsequentes as já representadas na sequência original também pode se constituir numa forma auxiliar ser interessante de representação na busca da generalização.
Os alunos, após a observação, devem sempre ser questionados a falar sobre o que veem em cada figura ou em cada situação-problema. Através de um processo argumentativo reflexivo, mediado pelo professor, é fundamental conduzir o processo ensino-aprendizagem à verbalização do comportamento da sequência e, por conseguinte, a uma expressão simbólica que retratava o contexto da situação-problema para diferentes situações.
A todo instante, durante o processo de elaboração do pensamento algébrico, os alunos devem ser instigados a explicitar suas falas e seus procedimentos. Acreditamos que isto contribui para realçar e ativar o pensamento, (re)construindo-o ao longo do diálogo. À medida que a linguagem cotidiana ficar carregada de significados, esse pensamento começa a ficar encorpado, tomar forma e, por conseguinte, sua expressão tornar-se-á possível.
O caminho para se elaborar e expressar determinada regularidade na linguagem algébrica, deve dar-se por meio de uma conversa dialógica com o texto. Assim, estamos de acordo com Vygotsky (2001), quando este afirma que a elaboração de um pensamento de caráter mais geral perpassa e se constitui pela linguagem, presente neste mesmo texto.
Dentro deste contexto, enfatizamos novamente a importância de se interpretar o texto escrito. Consideramos relevante falar o máximo possível sobre seu contexto, produzir significados via linguagem, para que, pela troca de ideias na via da experimentação, amadureça um pensamento que retrate genericamente a situação em estudo.
O desenvolvimento de um pensar algébrico elaborado a partir de uma problematização dialógica contextualizada pressupõe, no entendimento de Lins (1994), que esse conhecimento seja constituído a partir da enunciação do texto. Para o autor, não há como falar sobre um contexto sem ter elaborado o conhecimento que o constitui. Em seu estudo sobre o Modelo Teórico dos Campos Semânticos, ao fazer uma análise epistemológica da álgebra e do pensamento algébrico, ele afirma que:
conhecimento é uma crença-afirmação junto com uma justificação para a crença-afirmação. Indicamos, desta forma, que conhecimento é algo do domínio da enunciação – e que, portanto, todo conhecimento tem um sujeito – e não do domínio do enunciado; podemos também expressar este fato dizendo que conhecimento é do domínio da fala, e não do texto. Desde este ponto de vista, a Matemática é um texto, e não conhecimento; tem-se conhecimento apenas na medida em que pessoas se dispõem a enunciar este texto. A um conhecimento que fala deste texto – a Matemática – chamaremos, naturalmente, de conhecimento matemático. […] O MTCS indica que o mesmo texto, falado com diferentes justificações, constitui diferentes conhecimentos. Uma criança de 5 anos acredita – e diz – que “2 + 2 = 4,” o mesmo que um matemático acredita – e diz. Mas as justificações de cada um são provavelmente distintas: a criança exibe os dedos, o matemático fala de conjuntos. Estão constituídos conhecimentos diferentes. A álgebra, como a Matemática, é um texto, e falaremos de conhecimento algébrico sempre que se enuncie, que se fale um conhecimento relativo a este texto, isto é, cuja crença-afirmação seja reconhecida como pertencendo a este texto (LINS, 1994, p. 29, itálico do autor).
Na perspectiva sócio-histórica, a formação dos conceitos é um processo, não um resultado da transmissão de palavras ou definições que expressam uma generalização. No entanto, palavras que expressam conceitos podem ser utilizadas na comunicação, antes que os mesmos tenham sido formados. A palavra pode ajudar nesse processo, mesmo que assuma significados diferentes no caminho da formação do conceito.
Observe que no ensino tradicional de matemática prioriza-se a resposta correta de um problema e no trabalho de produção de significados para o texto matemático a ênfase está na produção de significados sobre a linguagem escrita do texto. Esta produção de significados necessita ter procedimentos que auxiliem na sua efetivação. A observação visual, os gestos produzidos sobre cada situação proposta, seguidos da produção de frases com justificações pelo uso da linguagem oral, da linguagem escrita e da linguagem matemática, constituem tais procedimentos e permitem o surgimento de várias enunciações viáveis para as distintas formas de linguagem que vão surgindo.
Cada situação-problema trabalhada deve ser percebida pelos alunos como um desafio transponível. O entendimento matemático dessas situações deve perpassar, obviamente pelo entendimento linguístico dos aprendentes. Os alunos, pela manifestação da linguagem, em suas várias formas, precisam ser motivados a visualizarem as diferentes maneiras de se ver e interpretar cada questão, percebendo a existência de outros significados, possibilitados pelas ações reflexivas discutidas nos pequenos grupos. Segundo Vygotsky (2001, p. 111), “a relação entre pensamento e linguagem modifica-se no processo de desenvolvimento […]”, daí a importância da realização das atividades de forma interativa.
Para Lins (1994), esse conhecimento elaborado provém da junção de uma crença-afirmação e uma justificação. Para Vygotsky (2001, p. 12), “[…] a generalização se torna possível se há desenvolvimento da comunicação”.
É no trabalho de grupo que se evidencia com facilidade as funções que estão em fase de amadurecimento nos alunos. A zona de desenvolvimento proximal proposta por Vygotsky (2001) mostra o desenvolvimento mental de modo prospectivo no desenrolar das atividades desenvolvidas em grupo. O trabalho dialógico na zona de desenvolvimento proximal impulsiona a aprendizagem pela produção de significados entre os sujeitos interlocutores.
Acreditamos que enfatizar o uso da linguagem para uma efetiva constituição do pensamento algébrico, através de um processo que cria espaços para ativar o pensamento sobre situações-problema, engendradas por atividades que permitem estabelecer um modelo matemático que retrate a existência de um padrão de raciocínio dentro do contexto proposto, é um desafio salutar e de grande valia no processo de elaboração e desenvolvimento do pensamento algébrico.
Segundo Vygotsky (2001), à medida que o aluno atribui significados para as palavras pertencentes ao contexto, inicia-se o processo de formação do conceito que, quando internalizado, constitui uma generalização. Como consequência, inicia-se a elaboração do pensamento algébrico pela atribuição de significados dados às palavras, explicitando-se a situação-problema de forma generalizada. Nas palavras de Freitas (1995, p. 158), “[…] o sentido das coisas é dado ao homem pela linguagem”.
No entendimento de Vygotsky (2001), a apropriação da linguagem e o desenvolvimento do pensamento algébrico pelo aluno ocorrem pela mediação dos signos, que busca na linguagem significados que, quando apreendidos, conduzem à generalização. Nas escolas ainda não se dá a devida ênfase à concepção de que o pensamento ocorre pela linguagem. Não raro, constatam-se situações de sala de aula nas quais o aluno, ao tentar auxiliar seu colega, responde que somente sabe fazer, não explicar. Nesse caso, fica evidenciada a deficiência da formação de conceitos e da generalização.
Para Giardinetto (1999, p. 27), “[…] a linguagem orienta as atividades do pensamento […]” e essa premissa encontra respaldo em Vygotsky (2001), que considera o pensamento um saber socialmente construído pela produção de significados do aluno, através de discussões, falas e interpretações acerca de situações-problema. Esse saber, favorecido pela linguagem oral e pela argumentação dos atores, gera a elaboração do significado e propicia a (re)elaboração dos conhecimentos prévios dos mesmos.
Para Nobre; Amado e Ponte (2014), que consideram o desenvolvimento do pensamento algébrico uma das grandes finalidades do ensino de matemática, ressaltam que:
[…] as representações escritas produzidas pelos alunos, em particular, na resolução de problemas são poderosas ferramentas que devem ser desenvolvidas por constituírem uma componente essencial da aprendizagem, possibilitando a organização e a comunicação de ideias. Em particular, constituem um meio para a aprendizagem progressiva de métodos formais algébricos, que são umas das componentes importantes do trabalho em Álgebra. (NOBRE; AMADO e PONTE, 2014, p. 2).
Quando o professor atua na zona de desenvolvimento proximal, ele oportuniza pela interlocução novas aprendizagens, promove o desenvolvimento do pensamento algébrico e incentiva o aluno a resolver situações-problema, compartilhando ideias e argumentos com outros colegas. Capacita, assim, os alunos a produzir em equipe, favorecidos pelo diálogo argumentativo que oportuniza a (re)construção dos saberes presentes na situação-problema e seus saberes prévios. Um trabalho educativo na zona de desenvolvimento proximal favorece o professor com um diagnóstico da turma e permite, pela linguagem, que o aluno organize seu pensamento na busca de pistas com seus colegas mais experientes para solucionar os problemas que momentaneamente ele não consegue resolver.
Vive-se um momento histórico privilegiado, cujas tendências indicam predominância no campo da comunicação e da informação, que por sua vez se baseiam fortemente na cibernética e na matemática. Nesta última, o aluno deve produzir significados para o texto, internalizar os signos, modificar a realidade circundante, numa ação dialética, em substituição a uma linguagem mecanizada, não apropriada para a atual conjuntura de desenvolvimento da humanidade. Quando o conhecimento matemático começa a aflorar e fluir, os participantes sentem-se gratificados e adquirem uma certa familiaridade com o pensar algébrico, tornam-se capazes de lidar com os signos e os conceitos matemáticos.
Segundo Marques (2000, p. 29), o conhecimento como resultado da vida social não pode ser realizado sem a presença e a interlocução dos participantes. Para o autor, “[…] os homens aprendem uns dos outros e uns com os outros, […]”. Para Demo (1996, p. 68), essa perspectiva se constitui com “[…] trabalho de equipe, no sentido específico do conhecimento construído a várias mãos”. Essa postura do autor passa a constituir no limiar do milênio, “[…] a maneira mais efetiva de superar o paradigma da consciência, para consolidar o da comunicação” (DEMO, 1996, p. 68).
Nesse contexto, a sala de aula passa a ser vista como uma comunidade emergente, atores em interação, produzindo significados e apropriando-se de significados histórico-socialmente construídos pela interlocução. A argumentação dialógica propicia, para a matemática, uma aproximação entre o significante – texto matemático, e o significado – conhecimento matemático (FIORENTINI, 1995).
A partir do momento em que os alunos começam a construir o significado das palavras contidas no texto matemático, possibilitam que o pensamento se realize nelas. Para Vygotsky (2001, p. 398), “[…] o significado da palavra não é senão uma generalização ou conceito”. Portanto, o desenvolvimento e a apropriação do pensamento algébrico pode se constituir a partir da exploração do texto matemático, sua representação pode ser realizada usando-se um raciocínio aritmético, algébrico ou outra forma de representação, a qual dependerá das características do texto.
Portanto, se a linguagem pressupõe dialogia, e se há uma relação íntima entre linguagem e pensamento, entre linguagem e atividade prática, uma forma bastante profícua dos educadores promoverem o desenvolvimento cognitivo de seus alunos é criar situações práticas que os motivem a interagir e exercitar a linguagem.
A escassez desta postura didática, na perspectiva de Selbach et al. (2010),
É por esse motivo que aulas que se fundamentam apenas no domínio de regras nada significam e raramente educam, pois muitas vezes são apenas técnicas que jamais se transformarão em conhecimentos. São ferramentas úteis apenas na hora exata em que são usadas, em nada servindo para o depois. (SELBACH et al., 2010, p. 22).
O desenvolvimento do pensamento algébrico e sua apropriação discente sugerem uma interação permanente entre professor e alunos, o que, por sua vez, requer um trabalho educativo-coletivo, uma aprendizagem cooperativa e colaborativa entre os participantes do processo. Fiorentini; Miorim e Miguel (1993a) manifestaram a importância da relação que se estabelece entre pensamento e linguagem. Acreditam que, dialeticamente, pela atribuição de significados à linguagem na observação e análise de situações-problema, seja possível perceber a presença, o desenvolvimento e a apropriação do pensamento algébrico.
Ler matematicamente uma informação é ter consciência e compreensão da mensagem impressa na linguagem simbólica. Atribuir significados à ideia traduzida corresponde a aproximar o fazer algébrico do mundo vivido. O entendimento do significado da mensagem lida possibilita inseri-la nas relações que podem ser estabelecidas com a realidade.
Muitos termos utilizados na linguagem cotidiana já estão recheados de ideias e significados matemáticos. Percebemos que o aluno compreende significados, estabelece relações entre estes termos e o seu mundo existencial extra-escolar, enquanto que na atividade matemática escolar, essas mesmas palavras lhe são desprovidas de significação, ‘vazias’. Esta constatação nos leva a uma reflexão, a um desenvolvimento do exercício argumentativo no sentido de conectar, significativamente a linguagem matemática formal a outros contextos.
O mundo vive o paradigma da intersubjetividade ou da comunicação (MARQUES, 1993), atravessa um momento histórico, cujas mudanças sociais, culturais e econômicas são profundas em todos os segmentos da sociedade.
A reflexão a que nos propusemos permite um ‘novo olhar’ sobre a nossa atividade docente, o papel discente no processo ensino-aprendizagem numa abordagem dialógica, o entendimento da realidade circundante e a (re)construção do conhecimento desta realidade, renovando e transformando nossos saberes.
3. CONSIDERAÇÕES FINAIS
Sabemos que o pensamento algébrico está presente nas atividades algébricas, assim como, faz parte do desenvolvimento humano e, como tal, surge inicialmente para resolver necessidades práticas, estando bastante presente em nosso cotidiano de várias formas.
Acreditamos que o pensamento algébrico não é nato, portanto, precisa ser desenvolvido. Nesse sentido, a escola é um local privilegiado para o seu desenvolvimento e constituição, cabendo aos docentes o papel da mediação do processo ensino-aprendizagem.
A exploração de sequências repetidas, como as sugeridas nesta reflexão, pode contribuir tanto no desenvolvimento quanto na apropriação do pensamento algébrico. Através dessas situações-problema, a linguagem algébrica surge da produção de significados para cada contexto, desenvolvendo-se gradativamente, até ser internalizada, momento em que se inicia sua apropriação.
O pensamento algébrico teria pouco sentido se tivesse que se sustentar apenas pela atividade algébrica. Sua presença e manifestação extrapolam o campo da matemática dita algébrica. Assim como a aritmética não pode se restringir e ser validada como campo da matemática que trata apenas de regras e números, o pensamento algébrico também não diz respeito somente a atividades da álgebra. Os pensamentos algébrico e aritmético têm sustentação em suas linguagens específicas, cujos signos foram socialmente construídos e apresentam significados diferentes em contextos distintos.
Esses pensamentos, segundo Vygotsky (2001), só poderão ser desenvolvidos quando os significados produzidos nas interlocuções forem internalizados já que, nessa perspectiva, as capacidades intelectuais dos sujeitos são desenvolvidas num processo contínuo pela linguagem significada.
O desenvolvimento do pensamento algébrico torna-se possível pela introdução da linguagem simbólica, num processo que se inicia pela significação da linguagem cotidiana, perpassando pela observação, discussão e significação de cada situação-problema. Decorre de uma interlocução dialógica reflexiva do ato de ler e significar a linguagem expressa no texto matemático. O pensamento, expresso simbolicamente pela linguagem, reflete o nível de conhecimento consolidado. Ambos, pensamento e linguagem, tornam-se fundamentais para a compreensão do mundo e na comunicação das ideias matemáticas.
Acreditamos que a interlocução docente, competente na organização e execução da prática pedagógica e as reflexões dialógicas sobre cada situação-problema podem permitir uma nova leitura da atividade algébrica, alavancando, por conseguinte, todo o processo ensino-aprendizagem da álgebra para uma compreensão da realidade circundante.
A reflexão, embora longe de ser conclusiva, pode corroborar nas atividades do ensino da álgebra, contribuindo com que o estudante desenvolva um pensamento que o auxilie na busca de padrões e analogias, comumente enfrentadas em situações-problema do cotidiano.
Esta reflexão nos leva à percepção de que a linguagem algébrica está presente nas relações estabelecidas entre a linguagem cotidiana, os símbolos, os números, as operações aritméticas e em situações diversas da atividade humana. Traz subjacente que o pensamento algébrico se manifesta a partir da produção de significados sobre tais situações e este fato exige dos educadores uma atenção especial para a linguagem e suas diferentes formas de manifestação.
Contudo, a esta breve reflexão e com todo respeito que é devido ao referencial teórico adotado, poderia se chamar de uma primeira tentativa de aproximação com o que de fato possa ser entendido como pensamento algébrico. Se nos aprofundarmos no tema, verificaremos que se torna cada vez mais difícil definir, claramente, o que de fato caracteriza e constitui o pensamento algébrico. Seria esse uma forma de pensar a partir de um conhecimento algébrico? Quais seriam, então, as habilidades e as características que permeariam indubitavelmente tal pensamento?
Sabemos também que ainda não existe um consenso entre os estudiosos a respeito do que realmente caracteriza tal pensamento e o pensar algebricamente. Pra nós ficou evidente e espero que os leitores tenham percebido a importância que tem no processo ensino-aprendizagem a mediação com o social, com o concretamente vivido, pois possibilita aos discentes, pelo viés da linguagem, a compreensão do texto matemático, que comunica ideias e que é constituído de sinais e de signos. No entanto, a questão da constituição do pensamento algébrico continua um desafio e deve ser para os docentes motivo permanente para um (re)começar a partir do aprendido.
Esse olhar, voltado para a produção do conhecimento algébrico a partir de uma perspectiva dialógica, sugere ao educador outra dinâmica de trabalho pedagógico, mais reflexiva e crítica sobre sua prática. Possibilita ao educador perceber que suas aulas de álgebra podem, no âmbito da própria escola, representar uma alavanca para compreender a realidade circundante. Considera o processo de (re)construção do conhecimento como social, histórico e contextualizado, no qual a interlocução é indispensável.
Ao finalizar a reflexão, enfatizamos que a capacidade humana de identificar padrões nas sequências repetidas, sugeridas ao longo do texto para a atividade algébrica, certamente contribuirá com educadores e estudantes de matemática, na perspectiva de compreenderem melhor sobre como pedagogicamente podemos desenvolver e constituir uma forma de pensar e de nos expressar algebricamente.
REFERÊNCIAS
BRASIL. Ministério da Educação. Base Nacional Curricular Comum. Brasília: 2016.
CARMO, P. F. Um estudo a respeito da generalização de padrões nos livros didáticos de Matemática do Ensino Fundamental. PUC, 2014.
CARVALHO, Maria Cecília Costa e Silva. Padrões numéricos e sequências. São Paulo: Moderna, 1997. 79 p.
COXFORD, A. F.; SHULTE, A. P. As ideias da álgebra. Trad. De Hygino H. Domingues. São Paulo: Atual, 1995. 285 p.
DEMO, Pedro. Pesquisa e construção de conhecimento: metodologia científica no caminho de Habermas. 3.ed. Rio de Janeiro: Tempo Brasileiro, 1996. 125 p.
FARIAS, Sandra Alves; BORTOLANZA, Ana Maria Esteves. O papel da linguagem escrita nos processos de ensino e aprendizagem: um estudo teórico. Educação & Linguagem, v. 18, n. 2, p. 63-85, 2015.
FIORENTINI, Dario. Alguns modos de ver e conceber o ensino da matemática no Brasil. Zetetiké, Campinas, ano 3, n. 4, p. 1-37, 1995.
FIORENTINI, Dario; MIORIM, Maria Ângela; MIGUEL, Antonio. Contribuição para um repensar … a educação algébrica elementar. Pro-Posições, Campinas, v. 4, n. 1 [10], p. 78-91, mar. 1993a.
_____. Ressonâncias e dissonâncias do movimento pendular entre álgebra e geometria no currículo escolar brasileiro. Zetetiké, Campinas, ano 1, n. 1, p. 19-39, mar. 1993b.
FREITAS, Maria Teresa de Assunção. Vygotsky e Bakhtin: psicologia e educação: um intertexto. 2.ed. São Paulo, Ática, 1995. 168 p.
GIARDINETTO, José Roberto Boettger. Matemática escolar e matemática da vida cotidiana. Campinas: Autores Associados, 1999. 128 p.
IMENES, L. M.; LELLIS,M. Matemática. 4 volumes. São Paulo: Scipione, 1997.
LINS, R. C.; GIMENEZ, J. Perspectivas em aritmética e álgebra para o século XXI. Campinas: Papirus, 1997. 176 p.
LINS, Rômulo Campos. O modelo teórico dos campos semânticos: uma análise epistemológica da álgebra e do pensamento algébrico. Dynamis, Blumenau, v.1, n. 7, p. 29-39, abr./jun, 1994.
LORENZATO, Sérgio; VILA Maria do Carmo. Século XXI: qual matemática é recomendável? Zetetiké, Campinas, ano 3, n.4, p. 41-49, 1993.
MACHADO, Nilson José. Matemática e língua materna: análise de uma impregnação mútua. 3.ed. São Paulo: Cortez, 1993.
MARQUES, Mario Osório. Conhecimento e modernidade em reconstrução. Ijuí: Editora UNIJUÍ, 1993. 126 p.
_____. A aprendizagem na mediação social do aprendido e da docência. 2.ed. Ijuí: Editora UNIJUÍ, 2000. 144 p.
Mestre, C. & Oliveira, H. (2011). O pensamento algébrico e a capacidade de generalização de alunos do 3.º ano de escolaridade do ensino básico. In C. Guimarães & P. Reis (Orgs.) Professores e infâncias: Estudos e experiências (pp. 201-223). São Paulo: Junqueira & Marin Editores.
NOBRE, S.; AMADO, N.; PONTE, J.P. Representações na aprendizagem de sistemas de equações. Disponível em: http://cmup.fc.pt/cmup/eiem/grupos/documents/14.Nobre_Amado_Ponte.pdf. Acesso em: 10 jan. 2014.
SELBACH, S. et al. Matemática e Didática. Petrópolis: Vozes, 2010.
SOUZA, Eliane Reame de; DINIZ, Maria Ignez de Souza Vieira. Álgebra: das variáveis às equações e funções. 2.ed. São Paulo: IME-USP, 1996. v. 5.
VALE, I.; PIMENTEL, T. Padrões e Conexões Matemáticas no Ensino Básico. Educação Matemática, n. 110, p. 33-38, 2011.
VYGOTSKY, Lev Seminovich. A formação social da mente: o desenvolvimento dos processos psicológicos superiores. 6.ed. São Paulo: Martins Fontes, 1998. 191 p.
_____. A construção do pensamento e da linguagem. Trad. De Paulo Bezerra. São Paulo: Martins Fontes, 2001. 496 p.
APÊNDICE – REFERÊNCIA DE NOTA DE RODAPÉ
7. Segundo Lins (1994), consiste em dizer pelo uso natural da linguagem cotidiana, porque se acredita que determinada frase produzida sobre uma situação-problema é verdadeira. Assim, os modos de produção de significados sobre diferentes contextos, geram justificações, que por sua vez, podem se aproximar do que entendemos que seja pensamento algébrico.
[1] Mestrando em Desenvolvimento Rural Sustentável, UNIOESTE: Universidade Estadual do Oeste do Paraná, 2020. Especialista em Matemática e Física, UNIPAR, Conclusão em 2010, Graduação em Matemática com ênfase em Física, UNIPAR, conclusão em 2007.
[2] Mestrado em Educação nas Ciências – Matemática. UNIJUI: Universidade Regional do Noroeste do Estado do Rio Grande do Sul, RS. Início: 2.001. Conclusão: 2.003. Especialização: Ensino de Ciências. FAFIG: Faculdade Estadual de Filosofia, Ciências e Letras de Guarapuava. Início: 1.987. Término: 1.988. Graduação em Matemática. UPF: Universidade de Passo Fundo, RS. Início: 1.984. Conclusão: 1.987. Graduação em Ciências 1º Grau. FACIP: Faculdade de Ciências e Pedagogia de Lages, SC. Início: 1.981. Conclusão: 1.984.
[3] Graduanda em Agronomia – UNIOESTE – Universidade Estadual do Oeste do Paraná. Graduanda de Administração – Unip – Universidade Paulista.
[4] Especialista Em Educação Matemática E Especialista Em Física Educacional.
[5] Pós-Doutor Em Ciências Ambientais.
[6] Especialização em Ensino de Ciências Exatas – Matemática, Física e Química. UNIOESTE – Universidade Estadual do Oeste do Paraná. Graduação: Ciências – Licenciatura Plena – Habilitação Matemática. UNIJUI: Universidade Regional do Noroeste do Estado do Rio Grande do Sul, RS. Graduação: Ciências – Licenciatura de 1º. Grau. UNIJUI: Universidade Regional do Noroeste do Estado do Rio Grande do Sul, RS.
Enviado: Maio, 2021.
Aprovado: Junho, 2021.
