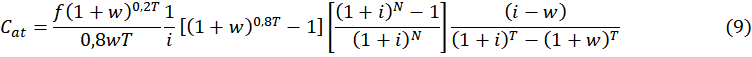ARTICLE ORIGINAL
ROCHA, Matheus Carneiro [1], ARAÚJO, Jamille Carla Oliveira [2], SANTOS, Neuma Teixeira Dos [3]
ROCHA, Matheus Carneiro. ARAÚJO, Jamille Carla Oliveira. SANTOS, Neuma Teixeira Dos. (IN) justice contributive dans le régime général de sécurité sociale : RGPS du point de vue de la science actuarielle du point de vue du revenu et du facteur actuarielle de sécurité sociale. Revista Científica Multidisciplinar Núcleo do Conhecimento. 04 année, Ed. 06, vol. 03, p. 135-161. juin 2019. ISSN: 2448-0959.
RÉSUMÉ
Les questions liées à la sécurité sociale publique ont suscité une large réduction entre la société et le gouvernement. Le citoyen moyen se soucie de la juste mesure entre ce qu’il paie dans le présent et combien il recevra de la retraite à l’avenir. Dans ce cadre, cet article vise à définir selon les fondements de la science actuarielle, la juste mesure entre la valeur des cotisations (paiements) et la valeur des prestations (retraite) gérées par le Régime général de sécurité sociale – RGPS comme un outil de justice sociale .in). La méthodologie utilisée pour obtenir tous les paramètres pertinents pour le RGPS ainsi que pour le régime actuarielle de sécurité sociale a été la création de situations impliquant des hommes et des femmes dans des conditions spécifiques d’entrée dans le système de sécurité sociale de l’âge initial, l’âge de la retraite et le salaire de cotisation et à partir de ces données d’entrée, les valeurs de cotisation et les avantages sociaux ont été calculées par le biais du programme Matlab , où les calculs ont été opérationnels comme routine de calcul. Les résultats ont été segmentés par le sexe (homme ou femme) et la fourchette de revenu, il a été observé que le taux de cotisation à la sécurité sociale, le paramètre le plus important pour définir la valeur des cotisations au RGPS, de 28% à 31% est très élevé par rapport au taux calculé par la science actuarielle de 16% à 17% pour les hommes et de 13% à 14% pour les femmes. Il est conclu que pour le citoyen ordinaire assujetti aux règles du RGPS en vigueur, les montants des cotisations versées qui reflètent les prestations de retraite reçues diffèrent de la mesure équitable, calculée par la science actuarielle, par conséquent, il n’a pas été observé des facteurs qui attestent que le RGPS est juste pour le contribuable et donc pour la société.
Mots-clés: Sécurité sociale, RGPS, actuariat.
1. INTRODUCTION
Le système de retraite public est géré par l’Institut national de la sécurité sociale (INSS) a été mis en œuvre par la loi no 8.029 du 12 avril 1990 et réglementé par le décret no 99.350 du 27 juin 1990. Il régit la question de la sécurité sociale dans le pays, qui est chargé de l’INSS de gérer et de maintenir les services de sécurité sociale issus du Système général de sécurité sociale – RGPS, en accompagnateur r. 8.213 du 24 avril 1999, encadre essentiellement les travailleurs du secteur privé et le système de sécurité sociale propre (RPPS) des fonctionnaires.
Le point fondamental de tout système de sécurité sociale est de savoir comment il sera financé, c’est-à-dire d’assurer un flux continu de ressources pour couvrir les dépenses avec des prestations administratives et des dépenses. En outre, Iyer (2002), il est nécessaire d’égaliser les flux de ressources proportionnelles à la période de cotisation et le salaire final du contribuable.
Les conditions de cotisation et le taux de cotisation apparaissent naturellement dans le domaine central des discussions en matière de sécurité sociale, puisque c’est la société dans son ensemble qui finance ce système.
La dynamique complexe des systèmes de sécurité sociale est largement discutée par Iyer (2002), qui informe que les paramètres appliqués influencent le système de sécurité sociale sont des aspects démographiques et économiques, la dynamique même du nombre de personnes de la population active, étant celui qui contribue au système et le nombre de personnes à la retraite ou qui tirent profit d’une sorte de bénéfice de ce système.
Ainsi, avec l’augmentation du nombre de pensions et de prestations d’aide sociale, ainsi que la réduction de la population économiquement active, c’est-à-dire le nombre de contribuables de la sécurité sociale, on affirme qu’elle apporte un changement significatif dans le profil démographique, qui peut conduire à l’augmentation des dépenses de sécurité sociale, à partir de 2050, à dix fois la valeur du produit intérieur brut (PIB). Ce fait, élevé pour une société à payer afin de ne pas affecter d’autres activités, impliquant des politiques publiques importantes selon Cruz, (2015).
Selon Campani et Dias da Costa (2016) les dépenses consacrées aux retraites publiques sont stratoferically élevés, selon les fonctionnaires du gouvernement est dans la maison de centaines de milliards de reais et dans un peu plus de 50 ans, les dépenses seront supérieures à 40% des recettes budgétaires de l’Union. Malgré la taille consacrée à la sécurité sociale, personne n’a débattu de la question de savoir si la valeur des cotisations versées et reçues ainsi que les taux d’actualisation appliqués sont vraiment équitables.
Pour l’analyse des systèmes de sécurité sociale. Comprendre comment les paramètres complexes et stochastiques se rapportent au fil du temps est un terme clé pour d’autres aspects des mathématiques actuarielles des systèmes de sécurité sociale (Afonso et Lima, 2011).
L’intérêt de l’auteur pour l’étude sur la justice actuarielle est devenu encore plus clair lors de la lecture des travaux de Giambiagi et Afonso (2009) qui positionne le système de sécurité sociale idéal comme actuariellement équilibré entre la valeur actuelle prévue actualisée un taux d’intérêt égal au flux de prestations reçues.
Le sujet a une pertinence sociale pour tenter de vérifier en justice s’il y a un besoin de réforme des retraites, compte tenu des changements récents liés à la non-incidence du facteur de sécurité sociale dans le temps de cotisation, établi par la nouvelle loi nº 13.183/2015, reflètent la viabilité économique et financière de la sécurité sociale.
Le nœud de cela est la question suivante: y a-t-il justice dans le système de contribution au RGPS du point de vue de la science actuarielle? Autrement dit, le revenu et le facteur actuariel appliqué peuvent déterminer la justice du souvenir contributif?
2. CADRE THÉORIQUE
2.1 FLUX DE COTISATIONS RGPS – RÉGIME GÉNÉRAL DE SÉCURITÉ SOCIALE
L’INSS (Institut national de la sécurité sociale) a été mis en œuvre par la loi no 8 029 du 12 avril 1990 et réglementée par le décret no 99.350 du 27 juin 1990. C’est à l’INSS de gérer et de maintenir les services de sécurité sociale issus du Système général de sécurité sociale – RGPS, dans le canapé accomb de la loi no 8 213 du 24 avril 1999.
Le RGPS dispose d’un important système d’avantages sociaux pour le citoyen qui est retraite par temps de cotisation (ATC). Ce système de retraite comporte trois règles, à savoir le progressif 85/95, les 30/35 ans de cotisation et la règle de la retraite proportionnelle. Comme la règle actuelle est progressive 85/95, c’est celle sur laquelle on travaillera.
La contribution au RGPS est caractérisée comme une distribution simple, où les entreprises contribuent autour de 20% et le taux restant est banc par le travailleur. La contribution au travailleur est calculée en fonction du revenu du contribuable (), où elle est grandement contribuée par le taux de cotisation (c) selon la fourchette de revenu, selon le tableau 1 disponible sur le site Web de l’INSS.
Tableau 1 – Taux de cotisation selon l’échelle salariale 2017 du RGPS.
| Salaire de contribution (R$) | Taux |
| Jusqu’à 1 659,38 | 8% |
| De 1 659,39 à 2 765,66 | 9% |
| De 2 765,67 à 5 531,31 | 11% |
Source – INSS (2019).
Ensuite, le flux de contributions ou de valeur actualisée des contributions (VPC) est calculé simplement en fonction de l’équation 1. L’accumulation de ressources favorisées par l’équation 1 est en augmentation et progressive.
2.2 FACTEUR DE SÉCURITÉ SOCIALE ET FLUX DE PRESTATIONS DANS LE RGPS
Le facteur de sécurité sociale a été institué dans le gouvernement FHC par le biais de l’amendement constitutionnel 20 en 1998. L’année suivante, par la loi 9.876, le facteur de sécurité sociale a vu le jour avec la mission de décourager les retraites anticipées, car plus le temps de cotisation est long, plus le montant de la retraite a été reçu et vice versa. L’équation 2 montre la manière de calculer le facteur de sécurité sociale (Penafieri et Afonso, 2013).
Où:
Tc : temps de contribution.
α: taux de cotisation (0,31).
Es: espérance de vie donnée par le tableau de mortalité IBGE pour les deux sexes.
Id: âge au moment de la retraite.
Par conséquent, l’équation 2 montre la relation entre trois variables importantes, le moment de la cotisation, l’âge au moment de la retraite et l’espérance de vie. En termes mathématiques, plus le temps de cotisation est long, plus le facteur de sécurité sociale est important, plus le temps et l’âge au moment de la retraite sont longs, plus le facteur de sécurité sociale est élevé et dans la direction opposée, plus l’espérance de vie est élevée, plus le facteur de sécurité sociale est faible.
La loi 9.876/99 a été complétée par le décret 3265/99 institué un changement dans le RGPS dans le calcul du flux de la retraite ou du salaire des prestations (Sb), par conséquent, le salaire sera calculé en multipliant le facteur de sécurité sociale (f) par la moyenne arithmétique réelle M des salaires de cotisation 80% plus élevés, selon l’équation 3.
L’équation 4 fait partie intégrante du calcul des prestations de retraite par temps de cotisation. L’équation signifie que la moyenne des salaires de cotisation 80 % plus élevés, Tc : représente le temps de cotisation,0,2Tc représente 20 % du temps de cotisation en raison de l’interprétation de la règle constitutionnelle de l’amendement Nº 20.
Où est la valeur du salaire de la personne dans le temps t, w0 signifie le salaire initial du contribuable, h signifie le taux de croissance de l’économie par an et g est le taux de croissance des salaires par année, les paramètres de l’équation 5 combinés expliquent la croissance progressive et exponentielle du revenu du contribuable au fil du temps.
Les paramètres importants pour le RGPS sont insérés dans l’économie comme variables exogènes au système de sécurité sociale du RGPS. L’une des variables est le salaire des contribuables, ce qui suit le modèle mathématique proposé par Gremaud et Patrick (2004); Penafieri et Afonso (2013) selon l’équation 5 et précédemment présentés dans l’équation 4.
2.3 NOTIONS DE MATHÉMATIQUES ACTUARIELLES
Filho (2010) présente les notions importantes d’hypothèses actuarielles, un paramètre important à considérer est le conseil de survie. La littérature a une série de tableaux, mais celui que l’auteur a utilisé dans l’élaboration de ce travail était la planche de survie élaborée par IBGE. L’importance principale de la commission de survie est d’obtenir l’espérance de vie et la probabilité de survie dans une coupe donnée de la table.
Les notions présentées par Afonso et Lima (2011) sont conformes à Filho (2010) concernant la notion de probabilité d’un individu dans l’âge x rester en vie jusqu’à l’âge x t ans. Cette probabilité est représentée par Px selon l’équation 6. Ix+t représente sur le tableau de survie le nombre d’individus dans la coupe qui correspond à l’âge x+t Ix, ce qui représente la quantité hypothétique d’individus dans la coupe de la table de survie à l’âge x.
De même, l’équation 6 la probabilité qu’une personne meurt en t ans peut donc être calculée la différence dans chaque cohorte d’individus qui sont morts entre les intervalles x et x-t divisé par le nombre d’individus dans la cohorte x est donnée par l’équation 7.
La lecture de l’article écrit par Afonso et Lima (2011) était importante pour ce travail, car les auteurs abordaient le thème du régime de sécurité sociale du point de vue actuariel par rapport au RGPS à l’ordre du jour du système de contribution en question. La base théorique du modèle de contribution et d’accumulation des prestations de sécurité sociale a été largement présentée dans l’article.
La figure 1 montre deux côtés distincts, la gauche représente la période contributive, c’est-à-dire que ce sont les valeurs monétaires qui sont régulièrement versées par le contribuable au système de sécurité sociale. Le côté droit représente la période de réception de la retraite étant cette période où le bénéficiaire reçoit son salaire de prestations jusqu’à son décès au cours de la période w.
Figure 1 – Flux de contributions et de flux d’avantages en fonction du temps.
Des mathématiques financières le flux contributif au fil du temps, devrait être amené à la valeur actuelle pour l’âge x se multipliant par le facteur d’escompte composé vt selon l’équation 8, où t est la période de temps et je suis le taux d’actualisation pour l’effet de calcul varie entre 1% à 3% comme suggéré dans Afonso et Lima (2011).
2.4 FACTEUR ACTUARIELLE DE SÉCURITÉ SOCIALE DANS LE RAP – RÉGIME ACTUARIAL DE SÉCURITÉ SOCIALE
L’affirmation sur la justice actuarielle a suscité l’intérêt de l’auteur, cet intérêt est devenu encore plus clair lors de la lecture de l’œuvre de Giambiagi et Afonso (2009) qui positionne le système de sécurité sociale idéal comme actuariellement équilibré entre la valeur actuelle prévue, escomptant un taux d’intérêt égal au flux de prestations reçues. Ainsi, pour un juste équilibre actuariel, il est essentiel de calculer le taux de cotisation actuarielle (Cat) basé sur l’équation 9, où f représente le facteur de sécurité sociale, w signifie le taux de progression des salaires, je suis le taux d’actualisation, T est la période de cotisation et N est la limite d’âge de la planche de survie utilisée, dans le cas de ce travail, c’est la planche IBGE 2017.
Après les études précédentes, il est devenu clair la différence substantielle entre les deux approches pour calculer le flux des contributions l’une basée sur le RGPS et l’autre basée sur la science actuarielle. Le RGPS tel qu’il est déjà présenté accumule les cotisations par le biais d’un pourcentage, sans critère actuarielle, qui met l’accent sur le revenu. L’autre actuariellement équitable comme cela a également été présenté, le facteur ou le pourcentage de multiplication est obtenu par des critères rigoureusement scientifiques basés sur les mathématiques actuarielles.
2.5 FLUX DE CONTRIBUTIONS DANS LE RAP
Les contributions selon Afonso et Lima (2011) peuvent être décrites mathématiquement par la formulation actuarielle montrée dans l’équation 10. Ainsi, le VPC signifie que la valeur actuelle des cotisations est obtenue à la valeur actuelle mise à jour par le facteur d’escompte composé donné par le produit vt par Px et multiplié par la durée de revenu donnée par CatWt, où Cat est donné par l’équation 10 et Wt est donné par l’équation 5. Le flux de contributions est décrit comme une série limitée de paiements variables temporaires immédiats.
Par conséquent, nous avons pensé à une situation hypothétique liée à la situation de la retraite par temps de cotisation à partir de quatre données sur les intrants (sexe, âge d’entrée, âge de la retraite et revenu initial), où les résultats pourraient être facilement reproduits, de sorte qu’il était possible de nourrir la discussion sur la cohérence du système RGPS et, par conséquent, la justice en versant un certain montant mensuel à l’INSS pour prendre sa retraite avec un certain montant.
2.6 VALEUR ACTUALISÉE DU FLUX DE PRESTATIONS DE RETRAITE DANS LE RAP
Le calcul du flux de prestations se traduira par le salaire de prestations, le même montant calculé par le RGPS dans l’équation 3. Le Régime actuarielle de sécurité sociale cherche à calculer, comme dans l’article d’Afonso et Lima (2011), la valeur actuelle du flux de prestations, car il aidera à interpréter le degré de distance entre les cotisations au RGPS par rapport au régime actuarial de sécurité sociale. Le calcul de la valeur actuelle du flux de prestations dans le RAP est donné par l’équation 11, où Sb est le salaire de prestations et FA est le facteur actuariel.
Le facteur actuel de l’équation 12 est obtenu par le produit entre le taux d’escompte composé Vt de l’équation 8 avec la probabilité de survie Px de l’équation 6. Par conséquent, le facteur actuel FA est donné par l’équation 11.
Sur la base de ces informations provenant du calcul de la valeur actuelle du flux d’avantages dans le RAP et du facteur actuel de l’équation 10, certaines études sur le thème présenté suivent.
3. ÉTUDES ET HYPOTHÈSES DE RECHERCHE ANTÉRIEURES
Dans cette section des travaux d’achèvement du cours est présenté selon le tableau 01, la disposition générale des œuvres qui contribuera à la vision de l’auteur et le soutien théorique.
Tableau 1 – Études principales sur le thème
| Citations | OBJECTIFS | Résultats | APPLICATIONS DANS L’ÉTUDE |
| Iyer, (2002) | Analyser et développer les mathématiques des systèmes de sécurité sociale en vue d’une formulation intégrale et différentielle. | Les mathématiques actuarielles des systèmes de sécurité sociale montrent comment les systèmes de sécurité sociale sont développés dans leurs aspects de l’équilibre actuarielle. | Les systèmes de sécurité sociale présentés dans ce travail comprennent les plus adoptés au monde, tels que le système de distribution simple (utilisé au Brésil) et le système de capitalisation directe. |
| Gilat, (2006) | Matlab with Engineering Applications est l’un des manuels standard utilisés dans les cours de génie mécanique, d’électricité et etc. | L’auteur a utilisé ce livre pour aider à la création de la routine des calculs de la sécurité sociale du système général de sécurité sociale et pour le régime actuarial de sécurité sociale, la routine de calcul est compilée dans le chapitre annexe. | Les applications Matlab comme outil de solution et de programmation. |
| Chapman, (2006) | Manuel pour les applications concept de structure de programmation dans Matlab. | La programmation de Matlab for Engineers était un autre manuel largement utilisé par l’auteur. Avec le livre de Gilat (2006), l’auteur a formé davantage pour développer les routines des calculs de sécurité sociale. | La contribution de cet auteur à ce travail a été d’élucider les concepts de la structure de décision, si – sinon – autre – fin, de juger les valeurs salariales et d’appliquer correctement les taux de cotisation au RGPS et au régime actuarielle de sécurité sociale, en détournant le flux de routine entre un chemin et l’autre. En plus de collaborer pour l’entrée de style pour les structures de répétition de fin, calculer de façon limitée la valeur des taux d’actualisation composés pour apporter les valeurs de contribution et les avantages à la valeur actuelle. |
| Giambiagi & Afonso, (2009) | Calculez ce qui serait un taux équitable d’un point de vue actuariel. | La principale conclusion des auteurs est que le taux de sécurité sociale en vigueur appliqué au RGPS de 31% est excessif pour certains groupes de revenus. C’est à travers ce travail que l’auteur a élaboré le thème de la justice dans le RGPS du point de vue des contributions et des avantages reçus par les utilisateurs. | Le calcul du taux de cotisation actuariellement équilibré à la sécurité sociale : une demande dans le cas brésilien, est un article de publication du professeur Giambiagi, est l’un des grands chercheurs des questions de sécurité sociale au Brésil. |
| Gonçalves & Letieri, (2010) | Cotisations de sécurité sociale : Analyse des états financiers des municipalités de Pernambuco en vue de la responsabilisation. | Il s’agissait d’un travail d’achèvement des cours consulté par l’auteur, dont l’importance était la description des systèmes de sécurité sociale à régime fermé. | Les fondements théoriques et les lois de sécurité sociale mentionnés dans cette étude ont été largement consultés, pour cette raison l’auteur a utilisé cette publication comme référence. |
| Plamondon, et al., (2011) | Décrire et analyser les questions macroéconomiques qui influencent la dynamique du flux de contributions et d’avantages sociaux. | La principale conclusion des auteurs était la relation positive entre le taux de progression des salaires, le niveau de développement économique et le taux d’actualisation composé. | Pratique actuarielle de la sécurité sociale, ce travail a eu un impact sur l’étude de la sécurité sociale du point de vue actuarielle. |
| Afonso & Lima, (2011) | Relier les aspects des mathématiques actuarielles, car il s’agit de risque biométrique et de réduction composée. | Elle a conclu que, en maintenant des facteurs biométriques et macroéconomiques, le revenu influe fortement sur le profil contributif de l’individu lié au RGPS. | Analyse des aspects distributifs de la retraite par temps de cotisation de l’INSS avec l’emploi des mathématiques actuarielles, |
| Lima, Wilbert, Pereira, & Paulo, (2012) | Étudier le facteur de sécurité sociale, l’un des principaux paramètres pour calculer le montant des prestations qui recevront pour le temps de cotisation. | La principale conclusion de ce travail est la corrélation positive entre le facteur de sécurité sociale et le montant des ressources que le gouvernement fédéral a déjà économisés dans les coffres publics depuis le jour où le facteur de sécurité sociale sur les pensions accordées est entré en vigueur. | L’impact du facteur de sécurité sociale sur le grand nombre de la sécurité sociale, cet article cite Afonso et Lima (2011). |
| Penafieri & Afonso, (2013) | Créer un facteur actuariellement équitable de sécurité sociale (FPAJ) qui est moins « punitif » pour les retraites anticipées. | Les auteurs enquêtent sur la justice actuarielle du facteur sécurité sociale sur les cotisations du RGPS. Les auteurs ont conclu que le facteur de sécurité sociale réduit la valeur de l’avantage des contribuables bien au-delà des valeurs d’équilibre actuarielle. Les auteurs se substituent au facteur actuel de sécurité sociale. | Discuter de la justice sociale est une question importante et très débattue, car elle est un facteur d’équilibre social, d’où son importance. |
Source: Préparé par les auteurs (2019).
La dynamique complexe des systèmes de sécurité sociale est largement discutée par (Iyer, 2002); Gremaud et Patrick (2004). Selon ces auteurs, les paramètres qui influencent le système de sécurité sociale peuvent être modélisés en adoptant les hypothèses suivantes :
H1 : Le contribuable n’est pas au chômage pendant la période contributive, c’est-à-dire que son revenu est caractérisé comme une fonction continue.
H2 : Les valeurs des paramètres économiques sont considérées comme constantes tout au long de la période contributive.
H3 : Les pensions en question sont exclusivement pour le temps de cotisation, ne sont pas considérées comme des retraites en raison de la maladie, de l’invalidité et du décès.
L’objectif du travail n’inclut pas l’évaluation précise de l’effet du taux de croissance économique, de l’inflation réelle et du taux de progression des salaires qui différencient les professions, l’éducation et etc. L’auteur a adopté des valeurs autour des valeurs moyennes utilisées dans l’œuvre de Gremaud et Patrick (2004), en outre, il devient impossible de prédire comment les paramètres économiques se comporteront au fil des décennies.
Ainsi, à partir de ces études, il a été possible de construire les analyses, les discussions et la méthodologie du présent dans l’œuvre. Par conséquent, la section suivante à présenter est la méthodologie, cela commence par une brève histoire du RGPS, puis sera présenté la théorie actuarielle pour l’élaboration de concepts importants sur la justice dans les cotisations aux prestations, le prochain sujet abordera les routines de calculs développés par la ressource computationnelle et ses implications dans le calcul de la sécurité sociale.
4. MÉTHODOLOGIE
L’étape initiale de la phase méthodologique, en plus de l’étude précédente présentée dans le chapitre de l’examen de la littérature, est la structuration de la ressource computationnelle qui a été utilisée. Le programme utilisé dans ce travail était Matlab.
Le programme de simulation de MATLAB a été développé et structuré pour demander à l’utilisateur quatre informations : le sexe de la personne (homme ou femme), l’âge initial, l’âge de la retraite et le salaire ou le revenu initial d’entrée dans le système de sécurité sociale.
Certaines hypothèses simplificantes ont été prises en compte : les cotisations sont initerruptas, sans tenir compte des effets de l’impôt sur le revenu et de l’inflation sur le calcul des cotisations et des recettes des prestations. La figure 02 affiche l’écran d’insertion des données d’entrée directement sur l’écran de commande lorsque le programme est en cours d’exécution.
Sur la base d’Afonso et Lima (2011) et Giambiagi et Afonso (2009), six événements de simulation des calculs de la sécurité sociale ont été développés groupés par sexe, trois variations pour les hommes et trois variations pour les femmes. Tous les paramètres de simulation étaient les mêmes pour les deux sexes, à l’exception du revenu (1 200, 2 500 et 5 000).
Figure 2 – Écran rapide de commande Matlab avec les entrées de données initiales pour les calculs de simulation.

À partir de ces quatre renseignements sur les entrées, comme l’illustre déjà la figure 2, les calculs du SGPS et du régime actuariel de sécurité sociale sont effectués de façon séquentielle selon le programme ou la routine de calcul.
Le prochain chapitre sera les résultats et les discussions, dans ce chapitre sera montré les tableaux et les graphiques impliquant les équations présentées dans la méthodologie, ainsi que sera présenté les mathématiques de la RGPS pour les calculs de la contribution et la retraite par rapport aux calculs du système de sécurité sociale, selon les préceptes de la science actuarielle.
5. RÉSULTATS ET DISCUSSIONS
5.1 PARAMÈTRES ET CONSTANTES D’ENTRÉE
La routine des calculs de sécurité sociale est structurée dans l’entrée et la sortie des données, tout comme le comportement des fonctions mathématiques, la routine fonctionne à partir des constantes précédemment configurées, modifiant ainsi les données d’entrée si vous modifiez les données de sortie.
Le tableau 1 présente la saisie des données et les constantes pour les calculs de la sécurité sociale du RGPS et du Régime actuariel de pension, tous deux calculés de façon séquentielle selon la routine écrite dans le Matlab disponible à l’Annexe de ce travail.
Les constantes ont été supposées comme des valeurs moyennes pour quelle que soit la situation initiale. Sans aucun doute, les constantes sont la partie cruciale de l’œuvre ainsi que la partie la plus compliquée de justifier ses valeurs adoptées, donc les valeurs adoptées peuvent être justifiées selon les œuvres de Giambiagi et Afonso (2009); Plamondon, et coll.(2011); Gremaud et Patrick (2004) et Afonso et Lima (2011) pour valoriser les chiffres macroéconomiques : taux de croissance, taux d’actualisation, taux de progression des salaires.
Les valeurs des paramètres d’entrée et les valeurs des constantes sont présentées selon le tableau 2.
Tableau 2 – Entrée et paramètres constants de sécurité sociale.
| Données d’entrée | Constantes | ||
| Age d’entrée (Femme) | 30 ans | Taux de croissance économique | 1% par an |
| Age d’entrée (Homme) | Taux d’actualisation | 6% par an | |
| Age de la retraite (femme) | 60 ans | ||
| Age de la retraite (Homme) | 65 ans | ||
| Salaire de départ (les deux) | R$ 1.200,00 | Taux de progression des salaires | 0,25% par an |
| R$ 2.500,00 | 0,5 % par an | ||
| R$ 5 000,00 | 1,2 % par an | ||
Source – Préparé par les auteurs.
Les données de l’âge d’entrée et de sortie ont été sélectionnées selon les règles de retraite selon le temps de cotisation selon l’insss. Le salaire initial a été défini à trois niveaux pour les deux sexes, parce que l’important ici est de tester la justice actuarielle dans les mêmes circonstances macroéconomiques, en ne variant que le facteur biométrique (sexe), l’âge d’entrée et de retraite et le salaire initial qui caractérise, en termes généraux, la classe de l’individu dans les basses (1 200,00 $), la moyenne (2 500 $R) et la haute (5 000 $R).
5.2 COTISATIONS DE SÉCURITÉ SOCIALE AU RGPS
Le tableau 3 montre les flux de cotisation moyens découlant des calculs de la sécurité sociale du RGPS en fonction de l’âge de la retraite, de l’âge d’entrée et du revenu initial. La valeur moyenne des cotisations entre les niveaux de salaire entre personnes de même sexe, en raison de la différence de revenu initiale.
Tableau 3 – Contributions moyennes par sexe et revenu initial versés par les contribuables au SPRR.
| Homme | ||||
| L’âge de la retraite | Age d’entrée | Revenu initial (R$/mois) | Contributions moyennes
(R$/mois) |
Total cumulatif (R$) |
| 65 ans | 30 ans | 1.200,00 | 122,00 | 52.703,68 |
| 30 ans | 2.500,00 | 300,58 | 129.850,26 | |
| 30 ans | 5.000,00 | 848,02 | 366.342,67 | |
| Femme | ||||
| L’âge de la retraite | Age d’entrée | Revenu initial (R$/mois) | Contributions moyennes
(R$/mois) |
Total cumulatif (R$) |
| 60 ans | 30 ans | 1.200,00 | 117,99 | 43.891,86 |
| 30 ans | 2.500,00 | 288,61 | 107.363,77 | |
| 30 ans | 5.000,00 | 797,28 | 296.587,50 | |
Source – Préparé par les auteurs.
Le total cumulatif diffère considérablement d’un homme à l’autre en raison du délai de cotisation étant plus court dans le cas des femmes, puisqu’elles prennent leur retraite 5 ans plus tôt par rapport aux hommes. Il n’a pas été observé l’application de concepts actuariels dans les contributions au RGPS, qui selon Penafieri et Afonso (2013) représente un déséquilibre actuariel compromettant la justice des contributions au RGPS.
5.3 FACTEUR DE SÉCURITÉ SOCIALE
Le calcul du facteur de sécurité sociale a été effectué selon l’équation 2. Lorsque les calculs ont été effectués selon les lignes directrices déjà présentées dans la méthodologie du RGPS, remplissant les conditions nécessaires à la retraite par le temps de cotisation, le facteur sécurité sociale n’agira pas comme une réduction de la valeur de la prestation de retraite reçue par le contribuable, d’autre part si le contribuable prend sa retraite avant que les conditions légales et nécessaires ne soient remplies, le facteur de sécurité sociale réduira la valeur de la prestation de retraite.
Le revenu initial n’influe pas sur la valeur du facteur de sécurité sociale, comme le suggère le tableau 4. La différence de valeur pour les hommes égales à 1.0000 et pour les femmes égales à 0.6561 est due à la réduction du temps de cotisation de 5 ans pour les femmes et aussi par les différences biométriques, puisque les hommes ont une espérance de vie plus faible par rapport aux femmes, selon le plan de survie de IBGE 2017.
Tableau 4 – Facteur de sécurité sociale segmenté par sexe.
| Homme | ||
| L’âge de la retraite | Age d’entrée | Facteur de sécurité sociale |
| 65 ans | 30 ans | 1,0000 |
| Femme | ||
| L’âge de la retraite | Age d’entrée | Facteur de sécurité sociale |
| 60 ans | 30 ans | 0,6561 |
Source – Préparé par les auteurs.
Dans la pratique, la réduction du facteur sécurité sociale a été prévue pour les femmes dans le RGPS comme un moyen d’imprégner une plus grande équité entre les sexes, selon Penafieri et Afonso (2013), mais certains ne sont pas d’accord avec cela, selon Afonso et Lima (2011), le facteur de sécurité sociale plus faible punit les femmes aggrave encore les différences historiques de revenus entre les hommes et les femmes. Il est salutaire de revoir que le facteur de sécurité sociale a été partiellement élaboré sur la base de critères biométriques, car il prend en compte l’espérance de vie telle que divulguée par l’IBGE, bien que le facteur controversé de la sécurité sociale décourage les retraites anticipées et équilibre l’espérance de vie plus longue des femmes avec l’espérance de vie plus courte des hommes.
5.4 PRESTATIONS DE SÉCURITÉ SOCIALE RGPS
Les résultats des calculs des avantages selon les paramètres du tableau 2, générés à partir de l’équation 3, les résultats présentés selon le tableau 5.
Tableau 5 – Flux de prestations RGPS aux contribuables, séparés par sexe et revenu initial.
| Homme | |||
| L’âge de la retraite | Age d’entrée | Revenu initial (R$/mois) | Avantages
(R$/mois) |
| 65 ans | 30 ans | 1.200,00 | 1.568,19 |
| 2.500,00 | 3.450,88 | ||
| 5.000,00 | 8.062,30 | ||
| Femme | |||
| L’âge de la retraite | Age d’entrée | Revenu initial (R$/mois) | Avantages
(R$/mois) |
| 60 ans | 30 ans | 1.200,00 | 989,68 |
| 2.500,00 | 2.160,28 | ||
| 5.000,00 | 4.931,19 | ||
Source – Préparé par les auteurs.
Il est important de noter que les hommes recevront une valeur de prestation de retraite plus élevée que leur propre revenu initial, en rappelant que le revenu initial augmentera à la suite de l’équation 5. Dans le cas des femmes, elles recevront moins de prestations de retraite qu’elles n’ont commencé à cotiser au RGPS. La différence entre le comportement des prestations versées aux hommes et aux femmes est due au facteur de sécurité sociale, car selon le tableau 4, les hommes ont un facteur de sécurité sociale égal à 1.0000 et les femmes égales à 0.6561.
En raison de ce qui a été exposé, le comportement des cotisations au RGPS ne suggère pas de suivre les préceptes actuariels, parce que la contribution est calculée en multipliant le revenu du contribuable avec des pourcentages selon le tableau 1. En ce qui concerne les prestations versées aux retraités par le RGPS, il existe des preuves de la présence de concepts de sciences actuarielles, en cherchant dans l’équilibre de thèse et la justice entre les contribuables masculins et féminins compte tenu de leurs caractéristiques biométriques cristallisées dans le conseil de survie de l’IBGE 2017.
Les questions de cotisation sont sensibles à l’opinion publique autant que les prestations reçues par le temps de cotisation, parce qu’elles influencent la qualité de vie du contribuable au moment délicat de la vie, lorsque les années facturent les jours des jeunes, par conséquent, la perte de la capacité de travail a une incidence directe sur le revenu de la personne.
5.5 Le RGPS COMPARED À L’ACTUARIAL SOCIAL SECURITY REGIME
Cette section est consacrée au comportement des valeurs de la sécurité sociale du point de vue de la science actuarielle et se compare aux valeurs de sécurité sociale du RGPS montrées dans la section précédente.
Les contributions du point de vue de la science actuarielle sont présentées selon le tableau 6 de la dernière colonne.
Tableau 6 – Différence entre les contributions au RGPS pour l’actuarielle séparée par les sexes.
| Homme | ||||
| L’âge de la retraite | Age d’entrée | Revenu initial (R$/mois) | Contributions moyennes – RGPS
(R$/mois) |
Contribution moyenne actuarielle (R$) |
| 65 ans | 30 ans | 1.200,00 | 122,00 | 88,43 |
| 30 ans | 2.500,00 | 300,58 | 206,47 | |
| 30 ans | 5.000,00 | 848,02 | 483,74 | |
| Femme | ||||
| L’âge de la retraite | Age d’entrée | Revenu initial (R$/mois) | Contributions moyennes – RGPS
(R$/mois) |
Contribution moyenne actuarielle (R$) |
| 60 ans | 30 ans | 1.200,00 | 117,99 | 87,30 |
| 30 ans | 2.500,00 | 288,61 | 190,92 | |
| 30 ans | 5.000,00 | 797,28 | 438,19 | |
Source – Préparé par les auteurs.
Il est évident que l’augmentation de la moyenne des valeurs de cotisation à mesure que le revenu de cotisation initial augmente tant pour le SPRR que pour le régime actuariel, il est également clair la différence substantielle entre la moyenne des cotisations au RGPS pour l’actuariat. La différence considérable entre les contributions est le résultat des fondations postulées par la science actuarielle, où le taux de cotisation est nettement inférieur, selon le tableau 6, par rapport au taux RGPS.
Tableau 6 – Taux de cotisation au RGPS par rapport au taux du régime actuarial de sécurité sociale.
| Salaire de contribution (R$) | Taux | Tarif général : travailleur et entreprise | Homme de taux actuarielle | Taux actuarielle Femmes |
| Jusqu’à 1 659,38 | 8% | 8%+20% = 28% | 16% | 13% |
| De 1 659,39 à 2 765,66 | 9% | 9%+20% = 29% | 17% | 14% |
| De 2 765,67 à 5 531,31 | 11% | 11%+20% = 31% | 17% | 14% |
Source – Préparé par les auteurs.
Il est évident que, selon le tableau 6, le taux actuariel est plus faible dans les deux sexes et dans les fourchettes de revenu initiale que les taux du RGPS. Giambiagi et Afonso (2009) sont arrivés à la même conclusion.
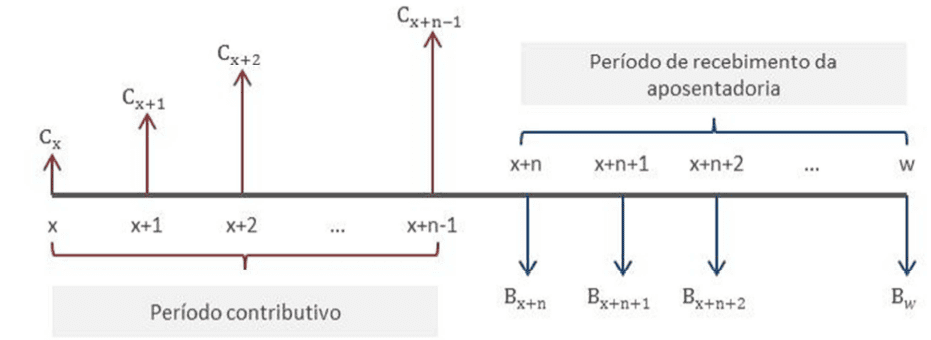
Le système de contribution au RGPS est très différent du Régime actuariel sous tous ses aspects, ce qui est évident lorsque l’on perçoit les valeurs de contribution accumulées au fil des ans. Le premier chiffre montre la relation entre les contributions au RGPS et le Régime de contribution actuarielle. Le comportement des courbes est clairement divergent, où le RGPS tend à toujours augmenter ses valeurs de contribution au fur et à mesure que le temps progresse, en face de cela, le régime actuariel montre que les valeurs de contribution diminuent. De plus, un aspect important est possible à l’intersection entre les deux graphiques, où, dès l’âge de 11 ans, le régime de cotisation actuarielle devient plus avantageux financièrement pour le contribuable par rapport au RGPS.
Figure 1 – Contribution au RGPS des systèmes de sécurité sociale et au régime actuarial de sécurité sociale en fonction du temps pour les hommes dont le revenu initial est de 1 200,00 R$
Le comportement divergent des courbes de la figure 1 est justifié par l’absence de considérations biométriques dans le système d’accumulation du RGPS, dans lequel, dans le régime actuariel de contribution, il est évident la présence d’hypothèses actuarielles, parce que la tendance est de diminuer la probabilité de survie du contribuable au fil du temps, tel que présenté dans le Cadre théorique.
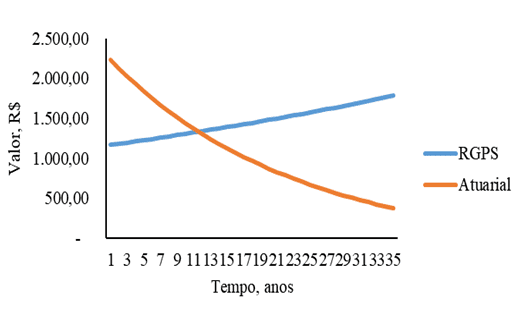
La figure de comportement similaire 1 peut être indiquée dans la figure 2. À la figure 2, le revenu de cotisation initial de la femme s’élève à une valeur proche de 2 000 $R et finit par atteindre 500 $R près de la 30e année de cotisation et les femmes dans la figure 2, toutefois, la différence réside dans la contribution actuarielle totale qui est plus élevée, en observant que la 1ère année de cotisation à la valeur totale se situe entre 2 000 $R et 2 500 $R près du point médian des deux valeurs (R$ 2 250,00).
Figure 2 – Contribution au RGPS des systèmes de sécurité sociale et au régime actuarial de sécurité sociale en fonction du temps pour les femmes dont le revenu initial est de 1 200,00 R$
Une autre différence réside dans la figure 1 par rapport à la figure 2, c’est dans le moment de l’intersection entre les deux courbes, dans le graphique 1, l’intersection est proche des 11 années de contribution, au cours desquelles, dans le graphique 2, est proche de 9 ans.
La différence de temps de contribution actuarielle des chiffres 1 et 2 suit également la même logique que les graphiques 3 et 4. Le revenu initial de 2 500,00 R$ hommes et femmes suit les mêmes caractéristiques de la courbe actuarielle des chiffres 1 et 2. Ci-dessous la figure 3.
Figure 3 – Contribution au RGPS des systèmes de sécurité sociale et au régime actuarial de sécurité sociale en fonction du temps pour les hommes dont le revenu initial est de 2 500,00 $R.
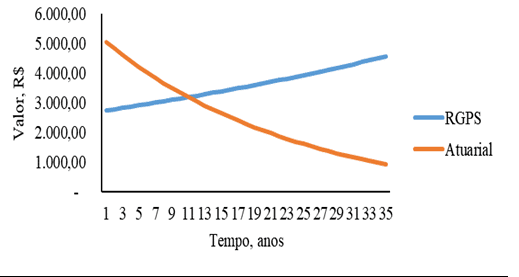
[/caption]La différence réside dans les cotisations totales, puisque plus le revenu initial sera élevé, car les hommes ont une espérance de vie plus faible et prennent leur retraite plus tard, de sorte que les chiffres 1, 2, 3 et 4 montrent que les hommes dans le système actuariel contribuent des valeurs plus élevées chaque année par rapport aux femmes.
Figure 4 – Contribution au RGPS des systèmes de sécurité sociale et au régime actuarial de sécurité sociale en fonction du temps pour les femmes dont le revenu initial est de 2 500 ,00 $R.
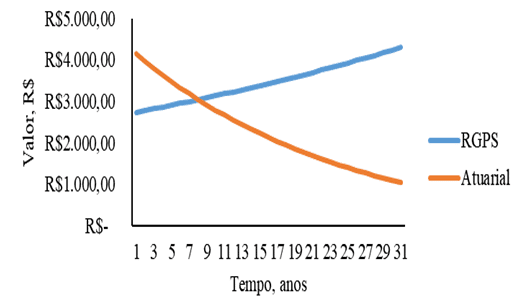
[/caption] Les chiffres 5 et 6 ont un comportement similaire aux autres chiffres, mais l’échelle salariale initiale est de 5 000 $R pour les deux sexes dans les chiffres 5 et 6.
L’effet du revenu initial sur les cotisations aturais montre que plus le revenu initial est élevé, plus les cotisations actuarielles sont élevées. Les hommes qui cotisent 5 000 $R contribuent un peu plus de 10 000 $R la première année, la contribution totale des femmes un peu moins de 10 000 $R la première année.
Figure 5 – Contribution au RGPS des systèmes de sécurité sociale et au régime actuarial de sécurité sociale en fonction du temps pour les hommes dont le revenu initial est de 5 000 $R.
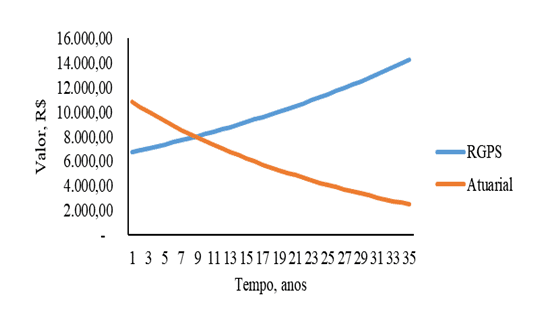
En ce qui concerne le comportement du point d’intersection entre le système contributif du RGPS et l’actuariat dans les chiffres 5 et 6, figure 5 des hommes la valeur de l’intersection est proche de 9 ans et combien celle des femmes figure 6 est proche de 5 ans. Cette divergence dans le comportement du point d’intersection peut être justifiée étant donné les caractéristiques actuarielles entre les hommes et les femmes.
L’homme représenté à la figure 5 diffère des hommes représentés dans les chiffres 1 et 3, en raison des caractéristiques macroéconomiques qui reflètent la contribution et le temps pour le système de contribution devient avantageux par rapport à la RGPS. Toutefois, lorsque les chiffres 5 et 3 n’ont pas beaucoup de différence dans le temps d’intersection des revenus initiaux de 2 500 $R et de 5 000 $R, la différence devient plus évidente au moment de l’intersection à mesure que le revenu augmente. Cela donne à penser que plus le revenu de la personne est élevé quel que soit le sexe, moins il compensera le RGPS
Figure 6 – Contribution au RGPS des systèmes de sécurité sociale et au régime actuarial de sécurité sociale en fonction du temps pour les femmes dont le revenu initial est de 5 000 $R.
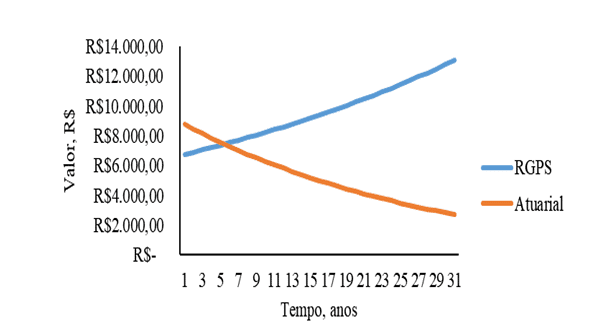
[/caption]
La figure 6 correspond au graphique des femmes dont le revenu initial est de 5 000 $R. En observant ce graphique, il est évident que le système actuariel pour les femmes de l’ordre de 5 000 $R intercepte le graphique avec le RGPS dans un délai proche de 5 ans, c’est le plus bas thème d’interception entre les courbes démontrée dans tous les chiffres de 1 à 5. Par conséquent, pour les femmes qui gagnent un revenu initial de 5 000 $R de la période de cotisation de cinq ans, le système de cotisation actuarielle est plus avantageux par rapport au RGPS.
Les graphiques indiquent la même tendance, la contribution au RGPS est en opposition au régime actuariel, dans les cas où il y avait un comportement particulier, les contributions au RGPS commencent à un niveau inférieur par rapport à l’actuariat, que le temps passe les contributions à la RGPS augmente, tandis que les contributions au régime actuariel diminuent. Ce comportement est justifié compte tenu des caractéristiques de chaque système particulier.
En plus des contributions étant plus élevées dans le RGPS, ce comportement d’élévation devient évident à partir du point d’intersection des deux courbes dans les graphiques 1 à 6. Il est suggéré qu’après les 6 années de cotisation, le RGPS cesse d’être avantageux et devient beaucoup plus lourd pour le contribuable par rapport au régime actuarial de sécurité sociale.
Figure 7 – Courbe des facteurs actuariels pour les hommes et les femmes en fonction du temps.
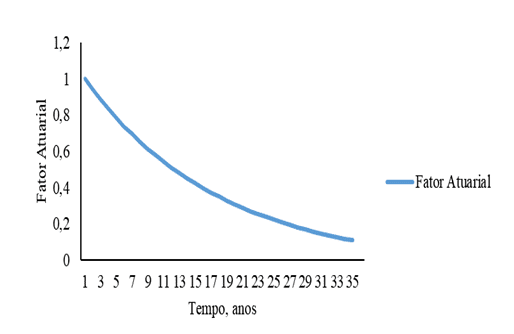
[/caption]Dans le RGPS à mesure que le revenu augmente au fil du temps, les cotisations augmentent également en raison de l’équation 1. Contrairement au RGPS, le Régime actuariel se désintègre de la valeur des cotisations en raison du facteur actuariel, diminuant en fonction du temps selon la figure 7 de l’équation 11. Cette diminution est influencée par la probabilité de diminution de survie, comme l’équation 6 et le taux d’actualisation diminuent également, l’équation 8.
6. CONCLUSION
Des études antérieures ont été menées pour comprendre comment les paramètres de la sécurité sociale sont calculés dans la pratique, la base pour le calcul du RGPS pour la retraite par le temps de cotisation, les valeurs de cotisation au RGPS, le facteur de sécurité sociale et le salaire des prestations.
La deuxième étape a été l’étude de la théorie actuarielle sur les conseils de survie et les mathématiques actuarielles. La troisième étape a été d’opérationnaliser les calculs des valeurs théoriques et pratiques par l’intermédiaire de Matlab, un programme informatique, et une comparaison ultérieure des résultats obtenus.
Dans la troisième étape, comme nous l’avons déjà mentionné, un code de programmation structuré a été élaboré à Matlab, où le système de sécurité sociale du monde réel et du monde actuariel a été calculé, à commencer par quatre variables d’entrée (homme ou femme, âge d’entrée, âge de la retraite et revenu initial). Les calculs ont été répétés six fois plus que les suivants, trois fois pour les hommes tous ayant le même âge d’entrée 30 ans, avec le même âge de la retraite 65 ans, cependant avec des revenus différents (1 200, 2 500, 5 000). La même procédure a été répétée pour les femmes ne différant qu’à l’âge de la retraite 60 ans.
La grande question à laquelle ce travail de conclusion de cours a cherché à répondre avec un effort absolu dans les trois étapes était la suivante : « Y a-t-il justice dans le système de contribution au RGPS du point de vue de la science actuarielle? Autrement dit, le revenu et le facteur actuariel appliqué peuvent déterminer la justice du souvenir contributif? ”
Il est conclu que le RGPS n’est pas juste pour répondre à la première partie de la question, parce que du point de vue de la science actuarielle qui cherche l’équilibre, le comportement des courbes de contribution du RGPS et du Régime actuarielle de pension présentent une tendance et des valeurs très distinctes, puisque la tendance de la courbe de contribution du RGPS est une augmentation progressive, d’autre part , la courbe du régime actuariel tend à diminuer progressive.
Ces travaux confirment, comme l’ont confirmé Giambiagi et Afonso (2009), le taux de sécurité sociale facturé par l’INSS par le biais du RGPS est trop élevé, où l’augmentation continue de la contribution met la pression sur la poche du contribuable âgé principalement au cours des dernières années de cotisation. L’effet inverse a été démontré par le Régime de pensions actuarielles.
Répondant maintenant à la deuxième et dernière partie de la question, il y a des éléments de preuve qu’il est possible de déterminer le juge des souvenirs contributifs du point de vue de la justice actuarielle, parce que le facteur actuariel qui aura une incidence sur le revenu de cotisation est obtenu par des fonctions biométriques fondées sur la science actuarielle.
Le RGPS calcule la valeur des cotisations au moyen d’un pourcentage qui se concentrera sur le revenu, sans informer l’entreprise de la façon dont elle a atteint un tel pourcentage et à quel point elle peut être équitable non seulement pour le contribuable, mais aussi pour l’institution qui paie. Toutefois, parce que le revenu mensuel de retraite présumait la même chose tant pour le RGPS que pour le Régime actuarial de pension, il y a beaucoup plus de contribue au RGPS par rapport à l’actuariat.
Les valeurs des cotisations et des prestations diffèrent entre le même sexe en raison du revenu initial, ce qui influence le taux de progression des salaires et le taux de cotisation, ce qui a entraîné une augmentation du montant de la contribution versée au RGPS. Dans la comparaison intergender, il y avait une différence substantielle, parce que les femmes prennent leur retraite plus tôt et ont une espérance de vie plus longue, selon la planche de survie, déterminant un montant inférieur à payer en cotisation au système de sécurité sociale, en revanche, ils reçoivent moins de prestations de retraite par rapport aux hommes.
La question de la sécurité sociale n’est pas épuisée, car le sujet est vaste et d’un grand intérêt pour la société. Compte tenu de cela, afin d’élargir les discussions, par conséquent, comme des suggestions pour des travaux futurs sont proposées l’analyse des raisons qui génèrent le déséquilibre actuariel dans le RGPS, une autre suggestion est de comparer les plans de sécurité sociale offerts sur le marché qui peuvent aborder les critères actuariels, une autre suggestion est de travailler sur la construction d’une application computationnelle visant à l’enseignement de la science actuarielle.
7. RÉFÉRENCES
- Afonso, L. E., & Lima, D. d. . Uma Análise dos Aspectos Distributivos da Aposentadoria por Tempo de Contribuição do INSS com o Emprego de Matemática Atuarial. Revista Gestão & Políticas Públicas, pp. p. 7-33.2011.
- Chapman, S. J. Programação em Matlab para Engenheiros. São Paulo: Thomson.2006.
- Filho, A. C. (2010). Cálculo Atuarial Aplicado (2ª ed.). São Paulo: Atlas.
- Giambiagi, F., & Afonso, L. E. Cálculo da Alíquota de Contribuição Previdenciária Atuarialmente Equilibrada: Um Aplicação ao Caso Brasileiro. rbe, v. 63, pp. p. 153-179.2009
- Gilat, A. Matlab com Aplicações em Engenharia (2ª ed.). Porto Alegre: Bookman.2006.
- Gonçalves, & Letieri, V. . Contribuições Previdenciárias: Uma análise nas Demonstrações Contábeis de Prefeituras de Municípios Pernambucanos com Vistas à Accountability. Universidade Federal de Pernambuco (Dissertação de Mestrado), p. 113. Recife, PE.2010.
- Gremaud, R. F., & Patrick, A. Regime de Previdência dos Servidores Públicos: Equilíbrio Financeiro e Justiça. p. 19.2004.
- HEITOR CAMPANI, C., & DIAS DA COSTA, T. R. Pensando na aposentadoria: PGBL, VGBL e autoprevidência. Universidade Federal do Rio de Janeiro. Rio de Janeiro: COPPEAD. doi:1518-3335.2016.
- IBGE. (s.d.). Acesso em 21/10/2018 de Outubro de 2018, disponível em http://sa.previdencia.gov.br/site/2016/07/TABUASDEMORTALIDADEIBGE2014_EXTRAPOLADAS.xls
- Iyer, S. Matemática Atuarial de Sistemas de Previdência Social (Vol. v. 16). Brasília, DF: Ministério da Previdência e Assitência Social.2002.
- Lima, D. V., Wilbert, M. D., Pereira, J. M., & Paulo, E. O Impacto do Fator Previdenciário nos Grandes Números da Previdência Social. Revista de Contabilidade & Finanças – USP, v. 23(n. 59), pp. p. 128-141.2012.
- COSTA, Raimundo Nonato Vieira, ARAUJO, Jamille Carla Oliveira, SILVA, Leidian Moura da Nascer, Crescer e Sobreviver: Uma Análise das Modalidades de Aposentadoria da Previdência Privada sob os Planos PGBL e VGBL. (2018). XV Congresso USP de Iniciação Científica em Contabilidade, (p. p. 20). São Paulo.
- Penafieri, A. C., & Afonso, L. E. . O Impacto da Mudança da Regra de Cálculo das Aposentadorias por Tempo de Contribuição do INSS: o Fator Previdenciário é Atuarialmente Justo? Economia Apicada, v. 17, 2013. pp. p. 667-694..
- Plamondon, P., et. al.. (2011). Prática Atuarial na Previdência Social (Vol. v. 33). (S. d. Brasil, Trad.) Brasília, DF, Brasil. 2011.
- Rodrigues, J. A. . Gestão de Risco Atuarial. São Paulo: Saraiva. 2008.
[1] Maîtrise en génie mécanique (UFPA); Diplôme en génie mécanique (UFPA); Diplôme en sciences comptables (UFRA)
[2] Master en administration des affaires, MBA Comptabilité, expertise, audit et contrôle, Baccalauréat en Comptabilité
[3] Doctorant en éducation en sciences et mathématiques; Maîtrise en génie électrique; Spécialisation en éducation environnementale et durabilité; Baccalauréat en mathématiques.
Soumis : mai 2019.
Approuvé : juin 2019.