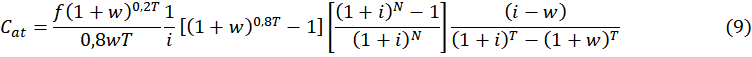ORIGINAL-ARTIKEL
ROCHA, Matheus Carneiro [1], ARAÚJO, Jamille Carla Oliveira [2], SANTOS, Neuma Teixeira Dos [3]
ROCHA, Matheus Carneiro. ARAÚJO, Jamille Carla Oliveira. SANTOS, Neuma Teixeira Dos. (IN) beitragsabhängige Justiz im allgemeinen System der sozialen Sicherheit: RGPS unter dem Gesichtspunkt der versicherungsmathematischen Wissenschaft unter dem Gesichtspunkt des Einkommens und des faktors der versicherungsmathematischen sozialen Sicherheit. Revista Científica Multidisciplinar Núcleo do Conhecimento. 04-Jahr, Ed. 06, Band 03, S. 135-161. Juni 2019. ISSN: 2448-0959.
ZUSAMMENFASSUNG
Fragen im Zusammenhang mit der öffentlichen sozialen Sicherheit haben zu einer breiten Debatte zwischen Gesellschaft und Regierung geführt. Der Durchschnittsbürger kümmert sich um die gerechte Maßnahme zwischen dem, was er in der Gegenwart zahlt, und dem, was er in Zukunft aus der Rente erhalten wird. Vor diesem Stellenziel zielt dieser Artikel darauf ab, nach den Grundlagen der versicherungsmathematischen Wissenschaft die gerechte Maßnahme zwischen dem Wert der Beiträge (Zahlungen) und dem Wert der Leistungen (Ruhestand) zu definieren, die vom Allgemeinen System der sozialen Sicherheit verwaltet werden – RGPS als Instrument der sozialen (In-)Justiz. Die Methode, die verwendet wurde, um alle Parameter zu erhalten, die für das RGPS sowie für das versicherungsmathematische System der sozialen Sicherheit relevant sind, war die Schaffung von Situationen, in denen Männer und Frauen unter bestimmten Bedingungen des Eintritts in das System der sozialen Sicherheit mit dem Anfangsalter, dem Rentenalter und dem Beitragsgehalt beteiligt waren, und aus diesen Inputdaten wurden die Beitragswerte und Leistungen im Rahmen des Matlab-Programms berechnet. , wobei Berechnungen als Berechnungsroutine operationalisiert wurden. Die Ergebnisse waren nach Geschlecht (männlich oder weiblich) und Einkommensbereich segmentiert, es wurde beobachtet, dass der Beitragssatz der sozialen Sicherheit, der wichtigste Parameter zur Definition des Wertes der Beiträge zum RGPS, von 28 % bis 31 % im Vergleich zu der von der versicherungsmathematischen Wissenschaft berechneten Quote von 16 % bis 17 % für Männer und 13 % bis 14 % für Frauen sehr hoch ist. Es wird der Schluss gezogen, dass für den normalen Bürger, der den geltenden Regeln des RGPS unterliegt, die Höhe der gezahlten Beiträge, die die erhaltenen Altersleistungen widerspiegeln, von der gerechten Maßnahme abweichen, die von der versicherungsmathematischen Wissenschaft berechnet wird, daher wurden keine Faktoren beobachtet, die bezeugen, dass das RGPS dem Steuerzahler und damit der Gesellschaft gerecht ist.
Schlagworte: Soziale Sicherheit, RGPS, versicherungsmathematische Wissenschaft.
1. EINFÜHRUNG
Das öffentliche Rentensystem wird vom Nationalen Institut für soziale Sicherheit (INSS) verwaltet, das durch das Gesetz Nr. 8.029 vom 12. April 1990 umgesetzt und durch das Dekret Nr. 99.350 vom 27. Juni 1990 geregelt wurde. Sie regelt die Frage der sozialen Sicherheit in dem Land, das für die INSS für die Verwaltung und Aufrechterhaltung der Sozialversicherungsdienste zuständig ist, die sich aus dem Allgemeinen Sozialversicherungssystem – RGPS , in der Frage von 8.213 vom 24. April 1999 – im Wesentlichen um die Arbeitnehmer des privaten Sektors und des eigenen Sozialversicherungssystems (RPPS) der öffentlichen Bediensteten ableitet.
Der grundlegende Punkt eines jeden Systems der sozialen Sicherheit ist, wie es finanziert wird, d. h. einen kontinuierlichen Fluss von Ressourcen zu gewährleisten, um Ausgaben mit Verwaltungsleistungen und -ausgaben zu decken. Auch, Iyer (2002), ist es notwendig, die Ströme von Ressourcen proportional zur Beitragsperiode und das endgültige Gehalt des Steuerzahlers zu gleichen.
Die Begriffe Beiträge und Beitragssatz ergeben sich natürlich im zentralen Diskussionsfeld, wenn es um die soziale Sicherheit geht, da es die Gesellschaft als Ganzes ist, die dieses System finanziert.
Die komplexe Dynamik der Systeme der sozialen Sicherheit wird von Iyer (2002) ausführlich diskutiert, der darüber informiert, dass die angewandten Parameter das Sozialversicherungssystem in demografischen und wirtschaftlichen Aspekten beeinflussen, die Dynamik der Zahl der Erwerbstätigen, die zum System beiträgt, und die Zahl der Rentner oder die, die von diesem System profitieren.
Mit der Zunahme der Zahl der Renten und Sozialhilfeleistungen sowie der Verringerung der Erwerbsbevölkerung, d. h. der Zahl der Steuerzahler der sozialen Sicherheit, wird also bestätigt, dass sie eine wesentliche Veränderung des demografischen Profils mit sich bringt, was zu einer Erhöhung der Sozialversicherungsausgaben von 2050 auf das Zehnfache des Wertes des Bruttoinlandsprodukts (BIP) führen kann. Diese Tatsache, erhöht für eine Gesellschaft zu zahlen, um andere Aktivitäten nicht zu beeinflussen, mit wichtigen öffentlichen Politik nach Cruz, (2015).
Laut Campani und Dias da Costa (2016) sind die Ausgaben für öffentliche Renten stratoferisch hoch, nach Angaben der Regierungsbeamten ist im Haus von Hunderten von Milliarden von Reais und in etwas mehr als 50 Jahren werden die Ausgaben mehr als 40% der Haushaltseinnahmen der Union sein. Trotz der Höhe der Sozialversicherung hat niemand darüber diskutiert, ob der Wert der gezahlten und erhaltenen Beiträge sowie die angewandten Diskontsätze wirklich gerecht sind.
Für die Analyse der Systeme der sozialen Sicherheit. Zu verstehen, wie komplexe und stochastische Parameter im Laufe der Zeit zusammenhängen, ist ein Schlüsselbegriff für andere Aspekte der versicherungsmathematischen Mathematik der Systeme der sozialen Sicherheit (Afonso und Lima, 2011).
Das Interesse des Autors an der Studie über versicherungsmathematische Gerechtigkeit wurde bei der Lektüre der Arbeit von Giambiagi und Afonso (2009), die das ideale System der sozialen Sicherheit als versicherungsmathematisch ausgewogen zwischen dem erwarteten Barwert gegenüber einem Zinssatz in Höhe des Leistungsflusses positioniert, noch deutlicher.
Das Thema hat soziale Relevanz für den Versuch, in der Justiz zu überprüfen, ob eine Rentenreform notwendig ist, angesichts der jüngsten Änderungen im Zusammenhang mit der Nichtinzidenz des Faktors der sozialen Sicherheit im Rentenalter für die Beitragszeit, die durch das neue Gesetz Nr. 13,183/2015 festgelegt wurde, die wirtschaftliche und finanzielle Tragfähigkeit der sozialen Sicherheit widerspiegeln.
Der Kern ist folgende Frage: Gibt es Gerechtigkeit im System des Beitrags zum RGPS aus der Sicht der versicherungsmathematischen Wissenschaft? Das heißt, der angewandte Einkommens- und Versicherungsfaktor kann die Gerechtigkeit der beitragsabhängigen Erinnerung bestimmen?
2. THEORETISCHEN RAHMEN
2.1 RGPS CONTRIBUTION FLOW – ALLGEMEINES SOZIALE SICHERHEITSSCHEMA
Das INSS (Nationales Institut für soziale Sicherheit) wurde durch das Gesetz Nr. 8,029 vom 12. April 1990 umgesetzt und durch das Dekret Nr. 99,350 vom 27. Juni 1990 geregelt. Es ist Die INSS ist es, die aus dem Allgemeinen Sozialversicherungssystem abgeleiteten Sozialversicherungsdienste – RGPS, in der Mitte des Gesetzes Nr. 8,213 vom 24. April 1999 zu verwalten und zu unterhalten.
Das RGPS verfügt über ein wichtiges Leistungssystem für den Bürger, der in den Ruhestand geht. Dieses Rentensystem hat drei Regeln, nämlich die progressive 85/95, die 30/35 Beitragsjahre und die Regel für den proportionalen Ruhestand. Da die derzeitige Regel progressiv 85/95 ist, wird daran gearbeitet werden.
Der Beitrag zum RGPS ist als einfache Verteilung gekennzeichnet, bei der Unternehmen etwa 20 % beisteuern und der verbleibende Satz vom Arbeitnehmer auf geerlegte wird. Der Beitrag zum Arbeitnehmer wird nach dem Einkommen des Steuerpflichtigen () berechnet, wobei er durch den Beitragssatz (c) entsprechend der Einkommensspanne erheblich beigesteuert wird, wie aus Tabelle 1 hervorgeht, die auf der INSS-Website verfügbar ist.
Tabelle 1 – Beitragssätze nach der Lohnspanne der RGPS-Beitragssätze 2017.
| Beitragsgehalt (R) | Rate |
| Bis zu 1.659,38 | 8% |
| Von 1.659,39 bis 2.765,66 | 9% |
| Von 2.765,67 auf 5.531,31 | 11% |
Quelle – INSS (2019).
Dann wird der Beitragsfluss oder der Gegenwartswert der Beiträge (VPC) einfach nach Gleichung 1 berechnet. Die Anhäufung von Ressourcen, die durch Gleichung 1 gefördert werden, nimmt zu und progressiv.
2.2 SOZIALE SICHERHEIT FACTOR UND FLOW OF BENEFITS IN RGPS
Der Faktor der sozialen Sicherheit wurde 1998 in der FHC-Regierung durch Verfassungsänderung 20 eingeführt. Im darauffolgenden Jahr entstand durch das Gesetz 9.876 der Faktor der sozialen Sicherheit mit dem Auftrag, Vorruhestandsregelungen zu entmutigen, denn je länger die Beitragszeit, desto höher die Höhe der erhaltenen Pensionierung und umgekehrt. Gleichung 2 zeigt die Art und Weise der Berechnung des Faktors der sozialen Sicherheit (Penafieri und Afonso, 2013).
Wo:
Tc:: Beitragszeit.
α: Beitragssatz (0,31).
Es: Lebenserwartung, die in der IBGE-Sterblichkeitstabelle für beide Geschlechter angegeben wird.
Id: Alter im Moment der Pensionierung.
Daher zeigt Gleichung 2 die Beziehung von drei wichtigen Variablen, dem Zeitpunkt des Beitrags, dem Alter zum Zeitpunkt des Ruhestands und der Lebenserwartung. In mathematischer Hinsicht: Je länger die Beitragszeit, desto höher der Faktor der sozialen Sicherheit, desto länger die Zeit und das Alter im Moment des Ruhestands, desto höher der Faktor der sozialen Sicherheit und in der entgegengesetzten Richtung desto höher die Lebenserwartung, desto niedriger der Faktor der sozialen Sicherheit.
Das Gesetz 9.876/99 wurde durch das Dekret 3265/99 ergänzt, mit dem eine Änderung des RGPS in der Berechnung des Renten- oder Leistungsentgelts (Sb) eingeführt wurde, so dass das Gehalt durch Multiplikation des Sozialversicherungsfaktors (f) mit dem realen arithmetischen Mittel M der 80 % höheren Beitragsgehälter gemäß Gleichung 3 berechnet wird.
Gleichung 4 ist ein Integral, das die Berechnungsgrundlage für die Altersversorgung nach Beitragszeit darstellt. Die Gleichung bedeutet den Durchschnitt der 80 % höheren Beitragsgehälter, Tc: stellt die Beitragszeit dar, 0,2Tc stellt 20% der Beitragszeit als Folge der Auslegung der Verfassungsregel des Änderungsantrags NO 20 dar.
Wo ist der Wert des Individuellen Gehalts in der Zeit t, w0 das Anfangsgehalt des Steuerpflichtigen, h bedeutet die Wachstumsrate der Wirtschaft pro Jahr und g die Rate des Lohnwachstums pro Jahr, die Parameter der Gleichung 5 zusammen erklären das fortschreitende und exponentielle Wachstum des Einkommens des Steuerzahlers im Laufe der Zeit.
Die für das RGPS wichtigen Parameter werden als exogene Variablen für das Sozialversicherungssystem des RGPS in die Wirtschaft eingefügt. Eine der Variablen ist das Gehalt der Steuerzahler, dies folgt dem mathematischen Modell von Gremaud und Patrick (2004); Penafieri und Afonso (2013) nach Gleichung 5 und zuvor in Gleichung 4 dargestellt.
2.3 NOTIONEn VON ACTUARIAL MATHEMATICS
Filho (2010) präsentiert die wichtigen Begriffe der versicherungsmathematischen Annahmen, ein wichtiger Parameter, der berücksichtigt werden muss, ist das Survival Board. Die Literatur hat eine Reihe von Tabellen, aber diejenige, die der Autor bei der Ausarbeitung dieses Werkes verwendet hat, war die von IBGE ausgearbeitete Überlebensplanke. Die Hauptbedeutung des Überlebensbretts ist es, die Lebenserwartung und die Überlebenswahrscheinlichkeit in einem gegebenen Schnitt der Tabelle zu erhalten.
Die von Afonso und Lima (2011) vorgestellten Vorstellungen entsprechen Filho (2010) hinsichtlich der Vorstellung von der Wahrscheinlichkeit, dass eine Person im Alter x bis zum Alter von x+t Jahren am Leben bleibt. Diese Wahrscheinlichkeit wird durch Px gemäß Gleichung 6 dargestellt. Ix+t stellt auf dem Überlebensbrett die Anzahl der Individuen im Schnitt dar, die dem Alter x+t Ix, entspricht, was die hypothetische Menge der Individuen im Schnitt der Überlebenstabelle im Alter x darstellt.
In ähnlicher Weise kann Gleichung 6 die Wahrscheinlichkeit eines Sterbens eines Individuums in t Jahren berechnet werden, daher wird die Differenz in jeder Kohorte von Individuen, die zwischen den x und x+t Intervallen dividiert durch die Anzahl der Individuen in Kohorte x gestorben sind, durch Gleichung 7 angegeben.
Die Lektüre des von Afonso und Lima verfassten Artikels (2011) war für diese Arbeit wichtig, da die Autoren das Thema des Sozialversicherungssystems aus versicherungsmathematischer Sicht im Vergleich zum RGPS auf der Tagesordnung des betreffenden Beitragssystems behandelten. Die theoretische Grundlage des Beitrags- und Akkumulationsmodells der Sozialleistungen wurde in dem Artikel ausführlich vorgestellt.
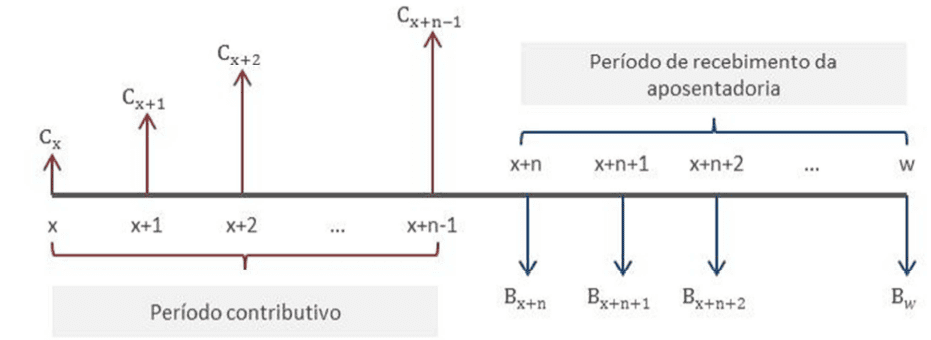
Abbildung 1 zeigt zwei unterschiedliche Seiten, die linke Seite stellt den Beitragszeitraum dar, d. h. es sind die monetären Werte, die der Steuerzahler regelmäßig an das Sozialversicherungssystem zahlt. Die rechte Seite stellt die Dauer des Eintritts in den Ruhestand dar, d. h. die Zeit, in der der Begünstigte sein Leistungsgehalt bis zu seinem Tod in der Zeit w erhält.
Abbildung 1: Beitragsströme und Leistungsströme in Abhängigkeit von der Zeit.
Aus der Finanzmathematik sollte der Beitragsfluss im Laufe der Zeit auf den Barwert für das Alter x Multiplikation mit dem Diskontfaktor Verbindung vt nach Gleichung 8 gebracht werden, wobei t der Zeitraum ist und i der Diskontsatz für den Berechnungseffekt variiert zwischen 1% und 3%, wie in Afonso und Lima vorgeschlagen (2011).
2.4 ACTUARIAL SOCIAL SECURITY FACTOR IN RAP – ACTUARIAL SOCIAL SECURITY REGIME
Die Behauptung über die versicherungsmathematische Gerechtigkeit weckte das Interesse des Autors, dieses Interesse wurde noch deutlicher bei der Lektüre der Arbeit von Giambiagi und Afonso (2009), die das ideale System der sozialen Sicherheit als versicherungsmathematisch ausgewogen zwischen dem erwarteten Barwert positioniert, indem ein Zinssatz in Höhe des Zuflusses der erhaltenen Leistungen diskontiert wird. Für ein faires versicherungsmathematisches Gleichgewicht ist es daher wichtig, den Versicherungsbeitragssatz (Cat) auf der Grundlage von Gleichung 9 zu berechnen, wobei f den Faktor der sozialen Sicherheit darstellt, w die Rate der Lohnprogression bedeutet, i der Diskontsatz, T ist die Beitragsperiode und N die Altersgrenze der verwendeten Überlebensplanke, im Falle dieser Arbeit ist es die IBGE 2017 Planke.
Nach den vorherigen Studien wurde der wesentliche Unterschied zwischen den beiden Ansätzen zur Berechnung des Beitragsflusses, der auf RGPS basiert, und dem anderen auf der Grundlage der versicherungsmathematischen Wissenschaft deutlich. Das bereits vorgelegte RGPS akkumuliert die Beiträge in einem Prozentsatz ohne versicherungsmathematische Kriterien, der sich auf das Einkommen konzentriert. Die andere versicherungsmathematische Fairness, wie auch dargestellt wurde, wird der Multiplikationsfaktor oder Prozentsatz durch streng wissenschaftliche Kriterien auf der Grundlage der versicherungsmathematischen Mathematik ermittelt.
2.5 BEITRAGSFLUSS IN RAP
Die Beiträge nach Afonso und Lima (2011) können mathematisch durch die in Gleichung 10 dargestellte versicherungsmathematische Formulierung beschrieben werden. So bedeutet der VPC, dass der Barwert der Beiträge zum Barwert erhalten wird, der durch den zusammengesetzten Diskontfaktor aktualisiert wird, der durch das vt Produkt von Px angegeben wird, und multipliziert mit dem von CatWt, angegebenen Einkommensbegriff, wobei Cat durch Gleichung 10 und Wt durch Gleichung 5 angegeben wird. Der Beitragsfluss wird als eine endliche Reihe von sofortigen temporären Variablenvorauszahlungen beschrieben.
Daher dachten wir an eine hypothetische Situation im Zusammenhang mit der Rentensituation durch Beitragszeit aus vier Eingabedaten (Geschlecht, Eintrittsalter, Rentenalter und Anfangseinkommen), in der die Ergebnisse leicht repliziert werden konnten, so dass es möglich war, die Diskussion über die Kohärenz des RGPS-Systems und damit die Justiz zu lenken, indem sie monatlich einen bestimmten Betrag an die INSS zahlte, um mit einem bestimmten Betrag in Rente zu gehen.
2.6 BARWERT DES FLUSSES DER ALTERSVERSORGUNG IN RAP
Die Berechnung des Leistungsflusses führt zum Leistungsgehalt, dem gleichen Betrag, der vom RGPS in Gleichung 3 berechnet wird. Das versicherungsmathematische System der sozialen Sicherheit versucht, wie in dem Artikel von Afonso und Lima (2011) den Barwert des Leistungsflusses zu berechnen, da es bei der Interpretation des Abstands zwischen den Beiträgen zum RGPS in Bezug auf das versicherungsmathematische System der sozialen Sicherheit behilflich sein wird. Die Berechnung des Barwerts des Leistungsflusses in RAP wird durch Gleichung 11 angegeben, wobei Sb das Leistungsgehalt und FA der versicherungsmathematische Faktor ist.
Der aktuelle Faktor der Gleichung 12 wird durch das Produkt zwischen dem zusammengesetzten Diskontsatz Vt der Gleichung 8 mit der Überlebenswahrscheinlichkeit Px der Gleichung 6 ermittelt. Daher wird der Stromfaktor FA durch Gleichung 11 angegeben.
Basierend auf diesen Informationen aus der Berechnung des Barwerts des Nutzenflusses in RAP und des aktuellen Faktors der Gleichung 10 folgen einige Studien zu dem vorgestellten Thema.
3. PREVIOUS STUDIEN UND FORSCHUNGSHYPOTHESEN
In diesem Abschnitt der Kursabschlussarbeit wird nach Tabelle 01, die allgemeine Gestaltung der Werke, die zur Vision und theoretischen Unterstützung des Autors beitragen wird vorgestellt.
Tabelle 1 – Hauptstudien zum Thema
| Zitate | ZIELE | Ergebnisse | ANWENDUNGEN IN DER STUDIE |
| Iyer, (2002) | Analysieren und entwickeln Sie die Mathematik der Systeme der sozialen Sicherheit mit Blick auf integrale und differenzierte Formulierung. | Die versicherungsmathematische Mathematik der Systeme der sozialen Sicherheit zeigt, wie die Systeme der sozialen Sicherheit in ihren Aspekten des versicherungsmathematischen Gleichgewichts entwickelt werden. | Zu den in dieser Arbeit vorgestellten Systemen der sozialen Sicherheit gehören die weltweit am weitesten verbreiteten, wie das einfache Verteilungssystem (in Brasilien) und das System der direkten Kapitalisierung. |
| Gilat, (2006) | Matlab with Engineering Applications ist eines der Standard-Lehrbücher, die im Maschinenbau, elektro- und etc.-Kursen verwendet werden. | Der Autor nutzte dieses Buch, um bei der Erstellung der Routine der Sozialversicherungsberechnungen des Allgemeinen Sozialversicherungssystems und für das versicherungsmathematische System der sozialen Sicherheit zu helfen, die Berechnungsroutine wird im Anhang Kapitel zusammengestellt. | Matlab-Anwendungen als Lösungs- und Programmierwerkzeug. |
| Chapman, (2006) | Lehrbuch zur Programmierung von Strukturkonzeptanwendungen in Matlab. | Programmierung in Matlab for Engineers war ein weiteres Lehrbuch, das vom Autor weit verbreitet war. Zusammen mit Gilats Buch (2006) gab es eine größere Ausbildung des Autors, um die Routinen der Sozialversicherungsberechnungen zu entwickeln. | Der Beitrag dieses Autors zu dieser Arbeit bestand darin, Konzepte der Entscheidungsstruktur aufzuklären, wenn sie – sonst – die Lohnwerte beurteilen und die Beitragssätze korrekt auf das RGPS und das versicherungsmathematische Sozialversicherungssystem anwenden, um den Fluss der Routine zwischen den einen Weg zu lenken. Neben der Zusammenarbeit für die Entition des Stils für -end Wiederholungsstrukturen, um endlich den Wert der zusammengesetzten Diskontsätze zu berechnen, um die Beitragswerte und Vorteile auf den Barwert zu bringen. |
| Giambiagi & Afonso, (2009) | Berechnen Sie, was aus versicherungsmathematischer Sicht ein fairer Satz wäre. | Die Wichtigste Schlussfolgerung der Autoren war, dass der auf das RGPS geltende Sozialversicherungssatz von 31 % für einige Einkommensgruppen übermäßig hoch ist. Durch diese Arbeit hat der Autor das Thema Gerechtigkeit im RGPS aus der Sicht der Beiträge und Leistungen der Nutzer ausgearbeitet. | Berechnung des versicherungsmathematisch ausgewogenen Sozialversicherungsbeitragssatzes: An Application to the Brazilian Case ist ein Publikationsartikel von Professor Giambiagi, einer der großen Forscher für Fragen der sozialen Sicherheit in Brasilien. |
| Gonçalves & Letieri, (2010) | Sozialversicherungsbeiträge: Eine Analyse im Jahresabschluss der Gemeinden von Pernambuco mit Blick auf die Rechenschaftspflicht. | Dies war ein KursAbschlussarbeit, die vom Autor konsultiert wurde, dessen Bedeutung die Beschreibung der Systeme der geschlossenen Sozialen Sicherheit war. | Die in dieser Studie erwähnten theoretischen Grundlagen und Sozialversicherungsgesetze wurden umfassend konsultiert, weshalb der Autor diese Veröffentlichung als Referenz verwendete. |
| Plamondon, et al., (2011) | Beschreiben und analysieren Sie makroökonomische Probleme, die die Dynamik des Beitrags- und Nutzenflusses beeinflussen. | Die wichtigste Schlussfolgerung der Autoren war das positive Verhältnis zwischen Lohnprogressionsrate, Höhe der wirtschaftlichen Entwicklung und zusammengesetzten Diskontsatz. | Die versicherungsmathematische Praxis in der sozialen Sicherheit, diese Arbeit, hatte einen Einfluss auf die Untersuchung der sozialen Sicherheit aus versicherungsmathematischer Sicht. |
| Afonso & Lima, (2011) | Beziehen Sie Aspekte der versicherungsmathematischen Mathematik, da es biometrische Risiko und zusammengesetzte Rabatt beinhaltet. | Sie kam zu dem Schluss, dass das Einkommen unter Beibehaltung biometrischer und makroökonomischer Faktoren das Beitragsprofil des mit dem RGPS verbundenen Individuums stark beeinflusst. | Analyse der Verteilungsaspekte der Rente nach Beitragszeit des INSS mit der Beschäftigung der versicherungsmathematischen Mathematik, |
| Lima, Wilbert, Pereira, & Paulo, (2012) | Untersuchen Sie den Faktor der sozialen Sicherheit, einen der wichtigsten Parameter, um zu berechnen, wie viel Leistung für die Beitragszeit erhalten wird. | Die wichtigste Schlussfolgerung dieser Arbeit ist die positive Korrelation zwischen dem Faktor der sozialen Sicherheit und der Höhe der Mittel, die der Bund seit dem Tag des Inkrafttretens des Sozialversicherungsfaktors für die gewährten Renten bereits in die öffentlichen Kassen eingespart hat. | Die Auswirkungen des Faktors soziale Sicherheit auf die große Zahl der sozialversicherung, zitierte dieser Artikel Afonso und Lima (2011). |
| Penafieri & Afonso, (2013) | Erstellen Sie einen versicherungsmathematisch fairen Sozialen Sicherheitsfaktor (FPAJ), der weniger “strafbar” für Vorruhestandsregelungen ist. | Die Autoren untersuchen die versicherungsmathematische Gerechtigkeit des Sozialversicherungsfaktors zu den Beiträgen des RGPS. Die Autoren kamen zu dem Schluss, dass der Faktor der sozialen Sicherheit den Wert des Nutzens der Steuerzahler weit über die versicherungsmathematischen Gleichgewichtswerte hinaus verringert. Die Autoren schaffen einen Ersatz für den aktuellen Faktor der sozialen Sicherheit. | Die Diskussion über die Gerechtigkeit der sozialen Sicherheit ist ein wichtiges und viel diskutiertes Thema, da es ein Faktor des sozialen Gleichgewichts und daher seine Bedeutung ist. |
Quelle: Erstellt von den Autoren (2019).
Die komplexe Dynamik der Systeme der sozialen Sicherheit wird von (Iyer, 2002) ausführlich diskutiert; Gremaud und Patrick (2004). Nach Diesen Autoren können die Parameter, die das Sozialversicherungssystem beeinflussen, durch die Annahme der folgenden vereinfachenden Hypothesen modelliert werden:
H1: Der Steuerpflichtige ist während der Beitragsperiode nicht arbeitslos, d.h. sein Einkommen wird als kontinuierliche Funktion bezeichnet.
H2: Die Werte der wirtschaftlichen Parameter werden während des gesamten Beitragszeitraums als konstant betrachtet.
H3: Die betreffenden Renten gelten ausschließlich für die Beitragszeit, gelten nicht als Renten aufgrund von Krankheit, Invalidität und Tod.
Das Ziel der Arbeit umfasst nicht die genaue Bewertung der Auswirkungen der Wirtschaftswachstumsrate, der realen Inflation und der Lohnprogression, die Berufe, Bildung usw. unterscheiden. Der Autor nahm Werte um die Mittelwerte an, die in der Arbeit von Gremaud und Patrick (2004) verwendet wurden, außerdem wird es unmöglich vorherzusagen, wie sich wirtschaftliche Parameter über Jahrzehnte verhalten werden.
So konnten aus diesen Studien die Analysen, Diskussionen und die Methodik der Gegenwart in der Arbeit erstellt werden. Daher ist der nächste Abschnitt, der vorgestellt werden soll, die Methodik, die mit einer kurzen Geschichte des RGPS beginnt, dann wird die versicherungsmathematische Theorie für die Entwicklung wichtiger Konzepte über Gerechtigkeit in Beiträgen zu Leistungen vorgestellt werden, das nächste Thema wird die Routinen der Berechnungen durch Rechenressourcen entwickelt und ihre Auswirkungen in der Berechnung der sozialen Sicherheit behandelt werden.
4. METHODIK
Der erste Schritt der methodischen Phase ist neben der vorherigen Studie, die im Kapitel der Literaturrezension vorgestellt wurde, die Strukturierung der verwendeten Rechenressource. Das Programm, das in dieser Arbeit verwendet wurde, war Matlab.
Das Simulationsprogramm in MATLAB wurde entwickelt und strukturiert, um den Benutzer vier Informationen zu fragen: Geschlecht der Person (Mann oder Frau), Anfangsalter, Rentenalter und Gehalt oder erstes Einkommen des Eintritts in das Sozialversicherungssystem.
Einige vereinfachende Hypothesen wurden berücksichtigt: Beiträge sind Initerruptas, ohne die Auswirkungen der Einkommensteuer und der Inflation auf die Berechnung der Beiträge und Der Einnahmen von Leistungen. Abbildung 02 zeigt den Einfügebildschirm der Eingabedaten direkt auf dem Eingabeaufforderungsbildschirm, wenn das Programm ausgeführt wird.
Basierend auf Afonso und Lima (2011) sowie Giambiagi und Afonso (2009) wurden sechs Simulationsereignisse von Sozialversicherungsberechnungen nach Geschlecht gruppiert, drei Variationen für Männer und drei Variationen für Frauen entwickelt. Alle Simulationsparameter waren für beide Geschlechter mit Ausnahme des Einkommens (1.200, 2.500 und 5.000) gleich.
Abbildung 2: Matlab-Eingabeaufforderungsbildschirm mit den ersten Dateneinträgen für Simulationsberechnungen.

Aus diesen vier Eingabeinformationen, wie bereits in Abbildung 2 dargestellt, werden die Berechnungen des RGPS und des versicherungsmathematischen Systems der sozialen Sicherheit nacheinander nach dem Programm oder der Berechnungsroutine durchgeführt.
Das nächste Kapitel wird die Ergebnisse und Diskussionen sein, in diesem Kapitel werden die Tabellen und Graphen mit den In-Methoden vorgestellten Gleichungen gezeigt, sowie die Mathematik des RGPS für die Berechnung von Beitrag und Ruhestand im Vergleich zu den Berechnungen des Sozialversicherungssystems, nach den Regeln der versicherungsmathematischen Wissenschaft.
5. ERGEBNISSE UND DISKUSSIONEN
5.1 INPUT PARAMETERS UND CONSTANTS
Die Routine der Sozialversicherungsberechnungen ist in Dateneingabe und -ausgabe strukturiert, ebenso wie das Verhalten mathematischer Funktionen, die Routine arbeitet von den zuvor konfigurierten Konstanten und ändert so die Eingabedaten, wenn Sie die Ausgabedaten ändern.
Tabelle 1 enthält die Dateneingabe und die Konstanten für die Berechnungen der sozialen Sicherheit des RGPS und des versicherungsmathematischen Rentensystems, die beide nacheinander nach der im Matlab verfügbaren Routine berechnet werden.
Die Konstanten wurden als Durchschnittswerte für die Ausgangssituation angenommen. Zweifellos sind die Konstanten der entscheidende Teil der Arbeit sowie der komplizierteste Teil der Rechtfertigung ihrer angenommenen Werte, daher können die angenommenen Werte nach den Werken von Giambiagi und Afonso (2009) gerechtfertigt werden; Plamondon, et al. (2011); Gremaud und Patrick (2004) und Afonso und Lima (2011) bewerten makroökonomische Zahlen: Wachstumsrate, Diskontrate, Lohnprogressionsrate.
Die Werte der Eingabeparameter und die Werte der Konstanten werden gemäß Tabelle 2 dargestellt.
Tabelle 2 – Eintrag und konstante Parameter der sozialen Sicherheit.
| Eingabedaten | Konstanten | ||
| Eintrittsalter (Frau) | 30 Jahre alt | Wirtschaftswachstum | 1% pro Jahr |
| Eintrittsalter (Mann) | Diskontsatz | 6% pro Jahr | |
| Rentenalter (Frau) | 60 Jahre alt | ||
| Rentenalter (Mann) | 65 Jahre alt | ||
| Einstiegsgehalt (beide) | R$ 1.200,00 | Lohnprogressionsrate | 0,25% pro Jahr |
| R$ 2.500,00 | 0,5% pro Jahr | ||
| R 5.000,00 | 1,2% pro Jahr | ||
Quelle – Vorbereitet von den Autoren.
Die Daten des Eintritts- und Austrittsalters wurden nach den Altersregeln nach Beitragszeit nach Angaben der Insss ausgewählt. Das Anfangsgehalt wurde auf drei Ebenen für beide Geschlechter festgelegt, da es hier darauf ankommt, die versicherungsmathematische Gerechtigkeit unter den gleichen makroökonomischen Umständen zu testen, wobei nur der biometrische Faktor (Geschlecht), das Eintritts- und Rentenalter und das anfangsbesoldt elektrisierte, im allgemeinen die Klasse des Individuums in niedrigen (1.200,00 R),B2(2.500,00) und hohen (5.000,00) Auds.
5.2 SOZIALE SICHERHEIT BEITRÄGE ZU RGPS
Tabelle 3 zeigt die durchschnittlichen Beitragsströme, die sich aus den Sozialversicherungsberechnungen des RGPS in Abhängigkeit von Rentenalter, Eintrittsalter und Anfangseinkommen ergeben. Der durchschnittliche Beitrag summt aufgrund der anfänglichen Einkommensdifferenz erheblich zwischen dem gleichgeschlechtlichen Lohnniveau.
Tabelle 3 – Durchschnittliche Beiträge, die nach Geschlecht und Anfangseinkommen der Steuerpflichtigen an das RGPS eingezahlt werden.
| Mann | ||||
| Rentenalter | Eintrittsalter | Anfangseinkommen (R/Monat) | Durchschnittliche Beiträge
(R/Monat) |
Gesamtsumme (R) |
| 65 Jahre alt | 30 Jahre alt | 1.200,00 | 122,00 | 52.703,68 |
| 30 Jahre alt | 2.500,00 | 300,58 | 129.850,26 | |
| 30 Jahre alt | 5.000,00 | 848,02 | 366.342,67 | |
| Frau | ||||
| Rentenalter | Eintrittsalter | Anfangseinkommen (R/Monat) | Durchschnittliche Beiträge
(R/Monat) |
Gesamtsumme (R) |
| 60 Jahre alt | 30 Jahre alt | 1.200,00 | 117,99 | 43.891,86 |
| 30 Jahre alt | 2.500,00 | 288,61 | 107.363,77 | |
| 30 Jahre alt | 5.000,00 | 797,28 | 296.587,50 | |
Quelle – Vorbereitet von den Autoren.
Die gesamtzahlsweise unterscheidet sich erheblich von Mann zu Frau, da die Beitragszeit bei Frauen kürzer ist, da sie 5 Jahre früher in Rente gehen als Männer. Es wurde nicht beobachtet, dass die Anwendung versicherungsmathematischer Konzepte in den Beiträgen zum RGPS, die nach Penafieri und Afonso (2013) ein versicherungsmathematisches Ungleichgewicht darstellt, das die Gerechtigkeit der Beiträge zum RGPS gefährdet.
5.3 SOZIALE SICHERHEIT
Die Berechnung des Sozialversicherungsfaktors erfolgte gemäß Gleichung 2. Wurden die Berechnungen nach den bereits in der Methodik für das RGPS dargelegten Leitlinien durchgeführt, die notwendigen Voraussetzungen für die Pensionierung durch Beitragszeit erfüllt, so wird der Faktor der sozialen Sicherheit nicht als Wertminderung der vom Steuerpflichtigen erhaltenen Altersrente wirken, während der Steuerpflichtige dagegen in den Ruhestand geht, bevor die rechtlichen und notwendigen Voraussetzungen erfüllt sind, der Faktor der sozialen Sicherheit den Wert der Altersrente verringert.
Das ursprüngliche Einkommen hat keinen Einfluss auf den Wert des Faktors der sozialen Sicherheit, wie in Tabelle 4 vorgeschlagen. Der Unterschied im Wert für Männer gleich 1.0000 und für Frauen gleich 0,6561 ist auf die Beitragszeit um 5 Jahre für Frauen reduziert und auch durch biometrische Unterschiede, da Männer haben niedrigere Lebenserwartung im Vergleich zu Frauen, nach der Überlebensplanke der IBGE 2017.
Tabelle 4 – Faktor der sozialen Sicherheit, segmentiert nach Geschlecht.
| Mann | ||
| Rentenalter | Eintrittsalter | Faktor der sozialen Sicherheit |
| 65 Jahre alt | 30 Jahre alt | 1,0000 |
| Frau | ||
| Rentenalter | Eintrittsalter | Faktor der sozialen Sicherheit |
| 60 Jahre alt | 30 Jahre alt | 0,6561 |
Quelle – Vorbereitet von den Autoren.
In der Praxis wurde der Rückgang des Faktors soziale Sicherheit für Frauen in der RGPS als eine Möglichkeit vorhergesagt, um mehr Gerechtigkeit zwischen den Geschlechtern zu gewährleisten, so Penafieri und Afonso (2013), aber einige sind nicht damit einverstanden, laut Afonso und Lima (2011) bestraft der niedrigere Faktor der sozialen Sicherheit Frauen weiter, was die historischen Einkommensunterschiede zwischen Männern und Frauen verschärft. Es ist heilsam zu überprüfen, ob der Faktor der sozialen Sicherheit teilweise auf der Grundlage biometrischer Kriterien ausgearbeitet wurde, da er die von ibGE offenbarte Lebenserwartung berücksichtigt, obwohl der umstrittene Faktor der sozialen Sicherheit von Vorruhestandsregelungen abschreckt und die längere Lebenserwartung von Frauen mit der kürzeren Lebenserwartung von Männern ausbalanciert.
5.4 RGPS SOZIALE SICHERHEIT BENEFITS
Die Ergebnisse der Berechnungen der Vorteile nach den Parametern der Tabelle 2, erzeugt aus Gleichung 3, die Ergebnisse nach Tabelle 5 dargestellt.
Tabelle 5 – Fluss der RGPS-Vorteile an die Steuerpflichtigen, getrennt nach Geschlecht und Anfangseinkommen.
| Mann | |||
| Rentenalter | Eintrittsalter | Anfangseinkommen (R/Monat) | Vorteile
(R/Monat) |
| 65 Jahre alt | 30 Jahre alt | 1.200,00 | 1.568,19 |
| 2.500,00 | 3.450,88 | ||
| 5.000,00 | 8.062,30 | ||
| Frau | |||
| Rentenalter | Eintrittsalter | Anfangseinkommen (R/Monat) | Vorteile
(R/Monat) |
| 60 Jahre alt | 30 Jahre alt | 1.200,00 | 989,68 |
| 2.500,00 | 2.160,28 | ||
| 5.000,00 | 4.931,19 | ||
Quelle – Vorbereitet von den Autoren.
Es ist wichtig zu beachten, dass Männer einen höheren Rentenwert als ihr eigenes Anfangseinkommen erhalten, wenn sie daran denken, dass das anfängliche Einkommen als Folge von Gleichung 5 wachsen wird. Bei Frauen erhalten sie weniger Altersgeld, als sie begonnen haben, sich an der RGPS zu beteiligen. Der Unterschied zwischen dem Verhalten der Leistungen für Männer und Frauen ist auf den Faktor der sozialen Sicherheit zurückzuführen, da Männer laut Tabelle 4 einen Sozialversicherungsfaktor von 1.0000 und Frauen 0,6561 haben.
Aufgrund der aufgedeckten Mittel deutet das Verhalten der Beiträge an das RGPS nicht darauf hin, den versicherungsmathematischen Vorschriften zu folgen, da der Beitrag berechnet wird, indem das Einkommen des Steuerpflichtigen mit den Prozentsätzen gemäß Tabelle 1 multipliziert wird. In Bezug auf die Leistungen, die die RGPS an Rentner zahlt, gibt es Beweise für das Vorhandensein von Konzepten der versicherungsmathematischen Wissenschaft, die in der These Ausgewogenheit und Gerechtigkeit zwischen männlichen und weiblichen Steuerzahlern suchen, da ihre biometrischen Eigenschaften im Survival Board von IBGE 2017 kristallisiert sind.
Die Fragen der Beiträge sind für die öffentliche Meinung ebenso sensibel wie die Leistungen, die durch die Beitragszeit erhalten werden, weil sie die Lebensqualität des Steuerzahlers in dem heiklen Moment des Lebens beeinflussen, wenn die Jahre die Tage der Jugend belasten, daher wirkt sich der Verlust der Arbeitsfähigkeit direkt auf das Einkommen der Person aus.
5.5 Das RGPS VERGLICHEN AUF DIE ACTUARIAL SOCIAL SECURITY REGIME
Dieser Abschnitt ist dem Verhalten der Werte der sozialen Sicherheit aus der Sicht der versicherungsmathematischen Wissenschaft gewidmet und vergleicht sich mit den Impagatwerten der sozialen Sicherheit des RGPS.
Beiträge aus der Sicht der versicherungsmathematischen Wissenschaft werden gemäß Tabelle 6 in der letzten Spalte dargestellt.
Tabelle 6 – Unterschied zwischen den Beiträgen zum RGPS für das versicherungsmathematische Getrennte nach Geschlechtern.
| Mann | ||||
| Rentenalter | Eintrittsalter | Anfangseinkommen (R/Monat) | Durchschnittliche Beiträge – RGPS
(R/Monat) |
Versicherungsmathematischer Durchschnittsbeitrag (R) |
| 65 Jahre alt | 30 Jahre alt | 1.200,00 | 122,00 | 88,43 |
| 30 Jahre alt | 2.500,00 | 300,58 | 206,47 | |
| 30 Jahre alt | 5.000,00 | 848,02 | 483,74 | |
| Frau | ||||
| Rentenalter | Eintrittsalter | Anfangseinkommen (R/Monat) | Durchschnittliche Beiträge – RGPS
(R/Monat) |
Versicherungsmathematischer Durchschnittsbeitrag (R) |
| 60 Jahre alt | 30 Jahre alt | 1.200,00 | 117,99 | 87,30 |
| 30 Jahre alt | 2.500,00 | 288,61 | 190,92 | |
| 30 Jahre alt | 5.000,00 | 797,28 | 438,19 | |
Quelle – Vorbereitet von den Autoren.
Es ist spürbar der Anstieg der durchschnittlichen Beitragswerte, da die anfänglichen Beitragseinnahmen sowohl für das RGPS als auch für das versicherungsmathematische System steigen, und es ist auch klar, dass der Durchschnitt der Beiträge zum RGPS für den Versicherungsmathematiker erheblich ist. Der erhebliche Unterschied zwischen den Beiträgen ist das Ergebnis der von der versicherungsmathematischen Wissenschaft postulierten Grundlagen, bei denen der Beitragssatz gemäß Tabelle 6 im Verhältnis zum RGPS-Satz deutlich niedriger ist.
Tabelle 6 – Beitragssatz zum RGPS im Vergleich zum Satz des versicherungsmathematischen Systems der sozialen Sicherheit.
| Beitragsgehalt (R) | Rate | Allgemeiner Tarif: Arbeitnehmer + Unternehmen | Versicherungsmathematische Rate Man | Versicherungsmathematische Rate Frauen |
| Bis zu 1.659,38 | 8% | 8%+20% = 28% | 16% | 13% |
| Von 1.659,39 bis 2.765,66 | 9% | 9%+20% = 29% | 17% | 14% |
| Von 2.765,67 auf 5.531,31 | 11% | 11%+20% = 31% | 17% | 14% |
Quelle – Vorbereitet von den Autoren.
Es ist offensichtlich, dass nach Tabelle 6 der versicherungsmathematische Satz sowohl bei den Geschlechtern als auch in den anfänglichen Einkommensbereichen niedriger ist als die RGPS-Sätze. Giambiagi und Afonso (2009) kamen zu diesem Schluss.
Das Beitragssystem zum RGPS unterscheidet sich in all seinen Aspekten sehr vom versicherungsmathematischen Regime, das zeigt sich, wenn man die im Laufe der Jahre angesammelten Beitragswerte wahrnimmt. Die erste Abbildung zeigt die Beziehung zwischen den Beiträgen zum RGPS und dem Versicherungsmathematischen Beitragsregime. Das Verhalten der Kurven ist deutlich divergierend, wo das RGPS dazu neigt, seine Beitragswerte im Laufe der Zeit immer zu erhöhen, im Gegensatz dazu zeigt das versicherungsmathematische Regime, dass die Beitragswerte abnehmen. Darüber hinaus ist ein wichtiger Aspekt an der Schnittstelle zwischen den beiden Schaubildern möglich, wo ab dem 11. Lebensjahr die Versicherungsmathematische Beitragsregelung für den Steuerzahler im Vergleich zum RGPS finanziell vorteilhafter wird.
Abbildung 1: Beitrag zu den Systemen der sozialen Sicherheit RGPS und versicherungsmathematische sozialversicherungssystem als Funktion der Zeit für Männer mit einem Anfangseinkommen von 1.200,00 R.
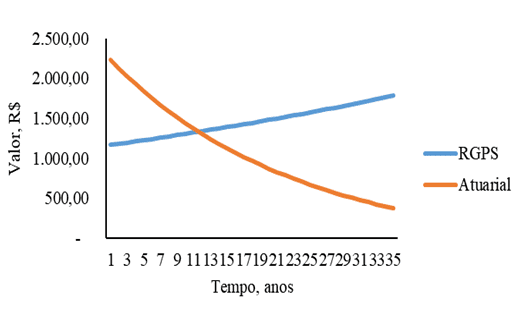
Das unterschiedliche Verhalten der Kurven in Abbildung 1 wird durch das Fehlen biometrischer Erwägungen im Akkumulationssystem zum RGPS gerechtfertigt, in dem im versicherungsmathematischen Beitragsregime offensichtlich das Vorhandensein versicherungsmathematischer Annahmen erkennbar ist, da die Tendenz besteht, die Überlebenswahrscheinlichkeit des Steuerzahlers im Laufe der Zeit zu verringern, wie im Theoretischen Rahmen dargestellt.
Ähnliches Verhalten Abbildung 1 kann in Abbildung 2 dargestellt werden. In Abbildung 2 beläuft sich das anfängliche Beitragseinkommen der Frau auf einen Wert von fast 2.000,00 R und auf 500,00 R 500,00 in der Nähe des 30. Beitragsjahres und der Frauen in Abbildung 2, Die Differenz besteht jedoch in der Gesamtversicherungsbeitrag, die höher ist, unter Beachtung des 1. Beitrags zum Gesamtwert ist zwischen 2.000,00 und 2.500,00 R in der Nähe der Mitte der beiden Werte (R. 2.250,00).
Abbildung 2: Beitrag zu den Systemen der sozialen Sicherheit RGPS und versicherungsmathematische Sozialversicherungssystem als Funktion der Zeit für Frauen mit einem Anfangseinkommen von 1.200,00 R.
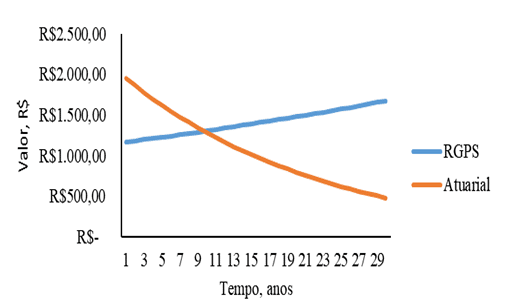
[/caption]Ein weiterer Unterschied ist in Abbildung 1 in Bezug auf Abbildung 2 in der Zeit des Schnitts zwischen den beiden Kurven, in Schaubild 1 ist der Schnittpunkt nahe an den 11 Beitragsjahren, in der in Schaubild 2 fast 9 Jahre liegen.
Die Differenz in der versicherungsmathematischen Beitragszeit der Abbildungen 1 und 2 folgt ebenfalls der gleichen Logik wie Schaubild 3 und 4. Das anfängliche Einkommen von 2.500,00 R. männer und frauen folgt den gleichen Merkmalen der versicherungsmathematischen Kurve der Abbildungen 1 und 2. Unten Abbildung 3.
Abbildung 3: Beitrag zu den Systemen der sozialen Sicherheit RGPS und versicherungsmathematische Sozialversicherungssystem als Funktion der Zeit für Männer mit einem Anfangseinkommen von 2.500,00 R.
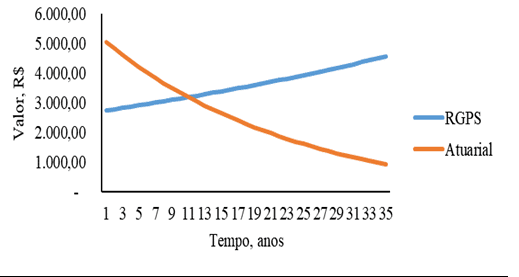
[/caption]Der Unterschied liegt in den Gesamtbeiträgen, da je höher das Anfangseinkommen die Beiträge sein wird, da Männer eine niedrigere Lebenserwartung haben und später in Rente gehen, so dass die Zahlen 1, 2, 3 und 4 zeigen, dass Männer im versicherungsmathematischen System jährlich höhere Werte im Verhältnis zu Frauen beisteuern.
Abbildung 4: Beitrag zu den Systemen der sozialen Sicherheit RGPS und versicherungsmathematische Sozialversicherungssystem als Funktion der Zeit für Frauen mit einem Anfangseinkommen von 2.500,00 R.
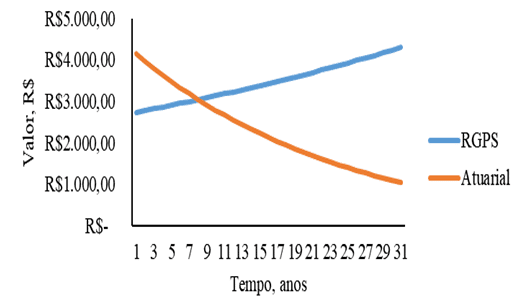
[/caption]Die Abbildungen 5 und 6 weisen ein ähnliches Verhalten wie die anderen Zahlen auf, die anfängliche Gehaltsspanne beträgt jedoch 5.000,00 R für beide Geschlechter in den Abbildungen 5 und 6.
Die Auswirkungen des Anfänglichen Einkommens auf die Aturais-Beiträge zeigen, dass je höher das Anfangseinkommen, desto höher die versicherungsmathematischen Beiträge. Männer, die 5.000,00 R.-Dollar beisteuern, tragen im ersten Jahr etwas mehr als 10.000,00 R. bei, Frauen insgesamt knapp unter 10.000,00 R im 1. Jahr.
Abbildung 5: Beitrag zu den Systemen der sozialen Sicherheit RGPS und versicherungsmathematische sozialversicherungssystem als Funktion der Zeit für Männer mit einem Anfangseinkommen von 5.000,00 R.
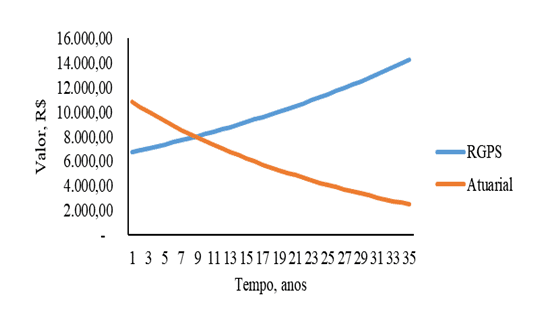
In Bezug auf das Verhalten des Schnittpunkts zwischen dem beitragspflichtigen System des RGPS und dem Versicherungsmathematik in den Abbildungen 5 und 6, Abbildung 5 der Männer, beträgt der Wert der Schnittmenge fast 9 Jahre und wie viel der Frauen figur 6 fast 5 Jahre beträgt. Diese Divergenz im Verhalten des Schnittpunkts kann angesichts der versicherungsmathematischen Merkmale zwischen Männern und Frauen gerechtfertigt werden.
Der in Abbildung 5 dargestellte Mann unterscheidet sich von den in den Abbildungen 1 und 3 dargestellten Männern, da die makroökonomischen Merkmale, die den Beitrag und die Zeit zum Beitragssystem widerspiegeln, im Verhältnis zum RGPS vorteilhaft werden. Wenn die Zahlen 5 und 3 in den Anfangseinkommen von 2.500,00 und 5.000,00 R keinen großen Unterschied in der Zeit der Schnittmenge haben, wird der Unterschied mit zunehmendem Einkommen in der Zeit der Schnittmenge deutlicher. Dies deutet darauf hin, dass je höher das Einkommen des Einzelnen unabhängig vom Geschlecht, desto weniger wird es für die RGPS
Abbildung 6- Beitrag zu den Systemen der sozialen Sicherheit RGPS und versicherungsmathematische Sozialversicherungssystem als Funktion der Zeit für Frauen mit einem Anfangseinkommen von 5.000,00 R.
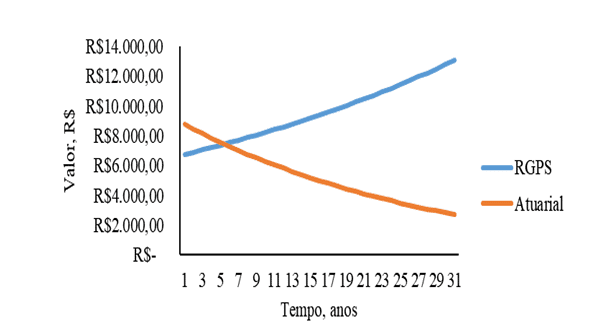
[/caption]Abbildung 6 entspricht der Grafik der Frauen mit einem Anfangseinkommen von 5.000,00 R. Die Beobachtung dieses Graphen ist offensichtlich, dass das versicherungsmathematische System für Frauen im Bereich von 5.000,00 R.-Dollar das Diagramm mit dem RGPS in der Zeit nahe 5 Jahren abfängt, dies ist das niedrigste Thema des Abfangens zwischen den Kurven, die in allen Zahlen von 1 bis 5 nachgewiesen werden. Für Frauen, die ab den 5 Beitragsjahren ein Anfangseinkommen von 5.000,00 R. verdienen, ist das versicherungsmathematische Beitragssystem daher im Vergleich zum RGPS vorteilhafter.
Die Graphiken deuten auf den gleichen Trend hin, der Beitrag zum RGPS steht im Gegensatz zum versicherungsmathematischen Regime, in Fällen, in denen es ein eigenartiges Verhalten gab, beginnen die Beiträge zum RGPS auf einer niedrigeren Ebene in Bezug auf den Versicherungsmathematiker, da die Zeit die Beiträge zum RGPS erhöht, während die Beiträge zum versicherungsmathematischen Regime sinken. Dieses Verhalten ist angesichts der Eigenschaften jedes einzelnen Systems gerechtfertigt.
Zusätzlich zu den höheren Beiträgen im RGPS wird dieses Höhenverhalten vom Schnittpunkt der beiden Kurven in den Diagrammen 1 bis 6 deutlich. Es wird vorgeschlagen, dass das RGPS nach den 6 Beitragsjahren nicht mehr vorteilhaft ist und für den Steuerzahler im Verhältnis zum versicherungsmathematischen System der sozialen Sicherheit viel schwerer wird.
Abbildung 7 – Versicherungsmathematische Faktorkurve für Männer und Frauen in Abhängigkeit von der Zeit.
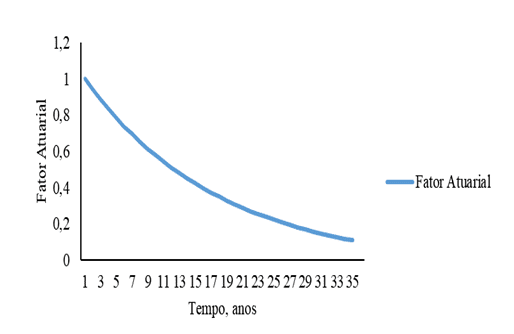
[/caption]In RGPS, wenn das Einkommen im Laufe der Zeit steigt, steigen auch die Beiträge aufgrund von Gleichung 1. Im Gegensatz zum RGPS zerfällt das versicherungsmathematische Regime mit dem Wert der Beiträge als Folge des versicherungsmathematischen Faktors und nimmt als Funktion der Zeit gemäß Abbildung 7 der Gleichung 11 ab. Dieser Rückgang wird durch die Wahrscheinlichkeit einer Überlebensabnahme beeinflusst, da Gleichung 6 und der Diskontsatz ebenfalls abnehmen, Gleichung 8.
6. FAZIT
Frühere Studien wurden durchgeführt, um zu verstehen, wie die Parameter der sozialen Sicherheit in der Praxis berechnet werden, die Grundlage für die Berechnung des RGPS für den Ruhestand nach Beitragszeit, die Werte des Beitrags zum RGPS, der Faktor der sozialen Sicherheit und das Leistungsgehalt.
Der zweite Schritt war das Studium der versicherungsmathematischen Theorie auf Überlebenstafeln und versicherungsmathematische Mathematik. Der dritte Schritt bestand darin, die Berechnungen theoretischer und praktischer Werte durch Matlab, ein Computerprogramm, und einen späteren Vergleich der erzielten Ergebnisse zu operationalisieren.
Im dritten Schritt wurde, wie bereits erwähnt, in Matlab ein strukturierter Programmierkodex entwickelt, in dem das Sozialversicherungssystem der realen und der versicherungsmathematischen Welt berechnet wurde, beginnend mit vier Eingabevariablen (Mann oder Frau, Eintrittsalter, Rentenalter und Anfangseinkommen). Die Berechnungen wurden sechsmal wie folgt wiederholt, dreimal für Männer mit dem gleichen Eintrittsalter von 30 Jahren, mit dem gleichen Rentenalter von 65 Jahren, jedoch mit unterschiedlichen Einkommen (1.200, 2.500, 5.000). Dasselbe Verfahren wurde für Frauen wiederholt, die sich nur im Rentenalter von 60 Jahren unterschieden.
Die große Frage, die diese Kursabschlussarbeit mit absoluter Anstrengung in den drei Schritten beantworten wollte, lautete: “Gibt es Gerechtigkeit im System des Beitrags zum RGPS aus sicht der versicherungsmathematischen Wissenschaft? Das heißt, der angewandte Einkommens- und Versicherungsfaktor kann die Gerechtigkeit der beitragsabhängigen Erinnerung bestimmen? ”
Es wird der Schluss gezogen, dass das RGPS nicht fair ist, den ersten Teil der Frage zu beantworten, denn aus der Sicht der versicherungsmathematischen Wissenschaft, die das Gleichgewicht sucht, weist das Verhalten der Beitragskurven des RGPS und des versicherungsmathematischen Rentenregimes eine sehr ausgeprägte Tendenz und Werte auf, da der Trend der Beitragskurve des RGPS andererseits progressiv zunimmt. neigt die versicherungsmathematische Regimekurve zu einer progressiven Abnahme.
Diese Arbeit bestätigt, wie Giambiagi und Afonso (2009) bestätigthaben, dass der sozialversicherungspflichtige Satz, den das INSS über das RGPS berechnet, zu hoch ist, wo die kontinuierliche Beitragserhöhung vor allem in den letzten Beitragsjahren Druck auf die Tasche der älteren Steuerzahler ausübt. Die versicherungsmathematische Rentenregelung zeigte eine gegenteilige Wirkung.
Nun, als ich den zweiten und letzten Teil der Frage beantwortet, gibt es Beweise dafür, dass es möglich ist, die Gerechtigkeit der beitragsabhängigen Erinnerung unter dem Gesichtspunkt der versicherungsmathematischen Gerechtigkeit zu bestimmen, da der versicherungsmathematische Faktor, der das Beitragseinkommen beeinflussen wird, durch biometrische Funktionen auf der Grundlage der versicherungsmathematischen Wissenschaft erzielt wird.
Das RGPS berechnet den Wert der Beiträge anhand eines Prozentsatzes, der sich auf das Einkommen konzentriert, und informiert das Unternehmen nicht darüber, wie es einen solchen Prozentsatz erreicht hat und wie fair er nicht nur für den Steuerzahler, sondern auch für das Institut, das zahlt, sein kann. Da das monatliche Renteneinkommen sowohl für das RGPS als auch für das versicherungsmathematische Rentensystem gleich angenommen wurde, trägt das RGPS jedoch im Verhältnis zum versicherungsmathematischen System wesentlich mehr zum RGPS bei.
Die Werte der Beiträge und Leistungen unterscheiden sich je nach Geschlecht aufgrund des ursprünglichen Einkommens, was sich auf die Lohnprogression und den Beitragssatz ausdeufliert, was zu einem höheren Beitragsbetrag für das RGPS führte. Im Intergender-Vergleich gab es einen erheblichen Unterschied, da Frauen früher in Rente gehen und eine längere Lebenserwartung haben, je nach Überlebensplanke, die einen niedrigeren Beitragsbetrag für das Sozialversicherungssystem festlegt, während sie im Vergleich zu Männern weniger Rentenleistungen erhalten.
Die Frage der sozialen Sicherheit ist nicht erschöpft, weil das Thema breit angelegt ist und für die Gesellschaft von starkem Interesse ist. Angesichts dessen, um die Diskussionen zu erweitern, ist daher, da Vorschläge für künftige Arbeiten die Analyse der Gründe vorgeschlagen werden, die das versicherungsmathematische Ungleichgewicht im RGPS erzeugen, ein weiterer Vorschlag darin, die auf dem Markt angebotenen Sozialversicherungspläne zu vergleichen, die sich den versicherungsmathematischen Kriterien annähern können, ein weiterer Vorschlag ist, an der Erstellung eines Berechnungsantrags zu arbeiten, der auf die Vermittlung von Versicherungsmathematik abzielt.
7. VERWEISE
- Afonso, L. E., & Lima, D. d. . Uma Análise dos Aspectos Distributivos da Aposentadoria por Tempo de Contribuição do INSS com o Emprego de Matemática Atuarial. Revista Gestão & Políticas Públicas, pp. p. 7-33.2011.
- Chapman, S. J. Programação em Matlab para Engenheiros. São Paulo: Thomson.2006.
- Filho, A. C. (2010). Cálculo Atuarial Aplicado (2ª ed.). São Paulo: Atlas.
- Giambiagi, F., & Afonso, L. E. Cálculo da Alíquota de Contribuição Previdenciária Atuarialmente Equilibrada: Um Aplicação ao Caso Brasileiro. rbe, v. 63, pp. p. 153-179.2009
- Gilat, A. Matlab com Aplicações em Engenharia (2ª ed.). Porto Alegre: Bookman.2006.
- Gonçalves, & Letieri, V. . Contribuições Previdenciárias: Uma análise nas Demonstrações Contábeis de Prefeituras de Municípios Pernambucanos com Vistas à Accountability. Universidade Federal de Pernambuco (Dissertação de Mestrado), p. 113. Recife, PE.2010.
- Gremaud, R. F., & Patrick, A. Regime de Previdência dos Servidores Públicos: Equilíbrio Financeiro e Justiça. p. 19.2004.
- HEITOR CAMPANI, C., & DIAS DA COSTA, T. R. Pensando na aposentadoria: PGBL, VGBL e autoprevidência. Universidade Federal do Rio de Janeiro. Rio de Janeiro: COPPEAD. doi:1518-3335.2016.
- IBGE. (s.d.). Acesso em 21/10/2018 de Outubro de 2018, disponível em http://sa.previdencia.gov.br/site/2016/07/TABUASDEMORTALIDADEIBGE2014_EXTRAPOLADAS.xls
- Iyer, S. Matemática Atuarial de Sistemas de Previdência Social (Vol. v. 16). Brasília, DF: Ministério da Previdência e Assitência Social.2002.
- Lima, D. V., Wilbert, M. D., Pereira, J. M., & Paulo, E. O Impacto do Fator Previdenciário nos Grandes Números da Previdência Social. Revista de Contabilidade & Finanças – USP, v. 23(n. 59), pp. p. 128-141.2012.
- COSTA, Raimundo Nonato Vieira, ARAUJO, Jamille Carla Oliveira, SILVA, Leidian Moura da Nascer, Crescer e Sobreviver: Uma Análise das Modalidades de Aposentadoria da Previdência Privada sob os Planos PGBL e VGBL. (2018). XV Congresso USP de Iniciação Científica em Contabilidade, (p. p. 20). São Paulo.
- Penafieri, A. C., & Afonso, L. E. . O Impacto da Mudança da Regra de Cálculo das Aposentadorias por Tempo de Contribuição do INSS: o Fator Previdenciário é Atuarialmente Justo? Economia Apicada, v. 17, 2013. pp. p. 667-694..
- Plamondon, P., et. al.. (2011). Prática Atuarial na Previdência Social (Vol. v. 33). (S. d. Brasil, Trad.) Brasília, DF, Brasil. 2011.
- Rodrigues, J. A. . Gestão de Risco Atuarial. São Paulo: Saraiva. 2008.
[1] Master in Maschinenbau (UFPA); Abschluss in Maschinenbau (UFPA); Abschluss in Rechnungswesen (UFRA)
[2] Master in Betriebswirtschaftslehre, MBA Accounting Management, Expertise, Audit und Control, Bachelor of Accounting
[3] Doktorand in Naturwissenschaften und Mathematik; Master in Elektrotechnik; Spezialisierung in Umwelterziehung und Nachhaltigkeit; Bachelor-Abschluss in Mathematik.
Eingereicht: Mai 2019.
Genehmigt: Juni 2019.