ARTIGO ORIGINAL
MUATOCUANE, Justino Almeida [1]
MUATOCUANE, Justino Almeida. Novos métodos para construção da oval: face definida por direções com iguais coeficientes de redução na perspectiva dimétrica. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano. 06, Ed. 11, Vol. 03, pp. 29-40. Novembro 2021. ISSN: 2448-0959, Link de acesso: https://www.nucleodoconhecimento.com.br/arquitetura/construcao-da-oval
RESUMO
Muito pouco se trabalha com a perspectiva dimétrica devido à dificuldade de construção de arcos de circunferências em uma das suas faces. Este artigo, tem como objetivo, descrever dois novos métodos para a construção da oval dimétrica na face com o mesmo coeficiente de redução. Vários estudos acadêmicos, inerentes a perspectiva ortogonal na área do Desenho técnico, têm afirmado ser difícil desenhar arcos de circunferência na face com o mesmo coeficiente de redução da perspectiva dimétrica, fazendo com que esta perspectiva seja menos aproveitada. Assim sendo, a questão de estudo apresentada é: Como construir arcos de circunferência na face com o mesmo coeficiente de redução da perspectiva dimétrica? Este estudo trata-se de uma pesquisa aplicada, com o processo de pesquisa bibliográfica. Na conclusiva, foi possível observar que os dois métodos aqui desenvolvidos atendem ao objetivo principal deste estudo, pois demostraram ser eficazes na apresentação do resultado, que é a oval dimétrica.
Palavras-chave: perspectiva axonométricas, oval, dimétrica, coeficiente de redução.
INTRODUÇÃO
Não fazendo parte deste tema o estudo amplo da perspectiva, é primordial ter-se em conta que ela se divide em dois grupos, a Cilíndrica ou Paralela em que temos: a axonometria obliqua e a Ortogonal que apresenta a axonometria ortogonal Isométrica, Dimétrica, Trimétrica e a Militar. A Cónica ou Central na qual se têm: com um ponto de fuga, dois pontos de fuga e três pontos de fuga.
Novos métodos para construção da Oval: Face definida por direções com iguais coeficientes de redução na Perspectiva Dimétrica, é o tema proposto neste presente trabalho que visa apresentar duas formas para a construção da oval dimétrica em faces definidas pelo mesmo coeficiente de redução. Trata-se de dois eixos, o do comprimento e o da altura que em perspectiva dimétrica formam faces com o mesmo coeficiente.
Visto que, sendo essa perspectiva uma das frequentemente usada apresente mais dificuldades na representação de arcos de circunferências, para se apresentar os novos métodos cá propostos, houve primordialmente a necessidade de fazer-se uma abordagem a cerca dessa perspectiva, qual é o seu comportamento e como ela é obtida, por último apresentar os resultados propostos.
Da Cunha (2017, p. 245) quando fala da utilização dos vários tipos de Perspectiva aponta como um dos inconvenientes “o facto de ser, normalmente, mais morosa a representação em projeções ortogonais, acontecendo isto, em especial, quando haja arcos de circunferências ou outras curvas a representar.”
Das várias formas de construção de ovais atualmente difundidas, sendo dado o eixo maior, o eixo menor ou até sendo dado dois eixos maior e menor. Nenhuma delas ajuda-nos na obtenção de arcos de circunferências e curvas na perspectiva dimétrica nas faces com o mesmo coeficiente de redução. Essa é a razão deste artigo, preencher uma lacuna no que diz respeito a falta de métodos que foram designados especialmente para uma aplicação específica, poderão ajudar-nos na construção de ovais dimétricas em faces definidas com o mesmo coeficiente de redução.
Então, esse artigo é de grande valia, pois traz consigo novos métodos que vão nos ajudar a construir a oval dimétrica na face com o mesmo coeficiente de redução, que não é algo até então considerado fácil de o fazer, chegando às vezes a se dizer que essa perspectiva menos é usada devido à dificuldade que se encontra na construção de arcos de circunferências.
Podemos ver isso quando Ribeiro (2015, p. 14) fala da perspectiva axonométrica ortogonal dimétrica afirma que “Esse método é raramente usado devido à dificuldade de desenhar circunferência através desta perspectiva.”
O objetivo geral deste artigo consiste em:
Descrever dois novos métodos para a construção da oval Dimétrica na face com o mesmo coeficiente de redução.
Esses métodos serão apresentados após uma breve descrição da perspectiva Dimétrica.
Tendo como objetivos específicos:
Definir a perspectiva axonométrica ortogonal Dimétrica;
Apontar os métodos para construção da oval dimétrica em faces de igual coeficiente de redução;
Citar os passos para construção das ovais dimétricas.
Para a realização deste trabalho dotou-se uma pesquisa experimental, com uma finalidade aplicável. Está dividido no campo do desenvolvimento em duas partes, a primeira na qual dá-se uma visão acerca da Perspectiva ortogonal dimétrica e na segunda onde se explora de uma maneira explicativa os métodos de construção de oval dimétrica na face com o mesmo coeficiente de redução.
ABORDAGEM ACERCA DA PERSPECTIVA DIMÉTRICA
Perspectiva axonométrica é a representação rigorosa através de três eixos fundamentais: OX, OY e OZ. Os quais representam o comprimento, largura e altura.
A perspectiva dimétrica faz parte das perspectivas axonométricas ortogonais, que segundo Bornancini; Petzold e Júnior (2018, p. 7) são sistemas de perspectivas no qual o objeto colocado de modo que as suas três direções fundamentais sejam oblíquas em relação ao quadro, é representado sobre o mesmo por meio de uma projeção cilíndrica ortogonal.
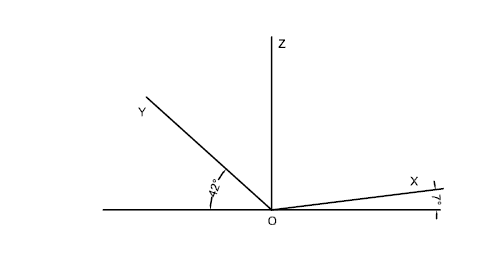
“Calculando os valores dos ângulos das direções axonométricas principais com a horizontal de referência um ângulo é de 7˚ e outro de 41˚30ˈ, embora na prática este seja sempre substituído pelo de 42˚ por uma questão de facilidade de medida.” (CARREIRA, 1972, p. 306).
Perspectiva ortogonal dimétrica é aquela em que nos três eixos tem-se dois com o mesmo coeficiente de redução juntamente com o ângulo, e um diferente.
Coeficiente ou fator de redução é a relação entre a projeção de um segmento da reta e a sua verdadeira grandeza (nas projeções axonométricas ortogonais é sempre menor que a unidade). O coeficiente de redução também é denominado de coeficiente de transformação, alteração ou encurtamento. (BORNANCINI; PETZOLD E JÚNIOR, 2018, p. 9)
Essas reduções ou encurtamentos de cada aresta são de 0.94, 0.94 e 0.47, no entanto por se tratar de um desenho essencialmente prático adoptou-se valores exatos: OX=1, OZ=1 e OY=1/2. (CARREIRA, 1972, p. 306).
Figura 1: Sistema de representação em perspectiva Dimétrica.
CONSTRUÇÃO DE OVAIS DIMÉTRICAS NA FACE DEFINIDA POR DIREÇÕES COM IGUAIS COEFICIENTES DE REDUÇÃO
Nos estudos acerca da construção de ovais Dimétricas, Da Cunha (2017) destaca que nas faces correspondentes a direção com o mesmo coeficiente de redução pode recorrer-se à oval, tal como se faz para a elipse isométrica. Pelos meios dos lados da perspectiva do quadrado levantam-se perpendiculares, cujos pontos de cruzamento definem os quatro centros da oval.
Testando essa afirmação não se conclui a obtenção dos quatro centros da oval o que nos leva a ressaltar a dificuldade de representação de arcos.
Da Cunha (2017) afirma que o facto de a perspectiva isométrica as elipses serem iguais, qualquer que seja o plano isométrico considerado, constitui uma apreciável vantagem deste tipo de perspectiva.
Assim, conclui-se que essas construções aplicadas em perspectiva dimétrica seguem métodos diferentes, pois nas faces definidas pelas direções a 90˚ e 42˚ tem-se Elipses, que podem ser construídas usando processos já conhecidos sendo o mais viável o do retângulo circunscrito. Nas faces pelas direções de 90˚ e 7˚ tem-se Ovais.
As ovais dimétricas nas faces com o mesmo coeficiente de redução podem ser construídas usando dois métodos: Método Arãoniano e o Método Duplo.
MÉTODO ARÃONIANO
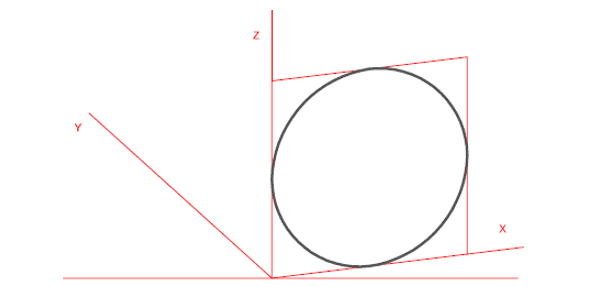
A Oval construída através de dois triângulos equiláteros e um retângulo. Têm quatro eixos, dois maiores obtidos através da intersecção de quatro arestas dos triângulos e outros dois obtidos através da intersecção dos lados menores do triângulo com a diagonal maior do quadrilátero propriamente dito que é determinado pelo raio da circunferência da figura em questão.
Figura 2: Oval em Perspectiva Dimétrica.
PASSOS DE CONSTRUÇÃO
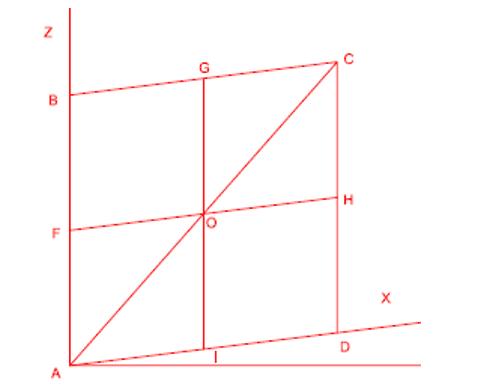
1 – Construído um quadrilátero propriamente dito obtido através do raio da figura pretendida. Determina-se a diagonal maior e une-se os pontos médios do quadrilátero de maneira a obter dois segmentos concorrentes no ponto O.
Figura 3: Primeiro passo.
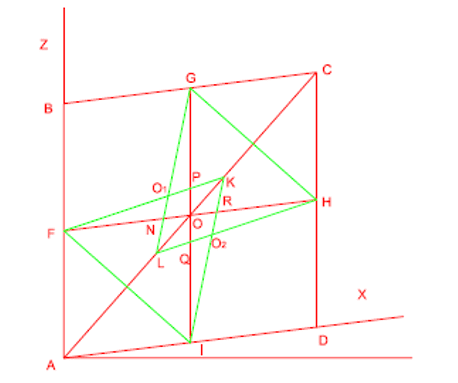
2 – Unindo o ponto médio do lado com o ponto médio do lado , obtêm-se uma aresta do triângulo equilátero, que através dele obtêm-se as restantes arestas. Fazendo o mesmo, unindo o ponto médio do lado com o ponto médio do lado obtêm-se uma aresta do segundo triangulo, sendo as duas restantes iram intersectar-se com duas do primeiro triangulo obtendo dois eixos: O1 e O2.
E com dois segmentos obtendo os pontos N, P, Q e R.
Figura 4: Segundo passo.
3 – Construir um retângulo a partir dos pontos N, P, Q e R. os lados menores do retângulo se intersectando com a diagonal obtendo os pontos O3 e O4.
Figura 5: Terceiro passo.
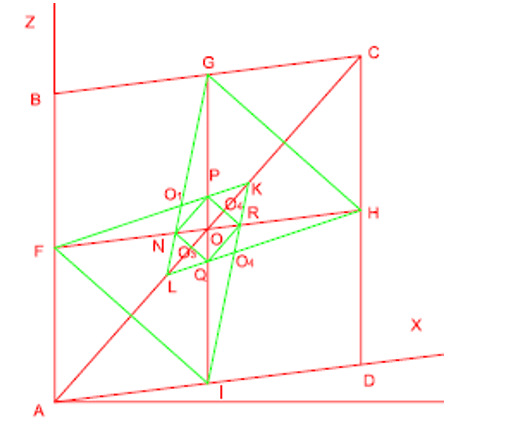
4 – Com a ponta seca do compasso em O1 abertura até H constrói-se um arco HI. O2 abertura até F constrói-se um arco FG. O3 abertura até F constrói-se um arco FI. O4 abertura até G constrói-se um arco GH. E por fim temos oval dimétrica.
Figura 6: Quarto passo.
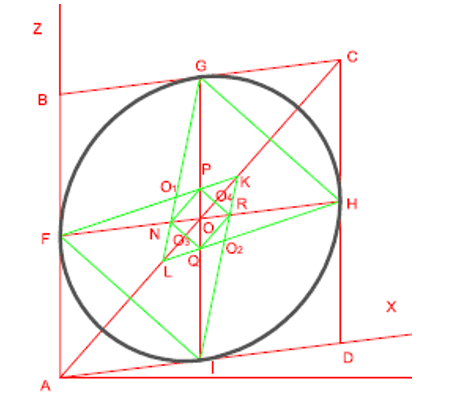
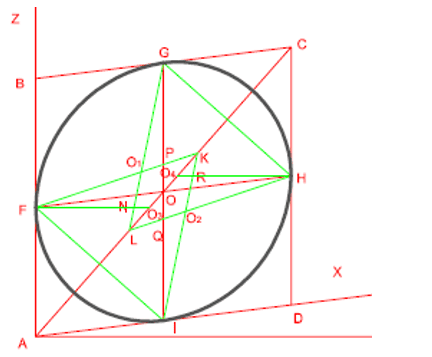
MÉTODO DUPLO
A Oval construída através do método duplo apresenta quatro eixos que são obtidos através de dois triângulos equiláteros e dois segmentos de reta perpendiculares a lados que sejam paralelos ao eixo das alturas, que tenham o seu início nos pontos médios.
Este método não se distingue no que concerne na obtenção dos triângulos equiláteros do método anterior, ou seja, segue os mesmos passos de construção até o segundo passo dos quais fiz menção para a oval construída através Método Arãoniano.
PASSOS DE CONSTRUÇÃO
2 – Unindo o ponto médio do lado com o ponto médio do lado , obtêm-se uma aresta do triângulo equilátero, que através dele obtêm-se as restantes arestas. Fazendo o mesmo, unindo o ponto médio do lado com o ponto médio do lado obtêm-se uma aresta do segundo triangulo, sendo as duas restantes iram intersectar-se com duas do primeiro triangulo obtendo dois eixos: O1 e O2. E com dois segmentos obtendo os pontos N, P, Q e R.
Figura 7: Segundo passo.
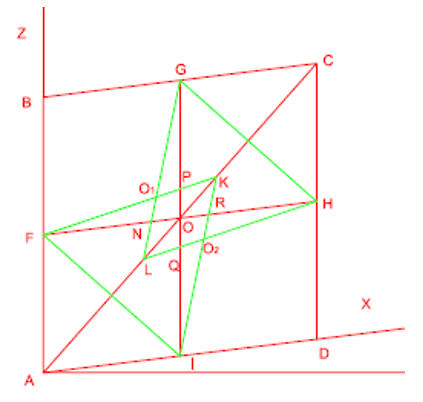
3 – Partindo do ponto F e H traçam-se dois segmentos de retas até intersectarem a diagonal maior, obtendo os eixos O3 e O4.
Figura 8: Terceiro passo.
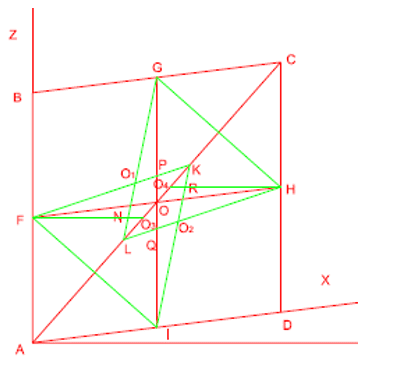
4 – Com a ponta seca do compasso em O1 abertura até H constrói-se um arco HI. O2 abertura até F constrói-se um arco FG. O3 abertura até F constrói-se um arco FI. O4 abertura até G constrói-se um arco GH. E por fim temos oval dimétrica.
Figura 8: Quarto passo.
CONSIDERAÇÕES FINAIS
Considera-se morosa a representação de arcos e outros elementos curvos na perspectiva axonométrica ortogonal dimétrica, pois à não existência de métodos que nos ajudam a representá-los é a causa desta dificuldade.
A apresentação destes dois Métodos, o Arãoniano que é a construção da oval através de dois triângulos equiláteros e um retângulo e o Duplo tratando-se da obtenção da oval a partir de dois triângulos equiláteros e dois segmentos de reta perpendiculares. Estas são propostas claras para a representação destes elementos, uma representação parcial (arcos e curvas) ou total da oval.
Existe possibilidades de novos estudos partindo destes resultados. Pois são dois métodos que abrem espaço para certas avaliações de cada um.
REFERÊNCIAS
BORNANCINI, José Carlos M; PETZOLD, Nelson Ivan; JÚNIOR, Henrique Orlandi. Desenho Técnico Básico: Fundamentos Teóricos E Exercícios À Mão Livre. 3ª ed. Brasil: Universidade Federal do Rio Grande do Sul. 7 p. Volume II. Disponível em: <https://www.google.com/url?sa=t&source=web&rct=j&url=https://www.ufrgs.br/destec/wp-content/uploads/2018/08/DESENHO-T%25C3%2589CNICO-B%25C3%2581SICO-VOL2.3ED.pdf&ved=2ahUKEwjmj4KF6vnmAhWHWhUIHZ7QBTQQFjALegQIBBAB&usg=AOvVaw1QYpSO26OcfcgzE-GPo-d->, Acesso em: 07 Dez. 2019.
CARREIRA, António. Compêndio de desenho: Para 3˚ ciclo do Ensino Liceal. 2ª. ed. Lisboa: Depositaria Livraria Sa da Costa, 1972. 306 p.
DA CUNHA, Luís Veiga. Desenho Técnico. 17ª. ed. Lisboa: Fundação Calouste Gulbenkian, 2017. 242 – 245 p.
RIBEIRO, Laura de Aquino. Apostila de Perspectivas. Universidade Federal Fluminense, Niterói – RJ. 2015. 14 p. Disponível em: <https://www.google.com/url?sa=t&source=web&rct=j&url=https://desenhobasicouff.weebly.com/uploads/7/1/0/5/7105339/apostila_perspectivas_laura.pdf&ved=2ahUKEwi1uLWq6PnmAhVhoXEKHc79DmQQFjAKegQIBBAB&usg=AOvVaw3dhOp1T6NhujdXodQvauF0>. Acesso em: 08 Jan. 2020.
[1] Licenciatura em Ensino de Educação Visual.
Enviado: Fevereiro, 2020.
Aprovado: Novembro, 2021.
