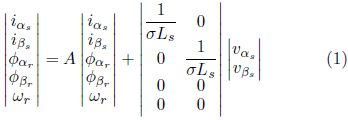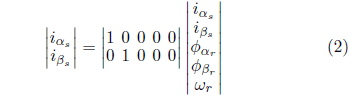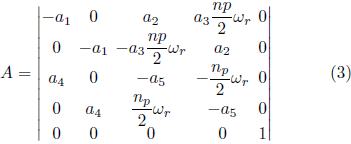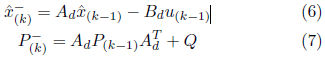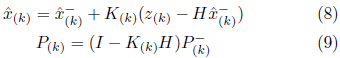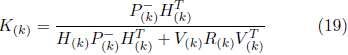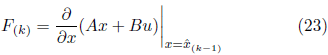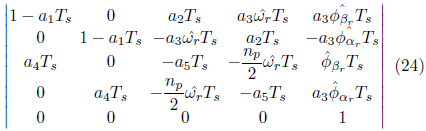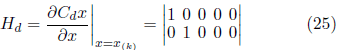ORIGINAL ARTICLE
LOPES, Leonardo de Magalhães [1], PEIXOTO, Zélia Myriam Assis [2]
LOPES, Leonardo de Magalhães. PEIXOTO, Zélia Myriam Assis. An Extended Kalman Filter, with pre-adjusted covariance matrices, applied to the sensorless speed control of three-phase induction motors. Revista Científica Multidisciplinar Núcleo do Conhecimento. Year 05, Ed. 09, Vol. 02, pp. 109-126. September 2020. ISSN: 2448-0959, Access Link: https://www.nucleodoconhecimento.com.br/electrical-engineering/kalman-filter, DOI: 10.32749/nucleodoconhecimento.com.br/electrical-engineering/kalman-filter
SUMMARY
With the emergence of sensorless control methods, there was a need for the use of estimators and/or state observers to give it the robustness and precision required in the drive of induction motors. This work deals with the application of the Extended Kalman Filter (EKF) in the estimation of rotor speed and position, aiming at the implementation of the indirect vector control technique in a sensorless speed control system for three-phase induction motors. The mathematical development of the system state variables associated with the EKF stochastic process is presented in this study, and point out its application under variable speed and load conditions, which are imposed on these motors in everyday life. The sensorless control strategy was tested through routine lines in the Matlab® software, simulating operating conditions of this type of engine, being proven its performance, as well as the convergence times consistent with the usual requirements of high performance systems. The main contributions of this work are the use of a reduced-order EKF (ROEKF) and the preset of covariance matrices to accelerate convergence in speed and position estimates for future implementations in currently accessible digital signal processors.
Keywords: EKF, Extended Kalman Filter, Induction Motors, Sensorless, AC electric drive systems.
1. INTRODUCTION
In recent decades, the applications of alternating current (AC) drive systems, associated with vector control techniques with speed and/or position monitoring by means of electromechanical sensors, have established themselves as a low cost alternative, greater mechanical robustness and high performance, equating to the CC drives precursors. However, the use of electromechanical transducers still includes limitations regarding maintenance costs, reliability, mechanical robustness and restrictions on operation in harsh environments (DADKHAH et al., 2015).
In this context and from the emergence of digital high-speed signal processors, the systems of speed control and/or sensorless position, although they imply the increase in the mathematical and computational complexity of the control models, have been increasingly used as they contribute to the mechanical robustness and variation of machine parameters and uncertainties intrinsic to the measurements of electrical signals (BARUT et al., 2008).
Several studies have been developed aiming at sensorless systems, where the sliding mode technique, adaptive systems by reference model (Model Reference Adaptive System) and Extended Kalman Filter (EKF – Extend Kalman Filter), among others (VIEIRA et al., 2014).
Rudolf Emil Kalman presented, in 1960, a recursive solution to the problem of discrete linear filtering from the model in the space of states plus stochastic plots referring to measurement noises and modeling errors. However, the initial version of the Kalman Filter (KF – Kalman Filter) has limitations in relation to nonlinear characteristics such as induction motors (IM), nonlinearities related to
relationship between electromagnetic velocity and flows as well as the presence of time-varying parameters associated with these variables (BARUT et al., 2007).
An alternative to KF is the Extended Kalman Filter (EKF) whose structure can be applied to linearized systems around a specific point of operation. Other variants of the Kalman Filter are available, such as the Unscented Kalman Filter (UKF) Akin et al. (2003), the EKF Combined S. Bogosyan and Gokasan (2007), Bi Input-extended Kalman Filter (Bi-EKF), among others.
In Barut (2010), the UKF is associated with the nonlinear model of MI and a method of filtering the covariance matrix. This combination generated the SRUKF (Square Root UKF), with improvements in accuracy compared to the UKF version.
In Jafarzadeh et al. (2013), the real-time implementation of the full-order EKF estimator with double input or Bi-EKF is described. The Bi-EKF is based on two mathematical models, one for the stator flow and the other for the rotor flow in the stationary frame, providing the complete estimation of all induction motor states in conjunction with the stator and rotor resistances, in a wide speed range (BARUT et al., 2012).
Another method derived from EKF is the Reduced-Order Extended Kalman Filter (ROEKF) which, with fewer variables, provides the reduction of processing time and estimation errors without compromising system performance (YIN et al., 2013) (LEITE et al., 2004).
The estimation of the speed/position of IM requires the knowledge of the voltages and currents of the stator, but the total number of variables and parameters to be treated can extend up to 10, making online processing impossible. It is worth noting that the accuracy of the estimates of the control variables depends heavily on the parameters of MI and the signal noise ratio (SNR) of the measured signals (LEITE et al., 2004).
This work proposes the application of a Reduced Order Extended Kalman Filter, especially a 5th order ROEKF, for estimating the speed and position of a three-phase induction motor based on the orthogonal components of the stator current and rotor flow.
Aiming at reducing processing time and future implementation using the Texas Instrument Manufacturer’s digital signal processor, model TMDSHVMTRPFCKIT, an alternative to the 6th and 7th orders EKFs usually applied that include stator current components, rotor electromagnetic flows and stator and rotor resistances (DADKHAH et al., 2015) (BOGOSYAN and GOKASAN, 2007) (BARUT, 2010) (BARUT et al., 2012).
The main contributions of this work refer to the ROEKF analyses in relation to the accuracy and convergence of the speed estimation under different operating and load conditions as well as the adaptation, development and testing of the techniques of off-line tuning of the covariance matrices of the modeling errors and measurements.
2. THEORETICAL FRAMEWORK
In this section will be presented the fundamental concepts related to the mathematical model of three-phase MI, Extended Kalman Filter and offline tuning techniques of the covariance matrices, necessary for the development of the 5th order ROEKF for application in a sensorless velocity control system (AMEID et al., 2016).
2.1 THE MATHEMATICAL MODEL OF THE THREE-PHASE INDUCTION MOTOR – MI
The mathematical model of MI can be described, in the stationary reference, by the components of the stator current
and rotor flowand rotor
and rotor speed
, according to equations 1 to 3 (KRAUSE et al., 2013):
2.2 THE EXTENDED KALMAN FILTER – EKF
The EKF is based on the continuous version of the Kalman Filter, represented by the following barut discrete linear equations (2010):
Where Ad and Bd are, respectively, the discrete arrays of parameters and process inputs, and W contains the plots related to system modeling errors.
The equation of the measuring variable z(k) is given by:
H being the observation matrix and v(k), the measurement noise. Both w(k) and v(k) are white noises with zero mean, independent of each other and with normal probability distribution. Kalman’s estimator presents two steps for estimation, prediction and correction. In the prediction stage, one should predict the projection of the state in the forward step
, as well as the uncertainty in the estimation
.
is the covariance matrix of the estimator error in the instant before the current observation,
is the transposition of the discrete matrix of parameters and Q is the covariance matrix of the process noises.
The correction step, necessary to achieve the estimated state, is formulated
through an equation that associates the estimated state in the prediction of the measure with the difference between the measured actual value and the predicted value. In the correction stage, you have the equations of updating the measurement as
well as the uncertainty of the estimation
.
Where P(k) is the covariance matrix of the current estimation error and I is the identity matrix.
The difference
indicates the divergence between the estimated a priori measure and the current measure z(k). The K matrix, called the Kalman Filter earnings matrix, makes it possible to minimize the covariance of the process error and is represented by: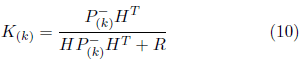
Recursively, the process is repeated from the estimated results a posteriori in the search for the prediction of a priori states.
Based on the KF version, the Extended Kalman Filter is a stochastic observer that uses noise-corrupted signals indicated for the estimation of variables in nonlinear systems represented by function f, being described generically according to equations (11) and (12):
As 
the noises w(k-1) and v (k) are not known at each step, the state vectors and measurements are approximate, considering w(k-1) = 0 and v(k) = 0 (BARUT et al., 2012):
The equations linearized through the functions F and H are Jacobian matrices calculated at each time interval. Similarly to KF equations, the steps of predicting and updating EKF measurements are written as: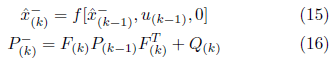
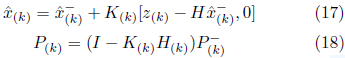
The filter gain is then calculated as:
3. DEVELOPMENT
3.1 EKF APPLICATION TO INDUCTION MOTOR CONTROL
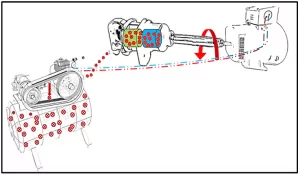
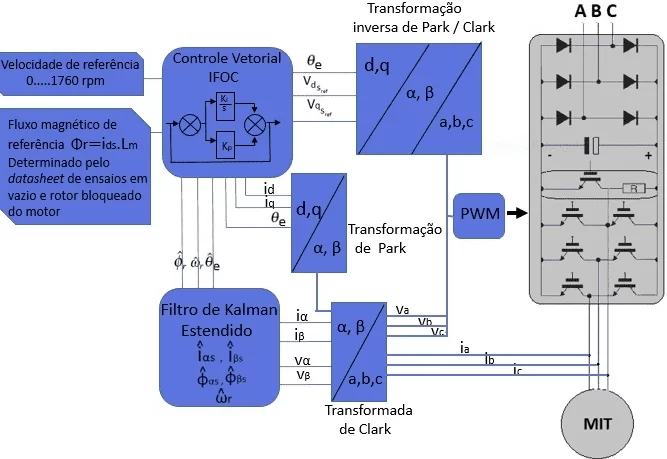
Figure 1 shows the sensorless speed control system associated with the Reduced Order Extended Kalman Filter. The proposed velocity control system is based on the indirect field oriented control (IFOC) technique, which presupposes the knowledge of rotor speed and position for transformations between reference axis systems, stator stress decoupling meshes and PI controllers used (LI and ZHONG, 2005).
Thus, the state vector to be estimated by ROEKF should be composed as:
Where the angle of the magnetic flow vector of the rotor and the estimated velocity
are calculated (EL-HALIM et al., 2012):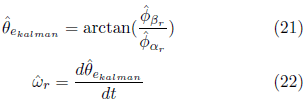
The main steps for the implementation of sensorless induction motor drive systems, using the ROEKF algorithm, are as follows (EL-HALIM et al.2012):
- Selection of the discrete induction machine model;
- Initialization of covariance matrices Q, P and R;
- Implementation of the ROEKF algorithm.
Figure 1. IFOC sensorless vector control with ROEKF speed estimator.
The diagram in Figure 2 presents the EKF operating steps.
Figure 2. EKF Operation Flowchart – Prediction and Correction Steps.
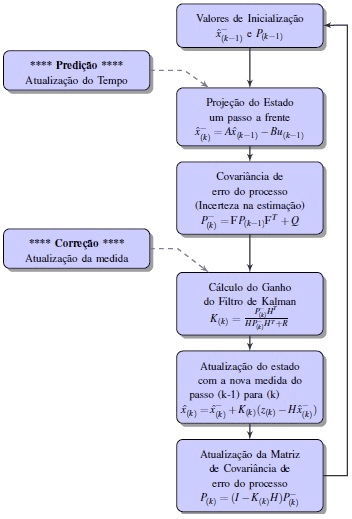
Initially, the initialization of the estimates
and the covariance matrix of p(k-1) errors are performed. Then, the update or projection of a step ahead of the state
and covariance of the errors of the estimates
, in the present state, is obtained from the array of engine parameters Ad and inputs Bd and u(k-1).
The Covariance Matrices P, Q and R, present in the process steps, are initialized according to the predisposition to uncertainties of the estimation process of the selected state variables.
The correction is made by the difference between the actual measured value and the predicted value. This difference is minimized by the action of the K gain on the estimate
and on the covariance of the error of the estimates of the P(k) system. Recursively, the values are updated, starting a new pet.
3.2 THE SPEED ESTIMATION USING EKF
Based on equations (15) to (19), the estimation of the MI velocity will be obtained using the expressions given below.
3.2.1 PREDICTION STEP
that is, F (k) is given by:
3.2.2 CORRECTION STEP
From equations (17) and (18), the vector of estimated states
and the covariances of estimation errors
are corrected according to the expressions:
At each measurement, the filter stores the matrices calculated in the previous step and returns to the beginning of the process in order to estimate the next
and
values and until EKF convergence is obtained.
3.3 OFF-LINE TUNING OF COVARIANCE MATRICES P and Q
The performance of the estimation is directly affected by the values chosen for the initialization of the Q, P and R covariance matrices, most often based on trial and error (RAYYAM et al., 2018). Several studies have been developed to meet the harmony of these matrices.
In Zerdali and Barut (2017), the authors use a differential evolution algorithm (DEA) and a multi-objective DEA (MODEA) associated with different adequacy functions.
Yin et al. (2017) uses a sequence of multiple EKF filters (MM-EKF), where different weights are assigned to each term of the set enabling the introduction of new information and, consequently, performance improvement and reduction of estimates error.
In Wallscheid et al. (2018), a joint project is presented to observe the speed, flow, torque and estimation of the electrical parameters of the IM by means of a UKF. Although the UKF showed a better linear approximation compared to the EKF, the UKF estimator showed greater sensitivity to the noise of the online measurements, leading to a lower accuracy of the speed and torque estimates.
The method proposed here for off-line tuning for the initialization of the Q and P covariance matrices was developed from Estevam et al. (2014), where the absence of mechanical equations in the EKF model hinders the convergence of speed estimation, usually obtained through the filter gain adjustment. The terms of the diagonal matrix P5x5, which are correlated with higher expectation of uncertainties in the estimation, and the terms of the diagonal matrix Q5x5 that are correlated with greater predisposition to noise of the estimation process should assume high values, respectively for p55 and q55, and lower values for q11 and q33. The influences of P and Q on the estimation of velocity were analyzed with the control system operating in open mesh, that is, the EKF is not influencing the logic of the PI controllers of the vector control.
The offline tuning of the matrices of covariance of estimation uncertainties, system noise and measurement P, Q and R, is based on knowledge about the dynamic behavior of the induction motor and the application of statistical tools through the expected value, mean, Gaussian probability distribution, variance and covariance. In this way, the values for the terms of the matrices are obtained.
4. SIMULATION RESULTS
The simulations were performed in MatLab®, considering the control in open mesh and in closed mesh using the values estimated by EKF.
The data used in the simulation were from the engine model 5K33GN2 – Marathon (Regal Beloit Corporations), available in www.regalbeloit.com/Products/Catalog. These characteristics were adopted in the simulations, aiming at the stage of practical implementation.
The speed profile included references at 90 rpm, 900 rpm and 1740 rpm, equivalent to 5%, 50% and 100% of the nominal speed of the induction motor, with frequency of skeying of IGBTs at 4kHz, under empty operating conditions and with load.
The values, estimated from the EKF algorithm, for the conjugate and electromagnetic flow, speed and mechanical position of the rotor were applied in place of the variables necessary for vector control.
The expressions (28), (29) and (30) indicate the tuned matrices for the simulation results. Where: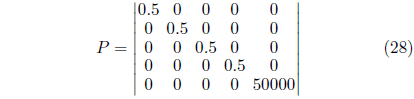
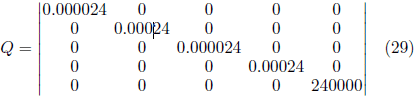
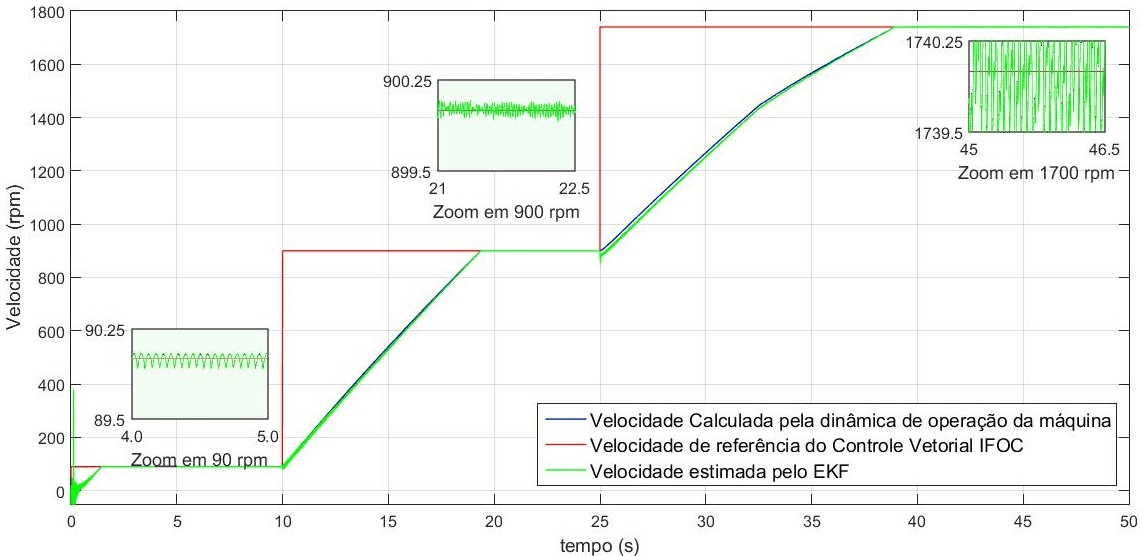
The graph shown in Figure 3 attests to EKF convergence in estimation accuracy, whether at speeds close to zero, intermediate speeds, or nominal velocity. The estimation presents values close to the reference speed and the speed calculated by the mathematical model of the induction motor.
Figure 3. Variable speed (90rpm, 900rpm and 1740 rpm).
The graph in Figure 4 shows the dynamic response of the EKF to the mechanical position of the rotor, with convergence in the estimation for values close to the mechanical position calculated by the mathematical model of the induction motor.
Figure 4. Position in radians in time (-π, 0, π).
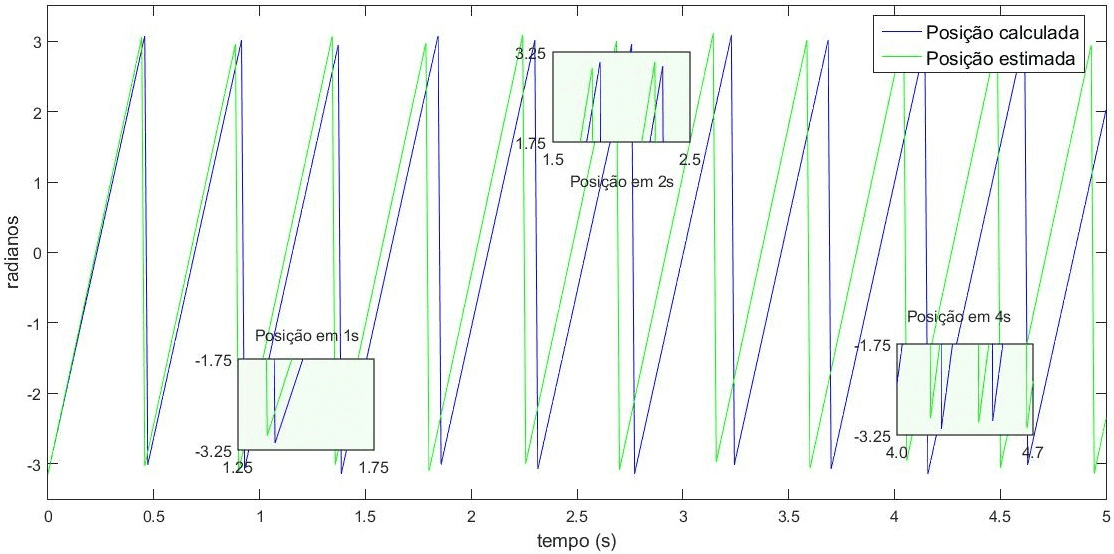
Taking the measurement of the position in radians in time, with trajectory ranging from π to π, the EKF estimator demonstrates precision and convergence at lower speeds, for example 90 rpm, as well as at average speeds. Deviations from the instant 25 seconds in Figure 3, where the speed is switched to 1740 rpm. In this case, the deviations are due to the logic of updating the estimates, which are directly linked to the P matrix of covariance of estimation errors. The uncertainties of the estimates present evidence due to the iterations of the values treated by the prediction phase and, later, correction of estimates.
The graph shown in Figure 5 outlines the variation in the mechanical position of the rotor in degrees.
Figure 5. Position in degrees 0°… 360° ranging with 90rpm, 900rpm, and 1740 rpm speed.
Where:
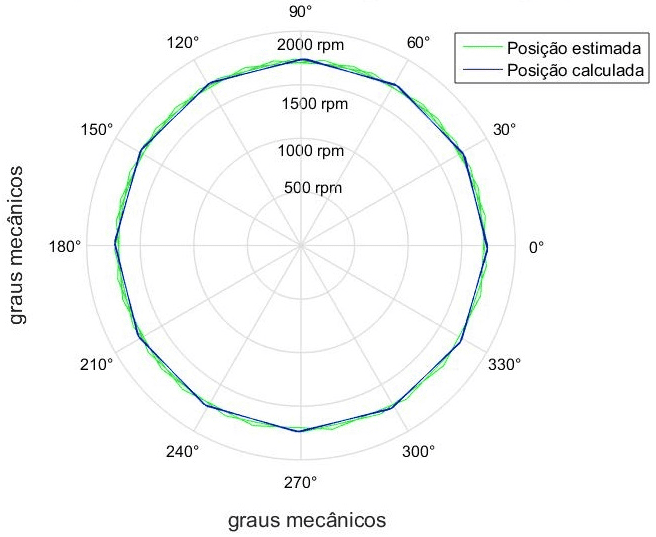
However, the presence of oscillations around the reference values is observed. These oscillations can be minimized by adjusting and tuning the EKF, basically on the q, r, p and k covariance matrices of the EKF. The largest oscillations stand out in operation at low and transient speeds.
When the P matrix of state estimator error covariance approaches zero, the Gain K matrix acts less intensely to minimize the discrepancy between the prediction values and the measures taken on the machine model.
If higher values are adopted for the elements of the noise covariance matrix (Q) there is a higher degree of uncertainty regarding the estimates of the system states, implying the increase of the K-gain matrix and an increase in the convergence speed of the estimation.
The increase in the values of the elements of the covariance matrix of the measurement noises of currents and voltages, R, implies the decrease of the matrix of the K gain, which acts in the reduction of the response speed of the EKF.
5. Conclusions
The simulated results indicate the viability of the estimator based on the indications of its ability to respond to the variations in speed imposed on the control system, as well as different load conditions imposed on the engine.
Induction motor operating conditions with different loads, up to 400N, or approximately 40kg of weight, were simulated. The charging values are based on the capacity of the engine mechanical torque, according to the manufacturer’s datasheet, being 1.1 N.m with a rated speed of 1725 rpm.
The EKF estimation presents convergence with the reference values and calculated values, according to the operation dynamics imposed on each load condition.
In possession of the results presented, it is expected to implement the solution in a hardware for digital control of engines using the digital signal processor of the Manufacturer Texas Instrument, model TMDSHVMTRPFCKIT with control plate F28035 and a three-phase asynchronous induction motor of squirrel cage type, model 5K33GN2, marathon manufacturer (Regal Beloit Corporations), available at PPGEE – PUCMINAS.
6. REFERENCES
AKIN, B., ORGUNER, U., and ERSAK, A. (2003). State estimation of induction motor using unscented Kalman Filter. IEEE Conference on Control Applications, 915-919.
AMEID, T., MENACER, A., TALHAOUI, H., HARZELLI, I., and AMMAR, A. (2016). Simulation and real-time implementation of sensorless field oriented control of induction motor at healthy state using rotor cage model and ekf. 8th International Conference on Modelling, Identification and Control, 695-700.
BARUT, M. (2010). Bi input-extended Kalman Filter based estimation technique for speed-sensorless control of induction motors. Energy Conversion and Management, 2032-2040.
BARUT, M., BOGOSYAN, S., and GOKASAN, M. (2007). Speed sensorless estimation for induction motors using extended Kalman Filters. IEEE Transactions on Industrial Electronics, 272-280.
BARUT, M., BOGOSYAN, S., and GOKASAN, M. (2008). Experimental evaluation of braided ekf for sensorless control of induction motors. IEEE Transactions on Industrial Electronics, 620-632.
BARUT, M., DEMIR, R., ZERDALI, E., and INAN, R. (2012). Real-time implementation of bi input-extended Kalman Filter-based estimator for speed-sensorless control of induction motors. IEEE Transactions on Industrial Electronics, 4197-4206.
DADKHAH, R., GIVI, H., and MEHDIPOUR, A. (2015). Parameter estimation of the induction motor using extended Kalman Filter for wide range speed control. The 6th International Power Electronics Drive Systems and Technologies Conference (PEDSTC2015), 137-142.
EL-HALIM, A.F.A., ABDULLA, M.M., and EL-ARABAWY, I.F. (2012). Simulation aides in comparison between different methodology of field oriented control of induction motor based on flux and speed estimation. 22nd International Conference on Computer Theory and Applications (ICCTA), 117-121.
ESTEVAM, E.G.A., PEIXOTO, Z.M.A., and FERREIRA, F.M.F. (2014). Aplicação EKF e as técnicas DTC-MTPA ao controle de velocidade sensorless do ipmsm. 20º Congresso Brasileiro de Automática, 1348-1355.
JAFARZADEH, S., LASCU, C., and FADALI, M.S. (2013). Square root unscented Kalman Filters for state estimation of induction motor drives. IEEE Transaction on Industry Applications, 92-99.
KRAUSE, P., WASYNCZUK, O., SUDHOFF, S., and PEKAREK, S. (2013). Analysis of Electric Machinery and Drive Systems. Wiley-IEEE Press, New Jersey.
LEITE, A.V., ARAUJO, R.E., and FREITAS, D. (2004). Full and reduced order extended Kalman Filter for speed estimation in induction motor drives: A comparative study. 35th Annual IEEE Power Electronics Specialists Conference, 2293-2299.
LI, J. and ZHONG, Y. (2005). Comparison of three Kalman Filters for speed estimation of induction machines. 40th Annual Meeting of the IEEE Industry Applications Society, 1792-1797.
RAYYAM, M., ZAZI, M., and BARRADI, Y. (2018). A new metaheuristic unscented Kalman Filter for state vector estimation of the induction motor based on ant lion optimizer. COMPEL – The international journal for computation and mathematics in electrical and electronic engineering, 1054-1068.
S. BOGOSYAN, M.B. and GOKASAN, M. (2007). Braided extended Kalman Filters for sensorless estimation in induction motors at high-low/zero speed. IET Control Theory and Applications, 987-998.
SHI, K.L., CHAN, T.F., WONG, Y.K., and HO, S.L. (2002). Speed estimation of an induction motor drive using an optimized extended Kalman Filter. IEEE Transactions on Industrial Electronics, 124-133.
VIEIRA, R., GASTALDINI, C.C., AZZOLIN, R.Z., and GRUNDLING, H.A. (2014). Sensorless sliding-mode rotor speed observer of induction machines based on magnetizing current estimation. IEEE Transactions on Industrial Electronics, 4573-4582.
WALLSCHEID, O., SCHENKE, M., and BÖCKER, J. (2018). Improving torque and speed estimation accuracy by conjoint parameter identification and unscented Kalman Filter design for induction machines. International Conference on Electrical Machines and Systems ICEMS, 1181-1186.
YIN, Z., LI, G., ZHANG, Y., LIU, J., SUN, X., and ZHONG, Y. (2017). Speed and flux observer of induction motor based on extended Kalman Filter and Markov chain. IEEE Transactions on Power Electronics, 7096-7117.
YIN, Z., ZHAO, C., LIU, J., and ZHONG, Y. (2013). Research on anti-error performance of speed and flux estimator for induction motor using robust Reduced-Order EKF. IEEE Transactions on Industrial Informatics, 1037-1046.
ZERDALI, E. and BARUT, M. (2017). The comparisons of optimized extended Kalman Filters for speed-sensorless control of induction motors. IEEE Transactions on Industrial Electronics, 4340-4351.
[1] Master in Electrical Engineering and Engineer in Electronics and Telecommunications.
[2] PhD in Electrical Engineering.
Submitted: August, 2020.
Approved: September, 2020.
