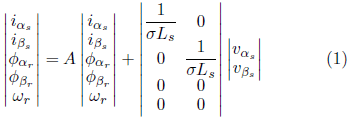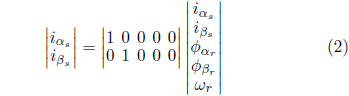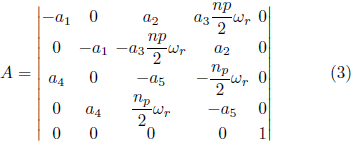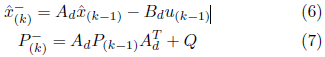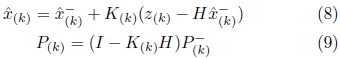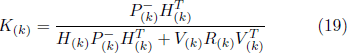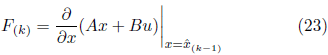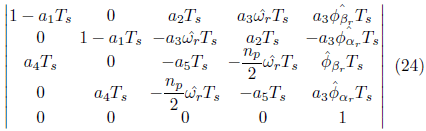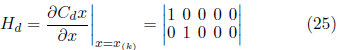ARTÍCULO ORIGINAL
LOPES, Leonardo de Magalhães [1], PEIXOTO, Zélia Myriam Assis [2]
LOPES, Leonardo de Magalhães. PEIXOTO, Zélia Myriam Assis. Un filtro Kalman extendido, con matrices de covarianza preestablecidas, aplicado al control de velocidad sin sensores de los motores de inducción trifásicos. Revista Científica Multidisciplinar Núcleo do Conhecimento. Año 05, Ed. 09, Vol. 02, págs. 109-126. Septiembre de 2020. ISSN: 2448-0959, Enlace de acceso: https://www.nucleodoconhecimento.com.br/engenharia-eletrica/filtro-de-kalman
RESUMEN
Con la aparición de métodos de control sin sensores, era necesario el uso de estimadores y/o observadores estatales para darle la robustez y precisión requeridas en el accionamiento de motores de inducción. Este trabajo se ocupa de la aplicación del Filtro Kalman Extendido (EKF) en la estimación de la velocidad y la posición del rotor, con el objetivo de la implementación de la técnica de control vectorial indirecto en un sistema de control de velocidad sin sensores para motores de inducción trifásica. El desarrollo matemático de las variables de estado del sistema asociadas con el proceso estocástico ekf se presenta en este estudio, y señala su aplicación bajo condiciones variables de velocidad y carga, que se imponen a estos motores en la vida cotidiana. La estrategia de control sin sensores se probó a través de líneas rutinarias en el Matlab® software, simulando las condiciones de funcionamiento de este tipo de motor, siendo probado su rendimiento, así como los tiempos de convergencia consistentes con los requisitos habituales de los sistemas de alto rendimiento. Las principales contribuciones de este trabajo son el uso de un EKF de orden reducido (ROEKF) y el preset de matrices de covarianza para acelerar la convergencia en las estimaciones de velocidad y posición para futuras implementaciones en procesadores de señales digitales actualmente accesibles.
Palabras clave: EKF, filtro Kalman extendido, motores de inducción, sin sensores, sistemas de accionamiento eléctrico de CA.
1. INTRODUCCIÓN
En las últimas décadas, las aplicaciones de sistemas de accionamiento de corriente alterna (CA), asociadas con técnicas de control vectorial con monitoreo de velocidad y/o posición mediante sensores electromecánicos, se han establecido como una alternativa de bajo costo, mayor robustez mecánica y alto rendimiento, equiparándose a los precursores de accionamientos de CC. Sin embargo, el uso de transductores electromecánicos sigue incluye limitaciones en cuanto a los costos de mantenimiento, fiabilidad, robustez mecánica y restricciones en el funcionamiento en entornos hostiles (DADKHAH et al., 2015).
En este contexto y a partir de la aparición de procesadores digitales de señal de alta velocidad, los sistemas de control de velocidad y/o posición sin sensores, aunque implican el aumento de la complejidad matemática y computacional de los modelos de control, se han utilizado cada vez más ya que contribuyen a la robustez mecánica y la variación de los parámetros de la máquina y las incertidumbres intrínsecas a las mediciones de señales eléctricas (BARUT et al., 2008).
Se han desarrollado varios estudios dirigidos a sistemas sin sensores, donde la técnica del modo deslizante, los sistemas adaptativos por modelo de referencia (Model Reference Adaptive System) y Extended Kalman Filter (EKF – Extend Kalman Filter), entre otros (VIEIRA et al., 2014).
Rudolf Emil Kalman presentó, en 1960, una solución recursiva al problema del filtrado lineal discreto del modelo en el espacio de estados más gráficas estocásticas que se refieren a ruidos de medición y errores de modelado. Sin embargo, la versión inicial del Filtro Kalman (KF – Kalman Filter) tiene limitaciones en relación con características no lineales como motores de inducción (MI),
relación entre la velocidad electromagnética y los flujos, así como la presencia de parámetros variables de tiempo asociados con estas variables (BARUT et al., 2007).
Una alternativa a KF es el filtro Kalman extendido (EKF) cuya estructura se puede aplicar a sistemas linealizados alrededor de un punto de operación específico. Otras variantes del filtro Kalman están disponibles, como el Unscented Kalman Filter (UKF) Akin et al. (2003), el EKF Combinado S. Bogosyan y Gokasan (2007), Bi Input-extended Kalman Filter (Bi-EKF), entre otros.
En Barut (2010), el UKF está asociado con el modelo no lineal de MI y un método de filtrado de la matriz de covarianza. Esta combinación generó el SRUKF (Square Root UKF), con mejoras en la precisión en comparación con la versión UKF.
En Jafarzadeh et al. (2013), se describe la implementación en tiempo real del estimador EKF de orden completo con doble entrada o Bi-EKF. El Bi-EKF se basa en dos modelos matemáticos, uno para el flujo del estator y el otro para el flujo del rotor en el bastidor estacionario, proporcionando la estimación completa de todos los estados del motor de inducción en conjunto con las resistencias del estator y del rotor, en un amplio rango de velocidad (BARUT et al., 2012).
Otro método derivado de EKF es el filtro Kalman extendido de orden reducido (ROEKF – Reduced-Order Extended Kalman Filter) que, con menos variables, proporciona la reducción del tiempo de procesamiento y los errores de estimación sin comprometer el rendimiento del sistema (YIN et al., 2013) (LEITE et al., 2004).
La estimación de la velocidad/posición de MI requiere el conocimiento de las tensiones y corrientes del estator, pero el número total de variables y parámetros a tratar puede extenderse hasta 10, lo que hace imposible el procesamiento en línea. Vale la pena señalar que la exactitud de las estimaciones de las variables de control depende en gran medida de los parámetros de MI y de la relación de ruido de señal (SNR – Signal Noise Ratio) de las señales medidas (LEITE et al., 2004).
Este trabajo propone la aplicación de un filtro Kalman extendido de orden reducido, especialmente un ROEKF de 5a orden, para estimar la velocidad y la posición de un motor de inducción trifásico basado en los componentes ortogonales de la corriente del estator y el flujo del rotor.
Con el objetivo de reducir el tiempo de procesamiento y la implementación futura utilizando el procesador de señal digital del fabricante de instrumentos de Texas, modelo TMDSHVMTRPFCKIT, una alternativa a las EK de 6a y 7a orden generalmente aplicadas que incluyen componentes de corriente de estator, flujos electromagnéticos del rotor y resistencias de estator y rotor (DADKHAH et al., 2015) (BOGOSYAN y GOKASAN, 2007) (BARUT, 2010) (BARUT et al., 2012).
Las principales contribuciones de este trabajo se refieren a los análisis ROEKF en relación con la precisión y convergencia de la estimación de la velocidad en diferentes condiciones de funcionamiento y carga, así como la adaptación, desarrollo y prueba de las técnicas de ajuste fuera de línea de las matrices de covarianza de los errores y mediciones de modelado.
2. MARCO TEÓRICO
En esta sección se presentarán los conceptos fundamentales relacionados con el modelo matemático de MI trifásico, Filtro Kalman Extendido y técnicas de ajuste offline de las matrices de covarianza, necesarias para el desarrollo del 5o orden ROEKF para su aplicación en un sistema de control de velocidad sin sensor (AMEID et al., 2016).
2.1 EL MODELO MATEMÁTICO DEL MOTOR DE INDUCCIÓN TRIFÁSICO – MI
El modelo matemático de MI puede ser descrito, en la referencia estacionaria, por los componentes de la corriente del estator
y el flujo del rotor
y a velocidad del rotor,
de acuerdo con las ecuaciones 1 a 3 (KRAUSE et al., 2013):
2.2 EL FILTRO KALMAN EXTENDIDO – EKF
El EKF se basa en la versión continua del filtro Kalman, representado por las siguientes ecuaciones lineales discretas Barut (2010):
Donde Ad y Bd son, respectivamente, las matrices discretas de parámetros y entradas de proceso, y W contiene los trazados relacionados con los errores de modelado del sistema.
La ecuación de la variable de medición z(k) se da por:
H siendo la matriz de observación y v(k), el ruido de medición. W(k) y v(k) son ruidos blancos con media cero, independientes entre sí y con distribución de probabilidad normal. El estimador de Kalman presenta dos pasos para la estimación, predicción y corrección. En la etapa de predicción, se debe predecir la proyección del estado en el paso hacia adelante
, así como la incertidumbre en la estimación
.
es la matriz de covarianza del error del estimador en el instante antes de la observación actual
,es la transposición de la matriz discreta de parámetros y Q es la matriz de covarianza de los ruidos del proceso.
El paso de corrección, necesario para alcanzar el estado estimado
, seformula a través de una ecuación que asocia el estado estimado en la predicción de la medida con la diferencia entre el valor real medido y el valor previsto. En la etapa de corrección, tiene las ecuaciones de actualización de la medición
,así como la incertidumbre de la estimación
.
Donde P(k) es la matriz de covarianza del error de estimación actual y yo es la matriz de identidad.
La diferencia
a indica la divergencia entre la medida a priori estimada y la medida actual z(k). La matriz K, llamada matriz de ganancias del filtro Kalman, permite minimizar la covarianza del error de proceso y está representada por: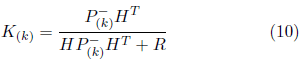
Recursivamente, el proceso se repite a partir de los resultados estimados a posteriori en la búsqueda de la predicción de los estados a priori.
Basado en la versión KF, el filtro Kalman extendido es un observador estocástico que utiliza señales dañadas por ruido indicadas para la estimación de variables en sistemas no lineales representados por la función f, siendo descrito genéricamente de acuerdo con las ecuaciones (11) y (12):
Como los ruidos w(k-1) y v (k) no se conocen en cada paso, los vectores de estado y las mediciones son aproximados, considerando w(k-1) á 0 y v(k) á 0 (BARUT et al., 2012):
Las ecuaciones linealizadas a través de las funciones F y H son matrices jacobianas calculadas en cada intervalo de tiempo. De forma similar a las ecuaciones de KF, los pasos para predecir y actualizar las mediciones EKF se escriben como: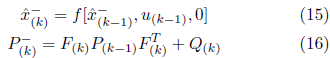
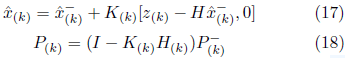A continuación, la ganancia del filtro se calcula como:
3. DESARROLLO
3.1 APLICACIÓN EKF AL CONTROL DEL MOTOR DE INDUCCIÓN
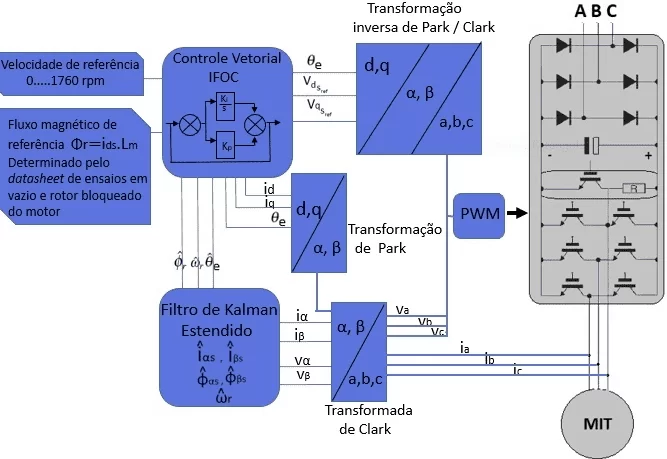
La Figura 1 muestra el sistema de control de velocidad sin sensores asociado con el Filtro Kalman Extendido de Orden Reducido. El sistema de control de velocidad propuesto se basa en la técnica de control orientado al campo indirecto (IFOC – Indirect Field Oriented Control), que presupone el conocimiento de la velocidad y la posición del rotor para las transformaciones entre sistemas de ejes de referencia, mallas de desacoplamiento de tensión de estator y controladores PI utilizados (LI y ZHONG, 2005).
Por lo tanto, el vector de estado que debe estimar ROEKF debe estar compuesto como:
Donde se calcula el ángulo del vector de flujo magnético del rotor y la
velocidad estimada (EL-HALIM et al., 2012):
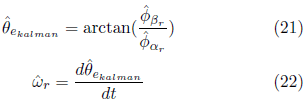Los principales pasos para la implementación de sistemas de accionamiento del motor de inducción sin sensores, utilizando el algoritmo ROEKF, son los siguientes (EL-HALIM et al.,2012):
- Selección del modelo de máquina de inducción discreta;
- Inicialización de matrices de covarianza Q, P y R;
- Implementación del algoritmo ROEKF.
Figura 1. Control vectorial sin sensores IFOC con estimador de velocidad ROEKF.
El diagrama en la Figura 2 presenta los pasos operativos EKF.
Figura 2. EKF Operation Flowchart – Pasos de predicción y corrección.
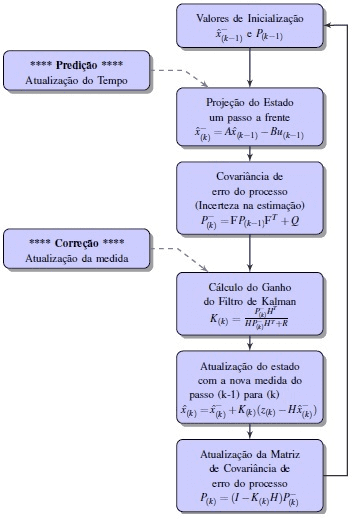
Inicialmente, se realiza la inicialización de las estimaciones 
y la matriz de covarianza de los errores p(k-1). A continuación, la actualización o proyección de un paso por delante del estado
y la covarianza de los errores de las estimaciones
, en el estado actual, se obtiene de la matriz de parámetros del motor Ad y las entradas Bd y you(k-1).
Las Matrices de Covarianza P, Q y R, presentes en los pasos del proceso, se inicializan de acuerdo con la predisposición a las incertidumbres del proceso de estimación de las variables de estado seleccionadas.
La corrección se realiza por la diferencia entre el valor medido real y el valor previsto. Esta diferencia se minimiza mediante la acción de la ganancia K en la estimación
y en la covarianza del error de las estimaciones del sistema P(k). Recursivamente, los valores se actualizan, iniciando una nueva mascota.
3.2 LA ESTIMACIÓN DE VELOCIDAD UTILIZANDO EKF
Sobre la base de las ecuaciones (15) a (19), la estimación de la velocidad de MI se obtendrá utilizando las expresiones que se indican a continuación.
3.2.1 PASO DE PREDICCIÓN
es decir, F(k) se da por:
3.2.2 PASO DE CORRECCIÓN
A partir de las ecuaciones (17) y (18), el vector de los estados estimados
y las covarianzas de los errores de estimación
se corrigen de acuerdo con las expresiones:
En cada medición, el filtro almacena las matrices calculadas en el paso anterior y vuelve al principio del proceso para estimar los siguientes valores
y
hasta que se obtenga la convergencia EKF.
3.3 AJUSTE FUERA DE LÍNEA DE LAS MATRICES DE COVARIANCIA PY Q
El rendimiento de la estimación se ve directamente afectado por los valores elegidos para la inicialización de las matrices de covarianza Q, P y R, la mayoría de las veces basadas en ensayo y error (RAYYAM et al., 2018). Se han desarrollado varios estudios para satisfacer la armonía de estas matrices.
En Zerdali y Barut (2017), los autores utilizan un algoritmo de evolución diferencial (DEA) y un DEA multiémtico (MODEA) asociado con diferentes funciones de adecuación.
Yin et al. (2017) utiliza una secuencia de múltiples filtros EKF (MM-EKF), donde se asignan diferentes pesos a cada término del conjunto que permite la introducción de nueva información y, en consecuencia, la mejora del rendimiento y la reducción del error de estimaciones.
En Wallscheid et al. (2018), se presenta un proyecto conjunto para observar la velocidad, el flujo, el par y la estimación de los parámetros eléctricos del MI mediante un UKF. Aunque el UKF mostró una mejor aproximación lineal en comparación con el EKF, el estimador UKF mostró una mayor sensibilidad al ruido de las mediciones en línea, lo que llevó a una menor precisión de las estimaciones de velocidad y par.
El método propuesto aquí para el ajuste fuera de línea para la inicialización de las matrices de covarianza Q y P se desarrolló a partir de Estevam et al. (2014), donde la ausencia de ecuaciones mecánicas en el modelo EKF dificulta la convergencia de la estimación de la velocidad, generalmente obtenida a través del ajuste de ganancia del filtro. Los términos de la matriz diagonal P5x5, que están correlacionados con una mayor expectativa de incertidumbres en la estimación, y los términos de la matriz diagonal Q5x5 que están correlacionados con una mayor predisposición al ruido del proceso de estimación deben asumir valores altos, respectivamente para p55 y q55, y valores más bajos para q11 y q33. Las influencias de P y Q en la estimación de la velocidad se analizaron con el sistema de control que funciona en malla abierta, es decir, el EKF no está influyendo en la lógica de los controladores PI del control vectorial.
El ajuste fuera de línea de las matrices de covarianza de incertidumbres de estimación, ruido del sistema y medición P, Q y R, se basa en el conocimiento sobre el comportamiento dinámico del motor de inducción y la aplicación de herramientas estadísticas a través del valor esperado, la media, la distribución de probabilidad gaussiana, la varianza y la covarianza. De esta manera, se obtienen los valores para los términos de las matrices.
4. RESULTADOS DE SIMULACIÓN
Las simulaciones se realizaron en MatLab®, teniendo en cuenta el control en malla abierta y en malla cerrada utilizando los valores estimados por EKF.
Los datos utilizados en la simulación eran del motor modelo 5K33GN2 – Marathon (Regal Beloit Corporations), disponible en www.regalbeloit.com/Products/Catalog. Estas características se adoptaron en las simulaciones, con el objetivo de en la etapa de aplicación práctica.
El perfil de velocidad incluía referencias a 90 rpm, 900 rpm y 1740 rpm, equivalentes al 5%, 50% y 100% de la velocidad nominal del motor de inducción, con frecuencia de captura de IGBT a 4 kHz, en condiciones de funcionamiento vacías y con carga.
Los valores, estimados a partir del algoritmo EKF, para el flujo conjugado y electromagnético, la velocidad y la posición mecánica del rotor se aplicaron en lugar de las variables necesarias para el control vectorial.
Las expresiones (28), (29) y (30) indican las matrices sintonizadas para los resultados de la simulación. Dónde:
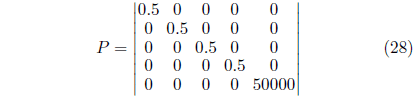
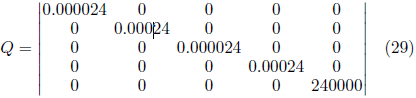
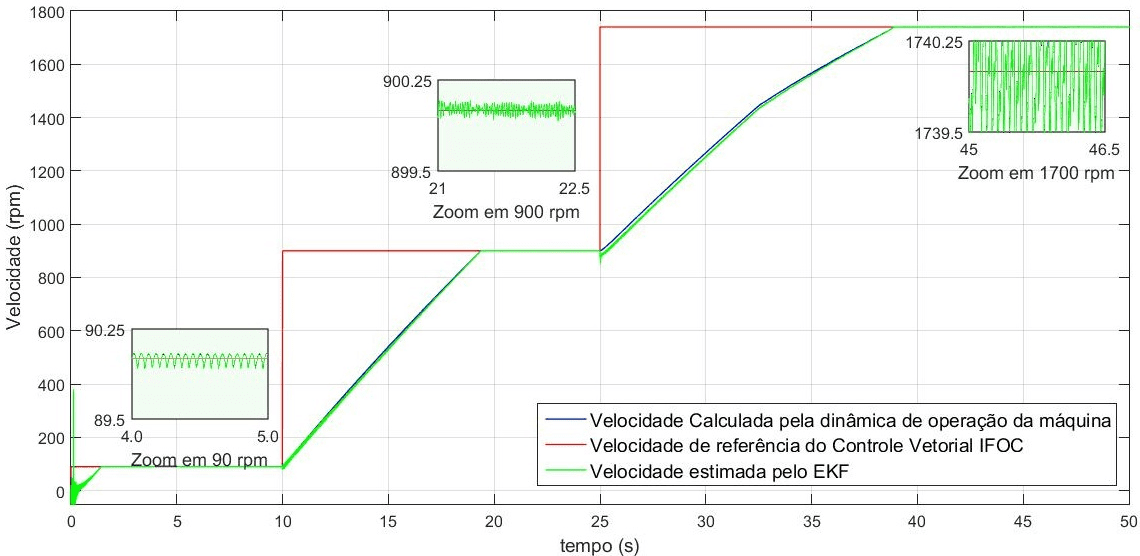
El gráfico que se muestra en la Figura 3 da fe de la convergencia ekf en la precisión de la estimación, ya sea a velocidades cercanas a cero, velocidades intermedias o velocidad nominal. La estimación presenta valores cercanos a la velocidad de referencia y a la velocidad calculada por el modelo matemático del motor de inducción.
Figura 3. Velocidad variable (90rpm, 900rpm y 1740 rpm).
El gráfico de la Figura 4 muestra la respuesta dinámica del EKF a la posición mecánica del rotor, con convergencia en la estimación de valores cercanos a la posición mecánica calculada por el modelo matemático del motor de inducción.
Figura 4. Posición en radianes en el tiempo (-π, 0, π).
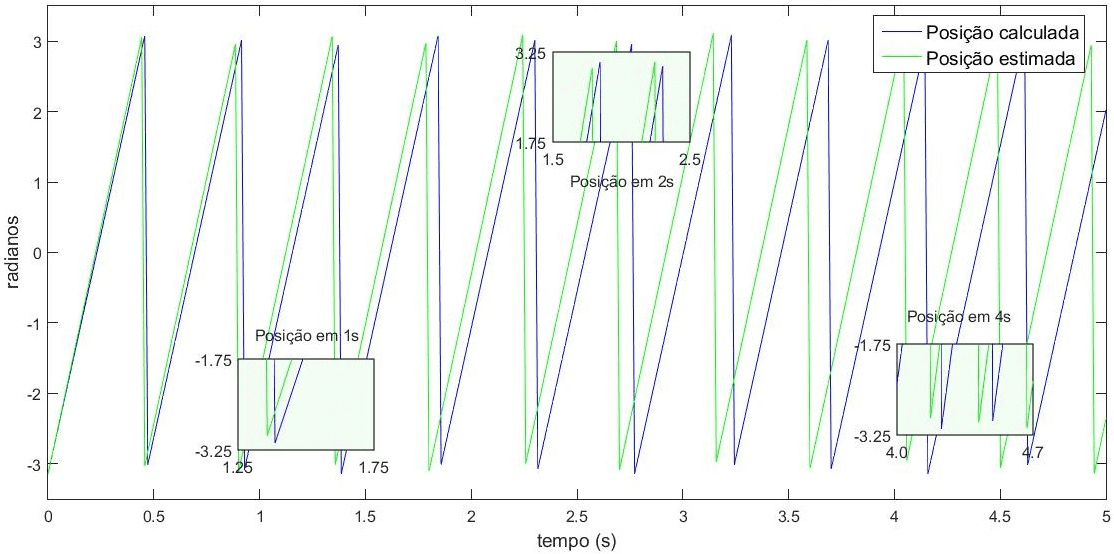
Tomando la medición de la posición en radianes en el tiempo, con una trayectoria que va desde π a π, el estimador EKF demuestra precisión y convergencia a velocidades más bajas, por ejemplo 90 rpm, así como a velocidades medias. Desviaciones del instante 25 segundos en la Figura 3, donde la velocidad se cambia a 1740 rpm. En este caso, las desviaciones se deben a la lógica de actualización de las estimaciones, que están directamente vinculadas a la matriz P de covarianza de errores de estimación. Las incertidumbres de las estimaciones presentan evidencia debido a las iteraciones de los valores tratados por la fase de predicción y, posteriormente, la corrección de las estimaciones.
El gráfico que se muestra en la Figura 5 describe la variación en la posición mecánica del rotor en grados.
Figura 5. Posición en grados 0o… 360o con 90 rpm, 900 rpm y 1740 rpm de velocidad.
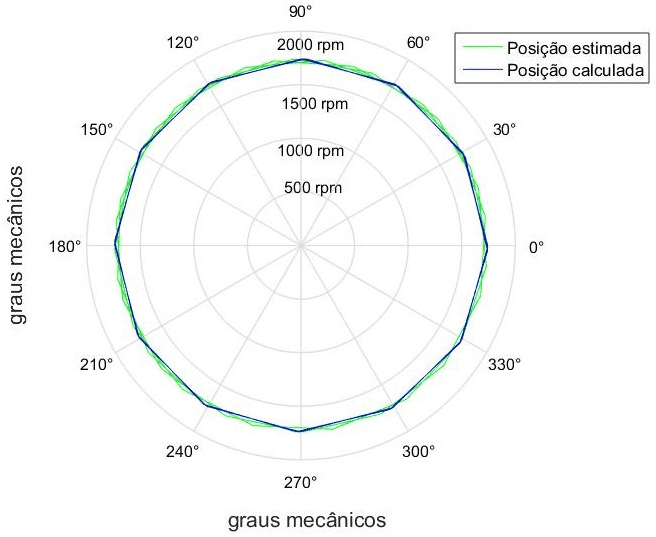
Dónde:
Sin embargo, se observa la presencia de oscilaciones alrededor de los valores de referencia. Estas oscilaciones se pueden minimizar ajustando y ajustando el EKF, básicamente en las matrices de covarianza Q, R, P y k del EKF. Las oscilaciones más grandes se destacan en funcionamiento a velocidades bajas y transitorias.
Cuando la matriz P de la covarianza de error del estimador de estado se acerca a cero, la matriz Gain K actúa con menos intensidad para minimizar la discrepancia entre los valores de predicción y las medidas tomadas en el modelo de máquina.
Si se adoptan valores más altos para los elementos de la matriz de covarianza de ruido (Q), existe un mayor grado de incertidumbre con respecto a las estimaciones de los estados del sistema, lo que implica el aumento de la matriz de ganancia K y un aumento en la velocidad de convergencia de la estimación.
El aumento en los valores de los elementos de la matriz de covarianza de los ruidos de medición de corrientes y voltajes, R, implica la disminución de la matriz de la ganancia K, que actúa en la reducción de la velocidad de respuesta del EKF.
5. Conclusiones
Los resultados simulados indican la viabilidad del estimador en función de las indicaciones de su capacidad para responder a las variaciones de velocidad impuestas al sistema de control, así como a las diferentes condiciones de carga impuestas al motor.
Se simularon condiciones de funcionamiento del motor de inducción con diferentes cargas, hasta 400N, o aproximadamente 40 kg de peso. Los valores de carga se basan en la capacidad del par mecánico del motor, según la hoja de datos del fabricante, siendo 1.1 N.m con una velocidad nominal de 1725 rpm.
La estimación EKF presenta convergencia con los valores de referencia y los valores calculados, de acuerdo con la dinámica de operación impuesta a cada condición de carga.
En posesión de los resultados presentados, se espera implementar la solución en un hardware para el control digital de motores utilizando el procesador de señal digital del fabricante Texas Instrument, modelo TMDSHVMTRPFCKIT con placa de control F28035 y un motor de inducción asíncrono trifásico de tipo jaula de ardilla, modelo 5K33GN2, fabricante de maratón (Regal Beloit Corporations), disponible en PPGEE – PUCMINAS.
6. REFERENCIAS
AKIN, B., ORGUNER, U., and ERSAK, A. (2003). State estimation of induction motor using unscented Kalman Filter. IEEE Conference on Control Applications, 915-919.
AMEID, T., MENACER, A., TALHAOUI, H., HARZELLI, I., and AMMAR, A. (2016). Simulation and real-time implementation of sensorless field oriented control of induction motor at healthy state using rotor cage model and ekf. 8th International Conference on Modelling, Identification and Control, 695-700.
BARUT, M. (2010). Bi input-extended Kalman Filter based estimation technique for speed-sensorless control of induction motors. Energy Conversion and Management, 2032-2040.
BARUT, M., BOGOSYAN, S., and GOKASAN, M. (2007). Speed sensorless estimation for induction motors using extended Kalman Filters. IEEE Transactions on Industrial Electronics, 272-280.
BARUT, M., BOGOSYAN, S., and GOKASAN, M. (2008). Experimental evaluation of braided ekf for sensorless control of induction motors. IEEE Transactions on Industrial Electronics, 620-632.
BARUT, M., DEMIR, R., ZERDALI, E., and INAN, R. (2012). Real-time implementation of bi input-extended Kalman Filter-based estimator for speed-sensorless control of induction motors. IEEE Transactions on Industrial Electronics, 4197-4206.
DADKHAH, R., GIVI, H., and MEHDIPOUR, A. (2015). Parameter estimation of the induction motor using extended Kalman Filter for wide range speed control. The 6th International Power Electronics Drive Systems and Technologies Conference (PEDSTC2015), 137-142.
EL-HALIM, A.F.A., ABDULLA, M.M., and EL-ARABAWY, I.F. (2012). Simulation aides in comparison between different methodology of field oriented control of induction motor based on flux and speed estimation. 22nd International Conference on Computer Theory and Applications (ICCTA), 117-121.
ESTEVAM, E.G.A., PEIXOTO, Z.M.A., and FERREIRA, F.M.F. (2014). Aplicação EKF e as técnicas DTC-MTPA ao controle de velocidade sensorless do ipmsm. 20º Congresso Brasileiro de Automática, 1348-1355.
JAFARZADEH, S., LASCU, C., and FADALI, M.S. (2013). Square root unscented Kalman Filters for state estimation of induction motor drives. IEEE Transaction on Industry Applications, 92-99.
KRAUSE, P., WASYNCZUK, O., SUDHOFF, S., and PEKAREK, S. (2013). Analysis of Electric Machinery and Drive Systems. Wiley-IEEE Press, New Jersey.
LEITE, A.V., ARAUJO, R.E., and FREITAS, D. (2004). Full and reduced order extended Kalman Filter for speed estimation in induction motor drives: A comparative study. 35th Annual IEEE Power Electronics Specialists Conference, 2293-2299.
LI, J. and ZHONG, Y. (2005). Comparison of three Kalman Filters for speed estimation of induction machines. 40th Annual Meeting of the IEEE Industry Applications Society, 1792-1797.
RAYYAM, M., ZAZI, M., and BARRADI, Y. (2018). A new metaheuristic unscented Kalman Filter for state vector estimation of the induction motor based on ant lion optimizer. COMPEL – The international journal for computation and mathematics in electrical and electronic engineering, 1054-1068.
S. BOGOSYAN, M.B. and GOKASAN, M. (2007). Braided extended Kalman Filters for sensorless estimation in induction motors at high-low/zero speed. IET Control Theory and Applications, 987-998.
SHI, K.L., CHAN, T.F., WONG, Y.K., and HO, S.L. (2002). Speed estimation of an induction motor drive using an optimized extended Kalman Filter. IEEE Transactions on Industrial Electronics, 124-133.
VIEIRA, R., GASTALDINI, C.C., AZZOLIN, R.Z., and GRUNDLING, H.A. (2014). Sensorless sliding-mode rotor speed observer of induction machines based on magnetizing current estimation. IEEE Transactions on Industrial Electronics, 4573-4582.
WALLSCHEID, O., SCHENKE, M., and BÖCKER, J. (2018). Improving torque and speed estimation accuracy by conjoint parameter identification and unscented Kalman Filter design for induction machines. International Conference on Electrical Machines and Systems ICEMS, 1181-1186.
YIN, Z., LI, G., ZHANG, Y., LIU, J., SUN, X., and ZHONG, Y. (2017). Speed and flux observer of induction motor based on extended Kalman Filter and Markov chain. IEEE Transactions on Power Electronics, 7096-7117.
YIN, Z., ZHAO, C., LIU, J., and ZHONG, Y. (2013). Research on anti-error performance of speed and flux estimator for induction motor using robust Reduced-Order EKF. IEEE Transactions on Industrial Informatics, 1037-1046.
ZERDALI, E. and BARUT, M. (2017). The comparisons of optimized extended Kalman Filters for speed-sensorless control of induction motors. IEEE Transactions on Industrial Electronics, 4340-4351.
[1] Máster en Ingeniería Eléctrica e Ingeniero en Electrónica y Telecomunicaciones.
[2] Doctor en Ingeniería Eléctrica.
Enviado: Agosto, 2020.
Aprobado: Septiembre de 2020.
