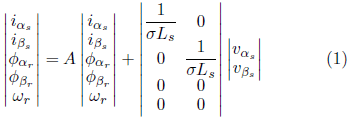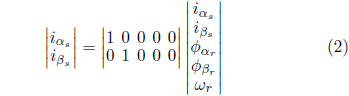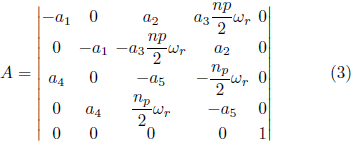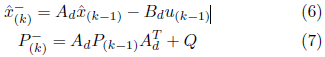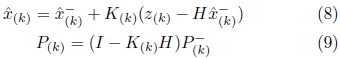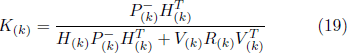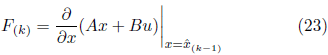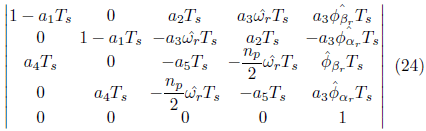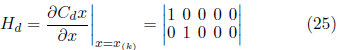ARTICOLO ORIGINALE
LOPES, Leonardo de Magalhães [1], PEIXOTO, Zélia Myriam Assis [2]
LOPES, Leonardo de Magalhães. PEIXOTO, Zélia Myriam Assis. Un filtro Kalman esteso, con matrici di covarianza preimpostate, applicato al controllo della velocità senza sensori dei motori a induzione a tre fasi. Revista Científica Multidisciplinar Núcleo do Conhecimento. Anno 05, Ed. 09, Vol. 02, pp. 109-126. settembre 2020. ISSN: 2448-0959, collegamento di accesso: https://www.nucleodoconhecimento.com.br/ingegneria-elettrica/filtro-kalman-esteso
RIEPILOGO
Con l’emergere di metodi di controllo senza sensori, era necessario l’uso di stimatori e/o osservatori statali per dargli la robustezza e la precisione richieste nella trazione dei motori a induzione. Questo lavoro riguarda l’applicazione dell’Extended Kalman Filter (EKF) nella stima della velocità e della posizione del rotore, mirando all’implementazione della tecnica di controllo vettoriale indiretto in un sistema di controllo della velocità senza sensori per i motori a induzione in tre fasi. Lo sviluppo matematico delle variabili di stato del sistema associate al processo stocastico EKF è presentato in questo studio, e sottolinea la sua applicazione in condizioni di velocità e carico variabili, che vengono imposte a questi motori nella vita di tutti i giorni. La strategia di controllo senza sensori è stata testata attraverso linee di routine nel software Matlab®, simulando le condizioni operative di questo tipo di motore, essendo provate le sue prestazioni, così come i tempi di convergenza coerenti con i soliti requisiti dei sistemi ad alte prestazioni. I principali contributi di questo lavoro sono l’uso di un EKF (ROEKF) a ordine ridotto e il preset di matrici di covarianza per accelerare la convergenza nelle stime di velocità e posizione per le implementazioni future nei processori di segnale digitali attualmente accessibili.
Parole chiave: EKF, Extended Kalman Filter, Induction Motors, Sensorless, AC electric drive systems.
1. INTRODUZIONE
Negli ultimi decenni, le applicazioni dei sistemi di azionamento a corrente alternata (CA), associate a tecniche di controllo vettoriale con monitoraggio della velocità e/o della posizione mediante sensori elettromeccanici, si sono affermate come alternativa a basso costo, maggiore robustezza meccanica e prestazioni elevate, equiparando ai precursori delle unità CA. Tuttavia, l’uso di trasduttori elettromeccanici include ancora limitazioni per quanto riguarda i costi di manutenzione, l’affidabilità, la robustezza meccanica e le restrizioni al funzionamento in ambienti difficili (DADKHAH et al., 2015).
In questo contesto e dall’emergere di processori digitali ad alta velocità, i sistemi di controllo della velocità e/o la posizione senza sensori, sebbene implicano l’aumento della complessità matematica e computazionale dei modelli di controllo, sono stati sempre più utilizzati in quanto contribuiscono alla robustezza meccanica e alla variazione dei parametri della macchina e delle incertezze intrinseche alle misurazioni dei segnali elettrici (BARUT et al., 2008).
Sono stati sviluppati diversi studi che mirano a sistemi senza sensori, dove la tecnica della modalità di scorrimento, i sistemi adattivi per modello di riferimento (Model Reference Adaptive System) e Extended Kalman Filter (EKF), tra gli altri (VIEIRA et al., 2014).
Rudolf Emil Kalman presentò, nel 1960, una soluzione ricorsiva al problema del filtraggio lineare discreto dal modello nello spazio degli stati più trame stocastistiche che si riferiscono ai rumori di misurazione e agli errori di modellazione. Tuttavia, la versione iniziale del filtro Kalman ((KF – Kalman Filter) presenta limitazioni in relazione alle caratteristiche non lineari come i motori a induzione (MI), le non
relazione tra velocità elettromagnetica e flussi, nonché la presenza di parametri variabili nel tempo associati a queste variabili (BARUT et al., 2007).
Un’alternativa a KF è l’Extended Kalman Filter (EKF) la cui struttura può essere applicata ai sistemi linearizzati intorno a un punto di funzionamento specifico. Sono disponibili altre varianti del filtro Kalman, come il Filtro Kalman Non profumato (UKF) Akin et al. (2003), l’EKF Combined S. Bogosyan and Gokasan (2007), Bi Input-extended Kalman Filter (Bi-EKF), tra gli altri.
In Barut (2010), l’UKF è associato al modello non lineare di MI e a un metodo per filtrare la matrice di covarianza. Questa combinazione ha generato l’SRUKF (Square Root UKF), con miglioramenti nella precisione rispetto alla versione UKF.
A Jafarzadeh et al. (2013), viene descritta l’implementazione in tempo reale dello stimatore EKF con doppio input o Bi-EKF. Il Bi-EKF si basa su due modelli matematici, uno per il flusso di stator e l’altro per il flusso del rotore nel telaio stazionario, fornendo la stima completa di tutti gli stati motori di induzione in combinazione con le resistenze di stator e rotore, in un’ampia gamma di velocità (BARUT et al., 2012).
Un altro metodo derivato da EKF è il filtro Ariduto Esteso Kalman (Reduced-Order Extended Kalman Filter) che, con meno variabili, fornisce la riduzione del tempo di elaborazione e degli errori di stima senza compromettere le prestazioni del sistema (YIN et al., 2013) (LEITE et al., 2004).
La stima della velocità/posizione di MI richiede la conoscenza delle tensioni e delle correnti dello stator, ma il numero totale di variabili e parametri da trattare può estendersi fino a 10, rendendo impossibile l’elaborazione online. Vale la pena notare che l’accuratezza delle stime delle variabili di controllo dipende in larga misura dai PARAMETRI di MI e dal rapporto di rumore del segnale (SNR – Signal Noise Ratio) dei segnali misurati (LEITE et al., 2004).
Questo lavoro propone l’applicazione di un filtro Kalman esteso a ordine ridotto, in particolare un ROEKF di quinto ordine, per stimare la velocità e la posizione di un motore a induzione a tre fasi basato sui componenti ortogonali della corrente dello stato e del flusso del rotore.
Con l’obiettivo di ridurre i tempi di elaborazione e l’implementazione futura utilizzando il processore di segnale digitale del Texas Instrument Manufacturer, il modello TMDSHVMTRPFCKIT, un’alternativa agli EKF del 6o e 7o ordine di solito applicati che includono componenti correnti di stator, flussi elettromagnetici del rotore e resistenze di stator e rotore (DADKHAHh et al., 2015) (BOGOSYAN E GOKASAN, 2007) (BARUT, 2010) (BARUT et al., 2012).
I principali contributi di questo lavoro si riferiscono alle analisi ROEKF in relazione all’accuratezza e alla convergenza della stima della velocità in diverse condizioni operative e di carico, nonché all’adattamento, allo sviluppo e alla sperimentazione delle tecniche di messa a punto off-line delle matrici di covarianza degli errori e delle misurazioni di modellazione.
2. QUADRO TEORICO
In questa sezione verranno presentati i concetti fondamentali relativi al modello matematico di MI a tre fasi, Extended Kalman Filter e tecniche di ottimizzazione offline delle matrici di covarianza, necessarie per lo sviluppo del ROEKF del quinto ordine per l’applicazione in un sistema di controllo della velocità senza sensori (AMEID et al., 2016).
2.1 IL MODELLO MATEMATICO DEL MOTORE A INDUZIONE IN TRE FASI – MI
Il modello matematico di MI può essere descritto, nel riferimento stazionario, dai componenti della corrente dello stato
e del flusso del rotore
e della velocità del rotor
e, secondo le equazioni da 1 a 3 (KRAUSE et al., 2013):
2.2 IL FILTRO KALMAN ESTESO – EKF
L’EKF si basa sulla versione continua del filtro Kalman, rappresentata dalle seguenti equazioni lineari discrete barut (2010):
Dove Ad e Bd sono, rispettivamente, le matrici discrete di parametri e input di processo e W contiene i grafici relativi agli errori di modellazione del sistema.
L’equazione della variabile di misurazione z(k) è data da:
H è la matrice di osservazione e v(k), il rumore di misurazione. Sia w(k) che v(k) sono rumori bianchi con media zero, indipendenti l’uno dall’altro e con distribuzione di probabilità normale. Lo stimatore di Kalman presenta due passaggi per la stima, la previsione e la correzione. Nella fase di previsione, si dovrebbe prevedere la proiezione dello stato nella fase in avanti,
così come l’incertezza nella stima
.
è la matrice di covarianza dell’errore dello stimatore nell’istante prima dell’osservazione corrente,
è la trasposizione della matrice discreta dei parametri e Q è la matrice di covarianza dei rumori di processo.
Il passaggio di correzione, necessario per ottenere lo stato stimato
,viene formulato tramite un’equazione che associa lo stato stimato nella stima della misura alla differenza tra il valore effettivo misurato e il valore stimato. Nella fase di correzione, si hanno le equazioni di aggiornare la misura
così come l’incertezza della stima
.
Dove P(k) è la matrice di covarianza dell’errore di stima corrente e I è la matrice di identità.
La differenza
indica la divergenza tra la misura a priori stimata e la misura corrente z(k). La matrice K, chiamata matrice di guadagni Kalman Filter, consente di ridurre al minimo la covarianza dell’errore di processo ed è rappres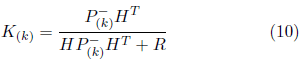
entata da:
In modo ricorsivo, il processo viene ripetuto dai risultati stimati a posteriori nella ricerca della stima di uno stato priori.
Basato sulla versione KF, il filtro esteso Kalman è un osservatore stocastico che utilizza segnali danneggiati dal rumore indicati per la stima delle variabili nei sistemi non lineari rappresentati dalla funzione f, essendo descritto genericamente in base alle equazioni (11) e (12):
Poiché i rumori w(k-1) e v (k) non sono noti ad ogni fase, i vettori di stato e le misure sono approssimativi, considerando w(k-1) – 0 e v(k) – 0 (BARUT et al., 2012):
Le equazioni linearizzate tramite le funzioni F e H sono matrici giacobite calcolate in ogni intervallo di tempo. Analogamente alle equazioni KF, i passaggi per prevedere e aggiornare le misurazioni EKF sono scritti come:
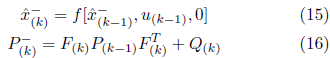
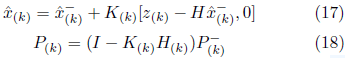Il guadagno del filtro viene quindi calcolato come:
3. SVILUPPO
3.1 APPLICAZIONE EKF PER IL CONTROLLO DEL MOTORE A INDUZIONE
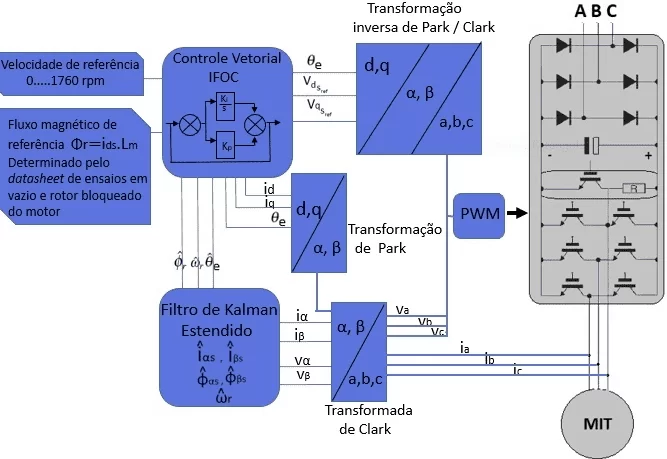
Figura 1 Mostra il sistema di controllo della velocità senza sensori associato al filtro Kalman esteso ordine ridotto. Il sistema di controllo della velocità proposto si basa sulla tecnica (IFOC – Indirect Field Oriented Control), che presuppone la conoscenza della velocità e della posizione del rotore per le trasformazioni tra i sistemi dell’asse di riferimento, le mesh di disaccoppiamento della sollecitazione statir e i controller PI utilizzati (LI e ZHONG, 2005).
Pertanto, il vettore di stato da stimare da ROEKF deve essere composto come:
Dove viene calcolato l’angolo del vettore di flusso magnetico del rotore e la 
velocità stimata (EL-HALIM et al., 2012):
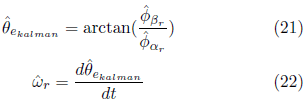I passaggi principali per l’implementazione di sistemi di azionamento motore a induzione senza sensori, utilizzando l’algoritmo ROEKF, sono i seguenti (EL-HALIM et al. 2012):
- Selezione del modello di macchina a induzione discreta;
- Inizializzazione delle matrici di covarianza Q, P e R;
- Implementazione dell’algoritmo ROEKF.
come illustrato nella Figura 1. Controllo vettoriale senza sensori IFOC con stima della velocità ROEKF.
Il diagramma in Figura 2 presenta i passaggi operativi EKF.
come illustrato nella Figura 2. Diagramma di flusso dell’operazione EKF – Passaggi di stima e correzione.
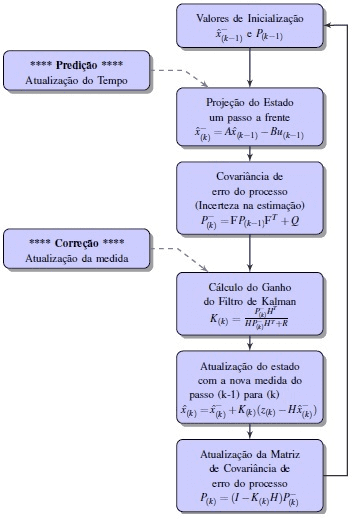
Inizialmente, viene eseguita l’inizializzazione delle stime
e della matrice di covarianza degli errori p(k-1). Quindi, l’aggiornamento o la proiezione di un passo avanti allo stato
e alla covarianza degli errori delle stime
, nello stato attuale, si ottiene dalla matrice di parametri del motore Ad e input Bd e you(k-1).
Le matrici di covarianza P, Q e R, presenti nelle fasi del processo, vengono inizializzate in base alla predisposizione alle incertezze del processo di stima delle variabili di stato selezionate.
La correzione viene effettuata dalla differenza tra il valore misurato effettivo e il valore previsto. Questa differenza è ridotta al minimo dall’azione del guadagno K sullastima
e dalla covarianza dell’errore delle stime del sistema P(k). In modo ricorsivo, i valori vengono aggiornati, avviando un nuovo animale domestico.
3.2 LA STIMA DELLA VELOCITÀ CON EKF
Sulla base di equazioni (15) a (19), la stima della velocità MI sarà ottenuta utilizzando le espressioni fornite di seguito.
3.2.1 FASE DI PREVISIONE
ad esempio F(k) è dato da:
3.2.2 PASSO DI CORREZIONE
Dalle equazioni (17) e (18), il vettore degli stati stimati
e la covarianza degli errori di stima
vengono corretti secondo le espressioni:
misurazione, il filtro memorizza le matrici calcolate nel passaggio precedente e torna all’inizio del processo per stimare i valor successivi
e
fino a quando non si ottiene la convergenza EKF.
3.3 REGOLAZIONE OFF LINE DELLE MATRICI DI COVARIANZA P E Q
Le prestazioni della stima sono direttamente influenzate dai valori scelti per l’inizializzazione delle matrici di covarianza Q, P e R, il più delle volte basate su tentativi ed errori (RAYYAM et al., 2018). Diversi studi sono stati sviluppati per soddisfare l’armonia di queste matrici.
In Zerdali e Barut (2017), gli autori utilizzano un algoritmo di evoluzione differenziale (DEA) e un DEA multi-obiettivo (MODEA) associato a diverse funzioni di adeguatezza.
Yin et al. (2017) utilizza una sequenza di più filtri EKF (MM-EKF), in cui a ogni termine del set vengono assegnati pesi diversi che consentono l’introduzione di nuove informazioni e, di conseguenza, il miglioramento delle prestazioni e la riduzione dell’errore di stima.
In Wallscheid et al. (2018), viene presentato un progetto congiunto per osservare la velocità, il flusso, la coppia e la stima dei parametri elettrici dell’IM mediante un UKF. Anche se l’UKF ha mostrato una migliore approssimazione lineare rispetto all’EKF, lo stimatore ukF ha mostrato una maggiore sensibilità al rumore delle misurazioni online, portando a una minore precisione delle stime di velocità e coppia.
Il metodo proposto qui per l’ottimizzazione off-line per l’inizializzazione delle matrici di covarianza Q e P è stato sviluppato da Estevam et al. (2014), dove l’assenza di equazioni meccaniche nel modello EKF ostacola la convergenza della stima della velocità, di solito ottenuta attraverso la regolazione del guadagno del filtro. I termini della matrice diagonale P5x5, che sono correlati con una maggiore aspettativa di incertezze nella stima, e i termini della matrice diagonale Q5x5 che sono correlati con una maggiore predisposizione al rumore del processo di stima dovrebbero assumere valori elevati, rispettivamente per p55 e q55, e valori inferiori per q11 e q33. Le influenze di P e Q sulla stima della velocità sono state analizzate con il sistema di controllo che opera in mesh aperta, cioè l’EKF non sta influenzando la logica dei controller PI del controllo vettoriale.
L’ottimizzazione offline delle matrici di covarianza delle incertezze di stima, del rumore del sistema e della misurazione P, Q e R, si basa sulla conoscenza del comportamento dinamico del motore di induzione e sull’applicazione di strumenti statistici attraverso il valore previsto, la media, la distribuzione della probabilità gaussiana, la varianza e la covarianza. In questo modo, si ottengono i valori per i termini delle matrici.
4. RISULTATI DELLA SIMULAZIONE
Le simulazioni sono state eseguite in MatLab®, considerando il controllo in mesh aperta e in mesh chiusa utilizzando i valori stimati da EKF.
I dati utilizzati nella simulazione provengono dal modello motore 5K33GN2 – Marathon (Regal Beloit Corporations), disponibile in www.regalbeloit.com/Products/Catalog. Queste caratteristiche sono state adottate nelle simulazioni, mirando alla fase di attuazione pratica.
Il profilo di velocità comprendeva riferimenti a 90 rpm, 900 rpm e 1740 rpm, equivalenti al 5%, 50% e 100% della velocità nominale del motore a induzione, con frequenza di skeying di IGBT a 4kHz, in condizioni operative vuote e con carico.
I valori, stimati dall’algoritmo EKF, per il flusso coniugato ed elettromagnetico, la velocità e la posizione meccanica del rotore sono stati applicati al posto delle variabili necessarie per il controllo vettoriale.
Le espressioni (28), (29) e (30) indicano le matrici ottimizzate per i risultati della simulazione. Dove:
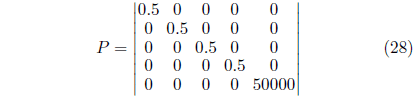
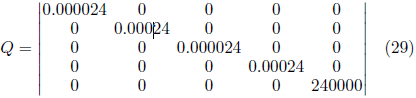
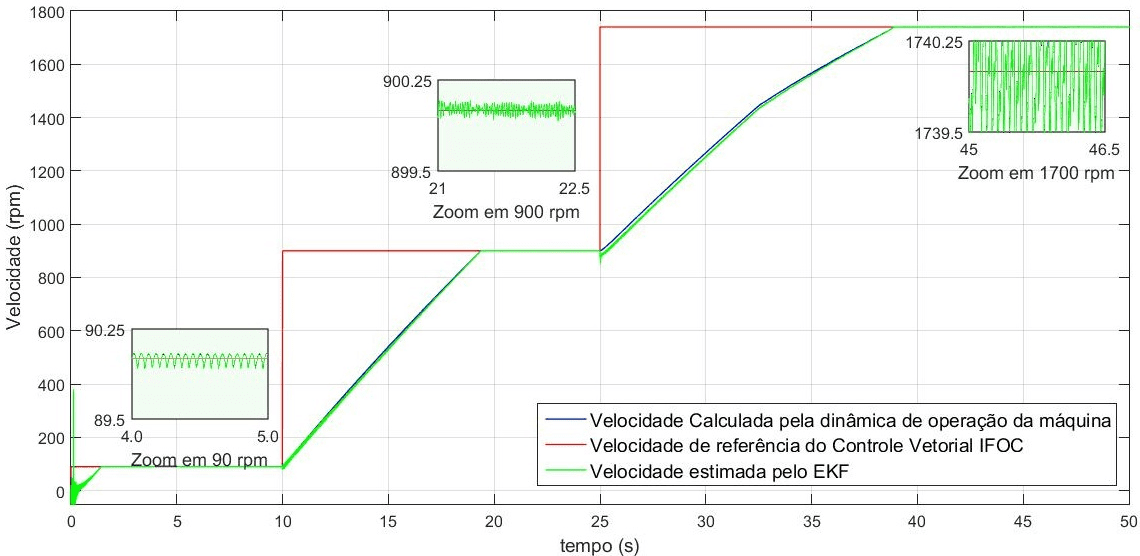
Il grafico mostrato nella Figura 3 attesta la convergenza ekf nella precisione di stima, sia a velocità vicine allo zero, velocità intermedie o velocità nominale. La stima presenta valori vicini alla velocità di riferimento e alla velocità calcolata dal modello matematico del motore di induzione.
come illustrato nella figura 3. Velocità variabile (90rpm, 900rpm e 1740 rpm).
Il grafico nella Figura 4 mostra la risposta dinamica dell’EKF alla posizione meccanica del rotore, con convergenza nella stima per i valori vicini alla posizione meccanica calcolata dal modello matematico del motore di induzione.
come illustrato nella Figura 4. Posizione in radianti nel tempo (-π, 0, π).
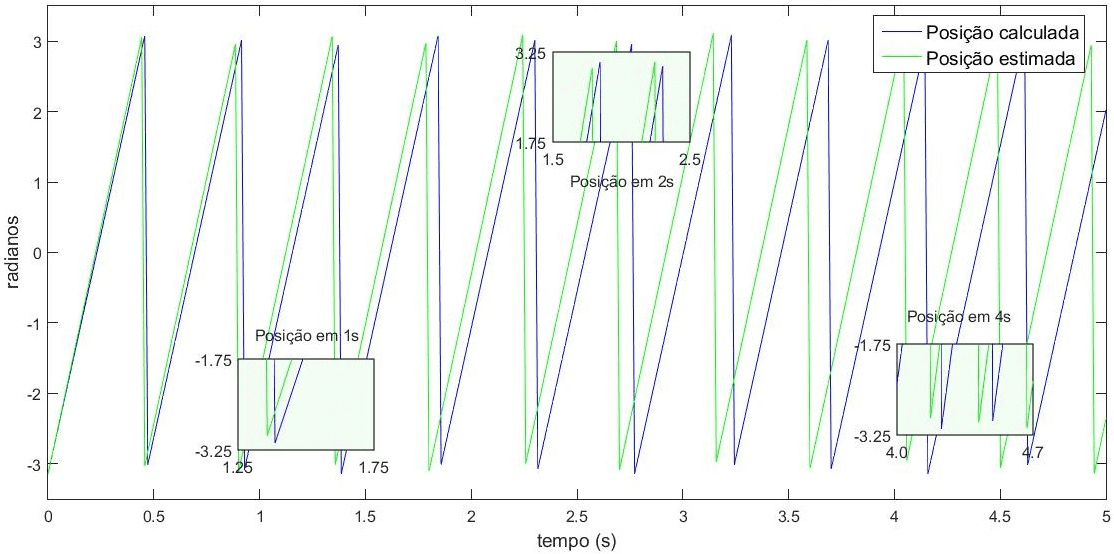
Prendendo la misurazione della posizione in radianti nel tempo, con traiettoria che va da π a π, lo stimatore EKF dimostra precisione e convergenza a velocità inferiori, ad esempio 90 rpm, così come a velocità medie. Deviazioni dall’istante 25 secondi in Figura 3, dove la velocità è commutata a 1740 rpm. In questo caso, le deviazioni sono dovute alla logica di aggiornamento delle stime, che sono direttamente collegate alla matrice P della covarianza degli errori di stima. Le incertezze delle stime presentano prove dovute alle iterazioni dei valori trattati dalla fase di stima e, successivamente, alla correzione delle stime.
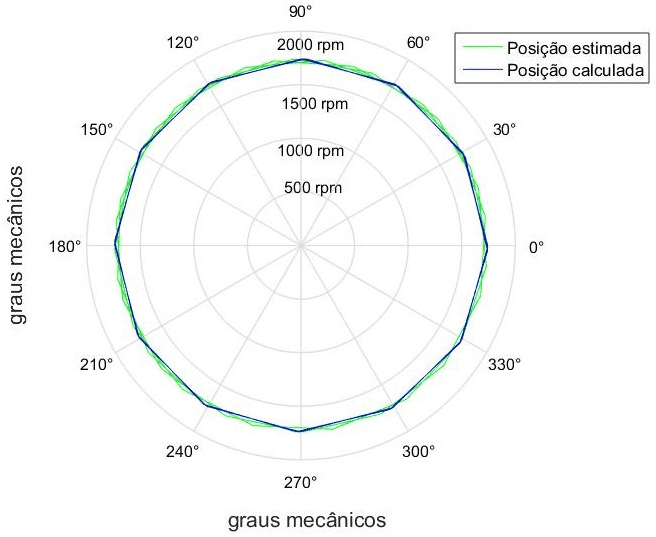
Il grafico mostrato nella Figura 5 delinea la variazione nella posizione meccanica del rotore in gradi.
come illustrato nella figura 5. Posizione in gradi 0… 360 gradi con velocità di 90 giri/min, 900 giri/min e 1740 giri/min.
Dove:
Tuttavia, si osserva la presenza di oscillazioni intorno ai valori di riferimento. Queste oscillazioni possono essere ridotte al minimo regolando e accordando l’EKF, fondamentalmente sulle matrici di covarianza Q, R, P e K dell’EKF. Le oscillazioni più grandi spiccano in funzione a basse e transitorie velocità.
Quando la matrice P della covarianza dell’errore dello stimatore di stato si avvicina a zero, la matrice Guadagno K agisce meno intensamente per ridurre al minimo la discrepanza tra i valori di stima e le misure adottate nel modello macchina.
Se vengono adottati valori più elevati per gli elementi della matrice di covarianza del rumore (Q), vi è un più alto grado di incertezza per quanto riguarda le stime degli stati del sistema, il che implica l’aumento della matrice di guadagno K e un aumento della velocità di convergenza della stima.
L’aumento dei valori degli elementi della matrice di covarianza dei rumori di misurazione di correnti e tensioni, R, implica la diminuzione della matrice del guadagno K, che agisce nella riduzione della velocità di risposta dell’EKF.
5. Conclusioni
I risultati simulati indicano la fattibilità dello stimatore in base alle indicazioni della sua capacità di rispondere alle variazioni di velocità imposte al sistema di controllo, nonché alle diverse condizioni di carico imposte al motore.
Sono state simulate le condizioni operative del motore a induzione con carichi diversi, fino a 400N, o circa 40 kg di peso. I valori di ricarica si basano sulla capacità della coppia meccanica del motore, secondo la scheda tecnica del costruttore, essendo 1,1 N.m con una velocità nominale di 1725 rpm.
La stima EKF presenta la convergenza con i valori di riferimento e calcolati, in base alle dinamiche di funzionamento imposte a ogni condizione di carico.
In possesso dei risultati presentati, si prevede di implementare la soluzione in un hardware per il controllo digitale dei motori utilizzando il processore di segnale digitale del Produttore Texas Instrument, modello TMDSHVMTRPFCKIT con piastra di controllo F28035 e un motore a induzione asincrona in tre fasi di tipo gabbia scoiattolo, modello 5K33GN2, produttore di maratona (Regal Beloit Corporations), disponibile pressoGEE PP – PUCMINAS.
6. RIFERIMENTI
AKIN, B., ORGUNER, U., and ERSAK, A. (2003). State estimation of induction motor using unscented Kalman Filter. IEEE Conference on Control Applications, 915-919.
AMEID, T., MENACER, A., TALHAOUI, H., HARZELLI, I., and AMMAR, A. (2016). Simulation and real-time implementation of sensorless field oriented control of induction motor at healthy state using rotor cage model and ekf. 8th International Conference on Modelling, Identification and Control, 695-700.
BARUT, M. (2010). Bi input-extended Kalman Filter based estimation technique for speed-sensorless control of induction motors. Energy Conversion and Management, 2032-2040.
BARUT, M., BOGOSYAN, S., and GOKASAN, M. (2007). Speed sensorless estimation for induction motors using extended Kalman Filters. IEEE Transactions on Industrial Electronics, 272-280.
BARUT, M., BOGOSYAN, S., and GOKASAN, M. (2008). Experimental evaluation of braided ekf for sensorless control of induction motors. IEEE Transactions on Industrial Electronics, 620-632.
BARUT, M., DEMIR, R., ZERDALI, E., and INAN, R. (2012). Real-time implementation of bi input-extended Kalman Filter-based estimator for speed-sensorless control of induction motors. IEEE Transactions on Industrial Electronics, 4197-4206.
DADKHAH, R., GIVI, H., and MEHDIPOUR, A. (2015). Parameter estimation of the induction motor using extended Kalman Filter for wide range speed control. The 6th International Power Electronics Drive Systems and Technologies Conference (PEDSTC2015), 137-142.
EL-HALIM, A.F.A., ABDULLA, M.M., and EL-ARABAWY, I.F. (2012). Simulation aides in comparison between different methodology of field oriented control of induction motor based on flux and speed estimation. 22nd International Conference on Computer Theory and Applications (ICCTA), 117-121.
ESTEVAM, E.G.A., PEIXOTO, Z.M.A., and FERREIRA, F.M.F. (2014). Aplicação EKF e as técnicas DTC-MTPA ao controle de velocidade sensorless do ipmsm. 20º Congresso Brasileiro de Automática, 1348-1355.
JAFARZADEH, S., LASCU, C., and FADALI, M.S. (2013). Square root unscented Kalman Filters for state estimation of induction motor drives. IEEE Transaction on Industry Applications, 92-99.
KRAUSE, P., WASYNCZUK, O., SUDHOFF, S., and PEKAREK, S. (2013). Analysis of Electric Machinery and Drive Systems. Wiley-IEEE Press, New Jersey.
LEITE, A.V., ARAUJO, R.E., and FREITAS, D. (2004). Full and reduced order extended Kalman Filter for speed estimation in induction motor drives: A comparative study. 35th Annual IEEE Power Electronics Specialists Conference, 2293-2299.
LI, J. and ZHONG, Y. (2005). Comparison of three Kalman Filters for speed estimation of induction machines. 40th Annual Meeting of the IEEE Industry Applications Society, 1792-1797.
RAYYAM, M., ZAZI, M., and BARRADI, Y. (2018). A new metaheuristic unscented Kalman Filter for state vector estimation of the induction motor based on ant lion optimizer. COMPEL – The international journal for computation and mathematics in electrical and electronic engineering, 1054-1068.
S. BOGOSYAN, M.B. and GOKASAN, M. (2007). Braided extended Kalman Filters for sensorless estimation in induction motors at high-low/zero speed. IET Control Theory and Applications, 987-998.
SHI, K.L., CHAN, T.F., WONG, Y.K., and HO, S.L. (2002). Speed estimation of an induction motor drive using an optimized extended Kalman Filter. IEEE Transactions on Industrial Electronics, 124-133.
VIEIRA, R., GASTALDINI, C.C., AZZOLIN, R.Z., and GRUNDLING, H.A. (2014). Sensorless sliding-mode rotor speed observer of induction machines based on magnetizing current estimation. IEEE Transactions on Industrial Electronics, 4573-4582.
WALLSCHEID, O., SCHENKE, M., and BÖCKER, J. (2018). Improving torque and speed estimation accuracy by conjoint parameter identification and unscented Kalman Filter design for induction machines. International Conference on Electrical Machines and Systems ICEMS, 1181-1186.
YIN, Z., LI, G., ZHANG, Y., LIU, J., SUN, X., and ZHONG, Y. (2017). Speed and flux observer of induction motor based on extended Kalman Filter and Markov chain. IEEE Transactions on Power Electronics, 7096-7117.
YIN, Z., ZHAO, C., LIU, J., and ZHONG, Y. (2013). Research on anti-error performance of speed and flux estimator for induction motor using robust Reduced-Order EKF. IEEE Transactions on Industrial Informatics, 1037-1046.
ZERDALI, E. and BARUT, M. (2017). The comparisons of optimized extended Kalman Filters for speed-sensorless control of induction motors. IEEE Transactions on Industrial Electronics, 4340-4351.
[1] Master in Ingegneria Elettrica e Ingegnere in Elettronica e Telecomunicazioni.
[2] Dottorato in Ingegneria Elettrica.
Inviato: agosto, 2020.
Approvato: settembre 2020.
