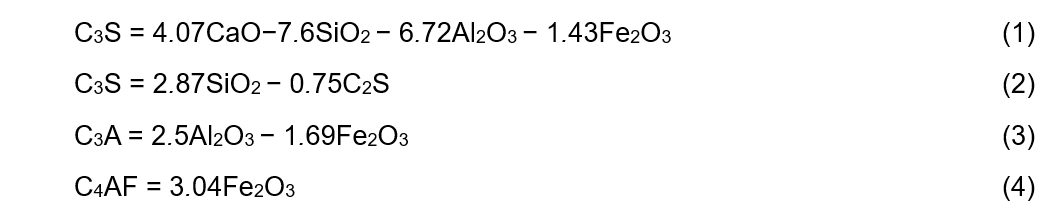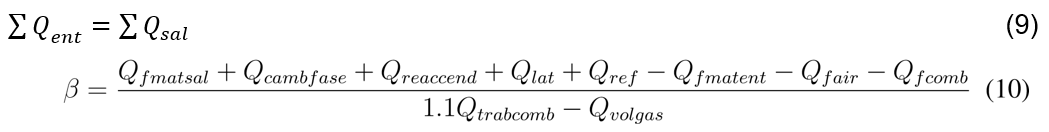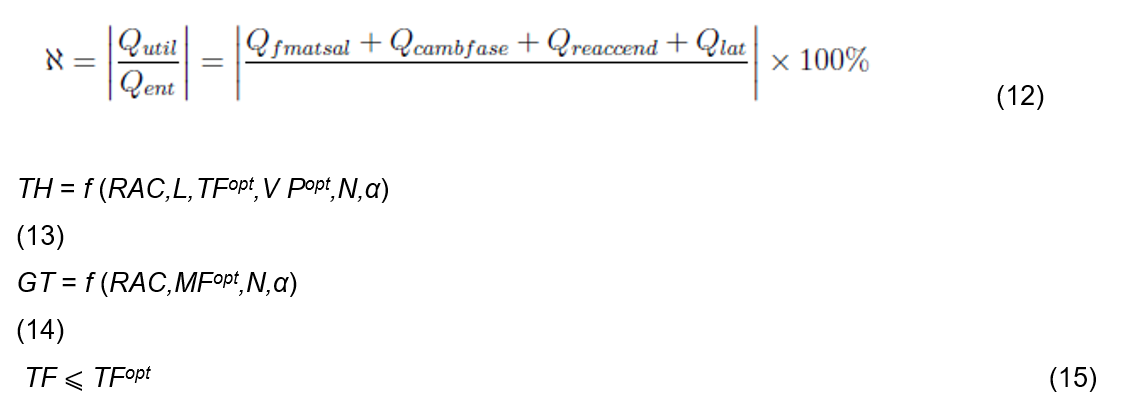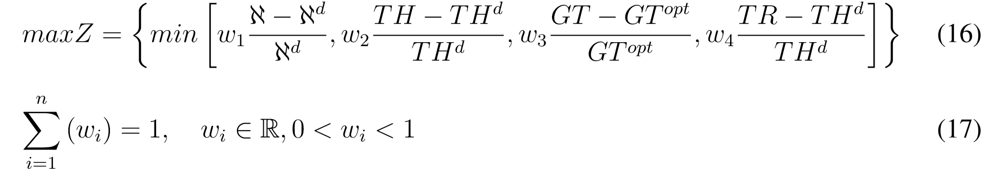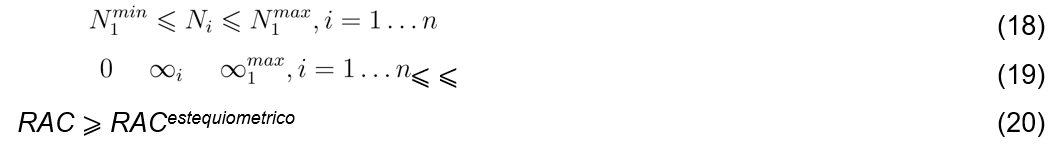ORIGINAL ARTICLE
HERNÁNDEZ, Yusdel Díaz [1], FIGUEREDO, Marcos Batista [2], NÉRI, Thais de Souza [3], SILVA, Alexandre do Nascimento [4]
HERNÁNDEZ, Yusdel Díaz. et al. Mathematical modeling of the rotary furnace operations for the production of clinker. Revista Científica Multidisciplinar Núcleo do Conhecimento. Year 08, Ed. 12, Vol. 01, pp. 139-157. December 2023. ISSN: 2448-0959, Access link: https://www.nucleodoconhecimento.com.br/engineering-mechanical-engineering/rotary-furnace-operations, DOI: 10.32749/nucleodoconhecimento.com.br/engineering-mechanical-engineering/rotary-furnace-operations
ABSTRACT
This paper presents a comprehensive system of mathematical models to describe, simulate, and optimize the operational and energetic aspects of rotary furnaces within the cement industry. To achieve this, we delve into the interaction between the furnace and other aggregates within the plant. We define the key variables governing the furnace’s operation through a meticulous analysis. Leveraging the power of genetic algorithms, we successfully validate the model’s performance under static and dynamic operational conditions. A pivotal aspect of our approach involves considering the behavior of combustion gases as analogous to a piston flow system. This consideration enhances our understanding of the complex processes occurring within the furnace. Furthermore, we establish shutdown criteria based on predetermined values obtained from the Case study facility: TR (Total Runtime) of 47 minutes, GT (Gas Temperature) at 97 percent, and ℵ (Agitation Speed) at 35 percent. These predefined values align with the desired outcomes of our objective function (Z). Through integrating and implementing our findings, a promising avenue emerges for improving the final product’s fuel consumption rate and quality. By concurrently addressing the plants and furnaces efficiency indicators, we set the stage for a more sustainable and productive operation in the cement industry.
Keywords: Cement rotatory furnace, Energy efficiency, Mathematical model, Operations.
1. INTRODUCTION
In general, the use of rotary kilns in the materials production industry began in the middle of the 19th century and the cement industry at the end of the 19th century. However, the use of this thermal aggregate did not become widespread until the first decade of the 20th century when Thomas Edison filed a patent allowing large-scale reproduction. With the tremendous technological advances of that century, rotary kilns underwent significant modifications in their mechanical and electrical components, automation, and types of fuels Hernandez, Ortiz and Herrera (2014), gradually improving their operability, control, and energy efficiency, among others. Despite these constant advances, these kilns are responsible for approximately 30 percent of the production cost and 65 percent of the energy use in the aggregate and cement clinker industry (Zanoli; Pepe; Rocchi, 2016).
On the other hand, modeling, or simulation of rotary kilns, either to improve automation and control or operation, is a very complex task due to the countless variables that involve from physical, chemical, and structural transformations of materials to hydrodynamic, thermal, kinetic, and mechanical processes (Kadri; Mouss; Mouss, 2012). In addition to the above, the study of the models describing the process is usually separated into two types of the static, which is explained by the heat balance, the degree of transformation, and the operation of the furnaces, and the dynamic, which involves the automation and control processes of the output variables or efficiency indicators of the furnace (Hernandez; Rivas-Perez; Moriano, 2018).
With the high demand for cement and the increase in fuel prices, one of the ways to achieve competitiveness in this type of company is the reduction of operating costs. Due to this, the evolution of the control and operation of rotary kilns are constantly evolving from PLC and PID management (Ortiz et al., 2003). However, most authors agree that the modeling control has advantages over traditional methods, so the Generalized Predictive Methods (GPC) and Dynamic Matrix (DMC) are the most used (Sezer et al., 2020).
On the other hand, these previously mentioned control tools are inconceivable without an operating model that establishes the correlation between the process variables. To discern this complex problem, several tools appear in the specialized literature, including machine learning, neural networks, regression models, genetic algorithms, and data mining, among others. For example, in Abioye et al. (2018) and Varun, Tejesh and Prashanth; (2018), numerical methods are applied to estimate the heat transfer and the heat involved in the chemical reactions along the kiln. As a result, the temperature profile of the kiln and the transformed clinker is obtained. Similarly, in Coral Medina and Fontalvo Alzate (2011), a pilot scale kiln is used to establish the degree of Clinker transformation as a function of the kiln rotation speed and inclination angle. For this purpose, the behavior of the combustion gases is considered to behave as a piston flow system. Based on a similar approach, Pereira, Ribeiro and Romero (2017), studies the combined heat and mass transfer to obtain a range of values of the critical Peclet number and obtains an optimum material transformation degree.
Others obtain a linear model describing the influence of the degree of fineness of the raw materials on the quality of the final product. The research estimates the dependence of the production cost and energy efficiency in thermal devices on the combustion process and thermal loss management. Similarly, Rodrigues et al. (2016) studies the endothermic chemical reactions in the furnace and establishes which can be disregarded during modeling for practical purposes because they have low energy consumption. Others, such as Anacleto et al. (2018), use combined energetic and exergy analysis to establish behavioral rules for the behavior of the transformed raw material along the rotary kiln. From the study of the available literature, it is inferred that the modeling of the operation is still insufficient. Hence, this research aims to obtain an operation model of rotary kilns for clinker production that increases the thermal aggregate’s efficiency indicators through simulation and multiobjective optimization tools.
This article is organized as follows: In section number 2, the interaction of the rotary kiln with the remaining aggregates of the plant is studied by identifying the coordinating variables and the set of mathematical models that explain it. Section 3 validates the model obtained using a comparison study with a reference plant. Finally, the conclusions and recommendations of the research are presented in the last section.
2. ANALYSIS AND SYNTHESIS OF THE OPERATING MODEL
Currently, there are as many approaches or strategies for modeling in engineering as there are types of models. Despite this, each of these strategies has joint edges from which a general methodology for dealing with these problems is derived (Díaz, 2017; Valdes and Ruiz, 2017). As part of this methodology, there is systems analysis and synthesis in engineering, which has proven to be an effective tool in multidisciplinary and multiobjective problems since it allows decomposing complex tasks into subtasks through the study of the variables that interrelate the subsystems to assemble them later and obtain solutions close to the global optimum of the more extensive system. From the previous idea, it is deduced that the operation model of rotary kilns to produce clinker has as a starting point the external analysis, that is, the study of the interrelation of this with the remaining technological aggregates of the plant.
2.1 EXTERNAL ANALYSIS OF THE OPERATING MODEL
Most large companies producing clinker and cement have a well-defined continuous or semi-continuous production process where the raw material is transformed from the ore through mechanical crushing, grinding, and screening preparation. Subsequently, clinker is obtained by sintering in kilns, which is then dried, mixed, and crushed until cement is obtained according to the desired brand. Thus, each aggregate’s operations are managed at a process pace controlled through the plant’s dispatch system. This way, the production plan is broken down into productive tasks for each area distributed over time, thus satisfying the efficiency and effectiveness indicators. In the case under study, operations are harmonized through the variables of coordination (VC), a brand of cement to be produced per batch (MFopt), production volume (VPopt), and minimum time required to finish the set (TFopt). This information is reviewed periodically; therefore, a minimum time to complete the batch is established to satisfy the plant-wide preference system and become a directive. Based on this feedback, the plant and area-sharing system results in a dispersed-conciliated steering structure. Fig. ?? shows in detail the steering scheme, although the (VC) of the remaining areas is not displayed because they are not the object of this research.
Figure 1: Reconciled dispersed management structure of a clinker processing plant
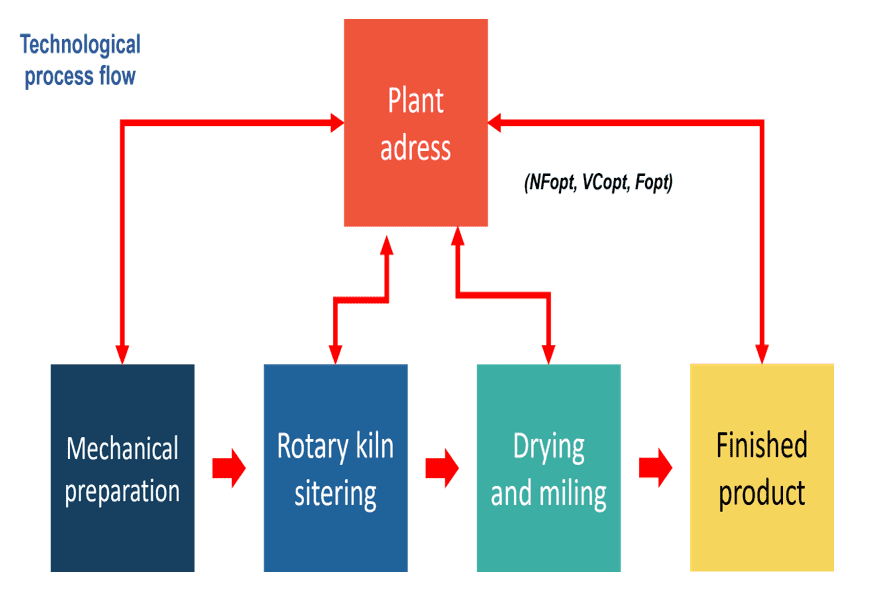
Subsequently, the mathematical models describing the coordination mentioned above variables are defined. When it is necessary to evaluate the (MFopt) most authors use Bogue’s Law, Eq. (1), (2), (3), and (4). This law allows estimating the four main phases of cement, namely tricalcium silicate (alite), bi-calcium silicate (belite), tricalcium aluminate, and tetra-calcium ferrite aluminate respectively, by disregarding those minority oxides present as impurities. Their accuracy and effectiveness are greater than 95 percent when estimating the final chemical composition of the cement using as a starting point the chemical composition of the raw materials introduced into the rotary kiln.
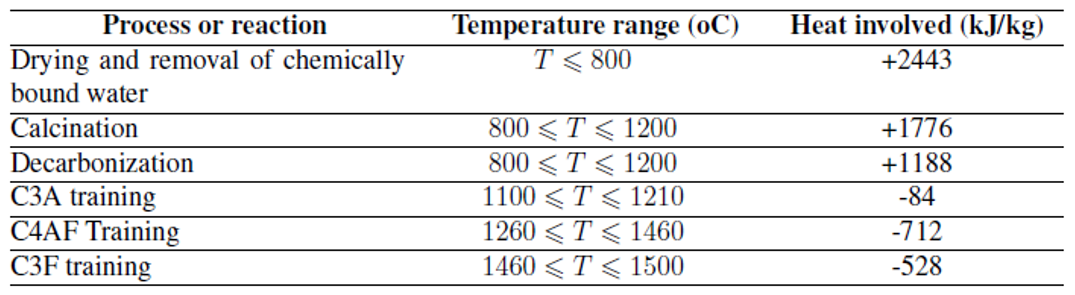
Likewise, the chemical reactions occurring in each temperature range and throughout the furnace are defined in Table 1, and the reaction heats. The mass flow of materials and the chemical energy involved in each transformation are then obtained by performing the corresponding mass balance, Eq. (5). The expression (m) defines the mass flow of materials in (kg/s). In the modeling of the clinker production process, the terms associated with the mass flow created and accumulated are usually neglected because it is considered to have a stationary behavior. This theoretical assumption is not entirely true, although several authors use it to simplify the modeling since during the initial heating of the kiln, quantities of CO2 are sometimes released in addition to the temporary formation of some intermediate chemical compounds such as C2F and the presence of impurities (less than 3 percent).
Table 1: Heat involved in various processes or reactions
On the other hand, the general model that allows the estimation of (TFopt) is usually expressed by Eq. (6). The variable depends on some process parameters defined as follows: (L) and (d) are the length and diameter of the kiln in meters, (θ) is the slope angle of the material when dry expressed in sexagesimal degrees. These two parameters under operating conditions do not usually vary. Unlike the variables (α), defined as the angle of inclination of the kiln and (N), the frequency of rotation of the equipment expressed in revolutions per minute usually varies in combination to satisfy the missing time previously requested by the plant management.
Finally, (φ) is a time reserve coefficient necessary to guarantee shutdowns due to unforeseen events.
Once defined (TFopt), it is possible to estimate (VPopt) since both variables are closely related Eq. (7). In the case of the average density of the mixture of materials (ρm) and the useful volume (%V) of the materials, several models explain them with sufficient accuracy. The first of these models depends only on the chemical composition of the dry raw materials (Qmentra), while the second one depends on the slope angle of the material (θ). As in expression (6), the working diameter and furnace length are considered constant for modeling purposes if the L/d ratio is within the design range between 15 and 20 percent.
2.2 INTERNAL ANALYSIS OF THE OPERATING MODEL
Once the plant management system has been analyzed and the variables for coordination with the other plant areas have been defined, as part of the systems analysis and synthesis methodology, the set of mathematical models that govern the operation of rotary kilns for clinker production is defined. For this purpose, the input variables (EV) or decision variables are defined, explicitly allowing the operation of the rotary kiln, and thus satisfying the efficiency indicators or output variables (EV). In the case under study, most authors agree that these variables are the (N), the (α), and the air-fuel ratio (RAC). The first two variables are closely related to the (TFopt) so that, to satisfy compliance with the time restrictions imposed by the steering system, a coherent combination of them is sought Eq. (8). It is necessary to clarify that the behavior of both is discrete because the electromechanical motor system of this type of furnaces only has punctual values to facilitate the automatic control. On the other hand, the (RAC) cannot be estimated directly during the production process because it depends on the specific fuel consumption (β) in (kgcomb/kgmaterial) which in turn depends on the thermal and mass behavior during the operation of the kiln. The possible values to be considered during the problem’s solution must satisfy a (VPopt) previously indicated by the plant management system.
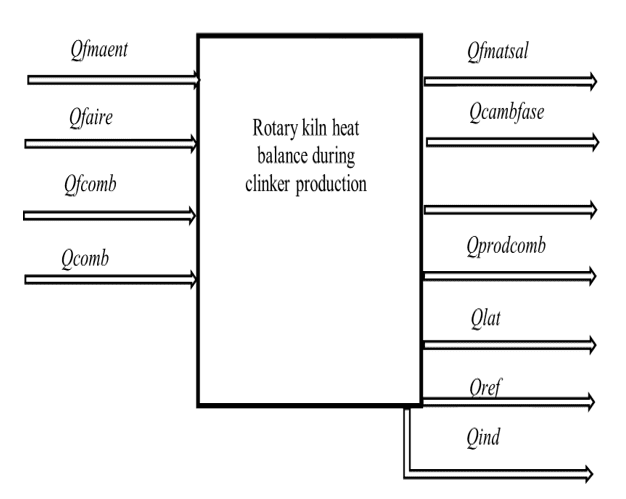
As the mass balance was defined in the previous section based on the raw materials, the heat balance of the furnace is carried out. Fig. 2 shows the input (Qent) and output (Qsal) heat to be considered in the modeling. This research does not present the expressions for estimating these heats because they are sufficiently explained in the available literature. Input heats are defined as (Qfmaent), (Qfair), and (Qfcomb), which is the energy contributed by the physical load of the filler materials, including material moisture, combustion air, and fuel, respectively. The heat of combustion (Qcomb) depends on the (β), so it must be estimated once obtained from the heat balance. To analyze the output heat, we have the physical heat that comes out with the clinker when evacuating the kiln (Qfmasal), the latent heat of phase change in the solid state of the silicates and aluminates (Qcambfase), and the heat of vaporization of the water present in the charge materials (Qlat). Also considered as losses are the heat expended in the endothermic reactions (Qreaccend) and given up by the furnace to the environment as thermal loss through the refractory walls (Qref). Finally, (Qind) and (Qprodcomb) depends on (β) and are estimated once calculated. By applying the heat balance Eq. (9) and clearing (β), the expression Eq. (10) is obtained where (Qtrabcomb) and (Qvolgas) are the low calorific value of the fuel to be used in (kJ/kgcomb) and the total volume of the combustion gas mixture at the temperature that is evacuated.
After estimating each variable, it finally determines the (RAC), necessary to guarantee each of the heats involved in the process of obtaining clinker Eq. (11) expressed in ![]() . In this model, (Υ) is a coefficient that depends on the temperature and pressure to which the fuel and air are subjected, while (Vaire) and (Vcombustible) are the volumetric flow of both substances inside the kiln burner.
. In this model, (Υ) is a coefficient that depends on the temperature and pressure to which the fuel and air are subjected, while (Vaire) and (Vcombustible) are the volumetric flow of both substances inside the kiln burner.
In the second stage, after defining each input or decision variable, it is necessary to determine the output variables expressed as rotary kiln efficiency indicators. Among them, the percentage energy efficiency (ℵ) has an essential place since it has a direct impact on production costs Eq. (12). In this model, the valuable heat (Qutil) is defined from the heat associated with´ the operations during the technological process, namely drying, sintering and decarbonization. Another output variable to consider is the temperature distribution (TH) in the atmosphere along the furnace zones Eq. (13) because it regulates the thermodynamics of the process. Similarly, the variable degree of transformation of materials (GT) is defined as an indicator of the quality of the final product since in the drying, mixing, and milling processes after the clinker production process; the chemical composition remains unchanged Eq. (14). Finally, the variable residence time of the material in the kiln (TR) is required since it is closely linked to the kinetics of chemical reactions and phase transformations that occur in the solid-state Eq. (15).
Once the coordination variables have been defined, as well as the mathematical models that relate the efficiency indicators (VS) as a function of the decision variables (VE), the conceptual mathematical model (14) or objective function (Z) is proposed. In the model, the terms associated with the superscript (d) describe the desired values close to the optimum of the variables (ℵ) and (TH). As a general criterion for energy efficiency, this value is usually considered equal to the reference value of the company designing the furnace.
Figure 2: Heat balance
Likewise, (THd) responds to the minimum theoretical temperature that each zone of the furnace must have to satisfy the chemical reactions and the change of phases in the solid state (Table 1). In addition, the terms associated with (GT) and (TR) that ensure the synchronization of the rotary kiln with the remaining aggregates of the plant without neglecting the quality of the final product are evaluated. The terms (w1), (w2), (w3), and (w4) are weight coefficients that reflect the importance given to each of the (VS) and must satisfy condition Eq. (16) and (17).
The model (16) is subject to the restrictions of the variables given by expressions Eq. (18), (19), and (20). Condition (18) obeys the range of permissible power in the electric motor that drives the furnace, while (19) responds to the maximum inclination established by design. In the case of Eq. (20), it is necessary to ensure complete combustion of the fuel and excess air.
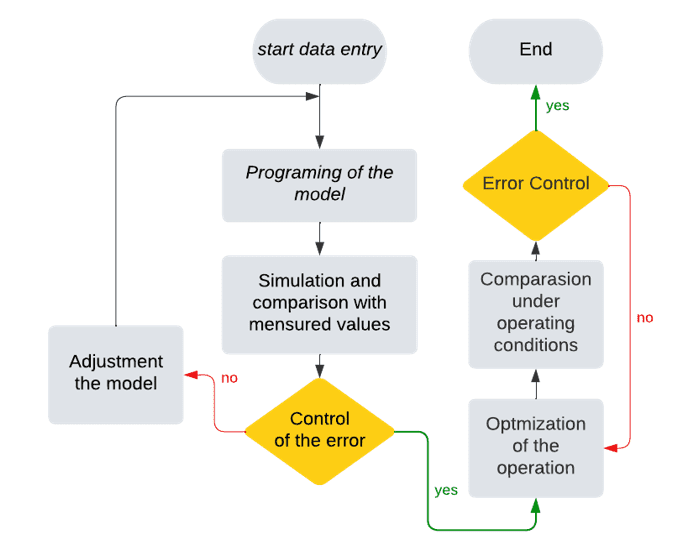
After formalizing the mathematical model, the most appropriate management structure to govern the system and the variables involved, the set of models is programmed in Matlab version R20R20 following the methodology shown in Fig. 3. It is necessary to add that for the adjustment and validation of the model, the values obtained by simulation are first compared with those of a furnace of a company taken as a case study, under static operating conditions. Subsequently, once the model has been adjusted, a genetic algorithm is applied to optimize the function (Z) with penalty for non-compliance with the constraints in the (VE). Once the system returns a set of optimal solutions, they are executed in the furnace Case of study. With the derived results, the comparison of the obtained solutions is carried out.
This reference furnace has the following characteristics: furnace length (L = 50m), working diameter (d = 3m), rotation frequency range (1.5rpm ⩽ N ⩽ 4.5rpm), maximum production capacity (Mmax = 55tons/hour), allowed dwell time radius (40min ⩽ TRper ⩽ 50min) and furnace inclination angle tolerance (0 ⩽ α ⩽ 50). In addition, it has two positions in each of the three zones of the furnace, allowing the taking of material and atmosphere temperatures with a type K thermocouple, the reading of the air and fuel flow at the burner inlet with two Coriolis meters, and the flow of gases leaving the furnace with an orifice pan meter. All measuring instruments are periodically checked and duly certified. Also, during each batch, three clinker samples are taken and analyzed to adjust the chemical composition.
Figure 3: Solution methodology and optimization of the system
3. ANALYSES OF RESULTS. VALIDATION OF THE MODEL
To implement the static model, the values previously obtained by simulation are compared with the values measured in the Case Study furnace under the same operating conditions, i.e., keeping the importance of (ℵ), (RAC), (TFopt), and (α) constant. The number of experiments to be performed is ten; each of these experiments is replicated three times, averaging the measured values. Unlike the dynamic model, the dynamic model studies the response capacity of the model to perturbations typical of real production conditions. Hence, the validation considers values of (VC) and (VE) that, in some way, represent the possible operating eventualities of the furnace.
3.1 STATIC MODEL VALIDATION
Table 2 shows the averaged results per batch together with the simulated values. It is pertinent to clarify that the temperature measured by zones (1), (2), and (3) are always taken at the same distance from the burner (DQ) as well as the material temperature (TM). Zone’s measured and simulated values meet the thermodynamic and kinetic requirements shown in Table 1, Zone’s measured and simulated values. The most relevant result is that a low difference is obtained between the simulated and measured values with a percentage error of less than four percent. The energy efficiency for the type of furnace studied is within the range of expected values according to Hernandez and Reyes (2015). Another result derived is that the (TR) satisfies the furnace design condition in all cases since it is less than 50 minutes, keeping the (GT) within the expected values in international standards. Plotting the total measured values of the variables (TH), (TM) versus (DQ) gives the temperature distribution along the kiln for the material (yellow color) and the kiln atmosphere (orange color). The temperature profile obtained is similar in terms of morphology and zone distribution to countless scientific works dedicated to the thermal study of rotary kilns in the cement industry. It is also interesting to note that the kiln temperature variable obtained by simulation (green simulated HT) practically overlaps with the real measured values.
Table 2: Experimental Data and Comparisons
| Simulated Diff | ||||||
| #Experiment | #1 | #2 | #3 | Average | value | % |
| Efficiency | 32.1 | 33.6 | 30.8 | 32.17 | 32.35 | 0.57 |
| TH (Zone 1) | 900 | 925 | 908 | 911 | 921 | 1.09 |
| TH (Zone 2) | 1459 | 1478 | 1473 | 1470 | 1487 | 1.14 |
| TH (Zone 3) | 1790 | 1782 | 1795 | 1789 | 1804 | 0.83 |
| TH (output) | 525 | 549 | 557 | 544 | 561 | 3.09 |
| TM (Zone 1) | 621 | 632 | 640 | 631 | 652 | 3.22 |
| TM (Zone 2) | 1125 | 1193 | 1154 | 1157 | 1174 | 1.42 |
| TM (Zone 3) | 1432 | 1397 | 1402 | 1410 | 1459 | 3.34 |
| TM (output) | 422 | 401 | 448 | 424 | 438 | 3.27 |
| GT (%) | 96.8 | 95.4 | 96.9 | 96.37 | 97.3 | 0.96 |
| TR | 42 | 47 | 44 | 44.33 | 46 | 3.62 |
| L | 15 | 30 | 45 | 50 | ||
Source: Authors, 2023.
From this result, it is inferred that the proposed static model explains the temperature distribution inside the kiln with robustness. The System previously admitted under static conditions is now subjected to a normally distributed combination of perturbations in the (VE). With the support of the mathematical assistant STATGRAPHICS, 100 random values of each variable are generated using upper and lower limits of the constraints Eq. (18), (19), and (20).
3.2 VALIDATION OF THE DYNAMIC MODEL
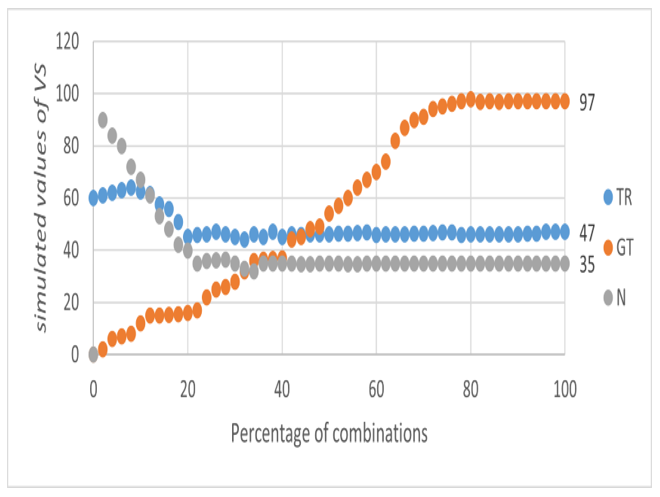
Likewise, we use as shutdown criteria preset values in the Case study facility of (TR = 47 minutes), (GT = 97 percent), and (ℵ= 35 percent), which correspond to the desired values of the objective function (Z). Fig. 5 shows the result obtained for the total combinations studied. The graph shows that the variables (TR) and (ℵ) converge rapidly to the desired values of the (VS) in the first iterations of the model (20 percent of the combinations). However, in the case of the variable (GT), the model takes time to reach values close to the desired one, needing to iterate approximately 70 percent of the total combinations. However, this result, besides being valid for satisfying the expected values of (GT), coincides to some extent with previous studies since this variable always depends on the compositions previously estimated in expressions (8) and (9), which generates a larger volume of data to be analyzed. Finally, the objective function (Z) value takes almost zero values, which presupposes the convergence of the global model.
Figure 4: Furnace temperature distribution by zone
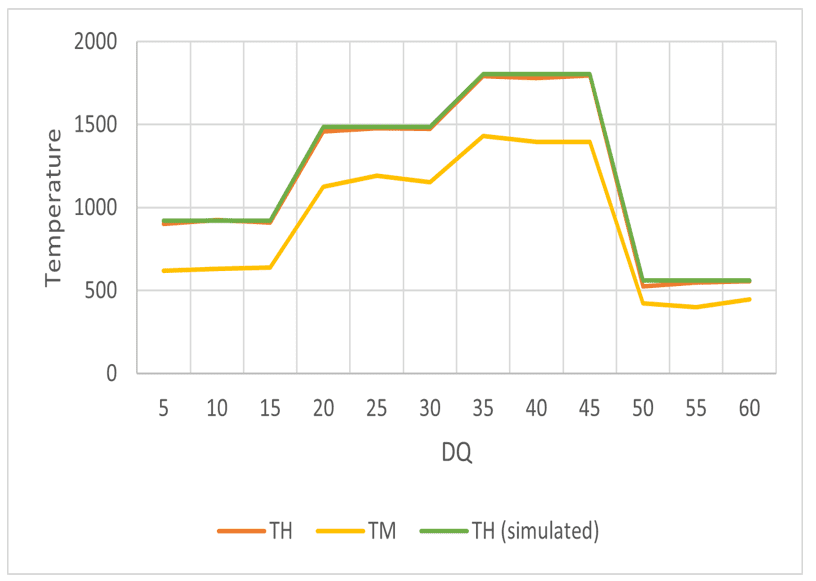
Figure 5: Behavior of the output variables in the model
4. CONCLUSIONS
A mathematical model that satisfactorily describes the static and dynamic operating conditions of rotary kilns in the cement industry was obtained. The system explained the behavior of the temperature distribution inside the kiln by zones with high accuracy. Also, the implemented optimization model of the output variables using genetic algorithms responds robustly to perturbations against various scenarios of the input variables as it manages to satisfy the kiln and plant efficiency indicators simultaneously. The potential benefits of the direct implementation of the model in the control system of the rotary kilns for clinker production are closely linked to the quality of cement, decrease in fuel consumption, and negative environmental impacts.
REFERENCES
ABIOYE, A. A. et al. Mechanical and microstructural characterization of ductile iron produced from fuel-fired rotary furnace. International Journal of Mechanical Engineering and Technology, 9(1):694–704, 2018.
ANACLETO, T. et al. Efeito da reação de calcinação nas análises energética e exergética de um forno rotativo empregado na produção de clínquer. Cerâmica, 64:507–518, 2018.
CORAL MEDINA, J. D.; FONTALVO ALZATE, M. G. G. Modeling and simulation of rotary kilns. application to cement production, annals […], VII Congreso colombiano de metodos numericos, 2011.
DÍAZ, Y. Modeling for the operation of radial installations for continuous casting of square section steels. 2017. Dissertation (Ph.D.) – Dept. Met. Eng, Moa. Hol. Univ., Cuba, 2017.
HERNANDEZ, A. M.; REYES, H. L. Behavior of fuels supply variable costs in electrical energy generation using gas and coal. IEEE Latin America Transactions, 13(9):2915–2921, 2015.
HERNANDEZ, J. S.; RIVAS-PEREZ, R.; MORIANO, J. J. S. Design of a generalized predictive controller for temperature control in a cement rotary kiln. IEEE Latin America Transactions, 16(4):1015–1021, 2018.
HERNANDEZ, O.; ORTIZ, P.; HERRERA, J. Cement rotary kiln model using fractional identification. IEEE Latin America Transactions, 12(2):87–92, 2014.
KADRI, O.; MOUSS, L. H.; MOUSS, M. D. Fault diagnosis of rotary kiln using svm and binary aco. Journal of mechanical science and technology, 26:601–608, 2012.
ORTIZ, O. et al. Steady state simulation of a rotary kiln for charcoal activation. Latin American applied research, 33(1):51–57, 2003.
PEREIRA, I.; RIBEIRO, D.; ROMERO, O. Three-dimensional modelling of heat transfer in wellbore during steam injection process. IEEE Latin America Transactions, 15(4):690–697, 2017.
RODRIGUES, D. et al. Modelagem matematica dos perfis de temperatura do gas, do solido e da parede do forno e dos perfis de concentracão das principais especies quımicas presentes no interior do forno rotativo empregado na produção de clınquer. Ceramica , 62:140–146, 2016.
SEZER, R. et al. Effects of furnace slope and rotational speed on the carbothermic reduction of celestite in a laboratory-scale rotary kiln furnace. Mining, Metallurgy & Exploration, 37(4):1273–1278, 2020.
VALDES, O. M.; RUIZ, J. A. Exploration of variable codes algorithm for linings materials and its thickness selection of steel casting ladles. IEEE Latin America Transactions, 15(8):1528–1535, 2017.
VARUN, V. S.; TEJESH, P.; PRASHANTH, B. Design and development of tilting rotary furnace. In IOP Conference Series: Materials Science and Engineering, volume 310, page 012084. IOP Publishing, 2018.
ZANOLI, S. M.; PEPE, C.; ROCCHI, M. Improving performances of a cement rotary kiln: a model predictive control solution. Journal of Automation and Control Engineering Vol, 4(4), 2016.
[1] PhD in Materials Engineering and Science (stricto sensu), Master in Materials Engineering (lato sensu), Metallurgical Engineer. ORCID: https://orcid.org/0000-0003-0381-3851. Currículo Lattes: https://lattes.cnpq.br/8250462277774753.
[2] PhD. ORCID: https://orcid.org/0000-0002-8193-5419. Currículo Lattes: http://lattes.cnpq.br/6235735011979354.
[3] PhD in Chemistry. ORCID: https://orcid.org/0000-0002-5739-7462. Currículo Lattes: http://lattes.cnpq.br/7216135300068165.
[4] Computational Modeling and Industrial Technology. ORCID: https://orcid.org/0000-0001-7436-8818. Currículo Lattes: http://lattes.cnpq.br/2937471014216142.
Submitted: November 13, 2023.
Approved: November 30, 2023.