ARTIGO ORIGINAL
SCHWANTES, Vilson [1], XAVIER, Márcio Pizzete [2], KRACKE, Elisa [3], GRAUNKE, Carla Kuhn [4], GONÇALVES JÚNIOR, Affonso Celso [5], SCHWANTES, Eloísa Bernardete Finkler [6]
SCHWANTES, Vilson. Et al. Importância Da Linguagem Para O Desenvolvimento Do Pensamento Algébrico. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano 06, Ed. 06, Vol. 02, pp. 112-141. Junho de 2021. ISSN: 2448-0959, Link de acesso: https://www.nucleodoconhecimento.com.br/educacao/pensamento-algebrico, DOI: 10.32749/nucleodoconhecimento.com.br/educacao/pensamento-algebrico
RESUMO
Este artigo é resultado de um trabalho investigativo que encontra fundamentação teórica nos escritos de Lins (1994), a respeito do Modelo Teórico dos Campos Semânticos, e no livro A Construção do Pensamento e da Linguagem de Vygotsky (2001). Teve a participação de alunos do ensino fundamental, onde situações-problema foram apresentadas em sessões de estudo, no intuito de entender-se a relação que existe entre pensamento e linguagem. Os alunos nem sempre percebem que a linguagem algébrica está presente nas relações estabelecidas entre a linguagem cotidiana, os símbolos e os números. Nas atividades propostas os alunos eram a todo instante instigados a pensar e falar sobre o que viam, produzindo significado sobre o contexto, representando-o na linguagem cotidiana e simbólica. Na resolução das situações-problema, mediadas pelos professores, queríamos compreender como ocorre o desenvolvimento do pensamento algébrico discente e sua constituição nos sujeitos. As reflexões e atividades realizadas com os alunos mostram que a organização, desenvolvimento e constituição do pensamento algébrico discente é possível pela internalização dos significados produzidos na interlocução, pela posse e mediação da linguagem significada, ocorrida na observação e comunicação das ideias matemáticas presentes em situações-problema. A pesquisa mostrou que o desenvolvimento do pensamento algébrico é possível introduzindo-se a linguagem simbólica, num processo que se inicia pela significação da linguagem cotidiana, perpassando pela observação, discussão e significação dos signos presentes em cada situação-problema.
Palavras-chave: Pensamento Algébrico, Linguagem, Produção de Significado, Generalização, Escrita Algébrica.
1. INTRODUÇÃO
Na prática pedagógica, no decorrer da história, muitos professores têm conduzido o processo ensino-aprendizagem seguindo tendências de acordo com suas concepções de matemática. O professor que, por exemplo, concebe a matemática como uma ciência pronta e acabada, terá uma prática pedagógica diferente daquela que a concebe como uma ciência viva em processo de construção permanente. De forma análoga, o professor que acredita na aprendizagem do aluno como imitador, repetidor de raciocínios e procedimentos terá uma prática diferente daquele que crê que o aluno aprende apropriando-se de conceitos a partir de ações conjuntas numa prática coletiva. O que diferencia estas posturas é que em um caso o professor age sobre o aluno e no outro o professor age com o aluno (FIORENTINI, 1995).
Na pesquisa realizada com os alunos, propusemos uma série de atividades (situações-problema) para que dialogicamente e em pequenos grupos eles pudessem pela comunicação das ideias matemáticas presentes em cada contexto, elaborar, comunicar e expressar o pensamento algébrico, numa perspectiva meta-operacional, ou seja, que vai além da postura normalmente adotada nas escolas.
Trata-se de um enfoque que compartilha a produção de significados entre participantes, numa dinâmica onde a qualidade da aprendizagem se sobrepõe à quantidade de conceitos. O percurso investigativo, segundo esta perspectiva, procura compreender intersubjetivamente o que permite um ser humano pensar algebricamente, buscando clarificar a relação que existe entre pensamento e linguagem para uma efetiva organização, desenvolvimento e verbalização do pensamento algébrico.
O estudo propõe, portanto, partir-se da comunicação das ideias matemáticas presentes na observação e análise de padrões e sequências repetidas. Inicia-se conversando sobre o texto [situação-problema], nas perspectivas de Lins (1994) e Vygotsky (2001). Acreditamos que a produção do pensamento algébrico perpassa pela resolução de situações-problema, que podem, pelo viés da linguagem, ajudar os alunos a se comunicarem matematicamente, tanto pela linguagem cotidiana quanto pela linguagem simbólica.
A discussão crítica e reflexiva do contexto de cada situação-problema, o questionamento das possibilidades interpretativas, a produção de significados e a elaboração dialógica do conhecimento matemático, presente ou oculto, perpassa tanto pela enunciação quanto pelo entendimento do texto, que se torna possível, segundo Vygotsky (2001) pela posse da linguagem e internalização dos significados produzidos sobre ela.
Conforme Freire (1987), o desafio consiste em se fazer uma leitura do mundo e na caminhada perceber e compreender as relações que se estabelecem entre o texto e seu contexto, relações estas também imbricadas dinamicamente na linguagem e na realidade.
Em síntese, ganha ênfase a construção de modelos e procedimentos. Nas atividades desenvolvidas com os alunos e nas falas correspondentes este aspecto ficou evidente. O trabalho trouxe subjacente a produção de significados sobre o texto em cada situação-problema, uma questão fundamental para o desenvolvimento do pensamento algébrico. Segundo Lins (1994), trata-se da possibilidade dialógica de se estabelecer pela problematização um pensar aritmeticamente, um pensar internamente e um pensar analiticamente.
Conversar a respeito de cada situação-problema e, especialmente, o que mais poderia ser verbalizado, criado e produzido para o contexto de cada situação proposta, foi fundamental. Nessa perspectiva, buscou-se seguidamente, questionar as falas, os significados produzidos no contexto de cada problema, fato que favoreceu o desenvolvimento do espírito crítico, a capacidade de argumentação e generalização.
Compartilhamos também o entendimento de Fiorentini; Miorim e Miguel (1993b) de que essa generalização não pressupõe e não requer a presença de uma linguagem estritamente simbólico-formal. A percepção de regularidades e a possibilidade de generalizá-las já representa um elemento caracterizador de um tipo de pensamento, que podemos denominar de pensamento algébrico. Para desenvolver o pensamento algébrico, o sujeito, segundo Lins (1994), precisa enunciar, falar sobre o texto.
Os participantes foram levados a reflexões sucessivas sobre as situações-problema propostas e sobre suas falas. Foram instigados a adotar uma postura investigativa e criativa que consideramos fundamental sempre. De acordo com Vygotsky (2001) e conforme Orlandi (2000, p. 19), “O sujeito não se apropria da linguagem num movimento individual. A forma dessa apropriação é social”.
2. DESENVOLVIMENTO
2.1 PRODUZINDO PENSAMENTOS E EXPRESSANDO IDEIAS PELA LINGUAGEM
Partimos dialeticamente[7] da observação de situações-problema e, pela via da comunicação das ideias matemáticas presentes em situações-problema, analisamos padrões e sequências com algum tipo de regularidade. O desenvolvimento do pensamento algébrico discente foi sendo elaborado e amadureceu a partir de conversações sobre o texto[8], na ótica dos escritos de Lins (1994), ou seja, de acordo com o Modelo Teórico dos Campos Semânticos, e do livro A Construção do Pensamento e da Linguagem de Vygotsky (2001).
Segue situação-problema trabalhada nas sessões de estudo. Lembramos que nossos interlocutores foram, a todo instante, motivados a produzir significados para o texto matemático. Interessava sempre significar ao máximo o texto e, através dessa produção, elaborar e validar conjecturas[9], que poderiam pela linguagem gerar um pensamento generalizante. Segue a primeira questão e o roteiro de questionamentos utilizado no ensaio empírico.
1) Observe a sequência de símbolos e depois responda:
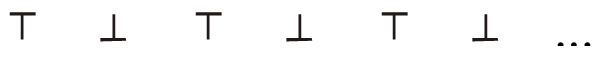
a) Os elementos desta sequência representam o que para vocês?
b) Qual o nono elemento da sequência?
c) Qual o décimo segundo (12º) elemento da sequência?
d) Qual o décimo quinto (15º) elemento da sequência?
e) Qual o vigésimo terceiro elemento da sequência?
f) Sem desenhar, qual o elemento que ocupa a centésima primeira (101ª) posição?
g) Escreva em palavras o comportamento desta sequência?
h) Como vocês procederam para encontrar o resultado?
i) Se alguém considerasse 
como sendo um elemento único, o que se poderia dizer sobre uma sequência formada por elementos repetidos na ordem:
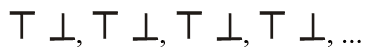Adaptado de Souza e Diniz (1996, p. 15).
A sequência de questionamentos foi desenvolvida com os alunos, em grupos e em momentos distintos. Os alunos foram motivados a observar a sequência de símbolos e, posteriormente, instigados a falar sobre ela, em relação ao que foi observado e ao que pôde ser percebido. Nesse momento dialógico, tem importância a mediação[10] docente proposta por Vygotsky (2001). Permitir aos alunos sentirem-se à vontade para conversar sobre as possíveis conjecturas elaboradas e suas possíveis validações, pode ser outra opção válida. À medida que o professor achar conveniente, pode propor as seguintes questões: Qual o 9º elemento da sequência? O 12º elemento da sequência? E o 15º elemento da sequência? Qual o 23º elemento da sequência?
Os questionamentos serviram de roteiro básico para a elaboração de um pensamento de caráter generalizante em que sua generalização não exigia, a princípio, o uso de uma linguagem simbólico-formal. Após observarem a sequência de símbolos, os alunos procuraram responder às questões de acordo com o roteiro de estudo proposto.
Analisando e comparando os resultados das falas dos alunos nos diferentes grupos, em relação aos questionamentos, observamos que para a questão houve diferentes formas de expressar, através da linguagem cotidiana, a mesma informação. As produções significativas destes quatro momentos distintos [quatro grupos], analisamos concomitantemente, conforme segue.
Para a aluna Caroline, por exemplo, a sequência representava “[…] uma letra é uma figura”. Para Angélica, “é uma sequência de símbolos. Iguais eles são, só que uns para cima e outros para baixo”. Para Douglas, os símbolos “são Ts”.
A aluna Talita percebeu imediatamente que a situação-problema se referia a uma sequência de dois símbolos que se repetiam ordenadamente. Assim, ela prontamente comunicou que “representam um número par e um número ímpar”, com o que Monique, sua irmã gêmea, concordou. Solicitei a Talita para explicar sua justificação. Talita respondeu: “É uma letra, virada [referindo-se ao T invertido], e outra não virada. Um número para cada um [a cada símbolo a aluna associou um número], só que aí, vai colocando: 1, 2, 3, 4, 5, 6, 7, 8 e assim por diante”. Solicitada para nomear os símbolos, a aluna assim se manifestou: “Que nem um T. É, pode ser um T. É um T, um na posição correta e um virado”, pensamento com o qual Monique também compartilhou.
Ao observar a sequência repetida, o aluno Daniel logo percebeu que se tratava “de uma letra T normal e uma invertida, infinitamente. Eu só vi um T normal e um invertido, só vi estes dois tipos”, concluiu o aluno, com o que Felipe, seu colega, manifestou concordância. A mesma observação foi feita por Jucilei. No entanto, para Camila, tratava-se de um símbolo “[…] em pé e outro deitado, que são iguais, só um sendo em pé e o outro invertido em uma sequência infinita”.
Quando discutiram sobre as questões b, c, d, e, f, através das quais pedia-se qual dos elementos [símbolos] estaria nas posições solicitadas, todos os alunos souberam responder corretamente, embora usassem procedimentos distintos. Destacamos, na sequência, algumas dessas falas.
Segundo a aluna Camila, para responder que elemento [símbolo] se encontrava em determinada posição, por exemplo, 9ª, 12ª, 15ª posição, “[…] a gente vai calculando assim, mentalmente, pela contagem”. Jucilei postulou: “[…] o primeiro elemento é um T normal e é ímpar, o segundo é invertido, é par”. A partir desta troca dialógica, Camila conseguiu completar seu raciocínio: “É, o T normal cai em casas ímpares e o T invertido cai em casas pares. O T que se encontra na posição 101 é para cima [normal], pois 101 é um número ímpar, então, cai o T normal nos números ímpares”.
Os alunos Caroline e Douglas, para generalizar essa situação, perceberam que nas múltiplas posições de 10 se encontrava sempre o T invertido e, a partir dessa informação, fizeram a contagem para encontrar o resultado do símbolo das posições intermediárias. Em seu relato Douglas disse:
Acho que contando, na posição 10 o T é para baixo [invertido]. Contando 20, 30, 40 e 50, sempre será invertido nessas posições. E se você está no 21, daí é o T normal. E, se você está no 31, 33, 41, aí também é o T normal. Por exemplo, na posição 101, esse já é o T normal. E, se você chegar no 200 [ducentésima posição], ele vai estar invertido, para baixo. E, se chegar no 201, ele é o T normal.
A aluna Monique em sua descrição explicou aos colegas que “[…] o T correto significaria um número ímpar. E um T virado, significaria um número par. E, como o número 101 é um número ímpar, então vai ser um T correto, nessa posição”. Questionada a respeito de que símbolo estaria na posição 350, Monique prontamente respondeu: “Seria um T virado, porque ele está em uma posição de número par”. Perguntamos então, qual símbolo se encontrava na posição 501. “Seria o T correto, porque está numa posição de número ímpar”, conclui a aluna com o aval de Talita.
Durante todo o diálogo a ideia básica consistia em levar os alunos a construir e explicitar, pelo uso natural da linguagem cotidiana, os seus pensamentos. Assim estavam, desde o princípio, realizando o que Lins (1994) considera uma justificação. Para este contexto, houve nos diferentes grupos, diferentes maneiras dos alunos expressarem, através do uso natural da linguagem cotidiana, o conhecimento elaborado a partir dos questionamentos e observações. Na questão a, por exemplo, a aluna Caroline percebeu na sequência a existência de uma letra e de uma figura, enquanto a aluna Angélica percebeu tratar-se de uma sequência de símbolos com um T na posição normal e outro na posição invertida. A aluna Talita percebeu que a situação-problema se referia a uma sequência de dois símbolos que se repetiam ordenadamente, um em posição par e o outro em posição ímpar.
Isto se justifica, segundo Lins (1994, p. 29), pelo Modelo Teórico dos Campos Semânticos que “[…] indica que o mesmo texto, falado com diferentes justificações, constitui diferentes conhecimentos” (itálico do autor). Para uma análise epistemológica da álgebra e do pensamento algébrico, o autor propõe este modelo, através do qual postula “[…] que conhecimento é uma crença-afirmação junto com uma justificação para a crença-afirmação” (LINS, 1994, p. 29, itálico do autor). A álgebra é um texto que passa a ser conhecimento algébrico à medida que se fale sobre esse texto, no sentido dessa crença-afirmação ser reconhecida como integrante desse texto. O pensamento algébrico é elaborado pelo aluno a partir do momento que este domina o texto algébrico utilizando-o para resolver situações-problema.
Segundo este modelo, o conhecimento a respeito de algo difere tanto entre professor e aluno quanto de aluno para aluno, porém todos são legítimos. A diferenciação entre esses conhecimentos não implica caráter de superioridade de um em relação ao outro. No ato dialógico, para cada crença-afirmação enunciada poderão existir várias justificações que podem constituir diferentes conhecimentos legítimos.
Na discussão sobre as questões b, c, d, e, e f, através das quais pedia-se qual dos elementos [símbolos] estaria nas posições solicitadas, as enunciações dos alunos confirmaram novamente a argumentação do autor. Camila em sua fala conseguiu demonstrar que quanto à posição do elemento na sequência o T normal cai em casas ímpares e o T invertido cai em casas pares, enquanto Caroline e Douglas utilizaram outro raciocínio, partindo das posições múltiplas de 10 para descobrir o símbolo das posições solicitadas. Talita e Monique em seus raciocínios associaram diretamente a posição dos Ts da sequência com os números ímpares e pares.
Instigados para descrever, em palavras, o comportamento dessa sequência e como procederam para tal, conforme as questões g e h, Talita disse: “[…] eu acho que seria assim, um T correto e um T virado”. Felipe e Taffarel perceberam que “em toda posição ímpar encontra-se um T normal”. Questionados sobre o que representava o T invertido na sequência, os dois alunos responderam simultaneamente: “Um número par”. Para Emerson, a sequência comportava-se, segundo a formação: “[…] Ts virados para baixo, serão os números pares e Ts para cima os números ímpares”. Para Camila, tratava-se de uma sequência “infinita com símbolos, sendo um normal e um invertido”.
Também exploramos a sequência repetida, conforme questão i, considerando cada par de Ts [
] como sendo um único elemento para as diferentes posições. Essa discussão foi importante, pela percepção que os alunos tiveram em relação a essa possibilidade, embora não interessante para o desenvolvimento do pensamento algébrico. Todos os grupos tiveram clareza de que essa caracterização não era interessante, por representar uma sequência constante para todas as posições.
Em situações de aprendizagem, o professor usa a linguagem para ensinar e aprender, e o aluno também aprende por meio da linguagem. Assim, em suas modalidades – oral e escrita – a linguagem é o elemento central do desenvolvimento do pensamento e da consciência humana (FARIAS; BORTOLANZA, 2015).
A primeira situação-problema trabalhada mostrou a importância da interação dos alunos com o texto, que é na e pela interação que se produz significados sobre esse texto. Os pensamentos produzidos podem ser generalizados, o que nos mostra que o desenvolvimento da linguagem possibilita o acesso aos bens simbólicos construídos social e historicamente.
2.2 A PRODUÇÃO DE SIGNIFICADOS PELA INTERAÇÃO COM O TEXTO
Apresentamos na sequência, os resultados das produções dos alunos, em relação à situação-problema 2. Tanto as falas dos alunos, quanto a análise que segue, trazem subjacente a ideia de que o conhecimento matemático é uma produção humana de significados construídos dialogicamente, na vivência e experiência dos seres humanos em diferentes situações da vida.
Segue a situação e o roteiro provisório de questionamentos utilizado nas sessões de estudo.
2) Observe as figuras geométricas e depois responda:
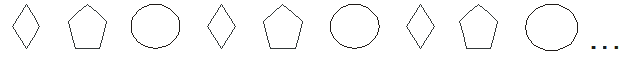
a) Iniciando da esquerda para a direita, vocês poderiam dizer o nome das figuras geométricas ali representadas?
b) Qual o 10º elemento da sequência? E o 11º elemento?
c) Qual o 13º elemento da sequência?
d) Qual o 19º elemento da sequência?
e) Qual o 23º elemento da sequência?
f) Sem desenhar, qual o elemento que ocupa a centésima [100ª] posição?
g) Escreva em palavras o comportamento dessa sequência?
h) Como vocês procederam para encontrar o resultado?
Adaptado de Souza e Diniz (1996, p. 18).
A sequência de questionamentos desta situação-problema foi desenvolvida com os alunos, em grupos e em momentos distintos. Embora para o desenvolvimento do tema central da pesquisa não fosse necessário que os alunos soubessem o nome das figuras geométricas da sequência, eles foram inicialmente instigados a falar sobre elas. Desta forma, após a observação das figuras, iniciamos pela questão a e pedimos aos alunos se já haviam visto essas figuras em algum lugar, se sabiam dizer o nome de cada uma.
Analisando e comparando os resultados das falas dos alunos nos diferentes grupos, em relação ao questionamento a, observamos que houve diferentes informações através do uso natural da linguagem cotidiana. Destacamos, na sequência, concomitantemente as falas mais significativas que ocorreram nas três sessões de estudo.
A primeira figura da esquerda [losango] foi imediatamente reconhecida pela aluna Angélica. O reconhecimento se deu pelo formato e pela sua utilização prática, não pelo nome específico. “É uma figura geométrica. As placas de sinalização das ruas também são assim” [referindo-se ao losango]. “Parecido também com a parte amarela da bandeira do Brasil”, complementou o aluno Douglas. Caroline também não se lembrou no momento do nome, porém lhe pareceu com algo já visto: “Uma pipa”, exclamou a aluna. Neste momento, Douglas lembrou que no ano anterior havia estudado em sala de aula essas e outras figuras geométricas, embora Caroline não lembrasse dessas aulas. Angélica lembrou que estudaram de fato essas figuras, porém não se recordou dos seus nomes.
De forma análoga, não ocorreu o reconhecimento do nome da segunda figura da sequência [pentágono], apenas sua visualização prática em situações do cotidiano. Angélica, após observá-la, mencionou que ela “[…] pode ser representada como uma casa”.
Em relação à terceira figura da sequência [círculo], quando questionados para pensar na possibilidade de não se tratar de um círculo, o aluno Daniel, prontamente exclamou: “Nós vamos discordar”. Esta figura foi identificada, segundo várias falas, como na de Felipe: “Sim, um redondo, também”.
Nesta questão os alunos apresentaram dificuldades para nomear algumas figuras geométricas, por isso, ao seu término fiz uma retomada reflexiva das discussões, esclarecendo as diferenças entre círculo, circunferência e a nomenclatura das figuras geométricas da sequência. A dificuldade para nomear figuras geométricas mostrou, de acordo com Lins e Gimenez (1997, p. 28), a necessidade de, na elaboração do conhecimento matemático, “[…] trabalhar com significados matemáticos […]”.
Uma reflexão a respeito desta problemática nos conduziu a compartilhar com Luria, Leontiev e Vigotsky (1991, p. 15) a ideia de que “trabalhar com objetos reais enquanto se desenvolvem os conceitos abstratos é uma etapa necessária da aprendizagem”. O não desenvolvimento da abstração pode acarretar uma má elaboração conceitual discente, conforme ocorreu em relação à nomenclatura das figuras geométricas. Para Vygotsky, é nas situações concretas que se encontram as referências para o trabalho com as ideias introduzidas pela linguagem matemática.
O fato de os alunos relacionarem as formas das figuras geométricas com situações do cotidiano em que estas aparecem, sem, no entanto, saber nomeá-las sob o ponto de vista da matemática formal, apesar de as terem estudado na escola, fez-nos compartilhar com Lins (1999, p. 90) o fato de que “tradicionalmente a escola negou os significados da rua, e se esforçou em tentar implementar o domínio dos significados da escola”. Possivelmente este problema seria evitado se a escola partisse dos saberes prévios dos alunos e a partir desses produzisse uma sistematização.
Esclarecer estas particularidades, nomear as figuras, foi importante. No entanto, não era nosso interesse aprofundar este assunto, por isso, acreditamos ser salutar concluí-lo. Contudo, torna-se mister alertar que estas dificuldades apresentadas pelos alunos trazem uma série de implicações pedagógicas que merecem uma atenção especial dos professores.
Na sequência dos questionamentos, discutimos com os alunos as questões b, c, d, e, através das quais pedia-se qual das figuras geométricas estaria na 10ª, 11ª, 13ª, 19ª, … posição. Todos os alunos souberam responder, embora tenham utilizado procedimentos distintos. Destaco, na sequência, algumas destas falas ocorridas nos diferentes grupos.
Quando perguntados sobre como procederam para dizer que figura geométrica se encontrava em determinada posição da sequência, alguns alunos passaram a explicitar o raciocínio que empregaram. A aluna Angélica disse ter dado continuidade à representação inicial da sequência, numerando-a. Assim, para dizer qual das figuras estava em determinada posição, ela “ia contando e numerando na sequência”, referindo-se às figuras e suas respectivas posições na sequência. Observamos que os alunos respondiam corretamente qual figura estava na posição solicitada, porém, fazendo para isso a contagem na sequência por eles numerada. Questionamos, então, se era necessário sempre numerar e contar na sequência para se saber que figura geométrica estaria numa posição qualquer. Caroline, prontamente disse: “Só pode ser numerando”, com o que Angélica concordou.
Para dizer que a figura geométrica estava em determinada posição, Felipe relatou: “Eu fui contando”, enquanto Daniel disse que bastava “[…] desenhar na sequência para encontrar a resposta”.
Interrogados sobre a possibilidade de uma regularidade no comportamento da sequência, Emerson relatou: “[…] sempre, losango, pentágono, círculo. Vão seguindo sempre a mesma ordem, quando termina o círculo, começa de novo, losango, pentágono, círculo”. “Sempre grupos de três figuras”, acrescentou Daniel. “Esse é o comportamento”, concluiu Felipe.
Emerson percebeu que na sequência de figuras, “o círculo, ela segue múltiplos de três. Ela sempre segue de três em três”. Taffarel, ao ouvir o colega, percebeu e compreendeu a dimensão dessa informação e compartilhou da ideia: “Múltiplos de três, daí vai dar para generalizar [a sequência]”. Para Felipe, “ele [o círculo] soma de três em três”.
Com o objetivo de sair do processo de contagem e expressar a sequência de figuras através de um pensamento de forma generalizada, solicitamos aos alunos que dissessem que figura se encontrava na posição 524. Nesse momento, os alunos mostraram-se visivelmente preocupados, no entanto, o raciocínio da contagem foi repetido. Alguns minutos depois, Emerson e Taffarel responderam: “É o pentágono”. Ao serem instigados a explicitar o raciocínio empregado, Taffarel relatou sucintamente aos colegas olhando para as anotações que havia feito em sua folha de atividades. “500, dava um pentágono, daí, vai cair no pentágono de novo” na posição 524. Ao serem questionados pelos colegas, não souberam expressar claramente o raciocínio que utilizaram para comprovar a afirmação.
Este raciocínio parece-nos altamente enxuto e abstrato, pois 24 corresponde para a sequência de figuras o marco ‘zero’ na teoria da congruência módulo 3. Embora os alunos não tivessem esse entendimento, a generalização desta situação-problema poderia ser vista como uma aplicação da congruência módulo 3, ou seja, duas posições se repetem quando o resto da divisão de sua diferença por 3 for zero. Assim, verificando quando o resto obtido na divisão de [524 – p] por 3 for zero, para p variando de 1 a 3, obtém-se a figura buscada que, no caso, corresponde àquela localizada na posição 2, isto é, o pentágono.
Somente na sessão de estudo subsequente, quando estas questões foram trabalhadas com o grupo das alunas Luma, Jucilei e Camila, houve uma compreensão diferenciada desde o princípio. Tanto Luma quanto Camila perceberam que uma das figuras estava numa posição privilegiada para a generalização da sequência. Respondendo à colega Jucilei, que procedia pela contagem para responder aos questionamentos, Luma disse: “Olha, eu não fiz assim. Que nem aqui [mostra na sequência as posições múltiplas de três], acaba no círculo. Daí eu vou até na posição 6, 9, 12, 15, é sempre um círculo, então a figura que cai nesta posição é sempre a mesma [referindo-se ao círculo nas posições múltiplas de três]”. O relato procedimental da observação de Camila foi semelhante: “Eu contei assim: A cada três números dava uma bola [referindo-se ao círculo], então é: 3, 6, 9, 12, … dava uma bola, 13 ia ser o losango”, primeiro elemento da sequência de figuras. Jucilei, após refletir sobre as falas das colegas, enunciou seu entendimento sobre a sequência de figuras assim: “Aí já é a tabuada de três”, o que determina em que posição se encontra o círculo.
Na tentativa de construir com os alunos um pensamento generalizado que expressasse qual figura geométrica se encontrava em determinada posição, indagamo-los no sentido de que falassem, sem desenhar, qual figura geométrica se encontrava na posição 100 [questão f]. Camila expôs seu entendimento dizendo: “Deixa eu pensar como é que eu fiz. Eu acho que eu contei a cada 30, dava uma bola, daí 60 dava bola, 90 outra bola, daí no 9 outra bola [90 + 9], daí depois o 100 vai ser um losango que é a primeira figura depois da bola”.
Para Jucilei, tratava-se de “uma sequência infinita de três figuras diferentes, sendo a primeira um losango, a segunda um pentágono e a terceira um círculo”. E sempre o círculo vai se repetir na posição 3, 6, 9, 12, já o losango e o pentágono não se repetem deste jeito [referindo-se às posições múltiplas de três]”, com o que os demais colegas concordaram. Para a aluna Jucilei estava claro que o círculo ocupava uma posição numericamente privilegiada, o que não ocorria, no seu entendimento, com o losango e o pentágono.
Neste grupo, também solicitamos aos alunos que dissessem qual figura se encontrava na posição 524. A aluna Luma expressou seu pensamento em relação a esta questão, justificando assim sua argumentação: “Se na posição 100 dá um losango, no 200 vai dar um pentágono, daí até 500, daí é um pentágono, daí contando até 520 dá um losango. E para 524, conta do 520 até 524 vai dar um pentágono”. Essa fala de Luma, assim como outras falas ocorridas nessa sessão de estudo, mostra claramente o quanto a álgebra se beneficia da aritmética e vice-versa, o que reafirma a posição de Lins e Gimenez (1997, p. 113), segundo os quais “a própria atividade aritmética envolve, naturalmente, um certo nível de generalidade”.
A possibilidade de generalizar esta atividade diretamente por meio da divisão por três foi percebida apenas no grupo da Talita e da Monique. As alunas conseguiram perceber que o círculo se encontrava sempre numa posição correspondente a um múltiplo de três. Para encontrar a figura correspondente a posição 524, 780, 1078, por exemplo, elas dividiram o número da posição por 3. Se a divisão fosse exata, a figura correspondente à posição seria um círculo, se o resto da divisão fosse 1, tratar-se-ia de um losango e se o resto fosse 2, de um pentágono. Através desta elaboração, as alunas realizaram relações por pensamento complexo que só na aparência têm o conceito. Elas usaram conceitos anteriores como, por exemplo, múltiplos de 3, para generalizar e encontrar a figura correspondente a uma posição qualquer.
Quando questionamos os alunos do grupo de Angélica, Douglas e Caroline sobre as questões f e g, a aluna Angélica enunciou em sua conjectura que o comportamento da sequência “podia ser determinado por números pares e números ímpares”.
Ao explicar sua forma de pensar, Angélica, assim como os demais alunos em outros momentos, estavam realizando o que Lins (1994) considera uma justificação. Os demais colegas, na tentativa de compreender o que Angélica tinha proposto, perceberam a impossibilidade da validação dessa conjectura. Douglas, imediatamente relatou: “Não serve, porque esse é o par [referindo-se à segunda figura – pentágono], daí, esse aqui também é par [referindo-se à quarta figura – losango]”. Douglas explicou aos colegas mostrando na sua folha de atividades que as figuras que se encontravam nas posições pares eram de formas geométricas diferentes e por isso a conjectura da colega não poderia ser validada. O fato de Angélica não ter encontrado um caminho válido para expressar o comportamento da sequência, não foi em vão.
A validade deste momento dialógico caracterizou-se pelo surgimento de uma oportunidade aos demais colegas de partilharem de ambas as informações, produzindo-se significado tanto na argumentação de Angélica, não válida, quanto na contra argumentação de Douglas, que era válida. Segundo Demo (1996), toda essa interlocução possibilitou, um “[…] conhecimento construído a várias mãos” (p. 68), ideia da qual também compartilho.
O debate argumentativo motivou os alunos para a busca de alternativas viáveis através do pensamento e da linguagem para a compreensão genérica da situação-problema. O importante desta dinâmica foi a possibilidade que se abriu no processo ensino-aprendizagem para a elaboração de justificativas para cada passo da resolução da situação em estudo, bem como a contra-argumentação dos colegas e a consequente rejeição de hipóteses falsas, a exemplo da explicação anterior de Douglas. Segundo Lins (1994) e Lins e Gimenez (1997), este estágio foi importante, pois, por meio dele, os alunos produziram significados e se apropriaram de conhecimentos.
É evidente que a produção de significados sobre o contexto de cada situação-problema pôde ser iniciada somente a partir do momento em que houve a apropriação do significado do texto pelo aluno. A investigação realizada com os alunos participantes da pesquisa convergiu na direção do que Lins e Gimenez (1997, p. 137) consideram que seja atividade algébrica, ou seja, “A atividade algébrica consiste no processo de produção de significado para a álgebra” (itálico dos autores).
As autoras Vale e Pimentel, em seu trabalho com padrões ressaltam que:
Muito do insucesso em matemática deve-se ao facto de os alunos recorrem apenas à memorização e não à compreensão. O primeiro passo para aprender a pensar matematicamente é aprender a descobrir padrões e estabelecer conexões. A procura de padrões deve constituir o núcleo das aulas em todos os temas, já que eles surgem nas fórmulas que descobrimos, nas formas que investigamos e nas experiências que fazemos. (VALE; PIMENTEL, 2011, p. 1).
Assim, à medida que os alunos começaram a produzir significados sobre um contexto, favorecidos ou não pela interlocução, eles adquiriram certas habilidades para comunicar-se consigo mesmos e com os outros. De acordo com Lins (1994, p. 33-34), pode-se concluir “[…] que o sujeito fala sempre para o outro, para o social, dentro da cultura a que pertence. Pode-se entender, assim, que interlocutores não são pessoas, indivíduos, mas precisamente modos de produzir significado”.
2.3 O PENSAMENTO ALGÉBRICO MEDIADO PELA LINGUAGEM SIMBÓLICA
A produção de significados sobre a linguagem está fundamentada na abordagem histórico-cultural para a educação de Vygotsky (2001), que postula ser a interação pela interlocução que garante, pelo viés da linguagem significativa, a (re)construção do conhecimento. Portanto, uma constituição dos saberes do plano social para o plano individual.
A reflexão a que nos propusemos procura mostrar que a constituição deste pensamento é possível a partir da linguagem, portanto, não é nato e precisa ser desenvolvido. Assim, os sujeitos produzem ideias relativas aos fatos observados sobre situações-problema e a compreensão sobre esses fatos se dá pela maturação e pela penetração da linguagem nesses contextos. Isto dialeticamente possibilita a generalização, segundo Vygotsky (2001), constituída a partir da e pela linguagem.
O desenvolvimento do pensamento algébrico, nessa perspectiva, contribui para a consolidação da aprendizagem algébrica, no sentido dos sujeitos, através dele, terem maiores possibilidades de (re)interpretar, com relativa autonomia, a realidade onde vivem e convivem. Essa também é a perspectiva de Demo (1996, p. 69) ao enfatizar que “A maneira humana de internalizar conhecimento não é repetir para decorar, mas aprender a aprender, saber pensar”.
Iniciamos outra sessão de estudo, apresentando aos alunos uma nova situação-problema. Passaremos a analisar concomitantemente, os resultados mais significativos das produções dos alunos, em relação a esta situação-problema, estando estes distribuídos em três grupos.
3) Observe a sequência representada abaixo, da esquerda para a direita e depois responda:
a) Quantos triângulos possui a próxima posição da sequência? Desenhe.
b) E a seguinte? Desenhe. Quantos triângulos ela possui?
c) Quantos triângulos têm a 7ª figura da sequência?
d) E a 10ª posição? A 15ª posição?
e) Como vocês procederam para encontrar os resultados? Alguém fez diferente? Como fez?
f) Seria possível representar cada posição da sequência através de uma operação matemática? Qual? Faça uma demonstração? Há outras possibilidades?
g) Compare cada posição com a quantidade de triângulos nela representados. O que você observou?
h) Escreva o comportamento de formação do número de triângulos dessa sequência.
i) Quantos triângulos têm uma posição qualquer dessa sequência? Represente matematicamente.
j) Na posição 100 desta sequência, existirão quantos triângulos? E na posição 500?
k) Quando multiplico 2 vezes n, considerando que o n seja um número inteiro positivo, o que representa sempre este resultado? Representa algum número especial?
Adaptado de Souza e Diniz (1996, p. 24).
Inicialmente, nesta atividade, os alunos foram motivados a observar e a desenhar a formação de outras posições, continuando a sequência de triângulos já existentes. Na continuidade, foram instigados a dizer quantos triângulos existem nas posições 7, 10, 15, etc., bem como explicitar, justificando, o procedimento adotado.
Nos três grupos em que trabalhamos nesta atividade, os alunos conseguiram dar respostas corretas aos questionamentos acima mencionados. Utilizaram-se inicialmente da linguagem cotidiana, atribuindo distintas justificações para explicitar seus procedimentos. Felipe, por exemplo, disse que conseguiu encontrar o número de triângulos das posições solicitadas “pela multiplicação por 2”.
Para explicar como encontrou o número de triângulos para diferentes posições, Luma comunicou seu pensamento através de um exemplo: “Eu fiz que nem na 15ª [posição], daí eu fiz 15 mais 15, dá 30”. Luma demonstrou ter compreendido que na sequência o número de linhas era constante e que na 15ª posição teríamos 15 triângulos em cada uma das duas linhas, o que a levou a utilizar-se da soma. Camila, aluna que participou do mesmo grupo de Luma, em seu relato disse: “Multipliquei o número dois, que é a quantidade de fileiras [linhas], pelo número obtido [posição solicitada]. Por exemplo, para a posição 15, fiz duas vezes 15, 30”.
Na representação de cada posição da sequência por meio de uma operação matemática, alguns alunos utilizaram a operação soma, e outros, se utilizaram da multiplicação. Monique percebeu que para encontrar o número de triângulos de determinada posição, “[…] tem 2 fileiras [referindo-se às duas linhas], e 3 colunas [correspondentes à figura da 3ª posição]. Então essa linha vezes esta coluna vai dar o resultado, entende [número total de triângulos da posição desejada]. Ou seja, aqui eu tenho 2 linhas e aqui eu tenho 3 colunas. Então, eu vou multiplicar 2 vezes 3, vai dar 6 triângulos”. Emerson comunicou seu pensamento por meio de um exemplo: “Pegando a sequência, se for 7ª [posição], aí multiplicando por 2”, encontra-se o número total de triângulos dessa posição, relatou o aluno. Talita e Monique observaram que seria possível também contar o número de triângulos em cada posição, no entanto, ter-se-ia que fazer a respectiva representação e isso, segundo as alunas, não era viável. “Dá para ir contando, mas, aí tem que ter muito papel”, concluem as alunas. Essas falas mostram a importância e a necessidade das generalizações na matemática.
Nas observações de Camila, sobre o comportamento dessa sequência, a aluna relatou que a figura seguinte possuía “2 triângulos a mais que a outra figura, a figura anterior”. Para Daniel, o número de triângulos de determinada posição é igual “à posição anterior mais 2”.
Raciocínio semelhante foi adotado por Felipe ao anunciar que com “mais 2 triângulos, dá a próxima posição”. O aluno ainda percebeu que para qualquer posição, o número total de triângulos é sempre par, assim ele comunicou: “Só tem números pares”. Luma ainda percebeu que o número total de triângulos de cada figura representa o conjunto dos múltiplos de 2. “Eu acho que são múltiplos de 2, aqui tem 2, daí aqui sempre é um múltiplo de 2” [diz apontando para a representação feita em sua folha de atividades]. Para Jucilei, na sequência há só triângulos e há um em cima do outro, também formam números pares como: 2, 4 e 6. É também a tabuada do 2”.
Dentro deste contexto e a partir deste momento, os alunos foram instigados a pensar sobre como se poderia calcular o número de triângulos para uma posição qualquer, utilizando-se de alguma expressão matemática. Emerson e Felipe sugeriram o uso de “uma letra” para a elaboração de um modelo matemático, generalizando a sequência. Solicitei uma explicação para essa enunciação. Emerson explicou, em seu modo de pensar, que para calcular o número de triângulos de determinada posição, seria interessante fazer “x vezes 2. x é a posição pedida, vamos supor 7ª, daí essa posição vezes 2, para saber o resultado que é 14 triângulos”. Felipe complementou esta informação, dizendo que: “Ao invés de x pode ser usado t, a, b, um número desconhecido, uma posição”. Camila sintetizou esta ideia ao dizer que bastava fazer “[…] 2 vezes alguma letra”.
Monique, através de sua fala, informou que percebeu que, para qualquer posição, o número total de triângulos representa sempre um número par, o que Felipe já havia observado em outro momento. “A quantidade multiplicada por 2, sempre vai dar par […] todos os números, até as posições ímpares, sempre vão dar uma quantidade par de triângulos”. Então ela concluiu que: “[…] o número de triângulos de uma figura é o dobro da posição”.
Nesse momento, perguntamos se alguém gostaria de explicar isto de forma diferente, ao que Jucilei exclamou: “Essa já matou”, referindo-se à explicação da colega Monique, o que provocou risos no grupo. Mesmo assim, Luma, que anteriormente havia encontrado o número total de triângulos de determinada figura através da soma, ao ser questionada para dizer genericamente como calcularia o número total de triângulos uma posição qualquer disse: “[…] só se fizesse que nem eu fiz aqui, mas daí seria um número imaginário. Então, seria x mais x. Um x representaria esse número aqui” [referindo-se a 1ª linha] e o outro x representaria o outro número aqui [mostrando a 2ª linha], o que dá como resultado 2x”.
Para Nobre; Amado e Ponte (2014), que consideram o desenvolvimento do pensamento algébrico uma das grandes finalidades do ensino de matemática, ressaltam que:
[…] as representações escritas produzidas pelos alunos, em particular, na resolução de problemas são poderosas ferramentas que devem ser desenvolvidas por constituírem uma componente essencial da aprendizagem, possibilitando a organização e a comunicação de ideias. Em particular, constituem um meio para a aprendizagem progressiva de métodos formais algébricos, que são umas das componentes importantes do trabalho em Álgebra. (NOBRE; AMADO e PONTE, 2014, p.2).
Ao longo deste desenvolvimento dialógico questionado, foi possível sentir a importância da produção de significados sobre o texto matemático, enfatizado por Lins (1994), além da necessidade da evolução das palavras pelo processo dialógico para chegar-se à generalização. Isto se confirma em Vygotsky (2001, p. 246), ao postular que “[…] os significados das palavras evoluem”, iniciando-se, por conseguinte, o processo de generalização.
Esta percepção pode ser traduzida nas palavras de Vygotsky (2001, p. 368), ao enfatizar que “Na medida em que se desenvolvem as relações de generalidade, amplia-se a independência do conceito […] e surge uma liberdade cada vez maior das operações semânticas em si e em sua expressão verbal”. Ainda, segundo esse autor, neste diálogo interativo os alunos usavam a linguagem exterior para comunicar seus pensamentos. À medida que esses pensamentos se tornavam compreensíveis, eram novamente utilizados para (re)elaborar novos pensamentos, caminhando-se para a formação de uma generalização sobre o contexto.
Partindo da premissa de que é preciso produzir significados sobre cada situação-problema, os alunos foram instigados a todo instante a dizer mais alguma coisa sobre cada contexto que fazia parte de nossa reflexão. Em relação à linguagem, compartilhamos com Vygotsky (2001) quando afirma que é ela que assume um papel preponderante para um efetivo desenvolvimento do ser humano, sustentando o pensamento.
Este caráter da linguagem passa a exigir uma mediação dialógico-comunicativa permanente e uma busca contínua em saber o que mais pode ser dito sobre cada situação-problema. Como o autor, acreditamos que quanto mais os alunos falam sobre o contexto de uma situação-problema, maiores e melhores são as possibilidades de representar genericamente seu contexto.
Esta atividade se diferenciou das situações-problema anteriores em relação à forma de se expressar o pensamento algébrico. Aqui, a expressão algébrica desta situação só se tornou possível pela introdução de uma letra, usada pelos alunos como símbolo representativo de uma posição genérica, enquanto nas situações anteriores a expressão foi possível através de um pensamento que não exigia o uso de uma linguagem estritamente algébrica.
O desenvolvimento do pensamento algébrico discente, nessa atividade, amadureceu à medida que os alunos se apropriaram da linguagem pelas interações mediadas pelos signos. De acordo com Vygotsky, são os significados produzidos para os conceitos algébricos que permitem, na ação pedagógica, a elaboração do pensamento algébrico.
2.4 CONTRIBUIÇÕES DA LINGUAGEM NA REPRESENTAÇÃO ALGÉBRICA DO PENSAMENTO
Segundo Vygotsky (2001), na linguagem há informação e através dela o pensamento é ativado. Um modelo algébrico, elaborado numa linguagem estritamente simbólica, mostra, nesta perspectiva, uma linguagem matemática oriunda do entrelaçamento da linguagem matemática com a linguagem cotidiana.
Seja a sequência de pontinhos que segue. Considere como sendo n a quantidade de pontinhos do lado de cada figura. Associe à ordem de cada figura na sequência o número de pontinhos que a constituem e depois responda:
a) Como vocês interpretam o que estão vendo nesta sequência?
b) Quando a figura tiver 5 pontinhos de lado, qual será o número total de pontinhos da figura?
c) Quando a figura tiver 6 pontinhos de lado, qual será o número total de pontinhos?
d) Quando a figura tiver 10 pontinhos de lado, qual será o número total de pontinhos?
e) Que raciocínio vocês utilizaram para encontrar esses resultados?
f) Elaborem uma tabela relacionando o número de pontinhos do lado da figura com o número total de pontinhos da respectiva figura.
g) Considerando que não se conhece o número de pontinhos do lado de determinada figura, como poderíamos representar o total de pontinhos dessa figura? Se preferirem, escrevam em palavras.
h) Indiquem através de uma expressão matemática a situação anterior.
i) Considerando que se conheça o total de pontinhos da figura, como poderíamos determinar o número de pontinhos de cada lado?
Adaptado de Bigode, 7ª série (2000, p. 134).
De forma análoga à atividade anterior, ao longo desta evidenciou-se novamente a importância da linguagem simbólica para a organização, generalização e representação de um pensamento. Após a leitura do enunciado da situação-problema, os alunos socializam entre si o que tinham visualizado e percebido.
Sobre como interpretavam o que estavam vendo nesta sequência, item a, Daniel falou que se tratava de “uma sequência de pontinhos que pode representar uma figura de tamanhos diferentes”, mas formam “um quadrado”, complementou Felipe. Camila observou que “todos os lados de cada figura têm a mesma quantidade de bolinhas”, portanto, para a aluna cada uma das figuras representa um “quadrado”. A observação de Luma diz respeito ao que acontecia de uma figura para a posterior, justificação que, para a pesquisa, reflete um outro conhecimento, tão importante quanto os demais produzidos: “Eu percebi uma coisa, que de lado, assim de lado, cada vez aumenta uma bolinha”. Em sua análise inicial, Jucilei se ateve à totalidade de bolinhas de cada uma das figuras. Em sua enunciação, observou que na primeira figura “[…] tem uma bolinha, na segunda tem 4, na terceira tem 9, na quarta 16”.
Dando continuidade, os alunos representaram, através de desenho, outras posições na sequência. Foram questionados sobre quantos pontinhos existem no total, quando a figura tiver 5, 6, 7, 8, 9 e 10 pontinhos no lado. Não foram percebidas dificuldades nessa fase do trabalho. No entanto, quando tiveram que falar sobre os raciocínios que utilizaram para encontrar esses resultados percebemos, novamente, pelas justificações, a constituição de distintos conhecimentos.
Cada aluno produziu um pensamento sobre um mesmo contexto e enunciou o seu significado de modo diferente. Para Emerson, bastava fazer “[…] o número de bolinhas de um lado, vezes ele mesmo”, pois se tratava de figuras quadradas. Taffarel ponderou que para encontrar o número total de pontinhos de determinada figura, deve-se multiplicar “a quantidade de bolinhas do lado 1, vezes o lado 2”. O aluno Daniel retomou este raciocínio e repetiu esta ideia dizendo que “o número total de bolinhas do lado 1 multiplicado pelo número total de bolinhas do lado 2, isto vai dar o total das bolinhas de cada figura”. Monique também percebeu que em cada figura “um lado é sempre igual ao outro e, sempre vai aumentando uma fileira de bolinhas de cada lado de uma figura para outra”.
Na sequência, desafiamos os alunos para a elaboração de uma expressão algébrica que fornecesse o número total de bolinhas para qualquer posição. A primeira conjectura foi assim enunciada pela aluna Jucilei:
x vezes x, porque eu não conheço um lado numa posição qualquer, daí eu também não vou conhecer o outro. Se nesse lado aqui eu tenho três bolinhas, desse lado [referindo-se ao outro lado] eu também tenho três. Se esse daqui eu não conheço [referindo-se a um lado de medida desconhecida], esse daqui eu também não posso conhecer [referindo-se ao outro lado desconhecido].
Luma complementou sintetizando essa ideia, dizendo que “x ao quadrado ou x vezes x” era a expressão que fornece o número total de bolinhas para qualquer posição. Camila disse que, para generalizar, ao invés de x, pode-se usar “b, qualquer b de bolinhas”. Taffarel sugeriu, então, que se utilizasse a expressão “b vezes b”, enquanto Emerson falou em “n vezes n”, ou ainda, conforme Felipe, “n ao quadrado”. Monique expôs seu pensamento assim: “Eu fiz multiplicando, um lado vezes o outro lado. E assim vai ser a mesma coisa do que ela [referindo-se ao raciocínio utilizado pela colega Jucilei], se eu não conheço um lado eu não vou conhecer o outro também”. Questionada sobre o que garante que posso chamar os dois lados de x, Talita respondeu: “Porque os lados das figuras são iguais”.
Empolgada com a situação-problema, a aluna Jucilei elaborou outra conjectura: “x mais x”. No entanto, logo percebeu que para a posição três, essa possibilidade não se validava, pois três mais três não dariam as nove bolinhas ali representadas. Mesmo não validada a conjectura, houve produção de significado nessa situação. Na sequência a aluna concluiu que para encontrar o número total de bolinhas para qualquer posição “[…] tem que ser x vezes x”. Monique retomou o raciocínio dizendo: “pode ser x ao quadrado”.
Apresentamos ao grupo de alunos a possibilidade de se saber o número de pontinhos do lado do quadrado, conhecendo-se o total de pontinhos da figura pertencente a essa sequência. Talita imediatamente mostrou ter percebido que essa situação retrata o inverso do que se tinha, até então, abordado. “É, tirar a raiz quadrada”. Nesse momento, Monique também exclamou: “Tira a raiz quadrada, isso mesmo!”. Essa percepção sobre o contexto de uma situação-problema foi interessante, embora tenha ocorrido apenas neste grupo, mas possibilitou a contextualização das operações inversas: potenciação e radiciação.
Faremos a seguir uma análise destas falas a respeito de cada uma das questões socializadas. Iniciaremos pela questão a, em que foi solicitado aos alunos falarem sobre suas interpretações a respeito do que viam na sequência. Daniel percebeu tratar-se de uma sequência de pontinhos que representavam figuras de tamanhos diferentes, um entendimento que partiu da ideia de espaço. Felipe e Camila ao observarem que a sequência era formada por figuras quadradas demonstraram um entendimento a partir de uma visualização geométrica. Luma, ao mencionar o que observava de uma figura para a posterior [aumento da quantidade de pontinhos nos lados], mostrou um entendimento a partir de uma visão dimensional enquanto Jucilei demonstrou pela sua enunciação uma visão global da quantidade total de pontinhos de cada figura em relação às demais.
Ao serem questionados sobre os resultados obtidos em relação às questões b até e, o aluno Emerson demonstrou em sua enunciação um pré-conceito de área do quadrado [lado vezes ele mesmo], Taffarel e Daniel demonstraram um pré-conceito mais geral de área de quadriláteros [lado 1 vezes lado 2]. Monique observou a quantidade de pontinhos que aumentava em cada figura quadrada em relação à anterior [aumentava uma fileira de bolinhas em cada lado], o que caracteriza que a aluna partiu do princípio de ampliação da área [observou o quanto aumentava].
Assim, os alunos conseguiram, cada qual, elaborar um conhecimento diferente a partir de uma mesma situação-problema. Esse conhecimento verbalizado através de diferentes justificações mostra, no contexto da situação-problema, que cada crença-afirmação justificada refletia modos distintos de produção de significados sobre uma mesma situação, os quais constituem segundo Lins (1994), conhecimentos diferentes. Esta situação mostrou, segundo o autor, como ocorre a constituição do conhecimento sobre o texto matemático.
Na pesquisa desenvolvida por Carmo (2014), o autor ressalta a importância do uso de padrões e sequências com algum tipo de repetição para introduzir a linguagem algébrica no ensino fundamental, enfatiza o quanto estas atividades podem trazer benefícios na aprendizagem da escrita algébrica, observando, porém, que, “[…] este tipo de atividade está sendo pouco utilizada para a introdução da linguagem algébrica, embora várias pesquisas e documentos oficiais mostram o potencial desse tipo de atividade para a iniciação do estudo da álgebra” (CARMO, 2014, p. 103).
Percebemos o quanto a produção de significados sobre esta situação-problema propiciou o desenvolvimento da capacidade de argumentação dos alunos e, por conseguinte, suas destrezas em elaborar um pensamento, expressando de forma simbólica e concisa suas falas. Para a elaboração do pensamento algébrico, nesta atividade, foi necessária ênfase reiterada ao uso natural da linguagem cotidiana e das outras formas de linguagem. Isto se constituiu em um aspecto fundamental no desenvolvimento e representação do pensamento algébrico discente, demonstrando que o ser humano produz pensamentos e expressa ideias pela linguagem.
Para Saraiva; Pereira e Berrincha (2010), “[…] o pensamento algébrico envolve, por um lado, a capacidade de cálculo e a capacidade de trabalhar com estruturas matemáticas usando os símbolos algébricos na resolução de problemas, e, por outro lado, envolve a capacidade de generalizar.” (SARAIVA; PEREIRA e BERRINCHA, 2010, p. 7).
Para nós ficou claro que a partir desta situação-problema, os alunos começaram a se sentir mais confiantes na elaboração das conjecturas validadas ou rejeitadas. Assim, começamos a notar que esses jovens iam elaborando, a cada dia, com maior facilidade a linguagem simbólica, pelo uso contínuo que dela fazíamos nas nossas sessões de estudo.
Percebemos nas diversas sessões de estudo que através da comunicação das ideias matemáticas presentes em situações-problema, à medida que os alunos, se apropriaram dos elementos simbólicos da linguagem algébrica, transformando este sistema de signos em instrumento do pensamento, conseguiam intersubjetivamente, constituir, verbalizar e expressar simbolicamente o contexto de cada situação-problema.
Portanto, segundo Vygotsky (2001), a constituição do pensamento algébrico é possível através da relação mediada por instrumentos e signos variados, destacando-se o conhecimento, a linguagem e o próprio pensamento algébrico.
Os princípios histórico-culturais nos ensinam que cabe à escola introduzir os sistemas conceituais, transacionando os significados, mesmo que isto gere dificuldades. O aluno se apropria da linguagem algébrica e constitui o pensamento algébrico à medida que faz o uso correto de sua linguagem. Fazer uso da linguagem cotidiana para se chegar na linguagem simbólica é fundamental, porém, a formação do pensamento algébrico perpassa pelo uso correto da linguagem algébrica.
3. CONSIDERAÇÕES FINAIS
Quando iniciamos esta pesquisa, estávamos ansiosos, angustiados e talvez um pouco temerosos em relação à performance dos alunos, tradicionalmente acostumados a receber as informações prontas e acabadas. No entanto, para esta investigação e no enfrentamento das situações-problema que nos acompanhariam ao longo das sessões de estudo, tínhamos que romper com o modo tradicional de ensino: Verbalização e audição em sala de aula. Os alunos haviam sido convidados para observar, relacionar, produzir significados, discuti-los com os seus pares, acostumando-se a ouvir do professor, ao invés de respostas, questionamentos e direcionamentos para as dificuldades que apareceriam.
Contudo nossa inquietação aumentava à medida que não podíamos prever a reação desses alunos frente a este tema. Seriam eles capazes de elaborar, por meio de signos, um pensamento que se constituiria em conhecimento? Nós conseguiríamos transformar a sala de aula num ambiente de aprendizagem coletiva, ao invés de um ambiente unidirecional de transferência de conhecimentos, ao qual estavam habituados? Conseguiríamos manter os alunos motivados e sintonizados em torno do foco central da pesquisa? Acostumados a calar, os alunos falariam mais e mais sobre cada situação-problema intencionalmente organizada?
Nas situações-problema, objetivou-se provocar os alunos no sentido de estes produzirem dialogicamente. Porém, nossa angústia consistia em saber se eles se empenhariam para expor suas ideias, estabelecendo relações dialógicas com os colegas e com o professor. Eles falariam à vontade frente a uma câmera [filmadora], presente na sala de aula? Que reação eles esboçaram em relação a uma série de palavras-chaves, que estariam perpassando os nossos encontros e o tema da pesquisa?
Conseguiriam identificar hermeneuticamente as sequências repetidas e especialmente falar sobre elas, percebendo padrões? A nossa postura como sujeitos organizadores da ação pedagógica, intervindo, questionando, provocando os alunos, dando-lhe direções para que caminhassem com os colegas na estruturação do conhecimento, seria aceita?
Apesar de muitas dúvidas e incertezas, pelos registros constantes neste trabalho, acreditamos que avançamos significativamente com os alunos na perspectiva de contribuir no desenvolvimento do pensamento algébrico.
Conforme já enfatizado, propusemos com os treze alunos participantes da pesquisa, a elaboração do pensamento algébrico através da apresentação de situações-problema, numa perspectiva meta-operacional, ou seja, que vai além da postura normalmente adotada nas escolas. Trata-se de um enfoque que compartilha comunicativamente a produção de significados dos participantes, numa dinâmica onde a qualidade da aprendizagem se sobrepõe à quantidade de conceitos. O percurso investigativo, segundo esta perspectiva, procura compreender intersubjetivamente o que permite um ser humano pensar algebricamente, buscando clarificar a relação que existe entre pensamento e linguagem para uma efetiva organização e desenvolvimento do pensamento algébrico.
O estudo propôs, partir-se da comunicação das ideias matemáticas presentes na observação e análise de padrões e sequências repetidas. Iniciamos conversando sobre o texto [situação-problema], nas perspectivas de Lins (1994) e Vygotsky (2001). Acreditamos que a produção do pensamento algébrico perpassa pela resolução de situações-problema, que podem, pelo viés da linguagem, ajudar os alunos a se comunicarem matematicamente, tanto pela linguagem cotidiana quanto pela linguagem simbólica.
A discussão crítica e reflexiva do contexto de cada situação-problema, o questionamento das possibilidades interpretativas, a produção de significados e a elaboração dialógica do conhecimento matemático, presente ou oculto, perpassa tanto pela enunciação, quanto pelo entendimento do texto, que se torna possível pela internalização dos significados produzidos sobre a linguagem.
Neste sentido, os alunos foram permanentemente desafiados a falar sobre o contexto de cada situação-problema. Em nenhum momento receberam a conjectura, regra, lei ou fórmula pronta, sempre tiveram a perspicácia e a sensibilidade de entender a necessidade de dialogar com os colegas. Perceberam ao longo das sessões de estudo a importância da comunicação das ideias matemáticas ali presentes, a relevância que existe no ouvir o relato das observações do outro. Enfim, perceberam a necessidade de comunicar argumentativamente os procedimentos para caminharem em direção ao conhecimento sistematizado.
Conforme Freire (1987), o desafio consiste em se fazer uma leitura do mundo e na caminhada perceber e compreender as relações que se estabelecem entre o texto e seu contexto, relações estas também imbricadas dinamicamente na linguagem e na realidade. Assim, aos seres humanos, tornar-se-ia mais significativo o desenvolvimento de um pensamento que auxilia a generalização de fatos e acontecimentos do que a costumeira decoreba de centenas de teoremas e fórmulas.
Em síntese, ganha ênfase a construção de modelos e procedimentos. Nas atividades desenvolvidas com os alunos e nas falas correspondentes este aspecto ficou evidente. O trabalho trouxe subjacente a produção de significados sobre o texto em cada situação-problema, uma questão fundamental para um desenvolvimento do pensamento algébrico. Segundo Lins (1994), trata-se da possibilidade dialógica de se estabelecer pela problematização um pensar aritmeticamente, um pensar internamente e um pensar analiticamente.
Conversar a respeito de cada situação-problema e, especialmente, o que mais poderia ser verbalizado, criado e produzido para o contexto existencial de cada situação proposta, foi fundamental. Nessa perspectiva, buscou-se de forma continuada, questionar as falas, os significados produzidos no contexto de cada problema, favorecendo o desenvolvimento do espírito crítico, a capacidade de argumentação e generalização.
Os participantes foram levados a reflexões sucessivas sobre as situações-problema propostas e sobre suas falas. Foram instigados a adotar uma postura investigativa e criativa que consideramos fundamental sempre. Para desenvolver o pensamento algébrico, o sujeito, segundo Lins (1994), precisa enunciar, falar sobre o texto.
Observamos ao longo da pesquisa que alguns alunos apresentaram certas dificuldades na recepção e ou compreensão das palavras pertencentes a determinadas situações-problema. Este tipo de dificuldade se constituiu, de certa forma, para esses alunos numa obstrução à constituição de um pensamento com capacidade de generalização e não permitiu a elaboração de relações mais abstratas.
Contudo, o trabalho investigativo que fizemos com os alunos mostrou que estes, na sua maioria, respondem às questões propostas, à medida que o contexto fica carregado de significações, possibilitadas pelo uso da linguagem, inicialmente, cotidiana. Acreditamos que a linguagem significa que contribuiu para o surgimento de um pensamento de caráter generalizante.
Momentos de aprendizagem com situações-problema contextualizadas podem contribuir para o surgimento de um pensar generalizante, expresso através de uma linguagem simbólica. Na pesquisa ele foi elaborado a partir do uso natural da linguagem cotidiana e da produção de significados sobre cada contexto.
Por fim, percebemos o quanto a linguagem é uma ferramenta linguística do pensamento permitindo que símbolos matemáticos possam ser internalizados pelos alunos quando lhes significam alguma coisa, possibilitando-lhes, então, lidar com objetos ausentes, levando-os à elaboração de abstrações e generalizações.
Durante as discussões, os alunos ainda manifestaram ter entendido que o pensamento algébrico não se restringe à matemática, estando presente na elaboração conceitual de qualquer disciplina. Isto para nós ficou claro em dado momento da pesquisa quando a aluna Luma, fez questão de enfatizar que sempre lembra de dois tipos de linguagem. A linguagem cotidiana e a linguagem simbólica. Segundo a aluna, são maneiras de você expressar algumas coisas. Ponderou ainda que existem mais tipos de linguagem, como a linguagem corporal, expressão através da arte, através de um quadro você pode passar alguma coisa para as pessoas, isto são tipos de linguagem.
Ao ouvir ou pensar sobre a palavra linguagem, os alunos lembraram que através dela você pode expressar o que você vê, sente e ouve. De modo geral os alunos mencionaram que que existem vários tipos de linguagem e entre elas está a linguagem matemática.
Especificamente sobre a linguagem matemática, afirmaram que podemos dizer que é uma linguagem universal, o mundo inteiro fala matemática da mesma forma. Ponderam que a forma de se fazer os cálculos aqui e no Japão é a mesma. Os alunos ainda citaram em sua reflexão a linguagem dos cegos, a linguagem cotidiana, algébrica, simbólica, as linguagens do computador, dos surdos-mudos, da matemática de modo geral, entre outras formas de comunicação utilizadas pelos seres humanos.
O que se queria na pesquisa, era que os alunos produzissem significado sobre cada situação-problema. Esta proposição foi bem compreendida é fundamental para a elaboração de um pensamento que pudesse ser caracterizado como algébrico. Não dar o peixe e sim ensinar a pescar constituía-se, a cada sessão de estudo, na chave que oportunizaria aos alunos tanto a elaboração do conhecimento quanto o aprofundamento do sentimento de confiança em suas capacidades afetiva, cognitiva, ética, de inter-relação pessoal e de inserção social, propiciando para todos, um agir com perseverança na busca de conhecimentos e da cidadania.
Quando instigamos os alunos a falarem sobre o que entendiam por pensamento algébrico, tema central da investigação e palavra-chave que perpassou nossas sessões de estudo, estes ressaltaram que se trata de um pensamento que se desenvolve com significados, atribuídos através da linguagem.
Percebemos que tiveram um entendimento que este pensamento se caracteriza por favorecer a abstração ou a generalização de uma ideia matemática. Ao longo das falas dos alunos, estes manifestaram uma critica a postura pedagógica de professores que se preocupam demasiadamente com a resolução de exercícios, sem aplicação prática.
Pelas falas dos alunos percebemos o quanto a capacidade humana de abstração e simbolização é uma característica singular é inerente à natureza intelectual da espécie humana. Através da exploração dialógica de situações-problema, como fizemos na pesquisa com adolescentes, pode-se desenvolver a capacidade de operar com signos, com mediações lógicas que nos reportam aos objetos sem que tenhamos que manipulá-los, permitindo-nos chegar a um pensamento algébrico que pela linguagem pode ser expresso.
De modo geral os alunos perceberam que o pensamento algébrico é um tipo de pensamento que traz subjacente à sua constituição um considerável grau de generalização. Desta forma, acreditamos que todo ser humano avança em termos de desenvolvimento cognitivo, à medida que consegue produzir, pelo viés da linguagem, significados sobre algo.
Embora o trabalho não seja conclusivo, aponta para uma metodologia interessante que possibilita a generalização das ideias matemáticas presentes em situações-problema e que pela linguagem, fundamental para o desenvolvimento do pensamento algébrico, pode conduzir os alunos, aos poucos, a escrever utilizando-se de símbolos matemáticos.
REFERÊNCIAS
BIGODE, A. J. L. Matemática hoje é feita assim. São Paulo: FTD, 2000, 7ª série, 335 p.
CARMO, P. F. Um estudo a respeito da generalização de padrões nos livros didáticos de Matemática do Ensino Fundamental. PUC, 2014.
DEMO, P. Pesquisa e construção de conhecimento: metodologia científica no caminho de Habermas. 3.ed. Rio de Janeiro: Tempo Brasileiro, 1996. 125 p.
FARIAS, S. A.; BORTOLANZA, A. M. E. O papel da linguagem escrita nos processos de ensino e aprendizagem: um estudo teórico. Educação & Linguagem, v. 18, n. 2, p. 63-85, 2015.
FIORENTINI, D. Alguns modos de ver e conceber o ensino da matemática no Brasil. Zetetiké, Campinas, ano 3, n. 4, p. 1-37, 1995.
FIORENTINI, D. et al. Ressonâncias e dissonâncias do movimento pendular entre álgebra e geometria no currículo escolar brasileiro. Zetetiké, Campinas, ano 1, n. 1, p. 19-39, mar. 1993b.
FREIRE, P. A importância do ato de ler: em três artigos que se completam. 18.ed. São Paulo: Autores Associados: Cortez, 1987.
LINS, R. C. O modelo teórico dos campos semânticos: uma análise epistemológica da álgebra e do pensamento algébrico. Dynamis, Blumenau, v.1, n. 7, p. 29-39, abr./jun, 1994.
LINS, R. C. Por que discutir teoria do conhecimento é relevante para a Educação Matemática. In: BICUDO, Maria Aparecida Viggiani (Org). Pesquisa em educação matemática: concepções perspectivas. São Paulo: Editora UNESP, 1999, p. 75-94.
LINS, R. C.; GIMENEZ, J. Perspectivas em aritmética e álgebra para o século XXI. Campinas: Papirus, 1997. 176 p.
LURIA, A. R. et al. Psicologia e pedagogia: investigações experimentais sobre problemas didácticos específicos. Trad. Maria Flor Marques Simões. 2.ed. Lisboa: Estampa, 1991. 153 p.
NOBRE, S. et al. Representações na aprendizagem de sistemas de equações. Disponível em: http://cmup.fc.pt/cmup/eiem/grupos/documents/14.Nobre_Amado_Ponte.pdf. Acesso em: 10 jan. 2014.
ORLANDI, E. P. Discurso e leitura. 5.ed. São Paulo: Cortez, 2000. 118 p.
SARAIVA, M. J. Sequência e expressões algébricas. Aprendizagem da resolução de equações a partir de igualdades numéricas. Projecto IMLNA. Instituto de Educação de Lisboa. Universidade da Beira Interior (2010). Disponível em: ˂http://www.apm.pt/filesMateriais_Sequencias e Equações-Equacoes _27Nov2010_4cfc0d6a04497.pdf˃. Acesso em: 14 jan. 2014.
SOUZA, E. R. de; DINIZ, M. I. de S. V. Álgebra: das variáveis às equações e funções. 2.ed. São Paulo: IME-USP, 1996. v. 5.
VALE, I.; PIMENTEL, T. Padrões e Conexões Matemáticas no Ensino Básico. Educação Matemática, n. 110, p. 33-38, 2011.
VYGOTSKY, L. S. A construção do pensamento e da linguagem. Trad. De Paulo Bezerra. São Paulo: Martins Fontes, 2001. 496 p.
APÊNDICE – REFERÊNCIA DE NOTA DE RODAPÉ
7. Dialética/dialeticamente nesta investigação, expressa a arte de buscar pelo diálogo, por meio da argumentação e contra-argumentação a ampliação de ideias e conceitos envolvidos na discussão. Na análise de fatos e situações-problema que permitem o desenvolvimento do pensamento, professor e aluno têm igual participação dialógica, estando um sempre à escuta do outro, (re)construindo juntos suas aprendizagens.
8. Texto ou texto matemático é entendido nesta pesquisa, segundo a perspectiva de Lins (1994), ou seja, uma situação-problema. Assim, a álgebra tanto quanto a matemática são vistas como um texto e, por isso, devem ser lidas e compreendidas como uma espécie de diálogo, uma interação entre leitor e autor, um tipo de comunicação realizada através de um sistema de signos. Caracteriza-se, ainda, como o centro da vivência entre professor e aluno, apresentando-se como meio para a discussão, para a reflexão ou criação de novas práticas.
9. Neste trabalho de pesquisa, conjectura é entendido como algo que antecede a busca de uma demonstração, uma regra, um padrão reconhecido, um modelo matemático, ou ainda, uma propriedade que para ser generalizada depende de validação. Portanto, trata-se de uma ideia ou hipótese que, momentaneamente, possui fundamentação incerta.
10. Aqui entendida como um processo que conduz os sujeitos ao pensamento, utilizando-se de instrumentos e signos para a formação [internalização] dos significados.
[1] Mestrado em Educação nas Ciências – Matemática. UNIJUI: Universidade Regional do Noroeste do Estado do Rio Grande do Sul, RS. Início: 2.001. Conclusão: 2.003. Especialização: Ensino de Ciências. FAFIG: Faculdade Estadual de Filosofia, Ciências e Letras de Guarapuava. Início: 1.987. Término: 1.988. Graduação em Matemática. UPF: Universidade de Passo Fundo, RS. Início: 1.984. Conclusão: 1.987. Graduação em Ciências 1º Grau. FACIP: Faculdade de Ciências e Pedagogia de Lages, SC. Início: 1.981. Conclusão: 1.984.
[2] Mestrando em Desenvolvimento Rural Sustentável, UNIOESTE: Universidade Estadual do Oeste do Paraná, 2020. Especialista em Matemática e Física, UNIPAR, Conclusão em 2010, Graduação em Matemática com ênfase em Física, UNIPAR, conclusão em 2007.
[3] Graduanda em Agronomia – UNIOESTE – Universidade Estadual do Oeste do Paraná. Graduanda de Administração – Unip – Universidade Paulista.
[4] Especialista Em Educação Matemática E Especialista Em Física Educacional.
[5] Pós-Doutor Em Ciências Ambientais.
[6] Especialização em Ensino de Ciências Exatas – Matemática, Física e Química. UNIOESTE – Universidade Estadual do Oeste do Paraná. Início: 1.997. Término: 1.988. (360h). Graduação: Ciências – Licenciatura Plena – Habilitação Matemática. UNIJUI: Universidade Regional do Noroeste do Estado do Rio Grande do Sul, RS. Início: 1.990. Conclusão: 1.992. Graduação: Ciências – Licenciatura de 1º. Grau. UNIJUI: Universidade Regional do Noroeste do Estado do Rio Grande do Sul, RS. Início: 1.986. Conclusão: 1.989.
Enviado: Agosto, 2020.
Aprovado: Junho, 2021.
