ARTIGO ORIGINAL
SCHWANTES, Vilson [1], XAVIER, Márcio Pizzete [2], KRACKE, Elisa [3], GRAUNKE, Carla Kuhn [4], GONÇALVES, Affonso Celso [5], SCHWANTES, Eloísa Bernardete Finkler [6]
SCHWANTES, Vilson. Et al. Manifestação E Verbalização Do Pensamento E Da Linguagem Algébrica Através Do Lúdico. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano 06, Ed. 06, Vol. 03, pp. 70-96. Junho de 2021. ISSN: 2448-0959, Link de acesso: https://www.nucleodoconhecimento.com.br/educacao/linguagem-algebrica, DOI: 10.32749/nucleodoconhecimento.com.br/educacao/linguagem-algebrica
RESUMO
Dificuldades na aprendizagem matemática são assunto rotineiro para alunos e professores na sala de aula. No intuito de contribuir no processo ensino-aprendizagem da disciplina, neste artigo trazemos o lúdico para o processo educativo, objetivando através do jogo e suas regras de funcionamento, permitir aos alunos a construção da aprendizagem matemática de forma prazerosa. A pesquisa mostra que o jogo pode proporcionar a construção do conhecimento matemático de forma natural e agradável, tornando-se um importante recurso pedagógico para atividades de ensino. Fundamentamo-nos no livro A Construção do Pensamento e da Linguagem de Vygotsky (2001), dada a relação que existe, segundo o autor, entre pensamento e linguagem. O estudo deixa claro que são os sentidos produzidos no processo de internalização da ideia (regra do jogo) que permitem a verbalização de seu funcionamento, constituição nos sujeitos do pensamento algébrico, levando os participantes da verbalização a generalização, representação e escrita simbólica do contexto. Nesse processo teve importância a produção de significados sobre o contexto, possibilitando, por meio das diferentes formas de linguagem, a elaboração do pensamento algébrico. Por fim, os resultados obtidos na pesquisa mostraram que o jogo, quando utilizado como recurso pedagógico, mediado pelo professor, contribui significativamente no processo ensino-aprendizagem.
Palavras-chave: Pensamento Algébrico, Linguagem, Lúdico, Produção de Significado, Generalização.
1. INTRODUÇÃO
1.1 DA PRODUÇÃO DO PENSAMENTO SOBRE O CONTEXTO À GENERALIZAÇÃO DA IDEIA DO JOGO
Jogos são atividades que exercitam, geram habilidade mental, despertam a imaginação e facilitam a aprendizagem. A atividade lúdica agrada, entretém, prende a atenção, entusiasma e ensina com maior eficiência, porque transmite informações de várias formas, estimulando diversos sentidos ao mesmo tempo, sem se tornar cansativo. Além disso, toda atividade que incorporar a ludicidade pode se tornar um recurso facilitador do processo de ensino e aprendizagem.
O procedimento didático mais adequado à aprendizagem de um determinado conteúdo é aquele que ajuda o aluno a incorporar os novos conhecimentos de forma ativa, compreensiva e construtiva, estimulando o pensamento operatório. Para que a aprendizagem se torne mais efetiva, é preciso substituir, nas aulas, as tarefas mecânicas que apelam para a repetição e a memorização, por tarefas que exijam dos alunos a execução de operações mentais (HAYDIT, 2011, p. 110).
Consideramos importante a construção do conhecimento de crianças, jovens e adultos, tanto pela inter-relação de uns com os outros, quanto pela influência sociocultural que ocorre entre todos ao longo de suas vidas. Fundamentado no livro A Construção do Pensamento e da Linguagem de Vygotsky (2001), esta pesquisa propõe com os alunos participantes a realização de uma atividade (situação-problema), chamada de truque de baralho. Trata-se de um jogo encontrado no livro Filosofia da Ciência – Introdução ao jogo e as suas regras, Rubem Alves (2000).
Esta atividade lúdica e a utilização de regras no seu desenvolvimento como elementos de aprendizagem, permite os participantes atuarem na “zona de desenvolvimento proximal” proposta por Vygotsky (2001), aflorando ao longo de seu desenvolvimento a manifestação e verbalização do pensamento e da linguagem algébrica através do lúdico.
O trabalho investigativo encontra-se fundamentado em Marques (2000), Demo (1996), Vygotsky (2001) e Lins e Gimenez (1997), à medida que estes autores acreditam que um trabalho numa perspectiva intersubjetiva não só dinamiza o aprendizado como também permite, pela discussão dialógica e reflexiva sobre cada contexto, a elaboração do conhecimento. Trata-se de uma perspectiva que visualiza o aluno como um sujeito que aprende com o outro.
A pesquisa objetivou levar os alunos a produzirem significados sobre a situação-problema lúdica proposta. Não dar o peixe e sim ensinar a pescar constituía-se na direção pedagógica que poderia oportunizar os alunos, tanto para a elaboração do conhecimento que verbalizasse a regra do jogo, quanto aprofundarem entre si o sentimento de confiança em suas capacidades, cognitiva, de inter-relação pessoal e de inserção social, propiciando para todos, um agir com perseverança na busca do conhecimento matemático que explicasse o funcionamento do jogo. No entendimento de Rego, a criança poderá utilizar materiais que servirão para representar uma realidade ausente. Nesses casos ela será capaz de imaginar, abstrair as características dos objetos reais e se deter no significado definido pela própria brincadeira (REGO, 1995, p. 81).
Segundo Guimarães et al. (2011, p. 10):
Os jogos devem ser utilizados como ferramentas de apoio ao ensino e que esta opção de prática pedagógica conduz o aluno a explorar sua criatividade. Sendo assim, dentro de um contexto educacional que o lúdico em sala de aula visa a finalidade de contribuir e auxiliar o educador no processo de ensino aprendizagem com o objetivo de desenvolver métodos de ensino que despertem na criança o interesse pela matemática.
O jogo sempre proporcionou ao ser humano um modo natural de relacionamento com o mundo. Além de favorecer a socialização dos alunos, através dele, os sujeitos se sentem desafiados, formulam hipóteses e conceitos, criam e recriam a própria vida, suas vivências, prazeres e conflitos, resolvendo-os e compensando-os por meio da imaginação subjacente ao lúdico.
O professor necessita pensar uma maneira de trabalhar com os conteúdos em sala de aula de modo que chame a atenção, ou seja, uma educação que promova mudanças e desperte o desejo e a curiosidade de seus alunos (JACOBSEN et al., 2013, p. 2).
Para a análise desta situação-problema, apresentamos uma breve reflexão sobre o uso do jogo em atividades de ensino e os resultados das produções dos alunos consideradas por nós mais significativas em relação à situação-problema truque de baralho.
2. DESENVOLVIMENTO DA ATIVIDADE LÚDICA
Seu desenvolvimento aconteceu em três momentos distintos, estando os alunos distribuídos em três grupos. Cada sessão de estudos foi iniciada com a leitura coletiva das instruções do jogo, contidas num texto entregue aos alunos, cujos resultados mais significativos apresentamos nesta sessão de forma concomitante.
Na sessão de estudo realizada para esta atividade, os três grupos de alunos evoluíram a partir do uso natural da linguagem cotidiana para um pensamento representado numa linguagem simbólico-formal. De acordo com Vygotsky (2001), foram os significados produzidos nas interações sociais em processo de internalização que permitiram o amadurecimento e a representação do pensamento algébrico pela linguagem simbólica.
Pelas manifestações dos alunos, durante seu desenvolvimento, esta foi uma das atividades que mais os envolveu. Após leituras de diversos autores e ouvir depoimentos de colegas professores, que já haviam trabalhado com jogos e enfatizado positivamente seu uso, bem como sua eficácia em situações de aprendizagem, utilizamo-nos dessa prerrogativa e pudemos constatar a validade do lúdico para um desenvolvimento do pensamento algébrico discente.
O leitor perceberá ao longo da produção de significados dos alunos sobre o contexto desta atividade que o uso do lúdico, como intervenção pedagógica, pode favorecer dialogicamente a elaboração de conjecturas. As validações dessas conjecturas reafirmam-se pelo desenvolvimento do pensamento algébrico expresso pela linguagem, que por sua vez, permite a generalização de situações-problema. Foi isso que percebemos através dos relatos dos alunos.
Constatamos nos alunos, durante a realização do jogo, especialmente através do empenho e satisfação demonstrados no decorrer da atividade, que eles haviam assumido como desafio o desvelamento dessa situação-problema, por acreditarem tratar-se de uma construção humana elaborada racionalmente sob uma ordem. A questão era decifrar o enigma e para isso teriam que observar atentamente meus movimentos e acima de tudo, segundo Demo (1996, p. 69), teriam que “[…] aprender a aprender, saber pensar”.
Nesta perspectiva, realizamos com os alunos esta atividade, denominada pelo autor de truque de baralho. Através dela, Alves (2000, p. 34), enfatiza que “o conhecimento só ocorre em situações-problema”. Esta afirmação foi uma boa razão para que os alunos se sentissem desafiados e motivados a exercitar suas capacidades de recriar soluções para situações-problema, desenvolvendo, no decorrer do processo, pelo uso natural da linguagem cotidiana, tanto a capacidade comunicativa quanto a busca de soluções para o contexto do jogo.
Em seu livro: Filosofia da Ciência – Introdução ao jogo e as suas regras, Rubem Alves (2000), propõe esta situação-problema que ele chama de truque de baralho. O problema consiste em organizar sobre uma mesa doze cartas de baralho: Ás, 2, 3, 4, 5, 6, 7, 8, 9, 10, valete e dama. A disposição das cartas é feita em círculo, como um mostrador de relógio, veja:
Figura 1. Cartas dispostas no formato das horas de um relógio.
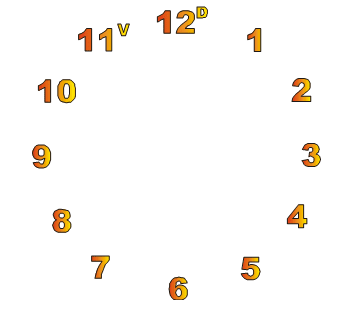
Com as cartas dispostas conforme mostra a figura, iniciamos o jogo fazendo a leitura coletiva das instruções de seu funcionamento conforme segue:
escolha uma hora, qualquer uma. Mantenha-a em segredo. Eu começarei a bater sobre as cartas (horas), pausadamente. A cada batida minha você deverá contar, mentalmente, em silêncio, até 20, a partir do número (hora) escolhido. Assim, se você tiver escolhido 4, quando eu der a 1ª batida você contará 5; na 2ª batida você contará 6, e assim sucessivamente, até 20. Quando você contar 20, eu estarei batendo na carta que você escolheu. E você terá de me dizer “acertou”. E isso porque, embora eu acerte sempre, eu não sei quando acerto. Você terá de acreditar em mim. Eu acerto sempre. Não há erros. O problema é: como é possível que isso aconteça? Os dados que lhe forneci são necessários e suficientes para você resolver o enigma. Tente resolver. Mas proceda logicamente. Não há truques. (ALVES, 2000, p. 19).
Após esta leitura inicial, comentamos com os alunos que considerávamos interessante que este jogo fosse realizado entre no mínimo três pessoas – nós, nas sessões de estudo, tínhamos sempre no mínimo quatro. Alguém que conheça as regras do jogo e que dê as batidas sobre as cartas – o relógio, um observador, para fazer as anotações dos números sobre os quais são dadas as batidas e, um jogador que pensa uma hora para ser adivinhada. Este anota silenciosamente e secretamente as horas a partir da hora pensada e avisa em voz alta quando sua contagem silenciosa chegar ao número combinado para o término do jogo, nesse caso, 20.
Salientamos a importância do observador e jogador sentarem lado a lado para confrontarem durante e depois do jogo encerrado suas anotações. A ideia era que, pelas observações e pelos registros realizados, descobrissem o segredo do jogo – idéia matemática – que permitiria a alguém acertar sempre a hora pensada por uma pessoa sem ver suas anotações e sem conhecer esta hora – número pensado.
Apresentamos na sequência uma tabela modelo, que segue, a qual poderia ser utilizada por um aluno observador. Esse aluno anotaria na tabela, caso desejasse, a partir da primeira quadrícula, os números sobre os quais o professor bateria.
Tabela – 1
| Número da batida |
Fonte: Autores.
Apresentamos também a tabela que poderia ser utilizada por um aluno jogador. Esse aluno anotaria, silenciosamente, a partir da 1ª quadrícula, caso assim desejasse, os números seguintes aos da hora pensada e avisaria a todos em voz alta quando suas anotações chegassem ao número combinado, nesse caso, 20.
Tabela – 2
| Número contado a partir da hora pensada *(4 h) |
Fonte: Autores.
* Nesse campo sugeri que fosse anotado o número correspondente a hora pensada. Neste exemplo, 4 horas.
Após a realização do jogo, por diversas vezes, ou ainda, após a realização de aproximadamente quatro rodadas, adivinhando sempre as horas distintas pensadas pelos alunos, questionamos os sobres:
a) O que observaram no procedimento do professor durante a realização do jogo?
b) O que mais conseguiram observar?
c) Existem regularidades? Quais são elas?
d) Esse jogo se constrói sob uma ordem? Qual a ordem?
e) Qual a condição para que o truque funcione sempre?
f) Escreva, em palavras, a ideia matemática que está por detrás do jogo.
g) Você seria capaz de escrever uma expressão matemática, um modelo matemático, uma lei que retrata a regra deste jogo? Use apenas símbolos para fazê-lo. O que significa cada símbolo que você usou na tua expressão?
h) Imaginemos que você escolha o número 12 – 12 horas, o maior número do relógio. Por quantas batidas minhas, no mínimo, não há formas de você chegar até 20, em sua contagem? Por quê?
i) Mas, se você escolheu 12, para que eu acerte, onde devo dar a 8ª batida?
j) E se você escolher o número 11? Explique.
OBS. Brinque com o jogo com os teus amigos, com vários amigos ao mesmo tempo e acerte a hora que cada um pensou. É divertido, você não acha?
k) Agora que você descobriu o truque, vamos experimentar com o número 25 ao invés do 20.
l) Qual seria o raciocínio necessário para que se acerte a hora pensada nessa nova condição? Tente expressar matematicamente essa ideia.
m) Seria possível fazer o mesmo jogo utilizando o número 15? Experimente.
n) Que raciocínio foi necessário empregar para acertar a hora pensada?
o) Qual é o menor número que pode ser utilizado como base de contagem para que esta regra [jogo] funcione sempre? Explique
p) No contexto desse jogo, para quais condições ele não funciona? Por quê?
q) O que é necessário para que o jogo funcione sempre?
r) O que mais gostariam de dizer?
Adaptado de Alves (2000, p. 18-19).
Esclarecemos aos alunos que atentassem para o fato de que acertaria sempre, mas não saberia quando acertaria, teria que para isso ser avisado por eles. Neste momento, Taffarel questionou: “Mas, o professor vai bater sempre na sequência?” Deixamos claro aos alunos que a resposta para este questionamento fazia parte da elucidação do segredo do jogo. Portanto, teriam que observar nossas batidas sobre as cartas e, pela observação, formular conjecturas que os auxiliassem tanto para compreender por que eu acertava sempre a hora por eles pensada, quanto para entender a ideia matemática que estava por detrás deste jogo e que permitia o seu funcionamento.
Motivados desde o princípio da atividade, neste momento os alunos já se encontravam de certa maneira ansiosos para compreender a ideia, o segredo do jogo, ou seja, a ideia matemática que me permitia acertar sempre a hora pensada pelos alunos, isto sem olhar suas anotações e sem saber o número [hora] por eles pensado. Toda a expectativa criada em torno do desafio de esclarecer o funcionamento do truque mostra-nos, segundo Vygotsky (1998, p. 136), que de fato para os alunos, “[…] a criação de uma situação imaginária pode ser considerada como um meio para desenvolver o pensamento abstrato”.
Dentre as rodadas realizadas nas três sessões de estudo, duas foram trabalhadas com quatro alunos em cada grupo e uma com cinco alunos. Transpareceu-nos naquele momento que todos os procedimentos estavam entendidos e os alunos preparados para o jogo.
Com o objetivo de clarificar e ajudar o leitor a compreender a dinâmica de cada sessão de estudo realizada, passamos a transcrever integralmente os procedimentos seguidos durante uma das sessões com o primeiro grupo.
Inicialmente retirámo-nos da sala para que os alunos do pequeno grupo – com 4 alunos, coletivamente combinassem uma mesma hora para ser por mim adivinhada. Alguns minutos depois, os alunos nos chamaram para dar início ao jogo. Pedimos, então, concentração a todos e iniciamos batendo aleatoriamente sobre as cartas contando silenciosamente até 7. Damos a 8ª batida sobre a dama e, a partir desta carta, sem contar, continuamos batendo sequencialmente no sentido anti-horário até que algum aluno dissesse ‘acertou’. À medida que um de nós batíamos sobre as cartas, cada aluno fazia as suas anotações na tabela. Neste jogo, enquanto um de nós batia, primeiramente de modo aleatório sobre a carta de número 4 – 4 horas, o aluno observador marcava em sua tabela o número 4.
Embora nós não soubéssemos, este grupo havia pensado o número 10 [10 horas] como sendo a hora que teria que ser por nós adivinhada. Por isso, para essa primeira batida nossa, o aluno jogador anotou em sua tabela o número seguinte ao da hora pensada, 11, seguindo as orientações enunciadas anteriormente pelo autor. Após bater sobre a carta 4, continuamos batendo aleatoriamente sobre os números 8, 10, 6, 2, 5 e 8. O aluno observador registrou-os em sua tabela e o aluno jogador pensou nos números seguintes ao que nós deveríamos adivinhar, 11, 12, 13, 14, 15, 16, 17, e os registrou em outra tabela, conforme segue.
Tabela 3. Tabela do aluno observador.
Cartas sobre as quais o professor batia
| 4 | 8 | 10 | 6 | 2 | 5 | 8 |
Fonte: Autores.
Tabela 4. Tabela do aluno jogador.
Número contado a partir da hora pensada
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
Fonte: Autores.
Após a 7ª batida aleatória [dada sobre o número 8], passamos a bater sequencialmente a partir do 12 [dama] no sentido anti-horário e o aluno observador continuou registrando em sua tabela os números sobre os quais eu batia: 12, 11, 10. A cada batida nossa o aluno jogador continuava sua contagem silenciosa, até chegar ao 20. O silêncio só era quebrado, em cada rodada, quando os alunos me interrompiam exclamando: “Acertou!”. Neste momento, sem ver as tabelas dos dois alunos, nós batíamos sobre a hora pensada por eles –10 horas, e dizíamos: Esta foi a hora por vocês pensada, a rodada está encerrada. Acertamos!
Tabela 5. Tabela do aluno observador
Cartas sobre as quais o professor batia
| 4 | 8 | 10 | 6 | 2 | 5 | 8 | Q(12) | J(11) | 10 |
Fonte: Autores.
Número contado a partir da hora pensada
Tabela 6. Tabela do aluno jogador
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
Fonte: Autores.
O leitor poderá observar pela anotação feita na tabela do aluno observador que a 2ª batida dei sobre o 8 – 8 horas. Atente também nesta tabela para as sete primeiras batidas minhas [4, 8, 10, 6, 2, 5 e 8]. São batidas dadas aleatoriamente, não apresentam nenhuma regularidade. Sua finalidade é despistar e confundir os alunos. Estas batidas representam um grau de dificuldade, um obstáculo para quem pretende desvendar o segredo do funcionamento do jogo. No entanto, precisam ser percebidas e levadas em conta, caso contrário, as chances para a elucidação do jogo ficam restritas.
Veja também que o aluno jogador continuou sua anotação, em ordem crescente, registrando na sua tabela o número 12, para essa segunda batida minha sobre o 8. Perceba que para cada batida minha sobre o mostrador de relógio, sua numeração contínua regular sequencial crescente, a partir da hora pensada [10], até chegar ao vinte, momento em que ele comunicava o término da rodada.
No jogo, realizado com o primeiro grupo, cujas anotações se encontram nas duas tabelas mostradas anteriormente, quando batemos sobre a carta de número 10, a aluna Luma exclamou: “Parou”. A contagem dos alunos do grupo havia chegado no vinte e restou-nos dizer: Vocês pensaram 10 horas, ao que os alunos, com um olhar desconfiado, pois sabiam que nós não éramos adivinho, balançaram a cabeça, demonstrando que sim, tinha realmente pensado 10 horas.
Neste jogo, sempre que o número de contagem combinado for 20, pode-se dar, sem medo de errar a hora pensada, sete batidas aleatórias sobre o mostrador de relógio, pois nenhum aluno irá exclamar acertou. Contudo é preciso prestar atenção e dar a 8ª batida sobre o 12 [dama], pois caso os alunos tenham pensado 12 horas, na 8ª batida a contagem deles chegará no 20 [12 + 8 = 20].
Neste sentido e levando em consideração que os alunos podem não ter pensado 12 horas [maior número do relógio], continuamos batendo, pois somente paramos de bater sobre as cartas quando os alunos nos avisam. Lembramos o leitor que acertamos sempre, mas não sabemos quando acertamos. Caso não tenhamos sido interrompidos, a partir da 8ª batida dada sobre a dama, continuamos batendo, só que agora regularmente, a 9ª batida sobre o valete –11 horas, depois sobre o 10 – 10 horas e assim por diante, sempre em ordem decrescente, aguardando que alguém diga: ‘Acertou’.
Por alguns instantes os alunos estavam perplexos diante do anteriormente ocorrido. Como poderíamos bater sobre a hora pensada, exatamente quando sua contagem silenciosa chegasse no 20? Imagine, agora, a reação desses alunos quando lhes dissemos que adivinharíamos, em uma mesma rodada, duas ou mais horas diferentes pensadas por dois ou mais alunos do grupo. Jucilei não se conteve e exclamou: “Ás duas horas? Os dois juntos?” Monique perguntou para as suas colegas: “[…] ele nunca erra?” A pergunta que não queria calar-se era: Como alguém poderia acertar, num mesmo jogo, a hora pensada por 5, 10 ou 15 pessoas, cada uma tendo pensado uma hora diferente? Qual seria o segredo? Ou será que não havia segredo? De fato, para os alunos isso era o máximo, algo fantástico e que eles queriam e tinham certeza de que iriam compreender.
Outra rodada foi iniciada com uma nova dinâmica. Agora, os grupos com 4 alunos formavam duas duplas, assumindo um aluno de cada dupla a função de preencher a tabela do aluno observador e o outro a do jogador, pensando cada dupla uma hora diferente para ser por mim adivinhada. A rodada acontecia conforme as orientações já mencionadas e nós adivinhávamos as duas horas diferentes pensadas pelas duas duplas de alunos.
Na sequência desta atividade, na realização de uma outra rodada, um de nós acertou a hora pensada por cada um dos alunos do grupo. Jucilei, nesta atividade e no momento em que acertamos a hora por ela pensada, levantou-se e exclamou: “Ah! Meu Deus! 12 [horas], acertou!”. Os demais alunos, da mesma forma como acontecera com Jucilei, ficaram impressionados. Isso para eles parecia mais uma façanha do que qualquer outra coisa, pelo menos nesse momento inicial.
Em cada grupo houve a realização de diversas rodadas e as consequentes anotações dos alunos em suas tabelas. Pedimos para que as guardassem, pois as informações nelas contidas seriam importantes para a elucidação da charada. Nas palavras de Ribeiro “O jogo favorece o desenvolvimento da criatividade, do senso crítico, da participação, da competição sadia, da observação, das várias formas de uso da linguagem e do prazer em aprender” (RIBEIRO; GOULART, 2013, p. 4.).
No terceiro grupo de alunos a expectativa se manteve, no entanto, foi trivial a primeira rodada realizada com eles. Eles haviam pensado o número 12 – 12 horas, o maior número do relógio. Assim que iniciamos pausadamente as batidas sobre as cartas, os alunos começaram sua contagem silenciosa até 20, a partir do 12, hora por eles pensada [13, 14, 15, 20]. Alguns instantes depois, nós já tínhamos dado sete batidas aleatórias [12 + 7 = 19] e quando damos a 8ª batida sobre a carta 12 [dama] a contagem silenciosa dos alunos chegou em 20, momento em que Taffarel e Daniel, quase que simultaneamente exclamaram: “Acertou!”.
Para os alunos este momento foi mágico: A 8ª batida, que para a nossa contagem significava o início das batidas não aleatórias [as 7 batidas anteriores eram aleatórias], para eles representou, naquele instante, apenas mais uma batida aleatória. Alguns alunos ficaram boquiabertos e ainda mais impressionados quando lhes disse que acertávamos sempre, porém, nunca sabíamos quando acertávamos, precisávamos ser avisados. Dissemos a eles ainda que no momento exato em que suas contagens silenciosas chegassem no 20, estaríamos batendo sempre sobre o número [hora] pensado por eles.
Neste grupo, após a realização de três rodadas, pedimos aos alunos que falassem sobre o que haviam observado. Taffarel imediatamente disse: “Você pegou do 12, daí fez [bateu] o 11, o 10, 9, 8, 7, 6 e assim por diante”. O aluno Felipe prontamente questionou o colega perguntando: “E as batidas que ele deu antes?” Taffarel respondeu confusamente: “[…] as batidas que ele deu antes, ele começou do 12, daí ele veio fazendo: 11, 10, 9, […]”, ao que Emerson perguntou: “Tá, mas quantas batidas ele deu antes?” [Silêncio]. Taffarel neste momento observou seus apontamentos e exclamou: “7 batidas! Daí a 8ª era no 12”. Na sequência os alunos cochicharam entre si. Felipe ainda disse que “[…] 8 mais 12, dá 20”.
Neste grupo foi Taffarel quem comunicou aos colegas a elaboração da primeira conjectura, porém, segundo o aluno, sua hipótese precisava ainda ser testada para poder ser validada. Assim, o aluno solicitou aos colegas que pensassem uma hora, iniciando posteriormente as batidas sobre o mostrador de relógio. Instantes depois de iniciar as batidas, seus colegas foram exclamando um a um: “Acertou, acertou, acertou”. Era a validação que lhe faltava para confirmar a sua hipótese inicial.
Como os demais alunos participaram ativamente desse momento, pedimos para que procurassem, agora, falar sobre os procedimentos observados durante as batidas de Taffarel sobre o mostrador de relógio. Emerson relatou que “depois da 7ª batida ele vai começar lá no 12, a 8ª batida e vem vindo pra baixo [ordem decrescente] até chegar no ás se você escolher o número 1 ou até ser interrompido se o número pensado for outro”. Felipe ainda acrescentou que depois das “7 batidas, daí ele vai pro 12 e começa pelo valete, 10, 9, 8, 7 […]”. Estes relatos demonstram que houve produção de significados, porém até este momento, os alunos não conseguiam expressá-los algebricamente.
Durante as primeiras rodadas, em cada um dos três grupos, houve entre os alunos a manifestação de cochichos e risos demonstrados através do semblante de cada um. As expressões faciais demonstravam ao mesmo tempo espanto, seriedade e preocupação em desvelar o enigma do jogo. Esta foi a impressão que tive ao assistir novamente as fitas de vídeo com as imagens dessas aulas. O olhar compenetrado de cada aluno sobre o ´mostrador de relógio´, fixado junto ao quadro-negro e, por conseguinte, sobre quais cartas eu batia, mostrou a imensa vontade que cada um deles tinha em desvelar e explicar como funcionava o truque de baralho.
As discussões e trocas de ideias entre os alunos, na tentativa de desvelar o enigma do jogo, propiciaram a elaboração de pensamentos que permitiram ao longo do processo a estruturação de conjecturas. Segundo o entendimento de Vygotsky (2001, p. 409), “todo pensamento procura unificar alguma coisa, estabelecer uma relação entre coisas. Todo pensamento tem um movimento, um fluxo, um desdobramento, em suma, o pensamento cumpre alguma função, executa algum trabalho, resolve alguma tarefa”.
Poderíamos ter apresentado aos alunos a solução deste problema, mas não era este o propósito da pesquisa. Nas atividades, interessava-me conseguir dos alunos, pela linguagem cotidiana num primeiro momento, tudo o que poderia ser pensado e dito sobre cada desafio que surgia. A ênfase dada para extrair dos alunos, pelas falas, o máximo de significados, encontra fundamentação nas palavras de Vygotsky (2001, p. 12), ao afirmar que “[…] a generalização se torna possível se há desenvolvimento da comunicação”.
A capacidade de argumentar e contra-argumentar, de produzir mais e mais significados se constituiria, num segundo momento, na chave para desvelar o modelo matemático presente ou oculto nesta situação-problema. Assim, nossa postura foi marcada pelo constante motivar e questionar cada um dos participantes, explorando suas capacidades de inventar soluções. Questionávamos a formulação de um pensamento sobre o contexto do jogo pela significação dos conceitos e os meios para se chegar a eles tinham que ser introduzidos na interlocução.
Surpreendemo-nos com a performance dos alunos durante a realização desta atividade. Todos estavam realmente empenhados e interessados em decifrar racionalmente o segredo, a ordem sobre a qual o jogo se sustentava. Compreendemos o estado emocional e o desejo dos alunos em desvendarem o funcionamento do jogo a partir dos escritos de Vygotsky (1998), ao afirmar que na atividade lúdica o desvelamento de suas regras constitui-se para as crianças uma “[…] fonte de prazer” (VYGOTSKY, 1998, p. 131).
O comportamento dos alunos durante a execução do truque de baralho, reflete-se no pensamento de Vygotsky (1998), ao analisar o papel do brinquedo no desenvolvimento cognitivo das crianças em idade pré-escolar. Os adolescentes, durante toda essa atividade lúdica, exercitarm suas capacidades de pensar, movidos pela possibilidade de satisfazerem suas regras e recriarem um modelo matemático que permitiria acertar sempre a hora pensada. Expressavam em seus semblantes um desejo, o de se emanciparem, assim como a criança busca no brinquedo o autocontrole.
Depois de ter realizado três e em alguns grupos quatro rodadas, seguidamente, crescia a convicção de que o caminho que nos conduziria na direção da elaboração de um modelo matemático, que viesse a retratar e explicitar o funcionamento deste jogo, perpassaria pela observação das regularidades subjacentes à atividade. Resolvemos, então, alertar os alunos para atentarem mais para a possibilidade de existirem, nos procedimentos utilizados por mim e pelos alunos que haviam testado suas conjecturas, certas regularidades.
Neste momento, Luma querendo um tempo para pensar disse: “Vai dar para pensar agora”, ao que Camila, sua colega acrescentou: “Já tem muita coisa para pensar”. Naquele momento, Monique já havia em voz baixa cochichado para as colegas do grupo, ventilando a possibilidade de ter encontrado uma solução para o enigma. De fato, ela havia elaborado uma conjectura, porém precisava testá-la para poder comunicar sua validação.
Após alguns cochichos entre os alunos do grupo, decidiram simular outra rodada com o intuito de averiguar a validade da conjectura elaborada pela aluna Monique, a respeito da regra do jogo. Esta saiu então da sala e os demais alunos permaneceram sentados ao redor da mesa. Combinaram cada qual uma hora para a colega adivinhar, chamando-a novamente para a sala. Ao retornar, os alunos cochicharam entre si e deram risadas, para dar vazão à grande expectativa criada. Será que Monique realmente teria elaborado uma conjectura que iria explicitar o funcionamento deste jogo, até então enigmático?
Monique começa então a bater pausadamente sobre as cartas do mostrador de relógio. Com uma das mãos segurou o quadro, que balançava um pouco com o impacto das batidas. Não demorou muito e Luma interrompeu as batidas da colega dizendo: “Acertou!”. Monique suspirou aliviada e emitiu um suave “ah!” Seguido de uma risadinha de felicidade. Ela realmente havia desvendado o segredo do jogo. No entanto, continuou a bater sobre as cartas para acertar as horas pensadas pelos demais colegas. Sem demora, Jucilei exclamou: “Acertou!”. Em seguida o mesmo aconteceu com os demais alunos.
Outros alunos também deram sinais de compreensão do funcionamento do jogo. Pedimos então que começassem a falar sobre o contexto dessa situação, explicitando o que permitiria um ser humano adivinhar a hora pensada por outro. De acordo com Vygotsky (2001), os alunos favorecidos pelo ato dialógico conseguiram carregar as palavras de significados, mostrando que o pensamento “é antes uma formação dinâmica que estática” (VYGOTSKY, 2001, p. 408).
Monique, referindo-se aos meus procedimentos anteriores, relatou aos seus colegas: “[…] ele conta sempre 7 números, é diferente e depois ele começa do 12, em ordem decadente”, querendo dizer decrescente. Neste sentido, Luma complementou: “É, é do diminutivo [referindo-se às batidas sobre as cartas em ordem decrescente] até que chega no número 20 [referindo-se à contagem silenciosa]”, com o que Jucilei e Camila concordaram, repetindo: “Até chegar no número 20”. Luma ainda chamou a atenção para o fato de não sabermos a hora pensada pela pessoa e, para acertarmos, a mesma pessoa tem que nos avisar. Sobre este aspecto Jucilei lembrou que isto é possível porque “[…] você bate lentamente, até que você vai pro outro número, a pessoa fala ‘acertou’, daí você sabe que acertou”.
Questionadas sobre a condição ou sobre o que precisava acontecer para que esse truque funcionasse sempre, Luma voltou a frisar que a 8ª batida “tem que ser no 12”, porém é preciso “contar primeiro sete batidas diferentes”, as quais, segundo Monique, consistem em “[…] confundir primeiro os participantes e depois é só bater na ordem decrescente, até acertar o número [hora pensada]”. Para Oliveira (1995), o comportamento das crianças é fortemente determinado pelas características das situações concretas em que se encontram. Nesta idade elas sempre desejam algo concreto, visível, real.
Em outro grupo de alunos, Caroline elaborou por primeiro uma conjectura, a qual foi testada e aplicada para os colegas. Neste grupo a aluna Angélica percebeu em suas anotações que Caroline havia dado 7 batidas aleatórias e depois apenas batidas sequenciais em ordem decrescente a partir da dama. Olhando para a sua tabela de apontamentos, Angélica disse: “Aqui tem 7 [números], nesta tabela. É primeiro no 1 depois no 5, 9, no 2, aí 7, 4, daí 6. Daí ela começa: 12, 11, 10, 9, 8, 7, 6, 5, 4”. Questionada sobre a forma como Caroline deu essas 7 batidas, Angélica simplesmente respondeu: “Misturado”, “em qualquer carta que ela quisesse”, acrescentou Douglas. Após um suspiro o aluno complementou: “É, e a 8ª batida ela começou do 12 pra baixo: 11, 10, 9, 8, 7, 6, 5 […]”.
Caroline descreveu sua observação em relação aos procedimentos que utilizamos para adivinhar a hora pensada pelos alunos, relatando: “Bom, eu observei que a gente conta até 7 e quando chega no número 8, bate na carta 12, que é a dama, depois vai indo para trás, que nem 11, 10, 9, […] até chegar no número 20 […] daí eles falam acertou, porque a gente não sabe que chegou no número 20”.
Esta postura foi importante e mostrou, segundo Marques (2001), que o caminho se faz ao caminhar e para isso conversar era preciso. No entendimento de Vygotsky (2001, p. 152), chega-se “[…] ao significado de uma palavra através de outra palavra […]”. De fato, a aluna Luma retomando a conversa ressaltou novamente que “a 8ª batida é sempre no 12 e que também você bate 7 números diferentes e a 8ª batida sempre você vai bater no 12”. Jucilei participou e compartilhou dessa ideia acrescentando que “depois da 8ª batida vai ser em ordem decrescente”. Camila também tinha tido essa compreensão e complementou em sua fala que após as batidas a esmo, para que o jogo funcionasse sempre era preciso continuar batendo sobre as cartas seguindo uma ordem, ou seja, batendo sequencialmente sobre “12, 11, 10, 9, 8 […]”, até a pessoa avisar que tínhamos acertado.
No entendimento de Caroline, existiam batidas irregulares [aleatórias] e regulares [sequências decrescentes a partir da dama] sobre as cartas. Segundo a aluna, “a irregular é quando você bate antes, as sete primeiras batidas [e] são pra confundir a pessoa”, ao que Angélica acrescentou “[…] irregular é bater misturado”.
2.1 A IMPORTÂNCIA DO ATO DIALÓGICO NA EXPRESSÃO ALGÉBRICA DE UMA IDEIA MATEMÁTICA
Faremos agora, um resumo sucinto da caminhada dialógica que ocorreu nos grupos e que permeou a busca de uma expressão matemática que representasse os pensamentos manifestados pelos alunos, através das distintas formas de linguagem, acerca das ideias que garantiam o funcionamento do jogo. Faremos também algumas considerações que consideramos fundamentais para uma efetiva elaboração, desenvolvimento e apropriação do pensamento algébrico. Destacaremos a importância do uso reiterado da linguagem em atividades lúdicas, especialmente quando estas são regidas por regras definidas, o que permite, ao longo de sua exploração, a constituição de um pensamento caracterizador da ideia do funcionamento do jogo e de sua representação por meio de uma expressão algébrica.
Vários alunos participantes da pesquisa apresentaram nesta atividade dificuldades para expressar matematicamente a ideia do jogo, cujo funcionamento haviam compreendido através de uma construção dialógica coletiva. Nas falas dos alunos evidenciou-se a compreensão de toda a dinâmica que permitia a um aluno adivinhar a hora que outro tinha pensado. Felipe, por exemplo, comunicou que era preciso “[…] bater 7 números, pra depois ir pro 12”. Emerson também compreendeu essa ideia e acrescentou que “antes de dar a 8ª batida ele [o professor] foi batendo em qualquer carta [aleatória] e, para ele descobrir o número escolhido por mim, que estava em silêncio, daí na 8ª batida tinha que começar no 12 e daí bater em ordem decrescente até chegar no número escolhido por mim”. Taffarel ainda observou em seus apontamentos que após a 8ª batida, na tabela do aluno observador, os números registrados [horas] iam diminuindo enquanto esses mesmos números, segundo o aluno, aumentavam na tabela do aluno jogador. No entanto, expressar essa ideia simbolicamente parecia representar um difícil degrau para os alunos.
Nossa postura investigativa, durante toda a realização da pesquisa, possuía um caráter ygotskiano, à medida que sempre voltávamos ao tema, numa tentativa dialógica de obter pela interlocução uma informação a mais, na expectativa de que essa informação pudesse fechar o circuito e possibilitar a conexão para uma comunicação da ideia do jogo, através de uma linguagem estritamente simbólica. No entanto, após muita conversa sobre o contexto da situação-problema, o aluno Daniel expressou a sua dificuldade e a dos colegas do grupo dizendo: “A gente só não consegue passar isso algebricamente”. Relatou ainda que compreenderam que “a 8ª batida é na dama e depois vem em forma decrescente pelo relógio”, até acertar a hora pensada. Porém, o aluno voltou a ressaltar que “[…] a gente não consegue passar isto algebricamente, para as letras”. Pedimos então se precisariam de uma ajuda, ao que Felipe me respondeu: “De duas”, significando mais de uma.
Continuamos insistindo mais um pouco e pedimos para que observassem os apontamentos realizados nas tabelas. Neste instante, o aluno Taffarel observou algo interessante nas anotações realizadas em uma de suas tabelas, em que o número a ser adivinhado era 10, exclamando: “Oh! 10 [hora a ser adivinhada, pensada pelo colega numa das atividades realizadas] mais 7 [batidas aleatórias], igual a 17, mais 3 [o que faltava para completar 20] que ele contou depois da dama [hora], dá 20”. Neste instante intervimos pedindo para que atribuíssem significado ao 7 e ao 10. Emerson chegou a falar em 7 mais x, como uma conjectura possível para a elucidação do enigma, porém, seu raciocínio foi interrompido por Taffarel, que conseguiu, em bom tom de voz, chamar a atenção de todos para a sua conjectura.: “É h = 20 – x. Agora esse x vai ser o que?”, indagou o aluno.
Emerson, percebendo a empolgação do colega, abandonou sua conjectura, pegou seus apontamentos e somou-se ao colega na tentativa de conseguirem expressar essa ideia matematicamente. Após pensar um pouco disse: “São as batidas”, ao que Felipe adicionou: “Irregulares e regulares”. Intervimos novamente solicitando que explicitasse o que estaria representando na expressão matemática o h e as batidas irregulares e as regulares, ao que Felipe e Taffarel responderam simultaneamente, “o h representa a hora pensada e as batidas irregulares e regulares, o x”.
A interlocução, que se seguiu a partir desse momento, clareou os significados dos termos presentes nesta expressão matemática e, por conseguinte, sua validação em outras situações do contexto deste jogo. Isto também foi produtivo, pois em seguida, questionados sobre outras possibilidades de se expressar matematicamente a ideia deste jogo, Taffarel comunicou e foi explicando outra conjectura por ele elaborada: “h [hora pensada] = x + y. As batidas regulares são o x e as batidas irregulares o y”. Ao tentarem validar a conjectura, perceberam que ela não se aplicava de forma geral para esse contexto, ou seja, funcionava para alguns casos [3+ 7 = 10, situação anterior], porém, não funcionava e não se aplicava para todas as situações deste jogo.
Sugerimos então a retomada da conjectura anteriormente elaborada pelo aluno Emerson [hora pensada = 7 mais x], porém, abandonada naquele momento, em função da comunicação de Taffarel. Exploramos essa possibilidade, porém, como esta mesma conjectura foi comunicada melhor numa outra sessão, com as alunas Monique, Talita, Luma, Jucilei e Camila, analisaremos a questão nas falas destas alunas. Elas apresentaram uma desenvoltura impressionante, tanto em relação à compreensão dessa situação-problema quanto para expressá-la matematicamente através de uma linguagem estritamente simbólico-formal.
Questionadas sobre por que eu batia na hora pensada quando sua contagem silenciosa chegava ao 20, Monique foi logo dizendo que era só somar “[…] 7 com o restante que eu vou contar na ordem decrescente a partir do 12”. Isto dito na linguagem cotidiana, fui logo perguntando qual seria então o modelo matemático que poderia representar essa ideia, numa linguagem simbólica, ao que Monique com naturalidade disse: “Eu acho que é: 7+x = h, ou então, h = 7+x”. Instigadas a explicitar significativamente cada termo da expressão, Monique disse que “7 vai representar as primeiras sete batidas aleatórias que eu vou dar”, “alternadas”, acrescentou Talita e “o x é o número de batidas a partir do 12, incluindo o 12”, completou Monique.
A aluna Luma percebeu que a letra x, nesta expressão, representava uma variável, isto é, para cada número pensado, para cada rodada seu valor variava. Neste sentido, a aluna comunicou que a expressão que retratava o funcionamento do jogo também podia ser expressa por “7+y =h ou h = 7+y, ou ainda h =7+a, qualquer letra, é, um número que você não sabe”.
Consideramos esta etapa como entendida e passamos a explorar uma outra questão que consideramos pertinente para se poder, em seguida, avançar e analisar com mais detalhes e profundidade os contextos para os quais este jogo funcionava, porque funcionava e para quais números de contagem ele eventualmente poderia não funcionar. Neste sentido, pedimos para que cada participante imaginasse e refletisse melhor sobre um fato que já havia ocorrido em dois momentos, ou seja: Caso alguém pensasse o número 12 – 12 horas, o maior número do relógio, por quantas batidas minhas, no mínimo, não haveria formas da contagem do aluno chegar ao número combinado, 20, e como isso poderia ser explicado?
A socialização desta abordagem foi interessante e mostrou a internalização de significados que havia ocorrido em relação à compreensão do jogo. No entendimento da aluna Luma, “12 com 8, chega no 20, daí tem que ser 12 com 7, que dá 19” para não adivinhar a hora pensada, 12 horas. Jucilei concordou com Luma e imediatamente acrescentou que “12 com 7 é igual a 19, daí a 8ª batida irá ser na dama”. Monique em seu raciocínio repetiu esta ideia e acrescentou que, “além da 8ª batida ter que ser na dama, a 9ª vai ser no número 11 [valete], porque 9 mais 11 vai dar 20”. Sobre esta mesma questão o aluno Taffarel, por exemplo, registrou sua compreensão dizendo que “7 mais 12 não dará 20 e assim [o professor] não será avisado [pelo aluno] que acertou” a hora pensada. Em sua reflexão, quando questionado por mim sobre a batida de número 8, o aluno disse que tem que ser “na dama e a 9ª batida no valete” com o que Daniel e Emerson também concordaram.
Além dos aspectos cognitivos, o jogo também a atende outras dimensões como o aspecto afetivo-emocional tão importante para o seu processo de desenvolvimento:
Ao brincar, afeto, motricidade, linguagem, percepção, representação, memória e outras funções cognitivas estão profundamente interligadas. A brincadeira favorece o equilíbrio para o processo de apropriação de signos sociais. Cria condições para uma transformação significativa da consciência infantil, por exigir das crianças formas mais complexas de relacionamento com o mundo. (OLIVEIRA, 2010, p. 164).
Consideramos como amadurecidas e compreendidas, uma série de questões e avançamos nos questionamentos. Pedimos, então, para que pensassem sobre a possibilidade de adivinhar-se a hora pensada por alguém, utilizando-se como base o número 25, ao invés do 20. Caso essa nova condição pudesse ser utilizada, pedi para que explicitasse os procedimentos que deveriam ser seguidos para que o truque continuasse funcionando.
Esta etapa da atividade também nos surpreendeu, dada a qualidade da produção dos significados comunicados pelos alunos. A aluna Jucilei não vacilou e foi logo dizendo: “Contaríamos 12 batidas [aleatórias] em vez de 7, depois a 13ª batida, iria ser na dama, no 12. Daí vai ser em ordem decrescente até chegar no número x” [referindo-se ao número – hora pensada]. A comunicação de Luma me pareceu simplesmente espetacular. Ela repetiu de certa forma o raciocínio da colega Jucilei, no entanto percebeu algo a mais presente no contexto deste jogo. Assim, Luma finalizou seu raciocínio destacando “[…] que tirando 13 sempre [do número combinado], vai dar o tanto de batidas alternadas, que te dá a resposta” [das batidas alternadas].
Esta ideia foi complementada por Jucilei que imediatamente acrescentou “que são 12 batidas aleatórias, se você diminui 13 de 25, daí vai dar o tanto de batidas aleatórias que você precisa saber” para acertar a hora pensada por alguém. Talita participou desta ideia e explicou este raciocínio utilizando-se da operação inversa. “Porque 13 mais 12, daria 25”. Esta interlocução mostrou, segundo Vygotsky (1998, p. 128), que “A ação regida por regras começa a ser determinada pelas ideias e não pelos objetos”.
Os demais alunos demonstraram esta mesma compreensão, comunicada com outras palavras. Destacamos aqui que a aluna Caroline enfatizou que após as batidas irregulares dadas sobre qualquer uma das cartas, seguem-se as batidas regulares, iniciando-se pela dama, depois valete, 10, 9, 8, continuando sequencialmente, sempre em ordem decrescente.
Os alunos Daniel, Emerson, Felipe, Taffarel e Maico já haviam manifestado o que Taffarel, neste momento, fez questão de repetir, ou seja: “O mais difícil é escrever [a ideia do jogo] na forma algébrica”. Mesmo assim, estes alunos surpreenderam com sua criatividade. Utilizando-se da linguagem cotidiana e das operações aritméticas básicas, Taffarel e Felipe construíram uma tabela, através da qual retrataram que: Qualquer número de contagem menos o número de batidas aleatórias, daria 13, menor número de contagem para o qual o jogo funciona sempre[7].
Nas palavras de Felipe, temos “[…] que pegar o número, estipulado, menos o número de batidas irregulares dadas nas cartas, assim, que vai dar sempre 13, menor número de contagem possível de ser utilizado para que o jogo funcione sempre”. Através deste raciocínio as batidas aleatórias somente serão conhecidas após conhecermos qual a ordem da batida sobre a dama [25 – 12 = 13]. Subtraindo 1 de 13 obtemos 12, que indica a quantidade de batidas aleatórias. Jucilei expressou seu pensamento ao relatar que “[…] com o 12 já não funciona, não tem como fazer [acertar sempre a hora pensada]”.
No entanto, ao tentar justificar sua crença-afirmação, em suas palavras transparecia uma certa limitação dessa ideia, dificultando o seu entendimento e uma compreensão mais detalhada. Talita, ao perceber a dificuldade da colega em se expressar, justificou que neste jogo, no qual dispomos os números [cartas] em círculo como em um mostrador de relógio, “se o número de contagem fosse 12 ou menor que 12 não daria certo porque um relógio tem como base 12 números. Então, não teria sobra de batidas aleatórias”.
Concluiu-se que para os números de contagem 12, 11 e menores, o jogo não funcionava, pois se faz necessário que haja uma diferença entre o número tomado como base de contagem e o maior número do relógio [12]. A diferença menos 1 representa as batidas aleatórias, que inexistem para números de contagem menores que 13, ou seja, 12 menos 1, que dá 11, não representaria um mostrador de relógio.
Compartilhamos com Demo (1996) quanto à comunicação anterior de Jucilei e à justificação de Talita, ao enfatizar que:
A construção de base empírica, quando for o caso, significa o esforço importante de emprestar concretude visível, experimentável, quantitativa à condução da hipótese de trabalho [na qual] o conhecimento empírico enriquece a argumentação, traduz familiaridade maior frente à problemática em foco […] (DEMO, 1996, p. 52).
Acreditamos ser interessante mostrar para o leitor a tabela mencionada anteriormente, elaborada por Taffarel e Felipe. Apresentamo-la com o propósito de elucidar como os alunos procederam para descobrir em que condições este jogo funcionaria sempre e, especialmente, a partir de quais números de contagem ele deixaria de funcionar.
Tabela – 7
| Número de contagem | Subtração [Menos] | Número de batidas aleatórias | Igual | Menor número para o funcionamento do jogo |
| 20 | – | 7 | = | 13 |
| 25 | – | 12 | = | 13 |
| 15 | – | 2 | = | 13 |
| 30 | – | 17 | = | 13 |
| 18 | – | 5 | = | 13 |
| 40 | – | 27 | = | 13 |
| 16 | – | 3 | = | 13 |
| 17 | – | 4 | = | 13 |
| 13 | – | 0 | = | 13 |
Fonte: Autores.
Na tabela apresentamos em negrito a última linha, ressaltando que após sua comunicação, os colegas de Taffarel e Felipe simularam algumas situações que acabaram validando-a. Estes alunos ainda ressaltaram que para o número de contagem 13, a primeira batida deve ser dada “[…] sobre a dama [e caso a hora ainda não tenha sido acertada, deve-se continuar as batidas], em ordem decrescente, 12, 11, 10 e assim por diante”. Chamaram novamente a atenção para o fato de o jogo funcionar somente para “os números de contagem maiores ou iguais a 13”.
Analisando em termos do relógio, a primeira carta a ser atingida por batidas regulares é a dama [12]. Portanto, 12 é uma constante fundamental do jogo. Se o nosso relógio tivesse 15 horas, então 15 faria o papel desta constante. A diferença entre o número de contagem n esta constante nos dá o número da batida sobre a carta referida por esta constante. Assim, 20 – 12 = 8; 25 – 12 = 13; 22 – 15 = 7, etc. A quantidade de batidas aleatórias é, portanto, 1 a menos do que os resultados acima, ou seja, respectivamente 7, 12, 6, etc. E, n menos cada uma dessas quantidades dá o menor número para o funcionamento do jogo: 13, 13, 16, etc. Achei interessante que os alunos encontraram primeiro a quantidade de batidas aleatórias através da observação de suas anotações.
3. CONSIDERAÇÕES FINAIS
O desenvolvimento desta atividade lúdica mostrou, pela alegria e satisfação dos alunos que é possível ensinar matemática por meio de jogos e o quanto o uso natural da linguagem cotidiana é importante na busca de uma generalização, tanto para justificar quanto para retratar matematicamente uma ideia, validando-a por meio de um modelo ou refutando-a.
Clarificou também que o pensamento se sustenta na e pela linguagem e que é o desenvolvimento da linguagem que faz aflorar o próprio pensamento, permitindo que uma pessoa adivinhe sempre a hora pensada por outra ou outras.
Durante as sessões de estudo procuramos promover linguisticamente a comunicação das ideias matemáticas presentes no contexto, propiciando aos alunos a organização do pensamento através da linguagem. Desta forma, pudemos perceber que quanto mais lhes era oportunizado a falar reflexivamente sobre determinado assunto, mais eles o compreendiam caminhando para um amadurecimento do processo que lhes permitiria, mais adiante, alcançar a generalização.
Motivar os alunos a falar sobre a situação-problema, intencionalmente planejada para uma atividade educativa, consistia em oportunizá-los a conectarem, pela linguagem cotidiana num primeiro momento e posteriormente pela linguagem matemática, seus conhecimentos e suas experiências a respeito do contexto. Ao justificarem suas falas, testavam suas ideias, explicitaram seus modos de pensar, percebiam o que realmente sabiam e o que mais precisavam saber.
Através desse exercício reflexivo sobre o contexto do jogo, refinavam conjecturas e, ao caminharem da linguagem cotidiana para a linguagem simbólica, produziam significados que, após internalizados os levava ao conhecimento, ou seja, a entenderem matematicamente qual era a regra do jogo e como ele poderia ser expresso matematicamente.
É, portanto, a linguagem que permitiu o pensar sobre o contexto do jogo, garantindo através de regras o seu funcionamento. É possível perceber através das falas dos alunos, ao longo da atividade, que um entendimento entre os seres humanos tornar-se-ia complicado sem a expressão mediadora da fala, que tem na palavra e sua significação um componente fundamental para a constituição do pensamento na forma generalizada.
É na e por meio da linguagem que o ser humano se utiliza especialmente de palavras, para organizar seu pensamento e para relacionar-se de forma mediada por instrumentos e por signos com o mundo e com os outros.
O que permitiu, segundo Vygotsky (1998), representar genericamente o pensamento matemático, subjacente ao truque de baralho, foi à linguagem no seu papel de formadora do pensamento. Esta atividade mostrou-se muito interessante por permitir, através do diálogo entre os alunos, a busca de uma generalização expressa matematicamente.
À medida que um aluno elaborava uma conjectura para explicitar matematicamente o funcionamento do jogo, ele próprio percebia a necessidade de validação da hipótese elaborada. Mais uma vez, junto com os colegas, pelo viés da linguagem, cada signo se constituía num algoritmo com um sentido único, permitindo o estabelecimento de relações, articulações, percepções, imaginações, numa perfeita conexão da linguagem, carregada de ideias, para a constituição de um pensamento generalizante.
Esta é uma das funções das letras no ensino da matemática algébrica: Representação simbólica e concisamente um pensamento, a comunicação de uma ideia ou de várias, simultaneamente. Segundo Vygotsky (2001), é sobre as palavras que produzimos, pela linguagem, sempre novos significados, oxigenamos através delas o pensamento, podendo representá-lo matematicamente. Esta linguagem concisa e ao mesmo tempo precisa pode traduzir nossos pensamentos, situações-problema do cotidiano, relatos e acontecimentos de forma generalizada e isto fascina e seduz o ser humano. Este pensamento generalizante, possível pela linguagem, privilegia a memória e a imaginação, nos faz pensar e nos conduz a uma leitura dinâmica do mundo, na medida que desvelamos os seus signos.
Esta situação-problema mostrou-nos que a linguagem possibilita ao ser humano uma via de acesso ao mundo pelo pensamento de modo geral e pelo pensamento algébrico de forma especial. As interações dialógicas possibilitam o desenvolvimento da linguagem. No entendimento de Vygotsky (1998), é nesta dinâmica que surgem as regras que validam as conjecturas que expressamos para representar situações-problema, através de uma linguagem estritamente simbólico-formal. Ainda de acordo como o autor (1998, 2001), o jogo regido por regras claramente definidas, sustentadas pela linguagem, ativa o pensamento, permite pela dialogicidade reiterada a internalização dos significados produzidose, por conseguinte, sua representação de forma geral, através de uma linguagem estritamente simbólica.
Ficou evidenciado o que Vygotsky (2001), chama de nível de desenvolvimento potencial. Sem dúvida, foram as interações dialógicas na zona de desenvolvimento proximal que propiciaram aos alunos a elaboração de conjecturas e suas respectivas validações ou refutações. Para Demo (1996), tratava-se da reelaboração de conhecimentos construídos a várias mãos a partir do conhecimento, ou seja, o raciocínio matemático que permitia adivinhar a hora pensada por alguém.
O desenvolvimento desta atividade mostrou que o jogo, quando utilizado como intervenção pedagógica, tanto desperta o interesse quanto desafia as crianças a desvendar o segredo que o envolve e a dominá-lo.
O trabalho investigativo utilizando o lúdico mostrou, segundo a perspectiva de Vygotsky (2001), que o pensamento está fundamentado na linguagem, ou seja, que a natureza conceitual do pensamento ocorre devido à linguagem. A pesquisa evidenciou que um efetivo aprendizado da matemática pode ocorrer a partir de atividades em grupo e que sua constituição requer a presença de uma segunda linguagem.
Foi por meio da linguagem cotidiana e da produção de significados sobre a situação-problema que os alunos chegaram, dialogicamente, a um amadurecimento no processo que os levou à formação de conceitos, abrindo caminhos para alcançarem a generalização. Trata-se da reconstrução do conhecimento através da interação comunicativa entre professores e alunos e entre os alunos, sem dar ênfase a um ou a outro.
Segundo Vygotsky (2001), são as interações sociais que oportunizam o desenvolvimento do pensamento e do ser humano como um todo. A elaboração de um pensamento matemático, pela linguagem, constitui-se não apenas pela interlocução com o outro, mas, de acordo com o autor, pelo discurso interior, uma espécie de diálogo que o sujeito estabelece consigo mesmo e que perpassa o processo de constituição do pensamento.
De acordo com o referencial teórico que adotamos neste trabalho investigativo, cremos que o ser humano, através de suas atividades rotineiras, pensa primeiramente em palavras, depois em símbolos. Assim, aos educadores, torna-se fundamental refletir mais sobre como os alunos desenvolvem e se apropriam da linguagem matemática, elaborada de forma intencional e não naturalmente.
Ao longo do desenvolvimento desta pesquisa com os alunos, percebemos o quanto a teoria histórico-cultural de Vygotsky, utilizada como aporte teórico, apresenta subsídios significativos que redirecionam nosso olhar sobre o ensino de matemática e suas questões mais imediatas, dentre elas, como um estudante, através da exploração de uma situação-problema pode manifestar e verbalizar, pelo pensamento e linguagem, o conhecimento algébrico.
Neste contexto, o desenvolvimento desta atividade lúdica mostrou que a interação entre os alunos foi fundamental para a manifestação e verbalização do pensamento e da linguagem algébrica. O trabalho em pequenos grupos favoreceu o desenvolvimento, pela linguagem, das capacidades de internalização deste pensamento pelos discentes. Foi também fundamental o papel docente como mediador e facilitador no processo de elaboração da aprendizagem para a constituição do conhecimento sistematizado.
Como implicações pedagógicas para um efetivo desenvolvimento de atividades lúdicas como esta, acreditamos ser o que vemos em muitas escolas brasileiras. Salas de aula medindo no máximo 48 m2 e comportando de 35 a 45 alunos. Estes fatos não inviabilizam o êxito do trabalho, mas exigem maior empenho docente.
Na sala de aula exige-se que o professor aja interativamente com a classe, que propicie possibilidades de fala a todos, fazendo a classe perceber que a construção do conhecimento matemático é um processo dinâmico que perpassa o ato comunicativo. No entanto, para a realidade atual de algumas escolas, especialmente públicas, cujas salas encontram-se superlotadas de alunos, há de se convir que se torna mais difícil conseguir resultados tão satisfatórios quanto os conseguidos com grupos menores.
Desafios à parte, o trabalho realizado com os 13 alunos, mostrou que a manifestação e verbalização do pensamento e linguagem algébrica é possível, perpassa e se constitui, segundo Vygotsky (2001), pelo viés da linguagem e, de acordo com Lins (1994) e Lins e Gimenez (1997), a partir da produção de significados sobre o contexto de cada situação-problema.
REFERÊNCIAS
ALVES, R. Filosofia da ciência: introdução ao jogo e a suas regras. 2.ed. São Paulo: Loyola, 2000. 223 p.
DEMO, P. Pesquisa e construção de conhecimento: metodologia científica no caminho de Habermas. 3.ed. Rio de Janeiro: Tempo Brasileiro, 1996. 125 p.
GUIMARÃES, E. et al. A importância dos Jogos Matemáticos na Aprendizagem nas Séries Iniciais. 2011. 20f. Centro Universitário Leonardo Da Vinci, Colíder.
HAYDT, R. C. C. Curso de didática geral. 1ed. São Paulo: Ática, 2011.
JACONBSEN, D. R. et al. Jogos eletrônicos: um artefato tecnológico para o ensino e para a aprendizagem In: ENCONTRO NACIONAL DE EDUCAÇÃO MATEMÁTICA, 11., 2013, Curitiba. Anais… Curitiba: SBEM, 2013. p. 1-14.
LINS, R. C.; GIMENEZ, J. Perspectivas em aritmética e álgebra para o século XXI. Campinas: Papirus, 1997. 176 p.
LINS, R. C. O modelo teórico dos campos semânticos: uma análise epistemológica da álgebra e do pensamento algébrico. Dynamis, Blumenau, v.1, n. 7, p. 29-39, abr./jun, 1994.
MARQUES, M. O. A aprendizagem na mediação social do aprendido e da docência. 2.ed. Ijuí: Editora UNIJUÍ, 2000. 144 p.
OLIVEIRA, M. K. de. Vygotsky: aprendizado e desenvolvimento um processo sócio-histórico. 3. ed. São Paulo: Scipione, 1995.
OLIVEIRA, N. C. N.; VALERIANO, W. P. O. A atividade orientadora de ensino: o lúdico e o recurso didático como mediadores no processo de ensino-aprendizagem em matemática. In: ENCONTRO NACIONAL DE EDUCAÇÃO MATEMÁTICA, 11., 2013, Curitiba. Anais… Curitiba: SBEM, 2013. p. 1-10.
OLIVEIRA, Z. de M. R. de. Educação Infantil: fundamentos e métodos. 5. ed. São Paulo: Cortez, 2010. (Coleção Docência em Formação).
REGO, C. T. Vygotsky: Uma perspectiva sociocultural da educação. 2. Ed. Rio de Janeiro: Vozes, 1995.
RIBEIRO, C. E.; GOULART, A. O ensino de probabilidade por meio de jogos na educação de jovens e adultos. In: ENCONTRO NACIONAL DE EDUCAÇÃO MATEMÁTICA, 11., 2013, Curitiba. Anais… Curitiba: SBEM, 2013. p. 1-15.
VYGOTSKY, L. S. A formação social da mente: o desenvolvimento dos processos psicológicos superiores. 6.ed. São Paulo: Martins Fontes, 1998. 191 p.
APÊNDICE – REFERÊNCIA DE NOTA DE RODAPÉ
7. Significa aqui o menor número de contagem para o qual a atividade pode ser realizada.
[1] Mestrado em Educação nas Ciências – Matemática.
[2] Mestrando em Desenvolvimento Rural Sustentável.
[3] Graduanda em Agronomia – UNIOESTE – Universidade Estadual do Oeste do Paraná. Graduanda de Administração – Unip – Universidade Paulista.
[4] Especialista Em Educação Matemática E Especialista Em Física Educacional.
[5] Pós-Doutor Em Ciências Ambientais.
[6] Especialização em Ensino de Ciências Exatas – Matemática, Física e Química. Graduação: Ciências – Licenciatura Plena – Habilitação Matemática. UNIJUI: Universidade Regional do Noroeste do Estado do Rio Grande do Sul, RS. Início: 1.990. Conclusão: 1.992. Graduação: Ciências – Licenciatura de 1º. Grau. UNIJUI: Universidade Regional do Noroeste do Estado do Rio Grande do Sul, RS. Início: 1.986. Conclusão: 1.989.
Enviado: Agosto, 2020.
Aprovado: Junho, 2021.

