ARTIGO ORIGINAL
SANTOS, Adecio da Silva [1]
SANTOS, Adecio da Silva. Demonstração da conjectura de Andrica para todos os primos gêmeos. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano 04, Ed. 04, Vol. 06, pp. 18-24. Abril de 2019. ISSN: 2448-0959
RESUMO
A Conjectura de Andrica é um dos problemas matemáticos até então sem nenhuma solução
apresentada. Esta conjectura está relacionada diretamente com a distância entre dois primos consecutivos. E recebeu esse nome em homenagem ao matemático Dorin Andrica. Nosso artigo mostra, pelo método de demonstração por redução ao absurdo, que essa conjectura é verdadeira para todo par de primos gêmeos. Através disto criamos um corolário da Conjectura de Andrica para os primos gêmeos, utilizando para tanto o APÊNDICE A (o qual traz uma demonstração que a quantidade de primos gêmeos é infinita).
Palavras-chave: Andrica, Conjectura, Demostração, Primos Gêmeos.
INTRODUÇÃO
A Teoria dos Números é uma das áreas da matemática que ainda possuem muitos
problemas em aberto. Um deles é a Conjectura de Andrica, a qual afirma que a desigualdade √Pn+1 – √Pn < 1 é verdade ∀n ∈ N, sendo Pn representação do n-ésimo número primo.
Segundo wikipedia: “A conjectura ainda não foi provada nem refutada, apesar de haver fortes indícios de que esta seja verdadeira.” (1)
Utilizando testes em computadores notou se que a conjectura é válida para números muito grandes. A título de curiosidade, o Portal do Geogebra disponibiliza (2), um programa para testar a conjectura para muitos números.
Os trabalhos acadêmicos, em português, sobre o assunto são muito raros. Porém, expomos neste artigo uma prova, utilizando o método de demostração por redução ao absurdo, da veracidade da Conjectura de Andrica é verdadeira para todo par de primos gêmeos. Baseando nos nesta conclusão, criamos e provamos o corolário: Se, ∀n ∈ N (gn +2,gn) são pares de primos gêmeos, então ![]() = 0 Note que a utilização de limites neste corolário só faz sentido caso a quantidade de primos gêmeos seja infinita. O que também é uma conjectura matemática em aberto. Mas ao final desse artigo deixamos no APÊNDICE A uma prova de tal infinidade.
= 0 Note que a utilização de limites neste corolário só faz sentido caso a quantidade de primos gêmeos seja infinita. O que também é uma conjectura matemática em aberto. Mas ao final desse artigo deixamos no APÊNDICE A uma prova de tal infinidade.
REFERENCIAL TEÓRICO
Conjectura Matemática é uma afirmação que muitos matemáticos acreditam que seja
verdadeira, mas ainda não provaram sua veracidade.
Uma destas conjecturas é a de Andrica. A qual afirma que a desigualdade √Pn+1 – √Pn < 1 é verdadeira ∀n ∈ N, sendo Pn a representação do n-ésimo número primo. Entretanto, argumentemos simplificadamente que a afirmação é válida para todos os números primos gêmeos. E analisaremos se é verdade isto. Mas para tanto usaremos os princípios lógicos, conforme Alencar Filho, do Terceiro Excluído e o da Não-Contradição. (3)
A partir daí, provaremos a Conjectura de Andrica para todos os Primos Gêmeos, através
de algumas manipulações algébricas. Depois disto criamos o corolário: Se, ∀n ∈ N, (gn +2,gn) são pares de primos gêmeos, então ![]() = 0. O qual é provado pelo uso do APÊNDICE A (que expõe uma demonstração da infinidade dos primos gêmeos) e por argumentações baseadas nas definições de limites e no Teorema do Sanduíche. Em particular, as definições e ao teorema anteriores mais a propriedade que diz que se uma sequência converge para 0 (zero) e outra sequência é limitada o produto das duas tende a 0 (zero) também são usadas na prova da infinidade dos números primos. Todas essas definições e propriedades de análise real são encontradas na referência (4). Por fim, deixamos ao leitor interessado as referências (5) e (6) que trazem mais informações sobre problemas matemáticos em aberto tais como a Conjectura (forte) de Goldbach, a
= 0. O qual é provado pelo uso do APÊNDICE A (que expõe uma demonstração da infinidade dos primos gêmeos) e por argumentações baseadas nas definições de limites e no Teorema do Sanduíche. Em particular, as definições e ao teorema anteriores mais a propriedade que diz que se uma sequência converge para 0 (zero) e outra sequência é limitada o produto das duas tende a 0 (zero) também são usadas na prova da infinidade dos números primos. Todas essas definições e propriedades de análise real são encontradas na referência (4). Por fim, deixamos ao leitor interessado as referências (5) e (6) que trazem mais informações sobre problemas matemáticos em aberto tais como a Conjectura (forte) de Goldbach, a
Conjectura de Legendre, a Conjectura de Collatz, entre outras.
DEMONSTRAÇÃO DA CONJECTURA DE ANDRICA PARA OS PRIMOS GÊMEOS
Nesta seção apresentaremos a conjectura de Andrica, a prova de sua veracidade para
todos os primos gêmeos e o corolário criado baseado em nosso resultado.
Conjectura de Andrica: A conjectura afirma que a desigualdade √Pn+1 – √Pn < 1 é verdadeira ∀n ∈ N, sendo Pn a representação do n-ésimo número primo.
Deixamos exposto, abaixo, uma prova da que está conjectura é verdadeira para todo par
de primo gêmeo.
Demonstração. Provemos que a conjectura é verdadeira para quaisquer pares de primos gêmeos. E para tanto suponhamos, por absurdo, que exista pelo menos um par de primos gêmeos, digamos (gk +2,gk) que não satisfaça a conjectura. Ou seja, que ∃k ∈ N tal que √Gk + 2 – √Gk ≥ 1.
Daí, tomando o par de primos gêmeos acima e baseando nos em manipulações algébricas,
as quais resultaram nas implicações sucessivas de cima para baixo a seguir, encontraríamos que
e elevando ao quadrado ambos os membros, desta última desigualdade, obteremos
as seguintes implicações (2Gk + 1)2 ≥ (2 √(gk+2)·(gk )2 4g2k + 4gk2 + 1 ≥ 4gk +8gk ⇒ 4gk +1 ≥ 8gk ⇒ 1 ≥ 4gk, ou seja, 1/4 ≥ Gk, mas isto é um ABSURDO!
Logo, a conjectura de Andrica é verdadeira para quaisquer pares de primos gêmeos.
Tomando posse desta ultima conclusão, podemos enunciar O Corolário da Conjectura
de Andrica para todos os Primos Gêmeos. Corolário da Conjectura de Andrica (para números primos gêmeos): Se, ∀n ∈ N, (gn +2,gn) são pares de primos gêmeos, então ![]() =0.
=0.
Demonstração. Pelo APÊNDICE A, sabemos que os pares de primos gêmeos são infinito. E
definindo gn como o n-ésimo número primo gêmeo, temos que √gn +2 −√gn < 1 ∀n ∈ N, onde (gn +2,gn) são pares de primos gêmeos, ∀n ∈ N. Agora, note que √gn +2−√gn < 1 ⇒
![]() 1 ∀n ∈ N. E isto nos garante que podemos tomar sempre o maior
1 ∀n ∈ N. E isto nos garante que podemos tomar sempre o maior
natural, ni.
CONSIDERAÇÕES FINAIS
Os grandes matemáticos dos séculos passados, tais como Euler (que tem o número
irracional “e” em sua homenagem), Hiemann (que conjecturou o mais famoso problema matemático, atualmente, em aberto: A hipótese de Hiemann) , Gaus, Hilbert (que listou os 23 maiores problemas da história da matemática), Cantor (que provou que os números reais são infinitos não enumeráveis) , Gödel (que provou o Teorema da Incompletude), entre outros, nos mostraram a beleza da matemática e de seu raciocínio lógico.
O prazer da descoberta e a honestidade da prova que um resultado, inquestionável, fazem
da matemática uma grande conquista da humanidade.
Este artigo explorou, através da Conjectura de Andrica, uma simples gota de um imenso
oceano de números, raciocínios e descobertas que a matemática tem a nos oferecer.
No mais esperamos, através deste trabalho, incentivar novos pesquisadores na área em
prol de navegarmos juntos no mar do conhecimento.
REFERÊNCIAS
- Portal do wikipedia. Disponível em: https://pt.wikipedia.org/wiki/Conjectura_de_Andrica.
Acesso em 14 de abril de 2019. - Portal do geogebra. Disponível em: https://www.geogebra.org/m/a3v2hpxc. Acesso em 17 de abril de 2019.
- ALENCAR FILHO, Edgard de. Iniciação à Lógica Matemática. 18 Ed. São Paulo: Nobel,
1975. - LIMA, Elon Lages Análise Real. vol. 1 Coleção Matemática Universitária, SBM,. Rio de
Janeiro, 2001. - Portal do ifba. Disponível em: http://www.ifba.edu.br/dca/Corpo_Docente /MAT/EJS.
Acesso em 14 de abril de 2019. - Portal do obaricentrodamente. Disponível em: https://www.obaricentrodamente.com/2014/01/
conjecturas-de-seba-sobre-distancia_25.html./PROBLEMAS_MATEMATICOS_DO_SECULO_XXI.pdf. Acesso em 14 de abril de 2019.
APÊNDICE A
Conjectura: Existe uma infinidade de números primos gêmeos.
Demonstração. Digamos que pn é a representação do n-ésimo número primo e suponhamos, por absurdo, que a quantidade de números primos gêmeos fosse finita sendo o número pk o maior primo gêmeo. Então, nossa suposição implica que ∀i ≥ 1 / pi+i > pi, os números pi+i + 2 são todos ímpares compostos. Agora, tomemos d1, d2, d3, ··· , dn sendo os maiores divisores de pk+1 +2, pk+2 +2, pk+3 +2, ··· , pk+n +2 respectivamente. Daí, temos as desigualdades abaixo e somando as, membro a membro, temos que
De (I) temos ainda que 2n  Além disto, a propriedade Arquimediana dos R nos garante que para cada soma
Além disto, a propriedade Arquimediana dos R nos garante que para cada soma 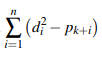 existe um natural Mn tal que
existe um natural Mn tal que 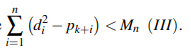
Por (II), (III) e pela transitividade obtemos: ![]() dividindo este ultimo resultado pelo termo (n · Mn) ficamos com
dividindo este ultimo resultado pelo termo (n · Mn) ficamos com 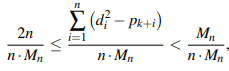 o que implica no seguinte
o que implica no seguinte
[1] Graduado e mestre em matemática.
Enviado: Abril, 2019
Aprovado: Maio, 2019
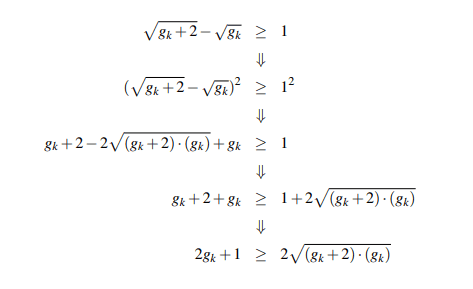




2 respostas
Prezado Sr professor Adécio da Silva Santos, interessante sua explanação e demonstração, peço minhas sinceras desculpas a todos(as) aqui presente desta Revista Científica, dentro de sua explanação e demonstração encontrei alguns pontos negativos ao afirmar que existe números primos gêmeos!!! com base em suas fórmulas apresentada na inicial: “A Teoria dos Números é uma das áreas da matemática que ainda possuem muitos
problemas em aberto. Um deles é a Conjectura de Andrica, a qual afirma que a desigualdade √Pn+1 – √Pn < 1 é verdade ∀n ∈ N, sendo Pn representação do n-ésimo número primo"., prove com números sua afirmação os números primos gêmeos e qual o valor da somatória usado em suas demonstrações?; em relação aos números primos, onde um Brasileiro afirma cientificamente que alguns números não são primos como todos(as) vem relatando de tempos passados, com uma simples PA(Progressão Aritmética), desvendei seus enigmas, onde afirmo cientificamente que não são primos e nem primos gêmeos: segue os números relatados a seguir: 2; 19; 41; 59; 61; 79; 101; 139; 179; 181; 199; 239; 241; 281; 359; 401; 419; 421; 439; 461; 479; 499; 521; 541; 599; 601; 619; 641; 659; 661; 701; 719; 739; 761; 821; 839; 859; 881; 919; 941; 1019; 1021; 1039; 1061; 1181; 1201; 1259; 1279; 1301; 1319; 1321; 1361; 1381; 1399; 1439; 1459; 1481; 1499; 1559; 1579; 1601; 1619; 1621; 1699; 1721; 1741; 1759; 1801; 1861; 1879; 1901; 1979; e mais alguns…… sendo assim "A Hipótese de Rielmann perde totalmente sua força" o autor Sr Sidney Silva.
Não entendo muito destas coisas, mas alguém, por favor, me corrija, por favor, se eu estiver errado:
1- Todo número primo pode ser escrito da forma (6k + 1) ou (6k +5), k sendo natural. A recíproca não é sempre verdadeira (nem sempre um número é 6k + 5, e é primo por isto. Por exemplo, 65 = 6.11 + 5, 65 não é primo);
.
2 – Todo número da forma (6k + 5) pode ser escrito da forma (6q – 1), q sendo natural:
6k + (5) => 6k + (6 – 1) => (6k + 6) – 1 => 6[k + 1] – 1. Fazendo [k + 1] = q => 6q – 1;
.
3 – Existem infinitos primos da forma (6k – 5).
.
Se 6q – 1 é um número primo, então [(6q-1 ); √((6q-1 )^2+ 24 q ) ], ou é um par de primos gêmeos, ou é ‘um primo e um quadrado’ (ou potência par) de um primo.
De forma que se há infinitos primos da forma 6q – 1, há portanto infinitos primos gêmeos.