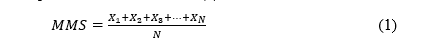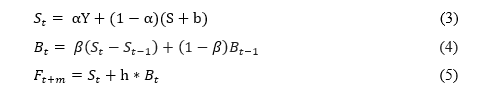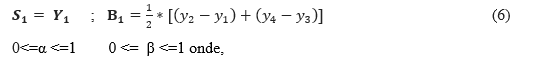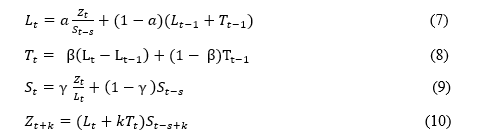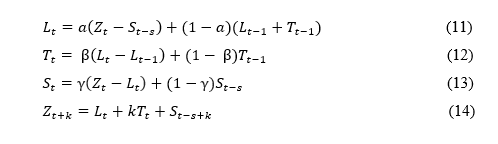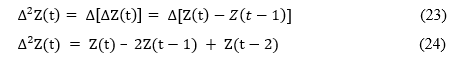ARTIGO ORIGINAL
MENDES, Nadielly Gomes [1], SILVA, Thiago Feitosa da [2], RODRIGUES, Arthur Rocha [3], COSTA, Karen Soares da [4], ESTELLER, Luchiana Fernandes Silva [5], NETO, Roberto Carlos Santiago [6], BESSA, Luiz Carlos Lopes [7]
MENDES, Nadielly Gomes. Estudo para reposição de estoque como princípio de seleção da previsão de demanda. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano 04, Ed. 09, Vol. 06, pp. 161-200. Setembro de 2019. ISSN: 2448-0959, Link de acesso: https://www.nucleodoconhecimento.com.br/engenharia-de-producao/reposicao-de-estoque
RESUMO
A previsão de demanda é fator importante para o planejamento estratégico das instituições aumentando sua capacidade competitiva. Estas previsões se baseiam em informações colhidas através de análise quantitativa ou qualitativa de fatores observados em um período de tempo. A presente pesquisa apresenta os métodos de previsão de demanda qualitativos e quantitativos, mas tomou-se como base o método quantitativo como forma de predição visando encontrar qual destes trará o maior grau de confiabilidade. O objeto de estudo deste trabalho foi a previsão de peças de reposição de uma usina sucroalcooleira. Foram testadas as técnicas de Média Móvel Simples, Suavização Exponencial Simples, Suavização Exponencial de Holt e Suavização Exponencial de Winter-Multiplicativo para realizar a predição e escolheu-se aquela que apresentou o menor desvio absoluto. O presente trabalho apresenta os métodos de previsão de demanda como forma de otimização dos processos com o objetivo geral de diagnosticar, através de técnicas estatísticas, qual o método de previsão que possa predizer a demanda mensal de uma usina sucroalcooleira com assertividade. Especificamente, pretende-se: i) coletar os dados da aquisição anual dos itens; ii) Analisar os dados coletados; iii) obter as previsões através de diversas técnicas distintas e identificar aquela que trouxer o melhor resultado. Os resultados demonstraram que, para os dados coletados, o método de Suavização Exponencial Simples apresentou o menor desvio em relação à demanda real e, portanto, configurou-se como o melhor método para realizar a predição. Esta pesquisa justificou-se pela importância da antecipação eficiente de possíveis ameaças e diagnóstico de oportunidades que a empresa tem no ramo de atuação, fazendo com que o planejamento estratégico de operações seja eficaz.
Palavras-chave: Previsão de demanda, métodos de previsão, métodos quantitativos.
1. INTRODUÇÃO
A capacidade de gerenciar processos, identificar falhas, sugerir melhorias e inovar, é um diferencial entre as empresas que estão em busca de se tornarem mais competitivas sem perder a qualidade. Pellegrini (2000) afirma que a previsão de demanda é a base para o planejamento estratégico de produção, vendas e finanças de toda e qualquer organização. Esta previsão permite que os administradores do negócio antevejam a necessidade de suprimento de material e/ou serviço e planejem de forma adequada suas ações.
De maneira estratégica são formados cenários para facilitar a identificação de gargalos e quando identificados realiza-se o tratamento dos elementos factíveis, ou seja, dados e fatos que dão uma previsão do que pode acontecer nos períodos que sucedem ao atual. Através desta previsão é que são trabalhados os elementos de planejamento como: quanto produzir, que tipo de máquina, equipamento, quantidade de peças a serem compradas e etc. Forno (2013).
Werner; Lemos e Daudt (2006) afirmam que presumir demanda possibilita utilizar a capacidade de produção de forma eficiente, reduz tempo de resposta ao cliente, evitar perda de vendas e diminuir estoques, propiciando à empresa a obtenção de melhores resultados financeiros. Quando se trata da influência do lucro empresarial, parte da indústria tem processos ineficientes, considerando-se que seja pela falta de planejamento.
As decisões devem ser assertivas, visto que o aumento dos lucros e a redução dos custos são os pontos chave das negociações e têm ligação direta com a permanência das empresas no mercado. O responsável por estas decisões, por sua vez, absorve as informações coletadas e só garante sucesso se os dados estiverem coerentes.
Para tanto, existem diferentes técnicas de previsão de demanda. O objeto de estudo deste trabalho será a utilização das técnicas de predição para prever a demanda anual de uma usina sucroalcooleira, localizada na região centro-oeste do Brasil. Desta forma, problematiza-se: qual a melhor técnica para prever a demanda de uma usina sucroalcooleira de modo a garantir a maior confiabilidade dos dados?
Tendo em vista a necessidade de planejamento e a importância de acompanhar os parâmetros do que é comprado com o que é de fato utilizado, o objetivo geral do presente trabalho é diagnosticar, através de técnicas estatísticas, qual o método de previsão que possa predizer a demanda da indústria supracitada com o maior grau de confiabilidade. Especificamente, pretende-se: i) coletar os dados da aquisição anual dos itens; ii) Analisar os dados coletados; iii) obter as previsões através de diversas técnicas distintas e identificar aquela que trouxer o melhor resultado.
Esta pesquisa justifica-se pela importância da previsão de demanda em antecipar com eficiência possíveis ameaças e diagnosticar as oportunidades que a empresa tem no ramo de atuação, fazendo com que o planejamento estratégico de operações seja eficaz. Em tempos passados a previsão de demanda era considerada como um diferencial, porém no cenário de hoje, a realidade é outra e essa se tornou obrigação das empresas visto que se bem aplicados, os métodos de previsão garantem a baixa dos custos e consequentemente o aumento do lucro empresarial.
2. REFERENCIAL TEÓRICO
Neste capítulo são apresentados de forma conceitual os métodos de previsão de demanda quantitativos e qualitativos, erro de previsão, estacionariedade a partir de revisão bibliográfica envolvendo consulta de artigos científicos, Conteúdos disponibilizados na internet e livros apresentando definições, metodologias e aplicações destes métodos.
2.1 PREVISÃO DE DEMANDA
De acordo com Proto (2003) gerir qualquer ambiente de negócio a fim de adequar os recursos da empresa e suas estratégias requerem análises e cálculos de estimativas ou até mesmo uma previsão de quais serão as necessidades do mercado.
O ponto inicial da previsão de demanda é o planejamento de vendas com base em dados históricos. Além disso, também devem ser consultadas pessoas que estão em contato direto com o cliente: vendedores, representantes, entre outros. As informações para a previsão também podem ser coletadas através de análise de mercado, pois esta influencia o comportamento de uma demanda. Com isso, Forno (2013) ressalta que a coleta de todos os dados a partir da análise de mercado gera uma melhor estimativa para prever o consumo futuro.
Os responsáveis pela empresa devem ter ciência de que para a previsão ser assertiva, a base de dados deve ser formada e mantida de forma eficiente com o histórico de vendas e deve conter explicações de variações quando ocorrer. Utilizam-se métodos matemáticos justificando o comportamento da demanda para compreender como os fatores internos e externos contribuem e influenciam na demanda, conforme afirma Queiroz (2003).
De acordo com Proto (2003), a base do sucesso da empresa é a previsão de demanda, pois esta é também a base fundamental para que as empresas desenvolvam os planos de capacidade de fluxo de caixa, fluxo de vendas, fluxo de produção, armazenamento de matéria-prima e produto acabado, mão de obra e compras, melhorando o nível de serviço e desenvolvendo de forma positiva um relacionamento com os clientes evitando perdas de vendas.
Mattar (1997) cita que a pesquisa qualitativa identifica a presença ou ausência de algo. Em outras palavras, para Seraponi (2000), quando o objeto de estudo não é bem conhecido, os métodos qualitativos devem ser utilizados, pois são capazes de revelar relações entre variáveis, motivações e comportamentos completamente inesperados, que não surgiriam utilizando um questionário estruturado.
2.2 MÉTODOS QUANTITATIVOS
Os métodos quantitativos podem ser de série temporal ou de correlação. Os métodos de séries temporais são baseados nos históricos que a empresa possui em um determinado tempo, podendo ser semana ou mês. Estes métodos, conforme Lin (2000), não procuram identificar os fatores que afetam o comportamento pelo fato de que o foco é dado ao que vai acontecer e não ao porquê está acontecendo, ao contrário do método de série causal.
Por sua vez Tubino (2007) afirma que os métodos de série temporal têm por finalidade modelar as demandas futuras e relacionar os dados históricos do produto com o tempo matematicamente, enquanto a correlação utiliza de uma ou mais variáveis que tenha alguma relação com a demanda do produto e associa esta variável aos dados históricos.
O coeficiente de correlação, o erro-padrão e o intervalo de confiança são indicadores da qualidade da regressão. O coeficiente de correlação r mostra a relação entre as variáveis dependente e independente. Valores positivos indicam variação no mesmo sentido das variáveis. Valores negativos indicam variáveis inversamente relacionadas. Um valor nulo significa que não existe relação. Quanto mais próximo r estiver de + 1,00, maior a correlação. O coeficiente de determinação r2 é o quadrado do coeficiente de correlação e varia de 0 a 1,00. Valores próximos a 1,00 são desejáveis e indicam que as variáveis dependente e independente estão fortemente correlacionadas. (ZAN, 2007, pág. 97)
Quanto aos métodos quantitativos, apresentar-se-á a média móvel simples; os métodos de suavização exponencial: Holt, Suavização exponencial simples, Winters; e o método de simulação de ARIMA.
2.2.1 MÉTODO DE MÉDIA MÓVEL SIMPLES
A média móvel simples não vai além de uma simples média aritmética onde são observados (X) como sendo os números mais recentes com os quais o valor da média será o valor da previsão subsequente conforme fórmula (1):
Onde X são os períodos de dados históricos passados (semana, mês, ano) utilizados para a análise e N a quantidade de períodos analisados.
No decorrer de um novo período (X), um novo dado de demanda real terá sucedido e o procedimento a ser adotado será o de adicionar o dado mais recente (xn) e abandonar o mais antigo (X1) a fim de que a previsão para o período seguinte seja computada. Desta forma mantem-se um número constante de observações que entram para o cálculo da média.
A vantagem do uso da técnica de média móvel para previsões consiste em sua simplicidade operacional e facilidade de entendimento, porém uma de suas limitações é a necessidade de armazenar um grande volume de dados principalmente se o número de períodos (n) for grande, é uma de suas limitações. (TUBINO, 2007).
Outra característica importante da técnica de média móvel simples é que a mesma fornece previsões de períodos posteriores, de curto e longo prazo. Por exemplo: Suponha-se que é desejada a previsão de demanda para o sétimo mês do ano, logo, seriam analisadas as vendas nos seis meses antecedentes e dividido também por seis, que foi a quantidade de períodos utilizados para análise como é apresentado no Quadro 1.
Assim tem-se a previsão para o mês de julho e o valor seria replicado para os meses seguintes. Após obter a demanda real do mês sete, substitui-se seu valor de previsão pela demanda real e calcula-se a nova previsão para o mês de agosto através da média dos últimos seis meses, ou seja, elimina-se o mês mais antigo. Daí o nome – média móvel.
2.2.2 MÉTODO DE SUAVIZAÇÃO EXPONENCIAL SIMPLES
O método de suavização exponencial simples proporciona uma média móvel com um peso exponencial de todos os valores observados anteriormente. Frequentemente, o modelo é apropriado para dados que não tem uma tendência previsível para cima ou para baixo e revisa continuamente o valor estimado com experiências recentes.
Para tanto, é utilizada a fórmula (2):
Onde:
Ft = Previsão para o período;
Yt = Demanda real observando o período;
(α) = Constante de suavização de nível
Segundo Pellegrini e Fogliatto (2001) quando se trata de suavização exponencial simples, deve-se ter uma estimativa inicial para . Se os dados históricos estiverem disponíveis usa-se a média simples das observações (N) mais recentes como , caso contrário utiliza-se o último dado observado ou faz-se uma subjeção. Quando os dados históricos estão disponíveis, pode-se usar uma média simples de N observações mais recentes como Ft; caso contrário, pode-se utilizar a última observação, ou fazer uma estimativa subjetiva.
Os valores dos coeficientes de ponderação determinam a sensibilidade do modelo em relações as alterações de média da série histórica. Modelos com α próximo de zero são pouco sensíveis. Esta sensibilidade aumenta quando α aproxima-se de um.
2.2.3 MÉTODO DE HOLT
O modelo de Holt, também conhecido como Suavização exponencial de dois parâmetros, emprega duas constantes de suavização. Para isso, utiliza de três equações, sendo elas:
A equação (3) indica a inclinação da série temporal, a equação (4) representa a tendência da série e a equação (5), por sua vez, calcula a previsão de demanda para os próximos períodos.
Valores iniciais:
(α) = Constante de suavização de nível
(β) = Constante de suavização de tendência
A equação (6), por sua vez, calcula o valor inicial da tendência.
Onde:
Ft = Previsão para o período;
Yt = Demanda real observando o período;
Tt = Tendência;
t = Nível onde a observação está no período t
H = horizonte observado
Para que o método de Hol t seja aplicado deve-se ter valores iniciais (L e T neste caso). Uma sugestão para estes cálculos é que o L seja igual ao último valor que está sendo observado na série temporal e calcular a média da declividade nas últimas observações de T, cita Pellegrini (2001).
2.2.4 MÉTODO DE WINTERS
Este modelo utiliza a suavização exponencial. É conhecido como uma extensão do modelo de Holt. Esse modelo se adapta a uma tendência de série linear, estacionaria ou periódica. Diferente dos modelos apresentados anteriormente, o modelo de Winters utiliza três constantes, sendo:
Alfa – Constante de enfraquecimento da média dos dados (0<=α <=1);
Beta – Constante de enfraquecimento da estimação da tendência (0 <= Beta <=1);
Gama – Constante de enfraquecimento de estacionaridade (0 <= γ <=1).
Para Pellegrini (2000) usa-se os modelos de Winters quando além de um componente de sazonalidade, verifica-se a ocorrência de tendência linear. Os modelos de Winters dividem-se em dois grupos: aditivo e multiplicativo. O modelo aditivo de Winters considera que a diferença entre o maior e menor valor de demanda dentro das estações permanece relativamente constante no tempo. Já no modelo multiplicativo, a amplitude da variação sazonal aumenta ou diminui como função do tempo.
No grupo multiplicativo do método Winters é utilizada a modelagem de dados sazonais onde há variância com o passar do tempo na amplitude do ciclo sazonal e o modelo aditivo que é usado na modelagem de dados sazonais onde há constante amplitude do ciclo sazonal com o passar do tempo.
As equações (7), (8) e (9) estimam os valores de nível, tendência e sazonalidade respectivamente, enquanto a equação (10) dá o valor da previsão pata o método de Winter- multiplicativos:
Já para os Winters aditivos utiliza-se das equações (11), (12) e (13) para estimar os valores de nível, tendência e sazonalidade respectivamente, enquanto a equação (14) dá o valor da previsão pata o método de Winter-Aditivo:
Onde:
L representa o nível;
T representa a tendência;
S representa a sazonalidade da série;
E Z t+k é a previsão para k períodos á frente
2.2.5 MÉTODO AUTO-REGRESSIVO INTEGRADO DE MÉDIAS MÓVEIS (ARIMA)
O modelo de previsão de demanda ARIMA como afirma Pellegrini (2001) “são modelos matemáticos que visam captar o comportamento da auto correlação entre os valores da série temporal, e com base nesse comportamento realizar previsões futuras.” Além disso, possuem uma ou mais raízes iguais a um e se comparado aos métodos de amortecimento quando a série é longa e bem comportada, apresenta bons resultados. Já em séries irregulares os resultados são inferiores.
2.3 ERRO DE PREVISÃO
O erro de previsão é a diferença entre o valor atual do período e o valor previsto para o mesmo período. É dado pela equação (15):
Onde:
Et é erro do período;
Yt é a observação atual do período;
Ft é a previsão para o mesmo período.
2.3.1 ERRO MÉDIO – MEAN ERROR (ME)
O erro médio representado pela equação (16) é a média de todos os erros detectados durante o período analisado e seu valor ideal seria igual à zero, ou seja, o erro médio tende a ser pequeno na medida em que os erros negativos e positivos se compensem.
2.3.2 ERRO PERCENTUAL MÉDIO – MEAN PERCENTAGE ERROR (MPE)
As medidas de erros anteriores dependem da escala utilizada nos dados. Neste sentido, podem ocorrer problemas ou resultados inexpressivos quando são utilizadas como parâmetro em diferentes intervalos de séries temporais. Assim, para que as comparações entre dados que possuam medidas diferentes possam ser realizadas, faz-se necessário à utilização de medidas percentuais do erro. Este, por seu lado, é definido pela equação (17):
As estatísticas MAPE, MAD e MSD são informações importantes para comparar os modelos de suavização e decidir se estes representam um bom ajuste aos dados obtidos.
2.3.3 ERRO PERCENTUAL ABSOLUTO MÉDIO – MEAN ABSOLUTE PERCENTAGE ERROR (MAPE)
O erro percentual absoluto médio é a média de todos os erros absolutos percentuais. O MAPE indica o tamanho médio do erro expresso em porcentagem do valor que está sendo observado e não leva em consideração se o valor é positivo ou negativo. Quando os valores são baixos, significa que MAPE está sendo calculado com precisão. O erro percentual absoluto médio pode ser calculado mediante a utilização da equação (18):
Onde são os nossos dados históricos passados, Zt são os valores que foram previstos para o período e é a quantidade de períodos que foram observados. Quanto menor for o valor de MAPE, melhor será o ajuste.
2.3.4 DESVIO PADRÃO ABSOLUTO DA MÉDIA – MEAN ABSOLUTE DEVIATION (MAD)
Calcula-se o desvio padrão absoluto da média a partir das previsões e dados históricos passados. O desvio padrão absoluto é a diferença do valor do dado histórico com a previsão, logo, calcula-se através da equação (19):
A média desse desvio é feita com os valores em módulo, isto se dá pois os valores passados podem variar entre positivo e negativo e se anularem. Sendo assim, calcula-se através da equação (20):
Onde são os nossos dados históricos passados, são os valores que foram previstos para o período e é a quantidade de desvio padrões absolutos que foram observados. Quanto menor for o valor de MAD, melhor será o ajuste.
De acordo com o site Portal Action (2018), o MAD representa o desvio padrão do ajuste em relação à média nas mesmas unidades dos dados. Isto quer dizer que se ajuntar série temporal durante o tempo e encontrar um MAD de 72, quer dizer que o nosso ajuste possui um desvio padrão da média de 72 dias.
2.3.5 DESVIO PADRÃO QUADRÁTICO DA MÉDIA – MEAN SQUARED DEVIATION (MSD)
A MSD ajusta as séries temporais. Segundo o site Portal Action (2018), quando temos um valor atípico no conjunto de dados analisados, essa medida é mais afetada que se este mesmo valor atípico aparecer em MAD. Sendo assim, obtem-se um MAD com resultado baixo e um MSD com resultado alto quando há um valor atípico no conjunto de dados. Para tanto, calcula-se a partir da equação (21):
Onde são os nossos dados históricos passados, são os valores que foram previstos para o período e é a quantidade de períodos que foram observados. Quanto menor for o valor de MSD, melhor será o ajuste.
2.4 ESTACIONARIEDADE
Uma série é estacionária quando se desenvolve aleatoriamente em torno de uma média constate como forma de estabilidade no decorrer do tempo. A maioria das séries encontradas, na prática, apresenta algum tipo de tendência, isto é, indica o comportamento de uma série que cresce, decresce ou permanece estável. Pode ser constante, linear ou exponencial.
A maioria dos procedimentos de análise estatística de séries temporais segundo o site Portal Action (2018), supõe que estas sejam estacionárias, portanto, será necessário transformar os dados originais se estes não formam uma série estacionária. A transformação mais comum consiste em tomar diferenças sucessivas da série original, até se obter uma série estacionária. Pra que uma série se torne estacionária, normalmente será suficiente usar uma ou duas diferenças. A primeira diferença Z(t) é definida pela equação (22):
A segunda diferença é definida pelas equações (23) e (24):
De modo geral, a n diferença de Z(t) é obtida utilizando-se a equação (25):
Gráfico 1- Representação de uma série estacionária
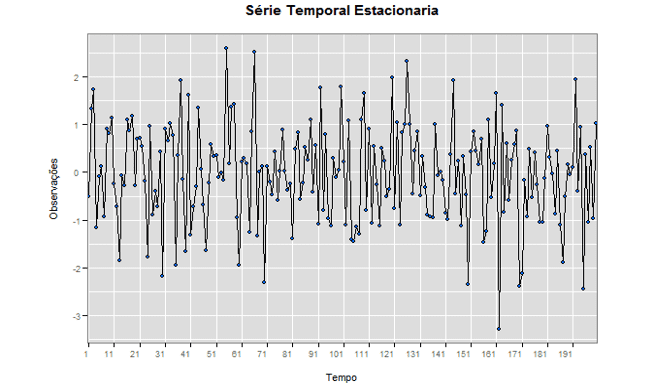
Uma série estacionária possui características onde seus valores variam em torno de uma média constante.
Gráfico 2 – Representação de uma série não estacionária

Uma série não estacionária, diferente da estacionária, apresenta um comportamento onde seus valores crescem e decrescem de forma aleatória sem estar em torno de uma média constante.
2.5 TRABALHOS CORRELATOS
A previsão de demanda para Santos (2017) não acontece de forma aleatória, mas necessita que uma abordagem seja selecionada a fim de tratar as informações de forma adequada. Ele cita também que a previsão de demanda partindo de uma abordagem de série temporal, parte de uma pressuposição de que os valores que influenciaram no passado, influenciarão também no futuro.
Loguércio e Ferreira (2017) cita que a previsão de demanda deve ser pautada a partir do conhecimento tanto mercado quanto de tendências e/ou dados históricos. Em se tratando dos modelos quantitativos, o autor enfatiza que as séries dos dados coletados costumam ser longas e a partir de sua coleta são identificados seus padrões de comportamento. Santos, Marques Junior e Bernardo (2015) em consonância com Loguércio e Ferreira citam que fica evidente que a previsão de demanda visa melhorar na tomada de decisão final da organização e que os objetivos destas ferramentas são obter um prazo, quantificar, por exemplo, a aquisição de matéria-prima e os recursos financeiros.
Para que uma empresa sobreviva no mercado Oliveira (2015) em seu trabalho cita que esta depende de uma previsão de demanda eficiente. Os impactos causados por uma má previsão são cruciais e definem a permanência da organização no mercado e quando os dados são precisos alavancam os lucros e garantes sua expansão.
A monografia de Furtado (2007) se baseia em um estudo que fora realizado em uma Companhia Siderúrgica e seu trabalho tem como objetivo principal selecionar um modelo de revisão que reduza o estoque diminuindo também a evasão de aditivos. Na visão do autor, a escolha de um método de previsão facilitaria no adiantamento de dados do futuro permitindo que a empresa realocasse melhor seus recursos para atender o mercado de forma eficiente.
A partir dos métodos de previsão de demanda quantitativos Carvalho (2016) promove um comparativo e definir o que traz melhor acurácia para a predição da demanda de gás natural a partir dos dados históricos da empresa. A conclusão foi de que a regressão linear simples apresentou o melhor ajuste aos dados.
Jesus (2016) utiliza dos métodos de previsão de demanda para identificar dentre a Média Móvel; Média Ponderada; Média Exponencial Móvel; Técnica de Regressão Linear Simples e Previsão de Sazonalidade Simples qual o melhor ajuste a partir das análises dos erros e visualização gráfica. O autor concluiu que a média exponencial móvel apresentou a melhor precisão para o caso da empresa de cerâmica.
Com objetivo de propor um método de previsão de demanda que apresentasse o menor erro de previsão na aquisição de adesivos de uma gráfica, Paganelli (2015) observou Erro Percentual Absoluto Médio (MAPE). O melhor método conforme definido pelo autor foi a previsão de demanda a partir do modelo sazonal de aditivo de Winter.
Com as observações iniciadas em 2013 e concluídas em 2014 Cordeiro (2015) utiliza dos dados de planejamento e controle de produção para basear a pesquisa e observa o desvio absoluto da média (MAD) como erro que definirá o melhor resultado da previsão. A autor considera em seu trabalho que o melhor método é o de média exponencial pois assume valor 0.9 para o coeficiente de ponderação alfa.
Tendo como base estudos dos dados históricos feitos em uma empresa de reabastecimento de água potável ao longo de dois anos Grando (2015) definiu em seu trabalho que o melhor método de previsão foi o de regressão linear, pois soluciona o problema de reabastecimento de água.
O estudo de Castro (2015) é feito em uma fábrica de bolsas. O autor analisa que a previsão de demanda proporciona aos tomadores de decisão uma visão ampla do futuro auxiliando na tomada de decisão de a gestão estratégica da empresa alicerçando a deliberação do que será produzido e comercializado.
Pessoa, Nobre e Veras (2018) apresentam em seu trabalho um estudo de caso baseado na aplicação dos métodos de previsão de demanda de três produtos com a coleta de dados feita dos dados sazonais do ano de 2017. Como resultado o autor concluiu que a media móvel ponderada dá um melhor lucro e melhora a produtividade.
Para identificar os problemas de planejamento e controle de produção Jesus (2016) utilizou do brainstorming e da matriz de Gut e, a partir da definição, o autor conclui que o melhor método de previsão é o de média móvel exponencial.
Tomando como base decisória o menor valor do desvio absoluto médio (MAD), Tahara et. al. (2014) aplica os métodos de previsão de demanda em uma montadora de automóveis utilizando a classificação ABC como metodologia que norteia seu trabalho. O autor concluiu que o método mais eficiente é o de Tendência Polinomial com grau 4, mas criticou que o processo precisa sempre ser renovado acompanhando a instabilidade da demanda.
Objetivando analisar as vendas de uma empresa de cerâmica Paiva e Negrão (2014) apropriam-se dos valores do Erro Percentual Absoluto Médio (MAPE) para definir qual a melhor técnica de previsão de demanda. O autor concluiu que a técnica com maior relevância para auxiliar o planejamento estratégico da empresa é o de Suavização Exponencial Dupla (Holt).
Com a finalidade de determinar a quantidade de material gasto para produzir móveis de uma empresa em Marabá, Silva (2018) utiliza dos métodos de previsão de demanda de média móvel para encontrar um número ideal de vendas de estante e quadro magnético no mês 12/2017.
Utilizando dos erros de previsão desvio absoluto médio (MAD) e o erro médio percentual absoluto (MAPE), Assumpção et. al. (2013) aplica as técnicas de previsão de demanda para projetar a demanda diária de sondas de uma empresa petrolífera. O autor pontua que o objetivo do trabalho foi alcançado e que a técnica utilizada foi à média exponencial.
Em um comparativo simples dos trabalhos analisados é possível observar que o método mais utilizado é o de média móvel exponencial, o que diferencia o presente trabalho destes que já foram publicados. Neste, o método que traz melhor acurácia da previsão é o método de Suavização Exponencial Simples. Fica claro que o erro do qual dos trabalhos tomam como base, em sua grande maioria é o Desvio Absoluto da Média (MAD) concordando com o presente trabalho que também se baseia nele. Em outros, o erro Médio Percentual Absoluto (MAPE) também é utilizado como base e em um dos casos, o MAD e MAPE são utilizados para prever a melhor demanda.
As técnicas de previsão de demanda são utilizadas em diversos segmentos e sua importância não se difere de segmento para segmento, mas permanece constante conforme a necessidade do ramo em que está sendo trabalhada.
3. METODOLOGIA
O presente estudo pode ser caracterizado como descritivo e aplicado. Descritivo, segundo Gerhardt et al (2009) busca analisar, verificar e descrever as relações entre fatos e fenômenos (variáveis), que neste caso, sob a forma de coleta de dados se referem à demanda de peças de reposição de estoque de uma usina sucroalcooleira. Aplicado, por buscar solucionar problema sendo de curto ou médio prazo, a partir da aplicação prática de conhecimentos obtidos.
A pesquisa bibliográfica foi realizada a partir de artigos científicos e livros relacionados à aplicação dos métodos de previsão de demanda. O trabalho também se caracteriza como estudo de caso, pois este, conforme Yin (2015) investiga “o caso” como fenômeno contemporâneo em especial quando o contexto e o fenômeno não estiverem tão evidentes. Também, consiste em uma pesquisa quantitativa, pois conforme Gerhardt et. al. (2009) este tipo de pesquisa segue uma linha de raciocínio lógico, se estrutura através de dados mediante controles já existentes e enfatiza sua objetividade na coleta e análise de dados diferentemente da pesquisa qualitativa.
O estudo limita-se na coleta de dados de peças utilizadas na reposição de estoque dos últimos doze meses. Analisar-se-á em primeira instância se a série é estacionária, ou seja, se as características estatísticas dos valores analisados são constantes ao longo do tempo.
Caso seja estacionária, utilizar-se-á os métodos de técnicas de previsão de demanda, sendo eles: Média móvel simples, Suavização exponencial simples que proporciona uma média móvel com um peso exponencial de todos os valores observados anteriormente, Holt também conhecido como Suavização exponencial de dois parâmetros e Winters que é conhecido como uma extensão do modelo de Holt. Esse modelo se adapta a uma tendência de série linear, estacionaria ou periódica. Caso não seja encontrada a estacionariedade, utilizar-se-á o Método auto-regressivo integrado de médias móveis (ARIMA).
O enfoque do estudo é definir a melhor técnica para prever a demanda de uma usina sucroalcooleira de modo a garantir a maior confiabilidade dos dados. Para que esta definição seja possível os métodos de previsão baseiam-se na ideia de que observações passadas contêm informações sobre o padrão da série temporal e a estatística MAD que compara os modelos de suavização e decide se estes apresentam um bom ajuste aos dados.
Para determinar o menor MAD foi utilizado um problema de programação não-linear, onde o objetivo era a minimização do MAD através da alteração dos coeficientes de ajuste. O problema de programação foi resolvido utilizando-se o Solver que é um complemento do Microsoft Excel®. Somente o método de média móvel simples não foi tratado por esta perspectiva por não possuir coeficiente de ajuste.
4. RESULTADOS E DISCUSSÕES
As usinas do ramo sucroalcooleiro vêm crescendo no Brasil e dessarte a necessidade de um maior acompanhamento quando se trata em prever demanda. Assim sendo, para uma previsão mais assertiva, os métodos de previsão estão sendo cada vez mais aprimorados uma vez que estoque parado é dinheiro parado.
A priori foram coletados os dados da empresa. Os dados utilizados para elaboração do presente trabalho são referentes aos meses de setembro/2017 a agosto/2018 sendo coletados a partir de um controle de aquisições que é planilhado pela empresa.
Quadro 1 – Dados sobre a demanda: Demanda Real
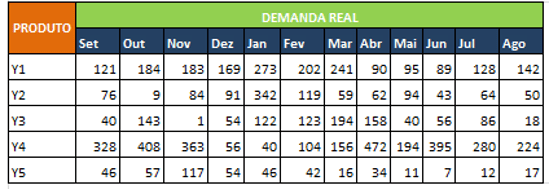
Nas Figuras a seguir são apresentados os dados da sazonalidade anual dos itens de forma individual.
Gráfico 3 – Dados sobre a demanda: Identificação da série estacionária do item Y1
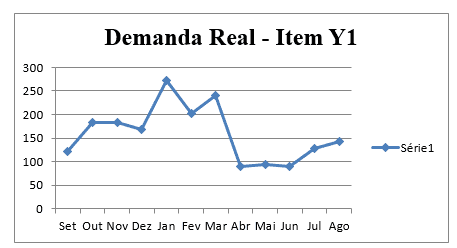
Gráfico 4 – Dados sobre a demanda: Identificação da série estacionária do item Y2
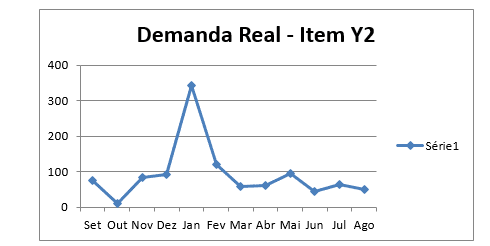
Gráfico 5 – Dados sobre a demanda: Identificação da série estacionária do item Y3
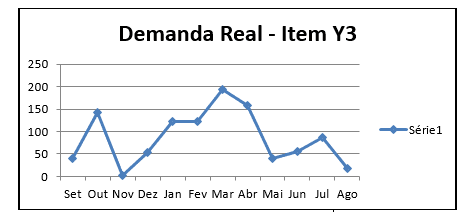
Gráfico 6 – Dados sobre a demanda: Identificação da série estacionária do item Y4
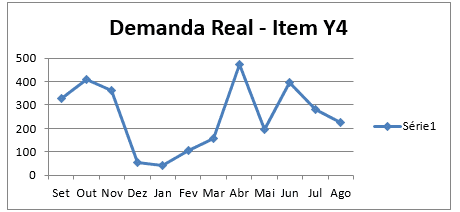
Gráfico 7 – Dados sobre a demanda: Identificação da série estacionária do item Y5
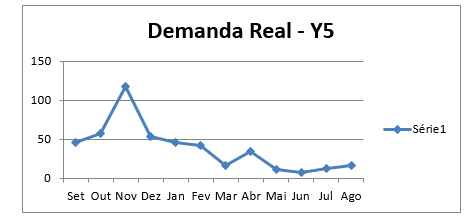
Abaixo são apresentados os dados da sazonalidade anual dos itens de forma agrupada.
Gráfico 8 – Dados sobre a demanda: Identificação da série estacionária
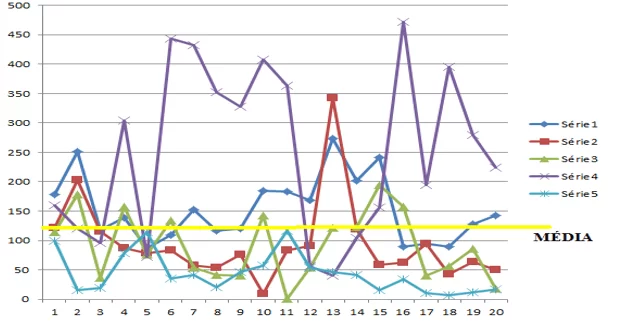
O teste de estacionariedade demonstrou que todas as sequencias numéricas avaliadas foram considerados estacionários, pois a variância se manteve constante em torno de uma média. Desta forma, viabiliza-se a utilização de técnicas baseadas em mínimos quadrados para realizar a predição. O teste de estacionariedade utilizado foi o KPSS criado por Denis Kwiatkowski, Peter C. B. Phillips, Peter Schmidt e Yongcheol Shin determina se a série temporal é estacionária ou não.
Para que a identificação fosse então possível, foram selecionados cinco itens do estoque de uma usina sucroalcooleira do centro-oeste do Brasil, denominados Y1, Y2, Y3, Y4 e Y5 mantendo assim o sigilo da descrição dos materiais em questão.
Levando em consideração as quantidades utilizadas nos últimos doze meses, é que se prevê a demanda do mês posterior. A seguir, serão apresentados os erros de previsão MAD, de cada um dos métodos quantitativos: Média Móvel Simples, Suavização Exponencial Simples, Holt e Winters multiplicativo a fim de comparar e, por conseguinte identificar como sendo a melhor previsão aquela que apontar o menor erro.
O Erro analisado foi o MAD que representa o desvio absoluto do ajuste em relação à demanda real nas mesmas unidades dos dados. Foi identificado com melhor acurácia para os valores do trabalho a série que apresentou o menor valor de MAD.
Fundamentado na identificação da estacionariedade, os métodos quantitativos foram aplicados a fim de prever a melhor demanda para o mês de setembro. Abaixo são apresentadas as tabelas cujos valores representam as análises da média móvel simples obtendo o MAD ideal conforme demonstrado nas Tabelas 1 a Tabela 5.
Tabela 1 – Método estatístico de previsão de demanda – Média Móvel Simples – Item 1
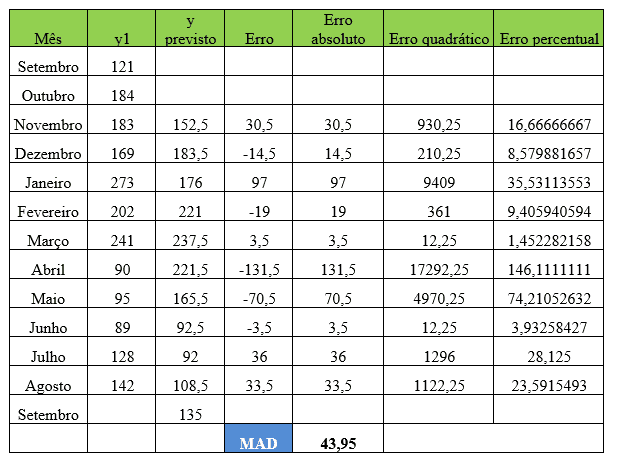
Observando os dados do item Y1 e utilizando dois meses para trazer a melhor acurácia para a análise, com o auxílio do Solver o Desvio Absoluto da Média (MAD) foi ajustado para 43,95. No mês de Agosto, a demanda real foi de 142 e a demanda prevista para o mês de Setembro foi de 135 peças.
Tabela 2 – Método estatístico de previsão de demanda – Média Móvel Simples – Item 2
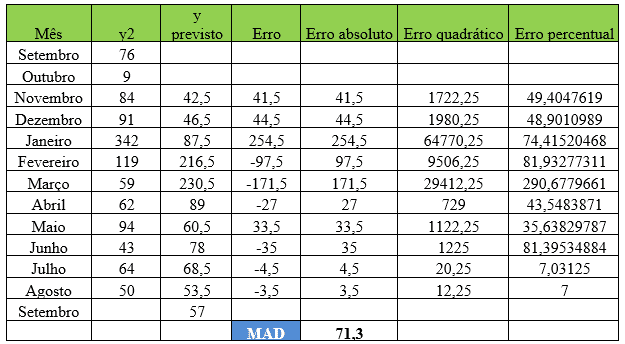
Analisando os dados do item Y2 e utilizando dois meses para trazer a melhor acurácia para a análise, com o auxílio do Solver o Desvio Absoluto da Média (MAD) foi ajustado para 71,3. No mês de Agosto, a demanda real foi de 50 e a demanda prevista para o mês de Setembro foi de 57 peças.
Tabela 3 – Método estatístico de previsão de demanda – Média Móvel Simples – Item 3
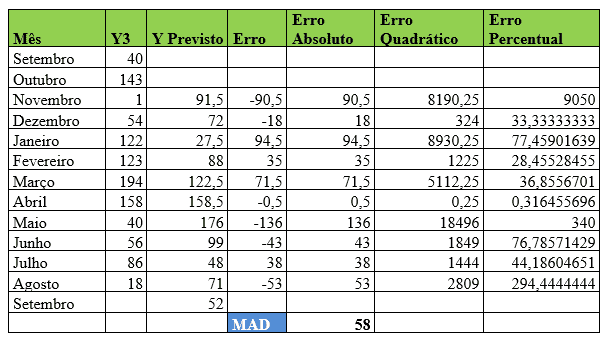
Verificando os dados do item Y3 e utilizando dois meses para trazer a melhor acurácia para a análise, com o auxílio do Solver o Desvio Absoluto da Média (MAD) foi ajustado para 58. No mês de Agosto, a demanda real foi de 18 e a demanda prevista para o mês de Setembro foi de 52 peças.
Tabela 4 – Método estatístico de previsão de demanda – Média Móvel Simples – Item 4
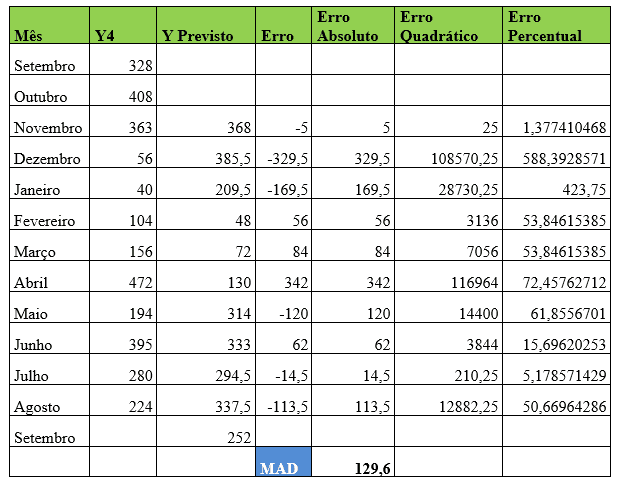
Observando os dados do item Y4 e utilizando dois meses para trazer a melhor acurácia para a análise, com o auxílio do Solver o Desvio Absoluto da Média (MAD) foi ajustado para 129,6. No mês de Agosto, a demanda real foi de 224 e a demanda prevista para o mês de Setembro foi de 252 peças.
Tabela 5 – Método estatístico de previsão de demanda – Média Móvel Simples – Item 5
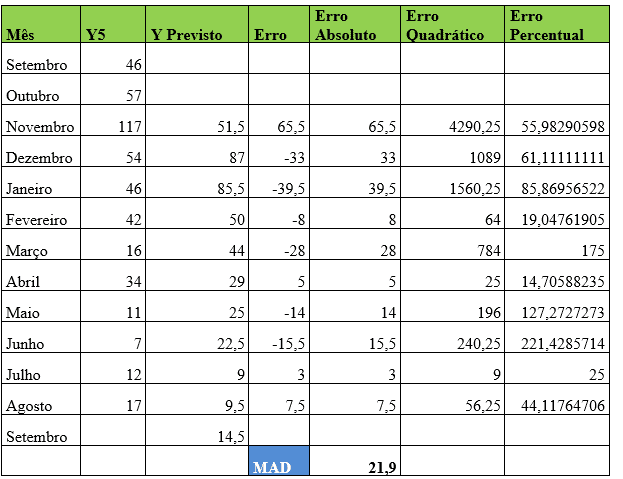
Já para o item Y5 utilizando dois meses para trazer a melhor acurácia para a análise, com o auxílio do Solver o Desvio Absoluto da Média (MAD) foi ajustado para 21,9. No mês de Agosto, a demanda real foi de 17 peças e a demanda prevista para o mês de Setembro foi de aproximadamente 15 peças.
Com o propósito de calcular a Suavização Exponencial Simples foram utilizados os mesmos valores para Y1, Y2, Y3, Y4 E Y5. Neste modelo o coeficiente de ponderação Alfa pode variar de zero a um sendo que suas alterações podem ser boas ou ruins para o resultado da previsão. Com o auxílio do Solver, foi feita a otimização desta variável. Abaixo são apresentadas as tabelas cujos valores representam as análises da Suavização Exponencial Simples obtendo o MAD das previsões conforme demonstrado nas Tabelas de 6 a 10.
Tabela 6 – Método estatístico de previsão de demanda – Suavização Exponencial Simples – Item 1
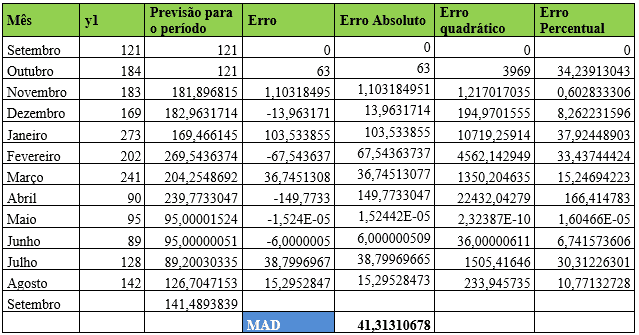
Em análise dos dados do item Y1foi identificado que o coeficiente de ponderação alfa assumiu valor de 0,966616112 ajustando o Desvio Absoluto da Média (MAD) para 41,31. Além disso, em agosto a demanda real foi de 142 e para o mês de setembro a previsão foi de que a empresa precisará adquirir 141 peças aproximadamente.
Tabela 7 – Método estatístico de previsão de demanda – Suavização Exponencial Simples – Item 2
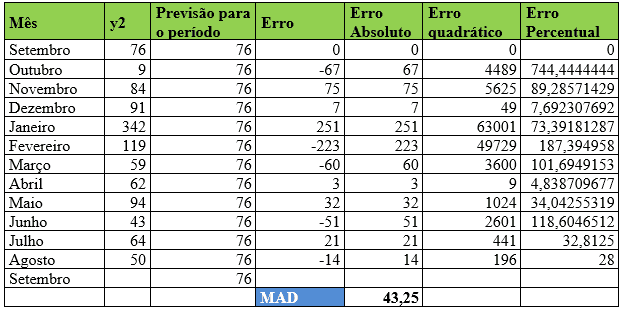
Observando os dados coletados do item Y2 o coeficiente de ponderação alfa assumiu valor de 0 ajustando o Desvio Absoluto da Média (MAD) para 43,25. Em agosto a demanda real foi de 50 e para o mês de setembro a previsão foi de que a empresa precisará adquirir 76 peças aproximadamente.
Tabela 8 – Método estatístico de previsão de demanda – Suavização Exponencial Simples – Item 3
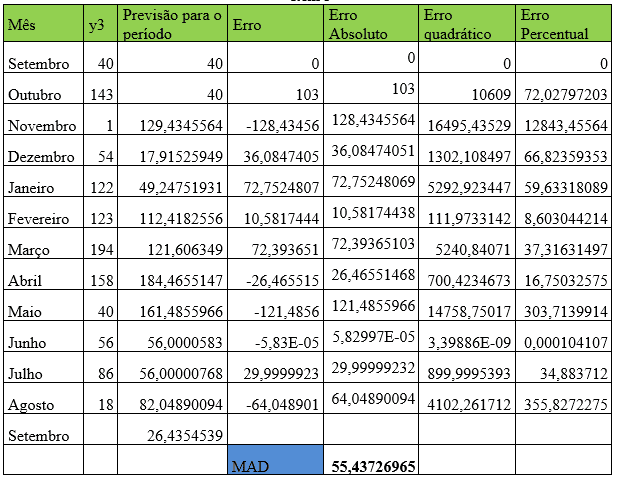
Considerando os dados coletados do item Y3 foi analisado que o coeficiente de ponderação alfa assumiu valor de 0,868296664 ajustando o Desvio Absoluto da Média (MAD) para 55,43. A demanda real de agosto foi de 18 e para o mês de setembro a previsão foi de que a empresa precisará adquirir 26 peças aproximadamente.
Tabela 9 – Método estatístico de previsão de demanda – Suavização Exponencial Simples – Item 4
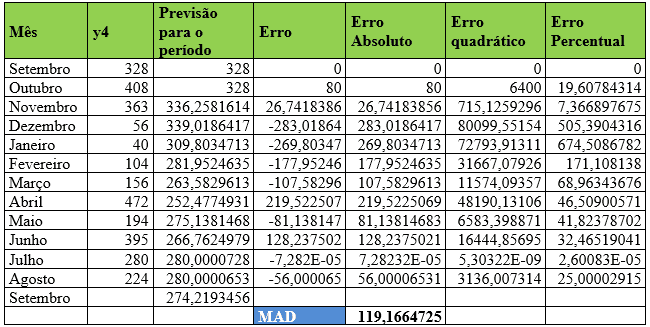
Já para o item Y4 o coeficiente de ponderação alfa assumiu valor de 0,10322702 ajustando o Desvio Absoluto da Média (MAD) para 119,16. Além disso em agosto a demanda real foi de 224 e para o mês de setembro a previsão foi de que a empresa precisará adquirir 274 peças aproximadamente.
Tabela 10 – Método estatístico de previsão de demanda – Suavização Exponencial Simples – Item 5
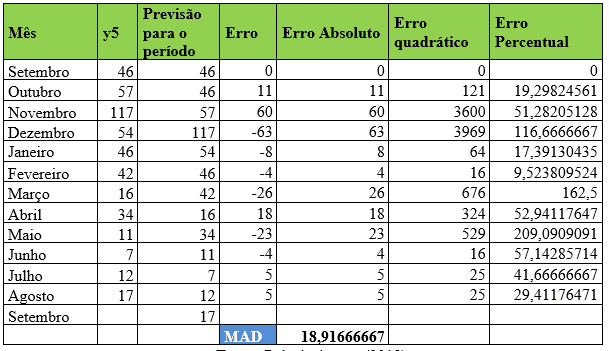
Para o item Y5 o coeficiente de ponderação alfa assumiu valor de 1 ajustando o Desvio Absoluto da Média (MAD) para 18,91. Além disso em agosto a demanda real foi de 17 e para o mês de setembro a previsão foi de que a empresa precisará adquirir 17 peças.
Com o propósito de calcular a Suavização Exponencial de Holt foram utilizados os mesmos valores para Y1, Y2, Y3, Y4 E Y5. Neste modelo os coeficientes de ponderação Alfa e Beta podem variar de zero a um sendo que suas alterações podem ser boas ou ruins para o resultado da previsão e h=1 sendo seu horizonte. Com o auxílio do Solver, foi feita a otimização desta variável. Abaixo são apresentadas as tabelas cujos valores representam as análises da Suavização Exponencial de Holt obtendo o MAD das previsões conforme demonstrado nas Tabelas de 11 a 15.
Tabela 11 – Método estatístico de previsão de demanda – Suavização Exponencial de Holt (Dupla) – Item 1
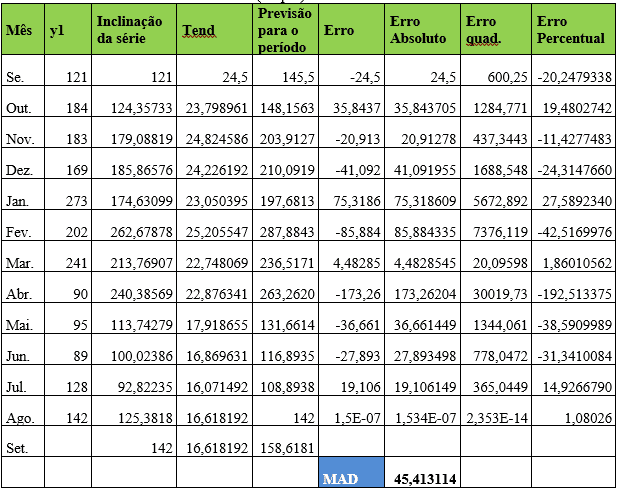
Averiguando os dados coletados para o item Y1 os coeficientes de ponderação alfa e beta assumem valores de 0,8629659 e 0,033157 respectivamente ajustando o Desvio Absoluto da Média (MAD) para 45,41. No mês de agosto, a demanda real foi de 142 e a demanda prevista para o mês de setembro foi de 158.
Tabela 12 – Método estatístico de previsão de demanda – Suavização Exponencial de Holt (Dupla) – Item 2
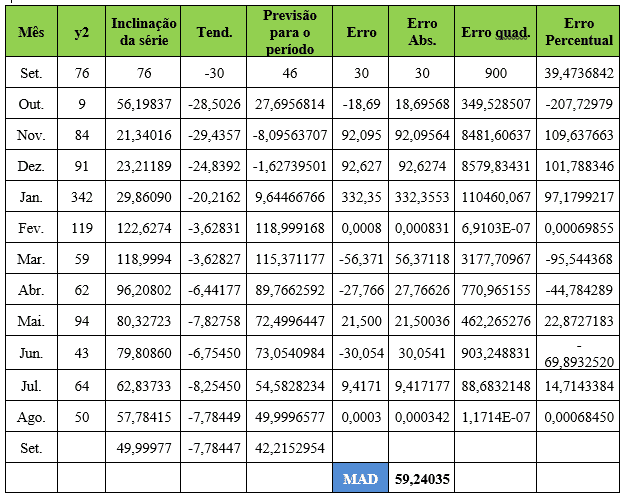
Para o item Y2 os coeficientes de ponderação alfa e beta assumem valores de 0,339945 e 0,14681808 respectivamente ajustando o Desvio Absoluto da Média (MAD) para 59,24. No mês de agosto, a demanda real foi de 50 e a demanda prevista para o mês de setembro foi de 42 aproximadamente.
Tabela 13 – Método estatístico de previsão de demanda – Suavização Exponencial de Holt (Dupla) – Item 3
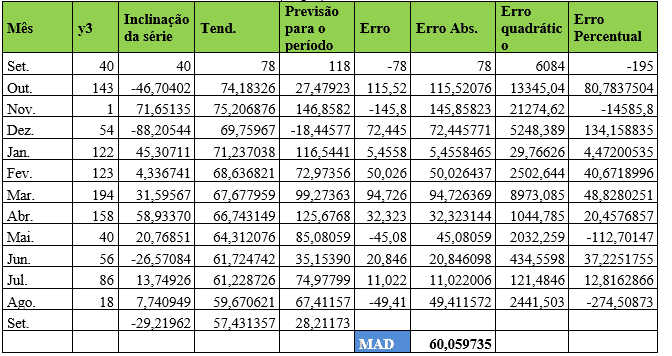
No item Y3 os coeficientes de ponderação alfa e beta assumem valores de 0,611590 e 0,023173 respectivamente ajustando o Desvio Absoluto da Média (MAD) para 60,059. No mês de agosto, a demanda real foi de 18 e a demanda prevista para o mês de setembro foi de 28.
Tabela 14 – Método estatístico de previsão de demanda – Suavização Exponencial de Holt (Dupla) – Item 4
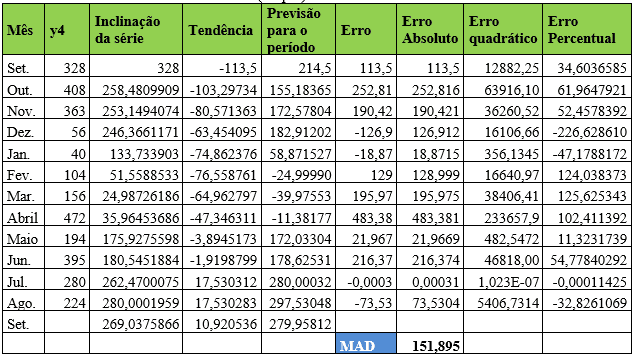
Já para o item Y4 os coeficientes de ponderação alfa e beta assumem valores de 0,387497717 e 0,2319788 respectivamente ajustando o Desvio Absoluto da Média (MAD) para 151,896. No mês de agosto, a demanda real foi de 224 e a demanda prevista para o mês de setembro foi de 280 aproximadamente.
Tabela 15 – Método estatístico de previsão de demanda – Suavização Exponencial de Holt (Dupla) – Item 5
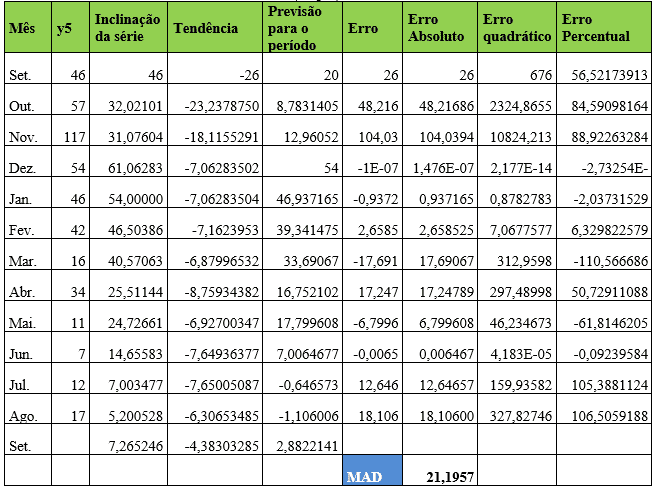
Considerando os dados coletados do item Y5 os coeficientes de ponderação alfa e beta assumem valores de 0,46234675 e 0,2297747 respectivamente ajustando o Desvio Absoluto da Média (MAD) para 21,195. No mês de agosto, a demanda real foi de 17 e a demanda prevista para o mês de setembro foi de 3 peças aproximadamente
Intentando calcular a Suavização Exponencial de Winter-Multiplicativo (Tripla), pois se trata de valores que não permanecem constantes, mas variam com o tempo foram utilizados os mesmos valores para Y1, Y2, Y3, Y4 E Y5. Neste modelo os coeficientes de ponderação Alfa, Beta e Gama podem variar de zero a um sendo que suas alterações podem ser boas ou ruins para o resultado da previsão e h=3 sendo seu horizonte. Com o auxílio do Solver, foi feita a otimização desta variável. Abaixo são apresentadas as tabelas cujos valores representam as análises da Suavização Exponencial de Holt obtendo o MAD das previsões.
Utilizando o método de previsão de demanda de Winters-multiplicativo, os coeficientes de ponderação alfa, beta e gama assumiram valor de 1 para todos os itens conforme demonstrado nas Tabelas de 16 a 20.
Tabela 16 – Método estatístico de previsão de demanda – Suavização Exponencial de Winter Multiplicativo (Tripla) – Item 1
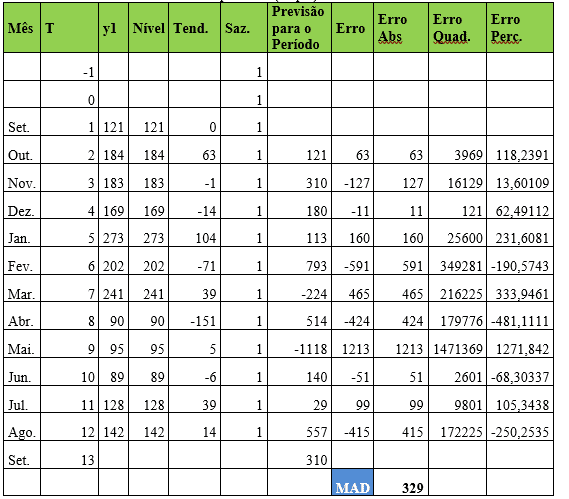
Dispondo dos dados do item Y1 observou-se que os coeficientes de ponderação alfa, beta e gama assumiram valor de 1 e o MAD foi ajustado para 329. A demanda real do mês de agosto foi de 142 e a previsão para o mês de setembro foi de 310
Tabela 17 – Método estatístico de previsão de demanda – Suavização Exponencial de Winter Multiplicativo (Tripla) – Item 2
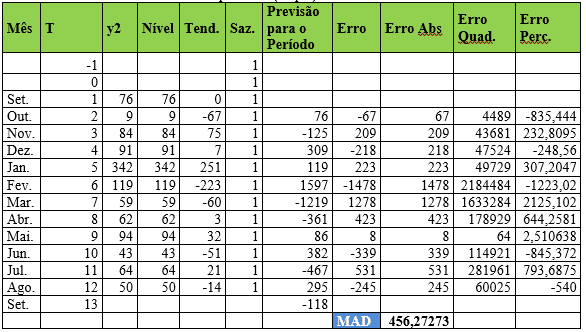
No item Y2 os coeficientes de ponderação assumiram valor de 1 e o MAD foi ajustado para 456,27. A demanda real do mês de agosto foi de 50 e a previsão para o mês de setembro foi de -118. Valores negativos não são interessantes pois indicam falha tanto processual quanto perdas lucrativas.
Tabela 18 – Método estatístico de previsão de demanda – Suavização Exponencial de Winter Multiplicativo (Tripla) – Item 3
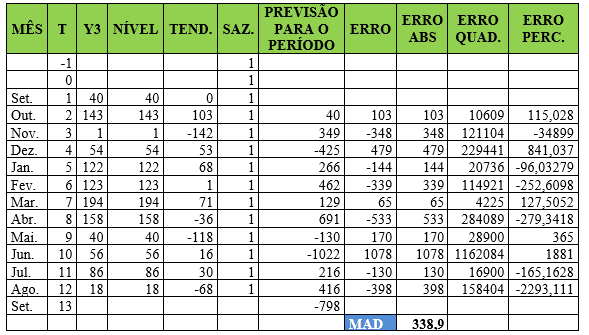
No item Y3 os coeficientes de ponderação assumiram valor de 1 e o MAD foi ajustado para 338,9. A demanda real do mês de agosto foi de 18 e a previsão para o mês de setembro foi de -798. Valores negativos não são interessantes pois indicam falha tanto processual quanto perdas lucrativas.
Tabela 19 – Método estatístico de previsão de demanda – Suavização Exponencial de Winter Multiplicativo (Tripla) – Item 4
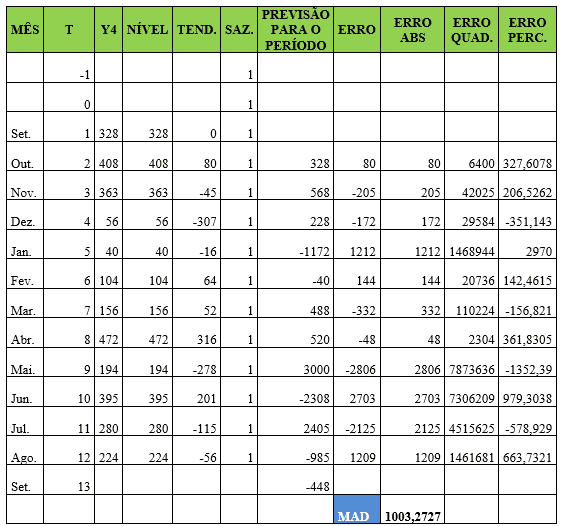
Já no item Y4 os coeficientes de ponderação alfa, beta e gama assumiram valor de 1 e o MAD foi ajustado para 1003,273. A demanda real do mês de agosto foi de 224 e a previsão para o mês de setembro foi de -448. Valores negativos não são interessantes pois indicam falha tanto processual quanto perdas lucrativas.
Tabela 20 – Método estatístico de previsão de demanda – Suavização Exponencial de Winter Multiplicativo (Tripla) – Item 5
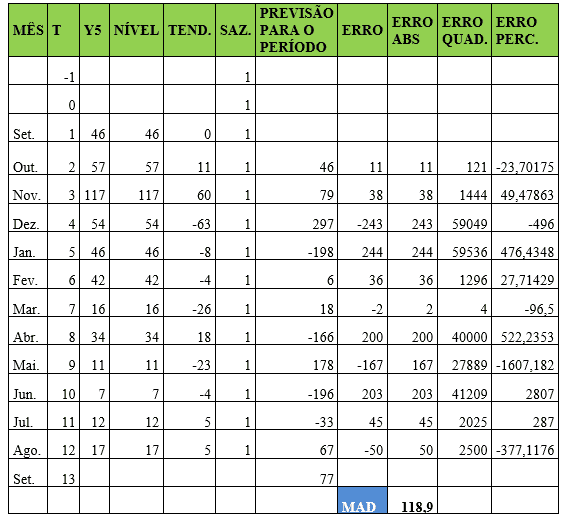
No item Y5 os coeficientes de ponderação alfa, beta e gama assumiram valor dw 1 e o MAD foi ajustado para 118,9. A demanda real do mês de agosto foi de 17 e a previsão para o mês de setembro foi de 77.
A comparação do Desvio Padrão Absoluto da Média (MAD) das previsões podem ser vistos na figura 10 extraída do Excel.
Tabela 25 – Comparação do Desvio Padrão Absoluto da Média (MAD)
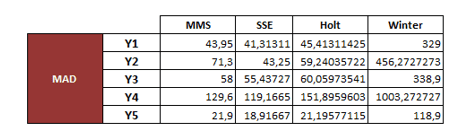
Foi possível identificar que a Suavização Exponencial Simples é a que apresentou o menor erro de previsão e, por este motivo, é o melhor método de previsão de demanda. Todos os itens obtiveram os menores valores de MAD se comparado com os demais.
5. CONCLUSÃO
A realização do trabalho permitiu o conhecimento da gama de possibilidades de previsão de demanda que as empresas podem aplicar para melhoria dos processos.
As técnicas de previsão de demanda são eficientes tanto para o processo de produção quanto para a mensuração de vendas e/ou compras que a empresa deve fazer. A partir da aplicação das técnicas de previsão quantitativas é que se consegue ver com clareza o melhor valor previsto.
É importante ressaltar que processo de previsão de demanda depende de coeficientes de ponderação, os quais fazem toda diferença nos valores previstos e com auxílio do solver é possível definir o melhor valor para alfa, beta e gama.
Conforme disposto no presente trabalho, o erro analisado foi o Desvio Absoluto da Média (MAD) e para a técnica de Suavização Exponencial Simples os itens Y1, Y2, Y3, Y4 e Y5 assumiram os valores de 41,31; 43,25; 55,43; 119,17 e 18,92 respectivamente.
Conclui-se que a técnica de Suavização Exponencial Simples é a que mantém os valores de previsão mais lineares se comparados com as outras técnicas e não assume valores negativos apontando uma eficiência ainda maior da previsão.
REFERÊNCIAS
ANTÔNIO, P. Pesquisa de mercado: ferramenta norteadora no processo decisório que antecede a tomada de decisão. Revista Eletrônica da Faculdade Metodista Granbery, nº 4, 2008.
ASSUMPÇÃO, R. C.; TAMMELA, I.; MEZA, E. B. M.; GUIMARÃES. M. S. Aplicação de Técnicas de Previsão de Demanda para Projetar os dias de Utilização de Sondas de Manutenção. XXXIII Encontro Nacional de Engenharia de Produção. Salvador: 2013.
CARVALHO, T. C; PEREIRA, K. R. A.; OLIVEIRA, M. A.; ANDRADE, A. R. O. Análise Comparativa entre Métodos De Previsão De Demanda – Um estudo aplicado a indústria de gás natural no Brasil. XXXVI Encontro Nacional de Engenharia de Produção, 2016.
CASTRO, A. F.; OLIVEIRA, A. L. G.; MOLIN FILHO, R. G. D.; SANTOS, M. A. R. Implantação das Técnicas de Planejamento e Controle da produção em uma Fábrica de Bolsas. XXXV Encontro Nacional de Engenharia de Produção: Fortaleza-CE, 2015.
CASTRO, R. A. de. Estudo do comportamento da demanda no varejo através de modelos de previsão. São Paulo, 2009.
CORDEIRO, B. A. F.; RANIERI, J. R.; RODRIGUES, N. A. C.; FERREIRA, V. T. S. Aplicação do Modelo de Média Exponencial para a Realização da Previsão de Demanda do Setor Leiteiro no Brasil. XXXV Encontro Nacional de Engenharia de Produção: Fortaleza-CE, 2015.
FORNO, A. J. D.; SILVA, P. B.; MIRANDA, R. G.; BORNIA, A. C.; FORCELLINI, F. A. Previsão de Demanda nas Organizações: resultados de 23 empresas do Brasil. Gestão e tecnologia para a competitividade: Rio de Janeiro, 2013.
FURTADO, M. R. Aplicação de um Modelo de Previsão da Demanda Total nos Credenciados Belgo Pronto. Monografia Submetida à Coordenação de Curso de Engenharia de Produção da Universidade Federal de Juiz de Fora, 2006.
GERHARDT, T. E.; SILVEIRA, D. T. Métodos de pesquisa. Universidade federal do Rio Grande do Sul, 2009.
GRANDO, M. L; PRADO, R. Estudo de Previsão de Demanda de Água Potável de um Município do Oeste do Estado de Santa Catarina. XXXV Encontro Nacional de Engenharia de Produção: Fortaleza-CE, 2015.
JESUS, G. M. K; SILVA, J. M.; GIRADE, C. Análise de Técnicas de Previsão de Demanda: Um Estudo de Caso em uma Cerâmica. XXXVI Encontro Nacional de Engenharia de Produção: Alagoas, 2016.
LIN, T. Y. Estudo de modelos de previsão de demanda. GV Pesquisa – FGV, 2000.
LOGUERCIO, B. A. N.; FERREIRA, J. S. J. Estudo de caso para determinação de modelo quantitativo de previsão de demanda em uma indústria têxtil. ENEGEP: Santa Catarina, 2017.
OLIVEIRA, M.; FREITAS, H. Focus Group – Pesquisa qualitativa: resgatando a teoria, instrumentalizando o seu planejamento. Revista de Administração, n. 3, 1998.
OLIVEIRA, I. H. I; RODRIGUES, L. L. F.; CASTORANI, R. R.; FAGUNDES, M. A. JACUBAVICIUS, C. Aplicação de Métodos de Previsão de Demanda para Redução de Custos na Gestão do Estoque. SEGET, 2015.
OLIVEIRA, V. M.; CORREIAS, S. E. N.; GOMEZS, C. R. P. O Policy Delphi como Método de Pesquisa para o Desenvolvimento de Framework: O Caso dos Papéis de Promoção do Consumo Sustentável no Contexto Brasileiro. Revista Capital Científico – Eletrônica, n. 2, 2018.
PAIVA, M. H. P.; NEGRÃO, L. L. L. Análise de Métodos de Previsão de Demanda: Aplicação na Indústria Cerâmica. XXXIV Encontro Nacional de Engenharia de Produção: Curitiba, 2014.
PAGANELLI, S. S.; LOPES, H. S.; RODRIGUES, M. R.; BARROS, G. P. Análises de Modelos Quantitativos de Previsão da Demanda: Ajuste e otimização de modelos à demanda do adesivo comum em uma gráfica na cidade de Belém-Pa. XXXV Encontro Nacional de Engenharia de Produção: Fortaleza-CE, 2015.
PELLEGRINI, F. R. Metodologia para Implementação de Sistemas de Previsão de Demanda. UFRGS – Escola De Engenharia Programa De Pós-Graduação Em Engenharia De Produção. Porto Alegre, 2000.
PELLEGRINI, F. R. P; FOGLIATTO, F. S. Passos para Implantação de Sistemas de Previsão de Demanda: Técnicas e Estudo de Caso. Revista PRODUÇÃO, v. 11 n. 1, 2001.
PESSOA, K; NOBRE, D.; VERAS; B. Análise Comparativa entre os Métodos de Previsão de Demanda em uma Indústria de Higiene Pessoal, Perfumaria e Cosméticos Localizada em Teresina-Pi. Piauí, 2018.
PORTAL action. Medidas de acurácia. Disponível em: <http://www.portalaction.com.br/se
ries-temporais/35-medidas-de-acuracia>. Acesso em: 14 de Maio de 2018.
PROTO, L. O. Z.. Previsão de demanda para planejamento da capacidade de empresa do setor cimenteiro. XXIII Encontro Nacional de Engenharia de Produção – Ouro Preto – MG, 2003.
QUEIROZ, A. A.. Método de previsão de demanda e detecção de sazonalidade para o planejamento da produção de indústrias de alimentos. XXIII Encontro Nacional de Engenharia de Produção – Ouro Preto – MG, 2003.
SANTOS DOS, T. S.; FERREIRA, L. H. M.; ROCHA, N. S.; LIMA, M. S. Previsão de Demanda e Gestão da Capacidade: um estudo de caso em um hotel no município de Marabá – PA. ENEGEP: Santa Catarina, 2017.
SANTOS, G. Q. V. MARQUES JUNIOR, J. A.; BERNARDO, Y. N. S. Previsão de demanda: Revisão bibliográfica e análise acadêmica atual. ENEGEP: Fortaleza, 2015.
SERAPONI, M. Métodos qualitativos e quantitativos na pesquisa social em saúde: algumas estratégias para a integração. n.1, pp.187-192.
SILVA, P. G. M. Previsão de Demandas e Gestão de Estoques, Estudo de Caso Realizado em uma Fábrica de Móveis no Município de Marabá-Pará. XXXVIII Encontro Nacional de Engenharia de Produção: Alagoas, 2018.
TAHARA, N. K. S.; LOBATO, H. M.; VERA, F. S.; RIBEIRO, A. S.; SILVA, A. L. C. P. Previsão de Demanda Previsão de um Veículo Classe a de uma Empresa do Setor Automobilístico. XXXIV Encontro Nacional de Engenharia de Produção, 2014.
TUBINO, D. F. Planejamento e controle de produção: teoria e prática. São Paulo: Atlas, 2007.
WERNER, L.; LEMOS, F. de O.; DAUDT, T. Previsão de demanda de níveis de estoque uma abordagem conjunta aplicada no setor siderúrgico. XIII SIMPEP: São Paulo, 2006.
YIN, R. K. Estudo de caso – Planejamento e métodos. São Paulo: Bookman, 5ª ed., 2015.
ZAN, G. L. Técnicas de previsão de demanda: um estudo de caso triplo com dados de venda de materiais eletro-mecânicos. 2007. Disponível em:< https://revista.feb.unesp.br/Ind
ex.php/gepros/article/viewFile/171/119>. Acesso em: 12 de Outubro de 2018.
[1] Graduada em Engenharia de Produção pelo Instituto Luterano de Ensino Superior de Itumbiara.
[2] Graduado em Administração de Empresas pela Universidade Norte do Paraná – UNOPAR.
[3] Graduando em Engenharia de Produção.
[4] Graduando em Engenharia de Produção.
[5] Graduando em Engenharia de Produção.
[6] Graduando em Engenharia de Produção.
[7] Graduando em Engenharia de Produção.
Enviado: Setembro, 2019.
Aprovado: Setembro, 2019.