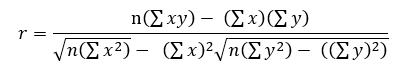ARTIGO ORIGINAL
SANTOS, Camila Regina da Silva [1], JÚNIOR, Osmar de Paula Oliveira [2], PEREIRA, José Wellington Abreu [3], GARCIA, Uelson Serra [4], FIGUEIREDO, Reginaldo Santana [5]
SANTOS, Camila Regina da Silva. Et al. Influência Do Preço Da Soja Em Grão No Preço Da Carne De Frango: Uma Análise Estatística. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano 03, Ed. 12, Vol. 07, pp. 69-84 Dezembro de 2018. ISSN:2448-0959
RESUMO
A carne de frango representa 50,6% do complexo de carne mundial e o consumo interno brasileiro é de 46,8%. O Brasil é o segundo maior produtor de soja mundial, desta produção, cerca de 80% é destinada para fabricação de ração animal. A demanda mundial para o consumo da carne de frango é cada vez crescente e seu preço, em certa medida é afetado pelo preço dos insumos necessários para atividade avícola. Neste contexto, o objetivo deste trabalho foi identificar a existência de correlação e o nível de significância entre as variáveis preço de soja em grão e o preço da carne de frango. Para isso, utilizou-se séries históricas do preço da soja em grão e carne de frango no período de 2007 a 2017. As variáveis foram submetidas à análises por meio do software IBM SPSS, onde foram analisadas o Coeficiente de Correlação de Pearson e a Regressão Linear das variáveis. Os resultados demostraram que existe forte correlação entre as variáveis e que o aumento no preço da carne de frango é explicado em 70,3% pelo o aumento preço da soja em grão.
Palavras-chave: Correlação, Regressão Linear, SPSS.
INTRODUÇÃO
Na atual conjuntura brasileira, o agronegócio tem exercido papel relevante na balança comercial e a produção agropecuária tem contribuído para o superávit das contas nacionais. Segundo o portal da Aveworld (2017), a balança comercial registrou, no mês de junho de 2017, um superávit de US$ 1,045 bilhão, resultando em um saldo positivo de US$ 37,261 bilhões e nas exportações, houve crescimento de 4,3%, em razão das vendas de produtos básicos e, principalmente, carne de frango e soja em grãos.
Neste contexto, para a próxima década, essa tendência têm grandes implicações diretas sobre o mercado da carne de frango e seus principais insumos, como, o milho e a soja. A principal implicação refere-se à segurança alimentar como resultado do crescimento na demanda mundial, devido à entrada de um bilhão de pessoas ao mercado consumidor. O crescimento quantitativo e qualitativo na demanda da carne de frango e, por consequência, do milho e da soja, está aumentando os preços desses produtos e a possibilidade de renda extraordinária (CONTINI et al, 2013).
O ranking da produção avícola é representado pelos EUA, Brasil e China. Os países que mais consomem carne de frango são: China, Indonésia, EUA e Brasil. O ranking mundial da produção de soja em grão é representado, principalmente, pelos EUA, Brasil e Argentina (FAOSTAT, 2018).
De acordo com dados do Departamento de Pesquisas e Estudos Econômicos (DEPEC, 2017), em 2016, a carne de frango representa 50,6% do complexo da carne (bovino, suíno e frango) mundial. Segundo essa mesma fonte, o consumo mundial da carne de frango representa 34,6% e no Brasil, esse percentual corresponde a 46,8%. Com relação a soja, cerca 80% da produção é utilizada na fabricação de rações, respondendo por 25% a 30% do volume da ração para aves e suínos (DEPEC, 2017).
Dada a importância para estes dois produtos, a soja em grão e a carne de frango, faz-se necessário conhecer a correlação destas duas variáveis e medir o nível de influência que uma representa sobre a outra no mercado do agronegócio brasileiro. Neste sentido, o objetivo deste trabalho foi identificar a existência de correlação e o nível de significância entre as variáveis preço de soja em grão e o preço da carne de frango no período compreendido entre julho de 2007 a junho de 2017.
O presente artigo, além desta introdução, está dividido em: revisão da literatura, metodologia, resultados e discussão, considerações finais e, por fim, referências.
2. REVISÃO DA LITERATURA
2.1 PRODUÇÃO DE CARNE DE FRANGO NO BRASIL
A produção de frangos de corte, atualmente, é considerada uma atividade econômica internacionalizada e uniforme, sem fronteiras geográficas de tecnologia. Podendo ser considerada um complexo industrial que não deve ser analisado apenas sob o aspecto de produção e distribuição, e sim por meio de uma abordagem sistêmica do setor. As características dessa atividade contribuem para aumentar a geração de emprego e de renda no campo. O sistema de integração desenvolvido no Brasil mostra-se ideal para pequenas propriedades (VIEIRA E DIAS, 2005).
Grande parte do destaque da produção de frangos no Brasil é devido à estruturação da cadeia produtiva do setor. Segundo Voila e Triches (2015), a cadeia produtiva do frango no Brasil é caracterizada pela utilização de modernos sistemas de planejamento, organização, coordenação dos elos, incorporação de novas tecnologias e técnicas gerenciais que se refletem no constante crescimento da produção. Albino e Taverni (2008) apud Paseto et al (2015) afirmam também que a cadeia produtiva de frango de corte tem sido uma das mais organizadas do país, destacando-se pelos resultados alcançados não só em produtividade, volume de abate, como também no desempenho econômico, o qual tem contribuído de forma significativa para a economia nacional.
Voila e Triches (2015) caracterizaram a cadeia produtiva de acordo com seus elos principais, sendo eles: avozeiro, matrizeiro, incubatório, aviário, frigorífico, varejista e consumidor final; e os elos auxiliares: pesquisa e desenvolvimento genético, medicamentos, milho, soja e outros insumos, equipamentos e embalagens, ou seja, são os segmentos a montante e a jusante da cadeia principal com a função de fornecer insumos e outras necessidades.
Outro aspecto da cadeia do frango, refere-se ao consumo de soja, um dos principais insumos da ração. Considerando que a taxa atual de conversão alimentar do frango, da ordem de 1,7 kg ração/1 kg frango, apresente uma melhoria da ordem de 5% na próxima década caindo para 1,6, a produção de carne de frango, estimada para 2020, de 109 milhões de toneladas, requererá 174 milhões de toneladas de ração. Assumindo a proporção de 35% de soja na composição da ração, serão empregadas, 61 milhões de toneladas de soja, ou seja, 28% das produções mundiais projetadas para 2020 (CONTINI et al, 2013).
A produção e os preços do milho e soja terão papel fundamental na dinâmica dessa cadeia na próxima década e o mundo deverá se constituir em regiões produtoras e consumidoras bem definidas, cabendo, ao Brasil, papel de destaque no abastecimento mundial dessa proteína (CONTINI et al, 2013).
Nos últimos 18 anos, o consumo de carne de frango no Brasil teve um aumento de 262%, saindo de um consumo per capita de 16,8 kg/hab.ano, em 1992, para 44 kg/hab.ano em 2010 (AGUIAIS, 2015).
No ano de 2016, as exportações de carnes totalizaram US$ 1,08 bilhão em abril, uma redução de 9,8% ante US$ 1,19 bilhão verificados no mesmo mês do ano de 2015. O principal item negociado no mês foi a carne de frango, com US$ 543,14 milhões (-11,2%). Em abril de 2017, o principal item negociado no mês foi a carne de frango, com a comercialização de 317,71 mil toneladas, houve variação negativa de 23% em relação a abril de 2016. O preço médio no mercado internacional passou de US$ 1.482 por tonelada para US$ 1.710 por tonelada (+15,3%) (MAPA, 2017).
Grandes produtores mundiais, EUA (2.498.000t), China (4.475.000t) e Índia (1.047.000t) apresentarão crescimentos importantes na produção de carne de frango entre 2012 e 2020, porém, esses incrementos serão acompanhados pelo aumento no seu consumo interno o que limita sua participação no mercado mundial. Nesse cenário, caberá ao Brasil, que, apesar do aumento previsto no consumo da ordem de 1.700.000t, produzirá um excedente exportável de 4.673.000t em 2020, um incremento de 1.066.000 nas suas exportações até 2020 (CONTINI et al, 2013).
2.2 PRODUÇÃO DE SOJA NO BRASIL
A soja representa o papel de principal oleaginosa produzida e consumida no mundo. Tal fato se justifica pela importância do produto tanto para o consumo animal, através do farelo da soja, quanto para o consumo humano, através do óleo. No Brasil, a partir dos anos 1970, a produção da soja passou a ter grande relevância para o agronegócio, verificada pelo aumento das áreas cultivadas e, principalmente, pelo incremento da produtividade pela utilização de novas tecnologias (SILVA et al, 2011).
Aproximadamente 90% da soja produzida no mundo é destinada à produção de óleo comestível e farelo, 4% tem outros usos e menos de 6% é destinada à alimentação humana direta. Em média, utiliza-se 20% de farelo de soja nas dietas animais, o que representa cerca de 70% do consumo mundial de farelo de soja. Ou seja, a soja, além de opção à dieta humana como fonte de proteína, é um insumo indispensável à produção de aves, suínos e bovinos e, portanto, seu consumo depende fundamentalmente do consumo de proteínas animais, notadamente as carnes (CONTINI et al, 2013).
A cadeia produtiva da soja é responsável por uma parcela significativa do Produto Interno Bruto (PIB) do agronegócio brasileiro. Ela é composta por empresas produtoras de máquinas, equipamentos e insumos agrícolas, por propriedades agrícolas produtoras de soja em grão, por indústrias de processamento como esmagadoras e refinarias que produzem óleo e farelo de soja, e todos os demais agentes – exportadores, atacadistas, varejistas, entre outros – que operam na produção e distribuição de soja em grão e derivados. A indústria da soja é importante atualmente tanto para a captação de moedas estrangeiras pelas exportações brasileiras de farelo, óleo e grãos, como para o suprimento do mercado interno de óleos comestíveis e concentrados protéicos (CONTE E FERREIRA FILHO, 2007). Segundo Agrolink (2017), os produtos do agro que apresentaram melhor desempenho se encontram no complexo soja (óleo, farelo e grãos).
A produção total mundial de soja em grãos é estimada em 344,67 milhões de toneladas. Os principais produtores mundiais são os Estados Unidos, o Brasil e a Argentina, que, juntos, são responsáveis por 82% da produção mundial (CONAB, 2018).
Segundo a EMBRAPA (2017), o Brasil é o maior produtor mundial de grão de soja correspondendo a uma produção de 113,923 milhões de toneladas, numa área plantada de 33, 890 milhões de hectares e com uma produtividade de 3.362 kg/ha, sendo o estado do Mato grosso o maior produtor da soja seguido pelos estados do Paraná e Rio Grande do Sul.
O complexo soja (grãos, farelo e óleo) teve participação de 52,5% nas exportações do agronegócio brasileiro em 2017 (MAPA, 2017). As exportações do complexo soja cresceram 12,6% em relação ao ano anterior, com US$ 4,55 bilhões, sendo a maior parcela obtida pelas vendas de soja em grãos, que alcançaram quantidade recorde de 10,43 milhões de toneladas, o que resultou em uma receita de US$ 3,95 bilhões. Somado a estes recordes, o preço médio do produto subiu 8,1% no período, passando de US$ 350 para US$ 378 por tonelada. O farelo de soja foi o segundo principal produto negociado pelo setor, saindo de US$ 470,11 milhões, para 1,33 milhão de toneladas embarcadas e preço médio, no período, de US$ 354 por tonelada. Já as vendas externas de óleo de soja totalizaram US$ 134,10 milhões, com alta no preço médio do produto e na quantidade comercializada, com 181,34 mil toneladas (MAPA, 2017). Roessing e Lazzarotto (2004) mostram que o complexo é responsável por gerar em torno de 5 milhões de postos de trabalho. A partir desse montante, pode-se assinalar que, para cada hectare de soja cultivado no Brasil, seria gerado, por todo o complexo, cerca de 0,24 emprego.
3. METODOLOGIA
3.1 APRESENTAÇÃO DOS DADOS AMOSTRAIS
Os dados para análise estatística foram coletados no Centro de Estudos Avançados em Economia Aplicada (CEPEA). Utilizaram-se duas séries históricas de dados mensais conforme a metodologia de preços do CEPEA. Os dados foram selecionados desde o mês de julho de 2007 até julho de 2017, com as variáveis soja em grão a granel com unidade de medida saca de 60 kg (preço – R$/ Saca 60 – kg), tipo exportação, conforme padrão Concex: até 14% de umidade, até 2% de impurezas, e limites máximos de 8% para grãos avariados (até 5% de ardidos) e 30% de grãos quebrados e frango inteiro abatido (congelado e resfriado), e frango vivo, de incubatórios, avicultores e associações, frigoríficos, atacadistas, representantes (intermediários) e agentes de supermercados, com unidade de medida (preço – R$/quilograma – kg). Os dados coletados apresentam o seguinte tratamento estatístico as médias regionais móveis que incluem os valores mais recente de cada colaborador, reportados nos últimos sete dias úteis, para cada um dos produtos. O cálculo diário é feito considerando apenas os valores que estejam no intervalo de dois desvios-padrão para cima e para baixo em relação à média da amostra.
As análises de dados deste estudo foram realizadas pelo software IBM Statistical Package for the Social Science (SPSS) usado para solucionar uma ampla variedade de problemas de negócios e de pesquisas no tratamento de dados estatísticos.
3.2 INFORMAÇÕES ESTATÍSTICA
Para identificar a confiabilidade das amostras no software e prosseguir com as análises é necessário, antes, aplicar o teste T-student, que fará a estatística de Teste para testar afirmativas sobre uma média populacional com o sigma (σ) desconhecido (TRIOLA, 2008). Após o teste T, realizou-se o Diagrama de Dispersão/ponto, que demostra a relação linear entre duas variáveis (x e y), e o Diagrama em Caixa (Boxplot) e identificação de outliers.
Como o exame visual de diagramas de dispersão é altamente subjetivo, usa-se o coeficiente de correlação linear (r) ou coeficiente de correlação de Pearson do produto de momento, que serve para medir a intensidade da relação linear entre os valores quantitativos emparelhados, x e y, em uma amostra e pode ser calculado conforme a equação 1. O valor de (r) deve sempre estar entre – 1 e + 1. Se (r) estiver muito próximo de zero não há correlação significativa entre x e y, se estiver próximo de – 1 ou + 1 existe uma relação linear significativa entre x e y, no primeiro caso (-1) será negativa perfeita, ou seja, o aumento dos dados de uma variável diminui a outra variável. A variável dependente tem relação inversamente proporcional a variável independente. No segundo caso (+1), há uma correlação positiva perfeita, ou seja, o aumento nos dados de uma variável proporciona o aumento de outra, estando a variável dependente diretamente relacionada com a independente. O coeficiente de correlação apresenta os níveis de significância de 0,01 ou 1%, 0,05 ou 5 % e 0,1 ou 10% (TRIOLA, 2008).
Segundo Filho et al (2009), valores extremos (0 ou 1) dificilmente são encontrados na prática. É importante discutir como os pesquisadores podem interpretar a magnitude dos coeficientes. Para Conhen (1988) e Dancey e Reidy (2006), os valores do coeficiente linear de Pearson podem ser interpretados da seguinte maneira:
- Se 0,10 < r < 0,30 a correlação linear é fraca;
- Se 0,40 < r < 0,6 a correlação linear é moderada;
- Se 0,70 < r < 1 a correlação linear é forte.
Equação 1 – Equação do Coeficiente de correlação linear
Onde:
n: número de pares de dados presentes;
Σ: representa a soma dos itens indicados;
Σx: soma de todos os valores de x;
Σx²: valores de x elevados ao quadrado um a um e depois somados;
(Σx)²: valores de x somados e o total elevado ao quadrado;
Σxy: cada valor de x multiplicado por seu correspondente valor de y, depois os produtos são somados;
r: coeficiente linear para uma amostra; e
p: coeficiente linear para uma população.
Em termos de análise estatística consideram-se duas hipótese, sendo Ho (hipótese nula) e H1 (hipótese alternativa). Essas hipóteses geram evidências suficientes quanto a existência ou não de uma correlação linear significativa entre duas variáveis (TRIOLA, 2008), onde:
H0:p = Não há correlação linear.
H1:p = Há correlação linear.
p>0,01;0,05;0,1(níveis de significância), aceita-se H0 e rejeita-se H1.
p<0,01;0,05;0,1(níveis de significância), rejeita-se H0 e aceita-se H0.
O critério de decisão é rejeitar a hipótese nula p= 0 se o valor absoluto da estatística de teste exceder os valores críticos; a rejeição de significa que há evidência suficiente para apoiar a afirmativa de uma correlação linear entre as duas variáveis. Se o valor absoluto da estatística de teste não exceder os valores críticos, então deixamos de rejeitar p= 0; isto é, não há evidência suficiente para se concluir que haja uma correlação linear entre as duas variáveis (TRIOLA, 2008).
Na análise da correlação de Pearson avalia-se os valores de Durbin-Watson (DW) que são utilizados para detectar a presença de autocorrelação (dependência) nos resíduos de uma análise de regressão. Os valores de DW devem ser comparados ao valor de dw com os valores críticos dL (limite crítico inferior) e dU (limite crítico superior) da tabela de Durbin-Watson (Portal Action, 2017), tendo-se assim as seguintes interpretações:
- se 0 ≤ dw < dL então, rejeitamos H0 (dependência);
- se dL ≤ dw ≤ dU então, o teste é inconclusivo;
- se dU < dw < 4-dU então, não rejeitamos H0 (independência);
- se 4-dU ≤ dw ≤ 4-dL então, o teste é inconclusivo;
- se 4-dL < dw ≤ 4 então, rejeitamos H0 (dependência).
Após a identificação da correlação linear entre x e y, pode-se estabelecer uma equação linear que expresse y em termos de x. Essa equação pode ser usada para prever valores de y para valores de x. A relação entre as duas variáveis é determinada através de uma reta chamada de reta de regressão, cuja equação é denominada de equação de regressão, a qual expressa uma relação entre x (chamada de variável explanatória, ou variável previsora ou variável independente) e y (chamada de variável resposta ou variável dependente).
A equação típica de uma reta é expressa pelos valores de intercepto e inclinação (TRIOLA, 2008):
Onde:
b0 representa o intercepto;
b1 representa a inclinação;
y representa o preço da carne de frango em (R$/kg);
x representa o preço da soja em grão saca de 60 quilograma em (R$/kg).
Na análise de regressão, existe um coeficiente de correlação ao quadrado (conhecido como o coeficiente de determinação, R² ) é uma medida da quantidade de variação em uma variável que é explicada pela outra (FIELD, 2009). Triola (2008) define R² como a proporção da variação em y que é explicada pela relação linear entre x e y, ou seja, o quanto do preço da carne de frango pode ser explicado pelo preço da soja em grão.
4. RESULTADOS E DISCUSSÃO
As séries históricas foram analisadas pelo software IBM SPSS gerando-se as seguintes saídas (outputs), Diagrama de Caixa (boxplot), Diagrama de Dispersão, Coeficiente de Correlação de Pearson e coeficiente de Regressão Linear. Os resultados e discussões podem ser observados nos tópicos seguintes.
4.1 DIAGRAMA DE DISPERSÃO
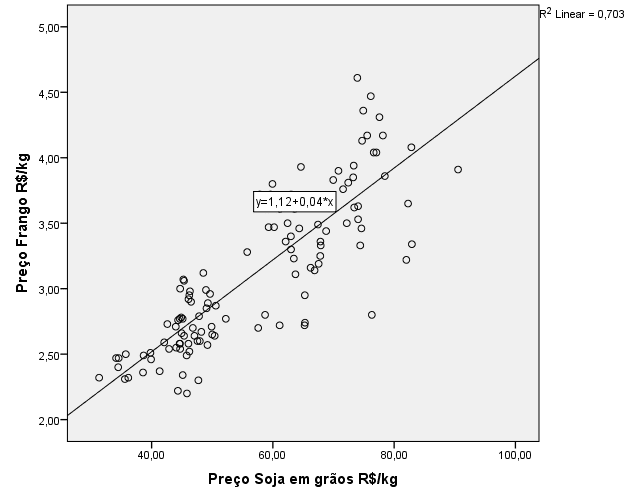
Como a pesquisa em análise faz o uso de duas variáveis, o mais indicado, conforme a literatura, é o Diagrama de Dispersão simples que, segundo Field (2009), é simplesmente um gráfico que coloca o escore de cada número de amostra em uma variável contra seu escore em outra. Observou-se que existe tendência geral dos dados preço da soja em grão e preço da carne de frango, porém, esta análise não é suficiente para afirmar um relacionamento entre as variáveis. Foram identificados poucos valores atípicos óbvios, pois a maioria dos pontos plotados no diagrama apresentam-se próximos uns aos outros. Os outliers (valores discrepantes, que situam-se distantes dos valores típicos) gerados, possivelmente, devem-se às especificidades da produção agropecuária, tais como: clima, manejo, perecibilidade e fatores fitossanitários. Segundo esta análise, observa-se pouca distorção no coeficiente de correlação, o que ocasiona uma correlação positiva, demostrando, assim, a confiabilidade dos dados coletados. Com esta análise, provavelmente o aumento no preço da soja provoca aumento do preço da carne de frango.
Gráfico 1. Diagrama de dispersão simples: preço da soja em grão e a carne de frango.
4.2 DIAGRAMA DE CAIXA (BOXPLOT)
Diagrama de Caixa é o gráfico de um conjunto de dados que consiste em uma linha que se estende do valor mínimo ao valor máximo, em uma caixa com linhas traçadas no primeiro quartil ou quartil inferior, Q1, na mediana ou segundo quartil Q2 e no terceiro quartil ou quartil superior, Q3, sendo que primeiro quartil separa os 25% inferiores dos valores ordenados dos 75% superiores, no segundo quartil separa os 50% inferiores dos valores ordenados dos 50% superiores e no terceiro quartil separa os 75% inferiores dos valores ordenados dos 25% superiores (TRIOLA, 2008).
Nesta análise observou-se para o preço da soja em grão e carne de frango o centro, a dispersão e a distribuição dos dados. Para a variável preço de soja em grão, os valores mínimo e máximo foram, respectivamente, 31,34 e 90,54. Com relação aos quartis Q1, Q2 e Q3 os valores foram, respectivamente 45,35; 58,27 e 68,11.
Para a variável preço da carne de frango, os valores mínimo e máximo foram, respectivamente, 2,20 e 4,61. Com relação aos quartis e , os valores foram, respectivamente, 2,64; 3,00 e 3,61.
Gráfico 2. Diagrama de Caixa (Boxplot): preço da soja em grãos saca de 60 kg.
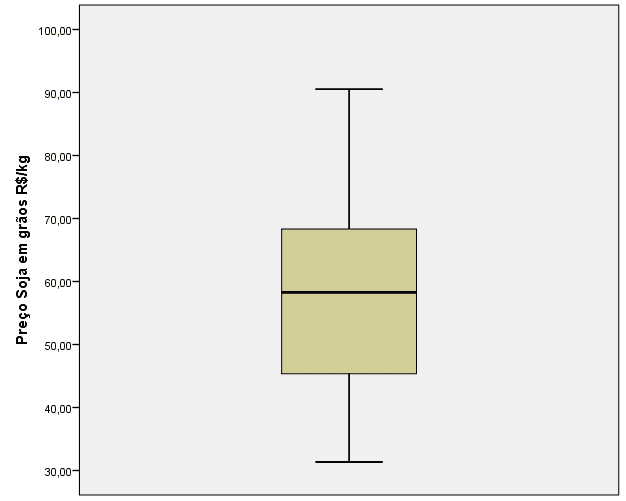
Gráfico 3. Diagrama de Caixa (Boxplot): preço da carne de frango.
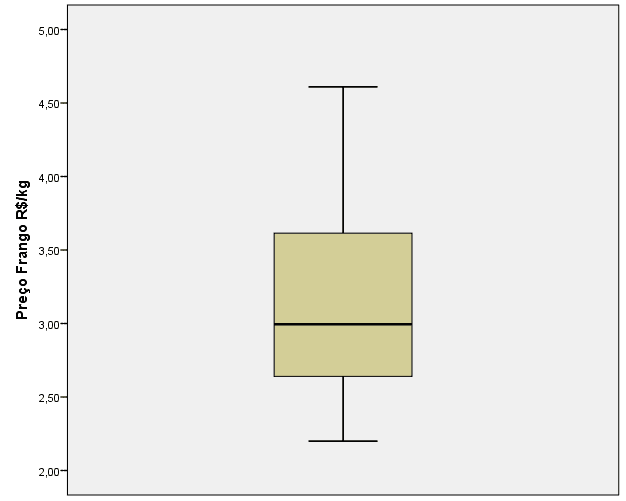
O diagrama demonstrou ausência de outliers, tanto para o preço da soja em grãos quanto para o preço da carne de frango. Podemos observar, nos dois diagramas, que o preço da soja tende a variar mais e ser maior do que o preço da carne de frango, como pode ser observado nos gráficos 2 e 3. Isso é explicado devido ao preço da soja em grão ser maior que o preço da carne de frango.
4.3 COEFICIENTE DE CORRELAÇÃO DE PEARSON
Observou-se que existe correlação entre o preço da soja em grão e o preço da carne de frango. Esta afirmativa pode ser evidenciada a partir do quadro 1, o qual demonstrou um coeficiente de correlação de Pearson com correlação positiva entre as variáveis analisadas, ou seja, o preço da carne de frango está positivamente relacionado com o preço da soja em grão com um coeficiente r = 0,838, considerado “forte”, significativo a p < 0,01 ou (Sig. (2 extremidades) menor que 0,01). Logo, rejeita-se a H0 (hipótese nula) de que não há correlação linear entre as duas variáveis e aceita-se a H1 (hipótese alternativa) que há correlação linear entre as variáveis, ou seja, o preço da soja em grão influencia na formação do preço da carne de frango. Esta correlação é explicada pela soja em grão constituir parte da ração alimentar da avicultura, sendo a soja em grão um bem complementar à produção de carne de frango.
| Correlações | |||
| Preço Soja Saca de 60 kg | Preço Frango R$/kg | ||
| Preço Soja Saca de 60 kg | Correlação de Pearson | 1 | ,838** |
| Sig. (2 extremidades) | ,000 | ||
| N | 120 | 120 | |
| Preço Frango R$/kg | Correlação de Pearson | ,838** | 1 |
| Sig. (2 extremidades) | ,000 | ||
| N | 120 | 120 | |
| **. A correlação é significativa no nível 0,01 (2 extremidades).
Fonte: dados da pesquisa. |
|||
Quadro 1. Coeficiente de Correlação de Pearson: preço da soja em grão e carne de frango.
4.4 COEFICIENTE DE REGRESSÃO LINEAR
No quadro 2 observou-se os valores de R e R². Tem-se um valor de R= 0,838, existindo apenas um previsor, o qual representa a correlação simples entre o preço da soja em grão e o preço da carne de frango. O valor de R² = 0,703, indica que o aumento preço da carne de frango pode ser explicado em 70,3 % pelo aumento do preço da soja em grão e 23,7% são explicados por outros fatores relacionados a produção da carne de frango. Evidenciou-se um Durbin-Watson (DW) = 0,428, com k = 2, dL = 1,66 e dU = 1,73 onde, 0 ≤ dw < dL, demostrando que existem evidências de uma correlação de dependência positiva entre o preço da soja em grão e o da carne de frango.
Quadro 2. Resumo do modelo: preditores e variável dependente.
| Resumo do modelob | |||||
| Modelo | R | R quadrado | R quadrado ajustado | Erro padrão da estimativa | Durbin-Watson |
| 1 | ,838a | ,703 | ,700 | ,31806 | ,428 |
| a. Preditores: (Constante), preço soja em grãos R$/kg | |||||
| b. Variável dependente: preço frango R$/kg
Fonte: dados da pesquisa. |
|||||
No quadro 3, podemos inferir que o F analisado corresponde a 278,925, que é significativo ao nível de P < 0,001. Logo, existe uma probabilidade menor do que 0,1% de que um valor F tão alto tenha ocorrido apenas por acaso (FIELD, 2009).
Quadro 3. ANOVA: preditores e variável dependente.
| ANOVA | ||||||
| Modelo | Soma dos Quadrados | df | Quadrado Médio | F | Sig. | |
| 1 | Regressão | 28,217 | 1 | 28,217 | 278,925 | ,000b |
| Resíduo | 11,937 | 118 | ,101 | |||
| Total | 40,154 | 119 | ||||
| a. Variável dependente: preço frango R$/kg | ||||||
| b. Preditores: (Constante), preço soja em grãos R$/kg
Fonte: dados da pesquisa. |
||||||
No quadro 4, observa-se os coeficientes que compõem a reta da regressão, sendo estes encontrados na coluna B onde b0= 1,115 ≈ 1,12 e b1= 0,35 ≈ 0,4, no qual b0 é o intercepto da reta e b1 é o gradiente de inclinação da linha de regressão. O modelo de regressão simples estimado pelo programa inferiu a seguinte equação:
y = 1,12 + 0,4x
Onde:
y = Preço da carne de frango;
x = Preço da soja em grão.
Logo:
Preço da carne de frango = 1,12 + 0,4. Preço da soja em grão
Esse modelo explica que quando a soja em grão estiver em falta no mercado, isto é, (quando x = 0), o preço da carne de frango será 1,12, então, podemos inferir que a mudança da variável preço da soja em grão influencia no previsor preço de carne de frango. Sendo assim, podemos afirmar que H1:p ≠ 0, onde p < 0,001, ou seja, existe significância entre o preço da soja em grão e o preço da carne de frango e que a variável preço da soja em grão tem contribuição significativa para prever os valores do preço da carne de frango.
Quadro 4. Coeficiente: variável dependente preço frango.
| Coeficientes | ||||||
| Modelo | Coeficientes não padronizados | Coeficientes padronizados | t | Sig. | ||
| B | Erro Padrão | Beta | ||||
| 1 | (Constante) | 1,115 | ,124 | 8,996 | ,000 | |
| Preço Soja em grãos R$/kg | ,035 | ,002 | ,838 | 16,701 | ,000 | |
Fonte: dados da pesquisa. |
||||||
5. CONSIDERAÇÕES FINAIS
Nesta análise, concluímos que existe correlação entre as duas variáveis, preço de soja em grão e preço da carne de frango. Sendo assim, rejeitou-se a hipótese nula de que não existe correlação linear entre as variáveis e aceitou-se a hipótese alternativa que existe correlação linear entre o preço da soja em grão e o preço da carne de frango. A hipótese alternativa apresentou uma correlação linear forte ao nível de 0,838 para o preço carne de frango/preço da soja em grão, o que significa uma correlação de 83,8% entre as variáveis, e para um r² = 0,703. O aumento do preço da carne de frango pode ser explicado em 70, 3% pelo aumento do preço da soja em grão. Nesse sentido, o preço da soja em grão tem forte influência na formação do preço da carne de frango, porém para se estabelecer liderança no mercado precisa-se levar em consideração que 29,7% desta variação no preço da carne de frango estão correlacionados com outras especificações agropecuárias.
O software IBM SPSS tem fundamental importância para análises estatísticas e consistências de fundamentação teórica da pesquisa, podendo ser utilizado para tratamento de dados e identificação de problemas de negócios agropecuários, onde existem variáveis correlacionadas.
REFERÊNCIAS
AGROLINK, (Portal). Exportações fecham semestre com recuo. Disponível em: <https://www.agrolink.com.br/noticias/exportacoes-fecham-semestre-com recuo_395366.html>. Acesso em: 13. Jan. 2018.
AGUIAIS, Edilson Gonçalves; FIGUEIREDO, Reginaldo Santana. Correlação entre consumo de carne de frango e renda no Brasil (2002-2009). Qualia: a ciência em movimento, v. 1, n. 1, p. 64-77, 2015.
AVEWORLD. Carne bovina e de frango ajudam no superávit da balança em junho. Disponível em: <http://www.aveworld.com.br/noticia/carne-bovina-e-de-frango-ajudam-no-superavit-da-balanca-em-junho/>. Acesso em: 17 Jul. 2017.
BRASIL. Ministério da Agricultura Pecuária e Abastecimento – MAPA. Soja lidera exportações do agronegócio brasileiro em abril. Disponível em: <http://www.agricultura.gov.br/noticias/soja-lidera-exportacoes-do-agronegocio-brasileiro-em-abril>. Acesso em: 15. Jul. 2017.
COHEN, Jacob. Statistical power analysis for the behavioral sciences. Hillsdale, NJ, Erlbaum, 1988.
CONAB. Companhia Nacional de Abastecimento. Análise Mensal. Soja abril de 2018. Disponível em: <file:///C:/Users/pc/Downloads/SojaZ-ZAnliseZMensalZ-ZAbril-2018.pdf>. Acesso em: 17 set. 2018.
CONTE, Luciane; FERREIRA FILHO, Joaquim Bento Souza. Substituição de fatores produtivos na produção de soja no Brasil. Revista de Economia e Sociologia Rural, Rio de Janeiro. v. 45, n. 2, p. 475-495, abr./jun. 2007.
CONTINI, Elísio; TALAMINI, Dirceu João Duarte; VIEIRA JUNIOR, Pedro Abel. Cenário mundial de commodities: frango, soja e milho. Disponível em: < https://ainfo.cnptia.embrapa.br/digital/bitstream/item/91011/1/final7198.pdf>. Acesso em: 20 de Out. 2018.
DANCEY, Christine; REIDY, John. Estatística sem matemática para psicologia: Usando SPSS para Windows. Porto Alegre, Artmed, 2006. 608p.
DEPEC – Departamento de Pesquisas e Estudos Econômicos. Junho de 2017. Carne Avícola. Disponível em: <https://www.economiaemdia.com.br/EconomiaEmDia/pdf/infset_carne_avicola.pdf>. Acesso em: 17 de Out. 2018.
______________. Junho de 2017. Soja. Disponível em: <https://www.economiaemdia.com.br/EconomiaEmDia/pdf/infset_soja.pdf>. Acesso em: 17 de Out. 2018.
FAO. Food and Agriculture Organization of the United Nations. Disponível em: <http://www.fao.org/faostat/en/#data>. Acesso em: 05 de Nov. 2018.
FIELD, Andy. Descobrindo a estatística usando o SPSS / Andy Field; tradução Lorí Viali. – 2. ed. – Porto Alegre, Artmed, 2009. 688p.
PASETO, Luísa; BARROS, Juliana Souza Granja; ALCÂNTARA, Milla Reis; PATINO, Marco Túlio Ospina. Cadeia produtiva de carne de frango: uma análise dos custos de produção do produtor e da agroindústria. In: Convibra 2015. Business Conference. Disponível em: <http://www.convibra.com.br/upload/paper/2015/30/2015_30_11656.pdf>. Acessado em: Acesso em: 22. Set. 2018.
ROESSING, Antônio Carlos; LAZZAROTTO, Joelsio José. Criação de empregos pelo complexo agroindustrial da soja. Londrina: Embrapa Soja, 2004. 50p. (Embrapa Soja. Documentos, 233). Disponível em: <https://www.infoteca.cnptia.embrapa.br/bitstream/doc/467980/1/documento233.pdf>. Acesso em: 09. Set. 2018.
SILVA, Ariana Cericatto; LIMA, Érica Priscilla Carvalho; BATISTA, Henrique Rogê. A importância da soja para o agronegócio brasileiro: uma análise sob o enfoque da produção, emprego e exportação. In: V Encontro de Economia Catarinense, 2011. Disponível em: <http://www.apec.unesc.net/V_EEC/sessoes_tematicas/Economia%20rural%20e%20agricultura%20familiar/A%20IMPORT%C3%82NCIA%20DA%20SOJA%20PARA%20O%20AGRONEG%C3%93CIO%20BRASILEIRO.pdf>. Acesso em: 09. Set. 2018.
TRIOLA, Mário F. Introdução à Estatística. 10 ed. Rio de Janeiro: LTC, 2008.
VIEIRA, Norberto Martins; DIAS, Roberto Serpa. Uma abordagem sistêmica da avicultura de corte na economia brasileira. Disponível em: <http://www.sober.org.br/palestra/2/394.pdf>. Acesso em: 13. Set. 2018.
VOILA, Márcia; TRICHES, Divanildo. A cadeia de carne de frango: uma análise dos mercados brasileiro e mundial de 2002 a 2012. Teoria e Evidência Econômica. – ano 21, n. 44, p. 126-148, jan./jun. 2015.
[1] Engenheira Agrônoma, Mestranda do Programa de Pós-graduação em Agronegócio da Universidade Federal de Goiás – UFG.
[2] Administrador, Doutorando do Programa de Pós-graduação em Agronegócio da Universidade Federal de Goiás – UFG.
[3] Administrador, Mestrando do Programa de Pós-graduação em Agronegócio da Universidade Federal de Goiás – UFG.
[4] Engenheiro Agrônomo, Mestrando do Programa de Pós-graduação em Agronegócio da Universidade Federal de Goiás – UFG.
[5] Pós-doutorado em Engenharia Industrial na Texas A&M University e Professor Adjunto do Programa de Mestrado e Doutorado em Agronegócios da Universidade Federal de Goiás – UFG.
Enviado: Novembro, 2018
Aprovado: Dezembro, 2018