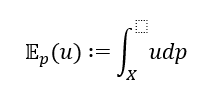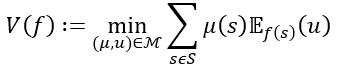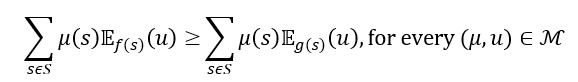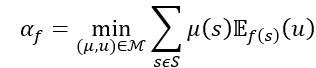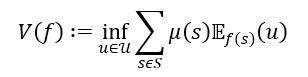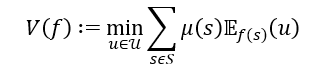Maxmin with multiple tastes and beliefs

ORIGINAL ARTICLE

LÉO, Bruno Beltrão ^[1]

LÉO, Bruno Beltrão. Maxmin with multiple tastes and beliefs. Revista Científica Multidisciplinar Núcleo do Conhecimento. Year 05, Ed. 11, Vol. 11, pp. 67-78. November 2020. ISSN:2448-0959, Access link in: https://www.nucleodoconhecimento.com.br/social-sciences/tastes-and-beliefs, DOI: 10.32749/nucleodoconhecimento.com.br/social-sciences/maxmin

ABSTRACT

This paper presents the main results of my doctoral thesis written in 2016 as part of the requirements to obtain the Doctor degree in the Doctoral Program in Economics at the University of Brasilia (UnB). It regards the axiomatization of a model of complete preferences under uncertainty that allows for a multiplicity of tastes and beliefs. As in Gilboa and Schmeidler (1989), the analysis is made in an Anscombe-Aumann setup and each act is evaluated by the worst-case scenario. The difference is that while in Gilboa and Schmeidler (1989) the multiple scenarios are composed of a set of priors, here they are composed of a set of probability-utility pairs. Thus, after imposing some postulates on preferences, we come to our main result, described in the form of a representation theorem (Theorem 1). A special case in which the multiple scenarios are a consequence of the multiplicity of tastes only is also axiomatized (Theorem 2).

Keywords: complete preferences, multiple tastes, multiple beliefs.

1. INTRODUCTION

In decision theory, at least in the last decades, we find a variety of papers that seek to model ambiguity aversion and demonstrate that such aversion is incompatible with most standard expected utility theory axioms. The literature generally assumes that ambiguity may arise from a multiplicity of beliefs, a multiplicity of tastes (utilities), or from both. Multiplicity of beliefs often is related to a lack of fully specified probabilities based on some scientific evidence. Multiplicity of tastes, or utilities, has to do with some sort of difficulty in comparing possible outcomes for oneself. That is, when facing a choice between alternatives that are not entirely understood or not promptly comparable, decision makers often find it difficult to express their preferences in a coherent manner. Von Neumann and Morgenstern (1947) already recognized this long ago. In this context, the completeness axiom turns out to be quite questionable and the literature on models of incomplete preferences under uncertainty that allow for the multiplicity of tastes and beliefs has become very intense these recent years.

For instance, in line with models of incomplete preferences we find the works of García del Amo and Ríos Insua (2002), Nau (2006), Seidenfeld, Schervish, and Kadane (1995), Ok, Ortoleva, and Riella (2012), Galaabaatar and Karni (2013), and Riella (2015). In particular, Nau (2006), Galaabaatar and Karni (2013), and Riella (2015) provide axiomatizations for Multi-prior Expected Multi-utility models under uncertainty. Ok et al. (2012), Galaabaatar and Karni (2013), and Riella (2015) also present axiomatizations for versions of the Single-prior Expected Multi-utility model. When preferences are complete, however, we find the works of Gilboa and Schmeidler (1989), Maccheroni (2002), Maccheroni, Marinacci, and Rustichini (2006), and Cerreia-Vioglio, Maccheroni, Marinacci, and Montrucchio (2011) as the most relevant ones.

As this work presents an axiomatization of a model of complete preferences under uncertainty in a broader scope, but similar to the one presented in Gilboa and Schmeidler (1989) (henceforth GS), let us briefly describe below the fundamental aspects of the GS model.

Gilboa and Schmeidler (1989) assumes that the decision maker is uncertainty averse and states several standard properties (axioms) of the preference relation. However, the usual independence axiom is replaced by a weaker and more appealing version of Independence that applies only when two generic acts are both mixed with the same constant act – the so-called certainty-independence (C-Independence) axiom. Given the experimental evidence, such as Ellsberg (1961), this new axiom is in fact more acceptable: “a decision maker who prefers (an act)  to (an act)  can more easily visualize the mixtures of    and  with a constant act  than with an arbitrary one, hence he is less likely to reverse his preferences” (GILBOA and SCHMEIDLER, 1989). Accordingly, by using the framework of Anscombe and Aumann (1963), Gilboa and Schmeidler (1989) provide an axiomatic foundation for the maxmin expected utility decision rule by characterizing preference relations over acts that have a numerical representation by a functional in a multi-prior expected single-utility model.

Maccheroni (2002) also axiomatizes a version of the GS model, in a world where there is only objective risk. In Maccheroni (2002)’s model, the decision maker is allowed to have multiple tastes (utilities) but a single belief (prior).

Although similar, our idea is more general than the GS model for in our case the decision maker not only is allowed to have a multiplicity of beliefs but also to have a multiplicity of tastes. In addition, we shall generalize Maccheroni (2002)’s model to the world of Anscombe-Aumann acts and thus obtain a Single-prior Expected Multi-utility model.

For that purpose, we will define an incomplete “induced” preorder and show that it satisfies a set of axioms that imply it will have a representation according to Riella (2015)’s main theorem. We then propose a modified version of Certainty Independence, as introduced by Dillenberger (2010), and show that this will lead us to the main result of the paper, which is a version of the Maxmin model of GS with multiple tastes and beliefs.

This paper is organized as follows.

Section 2 presents the framework, which coincides with the overall framework in Riella (2015). Just like Riella (2015), we impose the restriction that the prize space be a finite set. At the end of that section, we present our main result – a Multi-prior Expected Multi-utility representation theorem, for the case of complete preferences.

Section 3 presents a new postulate (the Extreme Objective and Subjective Bets Independence axiom) to the representation described in the main result (Theorem 1) in order to obtain a representation in which the agent has a single prior and multiple utilities. It turns out that in this case it is possible to work with a more general framework in which the prize space is a compact metric space (not necessarily finite).

Final Considerations section is devoted to describe the related literature and to present some conclusions. Additional results and complete proofs of the theorems presented in this paper can be found in Leo (2016) – the full version of the doctoral thesis, available in Portuguese only.

2. MAXMIN PREFERENCES WITH MULTIPLE PRIORS AND UTILITIES

2.1 FRAMEWORK

We will work in the setup of Anscombe and Aumann (1963) as it was reformulated by Fishburn (1970). Let X  be a compact metric prize space in general, but sometimes we will impose the restriction that X be a finite set. We will denote the elements of X by x, y, z, etc. We will write Δ(X) to represent the space of Borel probability measures on X.  We metrize Δ(X) in such a way that metric convergence coincides with weak convergence of Borel probability measures. The elements of Δ(X) are called lotteries and denoted by p, q, r, etc. The degenerate lottery that pays prize x ∈ X with probability one is denoted by denotes the linear space of all continuous real maps on X. The metric considered for C(X) is the supnorm. The expectation of any function with respect to a probability measure   is denoted by . That is,

Let S be a finite state space. We denote the space of probability measures on S by Δ(S). An act is a function that maps the state space S into the space Δ(X) of lotteries. We denote the space of all acts by . That is, . We metrize by the product metric and denote the elements of by f, g, h, etc. We follow the usual abuse of notation and write simply p to represent the constant act that returns the lottery p in every state of nature. Given that, we often write f(s) to represent the constant act that returns the lottery f(s) in every state of nature. For any subset T of S, and any two acts f and g, we write fTg to represent the act h such that h(s) = f(s) for every s ∈ T and h(s) = g(s) for every s ∈ S/T. Our primitive is a complete preorder (i.e., a reflexive and transitive binary relation) . As usual, the asymmetric part of this preorder is denoted by ≻, and its symmetric part by

In this section, we work with the special case of the setup described above in which X is a finite set. We will impose the following postulates on ≿.

Axiom 1 (Continuity). ≿ is a closed subset of .

Axiom 2 (Unambiguous Best). If   is such that for every  , then   for every

Axiom 3 (Extremal Elements Independence). If   is such that for  every , or    for every , then, for every f, g ∈  and

Axiom 4 (Uncertainty Aversion). For all , and .

Axiom 5 (One Side Mixture Monotonicity). If f, g and h in , and  are such that  for every , then .

The Continuity axiom is standard. That is, for any convergent sequences (f ^m) and (g^m) in F, with f ^m g^m  for each m, we have . We note that in the results of this paper that make use of a finite prize space X this property can be replaced by the weaker requirement that the sets and  are closed in [0,1], for any f, g  and h in F.

The Unambiguous Best axiom says that if a prize  is better than any other prize, then the act that returns the prize x in every state is unambiguously preferred to any other act, in the sense that even if we mix and an act f with some act g, the individual will still prefer the mixture with .

Extremal Elements Independence imposes that if x is the best or the worst prize, then the independence axiom holds when we mix a pair of acts with . We note that this is a particular case of Gilboa and Schmeidler (1989)’s C-Independence axiom in which the constant act used in that axiom necessarily pays the best or the worst prize with probability one.

The Uncertainty Aversion postulate is standard.

Finally, we have a strong monotonicity property that we label One Side Mixture Monotonicity. This property merges the Mixture Monotonicity axiom of Riella (2015) with the Dominance postulate of Galaabaatar and Karni (2013).

2.2 REPRESENTATION THEOREM

After imposing the restrictions described by the axioms above, we shall state our main result. First, let us consider the following definition.

Definition. Given a nonempty subset  , we say that  is n-bounded if there exist . We say that a nonempty subset is n-bounded if is an n-bounded subset of  . Finally, we say that a subset  is n-bounded if there exist in  with , for every for every .

We can now state the result.

Theorem 1. The following statements are equivalent.

1. There exists an n-bounded nonempty subset  of  such that the function    defined by

  represents ≿;

2. ≿ satisfies Continuity, Unambiguous Best, Extremal Elements Independence, Uncertainty Aversion and One Side Mixture Monotonicity.

Theorem 1 shows that the postulates discussed in this section are necessary and sufficient to characterize the version of Gilboa and Schmeidler (1989)’s multiple priors model in which the individual has multiple tastes and beliefs. A natural special case of Theorem 1 would be the version of the model above in which the individual has multiple tastes, but a single belief. We discuss this special case in Section 3, but first we give some intuition for the proof of Theorem 1 in Subsection 2.3 below.

2.3 PROOF SKETCH OF THEOREM 1

In what follows, we sketch the proof of Theorem 1; a complete proof can be found in Leo (2016). For now, we will focus only on the sufficiency part of the proof.

First, it is necessary to define a binary relation  by  , for every  and every , and show that such a relation satisfies the Continuity axiom. Afterwards, we show that for every  and ,  implies . Since is continuous, we use the same argument as in Lemma 1 of Dubra, Maccheroni, and Ok (2004) to show that it satisfies the Independence Axiom. We then show that for every pair of acts f and g in for every That is,satisfies the One Side Monotonicity postulate of Riella (2015).

The next step is to show that there exist in X such that, for any , and it is not true that Thus, as satisfies all the postulates in part 3 of Theorem 2 in Riella (2015), we know that there exists an n-bounded nonempty subset such that, for every pair of acts and only if,

We then let  be such that  for every  and every  in order to show that for every , there exists a unique  such that  . We then note that, for every pair We complete the proof by showing that, for every ,

3. MAXMIN PREFERENCES WITH A SINGLE-PRIOR AND MULTIPLE UTILITIES

In this section, we axiomatize the version of the representation of Theorem 1 where the agent has a single prior  and a set of utilities . It turns out that we can now work with the more general set up in which  is a compact metric space. The reason for that is inherently technical and is related to the results regarding the representation of incomplete preferences under uncertainty with indecisiveness in tastes and beliefs.

We will impose the following additional postulate on:

Axiom 6 (Extreme Objective and Subjective Bets Independence – EOSBI). Let be such that for every . Fix  and  . Then, for every  and ,

To understand the axiom above, first notice that can be seen as an objective lottery that pays the best prize, , with probability α and pays the worst prize, with probability . Similarly,  can be seen as a subjective lottery that pays if the event T is realized and pays  otherwise. The axiom then states that for comparisons between these two types of lotteries, the independence axiom holds.

3.1 REPRESENTATION THEOREM

We can now enunciate Theorems 2 and 3. For their proofs, please see Leo (2016).

Theorem 2. The following statements are equivalent.

1. There exist a nonempty and n-bounded subset of    and a priorsuch that the function  defined by

is continuous and represents ≿;

2. ≿ satisfies Continuity, Unambiguous Best, Extremal Elements Independence, Uncertainty Aversion, One Side Mixture Monotonicity and Extreme Objective and Subjective Bets Independence.

In addition to the fact that for the representation obtained in Theorem 2 we have a unique prior over the set of states of the world, we note also some other differences between Theorems 1 and 2. As we have mentioned above, Theorem 2 is true even when is an arbitrary compact metric space. However, while in Theorem 1 we can assume, without loss of generality, that the set  is compact, in Theorem 2 we cannot guarantee the same thing for the set , unless is finite. This has two consequences for the statement of Theorem 2. First, in Theorem 2 we cannot guarantee that the minimum utility of an act  is attained, so we have to use  instead of min. Second, without the compactness of the set  the representation alone does not ensure that the preorder ≿ is continuous and, consequently, we have to impose that. These problems do not happen when  is finite.

Formally, we have the following result:

Theorem 3. Suppose  is a finite set. The following statements are equivalent.

1. There exist a nonempty and n-bounded subset  and a prior  such that the function  defined by

represents ≿;

2. ≿ satisfies Continuity, Unambiguous Best, Extremal Elements Independence, Uncertainty Aversion, One Side Mixture Monotonicity and Extreme Objective and Subjective Bets Independence.

It is straightforward that our result reduces to Maccheroni (2002)’s when there is only one state of nature.

FINAL CONSIDERATIONS

The results presented in Leo (2016) are linked to two groups of papers – models associated with incomplete, or with complete preference relations.

When we consider models under uncertainty that allow for incompleteness due to the multiplicity of tastes and beliefs, let us first mention the work of Nau (2006) which presents an axiomatization for a model that works with a preorder as the primitive and relies on a postulate called Strong State-independence. In a few words, Nau’s postulate requires that whenever a weak preference between two arbitrary lotteries is preserved under an objective mixture with two conditional constant lotteries, both conditioned to a non-null common event, then the same preference is preserved under a mixture with the same constant lotteries conditioned on any other common event. It is worth to note that such axiom may be deemed to be a stronger version of Riella (2015)’s Mixture Separability axiom.

From a behavioral perspective and by investigating the classical Anscombe–Aumann model of decision-making under uncertainty with incomplete preferences, Ok et al. (2012) distinguish between the dual traits of “indecisiveness in beliefs” and “indecisiveness in tastes”. They do so by replacing the completeness assumption with the postulate that subjects can reduce subjective uncertainty to objective uncertainty, so as to obtain a single-prior expected multi-utility representation that may be viewed as the “dual” of the Knightian uncertainty model – the so-called multi-prior expected single-utility representation. Ok et al. (2012) characterize axiomatically their single-prior expected multi-utility model and show that, under independence and continuity, the two models can be jointly characterized by means of a partial completeness property.

In line with the work of Nau (2006), Galaabaatar and Karni (2013) extend the subjective expected utility model of decision making under uncertainty to include incompleteness due to multiplicity of tastes and beliefs to provide axiomatizations of the multi-prior expected multi-utility representation by making use of a strict partial order. Galaabaatar and Karni (2013) show that when a property that can be interpreted as a postulate of completeness of beliefs is added to their axiomatization of the multi-prior expected multi-utility representation, one obtains a single-prior expected multi-utility representation.

Additionally, in the scope of models of incomplete preferences, Riella (2015) provides an axiomatization of the multi-prior expected multi-utility representation and, like Nau (2006), uses a preorder as the primitive of the model. Riella (2015) adds three properties to obtain his result: the first is the Mixture Separability postulate, which is a weaker and simpler version of Nau’s Strong State-Independence postulate; the second, which is called One Side Monotonicity, is a natural adaptation of Galaabaatar and Karni (2013)’s Dominance axiom to the case of a preorder; the third one is the Mixture Monotonicity postulate. Moreover, just like Galaabaatar and Karni (2013), Riella (2015) also shows that if a completeness of beliefs axiom is added to his axiomatization of the multi-prior expected multi-utility representation, a single-prior expected multi-utility model is obtained. As an application, Riella (2015) provides a result in the spirit of the main result in Gilboa et al. (2010) for the single-prior expected multi-utility model and generalize the main result in Cerreia-Vioglio, Dillenberger, and Ortoleva (2015) to the case of multiple tastes under uncertainty.

For models of complete preferences, Gilboa and Schmeidler (1989) assumes uncertainty aversion and replaces the usual independence axiom by a weaker and more appealing version of independence that restricts the mixture to constant acts – the so-called certainty-independence (C-Independence) axiom. Thus, by using the framework of Anscombe and Aumann (1963), Gilboa and Schmeidler (1989) propose an axiomatic foundation of the maxmin expected utility decision rule by characterizing preference relations over acts that have a numerical representation by a functional in a multi-prior expected single-utility model. As shown in Section 4 of Leo (2016), it is possible to use Theorem 1 of the present paper to provide a somewhat simpler proof of the GS (1989) result.

In a world where there is only objective risk, Maccheroni (2002) proposes a maxmin multi-utility representation of complete preferences under uncertainty where a decision maker is allowed to have multiple tastes (utilities). Theorem 2 of the present paper is therefore a generalization of Maccheroni’s representation for the world of Anscombe-Aumann acts.

In a model similar to Gilboa and Schmeidler (1989), in the framework of Anscombe and Aumann (1963) for models of complete preferences, Maccheroni et al. (2006) characterize preferences for which there are a single utility function and an ambiguity index on the set of probabilities over the states of the world. Their ambiguity index intends to capture the decision maker ambiguity attitudes. Therefore, uncertainty could be viewed as the outcome of ambiguity, possibly resulting from the poor quality of the information on which agents base the choice of their model.

It is also worth to mention the work of Cerreia-Vioglio et al. (2011) regarding uncertainty averse preferences. They define a preference relation as uncertainty averse if it satisfies three basic axioms: Weak Order (thus, complete and transitive), Monotonicity and Convexity. Their main result is a representation for uncertainty averse preferences and relies on the original axioms of Gilboa and Schmeidler (1989), with the key exception of their independence assumption on uncertain acts, which they replaced by a much weaker axiom (Risk Independence), that applies only to constant acts. Their representation is, at the same time, general and rich in structure, and due to its generality, it is able to unify as special cases many of the choice criteria commonly used to model choices under uncertainty.

The analysis and results obtained in this paper raises a question concerning the axiomatization of the Multi-prior Expected Multi-utility model for the case when the prize space is not finite. The arguments used in the proof of Theorem 2 in Riella (2015) (which was used in the proof of our main result), and also in similar representations of the Multi-prior Expected Multi-utility model that have appeared in a variety of other papers, are valid only in finite dimensional spaces. It is worth to emphasize here that this is not only a technical issue. In many applications, like the ones that have the prize space to be a closed monetary interval (thus continuous and infinite), such a generalization turns out to be quite essential.

REFERENCES

ANSCOMBE, F. J.; AUMANN, R. J. (1963). A definition of subjective probability. Annals of Mathematical Statistics 34(1), 199.205.

BEWLEY, T. F. (2002). Knightian uncertainty theory: part i. Decisions in Economics and Finance 25(2), 79.110.

CERREIA-VIOGLIO, S.; DILLENBERGER, D.; ORTOLEVA, P. (2015). Cautious expected utility and the certainty effect. Econometrica 83(2), 693.728.

CERREIA-VIOGLIO, S.; MACCHERONI, F.; MARINACCI, M.; MONTRUCCHIO, L. (2011). Uncertainty averse preferences. Journal of Economic Theory 146, 1275.1330.

DILLENBERGER, D. (2010). Preferences for one-shot resolution of uncertainty and allais-type behavior. Econometrica 78(6), 1973.2004.

DUBRA, J.; MACCHERONI, F.; OK, E. A. (2004). Expected utility theory without the completeness axiom. Journal of Economic Theory 115, 118.133.

ELLSBERG, D. (1961). Risk, ambiguity, and the savage axioms. Quarterly Journal of Economics 75(4), 643.669.

FISHBURN, P. C. (1970). Utility Theory for Decision Making. New York: Wiley.

GALAABAATAR, T.; KARNI, E. (2013). Subjective expected utility with incomplete preferences. Econometrica 81(1), 255.284.

GARCÍA DEL AMO, A.; RÍOS INSUA, D. (2002). A note on an open problem in the foundation of statistics. Rev. R. Acad. Cien. Serie A. Mat. 96(1), 55.61.

GILBOA, I.; MACCHERONI, F.; MARINACCI, M.; SCHMEIDLER, D. (2010). Objective and subjective rationality in a multiple prior model. Econometrica 78(2), 755.770.

GILBOA, I.; SCHMEIDLER, D. (1989). Maxmim expected utility with non-unique prior. Journal of Mathematical Economics 18(2), 141.153.

LEO, B. B. (2016). Maxmin with Multiple Tastes and Beliefs (doctoral thesis). Available at: https://repositorio.unb.br/bitstream/10482/20734/1/2016_BrunoBeltraoLeo.pdf.

MACCHERONI, F. (2002). Maxmin under risk. Economic Theory 19, 823.831.

MACCHERONI, F.; MARINACCI, M.; RUSTICHINI, A. (2006). Ambiguity aversion, robustness, and the variational representation of preferences. Econometrica 74(6), 1447. 1498.

NAU, R. (2006). The shape of incomplete preferences. Annals of Statistics 34(5), 2430.2448.

OK, E. A.; ORTOLEVA, P.; RIELLA, G. (2012). Incomplete preferences under uncertainty: Indecisiveness in beliefs versus tastes. Econometrica 80(4), 1791.1808.

RIELLA, G. (2015). On the representation of incomplete preferences under uncertainty with indecisiveness in tastes and beliefs. Economic Theory 58(3), 571.600.

SEIDENFELD, T.; SCHERVISH, M. J.; KADANE, J. B. (1995). A representation of partially ordered preferences. Annals of Statistics 23(6), 2168.2217.

^[1] Doctor in Economics (Universidade de Brasília – UnB), Master in Economics (Universidade de Brasília – UnB), MBA in Finance and Capital Markets (Fundação Getúlio Vargas – FGV), Bachelor degree in Electrical Engineering (Universidade Federal de Pernambuco – UFPE).

Submitted: October, 2020.

Approved: November, 2020.