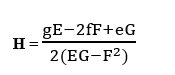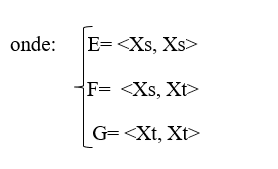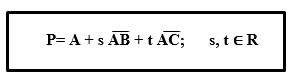ARTIGO ORIGINAL
COUTO, Louise de França e Silva [1]
COUTO, Louise de França e Silva. O plano euclidiano como superfície mínima. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano 03, Ed. 10, Vol. 09, pp. 28-36 Outubro de 2018. ISSN:2448-0959
RESUMO
No presente artigo são apresentados alguns conceitos sobre superfícies mínimas, e mais especificamente no plano euclidiano, fazemos um breve comentário histórico com as descobertas e a evolução deste conhecimento do campo da matemática, a Geometria Diferencial. Os resultados destas superfícies encantam os matemáticos e até os não matemáticos, por terem uma fácil visualização, e é uma teoria muito rica. A terminologia superfície mínima foi introduzida por Lagrange 1760. As superfícies mínimas são normalmente associadas com películas de sabão, que vamos explicar mais claramente no decorrer do artigo. Alguns exemplos de superfícies mínimas são: plano euclidiano, helicóide, catenóide e superfície de costa. Este artigo tem por objetivo não só mostrar o que são superfícies mínimas, mas também discorrer sobre uma em específico: o plano.
Palavra-chave: Superfícies mínimas, Geometria Diferencial, Plano Euclidiano.
INTRODUÇÃO
“A teoria da Superfície Mínima é conhecida como Problema de Plateau. E historicamente, esse assunto começa com Lagrange no século XVIII, que em sua famosa autobiografia, ele apresenta um algoritmo para o cálculo variacional. Em 1740, Euler através da rotação da catenária, obteve uma superfície mínima e deu o nome de “allyside” que mais tarde foi renomeado por catenóide por Plateau.” (Rodrigo Ristow, professor da UFPR).
O estudo da superfície de área mínima com borda específica e constante é um problema de cálculo variacional, segundo o professor Paulo Sérgio, visto dentro da geometria diferencial, e esta é uma linha de estudo que desperta grande interesse aos matemáticos, visto que é uma teoria abrangente com conexões profundas com funções analíticas de variáveis complexas e equações diferenciais parciais.
O questionamento conhecido como “problema de Plateau”, que deu origem às demais análises a respeito deste assunto, de forma simples e primitiva é: “Provar que para cada curva fechada C (contido) R³, existirá uma superfície M de área mínima, tendo C como limite”. Este questionamento ainda foi resolvido simultaneamente por outros pesquisadores, e versões posteriores e generalizações deste problema para dimensões mais altas inspiraram a criação de grandes matemáticos.
“Superfície Mínima é um dos principais tópicos da Geometria Diferencial, que desperta um interesse muito grande entre os matemáticos. Os resultados destas superfícies encantam por terem fácil visualização, e é uma teoria muito rica. Tem conexões profundas com funções analíticas de variáveis complexas e equações diferenciais parciais” segundo Esdriane Cabral Viana em sua dissertação de mestrado. A terminologia superfície mínima foi introduzida por Lagrange 1760. As superfícies mínimas são normalmente associadas com películas de sabão. Podem ser mostradas, por considerações físicas, que a película assume uma posição onde em seus pontos regulares a curvatura média é nula. E alguns exemplos de superfícies mínimas são: plano euclidiano, helicóide, catenóide e superfície de costa.
Este artigo tem por objetivo não só mostrar o que são superfícies mínimas, mas também discorrer sobre uma em específico: o plano euclidiano.
DESENVOLVIMENTO
O estudo da superfície de área mínima com borda específica e constante é um problema de cálculo variacional, visto dentro da geometria diferencial. Mas o que seria uma superfície mínima?
Por definição, superfície mínima é aquela à qual sua curvatura média é nula. Partindo deste princípio iremos focar nossas atenções no plano, que é um exemplo de superfície mínima, e demostrar a veracidade desta afirmação.
Como vimos o ponto chave para determinamos que o plano é uma superfície mínima, é calcular sua curvatura média, sendo assim veremos abaixo a definição deste conceito e como devemos proceder no cálculo desta curvatura.
Definição 1: Curvatura média de uma superfície, que iremos chamar de H, parametrizada* por X(u,v) é a semi-soma de K1 e K2, sendo estas as curvaturas principais da superfície, e é dada por:
Na definição 1 observamos a utilização do termo parametrizada, o que nos leva a outra discussão, o conceito de parametrização, e com relação ao plano, qual sua equação paramétrica. E só então, estabelecidos estes pré-requisitos poderemos calcular sua curvatura média.
Ao compararmos a reta com o plano, observamos a diferença entre unidimensional e bidimensional, pois na equação paramétrica da reta há a necessidade da variação de um parâmetro (t ∈ R) enquanto que no plano há a variação de dois parâmetros, (s, t ∈ R).
Como já vimos, a equação paramétrica do plano é bidimensional, então, dados A, B e C não-colineares contidos no plano π, temos:
De maneira análoga, porém agora em coordenadas temos:
Dados: A (a, b, c), B(a’, b’, c’) e C (a”, b”, c”)
→ →
1º passo: determinar os vetores A, AB e AC;
A = (a, b, c) AB = (a’ − a, b’ − b, c’ − c) AC = (a” − a, b” − b, c” − c)
2º passo: substituir na equação paramétrica do plano π, Tal que P = (x,y,z);
(x,y,z) = (a, b, c) + s(a’ − a, b’ − b, c’ − c) + t(a” − a, b” − b, c” − c)
s, t ∈ R
- O que nos dá a equação paramétrica do plano π:
X= a + s(a’ − a) + t(a” – a)
Y = b + s(b’ − b) + t(b” − b)
Z = c + s(c’ – c) + t(c” − c)
Agora para mostrarmos que a curvatura média dessa equação é igual a zero, vamos provar segundo o artigo de Lindeval Fernandes de Lima, como segue:
FÓRMULA DA PRIMEIRA VARIAÇÃO DA ÁREA
Teorema 1.3 (Primeira Variação da Área): Sejam M ⊂ R3 uma superfície, D ⊂ R2 um aberto, x : D ⊂ R2 → M uma parametrização de M e X : D × I → R3 uma variação normal de x, ou seja, X(p, t) = x(p) + tf(p)N(p), onde p = (u, v) ∈ D e f : D → R é diferenciável. Seja A(t) a área de Xt(D). Então ,
Definição 1.4. Dada uma superfície M, dizemos que M é mínima se, e somente se, a sua curvatura média H(p) é zero para todo ponto p ∈ M.
A palavra “mínima”, neste caso, está relacionada com o seguinte problema proposto por Lagrange em 1760: dada uma curva Γ fechada e simples, achar a superfície de área mínima que tem Γ como fronteira.
Suponha que exista uma solução M para o problema e considere a variação normal Ft de M, t ∈ (−ε, ε) dada por uma função f : M → R tal que f |Γ ≡ 0, ou seja, a variação fixa a fronteira. Como a área de M é mínima, temos então
que A(t) ≥ A(0), para todo t ∈ (−ε, ε) e para toda variação Ft. Sendo assim, A’(0) = 0, para qualquer f : M → R tal que f |Γ ≡ 0.
Pela fórmula da primeira variação da área,, a condição A’(0) = 0, para toda f, equivale ao fato que H = 0 em M. De fato, se H = 0, então A’(0) = 0 para toda f. Para mostrarmos que a recíproca é verdadeira, suponhamos que A’(0) = 0 para toda f, e que existe um certo p ∈ M tal que H(p) > 0. Escolhamos f tal que f(p) = H(p), f ≥ 0, e que f = 0 fora de um pequeno domínio D ⊂ M em torno de p. Para tal f temos A’(0) = −<0, contradizendo o fato de ser A’(0) = 0, o que mostra que H(p) = 0 para todo p ∈ M.
Concluímos que, se existe uma superfície M de área mínima com bordo Γ, então H = 0 em M. Podemos concluir que a curvatura média dessa superfície é igual a zero.
Um dos grandes contribuidores para o estudo de superfícies mínimas, Joseph Antoine Ferdinand PLATEAU (1801- 1883), estudou na Universidade de Liège, onde doutorou-se em física e matemática em 1829. Em 1835 foi professor de física experimental na Universidade de Gante. Plateau também estudou o fenômeno da capilaridade e tensão superficial (Statique expérimentale et théorique des liquides soumis aux seules forces moléculaires, 1873). O problema matemático da existência de uma superfície mínima com um dado contorno é denominado problema de Plateau. (A Superfície Mínima é, em Matemática, uma superfície em que fixados todos os pontos do bordo, quaisquer dois pontos são ligados por infinitas curvas, sendo que uma delas é uma catenária. O conceito matemático está intimamente ligado com as tensões físicas como as presentes na bolha de sabão.) O físico conduziu estudos extensivos de bolhas de sabão e formulou as leis de Plateau, que descrevem as estruturas formadas por tais bolhas de espuma. As bolhas têm forma poliédrica e são separadas pelos filmes finos de líquido (faces); as faces dos poliedros são superfícies curvas que se intersectam em linhas (designadas junções de PLATEAU1); estas junções intersectam-se em vértices, segundo o artigo: A Espuma como modelo para o Design Audiovisual. (Ver figura 1).
Figura 1
As superfícies mínimas também podem ser caracterizadas como superfícies de área mínima para uma dada borda fixa. Observe que uma esfera é uma “superfície mínima” no sentido de reduzir a área da superfície em relação ao volume, o que não a qualifica como uma superfície mínima no sentido usado pelos matemáticos. É interessante ressaltar que através das bolhas de sabão é possível obter visualizações de algumas superfícies mínimas, uma vez que sua obtenção analítica é extremamente difícil envolvendo a resolução de uma EDP não-linear. As bolhas de sabão, que se dão pela mistura de água com sabão e a argola, usada para soltar as bolhas no ar, ainda pode ser usada para explicar o que são superfícies mínimas. A película que se forma na argola antes que ela seja movimentada no ar é a primeira das superfícies mínimas: o plano. A segunda (catenóide) é obtida quando assopramos a argola e a película forma um bojo, antes de chegar a se fechar em bola. Devemos imaginar que a borda inicial formada pela argola seja mantida, ou seja, a superfície é limitada pelas duas bordas e vazada. A terceira (helicóide) é obtida se deformarmos a argola em forma de hélice. As formas que a película vai adquirir no espaço são as superfícies mínimas, ou as superfícies de menor área que cobre um determinado bordo (nesse caso, a argola). E ainda temos a mais nova superfície, descoberta por Celso Costa (1985), Superfície Costa, que tem a forma de um toro – como as bóias do tipo pneu que os banhistas usam para flutuar nas piscinas – com três buracos.
Superfície Costa (1985)
Em matemática, um plano é um objeto geométrico infinito a duas dimensões. Pode ser definido de várias formas equivalentes.
- Dando um ponto do plano e um vetor normal a esse plano;
- Dando um ponto do plano e dois vetores do plano;
- Dando uma reta do plano e um ponto do plano exterior a esta reta;
- Dando duas retas do plano;
- Dando três pontos não colineares.
Dois planos não paralelos no espaço
No Espaço euclidiano, um plano é uma superfície tal que, dada a quaisquer pontos na superfície, a superfície também contém a única linha reta que passa pelos pontos. A estrutura fundamental de dois planos sempre será a mesma. Na matemática isto pode ser determinado como “homomorfismo”. Informalmente, isso ocorre quando dois planos parecem o mesmo. Um plano pode ser unicamente determinado por um destes objetos:
- Três pontos não-colineares (não estão numa mesma reta);
- Uma reta e um ponto fora desta reta;
- Duas retas concorrentes (duas retas que se cruzam num único ponto);
- Duas retas paralelas distintas.
Como as linhas, os planos podem ser paralelos ou concorrentes. Diferentemente das linhas, os planos não podem ser deformes. Linhas traçadas em dois planos paralelos podem ser paralelas ou deformes, mas nunca concorrentes. Planos concorrentes podem ser perpendiculares, ou podem formar outros ângulos.
Três planos paralelos
No espaço euclidiano tridimensional, nós podemos explorar os seguintes fatos que não detêm, em dimensões superiores:
- Dois planos são ou paralelos ou concorrentes;
- Uma linha ou é paralela ou é concorrente num único ponto ou está contida no plano;
- Duas linhas perpendiculares para o mesmo plano devem ser paralelas entre si;
- Dois planos perpendiculares para a mesma linha devem ser paralelos entre si;
- O plano é uma superfície mínima.
CONSIDERAÇÕES FINAIS
No decorrer do artigo nós mostramos alguns exemplos de superfícies mínimas, e sua importância para os matemáticos, também falamos de um em especifico, o plano euclidiano, onde podemos provar que sua curvatura média é zero. Vimos sobre o problema de Plateau que é o problema matemático da existência de uma superfície mínima com um dado contorno. As superfícies mínimas também podem ser caracterizadas como superfícies de área mínima para uma dada borda fixa. Explicamos através das bolhas de sabão o que são superfícies mínimas. Mostramos que as formas que a película vai adquirir no espaço são as superfícies mínimas, ou as superfícies de menor área que cobre um determinado bordo. No espaço euclidiano tridimensional, nós vimos que o plano é uma superfície mínima. Vimos que o plano como superfície mínima tem grande importância não apenas para os matemáticos, mas, também para a física, e demais áreas afins, como já foi dito anteriormente, encanta pela sua fácil visualização.
REFERÊNCIAS
Um pouco sobre superfícies mínimas. Disponível em: <http://fatosmatematicos.blogspot.com.br/2009/09/um-pouco-sobre-superficies-minimas.html>. Acesso em: 02 de jun. 2014.
Superfície mínima. Disponível em: <http://pt.wikipedia.org/wiki/Superfíciemínima>. Acesso em: 02 de jun. 2014.
Plano (geometria). Disponível em: <http://pt.wikipedia.org/wiki/Plano_(geometria)>. Acesso em: 03 de jun. 2014.
CABRAL VIANA, Esdriane. Superfícies Regradas Mínimas no Espaço Euclidiano e no Espaço de Minkowski. Dissertação (Mestrado em Matemática) – Universidade Federal da Bahia, 2005.
REZENDE, Anamaria Amaral; Mazzilli, Clice de Toledo Sanjar. A espuma como modelo para o design audiovisual e suas relações. Tese de Doutorado.
FERNANDES LIMA, Lindeval. Superfícies Mínimas e de Curvatura Média Constante. Dissertação (Mestrado em Matemática) – Universidade Federal da Paraíba, 2003.
[1] Especialista em Ensino de Matemática – FAEL. Licenciada em Matemática – UEPA. Professora de Matemática.
Enviado: Outubro, 2018
Aprovado: Outubro, 2018
