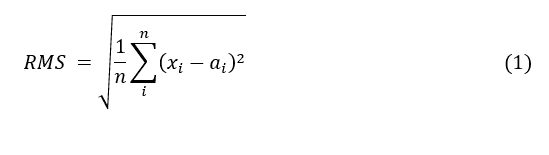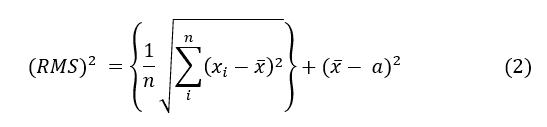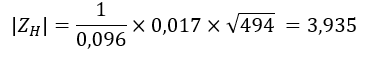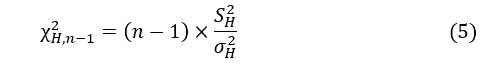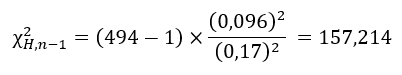ARTIGO ORIGINAL
FERREIRA, Flávia Renata [1], CINTRA, Jorge Pimentel [2]
FERREIRA, Flávia Renata. CINTRA, Jorge Pimentel. A avaliação da acurácia altimétrica dos dados Light Detection And Ranging (LiDAR). Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano 06, Ed. 02, Vol. 10, pp. 14-41. Fevereiro de 2021. ISSN: 2448-0959, Link de acesso: https://www.nucleodoconhecimento.com.br/geografia/acuracia-altimetrica, DOI: 10.32749/nucleodoconhecimento.com.br/geografia/acuracia-altimetrica
RESUMO
O LiDAR (acrônimo de Light Detection And Ranging) tem sido amplamente utilizado como tecnologia complementar de mapeamento. Este trabalho apresenta um breve panorama sobre os padrões de acurácia cartográfica no Brasil e no exterior, e em particular, trata da avaliação altimétrica dos dados obtidos pela tecnologia LiDAR. Foram empregados quatro procedimentos para avaliar a acurácia altimétrica dos dados LiDAR: a) um método baseado na exatidão cartográfica proposta pelo Decreto nº 89.817, que estabeleceu as Instruções Reguladoras das Normas Técnicas da Cartografia Brasileira, b) um método baseado na metodologia do Programa Nacional de Elevação Digital dos Estados Unidos (NDEP), c) um método proposto para quantificar a discrepância altimétrica das curvas de nível produzidas pela tecnologia LiDAR, e d) um método proposto para avaliar a discrepância altimétrica de todos os pontos LiDAR compreendidos entre curvas de nível consecutivas. O primeiro e o quarto métodos se adaptam melhor para uma avaliação geral de todos os dados da área, o segundo se aplica para uma avaliação de áreas cuja cobertura ou tipo de uso do solo são variados, e o terceiro método avalia as diferenças entre as curvas de nível produzidas a partir de dados LiDAR comparadas a um produto de referência. Com as conclusões e indicações deste trabalho, junto com uma avaliação numérica do resultado das aplicações, o usuário pode escolher os testes que pode ou deve empregar em seu caso concreto.
Palavras-Chave: Acurácia, Altimetria, Cartografia, Mapeamento, LiDAR.
INTRODUÇÃO
O princípio do funcionamento do LiDAR baseia-se na medição de distâncias por meio da obtenção da diferença de tempo entre a emissão de um pulso laser em direção a uma superfície e a detecção do sinal refletido (RENSLOW, 2012).
Este sensor remoto ativo, que pode ser empregado a partir de plataformas aéreas e terrestres, tem sido amplamente utilizado como tecnologia complementar em mapeamentos.
Cada pulso refletido passa a fazer parte de um conjunto de pontos com coordenadas planialtimétricas referenciadas a um Sistema Geodésico de Referência, graças à utilização do Sistema de Posicionamento Global por Satélites (GNSS) e do Sistema de Navegação Inercial (INS) durante a varredura.
Com as informações das coordenadas de cada ponto LiDAR, tornou-se possível avaliar a acurácia altimétrica de forma direta ou por interpolação, comparando a componente altimétrica de cada ponto com outro produto de referência para a mesma área.
As normas existentes para realizar a acurácia altimétrica preveem a comparação de coordenadas em certo número de pontos, usualmente 20 por produto cartográfico (MERCHANT, 1982), o que pode parecer insuficiente em muitos casos pois os levantamentos LiDAR trabalham com nuvens de milhões de pontos. Também por isso, torna-se necessário realizar procedimentos automatizados para o tratamento dessa grande quantidade de dados.
Como a avaliação da acurácia altimétrica dos dados LiDAR é um tema bastante relevante e ainda pouco explorado, justifica-se o presente trabalho, fruto de pesquisas e aplicações práticas.
1. CONTEXTUALIZAÇÃO SOBRE OS PADRÕES DE ACURÁCIA CARTOGRÁFICA
O termo acurácia é frequentemente confundido com o significado de precisão. A precisão é uma medida de dispersão de um conjunto de valores em torno de um determinado valor desse conjunto, denominado média. A precisão pode ser considerada como uma medida de consistência ou diferença entre medidas repetidas, embora possa ser sistematicamente incorreta. A medida usual da precisão é o desvio padrão ou o erro padrão (MONICO et al., 2009).
Já a acurácia é uma medida de tendência em torno do valor padrão ou de referência. Um sistema preciso como, por exemplo, o GNSS pode sistematicamente produzir medições tendenciosas devido à correção troposférica e ao uso de estações de base que não sejam de referência (MONICO et al., 2009).
As normas relativas à qualidade de dados geoespaciais necessitam de atualizações requeridas pelos avanços recentes nas ciências da geoinformação (ROBINSON et al., 1995; GARCIA-BALBOA, 2011; XAVIER et al., 2015).
Nero e Cintra (2005) realizaram um estudo comparativo sobre padrões de controle de qualidade em mais de 60 países e instituições que mostrou que todos eles consideram o mapeamento como um conjunto de cartas e, mais particularmente, os métodos focam no controle de uma carta e assim, o controle de qualidade de um mapeamento representa ou significa o controle de qualidade de uma ou mais cartas. Mas, no meio digital, vale a pena considerar o mapeamento como um todo, coisa que se procura fazer no presente trabalho.
1.1 EVOLUÇÃO DAS NORMAS RELACIONADAS À ACURÁCIA CARTOGRÁFICA
Em 2004, o National Digital Elevation Program (NDEP) publicou a diretriz Guidelines for Digital Elevation Data (NDEP, 2004), e a American Society for Photogrammetry and Remote Sensing (ASPRS) publicou a diretriz ASPRS Vertical Accuracy Reporting for LiDAR Data (ASPRS, 2004). Ambas não definiram valores específicos de acurácia, mas forneceriam métodos alternativos para realizar testes de acurácia dos dados LiDAR, onde os erros não seguem, necessariamente, uma distribuição normal de erro, como é comum para o caso do terreno com vegetação.
Em 2009, a National Oceanic and Atmospheric Administration (NOAA, 2009) publicou uma diretriz para o uso do LiDAR no mapeamento costeiro e na definição de limites territoriais marinhos dos Estados Unidos.
Em 2010, o US Geological Survey (USGS) publicou o documento LiDAR Guidelines and Base Specifications V.13, adotado pelo Memorando de Procedimentos Nº 61 da Federal Emergency Management Agency (FEMA), Standards for LiDAR and Other High Quality Digital Topography (FEMA, 2010). Mas, a FEMA também estabeleceu múltiplos valores de acurácia altimétrica com valores mais exigentes do que os valores estabelecidos pelo USGS para o mapeamento como um todo.
Em 2014, a ASPRS publicou o documento Positional Accuracy Standards for Digital Geospatial Data (ASPRS, 2014) que forneceu valores de acurácia horizontal e altimétrica para ortofotos digitais, mapeamento fotogramétrico e LiDAR, incluindo novos padrões LiDAR para a acurácia altimétrica de área sem vegetação (Non-vegetated Vertical Accuracy – NVA) e a acurácia altimétrica de área com vegetação (Vegetated Vertical Accuracy -VVA). Este documento substituiu o ASPRS Accuracy Standards for Large-Scale Maps (ASPRS, 1990) que se tornou obsoleto por se referir apenas a mapas com escala fixa.
Em 2015, o U.S. Army Corps of Engineers (USACE) publicou um manual que fornece diretrizes, novos padrões de acurácia, especificações técnicas e critérios de controle de qualidade para a execução de mapeamentos aerofotogramétricos e de LiDAR.
Em 2017, o Canada Centre for Mapping and Earth Observation (CCMEO) publicou um documento intitulado Federal Airborne LiDAR Data Acquisition Guideline. Este documento fornece especificações técnicas que têm a finalidade de garantir boa consistência na aquisição dos dados LiDAR, tanto para os levantamentos realizados no Canadá como os realizados em regiões fronteiriças aos Estados Unidos.
Lohani et al. (2018) fizeram uma revisão dos padrões existentes para dados LiDAR e elaboraram um catálogo dos requisitos técnicos necessários num projeto, incluindo aquisição dos dados, parâmetros de controle de qualidade, processamento e formato de entrega dos dados.
No Brasil, as diretrizes e bases das atividades cartográficas foram estabelecidas pelo Decreto-Lei nº 243, de 28 de fevereiro de 1967 (BRASIL, 1967).
Em 1984, foi instituído o Decreto nº 89.817 que estabeleceu as Instruções Reguladoras das Normas Técnicas da Cartografia Brasileira. O Artigo 8º deste Decreto especificou que o Padrão de Exatidão Cartográfica (PEC) seria um indicador estatístico de dispersão, relativo a 90% de probabilidade, que definiria a exatidão dos trabalhos cartográficos (BRASIL, 1984).
Em decorrência dos métodos e tecnologias disponíveis àquela época, esse Decreto previa um número mínimo de vinte pontos de verificação necessários à comprovação da acurácia dos documentos cartográficos.
Em 2008, foi instituída a Infraestrutura Nacional de Dados Espaciais (INDE) pelo Decreto nº 6.666, de 27 de novembro de 2008 (BRASIL, 2008).
O surgimento de novas geotecnologias contribuiu para que fosse realizada uma revisão dos padrões determinados pelo Decreto nº 89.817 resultando no desenvolvimento de uma nova especificação denominada Especificação Técnica para Aquisição de Dados Geoespaciais Vetoriais (ET-ADGV), publicada no ano de 2010 (CONCAR/DSG, 2011).
A ET-ADGV, então, estabeleceu um novo Padrão de Exatidão Cartográfica a ser aplicado aos Produtos Cartográficos Digitais (PEC-PCD).
O enquadramento das classes no PEC-PCD, como no Decreto de 1984, baseia-se nas estatísticas de 90% dos pontos coletados no produto cartográfico em relação às coordenadas dos pontos homólogos coletados na fonte de maior acurácia.
1.2 INDICADORES ESTATÍSTICOS DE ACURÁCIA
A norma brasileira (BRASIL, 1984) não menciona nenhuma fórmula ou método para se calcular a acurácia dos dados altimétricos como fez o NDEP (2004) e a ASPRS (2014), apenas recomenda que seja realizado um teste dos valores altimétricos medidos no documento cartográfico, comparando os valores medidos a uma referência três vezes mais acurada. Este teste utiliza, como parâmetros, os valores do PEC e do erro padrão que representam, respectivamente, 90% e 60,8% de nível de confiança dos dados testados.
Para a norma brasileira o erro padrão é interpretado como sendo o mesmo valor do desvio padrão e do erro médio quadrático. Já para a estatística, o desvio padrão é a dispersão da população dos dados; o erro padrão é o valor que representa o quanto a média da amostra se aproxima da média da população dos dados; e o erro médio quadrático é a média dos quadrados das diferenças entre os valores previstos (calculados) e os valores reais (conhecidos).
Deakin e Kildea (1999) esclarecem as relações dos termos estatísticos frequentemente utilizados na literatura de mapeamento, tais como, desvio padrão, variância e raiz do valor quadrático médio (RMS). No trabalho de Deakin e Kildea (1999), o RMS é expresso pela fórmula (1). O NDEP (2004) utilizou um modelo baseado nesta fórmula para o cálculo do erro médio quadrático (Root Mean Square Error – RMSE).
Onde:
RMS = raiz do valor quadrático médio;
Xi = valores medidos;
ai = um valor aceito (ou de referência)
n = número de amostras
Segundo Deakin e Kildea (1999), a fórmula (1) é adequada em modelos matemáticos em que o valor de ai é igual a zero. Quando o valor de referência for uma constante (a), diferente de zero, o cálculo do RMS desdobra-se na fórmula (2).
Onde:
RMS = raiz do valor quadrático médio;
Xi = valores medidos;
= a média da amostra; e
a = um valor constante, diferente de zero
n = número de amostras
A fórmula (2) traduzida em conceitos, significa:
(RMS)² = estimativa da variância + (estimativa da tendência)²
Para o caso em que o valor de referência for constante, se não houver tendência na amostra, a raiz do valor quadrático médio será igual ao desvio padrão.
O trabalho de Monico et al. (2009) utilizou a fórmula (3) a fim de obter a acurácia. Esta fórmula incorporou tanto a tendência (erros sistemáticos) quanto a precisão (erros aleatórios).
Onde:
MSE = erro médio quadrático
= variância da amostra (ou incerteza);
b = tendência (a média das discrepâncias entre os valores conhecidos e os valores medidos – Δ).
Nesta interpretação, se não houver tendência, o erro médio quadrático será igual à variância.
O trabalho de Merchant (1982), de onde deriva a norma brasileira (BRASIL, 1984), esclarece que o teste de acurácia pressupõe que os erros sistemáticos (que são interpretados como tendência por (MONICO et al., 2009) tenham sido eliminados ou que o produto a ser avaliado esteja isento destes erros.
Carvalho e Silva (2018) realizaram um trabalho de revisão dos métodos de análise da acurácia altimétrica no Brasil. Os autores recomendam que o uso de análises de tendência e precisão devem ser utilizados de forma cuidadosa, sendo importante realizar primeiramente um estudo sobre a normalidade dos dados amostrais. Verificada a possibilidade de não normalidade dos dados, deve-se evitar o uso destes tipos de análises para evitar resultados equivocados. Neste caso, uma possível solução é utilizar os padrões da ASPRS (2014), visto que estes contemplam a situação de distribuição não-normal para discrepância de dados altimétricos.
Neste trabalho foram aplicados quatro procedimentos para avaliar a acurácia altimétrica dos pontos LiDAR. Para efeitos do presente trabalho utiliza-se o termo acurácia ou exatidão supondo que a comparação dos valores altimétricos é realizada em relação a um valor tido como referência, isento de erro para efeitos práticos, e o parâmetro de avaliação de sua magnitude é o valor da média dos desvios de cada medida com relação ao seu correspondente valor de referência.
2. PRIMEIRO MÉTODO: AVALIAÇÃO DA DISCREPÂNCIA ALTIMÉTRICA DOS PONTOS LIDAR PELA ADAPTAÇÃO DA NORMA BRASILEIRA
A área de estudo de 22,75 km² foi obtida de um levantamento executado pela empresa Fototerra Atividades de Aerolevantamentos Ltda., no ano de 2012, no município de Campinas, cuja densidade de pontos LiDAR foi de 3-4 pontos por m². Para facilitar o processamento, a empresa executora fez uma redução do conjunto de dados por meio de um programa específico da empresa Trimble. Com o processo de redução, o total de pontos da área de estudo passou a ser 9.099.749, o que equivale a 0,4 pontos por m².
Uma forma de verificar a acurácia altimétrica dos pontos LiDAR é converter o conjunto de pontos, classificados como solo, para uma rede triangular irregular (TIN), em geral a conhecida triangulação de Delaunay, e comparar os valores altimétricos dessa TIN com os valores de controle, realizando uma interpolação na TIN por meio de programa SIG, para obter os pontos homólogos (com as mesmas coordenadas planas).
Esse procedimento é simples e requer apenas um programa SIG que disponibilize uma ferramenta para converter o conjunto de dados LiDAR em uma TIN e permita interpolações na mesma.
As diferenças entre os valores altimétricos devem ser submetidas a uma análise estatística que permite calcular a precisão e a medida da acurácia do conjunto de dados analisado. Essa análise é feita por analogia com a norma brasileira (BRASIL, 1984), complementada por mais dois testes da norma americana: teste t, de tendência e teste Qui-quadrado de precisão. Como se viu, a tendência deve ser eliminada.
A figura 1 apresenta a TIN resultante classificada por intervalos de valores altimétricos, conforme a legenda. Cada triângulo da TIN foi colorido de acordo com as cores pré-determinadas para os intervalos de altimetria.
Figura 1 – Conjunto dos Pontos LiDAR Convertidos numa TIN.
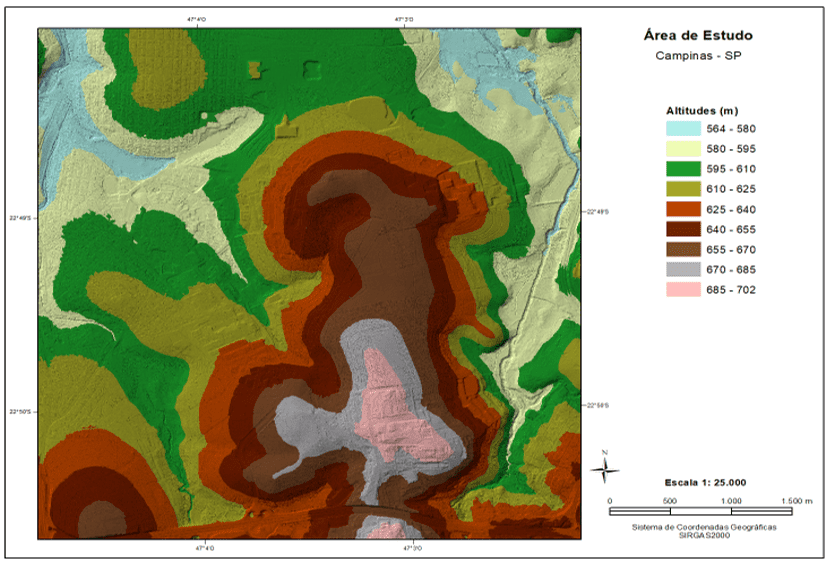
Dispunha-se de 4879 pontos cotados, provenientes da Base Cartográfica de Campinas, na escala 1:1.000, que recobriam a área de estudo e poderiam ser usados como dados de referência para analisar a acurácia altimétrica da TIN gerada a partir dos pontos LiDAR. Decidiu-se coletar os valores altimétricos de 500 pontos cotados bem distribuídos espacialmente para realizar essa análise.
As diferenças entre o valor altimétrico do ponto cotado no produto cartográfico e do ponto cotado na TIN (ΔH) foram submetidas a uma análise estatística, resultando nos valores mostrados na tabela 1 e na figura 2.
Tabela 1 – Valores da Análise Estatística.
| Estatística descritiva | |
| Média (m) | 0,018 |
| Desvio padrão (m) | 0,156 |
| Curtose | 57,585 |
| Média + 3*Desvio padrão (m) | 0,486 |
| Média – 3* Desvio padrão (m) | -0,450 |
| Assimetria | 1,840 |
| Contagem | 500 |
Fonte: A Autora
Os valores da curtose e assimetria, que estão fora do intervalo +0,5 e -0,5, preconizados pela teoria, indicam que a amostra não é normal e podem estar ocorrendo erros grosseiros. As diferenças entre os valores altimétricos (ΔH) deveriam estar dentro do intervalo determinado pela estatística, que é o valor da média (18 mm) mais/menos três vezes o desvio padrão (3 Sigma). O que está fora desse intervalo pode ser considerado como outlier ou erro grosseiro. No lote da amostragem havia 6 valores fora do intervalo aceitável, como se nota pela figura 2 (4 valores acima de 3 Sigma e 2 valores abaixo de 3 Sigma negativo no eixo de ΔH), e por isso, foram eliminados, depois da análise de cada caso.
Figura 2 – Gráfico das Discrepâncias Altimétricas para o Lote de Amostragem.
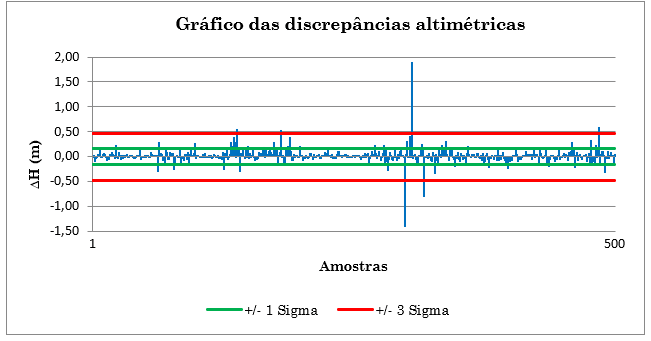
Procedeu-se a uma nova estatística descritiva para o lote da amostragem, tabela 2. Observa-se que o valor de curtose (K = 2,681) diminuiu muito, mas continua indicando uma distribuição leptocúrtica, mais afinada do que a curva normal (valores mais concentrados em torno da média do que a curva normal). O valor da assimetria (Sa = 0,392) está no intervalo (-0,5 ≤ Sa ≤ 0,5) o que é considerado uma distribuição aproximadamente simétrica, pela estatística clássica (BULMER, 1979). Com isso, os resultados melhoraram muito com relação à estatística anterior e os dados podem ser utilizados para as análises.
Tabela 2 – Nova Análise Estatística do Lote de Amostragem.
| Estatística descritiva | |
| Média (m) | 0,017 |
| Desvio padrão (m) | 0,096 |
| Curtose | 2,681 |
| Média + 3*Desvio padrão (m) | 0,306 |
| Média – 3* Desvio padrão (m) | -0,273 |
| Assimetria | 0,392 |
| Contagem | 494 |
Fonte: A Autora
A figura 3 mostra o gráfico das diferenças entre os valores altimétricos dos pontos cotados e da TIN. A média desse lote de amostragem ficou abaixo de 20 cm, como se vê pela primeira linha da tabela 2.
Figura 3 – Gráfico das Discrepâncias Altimétricas para o Lote de Amostragem Após a Exclusão dos Erros Grosseiros.
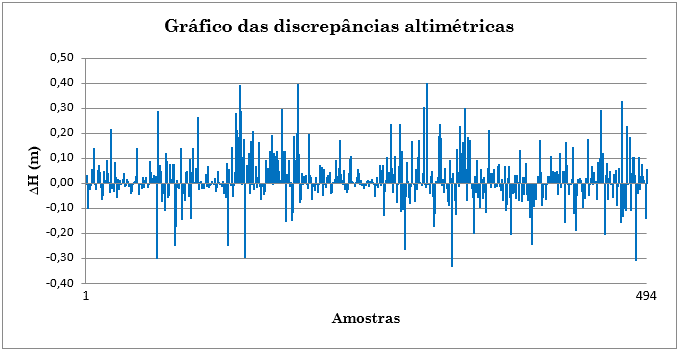
A norma brasileira de controle de qualidade não pede um teste de tendência, nem um teste de precisão das discrepâncias. De qualquer forma, foram aplicados para verificação.
O teste de tendência (teste t para pequenas amostras e teste Z para grandes amostras) revela se há existência de erros sistemáticos na amostra. O teste foi realizado seguindo a fórmula (4), tal como apresentado em mais detalhe por Cintra e Nero (2015):
Onde:
ZH = O valor de calculado
EP = S = Desvio padrão da amostra (σ – Sigma)
μ = média da amostra
n = número de amostras
Então o valor calculado de ZH é comparado com o valor obtido de uma tabela estatística Z(1-α/2) Esse valor depende do tamanho da amostra e do nível de significância (α), que é tradicionalmente tomado como 0,10 (nível de confiança de 0,90) e foi adotado no presente trabalho (CINTRA e NERO, 2015).
Da tabela estatística (ou valor calculado):
Z(1-α/2) = Z0,95 = 1,644853
Se 
> Z0,95, existe erro sistemático na componente H;
Se < Z0,95, não existe erro sistemático na componente H.
> Z0,95, e portanto, existe erro sistemático na componente H.
Para eliminar a tendência, basta subtrair a média da amostra (0,017 m) dos valores altimétricos das 494 amostras.
O teste de precisão, ou teste de qui-quadrado – ver Cintra e Nero (2015) – com a finalidade de saber se o lote de amostragem atende à norma brasileira de controle de qualidade, é realizado pela fórmula (5). Para realizar esse teste, o valor de 
da amostra deve ser comparado com um valor limite calculado 
para um certo tamanho da amostra (n) e um nível de confiança, que geralmente é de 90% (correspondendo a α = 0,10) (CINTRA e NERO, 2015).
Onde:
calculado para o lote de amostragem
n = número de amostras
= o quadrado do desvio padrão da amostra
= o quadrado do erro padrão da classe de mapeamento que se deseja testar
Para o valor de σH da classe A do PEC-PCD (Padrão de Exatidão Cartográfica para os Produtos Cartográficos Digitais), cujo valor é 0,17 m:
Se 
, a amostra atende a acurácia desejada;
Se 
, a amostra não atende a acurácia desejada.
geralmente aparece em tabelas até o valor correspondente a n – 1 (graus de liberdade) igual a 120. Para calcular valores acima desse limite, pode-se usar a fórmula (6) de Wilson–Hilferty, como se vê em Cintra e Nero (2015):
Onde:
df = n – 1 (graus de liberdade)
(cálculo auxiliar)
z = -1,645 (valor da curva normal com a mesma área de α = 0,10, à direita)
O valor limite é calculado usando a fórmula (6):
Como, 
, então, a amostra atende a acurácia desejada.
Pode-se dizer que este método consiste na aplicação da norma brasileira (BRASIL, 1984), que utiliza Merchant (1982) como referência, com a novidade de tomar uma amostra bem maior e, portanto, mais confiável do que aquilo que preconiza Merchant (1982), que adota 20 pontos de verificação por carta e não ao mapeamento como um todo (considerado contínuo). A outra contribuição do método é a sugestão de utilizar os pontos cotados como referência e utilizar a TIN para interpolar a cota no MDT LiDAR, nas mesmas coordenadas horizontais dos pontos cotados. Caso se tivesse dúvida sobre a qualidade dos pontos cotados se poderia fazer uma avaliação dos 500 pontos, através de uma amostragem, com checagem com GPS.
3. SEGUNDO MÉTODO: BASEADO NA METODOLOGIA DO PADRÃO NDEP
Escolheu-se, como um dos métodos para testar a acurácia altimétrica do LiDAR aquele preconizado pelo Programa Nacional de Elevação Digital dos Estados Unidos (National Digital Elevation Program – NDEP), que normatiza as especificações para a obtenção da acurácia altimétrica dos produtos obtidos pela tecnologia LiDAR. Essa metodologia foi utilizada para testar a área de estudo e ao final é comparada com os resultados das outras metodologias. A norma NDEP (2004) já supõe que a tendência tenha sido retirada e, portanto, examina previamente a acurácia.
Segundo a norma NDEP (2004), a acurácia altimétrica dos pontos coletados em solo nu pode ser avaliada segundo um padrão de distribuição normal, o RMSE. Os pontos coletados em áreas florestadas, arbustivas, campos agrícolas, capinzal ou mangue, devem ser avaliados utilizando a função estatística percentil 95.
Para realizar a seleção e coleta das amostras seguiu-se a orientação da norma de que os pontos de controle estivessem espaçados a intervalos de, pelo menos, 10% da distância diagonal do retângulo envolvente do conjunto de dados e, pelo menos, 20% dos pontos estivessem localizados em cada quadrante do conjunto de dados.
Decidido o critério de seleção, foram coletados os valores altimétricos da TIN, obtida com os pontos classificados como solo nu, nos mesmos locais (mesmas coordenadas planas) dos pontos cotados do produto cartográfico.
Aplicando os procedimentos do NDEP (2004) comparando os valores altimétricos de 86 pontos de controle com uma TIN gerada a partir de pontos LiDAR, chegou-se aos resultados da tabela 3.
Tabela 3 – Resumo da Acurácia Altimétrica.
| Categoria de Cobertura do Solo | Nº pontos
amostrais |
Acurácia determinada pelo RMSE | Acurácia determinada pelo Percentil 95 |
| Áreas abertas | 30 | 4,6 cm | – |
| Terrenos arbustivos/ árvores baixas | 26 | – | 32,4 cm |
| Áreas urbanas | 30 | 23,5 cm | – |
Fonte: A Autora
Além da metodologia do NDEP, é interessante realizar a estatística descritiva a fim de visualizar a distribuição dos dados (discrepâncias altimétricas), e perceber se ocorrem valores muito distantes da média.
Aplicando uma estatística descritiva aos dados, chegou-se aos resultados da tabela 4. O gráfico de distribuição das discrepâncias altimétricas é mostrado na figura 4.
Tabela 4 – Estatística Descritiva
| Média (m) | 0,035 |
| Desvio padrão (m) | 0,147 |
| Média + 3 x Desvio padrão (m) | 0,475 |
| Média – 3 x Desvio padrão (m) | -0,406 |
| Curtose | 20,892 |
| Assimetria | 3,874 |
| Contagem | 86 |
Fonte: A Autora
Figura 4 – Gráfico das Discrepâncias Altimétricas para o Lote de Amostragem.
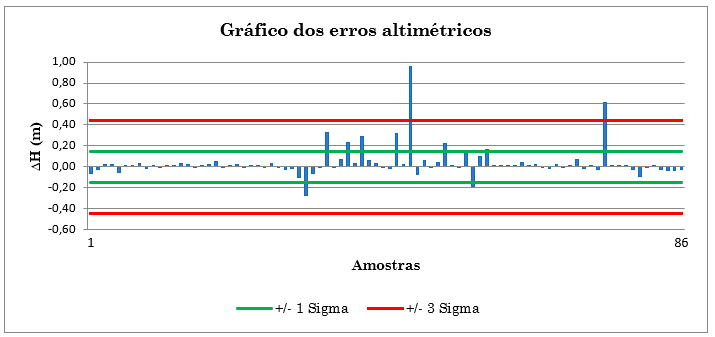
O gráfico mostra que existem 2 valores acima do intervalo aceitável, que é de 3 Sigma.
Um dos valores acima do intervalo aceitável (0,61 m), examinado, mostrou-se estar em local urbano, com dificuldade de avaliar a cota. O outro valor (0,962 m) corresponde a um terreno arbustivo. Estes dois valores devem ser eliminados e são considerados erros grosseiros.
Aplicando uma nova estatística descritiva aos dados, após retirar os erros grosseiros, chega-se aos resultados da tabela 5.
Tabela 5 – Estatística Descritiva.
| Média (m) | 0,017 |
| Desvio padrão (m) | 0,086 |
| Curtose | 5,713 |
| Assimetria | 1,225 |
| Contagem | 84 |
Fonte: A Autora
O gráfico da figura 5 mostra a nova distribuição dos dados, e a maior concentração dos dados (85%) ficou dentro de uma precisão de 7 cm.
Figura 5 – Gráfico das Discrepâncias Altimétricas para o Lote de Amostragem Após a Exclusão dos Erros Grosseiros.
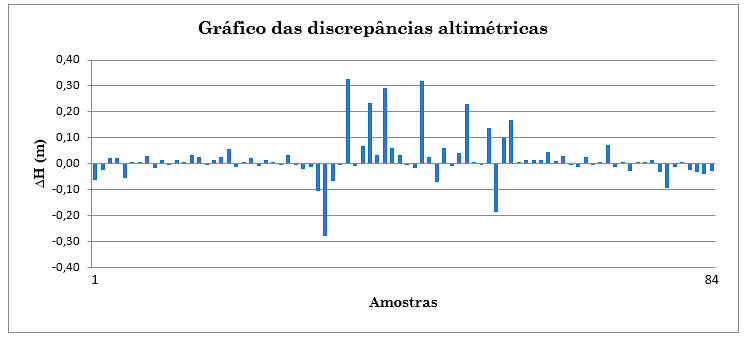
A aplicação dessa norma mostrou-se factível em nosso meio e terrenos e vale a pena considerá-la na execução de avaliação altimétrica.
4. TERCEIRO MÉTODO: QUANTIFICAÇÃO DA DISCREPÂNCIA ENTRE CURVAS DE NÍVEL
O terceiro método consiste numa forma de avaliar a acurácia altimétrica das curvas de nível obtidas a partir de pontos LiDAR, empregando-se analogicamente o Método dos Retângulos Equivalentes (MRE).
O Método dos Retângulos Equivalentes consiste em determinar os lados de um retângulo equivalente a duas curvas próximas, a partir das duas grandezas derivadas: área e perímetro. A área e o perímetro são indicadores que servem como medida do afastamento entre duas feições lineares. As dimensões dos retângulos equivalentes e, em particular seu lado menor, são utilizadas como estimadores das discrepâncias entre as representações de uma dada feição (FERREIRA e CINTRA, 1999).
Nesse experimento, decidiu-se testar a acurácia altimétrica das curvas de nível interpoladas pelos pontos LiDAR. O procedimento para esse experimento resumiu-se em sobrepor as curvas de nível procedentes do produto cartográfico e suas homólogas, procedentes da interpolação de pontos LiDAR, ou seja, duas curvas de mesmo valor altimétrico, com diferentes traçados. Onde as curvas não coincidiram formaram-se pequenas áreas ou polígonos (adotando o conceito do Método dos Retângulos Equivalentes), que correspondem a um erro (discrepância) que pode ser avaliado. Para medir esta discrepância foram comparados os valores altimétricos, em quarenta amostras, da borda externa da curva com os valores altimétricos de uma TIN (produzida pelas curvas de nível de referência, de equidistância de 1 m). Este procedimento foi realizado empregando ferramentas de um programa SIG.
As diferenças altimétricas foram medidas utilizando ferramenta computacional aliada ao conhecimento de tridimensionalidade proporcionado pelas redes irregulares triangulares – TIN’s (a TIN fornece a informação 3D, e o seu uso possibilita medir desníveis). Os polígonos gerados (de cor rosa na figura 6) foram sobrepostos à TIN (gerada pelas curvas de nível de referência do produto cartográfico) a fim de conhecer o valor altimétrico da TIN na fronteira ou borda que corresponde à curva de nível interpolada pelos pontos LiDAR, e determinar os locais que correspondem ao maior afastamento da curva de referência (a de cor preta na figura 6).
O conceito é que as duas bordas do polígono representam o mesmo valor altimétrico, e a borda correspondente à curva gerada pelos pontos LiDAR, quando comparada a um produto de referência (que é a TIN) pode estimar a discrepância altimétrica (ΔHTIN). A obtenção do valor altimétrico é realizada num programa SIG.
Figura 6 – Polígonos Sobrepostos à TIN.
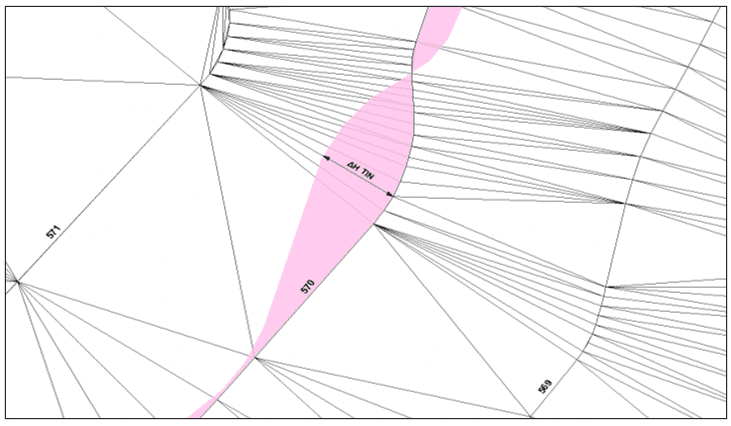
Coletando 40 amostras (as bordas mais discrepantes) para cada curva de nível, foram obtidas as discrepâncias altimétricas, média e desvio padrão para cada curva. A curva de nível de cota 700 m era menor e por isso só foi possível coletar 20 amostras. A tabela 6 mostra um resumo das estatísticas das discrepâncias altimétricas coletados para cada curva e um teste de tendência (ZH) para verificar a existência de erros sistemáticos nas amostras.
O valor de ZH foi calculado e comparado ao valor de Z0,95, que é um valor tabelado e corresponde a 1,645. O teste de tendência analisa as seguintes condições:
- Se 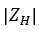> Z0,95, existe erro sistemático na componente altimétrica da amostra.
- Se 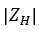< Z0,95, não existe erro sistemático na componente altimétrica da amostra.
Tabela 6 – Estatísticas das Discrepâncias Altimétricas para Cada Curva de Nível.
| Curvas de nível | Número de amostras | Média ΔHTIN (m) | Desvio padrão ΔHTIN (m) | Teste de tendência (ZH) |
| 570 | 40 | -0,010 | 0,273 | -0,232 |
| 580 | 40 | 0,150 | 0,558 | 1,700 |
| 590 | 40 | 0,028 | 0,372 | 0,476 |
| 600 | 40 | 0,062 | 0,330 | 1,188 |
| 610 | 40 | 0,020 | 0,153 | 0,827 |
| 620 | 40 | 0,033 | 0,160 | 1,304 |
| 630 | 40 | 0,096 | 0,357 | 1,701 |
| 640 | 40 | 0,054 | 0,253 | 1,350 |
| 650 | 40 | -0,012 | 0,096 | -0,791 |
| 660 | 40 | 0,024 | 0,132 | 1,150 |
| 670 | 40 | 0,027 | 0,181 | 0,943 |
| 680 | 40 | -0,023 | 0,267 | -0,545 |
| 690 | 40 | 0,195 | 0,564 | 2,187 |
| 700 | 20 | 0,041 | 0,880 | 0,208 |
Fonte: A Autora
A média, ou erro sistemático, para cada curva de nível corresponde a um deslocamento altimétrico convencionado como positivo ou negativo, como explicado anteriormente.
Como o desvio padrão é a dispersão da população dos dados, ele representa uma medida de precisão. Os valores do desvio padrão são altos, comparados com a média altimétrica, porque as amostras foram tomadas nos valores mais discrepantes, ora positivos, ora negativos.
As curvas de nível que apresentaram tendência no teste ZH foram:
- A curva 580 com discrepância altimétrica (média) de 15 cm e precisão (desvio padrão) de 56 cm;
- A curva 630 com discrepância altimétrica de 10 cm e precisão de 35 cm; e
- A curva 690 com discrepância altimétrica de 19 cm e precisão de 56 cm.
Ao final será feito uma análise comparativa apresentando os pontos fortes desse método.
5. QUARTO MÉTODO: AVALIAÇÃO DAS DISCREPÂNCIAS ALTIMÉTRICAS DOS PONTOS LIDAR SITUADOS ENTRE CURVAS DE NÍVEL CONSECUTIVAS
Além de realizar o controle de qualidade da altimetria sobre pontos LiDAR convertidos numa TIN, também é possível realizar o controle de qualidade de pontos LiDAR compreendidos em duas curvas de nível.
Esse método pode ser realizado transformando duas curvas de nível consecutivas num polígono e testar os valores altimétricos dos pontos LiDAR, compreendidos dentro desse polígono.
Foram testados valores altimétricos em vinte e três polígonos provenientes das curvas de nível de valor 680 m até 702 m (equidistância de 1 m entre as curvas).
Em cada um dos vinte e três polígonos, foram selecionados todos os pontos, classificados como “solo” pelo LiDAR, para que fosse tirada a diferença (∆H) entre o valor altimétrico de cada ponto LiDAR e o valor da altitude média do polígono a que o ponto pertence. As diferenças (∆H), em teoria, podem apresentar uma distância máxima de 0,5 m em relação à curva média, sem que se possa dizer que estão errados. Discrepâncias acima desse valor correspondem certamente a erros.
Com os valores de ∆H, procedeu-se a uma análise para cada polígono. O resumo da análise estatística dos vinte e três conjuntos de dados, com os respectivos valores de média, desvio padrão, curtose e assimetria estão na tabela 7.
Tabela 7 – Resumo da Análise Estatística.
| Polígono | Média (m) | Desvio padrão (m) | Curtose (m) | Assimetria (m) |
| 680-681 | -0,005 | 0,316 | -0,346 | -0,186 |
| 681-682 | -0,019 | 0,323 | -0,741 | 0,053 |
| 682-683 | -0,036 | 0,313 | -0,755 | 0,081 |
| 683-684 | -0,012 | 0,328 | -0,793 | 0,036 |
| 684-685 | -0,047 | 0,336 | -0,711 | 0,029 |
| 685-686 | 0,001 | 0,303 | -0,750 | -0,039 |
| 686-687 | -0,035 | 0,329 | -0,748 | 0,049 |
| 687-688 | -0,038 | 0,309 | -0,664 | 0,064 |
| 688-689 | 0,010 | 0,337 | -0,819 | -0,124 |
| 689-690 | 0,020 | 0,322 | -0,853 | -0,081 |
| 690-691 | -0,081 | 0,329 | -0,782 | 0,268 |
| 691-692 | -0,037 | 0,314 | -0,771 | 0,141 |
| 692-693 | -0,028 | 0,328 | -0,628 | 0,111 |
| 693-694 | -0,002 | 0,331 | -0,398 | 0,107 |
| 694-695 | -0,077 | 0,329 | -0,262 | -0,086 |
| 695-696 | 0,032 | 0,341 | -0,537 | -0,171 |
| 696-697 | -0,037 | 0,371 | -0,476 | 0,221 |
| 697-698 | -0,063 | 0,325 | -0,896 | 0,161 |
| 698-699 | 0,047 | 0,320 | -0,716 | -0,085 |
| 699-700 | -0,103 | 0,238 | 0,494 | -0,153 |
| 700-701 | -0,251 | 0,324 | 1,149 | -1,060 |
| 701-702 | -0,835 | 0,776 | -1,552 | 0,110 |
| 702-703 | -0,516 | 0,750 | 4,068 | -2,215 |
Fonte: A Autora
A média geral foi de (-0,092 m), ou seja, 9 cm, em módulo. Era de se esperar que a média geral se aproximasse de zero e não poderia haver, em tese, conjuntos de dados / distribuições com diferença maior, em módulo, do que 0,5 m, já que os pontos com discrepâncias superiores não estariam dentro das duas curvas de nível limitantes. A média passou de 0,5 m em módulo nos dois últimos polígonos (701-702 e 702-703).
Analisando as médias da componente ∆H dos vinte e três conjuntos de dados, chegou-se ao seguinte resultado: em três polígonos, a média da discrepância altimétrica foi menor que 1 cm; em treze polígonos, a média ficou entre 1 e 5 cm; em três polígonos, a média ficou entre 5 e 10 cm; em dois polígonos a média ficou entre 10 e 50 cm; e em 2 polígonos a média foi maior que 50 cm não passando de 83 cm.
A seguir, pôde-se fazer uma análise extensiva desses dados, à luz da norma brasileira quantificando a porcentagem de pontos acima de certo limite.
O Decreto Federal 89.817, de 20 de junho de 1984, determina que somente 10% das medidas tomadas no produto cartográfico avaliado, quando testados no terreno, ou nesse caso, por meio de um produto de referência, poderão apresentar erro superior ao padrão de exatidão cartográfica estabelecido, que atualmente é o PEC-PCD. Os valores limites em função da escala encontram-se na tabela 9.
Tabela 9 – Valores do PEC-PCD para Testar a Componente ΔH.
| Classe | PEC-PCD (m) | ||||
| 1:1.000 | 1:2.000 | 1:5.000 | 1:10.000 | 1:25.000 | |
| A | 0,17 | 0,17 | 0,34 | 0,84 | 1,67 |
| B | 0,33 | 0,33 | 0,66 | 1,67 | 3,33 |
| C | 0,40 | 0,40 | 0,80 | 2,00 | 4,00 |
| D | 0,50 | 0,50 | 1,00 | 2,50 | 5,00 |
Fonte: CONCAR/DSG, 2016
Dos vinte e três conjuntos de pontos analisados, o resultado desse experimento mostrou que:
a) Na escala 1:5.000: vinte atenderam a classe B e um atendeu a classe C;
b) Na escala 1:10.000: um atendeu a classe B; e
c) Na escala 1:25.000: um atendeu a classe B.
Como as diferenças (∆H) podem apresentar uma distância máxima de 0,5 m em relação à curva média, sem que se possa dizer que estão erradas, então, pode-se medir a magnitude do afastamento, maior que 0,5 m (para mais ou para menos) e comparar essa magnitude com o PEC-PCD.
Realizando uma nova análise dos conjuntos de pontos LiDAR compreendidos nos polígonos (somando 0,5 m aos valores do PEC-PCD – da tabela 10) chegou-se aos seguintes resultados:
a) Na escala 1:1.000: vinte atenderam a classe A e um atendeu a classe B;
b) Na escala 1:5.000: um atendeu a classe C; e
c) Na escala 1:10.000: um atendeu a classe B.
6. CONSIDERAÇÕES FINAIS
O primeiro e o segundo métodos avaliaram as discrepâncias altimétricas dos pontos LiDAR em relação a pontos de controle, por isso são pontuais. As diferenças entre estes dois métodos está na forma de aquisição das amostras. No primeiro método aplicou-se uma análise estatística aos valores medidos a fim de encontrar valores muito distantes da média e eliminá-los da amostra.
No segundo método seguiu-se a norma do NDEP (2004), que fornece valores métricos de acurácia por meio de fórmulas estatísticas. A partir dos experimentos deste trabalho, recomenda-se empregar o primeiro método precedendo o segundo método para, conjuntamente, realizar a avaliação da acurácia altimétrica, principalmente quando se quer fazer distinção entre os diversos tipos de cobertura do solo.
O terceiro método avaliou as diferenças entre 14 curvas de nível interpoladas a partir de pontos LiDAR e suas curvas correspondentes obtidas por outras técnicas. As médias das discrepâncias altimétricas variaram entre 1 cm e 19,5 cm. Os valores mais elevados de discrepâncias altimétricas revelados por este método podem ter ocorrido devido à redução de pontos LiDAR realizada pela empresa executora que, consequentemente, pode ter gerado curvas de nível inadequadas, ou porque as curvas de nível de referência não estavam definidas corretamente. Tal investigação é uma continuidade da pesquisa sobre este método.
O quarto método avaliou as discrepâncias altimétricas de todos os pontos LiDAR compreendidos numa área delimitada por duas curvas de nível consecutivas, correspondendo à equidistância de 1 metro, no caso. A abundância de valores possibilitou o enquadramento dos 23 conjuntos de dados analisados no padrão de exatidão cartográfica PEC-PCD. As médias das discrepâncias altimétricas dos 23 conjuntos de dados analisados variaram entre 1 mm e 83,5 cm. A vantagem deste método é poder avaliar uma grande quantidade de pontos LiDAR e não somente uma amostra.
O terceiro e quarto métodos, globais, detectaram discrepâncias maiores em pontos localizados: separação maior entre curvas de nível, que levam a erros altimétricos maiores em função da declividade (3º método), e valores discrepantes dos valores altimétricos definidos pelas curvas de nível analisadas (4º método). Os métodos pontuais (1º e 2º) não acusaram esses casos.
O primeiro, o terceiro e o quarto métodos se adéquam para uma avaliação da acurácia altimétrica geral da área, e o segundo método se adéqua para uma avaliação da acurácia altimétrica em áreas, cuja cobertura ou tipo de uso, são homogêneos por categorias: vegetação de diversos tipos, solo nu, edificações, por exemplo.
Estes quatro métodos não exigem demorados e caros procedimentos de campo. Trabalhos futuros podem estudar com mais detalhe essas anomalias localizadas.
AGRADECIMENTOS
Agradecimentos à Prefeitura Municipal de Campinas e às empresas Fototerra Atividades de Aerolevantamentos Ltda, e BASE Aerofotogrametria e Projetos S. A. pela cessão dos dados utilizados nesse trabalho.
REFERÊNCIAS
ASPRS. ASPRS Accuracy Standards for Large-Scale Maps, Photogrammetric Engineering and Remote Sensing, 56(7): 1068-1070, American Society for Photogrammetry and Remote Sensing (ASPRS), Bethesda, MD, 1990.
ASPRS. ASPRS Guidelines, Vertical Accuracy Reporting for LiDAR Data. American Society for Photogrammetry and Remote Sensing (ASPRS), Bethesda, MD, 2004.
ASPRS. ASPRS Positional Accuracy Standards for Digital Geospatial Data. American Society for Photogrammetry and Remote Sensing (ASPRS), Bethesda, MD, 2014.
BRASIL. Decreto-Lei nº 243, de 28 de fevereiro de 1967. Fixa as Diretrizes e Bases da Cartografia Brasileira e da outras providencias. Brasília, Diário Oficial da União, 28 de fevereiro de 1967. Disponível em: < http://www.planalto.gov.br/ccivil_03/decreto-lei/1965-1988/Del0243.htm>. Acesso em: 30/07/2018.
BRASIL. Decreto nº 89.817, de 20 de junho de 1984. Estabelece as Instruções Reguladoras das Normas Técnicas da Cartografia Nacional. Brasília, Diário Oficial da União, 22 de junho de 1984. Disponível em: < http://www2.camara.leg.br/legin/fed/decret/1980-1987/decreto-89817-20-junho-1984-439814-norma-pe.html> Acesso em: 13/07/2018.
BRASIL. Decreto nº 6.666, de 27 de novembro de 2008. Institui, no âmbito do Poder Executivo Federal, a Infraestrutura Nacional de Dados Espaciais (INDE), e dá outras providências. Brasília, Diário Oficial da União, 27 de novembro de 2008. Disponível em: <http://www2.camara.leg.br/legin/fed/decret/2008/decreto-6666-27-novembro-2008-584507-publicacaooriginal-107238-pe.html> Acesso em: 10/07/2018.
BULMER, Michael George. Principles of Statistics. New York: Dover Publications, 1979, 252 p.
CARVALHO, João Alberto Batista; SILVA, Daniel Carneiro. Métodos para avaliação da acurácia posicional altimétrica no Brasil. Revista Brasileira de Cartografia, Geodesia, Fotogrametria e Sensoriamento Remoto, vol. 70, n. 2, pp.725-744, abr./jun., 2018.
CINTRA, Jorge Pimentel; NERO, Marcelo Antônio. New method for positional cartographic quality control in digital mapping. Journal of Surveying Engineering, v. 141, n. 3, p. 04015001, 2015. R-1 EB80-N-72.004.
CONCAR/DSG. Especificação Técnica para a Aquisição de Dados Geoespaciais Vetoriais (ET-ADGV v.2.1.3). 2011.
CONCAR/DSG. Especificação Técnica para o Controle de Qualidade de Dados Geoespaciais (ET-CQDG v.1). 2016.
DEAKIN, Rodney Edwin; KILDEA, Daniel George. A Note on Standard Deviation and RMS, Australian Surveyor, 44:1, 74-79, 1999. DOI: 10.1080/00050326.1999.10441907
FEMA. Procedure Memorandum Nº. 61 – Standards for LiDAR and Other High Quality Digital Topography, Federal Emergency Management Agency (FEMA), Washington, D.C, September 27, 2010.
FERREIRA, Flávia Renata; CINTRA, Jorge Pimentel. A avaliação da acurácia altimétrica dos dados LiDAR utilizando a metodologia do programa nacional de elevação digital dos Estados Unidos. Anais do XXVII Congresso Brasileiro de Cartografia. Rio de Janeiro, p. 487-491, 2017.
FERREIRA, Flávia Renata. Propostas para a avaliação da acurácia altimétrica dos dados LiDAR. 2019. 202 p. Tese (Doutorado) – Escola Politécnica da Universidade de São Paulo, São Paulo, 2019.
FERREIRA, Luiz Felipe, CINTRA, Jorge Pimentel. Quantificação de discrepância entre feições lineares por retângulos equivalentes. Revista Brasileira de Cartografia, Geodesia, Fotogrametria e Sensoriamento Remoto, v. 1, n.51, p. 1-8, 1999.
GARCIA-BALBOA, José L. Normas de Calidad. En: Experto Universitário em Evaluación de La Información Geográfica (4a Edición). Master Universitário em Evaluación y Gestión de La Calidad de La Información Geográfica (1a Edición). Jaen: Universidad de Jaen, 2011.
LOHANI, Bharat; GHOSH, Suddhasheel; DASHORA, Ajay. A Review of Standards for Airborne LiDAR Data Acquisition, Processing, QA/QC, and Delivery. In: Sarda N., Acharya P., Sen S. (eds) Geospatial Infrastructure, Applications and Technologies: India Case Studies. Springer, Singapore, 2018.
MERCHANT, Dean Charles. Spatial Accuracy Standards for Large Scalle Line Maps. In: TECHINICAL CONGRESS ON SURVEYING AND MAPPING. Proceedings. v. 1, p. 222-231, 1982.
MIL-STD-105E. Sampling Procedures and Tables for Inspection by Attributes. May 10, 1989.
MONICO, João Francisco Galera; DAL PÓZ, Aluir Porfírio; GALO, Maurício. SANTOS, Marcelo Carvalho; OLIVEIRA, Leonardo Castro. Acurácia e precisão: revendo os conceitos de forma acurada. Boletim de Ciências Geodésicas, Curitiba, v. 15, nº 3, p.469-483, jul-set, 2009.
NDEP. Guidelines for Digital Elevation Data. National Digital Elevation Program (NDEP), version 1.0, p. 21 -35, 2004. <http://www.ndep.gov> Acesso em: 01/02/2016.
NERO, Marcelo Antônio; CINTRA, Jorge Pimentel. Controle de qualidade de mapas: Visão geral das normas de diversos países. Anais do XXII Congresso Brasileiro de Cartografia, Vol. 22, Sociedade Brasileira de Cartografia, Rio de Janeiro, 1–16, 2005.
NOAA. Light Detection and Ranging (LiDAR) Requirements. 2009 <https://www.ngs.noaa.gov/RSD/AirportSOW.pdf>. Acesso em: 11/06/2019.
NRCAN. Federal Airborne LiDAR Data Acquisition Guideline version 1.0 (Draft). 2017 <http://publications.gc.ca/collections/collection_2017/rncan-nrcan/M113-1-117-eng.pdf>. Acesso em: 13/06/2019.
RENSLOW, Michael S. Manual of Airborne Topographic LiDAR, American Society for Photogrammetry and Remote Sensing, Bethesda, 2012.
ROBINSON, Arthur H.; MORRISON, Joel L.; MUEHRCKE, Phillip C.; KIMERLING, A. Jon; GUPTILL, Stephen C. Elements of cartography. 6. ed. New York: John Wiley & Sons, 1995.
USACE. Engineering and design – photogrammetric and LiDAR mapping. Manual EM 1110-1-1000. Washington: U.S. Army Corps of Engineers (USACE), 2015.
XAVIER, Emerson M. A.; ARIZA-LOPEZ, Francisco J.; URENA-CAMARA, Manuel A. WPS for positional quality control applying the method proposed in UNE 148002. In: VI Jornadas Ibéricas de Infraestructuras de Datos Espaciales. Anais…, 2015. Sevilla, Spain.
[1] Doutorado em Engenharia de Transportes.
[2] Doutorado em Engenharia Civil.
Enviado: Agosto, 2020.
Aprovado: Fevereiro, 2021.
