ARTIGO ORIGINAL
MOURA, Tiago Rodrigues Coelho de [1]
MOURA, Tiago Rodrigues Coelho de. Demonstração do cálculo da linha neutra em vigas submetidas à flexão. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano 04, Ed. 10, Vol. 10, pp. 99-115. Outubro de 2019. ISSN: 2448-0959, Link de acesso: https://www.nucleodoconhecimento.com.br/engenharia-civil/calculo-da-linha
RESUMO
Um dos sistemas construtivos mais usado no Brasil é o concreto armado. Normalmente, as estruturas são constituídas por lajes, vigas, pilares e fundação. Todos esses elementos devem ser dimensionados e verificados a fim de resistir todos os esforços solicitantes. No dimensionamento, especificamente nas vigas e lajes, são feitas várias verificações. Uma das verificações, exigida pela norma vigente, é a posição da linha neutra. Essa linha neutra separa a região comprimida da região tracionada de um elemento submetido à flexão. Este estudo apresentou, de forma didática, o cálculo dessa linha neutra e as equações deduzidas para facilitar o trabalho dos profissionais de engenharia civil. Ao longo do texto, é exposto o passo a passo do cálculo para vigas com diversos tipos de seções transversais: retangular, I, T e trapezoidal. Todos os cálculos aplicáveis a vigas de concreto armado. Cada tipo de seção transversal resultou em equações diferentes. Normalmente, chega-se a equações do segundo grau para seções geometricamente retangulares e do terceiro grau para seções com partes triangulares.
Palavras-Chave: linha neutra, concreto, estruturas, flexão, vigas.
1. INTRODUÇÃO
Uma análise bem detalhada dos elementos estruturais é de grande importância para garantir a segurança das edificações. As normas da Associação Brasileira de Normas Técnicas (ABNT) amparam, de forma ampla, o dimensionamento de estruturas na construção civil, em especial, a NRB 6118 (ABNT, 2014) que trata das estruturas de concreto armado. Nessa norma estão previstas várias verificações, uma delas é a posição da linha neutra em vigas. A linha neutra é compreendida como um plano que separa duas regiões – a comprimida e a tracionada – num mesmo elemento quando submetido à flexão. Além das verificações especificadas nessa norma, a posição da linha neutra, em relação à fibra mais comprimida, é necessária para calcular a área de aço de tração da viga. Esse breve estudo tem a finalidade de demonstrar o desenvolvimento das equações desse parâmetro, nos elementos estruturais submetidos à flexão simples.
2. DESENVOLVIMENTO
2.1 LINHA NEUTRA EM VIGA DE SEÇÃO TRANSVERSAL QUALQUER.
A linha neutra, em um elemento sob flexão simples, separa a região comprimida da região tracionada. A Figura 1 exemplifica essas regiões em uma viga com carregamento uniforme. Nesse caso, todas as cargas transversais produzem um momento fletor que determina a posição dessa linha.
Figura 1 – Linha neutra em viga.
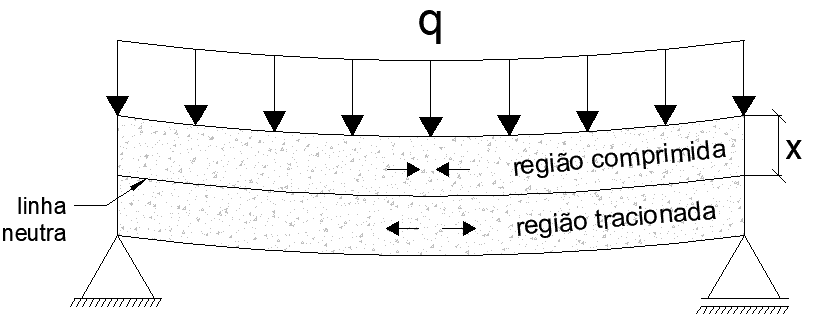
Nesses elementos, linha neutra é obtida em função do momento fletor na seção transversal. Fazendo o equilíbrio desse momento, em relação à região comprimida e ao aço tracionado, obtém-se a equação inicial do problema. Algumas observações previstas na NBR 6118 (ABNT, 2014) devem ser consideradas; a tensão efetiva na compressão do concreto é uma delas.
A tensão de pico do concreto, em acordo com o item 8.2.10 da NBR 6118 (ABNT, 2014), é 85% da tensão de cálculo. Essa consideração normativa visa garantir a segurança da região comprimida do elemento.
A posição de cálculo da linha é considerada em 80% da real. Esse modelo de cálculo é adotado para garantir, de forma homogênea, uma distribuição da tensão de compressão, conforme apresentado por Carvalho e Filho (2007). O esquema para demonstração dessa consideração está exposto na Figura 2, onde o gráfico de tensão real do concreto é substituído por outro equivalente, porém, de forma retangular.
Figura 2 – Linha neutra numa seção qualquer.
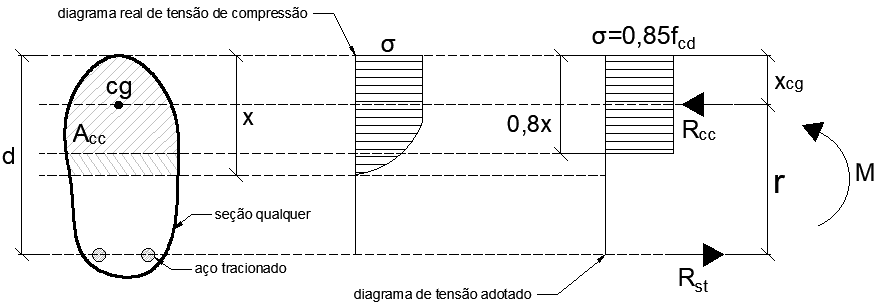
Os cálculos são baseados no equilíbrio de momento fletor da região comprimida do concreto e da tração do aço na seção transversal da viga. Conforme a Figura 2, podemos calcular a força na região comprimida (Rcc) em função da tensão e área.
Onde
Rcc: força de reação da região comprimida;
fcd: tensão de resistência de cálculo do concreto;
Acc: área de concreto sob compressão.
A força de reação da região comprimida é concentrada no centro de gravidade da área de concreto sob compressão. A distância (xcg) desse centro de gravidade até a face mais comprimida da viga pode ser calculado com as seguintes equações:
- Para um contorno da seção transversal definido por uma função f(x) num intervalo de “a” até “b”.
- Para uma seção transversal definida por figuras geometricamente conhecidas.
Ai: área das figuras geometricamente conhecidas;
ri: distância do centro de gravidade de cada Ai à face mais comprimida.
O momento fletor (M) na seção transversal analisada é o produto da força de reação da região comprimida (Rcc) pela distância (r) do centro de gravidade da área comprimida até a barra de aço tracionada, conforme pode ser visto na Figura 2.
Fazendo as manipulações algébricas da equação acima, chega-se a funções de graus diversos que variam de acordo com a seção transversal da viga. Normalmente, tem-se o grau 2 para seções retangulares. Uma das raízes dessas funções é a posição da linha neutra no elemento estrutural.
2.2 LINHA NEUTRA EM VIGA RETANGULAR
Com base no modelo apresentado no item 2.1 deste artigo, foi obtida a posição da linha neutra para uma viga retangular. A fórmula encontrada para esse tipo de seção transversal pode ser vista em diversos livros, mas o objetivo aqui é demonstrar a dedução da mesma.
A Figura 3 mostra a posição da linha neutra e o gráfico de tensão do concreto para uma viga de seção transversal retangular. O equilíbrio de momento é feito, dessa forma, tem-se a separação das regiões tracionada e comprimida.
Figura 3 – Linha neutra em viga retangular.
O equilíbrio de momento se dá pelo somatório do momento fletor solicitante e pelo momento gerado pala força de reação da região comprimida de concreto. Com isso, fazendo uso da equação 4, temos a expressão abaixo.
A área de concreto da região comprimida é calculada em função do modelo do gráfico de tensão adotado.
Fazendo a substituição da equação 6 na equação 5, temos a expressão final para o obter a posição da linha neutra.
Note que a equação 7 é do 2º grau e suas raízes podem ser facilmente encontradas, conforme demonstração a seguir. A maior raiz dessa equação é desprezada, pois, não tem sentido físico para o problema.
A posição da linha neutra é calculada com o uso da equação 8, porém, deve-se observar os limites estabelecidos pela NBR 6118 (ABNT, 2014). Esses limites visam garantir a segurança da estrutura.
2.3 LINHA NEUTRA EM VIGA I E VIGA T SEM MÍSULA
De modo semelhante às seções retangulares, encontra-se a linha neutra em outros tipos de vigas, aplicando o modelo apresentado no item 2.1 acima. Deve-se observar que as seções I e T não possuem as mesmas dimensões ao longo da altura, devido a isso, devem-se fazer os cálculos para duas hipóteses: linha neutra na mesa e linha neutra na alma. As Figuras 4 e 5 mostram os esquemas de todas as considerações feitas nesse tipo de viga.
Figura 4 – Linha neutra em viga I sem mísula.
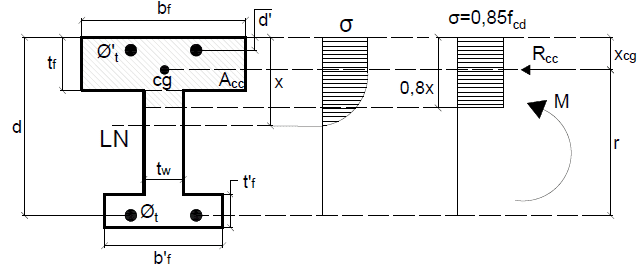
Figura 5 – Linha neutra em viga T sem mísula.
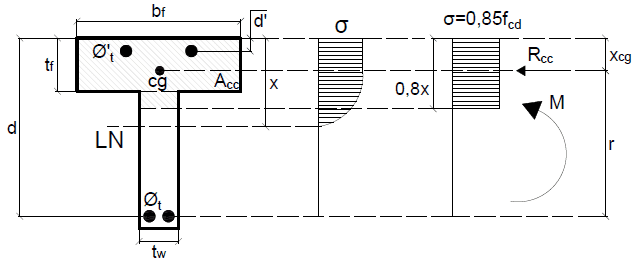
Quando a linha neutra passar na mesa da viga, é válida a equação 8, porém, deve se substituir o “bw” pelo “bf”, dessa forma temos a equação 9.
Quando a linha neutra passar sobre a alma da viga, é feito o mesmo equilíbrio de momento, porém, nessa parte, as mudanças ficam na área de concreto sob compressão (Acc) e no seu centro de gravidade. Isso ocorre devido à geometria da seção transversal. Usando a equação 3, encontra-se a distância desse centro de gravidade até a face mais comprimida da viga para esse tipo de seção.
A área de concreto comprimida fica conforme a equação 11.
Fazendo o equilíbrio de momento, com uso da equação 4, temos a expressão abaixo.
Observe que a equação 12 também é do 2º grau. Da mesma forma das seções retangulares, a maior raiz dessa equação é desprezada, pois, não tem sentido físico para o problema.
Para as vigas do tipo T e I, a posição da linha neutra (LN) é calculada com o uso das equações 9 e 13, respectivamente, para LN na mesa e LN na alma. Deve-se observar a espessura da mesa para determinar o limite de transição entre a mesa e a alma da viga. Devido aos limites estabelecidos pela NBR 6118 (ABNT, 2014), não se faz necessário o cálculo da linha neutra na mesa inferior da viga I.
2.4 LINHA NEUTRA EM VIGA I E EM VIGA T COM MÍSULA NA MESA
Nas estruturas correntes, é comum o uso de mísula nas vigas do tipo T e I. Esse tipo de viga pode ser calculado, de forma aproximada, conforme o item anterior. Mas, para encontrar resultados mais fidedignos, será apresentado aqui uma maneira de obter a posição da linha neutra vigas T e I com mísula.
As Figuras 6 e 7 exemplificam, de maneira objetiva, a forma da seção transversal e seus gráficos de tensões aproximados para esse tipo de viga.
Figura 6 – Linha neutra em viga I com mísula na mesa.
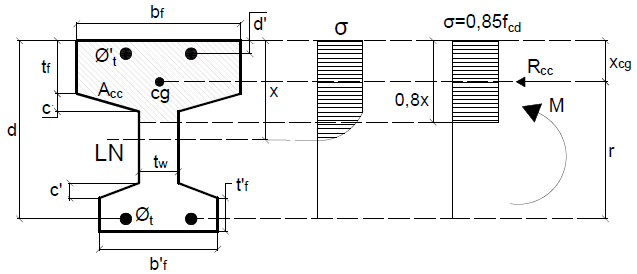
Figura 7 – Linha neutra em viga T com mísula na mesa.
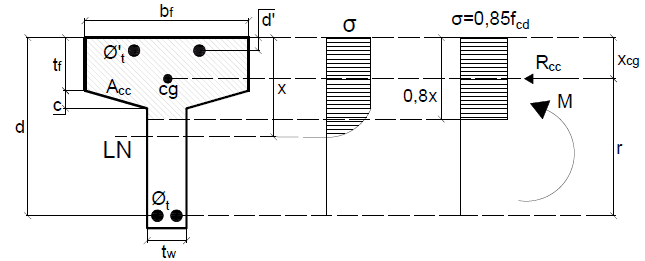
Nesse tipo de viga, há três hipóteses. A primeira é o caso da linha neutra passar na mesa da viga, com isso, é válida a equação 9. A segunda ocorre quando a linha neutra passa sobre a região com mísula. A terceira é o caso da linha neutra na alma da viga, nesse caso, teremos uma solução semelhante à equação 13, porém, com alguns ajustes em função da área de concreto sob compressão (Acc). Como a primeira hipótese já possui uma equação definida, iniciaremos neste item a dedução para a segunda hipótese. Com a aplicação da equação 3, encontra-se a distância do centroide da região sob compressão até a face mais comprimida da viga, conforme Figura 8.
Figura 8 – Centro de gravidade da área comprimida.
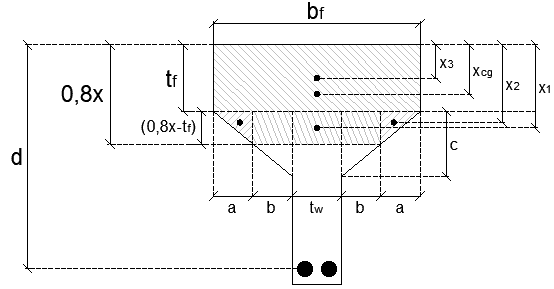
Nesse caso, onde há regiões triangulares na seção transversal, é mais complicada a dedução das equações. Devido a isso, iniciaremos com os cálculos das distâncias x1, x2 e x3 com suas respectivas áreas geométricas.
O valor de x1 é a distância do centro de gravidade do retângulo da região com mísula até a face superior da viga, conforme a Figura 8.
O valor de x2 é a distância do centro de gravidade dos triângulos à face superior da viga, conforme a Figura 8.
O valor de x3 é a distância do centro de gravidade do retângulo, referente à mesa, até a face superior da viga, conforme a Figura 8.
Cálculo da área 1 (A1) referente ao retângulo de x1.
Onde, por semelhança de triângulo, “b” é igual a:
Cálculo da área 2 (A2) referente aos dois triângulos de x2.
Onde, por semelhança de triângulo, “a” é igual a:
Cálculo da área 3 (A3) referente ao retângulo de x3.
Com as equações de A1, A2, A3, x1, x2 e x3, é possível calcular o centro de gravidade da área de concreto comprimida, substituindo-as na equação 3.
Fazendo o equilíbrio de momento, com uso da equação 4, temos a expressão abaixo.
Com a equação 21, pode-se calcular a posição da linha neutra na região com mísula. Note que essa equação é do 3º grau, com isso, se encontra três raízes. Uma dessas raízes, normalmente a menor, é a posição da linha neutra, as outras duas não terão sentido físico, por isso, devem ser desconsideradas.
Seguindo o mesmo procedimento, encontra-se a posição da LN para a terceira hipótese. Aplicando a equação 3, podemos encontrar a distância do centro de gravidade da área sob compressão até a face mais comprimida da viga. As medidas de cada dimensão, para aplicação das equações pertinentes, estão dispostas da Figura 9.
Figura 9 – Centro de gravidade da área comprimida.
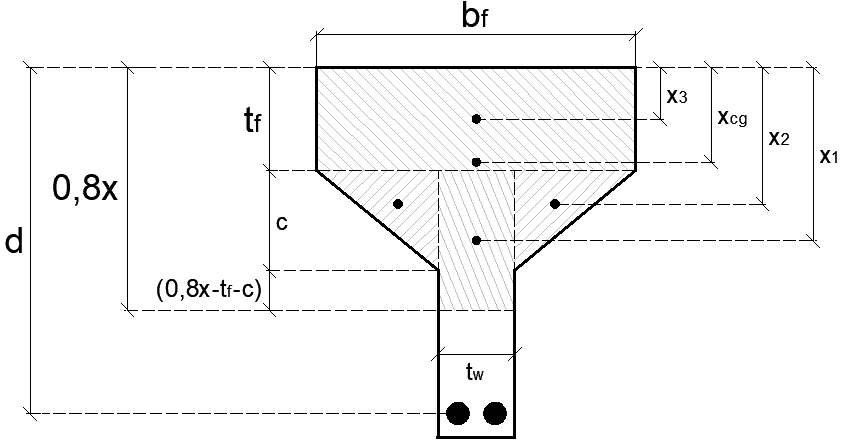
A fim de facilitar as manipulações algébricas, iniciou-se aqui a obtenção das distâncias x1, x2 e x3 e suas respectivas áreas geométricas. O valor de x1 é a distância do centro de gravidade do retângulo com hachura na alma até a face superior da viga.
O valor de x2 é a distância do centro de gravidade dos triângulos até a face superior da viga, conforme visto na Figura 9.
O valor de x3 é a distância do centro de gravidade do retângulo, referente à mesa, até a face superior da viga.
Cálculo da área 1 (A1) referente ao retângulo de x1.
Cálculo da área 2 (A2) referente aos dois triângulos de x2.
Cálculo da área 3 (A3) referente ao retângulo de x3.
Cálculo do centro de gravidade da área de concreto comprimida à face superior da viga.
Com o equilíbrio de momento na seção transversal da viga, usando a equação 4, temos a expressão abaixo.
Resolvendo a equação 29, encontram-se suas duas raízes. A menor delas é a posição da linha neutra na viga. A maior raiz deve ser desconsiderada para esse problema.
Para essa forma de viga, tipo T e I com mísula, a posição da linha neutra (LN) é obtida pelas equações 9, 21 e 30, respectivamente, para LN na mesa, LN na região com mísula e LN na alma. Da mesma forma que foi exposto no item 2.3, deve-se observar os limites estabelecidos pela NBR 6118 (ABNT, 2014).
2.5 LINHA NEUTRA EM VIGA TRAPEZOIDAL
Esse é um tipo de viga pouco usado, mas há algumas aplicações de acordo com a necessidade do projeto. Como pôde ser observado ao longo deste estudo, a obtenção da posição da linha neutra é feita pelo equilíbrio de momento na seção transversal. O modelo apresentado aqui está conforme a Figura 10, ou seja, não é válido para base maior na parte inferior.
Figura 10 – Linha neutra em viga trapezoidal.
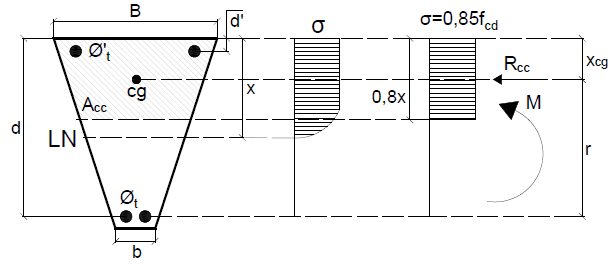
Figura 11 – Centro de gravidade da área comprimida.
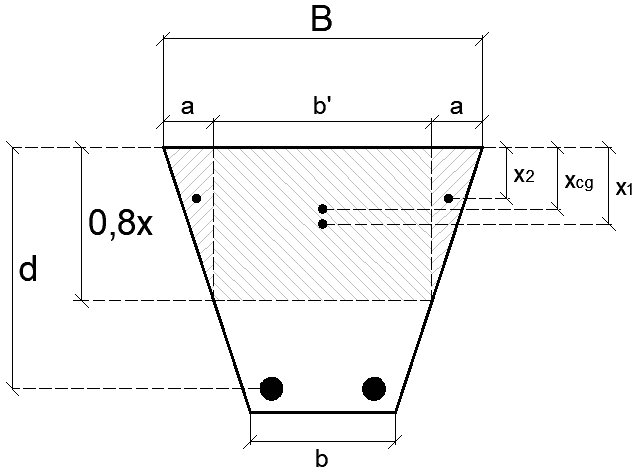
Para esse tipo de viga, em que há regiões triangulares na seção transversal, a equação para determinar a linha neutra é semelhante à viga T e I com mísula. O cálculo é iniciado com as distâncias x1 e x2 com suas respectivas áreas geométricas.
O valor de x1 é a distância do centro de gravidade do retângulo com hachura à face superior da viga, conforme indicado na Figura 11.
O valor de x2 é a distância do centro de gravidade dos triângulos à face superior da viga, conforme indicado na Figura 11.
Cálculo da área 1 (A1) referente ao retângulo de x1.
Onde, por semelhança de triângulo e de forma aproximada, b’ é igual a:
Cálculo da área 2 (A2) referente aos dois triângulos de x2.
Onde, por semelhança de triângulo e de forma aproximada, “a” é igual a:
Com as equações das áreas e as distâncias xi acima calculadas, aplicando a equação 3, tem-se o centro de gravidade da área de concreto comprimida.
Do mesmo modo das vigas anteriores, fazendo o equilíbrio de momento com a equação 4, temos a seguinte expressão.
Observe que a equação 36 é do 3º grau, com isso, ao resolvê-la, encontra-se três raízes. Normalmente, a menor raiz é a solução do problema. Esse tipo de equação não possui uma fórmula para resolvê-la, então, a melhor maneira é usar algum software. Há métodos interativos para solucionar polinômio com grau maior que dois. Um desses métodos é o de Gauss-Seidel apresentado por Boldrini et al (1980).
3. CONCLUSÃO
Mediante as analises feitas, ficou esclarecida a forma como é calculada a posição da linha neutra em vigas submetidas à flexão. Para outros tipos de seções transversais em vigas não abordadas aqui, pode-se seguir o mesmo modelo de cálculo demonstrado ao longo desse estudo. Ficou notório que quando a seção transversal é composta de figuras retangulares, chega-se a uma equação do 2º grau, já as que possuem alguma parte triangular, o problema é resolvido com equações do 3º grau. Para essas equações do 3º grau, é necessário adotar algum método matemático para encontrar as raízes, por exemplo, métodos iterativos, pois não há fórmulas para resolvê-las.
REFERÊNCIAS
ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 6118: projeto de estruturas de concreto: procedimento. Rio de Janeiro, 2014.
BOLDRINI, J. L. et al. Álgebra Linear. 3. ed. São Paulo: Harper & Row do Brasil, 1980.
CARVALHO, R. C.; FILHO, J. R. F. Cálculo e Detalhamento de Estruturas Usuais de Concreto Armado. 3. ed. São Carlos: EdUFSCar, 2007.
[1] Pós-graduado em Gestão de Obras na Construção Civil pela Faculdade Cidade Verde (FCV), Engenheiro Civil pelo Centro Universitário UNIEURO e técnico em Telecomunicações Aeronáuticas pela Escola de Especialista de Aeronáutica (EEAR).
Enviado: Agosto, 2019.
Aprovado: Outubro, 2019.



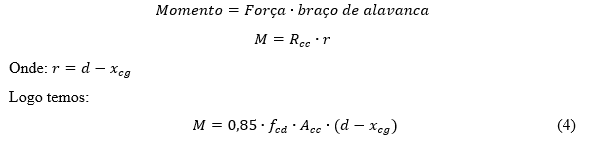


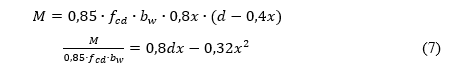
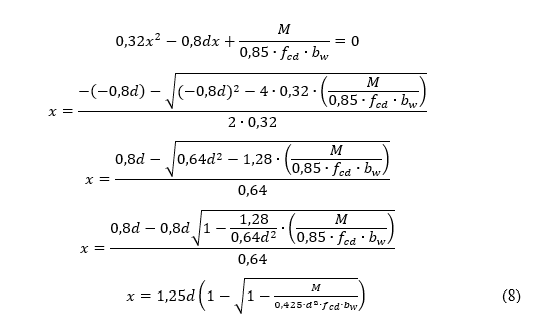
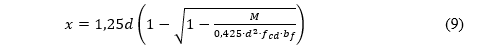

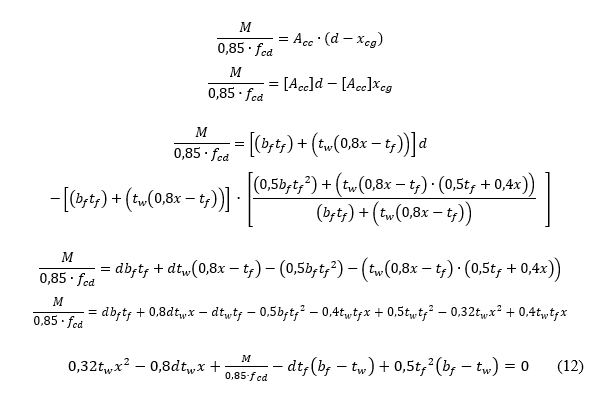
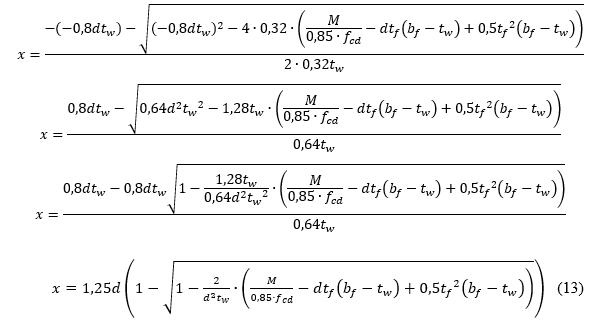

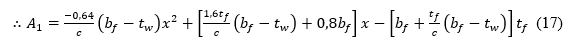
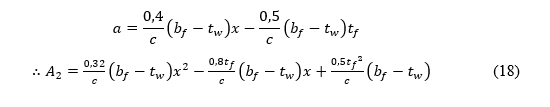
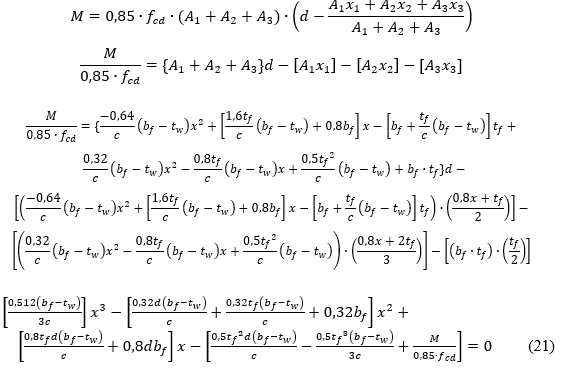


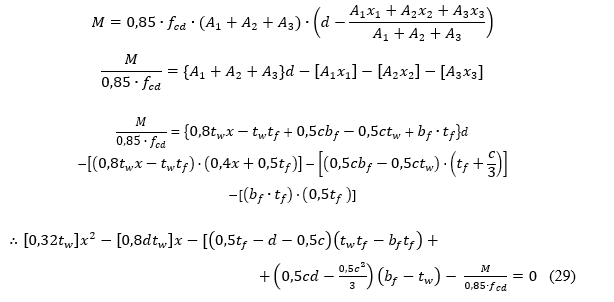
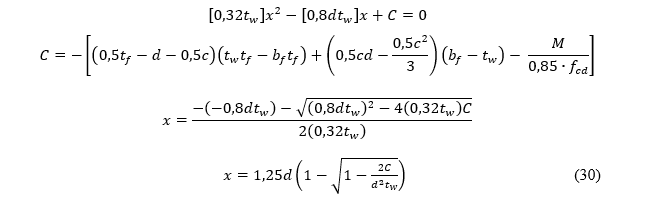
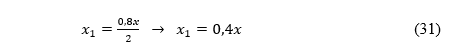
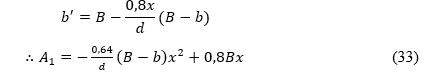
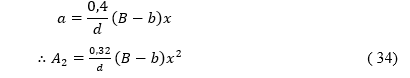
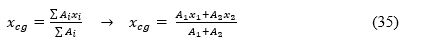
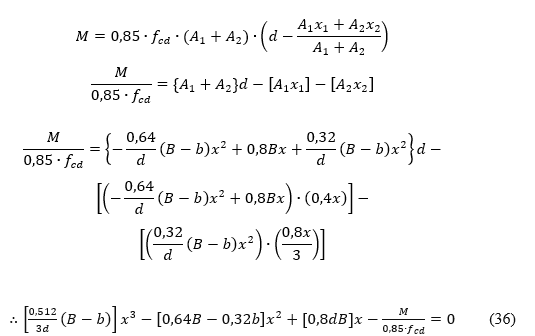

3 respostas
Parabéns Tiago pelo empenho e dedicação que você tanto demonstra. Pela área na qual você se graduou …. Parabéns pelo o artigo publicado…me sinto orgulhoso de ser seu amigo.
Muito obrigado! Forte abraço!
Parabéns Tiago achei seu artigo muito interessante . Serve ee base para o ensino de Resistência dos Materiais e Voncreto Armado.