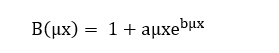ARTIGO ORIGINAL
MENDONÇA, Luan Carlos Ferreira de [1], FIGUEIREDO, Thales Gonçalves da Silva [2], GAVAZZA, Sérgio [3]
MENDONÇA, Luan Carlos Ferreira de. FIGUEIREDO, Thales Gonçalves da Silva. GAVAZZA, Sérgio. Atenuação de fótons em barreiras de proteção de concreto. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano. 07, Ed. 02, Vol. 05, pp. 66-106. Fevereiro de 2022. ISSN: 2448-0959, Link de acesso: https://www.nucleodoconhecimento.com.br/engenharia-civil/barreiras-de-protecao, DOI: 10.32749/nucleodoconhecimento.com.br/engenharia-civil/barreiras-de-protecao
RESUMO
A importância da proteção contra radiação ionizante está aumentando em paralelo com a evolução da medicina nuclear. O emprego de radiações na área da saúde inclui seções de diagnóstico e de radioterapia – desde que a sala de tratamento receba um nível de radiação que não seja deletério. Este trabalho ilustrará a eficácia do concreto como material de blindagem (ou barreira), para atenuação de raios gama monoenergéticos. Diante disso, foram traçadas as curvas da atenuação exponencial, do fator de crescimento (Buildup) e do fator de transmissão para diferentes energias do raio gama e espessuras do concreto. Obteve-se uma comparação entre métodos da Engenharia Nuclear para determinação dos fatores de Buildup – isto é, foi mostrado que ao calcular o fator de Buildup por Taylor, conseguem-se resultados próximos ao se utilizar o fator de Buildup de Berger. Diante deste contexto, o presente artigo tem como questão norteadora: Como o Engenheiro Civil pode projetar barreiras de proteção sabendo dos potenciais riscos de radiação, mantendo a segurança necessária? O objetivo geral é determinar os fatores de transmissão, em função da atenuação exponencial e do fator de Buildup, da radiação eletromagnética em blindagens de concreto, pois dessa maneira obtém-se uma equação de linha de tendência que possibilita ao engenheiro projetista determinar a espessura da barreira que assegure a devida proteção radiológica. Para o desenvolvimento deste estudo foi necessária uma pesquisa exploratória, através de revisão bibliográfica. Como houve a análise das informações obtidas, elucida-se uma pesquisa de forma qualitativa e quantitativa. Como conclusão deste estudo elaborou-se curvas dos fatores de transmissão de raios gamas em várias espessuras de concreto. Constatou-se que esses fatores de transmissão dependem da energia do raio gama e da espessura de concreto empregada. Finalmente, enfatiza-se a importância para o Engenheiro Civil obter os devidos conhecimentos técnicos ao se deparar com este tipo de projeto.
Palavras-chave: Radioterapia; Blindagem; Raios gama; Concreto; Fator de Transmissão.
1. INTRODUÇÃO
Com as crescentes inovações tecnológicas, a proteção radiológica tem papel fundamental contra os efeitos biológicos de radiações ionizantes em salas de diagnóstico/radioterapia. Segundo Podgorsak (2005), o engenheiro civil é um dos profissionais responsáveis pelo devido conhecimento das instalações médicas, com o propósito de diminuir o nível de radiação a um estágio que não seja deletério. O autor ainda destaca que:
Durante a fase de planejamento de uma instalação de equipamentos de radioterapia, um físico médico determina as espessuras exigidas de barreiras primárias e secundárias e fornece as informações ao arquiteto e engenheiro estrutural para incorporação no desenho arquitetônico da sala de tratamento. (PODGORSAK, 2005, p. 152)
Desta maneira, o cálculo das espessuras das barreiras (ou blindagens) nas salas de radioterapia é uma preocupação recorrente. Esses espaços podem abrigar aceleradores lineares de elétrons que produzem feixes de fótons de alta energia que chegam até 30 MeV (PAIVA, 2014).
Há medidas para garantir a qualidade do tratamento, de modo a minimizar as doses de radiação e evitar a exposição acidental. O princípio de segurança ALARA – As Low As Reasonably Achievable – postula que qualquer exposição à radiação ionizante deve ser mantida tão baixa quanto razoavelmente possível de ser executada (TAUHATA et al., 2014).
Já o autor Albuquerque (2014) acrescenta que, dentre os componentes usados na Construção Civil das salas, as blindagens são as que têm maior impacto sobre os custos das obras. Quando se trata de menores energias, são usadas pequenas espessuras, com emprego de materiais como revestimento de argamassas, utilização da barita como agregado miúdo e aditivos especiais, aplicados sobre a alvenaria, painéis de concreto ou gesso acartonado. Para energias mais elevadas, o concreto de massa específica normal (2,0 kg/dm³ a 2,8 kg/dm³) é bastante usado. Para a escolha do tipo de concreto a ser empregado na blindagem, Albuquerque alerta que o projetista deve, previamente:
(…) verificar que energia será blindada. O desempenho estrutural, a segurança contra incêndio, a segurança no uso e operação, a durabilidade, a manutenção e adequação ambiental da solução devem ser criteriosamente investigados, a fim de se conseguir uma solução segura, sob os diversos aspectos (ALBUQUERQUE, 2014, p. 2).
A utilização do concreto na Construção Civil, como blindagem em salas de radioterapia devido a “(…) duas propriedades primárias, sua força estrutural e sua capacidade de proteger da radiação” (FILMORE, 2004, p. 1). Em relação ao custo e propriedades, a autora Pomaro (2016, p. 1) especifica que o concreto é:
(…) um material relativamente barato e fácil de ser moldado em estruturas de várias formas. Suas boas propriedades de proteção contra nêutrons e raios gama, são devido ao seu teor intrínseco de água e densidade relativamente alta, respectivamente, tornando o material mais amplamente utilizado para proteção contra radiação.
Os autores Zorla et al. (2016) exemplificam concretos básicos de proteção contra radiação: serpentina, limonita, magnetita, hematita, ilmenita, ferrofósforo, barita, entre outros. Neste trabalho, o enfoque ficará para o concreto comum – o concreto comum. Waly e Bourham (2015, p. 1) apontam que “(…) ao modificar a composição do concreto com aditivos de densidade específica diferente irá alterar as características de blindagem de tal forma que poderá ter espessuras mais finas e coeficiente de atenuação linear maior”.
A radiação eletromagnética ionizante que será de interesse é o raio gama, pois induz danos em profundidades diversas no organismo dos seres vivos, culminando na morte de células. Desta forma, torna-se viável na terapia contra o câncer, podendo destruir ou regredir alguns tumores profundos sob a ação de feixes de radiação gama quando adequadamente aplicados (TAUHATA et al., 2014). Como menciona Podgorsak (2005), essas radiações podem vir a produzir danos ao núcleo tanto nas células sadias quanto nas tumorais. As técnicas para tratamentos estão evoluindo, possibilitando a irradiação com doses mais elevadas ao volume alvo e minimizando os danos nos tecidos sadios.
Seguindo este campo de ação, é imperativo para Engenharia Civil a realização do estudo e projeto das barreiras de proteção contra radiação, que a reduzam a níveis recomendáveis pelos órgãos regulatórios. Isso é conseguido pela determinação do fator de transmissão da barreira de proteção, que é o produto do coeficiente de atenuação linear pelo fator de crescimento (buildup) da radiação ao atravessar a espessura de material projetada para a barreira de proteção.
Diante deste contexto, o presente artigo tem como questão norteadora: Como o Engenheiro Civil pode projetar barreiras de proteção sabendo dos potenciais riscos de radiação, mantendo a segurança necessária? O objetivo geral da pesquisa é determinar os fatores de transmissão, em função da atenuação exponencial e do fator de buildup, da radiação eletromagnética em blindagens de concreto. No que tange aos objetivos específicos: Compreender as REM; caracterizar os processos de atenuação da REM com a matéria; apresentar o fator de crescimento (buildup) da REM; determinar o fator de transmissão da REM; traçar as curvas da atenuação exponencial, do fator de buildup e do fator de transmissão; comparar o fator de transmissão utilizando Taylor e Berger; relacionar o material de construção concreto com a REM.
Metodologicamente, este trabalho pauta-se em pesquisa bibliográfica, com o uso de fontes de grande notoriedade e respeito no tema, como artigos, dissertações de mestrado, teses de doutorado e livros. Para os modelos de cálculo foram utilizados os coeficientes de atenuação linear e os métodos tradicionais encontrados em Foderaro e Chilton, usando os fatores de Buildup de Taylor e Berger. Apresentando assim, de forma qualitativa e quantitativa, tanto por considerar os aspectos bibliográficos acerca do tema, quanto pela análise das informações obtidas para o cálculo dos fatores de transmissão, através de planilhas eletrônicas no Excel e gerando gráficos através da opção data import no Matlab. Do ponto de vista prático, é de suma importância que os valores aproximados e calculados teoricamente neste trabalho sejam confrontados com métodos de modelagem computacional, de modo a permitir a confiabilidade necessária nos dimensionamentos.
A primeira seção do trabalho discute sobre as diferentes radiações nucleares, bem como as interações do fóton com a matéria. A segunda seção apresenta um estudo sobre as blindagens e a utilização do concreto, como também aponta a geometria utilizada para atenuação dos fótons com a matéria. Ademais, é indicado as fórmulas de Taylor e Berger para a determinação do fator de Buildup. A terceira, destina-se aos cálculos e gráficos do Fator de Transmissão, juntamente com a análise dos resultados. PPor fim, na quarta seção, é realizada a conclusão do estudo, onde verifica-se uma equação ajustada para a determinação da espessura necessária do concreto, confrontando com a questão norteadora, que possibilita ao Analista de Blindagem, projetar barreiras de proteção com a segurança necessária.
2. RADIAÇÕES NUCLEARES
De acordo com Tauhata et al. (2014), os processos radioativos ocorrem a partir de ajustes ocorridos no núcleo atômico, ou em camadas eletrônicas, ou ainda nas interações que demandem subprocessos de estabilização com emissões de energias. Sobre a radiação nuclear:
Nome dado às partículas ou ondas eletromagnéticas emitidas pelo núcleo durante o processo de restruturação interna, para atingir a estabilidade. Devido à intensidade das forças atuantes dentro do núcleo atômico, as radiações nucleares são altamente energéticas quando comparadas com as radiações emitidas pelas camadas eletrônicas (TAUHATA et al., 2014, p. 19).
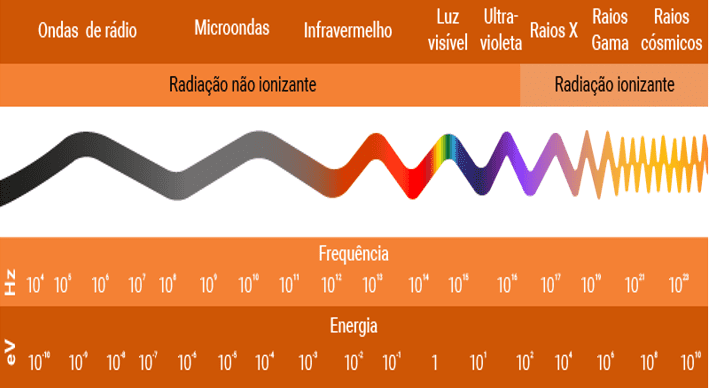
Didaticamente, as radiações podem ser divididas em ionizante e não ionizante. A última, como o próprio nome diz, não possui a capacidade de ionizar o meio, mas pode provocar vibrações de moléculas, gerando calor. A radiação ionizante, por outro lado, possui energia suficiente para arrancar elétrons e ionizar o meio (PODGORSAK, 2005). Na Figura 1, pode-se ver um esboço da distribuição de frequências e energias em conjunto com o tipo de radiação e seus respectivos comprimentos de ondas.
Figura 1 – Espectro eletromagnético (o conjunto de todos os tipos de radiação eletromagnética).
Ao interagir com a matéria, a radiação ionizante pode ser dividida em: diretamente ionizante e indiretamente ionizante. A primeira são as radiações que possuem carga, como as partículas alfa, beta e fragmentos de fissão. A segunda são as radiações que não possuem carga, como as radiações eletromagnéticas (raios gama e X), neutrinos e nêutrons (TAUHATA et al., 2014). Quanto ao alcance e atenuação das radiações:
As partículas carregadas quando interagem com um material, nele penetram até transferir toda sua energia, ou seja, possuem um alcance (range), cujo valor depende da sua energia, da densidade e tipo de material. Já as radiações eletromagnéticas, tipo gama e X, não possuem alcance, mas atenuação exponencial, dependente da sua energia e das características do material (TAUHATA et al., 2014, p. 103).
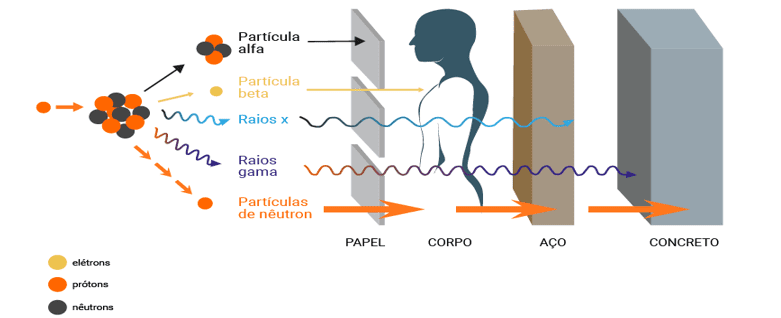
O engenheiro Gavazza (1986), conceitua que as radiações diretamente ionizantes são freadas no próprio núcleo ou no início da blindagem. Os neutrinos, por serem muito penetrantes, atravessam a blindagem sem serem afetados e essa característica faz com que a probabilidade de interagir com os materiais, incluindo o tecido humano, seja pequena, não havendo possibilidade de danos biológicos. As radiações indiretamente ionizantes, portanto, são as radiações que apresentam maiores possibilidades de penetrar e interagir no meio que os envolve. Logo, um material que atenue suficientemente essas radiações, automaticamente atenuará as demais a níveis desprezíveis. Esse fato é evidenciado na Figura 2, onde é possível observar que as radiações eletromagnéticas são extremamente penetrantes.
Figura 2 – Poder de penetração das radiações nucleares básicas.
2.1 RADIAÇÃO GAMA
A radiação gama, assim como os raios X, percorrem grandes espessuras antes de sofrer a primeira interação devido ao seu caráter ondulatório, ausência de carga e massa de repouso. Este poder de penetração, entretanto, depende da probabilidade ou secção de choque de interação para cada tipo de evento que pode absorver ou espalhar a radiação incidente (TAUHATA et al., 2014). Os mesmos autores, Tauhata et al. (2014, p. 13), explicam o efeito na transição nuclear: “Quando nucleons são deslocados para estados disponíveis, formando os estados excitados, no restabelecimento do equilíbrio eles emitem a energia absorvida sob a forma de radiação gama”. Na Figura 3 é evidenciada a emissão de um raio gama do núcleo.
Figura 3 – Representação da emissão de radiação gama pelo núcleo.
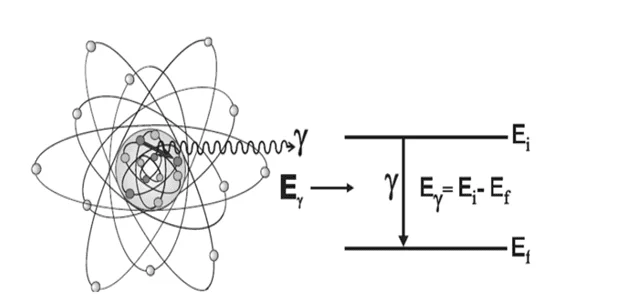
Se faz necessário ressaltar que as radiações eletromagnéticas serão sempre tratadas como um feixe de raios gama, onde cada raio gama se constitui num fóton do feixe considerado. Assim, se todos os raios gamas, ou fótons, de um feixe de raios gama, tiverem a mesma energia, o feixe é dito monoenergético. O presente estudo só considerará feixes monoenergéticos de raios gama, entendendo, ainda, como raios gama tanto o mesmo, como o raio X.
Como indica a autora Frutuoso (2015, p. 40), a diferença entre os raios X e gama está na origem da radiação: “os raios X são virtualmente idênticos aos raios gama, porém não de origem nuclear. São originárias, principalmente, da desaceleração de elétrons devido à proximidade da carga positiva de um núcleo”.
2.2 INTERAÇÃO DE FÓTONS COM A MATÉRIA
Os professores Chilton; Shultis e Faw (1984) enfatizam que, para a maioria dos estudos de proteção, quando a radiação eletromagnética interage com a matéria, as energias de 10 KeV a 10 MeV são mais importantes. Para esta faixa de energia, pode-se destacar: Efeito Fotoelétrico, Efeito Compton e Produção de Pares. O analista de blindagem pode precisar considerar também o espalhamento coerente (Rayleigh), radiação de aniquilação, fluorescência, entre outros. Estes últimos serão ignorados, pois foge do escopo deste trabalho. Na Figura 4 vê-se os principais processos de interação, dependendo tanto da energia dos fótons incidente, quanto do número atômico (Z) do meio absorvente.
Figura 4 – Interações da radiação eletromagnética com a matéria.
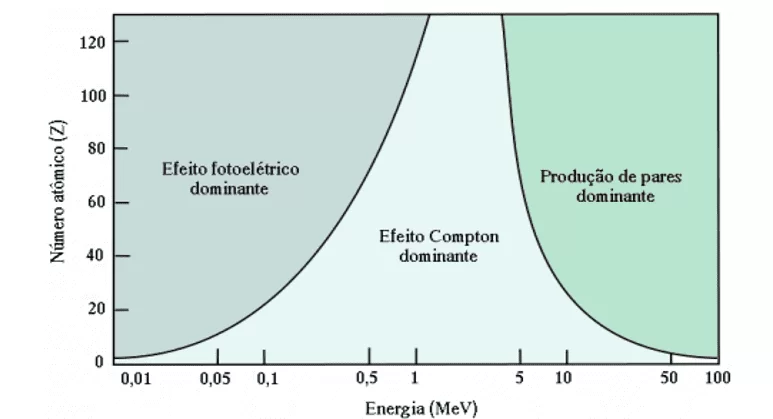
Medeiros (2018) fortifica que aparelhos utilizados em radioterapia são equipamentos capazes de acelerar elétrons a energias elevadas e lançá-los contra alvos metálicos para obtenção de fótons de bremsstrahlung (do alemão bremsen = quebrar, strahlung = radiação). A partir daí, dependendo da energia cinética dos elétrons primários e dos materiais que os fótons deverão atravessar, diferentes tipos de interação da radiação com a matéria podem ocorrer. Os tópicos a seguir apresentam conceitos fundamentais sobre os principais tipos de interação da radiação com a matéria mencionada.
2.2.1 EFEITO FOTOELÉTRICO
O físico Gleiser (1997) comenta que nesse efeito – descoberto por Hertz em 1887 – a radiação eletromagnética, atingindo uma amostra de metal eletricamente neutra, faz com que elétrons sejam removidos da superfície e o metal adquira uma carga positiva. A física clássica na época não era capaz de explicar esse evento, como por exemplo, o Eletromagnetismo de Maxwell. De modo a resolver o mistério, em março de 1905, Einstein estendeu a hipótese de Planck de que os átomos radiavam energia em pequenos pacotes, à própria luz – chamados de fótons. Einstein propôs que a luz de uma determinada frequência ocorria em múltiplos de pequenos pacotes, cada um com energia proporcional à frequência. Gleiser (2014, p. 54) complementa em seu outro livro:
Ao contrário da matéria comum que, mesmo em repouso, tem uma energia (E) igual a sua massa (m) multiplicada pelo quadrado da velocidade da luz (c²) – a famosa expressão E = mc² -, a luz nunca está em repouso. Sua energia é dada exclusivamente pela sua frequência (f), em uma fórmula extremamente simples, E = hf, onde h é a constante de Planck, uma constante da Natureza associada a efeitos quânticos.
Os autores Tauhata et al. (2014) relatam que no efeito fotoelétrico há a transferência absoluta da energia do fóton a um único elétron orbital, que fica excitado e é expelido do átomo com uma energia cinética (Ec) igual à diferença entre a energia do fóton incidente e a energia de ligação do elétron no átomo, conforme a Eq. (1). Onde hf corresponde à energia de ligação do fóton incidente e Be é a energia de ligação do elétron ao orbital. Na Figura 5 é ilustrado o processo fotoelétrico.
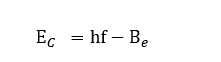 (1)
(1)
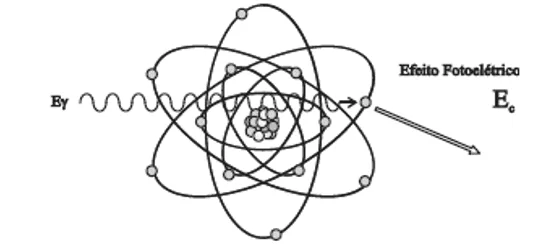
Depois de ejetar, o elétron – chamado de fotoelétron – percorre uma pequena distância e é rapidamente absorvido. A deficiência de um elétron devido à interação fotoelétrica causa a transição de um elétron de uma camada superior para a camada do elétron ejetado. Ocorre, assim, a emissão de radiação característica. A probabilidade deste processo ocorrer diminui com o aumento da energia dos fótons, mas aumenta com a elevação do número atômico do material. O efeito fotoelétrico é dominante em tecidos humanos para energias inferiores a 100 keV aproximadamente, sendo importante em imagens de raios X (FRUTUOSO, 2015).
Figura 5 – Representação do Efeito Fotoelétrico.
2.2.2 EFEITO COMPTON
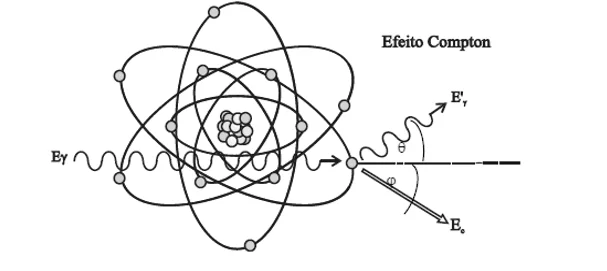
Neste efeito (ilustrado esquematicamente na Figura 6), a energia de um fóton é suficientemente maior que a energia de ligação de um elétron orbital, tornando-se improvável que esse fóton consiga transferir toda a energia a um único elétron e desaparecer, como no efeito fotoelétrico (MEDEIROS, 2018). O efeito dá-se preferencialmente em energias intermediárias, e o que ocorre é que o fóton:
(…) é espalhado por um elétron de baixa energia de ligação, que recebe somente parte de sua energia, continuando sua sobrevivência dentro do material em outra direção e com menor energia. Como a transferência de energia depende da direção do elétron emergente e esta é aleatória, de um fóton de energia fixa podem resultar elétrons com energia variável, com valores de zero até um valor máximo (TAUHATA et al., 2014, p. 81).
Figura 6 – Representação do Efeito Compton.
2.2.3 PRODUÇÃO DE PARES
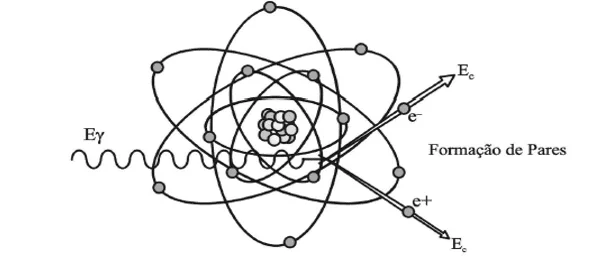
A produção em pares é um exemplo clássico da teoria da relatividade especial de Einstein, em que a energia pura do fóton é convertida em duas massas de elétrons (MARTIN, 2006). Essa energia realmente desaparece e é transformada em um par partícula/antipartícula – um elétron (e-) e um pósitron (e+) –, a partir de uma colisão com um núcleo. A transformação de energia em massa ocorre quando fótons de energia igual ou maior do que 1,02 MeV passam próximo a núcleos de número atômico elevado. Essas duas partículas transferem a sua energia cinética para o meio material, sendo que o pósitron volta a se combinar com um elétron do meio e dá origem a dois fótons, cada um com energia de 511 keV (TAUHATA et al., 2014). A Figura 7 mostra um esquema da produção de pares.
Figura 7 – Representação do Efeito de Produção de Pares.
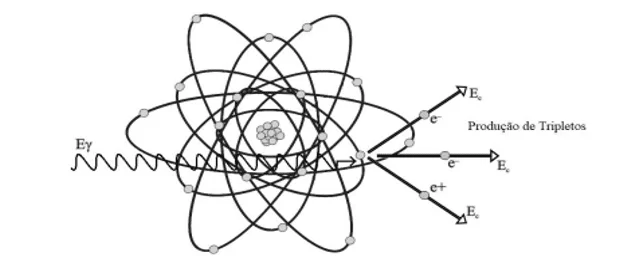
Medeiros (2018) alega que, embora com menor probabilidade, também pode ocorrer a produção de tripletos devido ao elétron gerador do campo ser ejetado (recebendo considerável energia cinética) juntamente com a produção do par elétron-pósitron. A energia mínima de um fóton para que este evento possa ocorrer deverá ser 2,044 MeV. O processo de produção de tripletos é ilustrado na Figura 8.
Figura 8 – Representação do Efeito de Produção de Tripletos.
3. BLINDAGENS
A blindagem – também nomeada como barreira ou escudo – caracteriza-se por ser peça essencial para fins de limitação de dose, pois é uma entidade física interposta entre a própria fonte de radiação ionizante e um objeto a ser protegido, de tal forma que o nível de radiação na posição daquele objeto será reduzido. Silva Neto (2016) aponta que os fatores tempo e distância em relação às fontes radioativas estão implícitos na habilidade e destreza de um técnico bem treinado para garantir a segurança contra exposições desnecessárias ou acidentais. Entretanto, quando se opera em níveis elevados de energia, além de colimadores, aventais, labirintos e outros artefatos, é necessário introduzir outro fator de segurança: a blindagem. A química Frutuoso (2015, p. 56) argumenta que:
O aumento da distância interposta entre a fonte de radiação e os lugares em que as pessoas se encontram constitui um meio eficaz para reduzir as doses de radiação, uma vez que esta varia com o inverso do quadrado da distância. Muitas vezes somente este recurso é insuficiente e, portanto, devem ser utilizados materiais como blindagem que absorvam a proporção necessária de radiação de modo que seja transmitida por eles uma dose menor que aquela correspondente aos limites autorizados.
Para o cálculo de blindagem das paredes de proteção, deve ser levado em consideração: a localização do gerador de radiação, as direções possíveis de incidência do feixe, o tempo de ocupação da máquina ou fonte, a carga de trabalho, os locais e áreas circunvizinhas, a planta da instalação (TAUHATA et al., 2014). Todas essas premissas devem obedecer sistematicamente às recomendações da CNEN – Comissão Nacional de Engenharia Nuclear. Em grande parte do mundo essa metodologia de cálculo se baseia principalmente no relatório 151 do NCRP – National Council on Radiation Protection and Measurements.
Julga-se necessário ser calculada a blindagem das portas das salas, sendo precedida de um labirinto que possa permitir espessuras e pesos de porta não muito elevados. Em energias superiores a 6 MeV, considera-se a radiação dos nêutrons, além dos raios gama produzidos pela captura desses nêutrons (BRAGA, 2016).
Um dos aspectos mais importantes é o critério para seleção do material a ser utilizado na blindagem e a sua espessura. Para Frutuoso (2015), esse processo depende do tipo de dispositivo emissor de radiação (radiação X ou gama, partículas alfa ou beta e nêutrons) e também da intensidade do feixe de radiação, porém deve ser levada em consideração a atividade do elemento radioativo, a potência do equipamento emissor de raios e se o valor da dose depois da utilização da blindagem corresponde a níveis aceitáveis.
3.1 MATERIAIS DE BLINDAGEM
Desde o projeto de construção da clínica, já existe um analista de blindagem calculando como a sala será construída – o projeto das barreiras é sempre realizado antes da construção do bunker. Um projeto final dessas salas é influenciado por muitos fatores além das propriedades de atenuação da blindagem. O projetista também deve estar ciente dos efeitos biológicos da radiação, mas também dos efeitos nas propriedades do material:
Também deve considerar os custos do material e da construção, a resistência estrutural, a manutenção, a confiabilidade e as limitações de peso e espaço. O ambiente físico da blindagem pode influenciar o design. Por exemplo, altas temperaturas podem impor tensões térmicas nas blindagens ou causar desidratação inaceitável em uma blindagem de concreto (CHILTON; SHULTIS e FAW, 1984, p. 366).
Dentre alguns tipos de materiais utilizados para blindagens em geral pode-se destacar: chumbo, urânio, tungstênio, grafite, aço, concreto e metais diversos (alumínio, zircônio e berílio). É importante notar as densidades desses materiais (tabela 1), uma vez que quanto maior for a densidade do material utilizado, menor será a espessura da barreira necessária para atenuar os fótons.
Tabela 1 – Densidade dos principais materiais para blindagem.
| Material | Densidade (g/cm³) |
| Aço | 7,87 |
| Alumínio | 2,7 |
| Berílio | 1,848 |
| Chumbo | 11,34 |
| Concreto Comum | 2,35 |
| Concreto Baritado | 3,5 |
| Concreto Magnetita | 3,55 |
| Concreto Ferrofósforo | 4,68 |
| Grafite | 1,7 |
| Tungstênio | 19,3 |
| Urânio | 19,05 |
| Zircônio | 6,489 |
Fonte: Elaborado pelos autores, 2019.
Como mostrado na tabela, o chumbo apresenta alta densidade e, mesmo sendo um material relativamente caro, é amplamente usado. Outros materiais, como o aço e concreto, são as escolhas mais comuns para projetos pois, além de boas densidades, possuem fácil disponibilidade e relativo baixo custo.
Uma consideração do ponto de vista econômico ao se projetar blindagens, é que a proteção fornecida não depende tanto da natureza do material, pois o mesmo grau de proteção pode ser conseguido por uma blindagem de chumbo fino ou por uma de concreto grosso. Por outro lado, o volume e o peso da blindagem influenciam nos custos finais de instalação (CHILTON; SHULTIS e FAW, 1984).
Importante abrir um paralelo: o uso do chumbo na proteção contra nêutrons é questionável. Enquanto o concreto apresenta um alto teor de hidrogênio, mostrando-se eficiente tanto para fótons quanto para nêutrons. O chumbo, mesmo tendo alta densidade, além de ser tóxico e possuir baixa resistência à tração – inadequado para projetos estruturais –, não é rico em hidrogênio em sua constituição e, por essa razão, as barreiras acabam sendo projetadas com espessuras mais elevadas. Outro aspecto levantado por Frutuoso (2015, p. 62) é que o chumbo “(…) só é aconselhado como blindagem nas portas. Embora esse material seja denso, lençóis ou lâminas de chumbo são difíceis de manusear”.
Apesar do cuidado relevante que o nêutron possui, ainda é uma realidade distante no que tange os custos envolvidos. O engenheiro Medeiros (2018) afirma que a teleterapia tem sido o método mais comum de radioterapia. Embora já existam equipamentos que trabalhem com feixes de prótons (uso de cíclotrons) ou nêutrons (muito restritiva devido à disponibilidade de um reator nuclear), a maioria dos equipamentos são os chamados aceleradores lineares de uso médico, ou simplesmente “linacs” – esses equipamentos geram feixes de elétrons e fótons. O autor concluiu que os linacs continuarão a ser o principal mecanismo para o tratamento de câncer por muitos anos.
Em particular, a interação dos nêutrons com a matéria é muito perigosa. Em certa etapa, o estudo teórico não é o suficiente, sendo exigido o uso de técnicas computacionais. Segundo Gavazza (1986), não se pode asseverar que, com todos os recursos teóricos e de cálculo disponíveis, seja possível garantir a determinação dos níveis “reais” de radiação no interior e nas proximidades de uma blindagem, principalmente no caso de nêutrons. Dessa forma, é sempre necessário avaliar os métodos de cálculo utilizados, testando-os contra resultados experimentais. O mesmo autor Gavazza (1986, p. 9) elucida a influência causada através do desenvolvimento computacional e o surgimento dos métodos numéricos:
Os projetos de blindagens envolvem cálculos de transporte de nêutrons e raios gama, em sistemas com geometrias complexas, muitas vezes através de vazios ou ainda em meios com espessuras equivalentes a vários livres caminhos médios (penetração profunda). Com o desenvolvimento dos computadores e o surgimento de métodos numéricos mais eficientes, as técnicas de cálculo evoluíram de “educadas” estimativas e métodos semi-empíricos para tratamentos mais rigorosos, baseados nas soluções da equação de transporte de Boltzamnn, através de programas computacionais sofisticados.
Medeiros (2018) sustenta que os fotonêutrons gerados pelo linac, ou mesmo nas paredes, piso e teto, contribuem para a dose no paciente, mas são usualmente desconsideradas no planejamento. O autor ainda reforça que não obstante:
(…) nêutrons possuem um papel importante de ordem prática, pois além de “contaminarem” o feixe principal de fótons, também podem espalhar-se por toda a sala de tratamento e pelo labirinto de entrada, demandando especial cuidado por ocasião do projeto de blindagem radiológica da porta de acesso ao bunker. Como a porta de acesso não pode ser construída com a mesma espessura de concreto que as paredes adjacentes de forma funcional e/ou econômica, há necessidade de utilizar-se materiais como o polietileno borado ou cádmio para garantir-lhe uma adequada blindagem contra nêutrons.
Não é difícil perceber que o estudo de blindagem é relativamente complexo e envolve alguns fatores que devem ser cuidadosamente analisados dependendo da finalidade. Frente a isso, para proceder à escolha do material para proteção, é necessário conhecer previamente todos os detalhes e ainda se as instalações apresentarão nêutrons envolvidos, pois, assim, qualquer material mencionado oferece boa proteção contra a radiação. Em seguida, efetua-se um balanço entre o volume e o custo final de cada blindagem, de modo a selecionar o melhor material, oferecendo tanto a proteção necessária quanto um menor impacto económico. Todavia, geralmente essa decisão não é fácil para o analista.
3.1.1 UTILIZAÇÃO DO CONCRETO
O estudo em questão limitou-se à blindagem para o concreto comum, por este ser muito utilizado de modo geral na Construção Civil. Albuquerque (2014) relata que o concreto convencional é muito usado e tem como vantagens o pequeno custo de aquisição, a tradição construtiva deste material, que é utilizado em larga escala no Brasil para a execução de estruturas de edifícios, e a disponibilidade de matérias-primas disponíveis em quase todas as regiões do país.
As salas de tratamento com megavoltagem, os bunkers, são mais comumente blindados com concreto comum a fim de minimizar os custos de construção. O efeito Compton é o modo predominante nesta faixa de energia. Nos casos em que a modalidade radioterápica é realizada através de baixa/média energia – radioterapia superficial –, o efeito fotoelétrico é o mais dominante, tornando o chumbo muito eficiente (PODGORSAK, 2005).
De acordo com Chilton; Shultis e Faw (1984), o concreto é preparado a partir de uma mistura, em peso, de cerca de 13% de cimento, 7% de água (incluindo água no agregado) e 80% de agregado. Deve-se observar que diferentes tipos de concreto podem ser preparados variando a natureza do agregado, em razão de melhorar as propriedades de atenuação dos fótons. Pois, assim, aumenta-se a densidade do concreto, sendo eficaz mesmo em espessuras reduzidas de blindagens, o que é, em geral, de grande interesse.
Ao referir-se a tal assunto, Albuquerque (2014) comenta que os concretos de elevada massa específica são produzidos como os concretos normais, formados por uma mistura de aglomerantes, agregados, adições e aditivos. Entretanto, é necessária a utilização de agregados de elevada massa específica.
Normalmente, esses agregados são minerais com presença acentuada de óxido de elementos químicos densos. Já os aglomerantes podem ser escolhidos entre os diversos tipos de cimentos Portland, produzidos e comercializados no Brasil – assim como os aditivos e as adições (ALBUQUERQUE, 2014).
Ao entender a influência causada pela densidade nos projetos, pode-se delimitar que, no estudo de blindagem, o principal fator é a energia do fóton. Deste modo, ao passo que a energia aumentar, o poder de absorção do material consequentemente diminui.
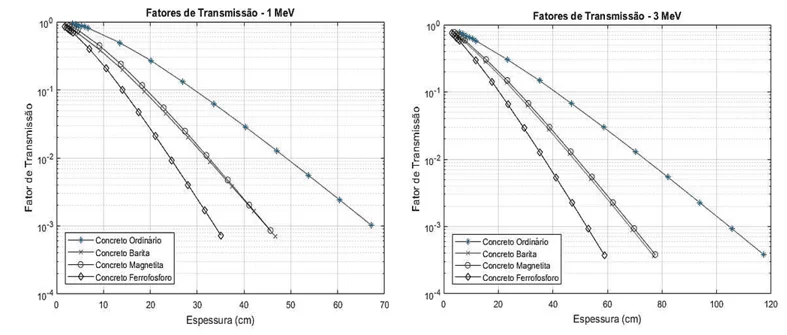
Cabe citar o trabalho de Mendonça e Ferreira (2018), que fornece uma visão sobre o desenvolvimento do concreto de alta densidade para barreiras de proteção. As demonstrações gráficas deste estudo teórico podem ser observadas na figura 9. Os autores indicam que, quanto maior a energia, maior será a transmissão na barreira de concreto. Nota-se também que, quanto maior a densidade do concreto, menor será o fator de transmissão para uma mesma energia. Isso também pode ser verificado quando se compara o comportamento de cada concreto para uma mesma faixa de energia. Os fatores de transmissão foram para energias de 1 MeV e 3 MeV de um raio gama de caráter monoenergético, sendo quatro tipos de composição química do concreto: Comum, Barita, Magnetita e Ferrofósforo. Observa-se que para o FT de 5×10-4 para o concreto comum/ordinário: a espessura chega perto dos 120 cm com 3 MeV e, quando o mesmo está com 1 MeV, a espessura está perto dos 70 cm.
Figura 9 – FT de diferentes tipos de concreto para as energias de 1 e 3 MeV.
Para materiais compostos comumente modelados em problemas de transporte de radiação, como o concreto, há compilações de dados atômicos convenientemente formatados para usar no MCNP – Monte Carlo N-Particle Transport – e em outros códigos. Um desses manuais é o Compendium of Material Composition Data for Radiation Transport Modeling que, como parâmetro de observação, lista vinte e cinco diferentes tipos de composição de concreto.
Não obstante, Pomaro (2016) relata que autores contemporâneos concordam que as informações técnicas necessárias para determinar um valor limite apropriado de radiação no que diz respeito à solidez das estruturas de concreto são pobres, especialmente no que se refere à avaliação de durabilidade do concreto. Assim, há a necessidade de mais testes experimentais que indiquem modelos preditivos de deterioração e validação do concreto. A autora ainda explica que preocupações com antigas usinas nucleares estão aumentando, sendo a principal razão para um novo interesse na avaliação dos danos radioativos das blindagens de concreto.
3.2 ATENUAÇÃO DE FÓTONS COM A MATÉRIA
3.2.1 GEOMETRIA DE FEIXE ESTREITO
Quando um feixe de raio gama monoenergético incide sobre um material absorvedor, parte do feixe de fótons é espalhada, parte é absorvida e uma fração o atravessa sem interagir e não é detectado. Tal feixe é estreito e, portanto, tem sua intensidade radiante significativamente reduzida. Quando são completamente removidos, no caso de feixe bem colimado e estreito, é caracterizada uma condição de boa geometria (TAUHATA et al., 2014). A representação esquemática se encontra na Figura 10.
Figura 10 – Geometria de feixe estreito.
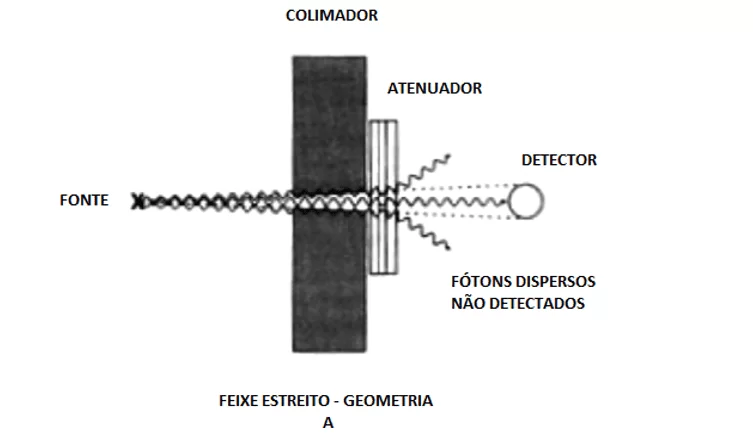
O autor Knoll (1979) relata que os raios gama monoenergéticos são colimados em um feixe estreito e autorizados a atacar um detector depois de passar por meio de um absorvedor de espessura variável, o resultado deve ser a atenuação exponencial simples dos raios gama. Sobre o assunto, Tauhata et al. (2014) afirma que é possível observar que a intensidade do feixe diminui a cada espessura de blindagem adicionada e, teoricamente, nunca se torna zero. A atenuação de um feixe de fótons por um material de espessura x é mostrado na Figura 11.
Figura 11 – Atenuação de um feixe de fótons por um material de espessura X.
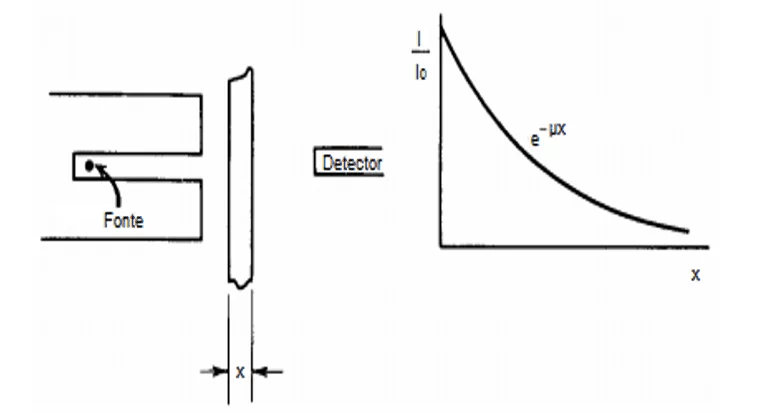
Para condições de boa geometria, a atenuação da radiação é dada pela lei de Beer-Lambert:
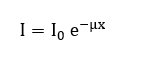 (2)
(2)
Onde:
I0: Intensidade do feixe antes de atravessar o material absorvedor.
I: Intensidade do feixe após atravessar o material absorvedor.
x: espessura do absorvedor.
μ: coeficiente de atenuação linear (cm-1).
Knoll (1979) certifica que o coeficiente de atenuação linear representa a probabilidade, por unidade de comprimento, de que uma radiação eletromagnética seja absorvida por um material. O coeficiente é a probabilidade de o feixe sofrer atenuação devido ao espalhamento compton, absorção fotoelétrica ou formação de pares, a Eq. (3) mostra o somatório :
(3)
Onde ![]() é o coeficiente de atenuação linear Compton total, K é o coeficiente de atenuação devido ao efeito fotoelétrico e τ é o coeficiente de atenuação linear devido à formação de pares.
é o coeficiente de atenuação linear Compton total, K é o coeficiente de atenuação devido ao efeito fotoelétrico e τ é o coeficiente de atenuação linear devido à formação de pares.
É surpreendente que μ seja uma constante, pois é o somatório dos coeficientes de processos de interações individuais, cada um dos quais é uma função da energia dos raios gama, número atômico, a massa e densidade do meio absorvente. No entanto, as intensidades de fótons medidos versus a espessura do absorvedor produzem consistentemente linhas retas quando plotadas em escalas semi-log (MARTIN, 2006).
3.2.2 GEOMETRIA DE FEIXE LARGO
Segundo Singh et al. (2013), a exposição a raios gama ocorre não apenas na radioterapia, mas também em indústrias, centros de pesquisa nuclear, reatores nucleares e armas nucleares. Logo, um detalhado estudo é necessário, principalmente devido a fatídicos acidentes nucleares (Fukushima, Chernobyl, Three Mile Island, etc).
Neste contexto, há uma indesejável situação enfrentada por físicos, engenheiros e oncologistas: as radiações secundárias. Esse processo pode ocorrer quando há acúmulo de fótons da parte colidida do feixe incidente, alterando o comportamento exponencial da atenuação do feixe, ocasionando assim, um crescimento na intensidade do feixe. Desta forma, determina-se o fator de Buildup, ou valor de correção, que é um fator multiplicativo inserido para obter a resposta corrigida aos fótons não colididos, incluindo a contribuição de fótons dispersos (SINGH et al., 2013).
Isso representa uma situação que o projetista se defronta no dia a dia: a má geometria – também descrito como “pobre geometria” –, ou seja, a geometria com feixe largo. Dificilmente consegue-se colimações perfeitas de boa geometria devido a muitas dificuldades experimentais. Neste caso, além dos fótons transmitidos alcançarem o detector, existe a possibilidade de que outros fótons possam ser detectados, como se tivessem sido transmitidos após interagirem com o meio material (determinada como radiação secundária). A representação do processo se encontra na Figura 12, onde é possível ver que alguns fótons são espalhados exatamente no detector.
Figura 12 – Geometria de feixe largo.
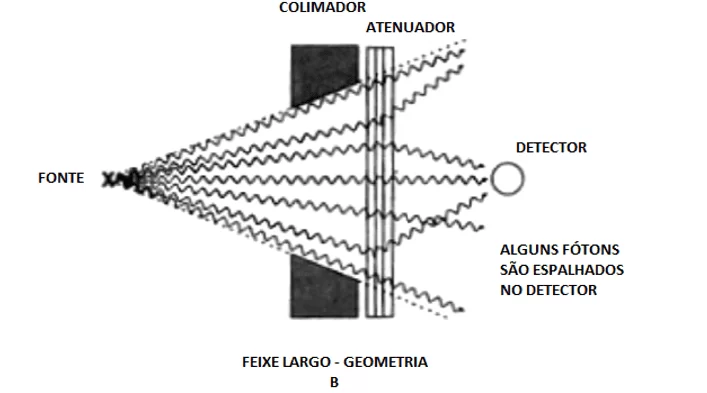
Como o detector contará os raios gama espalhados (secundários) bem como os diretos (primários), o sinal será maior que o registrado com boa geometria. Assim, a Eq. (1) não poderá dar a resposta correta, portanto a lei exponencial de Beer-Lambert é violada. Para que a equação continue a ser utilizada nessas situações, ela deve ser escrita como:
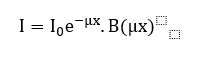 (4)
(4)
Onde:
![]() : fator multiplicativo da radiação
: fator multiplicativo da radiação
O fator de Buildup para um meio infinito pode ser definido pela Eq. (5). Onde a radiação total é a soma da radiação não colidida com a radiação espalhada. Como Wood (1981) comenta: “é a relação entre o fluxo do feixe largo e o fluxo do feixe estreito”.
 (5)
(5)
Shultis e Faw (2000) declaram que, de longe, o maior conjunto de dados de fatores de Buildup é em relação a uma fonte monoenergética e um detector situado em um meio homogêneo infinito com geometria de um ponto isotrópico (esta situação é a abordada no trabalho). Existem também outras geometrias como a de plano paralelo e o plano isotrópico.
Já Chilton; Shultis e Faw (1984, p.196) acrescentam que o sucesso do conceito dos fatores de Buildup na proteção de fótons é devido “(…) não apenas às regularidades dos coeficientes de interação dos fótons com a energia, mas também ao fato de que a radiação não colidida é o componente mais penetrante e, portanto, tende a dominar o processo de penetração”.
É significativo lembrar que para atenuação de fótons, o uso de atenuação exponencial e fatores de Buildup é uma técnica muito poderosa. Mas deve-se tomar cuidado quanto à extensão dessa técnica para problemas de atenuação de nêutrons, embora muito atraente, deve ser feita com cautela. A parcela não colidida para nêutrons é geralmente muito mais difícil do que para os fótons. Assim, não é muito prático utilizar esta técnica para nêutrons, pois o fator de Buildup depende fortemente da composição do material, o espectro de energia de nêutrons incidente e, acima de tudo, a geometria do problema particular (SHULTIS e FAW, 2000).
3.2.3 TIPOS DE BLINDAGEM CONTRA FÓTONS
As blindagens podem ser classificadas em dois tipos de camadas: 1) Blindagem de camada única: onde é possível ter um único elemento puro ou ligas de misturas homogêneas; 2) Blindagem multicamadas: como o próprio nome indica, é um tipo de blindagem onde há mais de uma camada. O valor de Buildup tende a ser diferente quando a blindagem é multicamadas comparada às de camada única (WOOD, 1981).
3.2.4 MÉTODOS EMPÍRICOS PARA O FATOR DE BUILDUP
Nos cálculos que envolvem o fator de Buildup, é conveniente ter uma expressão matemática para B. Uma variedade de fórmulas foi proposta, cujos parâmetros foram ajustados para dar uma estimativa razoável (WOOD, 1981). Essas fórmulas são baseadas em dados experimentais para reproduzir o fator de Buildup da radiação em situação de feixe largo.
Podem-se citar as fórmulas: Taylor, Linear, Quadrática, Capo, Berger e Geométrica. Para multicamadas: Kalos, Bowman-Trubey, Broder, Harima-Nishiwaki. Os autores Shultis e Faw (2000) comentam que as fórmulas de Taylor e Berger são muito usadas na prática, pois apresentam ampla aplicação em códigos computacionais. Neste trabalho, serão empregadas as fórmulas de Taylor e Berger – analisadas a seguir:
- Fórmula de Taylor: Especificamente, sugere-se que os Buildup de meio infinito sejam expressos com uma soma de dois exponenciais. A representação matemática se encontra abaixo:
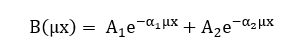 (6)
(6)
Onde: ![]() são valores tabelados em função do material e do valor da energia do raio gama e, A2 = 1- A1
são valores tabelados em função do material e do valor da energia do raio gama e, A2 = 1- A1
- Fórmula de Berger: Cerca de alguns anos após Taylor, Berger sugeriu adequar os valores:
(7)
Em que os parâmetros a e b são valores tabelados que dependem da energia, do meio atenuante e do tipo de resposta.
Ressalta-se que, além de métodos empíricos, existem os analíticos e os estatísticos. Analiticamente, o fator de Buildup pode ser resolvido através da equação de transporte de Boltzmann. Estatisticamente, a técnica de Monte Carlo é, atualmente, a técnica mais potente e comumente usada para analisar problemas complicados – esta técnica baseia-se em produtos típicos da era moderna do computador.
3.3 A INFLUÊNCIA DA GEOMETRIA FINITA NO FATOR DE BUILDUP
A geometria da fonte e a natureza do material são aspectos importantes a serem considerados por um analista de blindagem, porém outra situação deve ser também investigada: a influência da geometria finita.
Deve-se tomar conhecimento que muitas vezes é preciso utilizar o fator de correção (FC) para corrigir o valor de Buildup, por este indicar um valor maior que o necessário. A Figura 13 elucida um meio de corrigir o fator de Buildup de meio infinito (Binf), de modo a obter o fator de Buildup finito-adequado (Bfin) para um detector através de uma blindagem de espessura finita (CHILTON; SHULTIS e FAW, 1984).
Figura 13 – Fatores de correção para fatores de buildup de espessura finita.
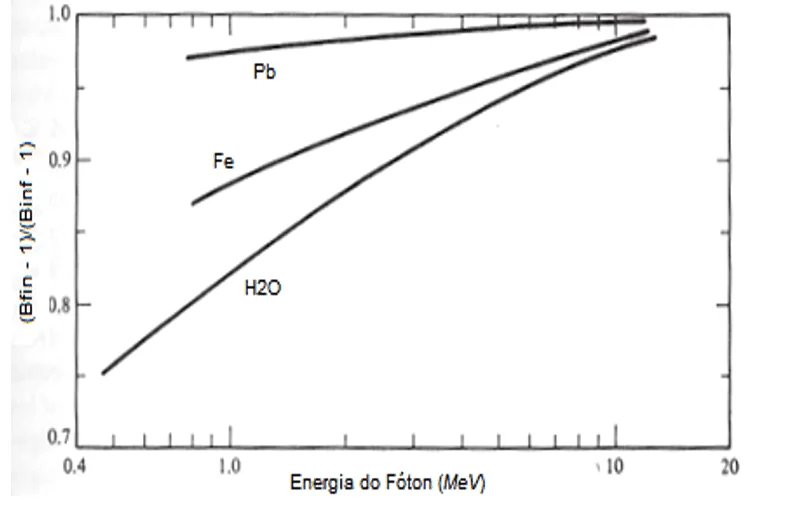
No sentido de simplificar o problema, o marcador gerado entre a energia correspondente e o material estudado será o valor do fator de correção (FC).
À medida que encontrar o FC – representante no eixo das ordenadas – é possível reformular e achar o valor de Buildup finito (Bfin). Onde o FC é dado por:
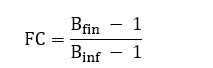 (9)
(9)
Assim, o Buildup finito-adequado (Bfin) pode ser escrito como:
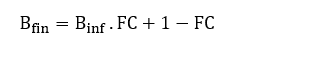 (10)
(10)
Para representar o concreto como material no fator de correção, normalmente utiliza-se os dados da água, conforme Spencer (1962, p. 82) comenta:
Uso de dados da água para representar o concreto dá resultados normalmente dentro da precisão de cálculo. Deve ser lembrado que perto da fonte, onde a contribuição total de fótons dispersos é uma parte relativamente pequena de resposta do detector, a diferença entre a água e o concreto é insignificante, certamente não tão grande que 10%; e com grandes penetrações a diferença pode ser maior que 10%.
Na Tabela 2 são apresentados os valores aproximados dos fatores de correção com suas energias correspondentes para o concreto (água).
Tabela 2 – Valores do FC para o Concreto usando dados da água.
| Material | E (MeV) | Fator de Correção (FC) |
| Concreto | 0,5 | 0,757 |
| 0,6 | 0,775 | |
| 0,7 | 0,790 | |
| 0,8 | 0,805 | |
| 0,9 | 0,815 | |
| 1 | 0,820 | |
| 2 | 0,874 | |
| 3 | 0,905 | |
| 4 | 0,930 | |
| 5 | 0,944 | |
| 6 | 0,953 | |
| 7 | 0,959 | |
| 8 | 0,964 | |
| 9 | 0,969 | |
| 10 | 0,974 |
Fonte: Elaborado pelos autores, 2019.
4. DETERMINAÇÃO DOS FATORES DE TRANSMISSÃO EM UMA BARREIRA DE CONCRETO
4.1 FATORES DE TRANSMISSÃO
A radiação gama, ao interagir com uma barreira de concreto, sofrerá a ação da atenuação exponencial e do fator de Buildup – ambos explicados em itens anteriores. O produto desses dois efeitos caracterizará o fator de transmissão (FT) da barreira, conforme a equação:
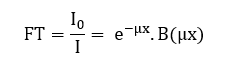 (11)
(11)
Mendonça e Ferreira (2018) relatam que o FT é o quanto da radiação é transmitida ao atravessar uma blindagem em um determinado material. Sendo que a atenuação exponencial é o termo que predomina no produto. Como o FT depende da energia da radiação incidente e das características do material, notou-se comportamentos diferentes para as curvas do FT em diferentes tipos de concreto.
Nos próximos itens serão apresentados os métodos para a determinação das curvas dos fatores de transmissão para diferentes espessuras do concreto comum. Para este estudo, foi realizada uma análise para os métodos tradicionais de cálculo de blindagem, usando fatores de Buildup de Taylor (FODERARO, 1978) e Berger (CHILTON, 1984) para energias de 1 MeV, 3 MeV e 6 MeV.
4.2 MÉTODO DE FODERARO
“The Photon Schielding Manual” (Manual de Blindagem de Fótons), desenvolvido por Anthony Foderaro, reúne todas as equações e tabelas de dados necessárias para executar talvez 90% dos cálculos de blindagem de fótons. De acordo com o Dr. Foderaro, este livro foi elaborado minuciosamente para atender as necessidades de analistas de blindagem e estudantes de radiações, deste modo, pode-se usar o manual com confiança (FRUTUOSO, 2015). Sendo assim, nos tópicos 4.2.1 e 4.2.2 serão apresentados os resultados dos Fatores de Transmissão utilizando-se os métodos de Taylor e Berger.
4.2.1 FT PELO MÉTODO DE FODERARO COM BUILDUP DE TAYLOR
Os resultados dos fatores de transmissão utilizando-se a fórmula de Taylor se encontram nos Quadros (1) a (3):
Quadro 1 – FT (1 MeV) para o concreto comum utilizando Taylor.
| μx (lcm) a | x (cm) b | FC c | Binf d | AE e | Bfin f | FT g |
| 0,0000 | 0,0 | 0,820 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
| 0,1490 | 1,0 | 0,820 | 1,2089 | 0,8616 | 1,1713 | 1,0091 |
| 0,2980 | 2,0 | 0,820 | 1,4206 | 0,7423 | 1,3449 | 0,9983 |
| 0,4470 | 3,0 | 0,820 | 1,6351 | 0,6395 | 1,5208 | 0,9726 |
| 0,5960 | 4,0 | 0,820 | 1,8525 | 0,5510 | 1,6990 | 0,9362 |
| 0,7450 | 5,0 | 0,820 | 2,0728 | 0,4747 | 1,8797 | 0,8923 |
| 0,8940 | 6,0 | 0,820 | 2,2960 | 0,4090 | 2,0627 | 0,8437 |
| 1,0430 | 7,0 | 0,820 | 2,5222 | 0,3524 | 2,2482 | 0,7923 |
| 1,1920 | 8,0 | 0,820 | 2,7514 | 0,3036 | 2,4361 | 0,7396 |
| 1,3410 | 9,0 | 0,820 | 2,9836 | 0,2616 | 2,6266 | 0,6871 |
| 1,4900 | 10,0 | 0,820 | 3,2190 | 0,2254 | 2,8195 | 0,6354 |
| 1,7880 | 12,0 | 0,820 | 3,6989 | 0,1673 | 3,2131 | 0,5375 |
| 2,0860 | 14,0 | 0,820 | 4,1916 | 0,1242 | 3,6171 | 0,4492 |
| 2,3840 | 16,0 | 0,820 | 4,6973 | 0,0922 | 4,0318 | 0,3717 |
| 2,6820 | 18,0 | 0,820 | 5,2163 | 0,0684 | 4,4574 | 0,3050 |
| 2,9800 | 20,0 | 0,820 | 5,7489 | 0,0508 | 4,8941 | 0,2486 |
a) Número de livres caminhos médio;
b) Espessura da blindagem;
c) Fator de correção;
d) Buildup infinito;
e) Atenuação exponencial;
f) Buildup finito-adequado;
g) Fator de transmissão.
Fonte: Elaborado pelos autores, 2019.
Quadro 2 – FT (3 MeV) para o concreto comum utilizando Taylor.
| μx (lcm) | x (cm) | FC | Binf | AE | Bfin | FT |
| 0 | 0,0 | 0,905 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
| 0,0852 | 1,0 | 0,905 | 1,0590 | 0,9183 | 1,0534 | 0,9674 |
| 0,1704 | 2,0 | 0,905 | 1,1181 | 0,8433 | 1,1068 | 0,9334 |
| 0,2556 | 3,0 | 0,905 | 1,1772 | 0,7745 | 1,1603 | 0,8986 |
| 0,3408 | 4,0 | 0,905 | 1,2364 | 0,7112 | 1,2139 | 0,8633 |
| 0,4260 | 5,0 | 0,905 | 1,2956 | 0,6531 | 1,2675 | 0,8279 |
| 0,5112 | 6,0 | 0,905 | 1,3549 | 0,5998 | 1,3212 | 0,7924 |
| 0,5964 | 7,0 | 0,905 | 1,4143 | 0,5508 | 1,3750 | 0,7573 |
| 0,6816 | 8,0 | 0,905 | 1,4738 | 0,5058 | 1,4288 | 0,7227 |
| 0,7668 | 9,0 | 0,905 | 1,5333 | 0,4645 | 1,4826 | 0,6887 |
| 0,8520 | 10,0 | 0,905 | 1,5929 | 0,4266 | 1,5366 | 0,6554 |
| 1,0224 | 12,0 | 0,905 | 1,7123 | 0,3597 | 1,6446 | 0,5916 |
| 1,1928 | 14,0 | 0,905 | 1,8319 | 0,3034 | 1,7529 | 0,5318 |
| 1,3632 | 16,0 | 0,905 | 1,9518 | 0,2558 | 1,8614 | 0,4762 |
| 1,5336 | 18,0 | 0,905 | 2,0720 | 0,2158 | 1,9702 | 0,4251 |
| 1,7040 | 20,0 | 0,905 | 2,1925 | 0,1820 | 2,0792 | 0,3783 |
Fonte: Elaborado pelos autores, 2019.
Quadro 3 – FT (6 MeV) para o concreto comum utilizando Taylor.
| μx (lcm) | x (cm) | FC | Binf | AE | Bfin | FT |
| 0,0000 | 0,0 | 0,952 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
| 0,0627 | 1,0 | 0,952 | 1,0282 | 0,9392 | 1,0268 | 0,9644 |
| 0,1254 | 2,0 | 0,952 | 1,0564 | 0,8821 | 1,0537 | 0,9295 |
| 0,1881 | 3,0 | 0,952 | 1,0845 | 0,8285 | 1,0805 | 0,8952 |
| 0,2508 | 4,0 | 0,952 | 1,1127 | 0,7782 | 1,1073 | 0,8616 |
| 0,3135 | 5,0 | 0,952 | 1,1408 | 0,7309 | 1,1340 | 0,8288 |
| 0,3762 | 6,0 | 0,952 | 1,1689 | 0,6865 | 1,1608 | 0,7968 |
| 0,4389 | 7,0 | 0,952 | 1,1969 | 0,6447 | 1,1875 | 0,7656 |
| 0,5016 | 8,0 | 0,952 | 1,2250 | 0,6056 | 1,2142 | 0,7353 |
| 0,5643 | 9,0 | 0,952 | 1,2530 | 0,5688 | 1,2408 | 0,7057 |
| 0,6270 | 10,0 | 0,952 | 1,2810 | 0,5342 | 1,2675 | 0,6771 |
| 0,7524 | 12,0 | 0,952 | 1,3369 | 0,4712 | 1,3207 | 0,6224 |
| 0,8778 | 14,0 | 0,952 | 1,3927 | 0,4157 | 1,3739 | 0,5711 |
| 1,0032 | 16,0 | 0,952 | 1,4485 | 0,3667 | 1,4270 | 0,5233 |
| 1,1286 | 18,0 | 0,952 | 1,5042 | 0,3235 | 1,4800 | 0,4787 |
| 1,2540 | 20,0 | 0,952 | 1,5597 | 0,2854 | 1,5329 | 0,4374 |
Fonte: Elaborado pelos autores, 2019.
4.2.2 FT PELO MÉTODO DE FODERARO COM BUILDUP DE BERGER
Os resultados dos fatores de transmissão utilizando-se a fórmula de Berger se encontram nos Quadros (4) a (6):
Quadro 4 – FT (1 MeV) para o concreto comum utilizando Berger.
| μx | x (cm) | FC | Binf | AE | Bfin | FT |
| 0,0000 | 0,0 | 0,820 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
| 0,1490 | 1,0 | 0,820 | 1,2171 | 0,8616 | 1,1781 | 1,0150 |
| 0,2980 | 2,0 | 0,820 | 1,4365 | 0,7423 | 1,3579 | 1,0080 |
| 0,4470 | 3,0 | 0,820 | 1,6581 | 0,6395 | 1,5396 | 0,9847 |
| 0,5960 | 4,0 | 0,820 | 1,8819 | 0,5510 | 1,7232 | 0,9495 |
| 0,7450 | 5,0 | 0,820 | 2,1080 | 0,4747 | 1,9085 | 0,9060 |
| 0,8940 | 6,0 | 0,820 | 2,3363 | 0,4090 | 2,0958 | 0,8572 |
| 1,0430 | 7,0 | 0,820 | 2,5669 | 0,3524 | 2,2849 | 0,8052 |
| 1,1920 | 8,0 | 0,820 | 2,7999 | 0,3036 | 2,4759 | 0,7517 |
| 1,3410 | 9,0 | 0,820 | 3,0352 | 0,2616 | 2,6688 | 0,6981 |
| 1,4900 | 10,0 | 0,820 | 3,2728 | 0,2254 | 2,8637 | 0,6454 |
| 1,7880 | 12,0 | 0,820 | 3,7551 | 0,1673 | 3,2592 | 0,5452 |
| 2,0860 | 14,0 | 0,820 | 4,2470 | 0,1242 | 3,6626 | 0,4548 |
| 2,3840 | 16,0 | 0,820 | 4,7487 | 0,0922 | 4,0739 | 0,3755 |
| 2,6820 | 18,0 | 0,820 | 5,2602 | 0,0684 | 4,4934 | 0,3075 |
| 2,9800 | 20,0 | 0,820 | 5,7818 | 0,0508 | 4,9210 | 0,2500 |
Fonte: Elaborado pelos autores, 2019.
Quadro 5 – FT (3 MeV) para o concreto comum utilizando Berger.
| μx | x (cm) | FC | Binf | AE | Bfin | FT |
| 0,0000 | 0,0 | 0,905 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
| 0,0852 | 1,0 | 0,905 | 1,0639 | 0,9183 | 1,0579 | 0,9715 |
| 0,1704 | 2,0 | 0,905 | 1,1279 | 0,8433 | 1,1158 | 0,9410 |
| 0,2556 | 3,0 | 0,905 | 1,1920 | 0,7745 | 1,1738 | 0,9090 |
| 0,3408 | 4,0 | 0,905 | 1,2561 | 0,7112 | 1,2318 | 0,8761 |
| 0,4260 | 5,0 | 0,905 | 1,3203 | 0,6531 | 1,2899 | 0,8424 |
| 0,5112 | 6,0 | 0,905 | 1,3846 | 0,5998 | 1,3480 | 0,8085 |
| 0,5964 | 7,0 | 0,905 | 1,4489 | 0,5508 | 1,4063 | 0,7746 |
| 0,6816 | 8,0 | 0,905 | 1,5133 | 0,5058 | 1,4645 | 0,7408 |
| 0,7668 | 9,0 | 0,905 | 1,5778 | 0,4645 | 1,5229 | 0,7074 |
| 0,8520 | 10,0 | 0,905 | 1,6423 | 0,4266 | 1,5813 | 0,6745 |
| 1,0224 | 12,0 | 0,905 | 1,7715 | 0,3597 | 1,6982 | 0,6109 |
| 1,1928 | 14,0 | 0,905 | 1,9010 | 0,3034 | 1,8154 | 0,5507 |
| 1,3632 | 16,0 | 0,905 | 2,0308 | 0,2558 | 1,9329 | 0,4945 |
| 1,5336 | 18,0 | 0,905 | 2,1608 | 0,2158 | 2,0506 | 0,4424 |
| 1,7040 | 20,0 | 0,905 | 2,2911 | 0,1820 | 2,1685 | 0,3946 |
Fonte: Elaborado pelos autores, 2019.
Quadro 6 – FT (6 MeV) para o concreto comum utilizando Berger.
| μx | x (cm) | FC | Binf | AE | Bfin | FT |
| 0,0000 | 0,0 | 0,952 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
| 0,0627 | 1,0 | 0,952 | 1,0282 | 0,9392 | 1,0269 | 0,9645 |
| 0,1254 | 2,0 | 0,952 | 1,0564 | 0,8821 | 1,0537 | 0,9295 |
| 0,1881 | 3,0 | 0,952 | 1,0846 | 0,8285 | 1,0806 | 0,8953 |
| 0,2508 | 4,0 | 0,952 | 1,1129 | 0,7782 | 1,1074 | 0,8618 |
| 0,3135 | 5,0 | 0,952 | 1,1411 | 0,7309 | 1,1343 | 0,8290 |
| 0,3762 | 6,0 | 0,952 | 1,1693 | 0,6865 | 1,1612 | 0,7971 |
| 0,4389 | 7,0 | 0,952 | 1,1975 | 0,6447 | 1,1880 | 0,7660 |
| 0,5016 | 8,0 | 0,952 | 1,2257 | 0,6056 | 1,2149 | 0,7357 |
| 0,5643 | 9,0 | 0,952 | 1,2539 | 0,5688 | 1,2417 | 0,7063 |
| 0,6270 | 10,0 | 0,952 | 1,2822 | 0,5342 | 1,2686 | 0,6777 |
| 0,7524 | 12,0 | 0,952 | 1,3386 | 0,4712 | 1,3223 | 0,6231 |
| 0,8778 | 14,0 | 0,952 | 1,3950 | 0,4157 | 1,3760 | 0,5720 |
| 1,0032 | 16,0 | 0,952 | 1,4514 | 0,3667 | 1,4298 | 0,5243 |
| 1,1286 | 18,0 | 0,952 | 1,5079 | 0,3235 | 1,4835 | 0,4799 |
| 1,2540 | 20,0 | 0,952 | 1,5643 | 0,2854 | 1,5372 | 0,4387 |
Fonte: Elaborado pelos autores, 2019.
4.3 CURVAS DE BUILDUP, FT E ATENUAÇÃO EXPONENCIAL
Nas Figuras 14 a 19 são apresentadas as curvas do fator de buildup, da atenuação exponencial e dos fatores de transmissão para as diferentes energias dos raios gama: 1 MeV, 3 MeV e 6 MeV – utilizando o concreto comum/ordinário como material base de blindagem. Para essas energias, foram empregadas as diferentes fórmulas de Buildup mencionadas – Taylor e Berger –, em situação de feixe largo.
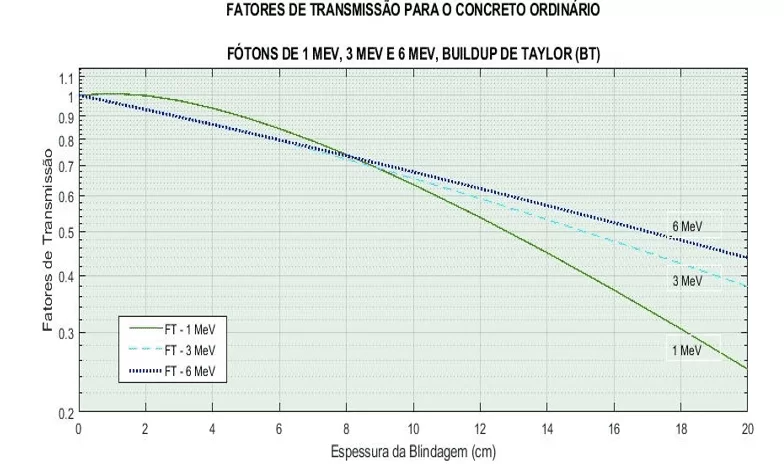
Na Figura 20 é abordada a comparação dos fatores de transmissão ao utilizar o buildup de Taylor e Berger para a energia de 1 MeV. Enquanto na Figura 21, são apresentados os fatores de transmissão para as três diferentes energias usando apenas o buildup de Taylor. A análise de resultados (tópico 4.4) servirá como identificação e detalhará as figuras 14 a 21.
Figura 14 – Curvas de BT, FT e AE para fótons de 1 MeV.
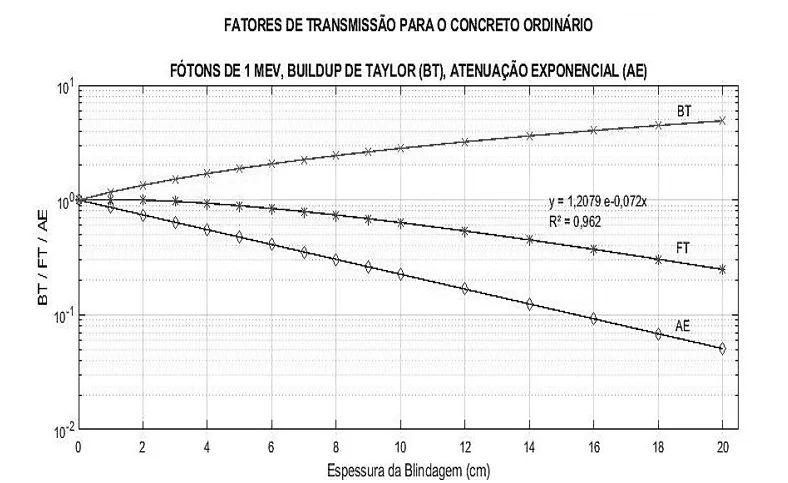
Figura 15 – Curvas de BT, FT e AE para fótons de 3 MeV.
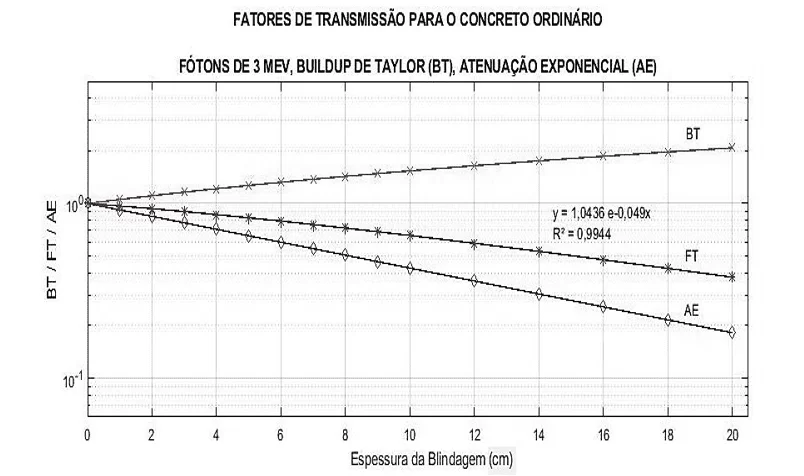
Figura 16 – Curvas de BT, FT e AE para fótons de 6 MeV.
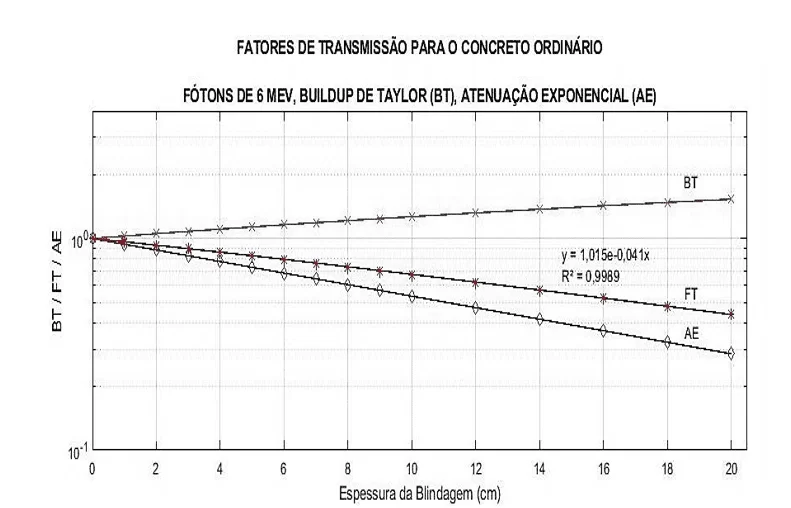
Figura 17 – Curvas de BB, FT e AE para fótons de 1 MeV.
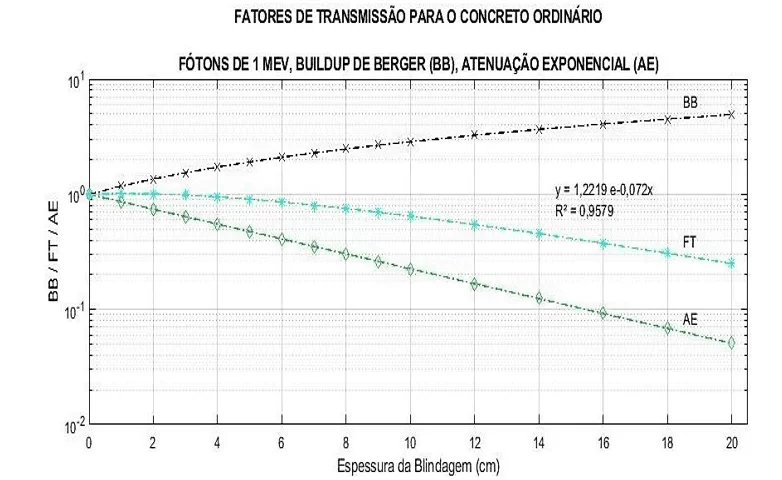
Figura 18 – Curvas de BB, FT e AE para fótons de 3 MeV.
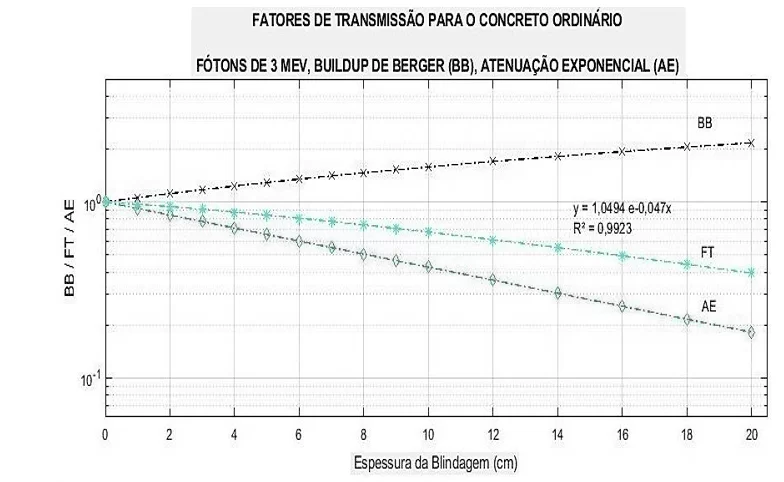
Figura 19 – Curvas de BB, FT e AE para fótons de 6 MeV.
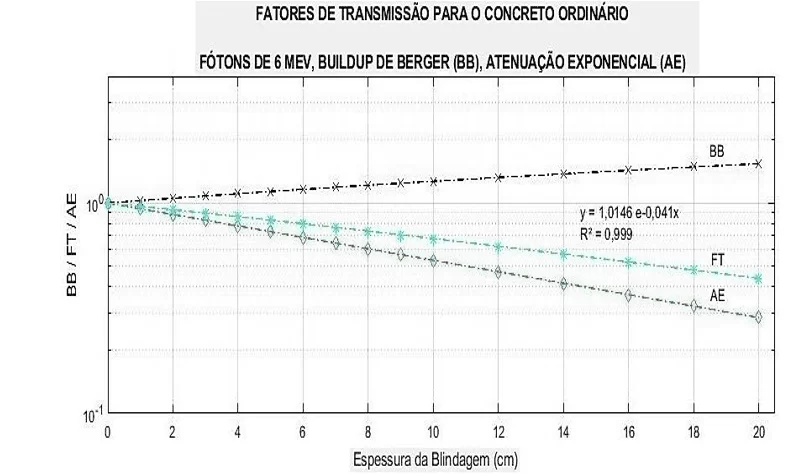
Figura 20– Comparação do FT ao utilizar Buildup de Taylor e Berger.
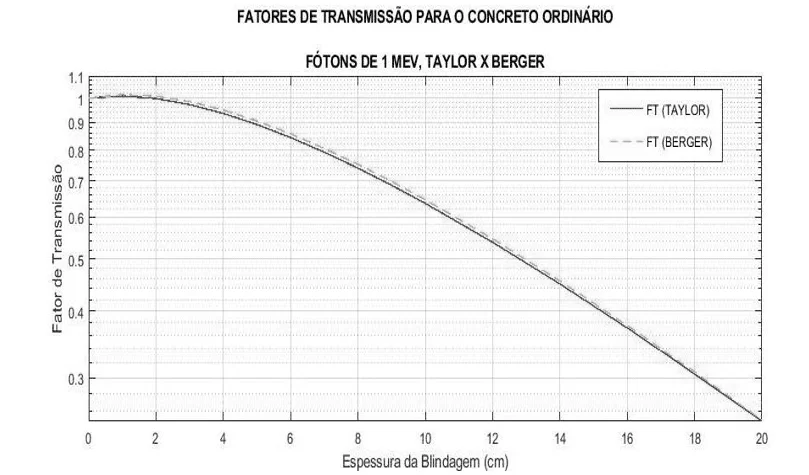
Figura 21– Comparação do FT para diferentes energias.
4.4 ANÁLISE DOS RESULTADOS
Da análise dos resultados constata-se que o fator de transmissão depende da energia da radiação e do meio material. O fator de transmissão é um produto da atenuação linear pelo fator de Buildup.
A atenuação linear diminui à medida que a energia da radiação aumenta. Verifica-se que a atenuação linear para 1 MeV é maior do que para atenuação para 3 MeV e maior ainda para 6 MeV.
O fator de Buildup utilizado nas fórmulas obtido na literatura, é para meio infinito, o que obrigou a uma correção baseada no gráfico da Figura 13, utilizando a metodologia proposta por Chilton, para se obter o Buildup para meio finito. O comportamento previsto para Buildup é de que ele aumente à medida que a energia da radiação diminua e que o número de livres caminhos médio (lcm) aumente.
Existem fórmulas empíricas para o cálculo de Buildup. Duas delas foram usadas nesse trabalho: de Taylor e de Berger. Nota-se muito boa concordância entre as duas curvas, podendo ser usada uma ou outra.
Da análise dos dados constata-se que o FT para energia de 1 MeV e para poucos livres caminhos médios é superior aos FT para energias de 3 MeV e 6 MeV. A partir de 10 cm (1,49 lcm para 1 MeV, 0,852 lcm para 3 MeV e 0,627 lcm para 6 MeV) os FT diminui à medida que a energia da radiação aumenta. Isso ocorre porque o FT é um produto da atenuação linear pelo fator de Buildup que têm comportamento diferente para espessuras menores ou maiores que 10 cm de concreto.
Os gráficos dos fatores de transmissão ajustados com uma linha de tendência apresentam a equação da curva ajustada. Essa equação ajustada possibilita que seja determinada a espessura necessária do concreto para uma determinada transmissão pretendida.
5. CONCLUSÃO
Mediante o estudo realizado, bem como os resultados apresentados e analisados anteriormente, podem ser obtidas algumas conclusões visando responder à questão norteadora sobre como o Engenheiro Civil pode projetar barreiras de proteção sabendo dos potenciais riscos de radiação, mantendo a segurança necessária. Nota-se a diversidade de interações de fótons com a matéria e riscos potenciais para as pessoas envolvidas. Há, portanto, a necessidade de alcançar um alto grau de segurança e confiabilidade, a fim de utilizar beneficamente essas fontes emissoras.
Como a área deste Trabalho de Conclusão de Curso é a Engenharia Civil, foi realizada uma avaliação simples dos efeitos envolvidos em uma blindagem padrão de concreto para radiação gama, buscando um cenário viável para a avaliação desses feitos com métodos consagrados de determinação de blindagens oriundos da Engenharia Nuclear.
As curvas dos fatores de transmissão por apresentarem a equação da linha de tendência possibilita ao engenheiro projetista determinar a espessura da barreira de concreto comum para obter o fator de transmissão que assegure a devida proteção radiológica recomendada pelos órgãos regulatórios – podendo utilizar as curvas de buildup de Taylor ou Berger. A linha de raciocínio e as considerações feitas mostram a importância de o engenheiro civil saber os efeitos dos fótons ao projetar barreiras de concreto – ou qualquer outro material.
Espera-se que além de despertar um senso crítico nos profissionais de Engenharia Civil, esta pesquisa sirva como ponto de partida para aqueles que pretendem iniciar os aprofundamentos nos estudos de blindagem contra raios gama.
Sugere-se a continuidade deste trabalho para os alunos de Engenharia Civil com as seguintes propostas:
- Realizar a análise dos FT para outros materiais de construção;
- Realizar o cálculo de Buildup por métodos de órgãos regulamentares e comparar com este trabalho. Pode-se também realizar o cálculo com outras fórmulas tradicionais, como as blindagens de multicamadas;
- Avaliar a possibilidade de incluir métodos experimentais;
- Realizar a análise da interação dos nêutrons com a matéria.
REFERÊNCIAS
ALBUQUERQUE, S.M. Estudo para o desenvolvimento e caracterização de concretos de massa específica elevada para proteção às radiações gama e X. 2014. Tese (Doutorado em Tecnologia Nuclear) – Universidade de São Paulo, São Paulo, 2014.
ATTIX, F.H. Introduction to Radiological Physics and Radiation Dosimetry. 2. ed, Weinheim: WILEY-VCH, 2004.
BRAGA, K.L. Estudo, utilizando o código MCNPX, da radiação espalhada e produzida pelas paredes de salas de radioterapia e seus feitos sobre doses equivalentes, doses efetivas e fatores de risco para carcinogênese radioinduzida nos pacientes. 2016. Dissertação (Mestrado em Engenharia Nuclear) – Instituto Militar de Engenharia, Rio de Janeiro, 2016.
BUSHBERG, J.T. et al. The Essential Physics of Medical. 2. ed, California: Imaging Lippincott Williams & Wilkins, 2001.
CHILTON, A.B.; SHULTIS, J.K.; FAW, R.E. Principles of Radiation Shielding. New Jersey: Prentice-Hall, 1984.
FILMORE, D.L. Literature Review of the Effects of Radiation and Temperature on the Aging of Concrete. Idaho: INEEL, 2004.
FODERARO, A. The Photon Shielding Manual. 2. ed, Pennsylvania: University Park, 1978.
FRUTUOSO, C.C. Análise aplicada da norma CNEN para instalações de medicina nuclear. Dissertação (Mestrado em Engenharia Nuclear) – Instituto Militar de Engenharia, Rio de Janeiro, 2015.
GAVAZZA, S. Cálculo de Parâmetros de um Experimento de Blindagem. 1986. Dissertação (Mestrado em Engenharia Nuclear) – Instituto Militar de Engenharia, Rio de Janeiro, 1986.
GLEISER, M. A dança do universo. São Paulo: Companhia das Letras, 1997.
______. A ilha do conhecimento. Rio de Janeiro: Record, 2014.
KNOLL, G.F. Radiation detection and measurements. New York: John Wiley & Sons, 1979.
MARTIN, J.E. Physics for radiation protection. 2 ed, Weinheim: Wiley-VCH, 2006.
MCCONN, R.J. et al. Compendium of Material Composition Data for Radiation Transport Modeling. Washington: Pacific Northwest National Laboratory, 2011.
MENDONÇA, L.C.F. e FERREIRA, V.C. Fatores de transmissão da radiação eletromagnética no concreto. 2018. Iniciação Científica (PIC UVA) – Universidade Veiga de Almeida, Rio de Janeiro, 2018.
MEDEIROS, M.P.C. Modelagem computacional de um acelerador linear e da sala de radioterapia para cálculo da dose efetiva em pacientes submetidos a tratamento de câncer de próstata. 2018. Tese (Doutorado em Engenharia Nuclear) – Universidade Federal do Rio de Janeiro, Rio de Janeiro, 2018.
PAIVA, E. Princípios do cálculo de blindagem em radioterapia. Revista Brasileira de Ensino de Física, Rio de Janeiro, v. 36. 2014. Disponível em: http://www.scielo.br/scielo.php?pid=S180611172014000300011&script=sci_abstract&tlng=pt. Acesso em: 6 ago. 2018.
PODGORSAK, E. B. Radiation oncology physics. a handbook for teachers and students. Vienna: IAEA, 2005.
POMARO, B. A Review on Radiation Damage in Concrete for Nuclear Facilities: From Experiments to Modeling, Modelling and Simulation in Engineering, Padova, 2016. Disponível em: https://www.hindawi.com/journals/mse/2016/4165746/. Acesso em: 22 ago. 2018.
SANTIAGO, A. Radioproteção – Tudo que você precisa saber. 2017. Disponível em: https://radioprotecaonapratica.com.br/radioprotecao-protecao-radiologica. Acesso em: 16 ago. 2018
SHULTIS, J. K.; FAW, R. E. Radiation Shielding. Illinois: Amer Nuclear Society, 2000.
SILVA NETO, P.F. Atenuação das radiações nucleares em diferentes tipos de materiais de construção. Trabalho de Conclusão de Curso (Graduação em Engenharia Civil) – Universidade Veiga de Almeida, Rio de Janeiro, 2016.
SINGH, T., KAUR, G., SINGH, P. S. Study of Gamma Ray Exposure Buildup Factor for Some Ceramics with Photon Energy, Penetration Depth and Chemical Composition. Journal of ceramics, 2013. Disponível em: https://www.hindawi.com/journals/jceram/2013/721606/. Acesso em: 10 fev. 2019.
SPENCER, L. V. Structure Shielding Against Fallout Radiation From Nuclear Weapons. Washington: National Bureau of Standards, 1962.
TAUHATA, L. et al. Radioproteção e Dosimetria: Fundamentos. 10. ed, Rio de Janeiro: IRD/CNEN, 2014.
WALY, E.-S. A.; Bourham, M.A. Comparative study of different concrete composition as gamma-ray shielding materials. Annals of Nuclear Energy. v.85, jan./jun. 2015. Disponível em: https://www.sciencedirect.com/science/article/pii/S0306454915002698. Acesso em: 30 ago. 2018.
WOOD, J. Computational Methods in Reactor Shielding, Oxford: Pergamon Press, 1981.
ZORLA, E. et al. Radiation shielding properties of high performance concrete reinforced with basalt fibers infused with natural and enriched boron. Nuclear Engineering and Design. v. 313. 2016. Disponível em: https://www.sciencedirect.com/science/article/pii/S0029549316305258. Acesso em: 15 ago. 2018.
[1] Graduação em Engenharia Civil. ORCID: 0000-0003-1573-5774.
[2] Graduação em Engenharia Civil. ORCID: 0000-0002-2985-4136.
[3] Orientador. ORCID: 0000-0001-5583-5054.
Enviado: Outubro, 2021.
Aprovado: Fevereiro, 2022.