A geometria hiperbólica e o reflexo de sua utilização para alunos do Ensino Médio

ARTIGO ORIGINAL

VOGADO, Gilberto Emanoel Reis ^[1], LOBATO, Fabricio da Silva ^[2], DIAS, Gustavo Nogueira ^[3], BARRETO, Wagner Davy Lucas ^[4], SILVA JUNIOR, Washington Luiz Da ^[5], PAMPLONA, Vanessa Mayara Souza ^[6], RODRIGUES, Alessandra Epifanio ^[7], ARAÚJO, Jamile Carla Oliveira ^[8], BARBOSA, Eldilene Da Silva ^[9], SILVA, Euvaldo Soares Da ^[10]

VOGADO, Gilberto Emanoel Reis. Et al. A geometria hiperbólica e o reflexo de sua utilização para alunos do Ensino Médio. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano 05, Ed. 09, Vol. 03, pp. 99-118. Setembro de 2020. ISSN: 2448-0959, Link de acesso: https://www.nucleodoconhecimento.com.br/educacao/geometria-hiperbolica, DOI: 10.32749/nucleodoconhecimento.com.br/educacao/geometria-hiperbolica

RESUMO

O trabalho a seguir apresenta como objetivo ampliar o conhecimento geométrico dos alunos e professores do ensino médio por meio do estudo da Geometria Hiperbólica. O texto foi estruturado em cinco partes: na primeira abordamos O nascimento da Geometria Hiperbólica, onde apresentamos resumidamente, um dos episódios mais fascinantes da História da Matemática. Explanamos sobre a Soma das medidas dos ângulos internos de um triângulo, apresentando resultados surpreendentes, onde reflete a importância do estudo da Geometria Hiperbólica, em seguida apresentamos por meio de figuras e um quadro comparativo, as principais diferenças entre as geometrias Euclidianas e Não-Euclidianas. O estudo da Geometria Hiperbólica promoveu uma reflexão sobre o desenvolvimento e a construção do conhecimento geométrico, destacando a busca incansável por cerca de 2000 anos de notáveis matemáticos e geômetras que tentaram demonstrar o Quinto Postulado de Euclides ou Postulado das Paralelas. A Geometria Euclidiana presente nos livros didáticos, é válida e consistente para descrever e representar pequenas medidas e formas que estão limitadas por uma superfície de curvatura nula.

Palavras Chaves: Geometria Hiperbólica, história da matemática, geometria euclidiana, postulado das paralelas.

1. INTRODUÇÃO

O estudo da geometria é de fundamental importância para a formação do aluno, porque é por meio dos seus conceitos que o estudante desenvolve o pensamento geométrico, que possibilita compreender, descrever e representar, de forma precisa e ordenada, o mundo em que vive.

Na educação básica, comumente o ensino da geometria limita-se à Geometria Euclidiana que está restrita a uma superfície plana, aprendemos que a soma dos ângulos internos de um triângulo qualquer é sempre igual a 180° e que, por um ponto externo a uma reta passa uma única reta paralela à reta dada. Mas essas afirmações são realmente verdadeiras? Os objetos e conceitos peculiares da Geometria Euclidiana que é limitado a uma superfície plana é apropriada para descrever o nosso mundo que é curvo? Essa geometria é consistente para mensurar distâncias intergalácticas ou subatômicas?  Ela é a única ferramenta de estudo das formas geométricas presentes em nosso mundo físico?

Com o objetivo  e finalidade de contrapor esses questionamentos e expandir o conhecimento geométrico dos alunos e professores do ensino médio, propomos o estudo da Geometria Hiperbólica.

Nesse sentido, o texto foi estruturado em cinco partes: na primeira abordamos O nascimento da Geometria Hiperbólica, onde apresentamos resumidamente, um dos episódios mais fascinantes da História da Matemática, a seguir explanamos sobre a Soma das medidas dos ângulos internos de um triângulo, apresentando resultados surpreendentes, na terceira parte a importância do estudo da Geometria Hiperbólica, em seguida apresentamos por meio de figuras e um quadro comparativo, as principais diferenças entre as geometrias Euclidianas e Não-Euclidianas. A quinta parte mostra a presença da Geometria Hiperbólica em algumas obras de Escher e como a professora de Matemática Daiana Tamina descobriu que o crochê possibilita a construção de modelos planos hiperbólicos no mudo real e como ela conseguiu provar por meio dessa técnica que o Quinto Postulado de Euclides estava incorreto.

2. O NASCIMENTO DA GEOMETRIA HIPERBÓLICA

A história da Matemática registra que por um período de quase dois mil anos, a Geometria de Euclidiana foi aceita como a única geometria possível, uma vez que somente ela possibilitava a leitura do universo.

O nome dado a essa geometria foi em homenagem a Euclides de Alexandria, um matemático grego que reuniu praticamente todo o conhecimento matemático desenvolvida até os seus dias, em uma obra de treze volumes, chamada de Os Elementos, que se tornou a base para os livros didáticos de geometria.

Nesta obra, pela primeira vez, a Matemática é apresentada de forma axiomática, ou seja, a partir de axiomas ou postulados, que são afirmações aceitas como verdadeiras sem a necessidade de demonstração, por serem de simples compreensão.

A Geometria Euclidiana tem como base cinco postulados e cinco noções comuns, dentre eles, o Quinto Postulado gerou muita discussão em torno de sua validade, sendo criticado por vários matemáticos, porque diferente dos outros, é complicado e pouco evidente, como veremos a seguir:

Na concepção de Euclid (1956) o 5º postulado é enunciado: “Se uma reta, ao cortar outras duas, forma ângulos internos, no mesmo lado, cuja soma é menor do que dois ângulos retos, então estas duas retas encontrar-se-ão no lado onde estão os ângulos cuja soma é menor do que dois ângulos retos”.

Este Postulado de Euclides, também conhecido como Postulado das Paralelas, não foi aceito pela comunidade matemática como um postulado, devido sua complexidade e a incerteza de sua validade, requerendo uma análise mais profunda, sua demonstração a partir dos quatro primeiros postulados e axiomas. Por isso, por cerca de 2000 anos, diversos matemáticos tentaram demonstrá-lo, dentre eles destacamos:

Claudius Ptolomeu propôs uma demonstração do 5º postulado a partir dos quatro primeiros. Para tanto, ele utilizou a vigésima nona proposição do primeiro livro de Euclides, que é equivalente ao Quinto Postulado, o que resultou em um ciclo vicioso.

Proclus Diadochus propôs uma demonstração do mesmo, a partir dos quatro outros postulados, aceitando que retas paralelas são equidistantes, que também é equivalente ao Quinto Postulado de Euclides.

Nasir al-Din al-Tusi (Nasiredin) tentou provar o Quinto Postulado, utilizando uma proposição-axioma, que por possuir um caráter de auto evidência não necessitou ser demonstrada. Mas essa proposição-axioma também era equivalente ao Quinto Postulado, resultando em um raciocínio cíclico em suas deduções.

John Wallis propôs uma demonstração a partir dos quatro primeiros, usando existência de triângulos semelhantes e não congruentes, que também é equivalente ao Quinto Postulado.

Giovanni Girolamo Saccheri escreveu a obra “Euclides Ab Omni Naevo Vindicatus” refere-se a uma das obras de geometria não euclidiana, onde também tentou fez como os anteriores, mas utilizando o método de redução ao absurdo, supondo a negação desse postulado, procurou chegar a uma contradição por meio de um quadrilátero com dois ângulos retos na base e dois lados verticais congruentes (VIEIRA, 2018, p.48) conhecido como “quadrilátero de Saccheri”. Ele sabia que a existência desses retângulos é equivalente ao Quinto Postulado. A negação obtida levou a dois casos: o caso em que os ângulos congruentes do topo são obtusos, que contradiz o segundo Postulado e o caso em que são agudos. Os resultados desenvolvidos são os conhecidos teoremas de Geometria Hiperbólica, que mostram a existência de duas retas paralelas assintóticas, que se aproximam à medida em que são prolongadas.

Johann Heinrich Lambert também tentou provar o Quinto Postulado de Euclides por redução ao absurdo, utilizando um quadrilátero que possui três ângulos retos, conhecido hoje como  “quadrilátero de Lambert”, o que resultou na dedução de uma série de resultados, mais tarde conhecidos como teoremas de Geometria Hiperbólica. Dentre esses resultados, o mais importante foi a dedução de que a soma dos ângulos internos de um triângulo é inversamente proporcional à sua área.

Ele considerou um quadrilátero com três ângulos retos como o da figura abaixo:

Figura 1 – Quadrilátero de Lambert.

A seguir ele supôs três hipóteses para o quarto ângulo:

1. Hipótese do ângulo reto, o que equivale ao quinto postulado de Euclides;
2. Hipótese do ângulo obtuso;
3. Hipótese do ângulo agudo.

Ele verificou que a primeira hipótese conduzia â geometria euclidiana e que a segunda poderia ser rejeitada, pois se o quarto ângulo fosse obtuso duas perpendiculares à mesma reta se intersectam e as propriedades da figuras seriam curvadas, transformando as linhas retas em círculos máximos, que se encontram em mais de um ponto, estando desprovidos das propriedades das linhas retas, o que refuta a hipótese do ângulo obtuso. Como ele não encontrou nenhuma contradição da terceira hipótese, “Lambert concluiu que quanto mais agudo fosse o ângulo, maior seria o quadrilátero. Essa análise levou Lambert a descobrir que a soma dos ângulos de um triângulo poderia ser inferior a dois ângulos retos”. (TERDIMAN, 1989. p.94)

O mais interessante é que Lambert iniciou seus estudos sobre Geometria Hiperbólica sem nenhuma pretensão de procurar contradições, quando ainda nem conhecia a obra de Saccheri e mesmo assim, obteve resultados surpreendentes. Dentre os quais merece destaque a descoberta de que “a área Δ de um triângulo é dada por  Δ = K(Π – α – β – ϒ), onde α, β e γ são as medidas dos ângulos internos de um triângulo em radianos e K > 0 é uma constante” (ANDRADE 2008, p. 9). Porque por meio desse resultado, ele provou que “A soma dos ângulos do triângulo decresce quando a área cresce”(ANDRADE 2008, p. 10), que está entre as propriedades mais extraordinárias da Geometria não Euclidiana.

2.1 JOHANN CARL FRIEDRICH GAUSS

Gauss tentou demonstrar o Quinto Postulado de Euclides, a partir dos quatro primeiros, mas logo convenceu-se que essa demonstração não era possível. Mais tarde ele desenvolveu uma série de resultados da Geometria Hiperbólica, compartilhando essas descobertas, por meio de correspondências, com vários matemáticos da época Ele foi o primeiro matemático a reconhecer a existência de uma geometria consistente diferente da euclidiana. Acredita-se que Gauss não publicou esses resultados por temer a rejeição de uma Geometria diferente da clássica que contestava a filosofia de Kant, aceita pela igreja, que aceitava o universo como euclidiano.

János Bolyai, assim como Gauss tentou demonstrar o Quinto Postulado de Euclides a partir dos quatro primeiros e logo se convenceu da impossibilidade de tal demonstração. Em uma carta escreveu a seu pai que havia descoberto a ideia básica de um novo sistema geométrico, criando um novo mundo a partir do nada. “A sua hipótese apoiava-se numa definição de paralelismo mais geral do que na Geometria de Euclides”

2.2 NIKOLAI IVANOVICH LOBACHEWSKY

Lobachewsky, assim como os anteriores, também tentou demonstrar o Quinto Postulado e logo se convenceu da impossibilidade desse feito, reconhecendo a existência de uma nova geometria, que ele chamou de pangeometria ou geometria imaginária, passou a desenvolver resultados da Geometria, Hiperbólica, sobre a qual publicou um trabalho em 1829. Talvez pelo fato desse trabalho ter sido publicado em russo, não despertou o interesse almejado, por isso, algum tempo ele publicou uma versão em alemão. Dessa forma, Gauss tomou conhecimento dessa obra, ficando surpreso ao constatar que Lobachewsky descobriu, quase simultaneamente a ele, os mesmos resultados da Geometria Hiperbólica.

Lobachewsky sugeriu uma nova Geometria na qual mais de uma reta paralela a uma reta da podiam ser traçadas por um ponto e onde a soma dos ângulos de um triângulo seria menor do que dois retos.

2.3 EUGENIO BELTRAMI

Mesmo diante de todos os estudos anteriores, que geraram duras críticas, bem fundamentadas, à Geometria Euclidiana, ela reinava absoluta. Foi em 1868 que Eugênio Beltrami provou definitivamente que o quinto postulado não podia ser demonstrado. A partir daí definiu-se a geometria hiperbólica.

Agora era necessário provar a consistência dessa nova geometria. Foi com esse objetivo que Beltrami introduziu modelos euclidianos na Geometria Hiperbólica, pois assim os axiomas da Geometria Hiperbólica passariam a ser interpretados e aceitos como verdadeiros, resolvendo de vez esse problema, uma vez que uma contradição na Geometria Hiperbólica seria automaticamente transferida para a Geometria Euclidiana, que é considerada consistente.

Ele introduziu um modelo parcial para a Geometria Hiperbólica, utilizando a pseudoesfera, superfície de revolução da curva denominada tratriz em torno de sua assíntota.

Figura 2: Superfície com curvatura negativa – Pseudo-esfera.

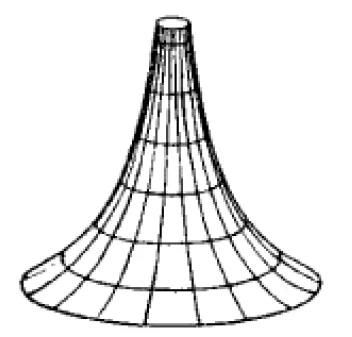
Como esse modelo representava parcialmente o plano hiperbólico, não era possível estender convenientemente as retas hiperbólicas até o infinito, desse modo a pseudoesfera não era totalmente adequada para a Geometria Hiperbólica, fazendo-se necessário desenvolver modelos completos para a Geometria Hiperbólica.

2.4 FELIX CHRISTIAN KLEIN

Em 1871 Felix Klein, um iminente geômetra, introduzir um modelo completo para a Geometria Hiperbólica, que ficou conhecido como o Modelo do Disco de Klein.

Figura 3: Modelo do Disco de Klein.

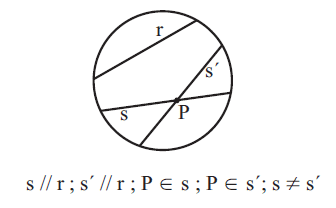
2.5 JULES HENRI POINCARÉ

O questionamento sobre a validade da Geometria Hiperbólica só foi resolvido na segunda metade do século XIX, quando o matemático francês Henri Poincaré introduziu um novo modelo, que ficou conhecido como o Disco de Poincaré. Nele o plano é uma região limitada por uma circunferência, onde as retas são constituídas pela intersecção não vazia de dois discos quaisquer.

No disco de Poicaré todos os postulados da Geometria Hiperbólica são provados com base nos postulados da geometria euclidiana, assim se houver inconsistência ou dúvida quanto à validade da Geometria Hiperbólica, “ela também recairá sobre a consistência da geometria euclidiana” (ANDRADE, 2008, p. 21).

Figura 4: Modelo do Semiplano Superior.

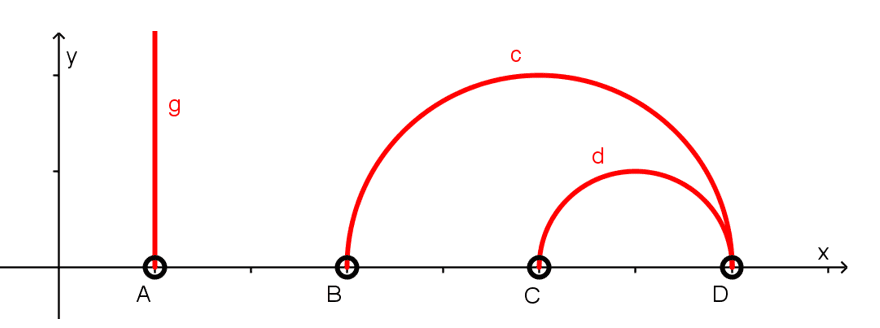
Figura 5: Modelo do Disco de Poincaré.

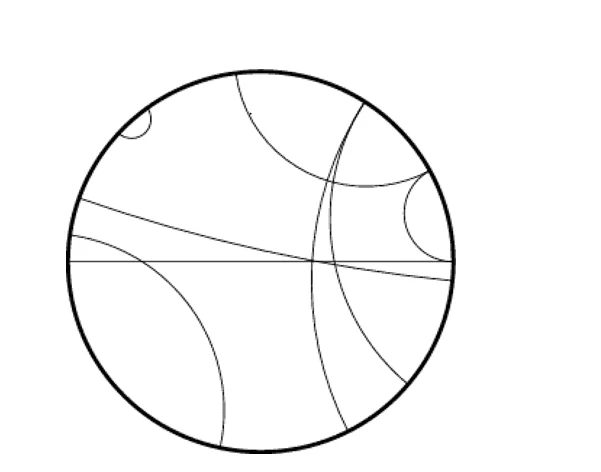
Na verdade o nascimento da geometria não-euclidiana é o resultado das discussões e das tentativas de demonstrar a validade do quinto postulado de Euclides que afirma que “Se uma reta, interceptando duas outras, forma ângulos internos de um mesmo lado cuja soma é menor que dois retos, então estas duas retas, se prolongadas indefinidamente, se encontram naquele lado cuja soma dos ângulos internos é menor que dois retos” ou conforme uma versão equivalente do matemático Playfair: “por um ponto fora de uma reta pode-se traçar uma única reta paralela à reta dada”.

Ao substituir o quinto postulado de Euclides por uma de suas negações, Janos Bolyai descobriu “um novo e estranho universo” (BARBOSA, 2008, p. 42).

A validade desse postulado depende diretamente da superfície geométrica considerada, ou seja, quando consideramos uma superfície sem curvatura (de curvatura nula), perfeitamente plana em todas as direções, o quinto postulado de Euclides é válido, mas se a superfície apresentar curvatura, ele não é válido e sua negação “torna-se um axioma que se junta aos quatro primeiros para estabelecer geometrias independentes e consistentes conhecidas como Geometrias Não-Euclidianas”. (PEREZ, 2015, p. 25)

Assim, ao considerarmos uma superfície com curvatura, ocorre a negação do quinto postulado de Euclides ou postulado das paralelas e neste caso ele deixa de ser um teorema, uma vez que, neste caso, ele é independente dos demais e sua demonstração torna-se impossível, o que resulta na construção de outras geometrias.

Por exemplo, se por um ponto fora de uma reta não passa nenhuma reta que seja paralela a essa primeira, ocorre o surgimento da Geometria Elíptica, mas se passam pelo menos duas retas paralelas isso originará a Geometria Hiperbólica.

Na superfície curva, temos a geodésica determinada pela menor distância entre dois pontos dessa superfície. A geodésica corresponde à reta na geometria Euclidiana.

A Geometria Hiperbólica foi desenvolvida simultaneamente por Gauss, Bolyai e Lobachewsky, mas o reconhecimento pela da descoberta foi atribuído a Lobachewsk, por ter sido o primeiro a publicar sobre esse assunto que ele chamou de Geometria Imaginária.

3. SOMA DAS MEDIDAS DOS ÂNGULOS INTERNOS DE UM TRIÂNGULO

Com certeza você já ouviu a afirmação: “a soma das medidas dos ângulos internos de um triângulo é sempre igual a 180°”. Por isso é natural que ao se deparar com a pergunta: qual é a soma das medidas dos ângulos interno de um triângulo? É comum o indivíduo responder: 180°. Mas essa resposta está realmente correta?

Na verdade, não é difícil provar que a resposta para esse questionamento depende da superfície que estamos considerando, ou seja, depende da geometria em que esse triângulo se encontra. Na geometria plana a soma das medidas dos ângulos internos de um triângulo mede 180° e, neste caso a afirmação está correta. No entanto, isso não ocorre na geometria esférica onde essa soma varia entre 180° e 540°, muito menos na Geometria Hiperbólica, onde essa mesma soma varia entre 0 e 180°.

A figura abaixo representa uma esfera de isopor onde foram fixados três alfinetes, sendo um no polo norte e os outros dois na linha do equador. Ao ligar os três pontos, dois a dois, por meio de um elástico, obtemos a forma de um triângulo que ocupa um oitavo da esfera, ou seja, este triângulo possui três ângulos retos, logo as somas dos ângulos internos de um triângulo da esfera, neste caso, é 540°. Dessa forma podemos afirmar que a soma dos ângulos internos de um triângulo depende da superfície onde o triângulo foi construído.

Figura 6: Triângulo da esfera.

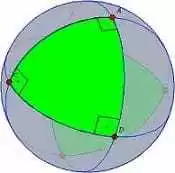
Para esclarecer melhor a situação veja a figura abaixo:

Figura 7: Soma dos ângulos internos de um triângulo.

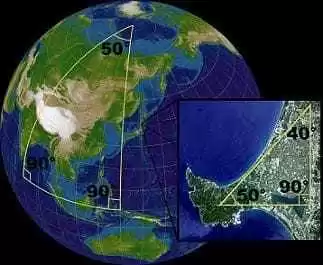
A figura destaca dois triângulos “construídos” na superfície terrestre. O triângulo da direita foi ampliado. Ele é extremamente pequeno em relação ao nosso planeta ele é aproximadamente plano, de modo que a soma dos seus ângulos internos são aproximadamente 180°. Se afastarmos progressivamente os vértices desse triângulo, a soma dos seus ângulos internos se aproximará de 540° à medida em esses vértices se aproximam da circunferência máxima. Portanto, a soma dos ângulos internos de um triângulo esférico varia entre 180° e 540°.

Figura 8: Soma dos ângulos internos de um triângulo em uma superfície hiperbólica.

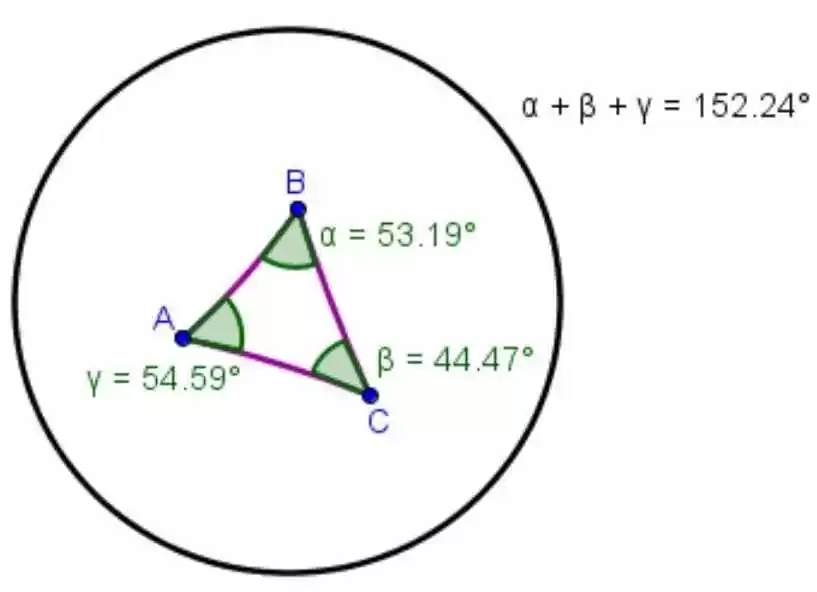
O que acabamos de expor pode ser verificado na figura abaixo:

Figura 9: Superfícies esféricas e hiperboloide.

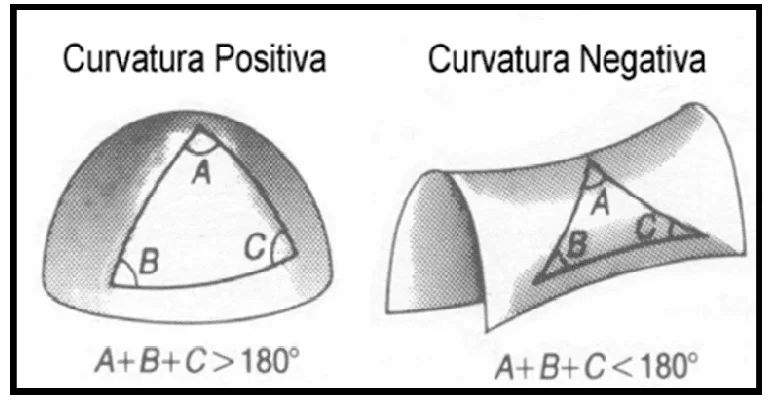
Note que quando construímos um triângulo em uma superfície que possui curvatura positiva a soma dos ângulos internos desse triângulo é maior que 180°, se a curvatura da superfície é negativa, essa soma é menor que 180° e quando essa curvatura é nula, a soma dos ângulos internos do triângulo dessa superfície é 180°.

Portanto, a soma dos ângulos internos de um triângulo depende da superfície em que o triângulo foi traçado, em uma superfície plana (com curvatura nula) essa soma é igual a 180°, na superfície hiperbólica (que possui curvatura negativa) a soma é menor que 180° e na superfície esférica (com curvatura positiva) a soma varia entre 180° e 540°.

4. ESTUDAR GEOMETRIA HIPERBÓLICA?

A Geometria Euclidiana não era capaz de responder perguntas relacionadas a certos fenômenos do Universo, não possibilitava a obtenção de medidas de grande escala ou medir grandes distâncias sobre a superfície da Terra onde temos que considerar a sua curvatura, porque nessa geometria a curvatura é nula, portanto ela só funciona no plano. Em virtude desse problema, surge a necessidade de desenvolver novas geometrias, que considerassem uma superfície curva, dessa forma, surgem as Geometrias Não-Euclidianas.

As Geometrias Não-Euclidianas possuem objetos e conceitos que podem representar descrever e estabelecer respostas consistentes para esses fenômenos, supracitados, que a Geometria Euclidiana não consegue responder.

Sendo assim, podemos afirmar que tanto o engenheiro quanto o carpinteiro fazem uso da geometria Euclidiana, mas como o marinheiro precisa considerar a curvatura de nosso planeta, neste caso é necessário fazer uso da Geometria Não Euclidiana.

A Geometria Hiperbólica considera todos os postulados da geometria euclidiana, com exceção do quinto postulado ou postulado das paralelas, que é substituído pelo postulado hiperbólico ou Axioma de Bolyai-Lobatchevsky que afirma: por um ponto exterior a uma reta passa mais de uma paralela, (RIBEIRO, 2012).

Os Parâmetros Curriculares Nacionais (BRASIL, 1998) visam a melhor compreensão do espaço físico, que está no entorno do indivíduo.

As formas hiperbólicas apresentam a vantagem de maximizar a área de uma superfície.

5. AS DIFERENÇAS ENTRE AS GEOMETRIAS EUCLIDIANAS E NÃO-EUCLIDIANAS

“Geometria neutra é um corpo de resultados obtidos a partir dos axiomas de Hilbert que não lançam mão do postulado das paralelas. Portanto, são proposições válidas nas geometrias euclidianas e hiperbólicas” (ANDRADE, 2013, p. 27 apud VIEIRA, 2018, p. 19).

A maior divergência entre as geometrias euclidiana e não-euclidiana giram em torno do quinto postulado de Euclides, como veremos a seguir:

Figura 10 – Representação do 5º Postulado de Euclides na Geometria Euclidiana.

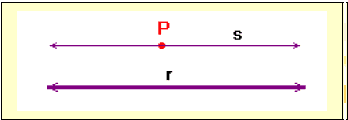
Dados um ponto P e uma reta r, existe uma única reta s que passa pelo ponto P e é paralela a r

Figura 11 – Representação do 5º Postulado.

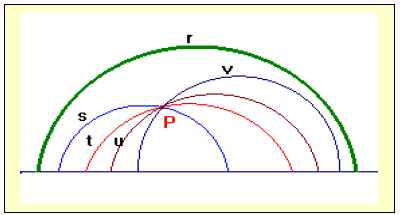
Na Geometria Hiperbólica  “por um ponto P fora de uma reta r passa mais de uma reta s paralela à reta r” (COUTINHO, 2001, p. 40).

Figura 12 – Representação do 5º Postulado de Euclides na Geometria Elíptica.

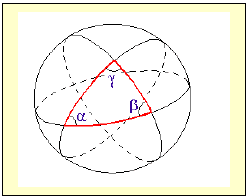
Na Geometria Elíptica “Quaisquer duas retas em um plano têm um ponto de encontro” (COUTINHO, 2001, p. 73).

Apresentamos um quadro comparativo com as principais diferenças dos conteúdos geométricos em cada uma das geometrias.

Quadro 1: Comparações entre alguns conteúdos geométricos nas diferentes geometrias.

CONTEÚDO MATEMÁTICA	GEOMETRIA EUCLIDIANA	GEOMETRIAS NÃO EUCLIDIANAS
		GEOMETRIA HIPERPÓLICA OU LOBACHEVSKIANA	GEOMETRIA ELÍPTICA OU REIMANIANA
Duas retas distintas intersectam	Um ponto	Um ponto	Em dois pontos antípodos.
Dada uma reta L e um ponto P exterior a L, existe(m)	Uma reta e só uma que passa por P e é paralela a L.	Pelo menos duas retas que passam por P e é paralela a L.	Não há reta que passa por P e é paralela a L.
Uma reta	É dividida em duas por um ponto	É dividida em duas por um ponto	Não é dividida em duas por um ponto
As retas paralelas	São equidistantes	Nunca são equidistantes	Não existem
Se uma reta intercede uma de duas paralelas	Intercede a outra	Pode ou não intercede a outra	Como não há paralelas, isto não ocorre.
A hipótese de Saccheri válida é a do	Ângulo reto	Ângulo agudo	Ângulo obtuso
Duas retas distintas perpendiculares a uma terceira	São paralelas	São paralelas	Interceptam-se
A soma das medidas dos ângulos internos de um triângulo é	Igual a 180º	Menor do que 180º	Maior que 180º
A área de um triângulo é	Independente da soma dos seus ângulos	Proporcional ao defeito da soma de seus ângulos	Proporcional ao excesso da soma de seus ângulos.
Dois triângulos com ângulos correspondentes iguais são	Semelhantes	Congruentes	Congruentes
Soma dos ângulos internos de quadrilátero	Igual a 360º	Menor do que 360º	Maior que 360º

(Fonte: Anais do X Encontro Nacional de Educação Matemática Comunicação Científica)

6. A UTILIZAÇÃO DO CROCHÊ PARA PROVAR QUE O QUINTO POSTULADO DE EUCLIDES ESTAVA INCORRETO

Em seu quinto postulado, conhecido como postulado das paralelas, Euclides afirma que “dada uma reta e um ponto exterior, existe somente uma reta contendo o ponto e paralela à reta dada”, ou seja, “dada uma reta e um ponto fora dessa reta, só existe uma única maneira de traçar uma segunda reta que passe pelo ponto e que seja paralela à primeira reta”, dessa forma qualquer inclinação ocasionará o cruzamento dessas retas em algum local do espaço.

Na tentativa de demonstrar esse postulado, alguns matemáticos se convenceram da impossibilidade de fazer essa demonstração, desenvolvendo uma nova geometria que contradizia o quinto postulado de Euclides, substituindo esse postulado pela hipótese:  por um ponto P externo a uma reta r passam mais de uma reta paralela à reta r. Essa hipótese é conhecida como Axioma da Geometria Hiperbólica ou Postulado Hiperbólico das Paralelas, e está representada na figura abaixo:

Figura 13 – Axioma da Geometria Hiperbólica.

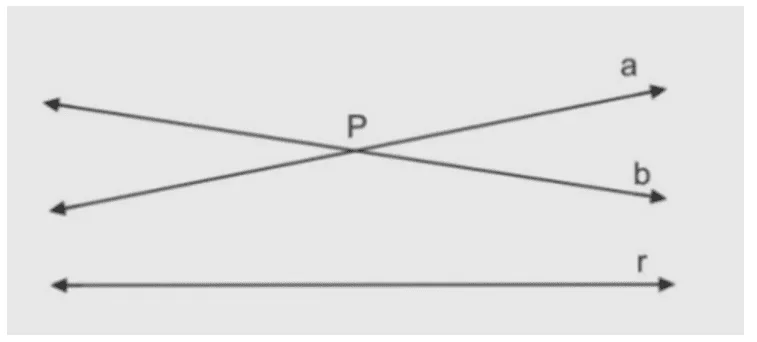
Assim surgiu a Geometria Hiperbólica, que foi chamada por Lobachewski de “Geometria Imaginária”, porque era difícil compreender sua existência.

Essa dificuldade permaneceu por um longo período, mesmo diante das evidências dos cálculos e estudos que asseguravam a consistência da Geometria Hiperbólica. Ela não faz muito sentido para os matemáticos, por parecer abstrata e irreal, sem aplicação prática e desprovido de sentido epistemológico.

O plano hiperbólico era normalmente representado por um círculo onde estavam inseridos semicírculos retos que possuíam a mesma medida entre si, com a mesma curvatura do espaço que se expande, por isso era difícil representá-lo por meio de um desenho.

A seguir apresentamos a representação de um plano hiperbólico:

Figura 14 – Representação de um plano hiperbólico.

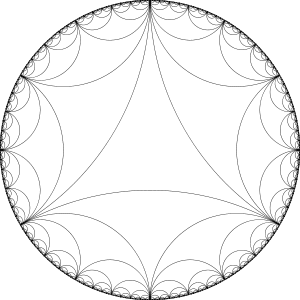
Na verdade, para ser mais preciso, é necessário falsear a superfície do papel ou da tela, para obtermos a ideia exata do plano hiperbólico.

Em 1926 o artista holandês Maurits Cornelis Escher, conhecido pelas suas xilogravuras, litografias e meios-tons (mezzotints), descobriu as transformações geométricas que hoje são conhecidas como isometrias  O contato de Escher com Bruno Ernst e outros matemáticos levaram-no a perceber a “Matemática” presente em sua obra. Dentre esses matemáticos, destaca-se Donald Coxeter, que lhe explicou os modelos de Geometria Hiperbólica, despertando o interesse de Escher em utilizar esses modelos, bem como a Matemática acadêmica em diversas de suas obras.  Nos quadros abaixo está registrada a utilização da Geometria Hiperbólica.

Figura 15 – Limite Circular I, 1958, Xilogravura e Limite Circular III, 1958, Xilogravura.

Figura 16 – Demonstração do erro do Quinto Postulado de Euclides.

Certamente Escher, assim como seus contemporâneos, não conseguia compreender as representações da Geometria Hiperbólica “fora” do papel, uma vez que ela era apenas conceitual, e os matemáticos não tinham certeza se essa nova geometria estava presente na natureza.

Foi em 1997 que a professora de Matemática Daiana Tamina descobriu que o crochê possibilita a construção de modelos planos hiperbólicos no mudo real que é tridimensional. Isso decorre de sua estrutura que cresce exponencialmente, quando se acrescenta dois pontos a cada um dos pontos existentes, originando curvaturas negativas, além de serem macios e moldáveis, o que corrobora para a compreensão do plano hiperbólico.

Note que as retas traçadas na superfície hiperbólica de crochê, parecem uma curva, mas, no entanto, são perfeitamente retas. Dessa forma a professora Daiana Tamina, conseguiu provar que o Quinto Postulado de Euclides ou Postulado das Paralelas estava errado, quando se trata de uma superfície hiperbólica: Para compreender melhor essa ideia, veja a figura 16.

A partir da situação evidenciada na representação acima, ela concluiu que pôr um ponto “X” fora de uma reta “A” passam infinitas retas paralelas a esta reta “A”.

Por mais de um século e meio os matemáticos tentaram imaginar a Geometria Hiperbólica, mas como o plano hiperbólico apresenta estruturas matemáticas demasiadamente complexas, sua concepção e representação é quase impossível de serem realizadas pelos seres humanos. Tudo isso fez com que os matemáticos firmassem a ideia de que não existem objetos ou formas hiperbólicas naturais em nosso mundo. “Mas planos hiperbólicos sempre existiram, as pessoas só não estavam procurando nos lugares certos”. (BARRUECO, 2015, p. 6)

“Alfaces, recifes de coral, algumas pétalas de flores, algumas lesmas marinhas, são todas representações naturais de planos hiperbólicos, estruturas matemáticas super complexas e difíceis de serem reproduzidas pelos seres humanos”. (BARRUECO, 2015, p. 6)

Podemos notar que a Geometria Hiperbólica está muito presente em nosso mundo, auxiliando na compreensão de fatos tangíveis e até mesmo intangíveis, corroborando com o desenvolvimento da Física Moderna, sendo utilizada sobretudo na teoria espacial da relatividade, dentre os quais merecem destaque, o espaço-tempo de Minkowski e o espaço giro vetorial.

CONSIDERAÇÕES FINAIS

O estudo da Geometria Hiperbólica promoveu uma reflexão sobre o desenvolvimento e a construção do conhecimento geométrico e notáveis matemáticos e geômetras que tentaram demonstrar o Quinto Postulado de Euclides ou Postulado das Paralelas. A negação desse postulado originou as Geometrias Não-Euclidianas.

A Geometria Euclidiana presente nos livros didáticos, é válida e consistente para descrever e representar pequenas medidas e formas que estão limitadas por uma superfície de curvatura nula, ou seja, o plano. O mesmo não se verifica diante da necessidade de descrever distancias intergalácticas ou subatômicas, ou um objeto inserido em uma superfície de curvatura negativa ou positiva, neste caso é necessário utilizar uma das geometrias não-euclidianas, pois elas possuem objetos e conceitos  capazes de descrever, representar e explicar de forma consistente certos fenômenos do Universo que não podem ser explicados pela Geometria Euclidiana.

Neste sentido a soma dos ângulos internos de um triângulo depende da curvatura da superfície em que ele se encontra. Quando a curvatura é nula, ou seja, no plano, a Geometria Euclidiana é a mais adequada, e o valor dessa soma é 180°, já quando essa curvatura é negativa  a Geometria Hiperbólica é mais adequada e a soma é menor que 180°, por outro lado essa soma será maior que 180° se a curvatura é positiva e, nesse casos, a Geometria Elíptica é mais consistente.

A Geometria Euclidiana é inconsistente quando estudamos superfícies com curvatura diferente de zero, por isso seus conceitos e objetos são incapazes de descrever, representar e explicar diversas formas do nosso mundo físico, portanto para que o aluno seja capaz de descrever e representar, de forma precisa e ordenada, o mundo em que vive é necessário que o mesmo estude as Geometrias Não-Euclidianas e em particular a Geometria Hiperbólica, que está muito presente em seu cotidiano.

REFERÊNCIAS

ANDRADE, P. F. A. Introdução à geometria hiperbólica plana: o disco de Poincaré. Fortaleza: Editora da UFC, 2008.

BARBOSA, J. L. Geometria hiperbólica. Rio de Janeiro: IMPA, 2008

BARRUECO, Caroline.  Comprovou, Graças ao Crochê, que Euclides Estava Errado. Disponível em: <https://noosfera.com.br/como-uma-delicada-forma-de-artesanato-revolucionou-nossa-maneira-de-perceber-a-matematica/>. Acesso em 18 de set de 2019.

BRASIL. Secretaria de Educação Fundamental. Parâmetros curriculares nacionais: matemática. Brasília: CNE/CES, 1998.

COUTINHO, L. Convite às geometrias não-euclidianas. Rio de Janeiro: Editora Interciência, 2001.

CRUZ, D. G; SANTOS, C. H. Algumas diferenças entre a geometria euclidiana e as geometrias não euclidianas – hiperbólica e elíptica – a serem abordadas nas séries do ensino médio. In X Encontro Nacional de Educação Matemática Educação Matemática, Cultura e Diversidade. Salvador-BA, 2010.

EVES, H. Introdução à história da matemática. Tradução Hygino Domingues. São Paulo: Editora Unicamp, 2008.

EUCLID. The Elements, Dover Publications, N.Y. , 1956.

HANSEN, V. L. Changes and trands in geometry curricula. In C. Mammana, & V. Villani (Eds.), Perspectives on the teaching of geometry for the 21st century. London: Kluwer Academic Publishers, p. 235-242, 1998.

PEREZ, Carlos Martinez. Fundamentos de geometria hiperbólica. Dissertação (mestrado) – Universidade Estadual Paulista, Instituto de Geociências e Ciências Exatas. 76 f. Rio Claro, 2015.

REIS, J. D. A. D. S. Geometria esférica por meio de materiais manipuláveis. Dissertação (Mestrado em Educação Matemática). UNESP, Instituto de Geociências e Ciências Exatas, Rio Claro, 2006.

RIBEIRO, R. D. G. L. O ensino das geometrias não euclidianas: um olhar sob a perspectiva da divulgação científica. Dissertação (Mestrado). Universidade de São Paulo, Faculdade de Educação, São Paulo, 2012.

TERDIMAN, E. W. A geometria hiperbólica e sua consistência. Dissertação (Mestrado em Matemática). Pontifícia Universidade Católica de São Paulo, São Paulo, 1989.

VIEIRA, Carlos Augusto do Nascimento. Sobre Geometrias Não-Euclidianas/Carlos Augusto do Nascimento Vieira. 64 f. Dissertação (Mestrado) – Universidade Federal do Cariri, Centro de Ciências e Tecnologia –Programa de Pós-graduação em Matemática em Rede Nacional, Juazeiro do Norte, 2018.

VIEIRA, Juniano Vergna. Os quadriláteros de Saccheri e o surgimento da geometria hiperbólica. Dissertação de mestrado, Universidade Federal do Espírito Santo. Mestrado Profissional em Matemática em Rede Naciona, 2018.

^[1] Doutorado em Educação Matemática. Mestrado em Geofísica. Especialização em Matemática Superior. Graduação em Licenciatura Plena em Matemática.

^[2] Graduação em Matemática.

^[3] Doutorado em Educação e Artes. Mestrado em Geofísica. Especialização em Gestão Escolar. Graduação em Matemática.

^[4] Mestrado em Ciências Ambientais. Mestrado profissional em Matemática. Especialização em Didática Da Matemática. Graduação em Matemática Licenciatura. Graduação em Ciência com Habilitação em Matemática.

^[5] Especialização em andamento em Antropologia Brasileira. Especialização em andamento em Educação do campo. Especialização em Matemática Financeira e Estatística. Especialização em Gestão Educacional e Docência da Educação Superior. Especialização em Fundamentos da Matemática Elementar. Graduação em andamento em Gestão Financeira. Graduação em Licenciatura Plena em Matemática.

^[6] Doutorado em Agronomia (Entomologia Agrícola). Mestrado em Matemática e Estatística. Especialização em Bioestatística. Graduação em Bacharelado em Estatística.

^[7] Doutorado em andamento em Ciência Animal. Mestrado em Ciência Animal. Graduação em Agronomia.

^[8] Doutorado em andamento em Ciências Contábeis. Mestrado em Administração. Especialização em MBA Gerência Contábil, Auditoria, Perícia e Controle. Graduação em Ciências Contábeis.

^[9] Doutorado em andamento em Agronomia. Mestrado em Administração. Especialização em MBA G. Contábil, Auditoria, Controladoria e Perícia. Aperfeiçoamento em Perito Judicial. Graduação em Ciências Contábeis.

^[10] Mestrado profissional em andamento em Mestrado Profissional em Ensino de Matemática. Especialização em Pós-Graduação Lato Sensu em Matemática. Graduação em Ciências – Matemática.

Enviado: Agosto, 2020.

Aprovado: Setembro, 2020.