ОРИГИНАЛЬНАЯ СТАТЬЯ
BELLAS, Leonardo Dias [1]
BELLAS, Leonardo Dias. Расчет числовой доли. Revista Científica Multidisciplinar Núcleo do Conhecimento. 05-й год, Эд. 12, Vol. 02, стр. 144-162. Декабрь 2020 года. ISSN: 2448-0959, Ссылка доступа: https://www.nucleodoconhecimento.com.br/математические-олимпиады/числовой-доли
РЕЗЮМЕ
В 2011 году этот автор сделал математическое логическое наблюдение и с тех пор изучает эту логику, которая касается того, что любое число может быть представлено последовательной цифрой от 1 до 9. Тем не менее, открытие того, что эта логика была о было сделано и другой существующий расчет Fibonacci последовательность была связана. Тем не менее, это исследование было разработано для записи информации об этой логике в отношении этого научного открытия расчета числовой пропорции, а также о логике численные пропорции и его связь с другими научными открытиями и концепциями, которые были разработаны другими математиками ранее. Для обсуждения и демонстрации этих математических наблюдений, которые ранее не наблюдались, и предоставления нового варианта более эффективного расчета, поскольку любое число может быть представлено последовательными цифрами от 1 до 9. Таким образом, с помощью расчета и логики нумеральной пропорции мы можем определить это, в дополнение к демонстрации его применимости в математике и современных науках.
Ключевое слово: Соотношение нумеров, последовательность Fibonacci
1. ВВЕДЕНИЕ
Цель этого исследования состоит в том, чтобы продемонстрировать это математическое открытие о численных пропорциях и показать его применимость в текущей математике. С помощью математических расчетов и демонстраций расчет числовой пропорции будет объяснен и применен путем лечения того, что любое число может быть представлено последовательной цифрой от 1 до 9. Эта последовательность от 1 до 9 является последовательной последовательностью, так как повторяется бесконечно и последовательно. И так показать свою связь с другим расчетом уже выполнены, что из последовательности Fibonacci , который является бесконечным коэффициентом двух последовательных мер. Иррациональное число называется (PHI) получено, с приблизительным значением 1,618, который также известен как золотое соотношение или золотая пропорция, в соответствии с математиком Leonardo de Pisa.
2. ЛОГИКА СООТНОШЕНИЯ ЧИСЛА АСПЕКТОВ
При демонстрации расчета соотношения цифр мы должны сделать несколько математических наблюдений, таких как пример логики соотношения цифр. Как по примеру в таблице ниже:
Таблица 1. Расчет соотношения логики и цифры

Таким образом, мы можем заметить, что все интеграторы, десятичные или цифры от 0.000000…0001 до Бесконечности, при добавлении к их последней переменной, являются последовательными от 1 до 9, то есть сумма цифр любого числа, будучи нейтральным нулем, является последовательной от 1 до 9 Бесконечно. Таким образом, с помощью этой логики мы можем заметить, что любое число может быть представлено последовательной цифрой от 1 до 9, следует более простой способ выразить эту логику.
Рисунок 1: Логика соотношения нумерового аспекта

Источник: автор.
3. РАСЧЕТ КОЭФФИЦИЕНТА ЧИСЛЕННЫЕ АСПЕКТЫ
Теперь давайте перейдите к расчету соотношения числа аспектов. В этом случае я использовал римский алфавит, но другой алфавит или другой символ / код может быть использован.
Рисунок 2: Расчет соотношения нумерового аспекта

Источник: автор.
Мы можем заметить, что независимо от того, используем ли мы целые числа или числа числовой пропорции, мы обнаруживаем, что в обоих вычислениях результаты одинаковы. Однако можно заметить, что использование логики числовых пропорций для получения результата проще. Поскольку вам не нужно использовать весь бесконечный алфавит целых чисел, только последовательность от 1 до 9. Этот расчет аналогичен тому, как если бы вы разбили бесконечное число целых чисел в последовательности от 1 до 9 (числовое значение). Любое число – это порядковый номер от 1 до 9.
Давайте посмотрим на имя João, целыми числами это число 1015115, а в цифровой логике это число 1616. Таким образом, мы видим, что и число 1015115, и число 1616, и сумма цифр до их последней переменной равна 5, таким образом мы можем составить шкала чисел, облегчающая операции с большим объемом, упорядочение и идентификация каждого элемента от 1 до 9.
Мы также можем применить расчет соотношения цифр в этих наблюдениях, в числах миллионов ниже:
Глядя в миллиарды тоже:
Мы такжеможем наблюдать в диплетах:
Здесь, в dizymas мы можем лучше наблюдать бесконечное происходит от 9 до 1.
Основой, или принципом, лежащим в основе этих рассуждений, является запись открытия этого расчета числовой пропорции, демонстрирующего, что любое и все числа могут быть представлены последовательным числом от 1 до 9 бесконечно. Четко наблюдаемые в логике и расчете численные пропорции, представленные здесь. Поэтому мы будем применять его значения с примерами математики и логики.
Таким образом, мы также можем наблюдать бесконечность от 1 до 9.
4. БЕСКОНЕЧНОСТЬ И ЛОГИКА СООТНОШЕНИЯ ЦИФР
Следующим примером является пример, идентифицяющий Бесконечность в логике соотношения числа аспектов:
Рисунок 3: Бесконечная логика соо
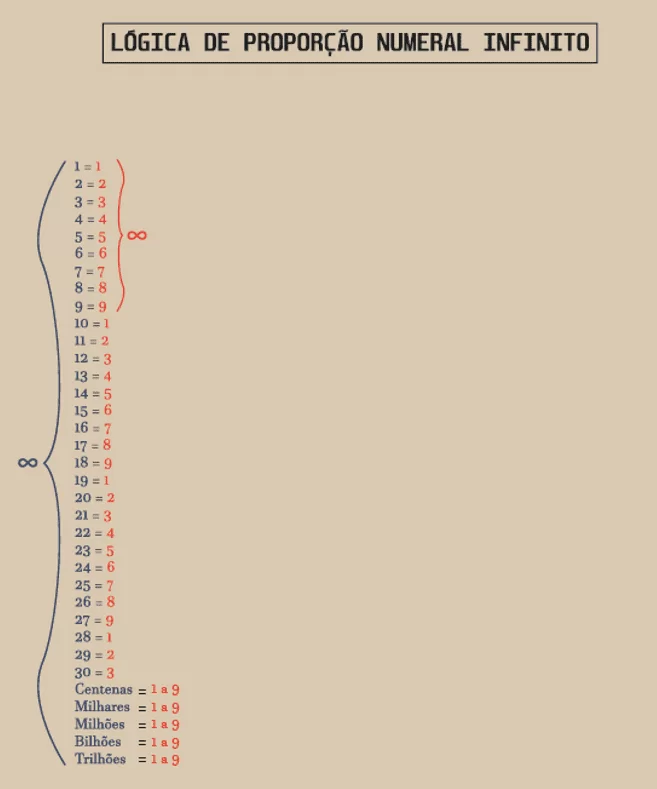
Глядя на приведенную выше диаграмму, можно перейти к бесконечности, как в целых числах, так и в цифрах. И, как говорилось ранее, вы разбиваете все числа на цифры, и смотрите на это вот так, где легче найти или сосчитать до бесконечности? Подсчет всех чисел, переживает тысячи, миллионы, миллиарды, триллионы и т.д. или считая только от 1 до 9? По логике наблюдения, вычисляя последовательное соотношение буквенных аспектов от 1 до 9, легче и проще найти и подсчитать до бесконечности.
5. ПРИЛОЖЕНИЯ ДЛЯ РАСЧЕТА КОЭФФИЦИЕНТА ЧИСЛА
Вычисление числовой пропорции может быть очень полезным, некоторое время назад было сделано научное открытие новой бинарной системы, которое является очень важным открытием системы для работы электро и комонических игр, съеденных с электро и так далее. Это намного эффективнее и безопаснее, чем нынешняя система. Это исследование было опубликовано в том же научном журнале, и ссылка будет в ссылках на эту работу. Но зная этот расчет числовой пропорции, оценивая открытие двоичной системы 2, и дало основу для определения логических различий между двоичными системами, как в этом случае ниже, где может быть распределена деральная пропорция катионов. (BELLAS, 2019)
Рисунок 4: Последовательность двоичной системы

Источник: Автор
Итак, глядя на две логики бинарных систем и используя расчет соотношения цифр, мы определяем логику в каждой системе, у нас есть в двоичной системе 1, последовательность из 6 повторений 1, 2, 4, 8, 7, 5. И логика двоичной системы 2, это последовательность из 2 повторений 3 и 6. В двух двоичных логиках числа удваивается до бесконечности, но в двоичной системе 1 она складывается до бесконечности в последовательности из 6 значений, а в двоичной системе 2 вы сбрасывают до бесконечности в последовательности из 2 значений. Таким образом, двоичная система 2 имеет больше математической логики и является более эффективной, чем двоичная система 1, математически и логически.
Одним из логических определений является, когда информация повторяется или имеет последовательность. В случае двоичной системы 1 она повторяется или имеет последовательность в 6-факторной логике, уже в двоичной системе 2 она повторяется или имеет последовательность в логике 2 факторов, поэтому двоичная система 2 проще, это логичнее. Два логических фактора проще, чем 6 логических факторов.
На Youtube есть видео под названием «O Segredo dos números 3, 6 e 9» – Неизвестные факты. В этом видео речь идет о наблюдениях Nikola Tesla относительно чисел 3 и 6, однако это видео не было справочным материалом для реализации научных открытий этой работы, а также двоичной системы 2, когда это исследование начало развиваться и Бинарные данные, а также наблюдения чисел 3 и 6, а также вычисление и логика числовой пропорции были выполнены другим способом и до доступа Nikola Tesla к информации об этом предложении в этом видео.
Тесла нашел соотношение цифр 3 и 6, но не относился к двоичному коду, не относился к двоичной системе и программированию, и не развивал расчет численного соотношения, но Тесла наблюдал связь двоичной системы с Fibonacci и нашел логические последовательные 1, 2, 4, 8, 7, 5 из двоичной системы 1, а также нашел последовательные 3 и 6 , но не относиться к двоичной системе, но он был ученым, который был ближе всего к поиску новой двоичной системы. (TESLA, Youtube)
И в открытии двоичной системы 2, последовательное сканирование 3 и 6 не были первым наблюдением, сделанным о двоичной системе 2, эта информация является частью, так же как и многие другие, сделанные во время научного открытия двоичной системы 2, такие как двоичный код, круглый пиксель, открытие нейтронов в двоичном программировании, а также определение 1 (один) равный Pi и другие различия между типом открытых и закрытых схем в бинарных системах и различиями в двоичном программировании.
Тем не менее, это видео помогает в основе логических аспектов, чтобы сделать научные, математические, логические и физические наблюдения этого исследования. Таким образом, чтобы сделать выводы этих исследований, информация о логической последовательности номеров Тесла 3 и 6 была неизвестна, и, наблюдая за видео Тесла, он наблюдал номера 3 и 6 в различных отношениях от того, как это наблюдалось в этом исследовании, в этих научных выводов, присутствующих здесь, последовательные сканы 3 и 6 наблюдались путем расчета соотношения цифр.
Это видео было позже наблюдается открытие и публикация двоичной системы 2, а также позднее публикация патентного процесса в INPI (Национальный институт промышленной собственности), но и для качества материала, потому что предмет имеет те же ссылки, и был хорошо цитируется одним из лучших физиков в современной науке, а также искать больше наблюдения по этому вопросу , это видео очень полезно.
Оно следует за этой цитатой от Tesla для того чтобы представить величину чего оно понять в математике и физике широта знания которая понять смысль номеров 3 и 6. ‘Если бы вы знали великолепие чисел 3, 6 и 9, то у вас был бы ключ к Вселенной” (TESLA, Youtube)
Рисунок 5: Цитата Никола Тесла 3 и 6.

Можно сказать, что наблюдение бесконечности от 1 до 9 и, таким образом, понимание того, что любое и все числа могут быть представлены этой последовательностью бесконечности, также имеет большое великолепие.
Двоичная система 2 – самое важное технологическое научное открытие сегодня, так как это передовая технология, компьютер с технологией двоичной системы 2 намного превосходит компьютер с современной технологией двоичной системы, и этот расчет является одним из самых сложных уравнений, которые мы имеем .
Есть несколько технических различий, которые демонстрируют превосходство двоичной системы 2 к двоичной системе 1, ниже будут приведены некоторые в качестве примеров:
1 – Разница в типе физической цепи, в двоичной системе 1 цепь открыта, то есть, это прерванная схема и в двоичной системе 2 цепь закрыта, то есть это непрерывная цепь, это создает большую разницу в превосходстве в производительности и реакции системы. Непрерывная схема более эффективна, чем прерванная цепь.
2 – Еще одно техническое отличие заключается в том, что в двоичной системе 1 схема работает только с двумя физическими и логическими элементами программирования отрицательный и положительный, в то время как двоичная система 2 работает с тремя физическими и логическими элементами программирования отрицательный, нейтральный и положительный, с этими тремя элементами в программировании схема закрывается из-за нейтрального, тем самым принося превосходную производительность и результат , в том числе влияющих на безопасность системы. Один из способов выразить себя технически в смысле безопасности двоичного программирования, является то, что двоичная система без нейтральной цепи открыта, так что ее дверь открыта небезопасно, и в двоичной системе с нейтральным цепь закрыта, поэтому его дверь закрыта, так что двоичная система 2 имеет больше безопасности.
3 – Другие аспекты в программировании физической логики систем, в двоичной системе 1 он работает только с 1 π (один PI) без нейтрального, в то время как в двоичной системе 2 физическая логика системы работает с 2 π (два PI) с нейтральным, это приносит большую разницу в типе виртуальной реальности систем, в двоичной системе 1 пиксель квадратный и в двоичной системе 2 пиксель круглый , непосредственно влияющих на тип реальности, измерения и графики системы, в результате чего больше качества, определения, скорости, гибкости и логики, а также увеличение обработки и мощности в объеме данных, таким образом, большую эффективность в логических аспектах в программировании двоичной системы 2. 2 π (два PI) с нейтральным больше, чем 1 π (один PI) без нейтрального.
4 – И еще одна важная техническая причина – это разница между двоичными кодами и логическими последовательностями систем, как объяснялось ранее, в двоичной системе 1 – это логическая последовательность из шести факторов, а в двоичной системе 2 – это логическая последовательность из двух факторов, и это Разница в последовательных и двоичных кодах напрямую влияет как на объем обработки данных, так и на скорость отклика двоичной системы 2, которая является более гибкой и логичной математически и физически. Последовательные 3 и 6 более логичны и эффективны, чем 1, 2, 4, 8, 7, 5.
Есть и другие технические различия и другая информация, но эти примеры выше, которые демонстрируют основные различия между системами, и набор этих технических различий между бинарными системами демонстрируют высокое качество одной системы по отношению к другой системе.
Открытие двоичной системы 2 программирования является одним из логических программ, которые мы в одной из самых сложных и высоких степеней, которая существует на сегодняшний день, и сделать математические, логические и физические наблюдения, используя только 0 (ноль) и 1 (один), то есть, видя системы в нуле и один, является большой проблемой.
Что касается схем и программирования бинарных систем, правильный способ, который мы можем выразить, является то, что компьютер он думает о нулях и один, так что научное открытие двоичной системы 2, является открытием нового способа или более эффективный способ для компьютера думать о нулях и них.
Двоичная система 2 является самой передовой технологией, которая существует сегодня. Двоичные системы являются системами, потому что они выполняют различные функции, они являются логическими схемами, а также программирование, двоичная система 2 является новой системой более эффективной и безопасной для работы электроники, и отличает двоичное программирование от другого через логическое расположение нулей и один.
Тем не менее, это исследование, чтобы продемонстрировать открытие расчета числовой пропорции, если вы хотите больше информации о двоичной системе 2, статья находится в ссылках на эту работу.
Двоичная система 2 работает с законами численным соотношением, она обрабатывает ваши данные от 1 до 9, тем самым будучи гораздо более эффективными. Двоичная система 2 также работает с уважением к законам Fibonacci, и это исследование имеет ссылку и связь также в расчете численой пропорции, потому что они практически одно и то же, два являются коэффициентом бесконечности, только новый математический способ расчета, выражения и наблюдения часть законов Fibonacci был обнаружен. Эти наблюдения выполняются здесь называется расчетом численными пропорциями.
После долгого времени изучения и исследования, и достижения наблюдений выше расчета численной пропорции, связь была найдена между этим открытием и другим исследованием, что из последовательности Fibonacci (PHI). Логика численой пропорции от 1 до 9 до Бесконечности напрямую связана с законами Fibonacci , которые также следуют математическим законам,
что с помощью мер серии Fibonacci при анализе коэффициента двух последовательных мер получается иррациональное число под названием (PHI) с приблизительным значением 1,618. И эта конъюнктура мер, основанных на этом количестве, называется Золотым Коэффициентом, или Золотым Коэффициентом, который находится, таким образом, в цветах, деревьях, волнах, в галактиках, оболочках, ураганах, в симметричном лице человека, в их костных суставах и в особенностях человека, их сердцебиении и в их ДНК. Также в преломлении света, предоставляемого электронами атомов, в вибрациях, в других, более проявлениях (TANURE, online, s/p).
И это объясняет, почему последовательность от 1 до 9. Ниже мы можем видеть, что следующий квадрант является удвоением всех предыдущих, например, 2 – это удвоение [1], 3 – это удвоение [1 и 2], 4 вдвое больше, чем [1, 2 и 3], 5 вдвое больше, чем [1, 2, 3 и 4] и так далее. И он всегда идет последовательно от 1 до 9, где 9 вдвое больше всех своих предшественников, таким образом повторяя логику бесконечности: 1 2 3 4 5 6 7 8 9, 1 2 3 4 5 6 7 8 9, 1 2 3 4 5 6 7 8 9. Всегда следующая цифра удваивает количество своих предшественников. Ниже приведен способ выражения последовательности Fibonacci.
Рисунок 6: Fibonacci-PHI последовательность
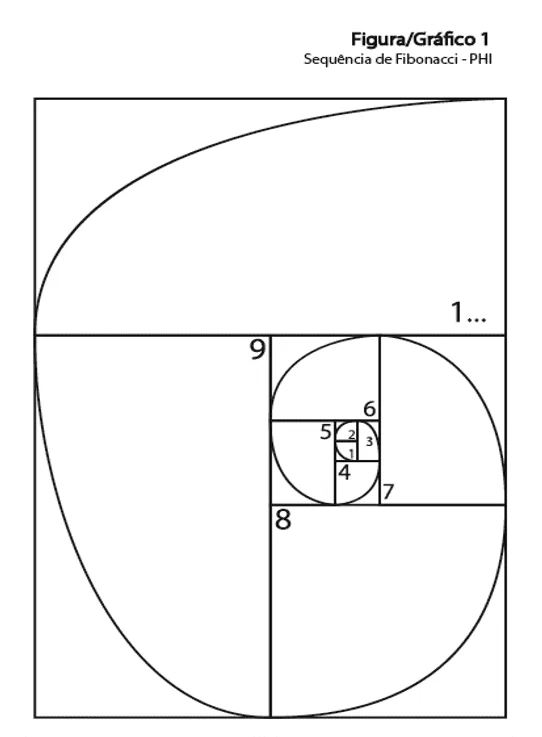
Глядя на приведенную выше диаграмму, мы приходим к выводу, что:
9 х PHI 1 Бесконечность (девять раз Fibonacci мера равна одной Бесконечности) или
9 x 1.618 й 1 Бесконечность или 1 единица.
ИЛИ 1 бесконечность No 1 единица (бесконечность равна одной единице)
Например, если математически найти меру Fibonacci , представляющую бесконечность в ракушке, эта ракушка представлена единицей 1, потому что этот коэффициент бесконечности присутствует или математически подписан в этой единице.
Мера цифры пропорции или последовательности Fibonacci , которая представлена коэффициентом и логикой пропорции для расчета и найдите бесконечность, потому что если вы обнаружите этот коэффициент или расчет, присутствующий в любом элементе, галактике, растении или животном, то это существо или элемент представлены 1 (одной) единицей в законах Fibonacci .
Все элементы и существа подписаны математически, физически и естественно с этим коэффициентом Бесконечности.
В каждом блоке есть математически подписанная Бесконечность.
Другая цитата, найденная о последовательности Fibonacci , говорит о логике соотношения, как помоялись ниже:
является последовательность чисел, которые следуют шаблону.
Последовательность Fibonacci является не более чем порядком интеграторов, который обычно отходит от нуля и один, в котором каждое следующее число соответствует сумме предыдущих двух цифр. Эта преемственность можно увидеть в различных явлениях природы.
Последовательность Fibonacci была названа итальянским математиком Леонардо де Пиза, также известным как Fibonacci. В 1202 году, из этой численной последовательности, математик сообщил о заранее популяции кроликов.
Формула Fibonacci
Преемственность Fibonacci – это последовательность интеграторов, начатая нулевой и одной, в которой каждый последующий термин соответствует сумме двух предыдущих чисел:
0,1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584… (Fibonacci последовательность – Эдука и Бразилия).
И здесь мы можем заметить разницу методов наблюдения между расчетом Fibonacci и этим математическим и логическим расчетом численным пропорцией. Логика нумеральной пропорции и последовательность Fibonacci – это одно и то же, но этот бесконечный коэффициент можно наблюдать этими двумя различными способами. Поскольку Fibonacci был отсылкой к разработке этого открытия логики нумеральной пропорции, потому что в двух наблюдениях они имеют один и тот же коэффициент бесконечности, только способ наблюдаемых изменений, поэтому мы также будем крестить расчет этой последовательности от 1 до 9 этого исследования Fiboleo, по причине взаимосвязи между именами авторов этих наблюдений.
Последовательный от 1 до 9, как доказано в расчетах, присутствующих в данном исследовании, логика цифрных пропорций и расчет числовой пропорции.
Вот более подробную информацию из Fibonacci последовательности котировки в интернет-поисках:
Этот метод применяется при анализе финансовых рынков, теории игр и информатики, а также биологических и естественных конфигураций. Натуральные модели. Последовательность Fibonacci также может наблюдаться при природных явлениях). (Fibonacci последовательность – Эдука и Бразилия).
Здесь, в этой цитате, мы видим, что она говорит о компьютерных науках, это также, где расчет доли цифры был применен для определения новой двоичной системы, как по примеру ранее в этом исследовании.
Проверьте больше цитат о расчете, ниже некоторые из них:
Подсолнечник: Ядра подсолнечника имеют семена, которые расположены в двойном наборе спирали. Большую часть времени это 21 по часовой стрелке и еще 34 против часовой стрелки.
Сосновый конус: после роста плодов семена образуют двойную спираль с восемью по часовой стрелке и еще 13 против часовой стрелки.
Раковина улитки: каждая часть раковины имеет размер, равный сумме двух предшественников. Известно, что у конхи три основные стороны, тогда, если предположить, что одна сторона имеет размер 2 (1 + 1), а другая 5 (3 + 2), третья будет 8 (5 + 3). (Последовательность Fibonacci: Educa + Brasil).
Таким образом, логика численного соотношения, которая является последовательной от 1 до 9, является коэффициентом Бесконечности, и поэтому мы можем выполнить то же наблюдение в последовательном Fibonacci, который также является бесконечным коэффициентом. Но изучение этого расчета очень эффективно для операций, где он имеет большой объем цифрных чисел, потому что мы можем идентифицировать их в более простой логической последовательности, любые числа представлены последовательными числами от 1 до 9 бесконечно.
ЗАКЛЮЧЕНИЕ
Заключение этого исследования направлено на запись открытия расчета числовой пропорции и логики числовой пропорции, и связать это открытие расчета числовой пропорции с расчетом Fibonacci, помимо демонстрации его применимости в математике и особенно в бинарных системах и относительно его применения по отношению к бесконечности.
Это исследование может обеспечить основание для новых научных открытий, как это уже произошло, и для исследований. Это может помочь людям думать о новых способах борьбы с числами, и это более простой новый способ расчета путем последовательности всех значений в Бесконечность от 1 до 9. В логике цифры бесконечность разбита с 1 на 9. Также представить новую информацию, новый способ о том, как наблюдать, выражать, находить, вычислять и расшифровывать Бесконечное.
СПРАВКА
BELLAS, L.D. Sistema Binário 2 – Código Fechado. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano 04, Ed. 02, Vol. 05, pp. 110-151. Fevereiro de 2019. ISSN: 2448-0959. Disponível em: https://www.nucleodoconhecimento.com.br/tecnologia/sistema-binario-2-codigo-fechado
TANURE, A.C. Proporção Áurea e Sequência Fibonacci. Pagasus Portal. Disponível em: http://pegasus.portal.nom.br/proporcao-aurea-e-sequencia-de-fibonacci/
TESLA, N. Os segredos dos números 3, 6 e 9. Youtube – Fatos Desconhecidos https://www.youtube.com/watch?v=c2M9ZfZ5h5A&t=682s
Sequência de Fibonacci. Educa+Brasil. Disponível em: https://www.educamaisbrasil.com.br/enem/matematica/sequencia-de-fibonacci
[1] Окончил факультет делового администрирования со специализацией во внешней торговле.
Отправлено: май 2020 года.
Утверждено: Декабрь 2020 года.