Nuova formulazione matematica del processo di diffusione molecolare ed elettrodiffusione nelle membrane cellulari

ARTICOLO ORIGINALE

SOUZA, Nathan Rodrigues Serpa ^[1]

SOUZA, Nathan Rodrigues Serpa. Nuova formulazione matematica del processo di diffusione molecolare ed elettrodiffusione nelle membrane cellulari. Revista Científica Multidisciplinar Núcleo do Conhecimento. Anno 06, Ed. 04, Vol. 15, pp. 34-63. aprile 2021. ISSN: 2448-0959, Link di accesso: https://www.nucleodoconhecimento.com.br/fisica-it/diffusione-molecolare

RIEPILOGO

La diffusione molecolare è un fenomeno fisico-chimico osservabile nella vita quotidiana, come semplici gas di un profumo che si espande attraverso una stanza chiusa, così come microscopicamente, l’assorbimento di ioni da parte di verdure e animali da parte delle cellule, attraverso canali ionici aperti della membrana plasmatica. Questo articolo di natura fisica propone la formulazione di una nuova equazione chiamata dall’autore di “Equazione di Nathan”, come estensione della nota prima legge di Fick, che mira a descrivere il fenomeno naturale della diffusione, a causa della variabile Forza risultante del sistema, che consentirà un’analisi generale delle forze che influenzeranno questo fenomeno , oltre ad estendere questa formulazione per descrivere il trasporto di ioni attraverso la membrana cellulare, una formulazione chiamata “Equazione di Nathan per l’elettrodiffusione nelle membrane cellulari”. Attraverso il metodo esplorativo, la ricerca bibliografica e gli strumenti matematici sono stati possibili per eseguire tali formulazioni, nonché per interpretarle. Dall’analisi dimensionale e dai postulati proposti dalla 1a Legge di Fick e dalla Legge di Graham per la diffusione, sotto forma di grafici basati su dati sperimentali e ipotetici per confrontare le somiglianze delle curve del grafico, è stato possibile confermare la validazione matematica e fisica per questa equazione, dimostrando di conservare le unità e concordando positivamente con i postulati presentati da quelle altre leggi già stabilite nell’ambiente fisico-chimico.

Parole chiave: Diffusione, Membrana Cellulare, Legge di Fick, Equazione di Nathan, Elettrodiffusione.

1. INTRODUZIONE

La diffusione molecolare è un fenomeno fisico-chimico osservabile quotidianamente, come semplici gas di un profumo che si espande attraverso una stanza chiusa, così come microscopicamente, l’assorbimento di ioni da parte di verdure e animali da parte delle cellule, attraverso canali ionici della membrana plasmatica. Questo processo di trasporto consiste nel movimento spontaneo e irreversibile di molecole situate in regioni ad alta concentrazione (ipertonica) ad altre con concentrazioni più basse (ipotoniche), la forza trainante per questo sono i potenziali chimici o termici della soluzione, e nel caso di membrane cellulari forze elettrostatiche insieme (DA SILVA, 2013).

Secondo Alberts (2009), la membrana presenta tessuto di carattere anfifilo, formato da fosfolipidi con un’estremità polare (fosfato radicale) e un altro non polare (coda di acido grasso). Alcune molecole polari o cariche come gli ioni hanno difficoltà ad attraversare per semplice diffusione al bistrato lipidico, spostamento fatto attraverso il trasporto di proteine o proteine che fanno canali, come i canali ionici. Oltre a presentare una polarità tra i media extracellulari con accumulo di cariche positive e il mezzo intracellulare con accumulo di cariche negative, comportandosi come un campo elettrico uniforme (MOREIRA, 2014).

Questo articolo esplorativo, con un metodo di analisi teorico-matematica, mira a stabilire una nuova formulazione matematica per la descrizione del processo di diffusione molecolare e trasporto ionico attraverso canali ionici di membrane cellulari, che tenga conto della Forza risultante del sistema (F_R), che consentirà un’analisi generale delle azioni nelle particelle. Le proposizioni esposte avevano come base teorica l’incontro di una raccolta bibliografica diversificata, nei campi delle scienze biologiche, chimiche e fisiche, così come l’analisi delle loro proposizioni dalla comprensione fisica e matematica dei risultati, sotto lo spettro di altre leggi che descrivono un certo aspetto dello stesso fenomeno in studio, come: Legge di Fick e Legge di Graham.

2. SVILUPPO

2.1 MATERIE E METODI

Questo articolo di bias esplorativo mira a stabilire formulazioni matematiche per descrivere il processo di diffusione molecolare e il flusso di ioni attraverso canali ionici aperti di membrane cellulari, a causa non solo del gradiente di concentrazione o del potenziale elettrico della membrana, ma per tenere conto delle forze costanti che operano in generale, formulazioni matematiche che sono chiamate dall’autore di : Equazione di Nathan e Equazione di Nathan per l’elettrodiffusione nelle membrane cellulari.

Per la costruzione matematica, la raccolta di materiale bibliografico di varie scienze era di grande rilevanza, come: Biologia Cellulare, Chimica e Fisica. Oltre alla revisione del materiale, dopo la costruzione matematica, è stata eseguita l’analisi dimensionale dell’equazione per verificare la conservazione delle unità e la loro validità, nonché la loro risposta positiva o negativa sui postulati delle leggi Fick e Graham per la descrizione del processo di diffusione, sulla base di grafici basati su dati sperimentali e ipotetici , al fine di confrontare i grafici creati dalle relazioni matematiche. Le conoscenze utilizzate saranno esposte di seguito:

2.2 SVILUPPO BIOLOGICO

Le cellule sono organizzate in tre parti: la membrana plasmatica, il citoplasma e il nucleo. Uno dei focus di questo lavoro accademico risiede nella comprensione del compartimento primario, la membrana cellulare, con circa 8 nanometri (nm) o 8 x 10^-9 metri (m), osservabili alla luce di un microscopio elettronico. La membrana non è completamente permeabile, consistente nella sua funzione principale, essendo una barriera selettiva che consente la separazione, nonché lo scambio di sostanze tra l’ambiente extra ed intracellulare (JUNQUEIRA e CARNEIRO, 2012).

Tuttavia, la sua permeabilità selettiva è dovuta alla composizione chimico-strutturale delle membrane cellulari, essendo composta da un bistrato di fosfolipidi, proteine e carboidrati. I fosfolipidi sono tessuti ampyfili, cioè contenenti parti polari e non polari, la testa idrofila (Fosfato Radicale) si trova di fronte all’esterno della cellula formando interazione elettrostatica con le molecole polari dell’acqua. La sua regione idrofobica è costituita dalle sue lunghe catene apolari di acidi grassi che possono facilmente interagire con altre sostanze liposolubili, di cui è più vantaggioso avere la coda rivolta verso la regione intracellulare. Pertanto, non tutte le sostanze sono in grado di attraversare la membrana cellulare ed entrare nella cellula per semplice diffusione, tuttavia, tale trasporto di diffusione è facilitato dal trasporto o dalle proteine ioniche che fanno canali quando vengono aperte (ALBERTS, 2009).

2.3 SVILUPPO CHIMICO

Secondo Taiz e Zeiger (2006), la diffusione è un fenomeno del trasporto di materia, in cui c’è un flusso di particelle dalle regioni con concentrazioni più elevate alle regioni con concentrazioni più basse, con l’obiettivo di promuovere lo stato di equilibrio o anche chiamato omeotasi. La descrizione matematica di tale processo è espressa dalla Prima Legge di Fick, proposta dal medico e fisiologo Adolf Eugen Fick (1829-1901), un’equazione differenziale in cui la Densità di Flusso (J) è direttamente proporzionale al Gradiente di Concentrazione (  ), e al Coefficiente di Diffusione (D) che dipende dall’elemento chimico in esame, come espresso di seguito (vedi equazione 2.1):

Questo flusso omogeneizzante è una conseguenza statistica del movimento casuale delle particelle, noto come Movimento Browniano, le molecole si spostano spontaneamente dalle regioni ipertoniche (Concentrazioni Maggiori) alle regioni ipotoniche (Concentrazioni inferiori). Il segno negativo nella legge di Fick indica che il flusso è nella direzione opposta al gradiente di concentrazione, essendo una legge lineare, non importa quanto sia grande la differenza di concentrazione tra due punti, il flusso rimane proporzionale al gradiente.

Altri importanti dettagli sulla Legge di Fick sono i seguenti: Relazione direttamente proporzionale all’Area di Diffusione (A) e inversamente proporzionale tra la dimensione delle particelle e la velocità di diffusione, o la sua Massa Molecolare (M). Cioè, maggiore è l’area, maggiore è la tassa di trasporto; inoltre, minore è la massa molecolare della particella, maggiore è la sua velocità di trasporto e maggiore è la sua velocità di diffusione.

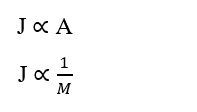
Secondo Brady e Huminston (1995), la Legge di Graham (vedi equazione 2.2), formulata dal chimico Thomas Graham (1805 – 1869) dopo i suoi studi sulla diffusione e l’effusione dei fluidi, stabilisce che la Velocità (u) di effusione e diffusione di due gas (δ1) e (δ2), nelle stesse condizioni di temperatura e pressione, è inversamente proporzionale alla radice quadrata delle loro Densità (d) o Massa Molecolare (MM), come espresso di seguito:

o 

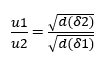
o

2.4

SVILUPPO FISICO

Uno dei concetti fondamentali di questo articolo è il noto “Principio Fondamentale della Dinamica” o “Seconda Legge di Newton”, che afferma: La forza risultante che agisce su un corpo è il prodotto della sua massa per l’accelerazione (F_R = m. a). Halliday (2016) afferma che devi prima scegliere il corpo che vuoi studiare e applicare la forza risultante come somma di tutte le forze che agiscono sul corpo in questione.

Secondo Tipler (2009), Work (W) è l’energia trasferita a un oggetto attraverso una forza che agisce sull’oggetto stesso. Per calcolare il lavoro che una forza fa su un oggetto quando viene spostato, usiamo semplicemente la componente di forza parallela allo spostamento dell’oggetto, la componente di forza perpendicolare allo spostamento non funziona. Il Lavoro (W) di una forza costante, in funzione di forze parallele (θ = 0°, 180°), può essere descritto attraverso questa equazione:

W = F. d. cosθ

Come [Cos(0°, 180°) = 1]; si può riscrivere l’equazione di lavoro come Integrale o in funzione della Variazione di una Distanza ΔX (vedi equazione 2.3), abbiamo:

Secondo Halliday (2016), l’energia è un concetto difficile da definire. Tuttavia, comprendiamo intuitivamente cos’è l’energia, dall’analisi degli effetti nelle diverse forme di essa, come: Energia Cinetica ed Energie Potenziali. Concettualmente per Tipler (2009), Kinetic Energy è associato a tutti i corpi che hanno massa e si muovono. Essere (m) la massa di un punto materiale e (u) la sua velocità scalare, rispetto a un dato riferimento. L’energia cinetica del punto materiale è data da (vedi equazione 2.4):

Per il moto uniformemente variato, il lavoro di forza risultante dal corpo misura la variazione di energia cinetica del corpo. Dal Teorema Lavoro-Energia (W = ΔK) si ottiene l’espressione che eguaglia il Lavoro di una Forza Costante (W) con la Variazione dell’Energia Cinetica (ΔK), come mostrato dalle equazioni (2.5) e (2.6):

Il moto uniformemente variato, secondo Marques (2016), è quello in cui una particella subisce una variazione di velocità (u0) in un’altra (u) a causa di una forza costante che promuove un’accelerazione (a) anch’essa costante, producendo anche uno spostamento (ΔX) . Questo tipo di movimento può essere equiparato senza tener conto del tempo, la cosiddetta “Equazione di Torricelli” (2.7):

Secondo Pimentel (2004), la forza trainante dei processi diffusivi nel mezzo liquido cellulare, è il cosiddetto potenziale chimico di qualsiasi soluzione, che è configurata come la capacità di tale soluzione di eseguire lavori sotto le particelle disciolte, in relazione al gradiente di concentrazione, una formulazione per il massimo potenziale chimico dell’acqua sarebbe (2.8):

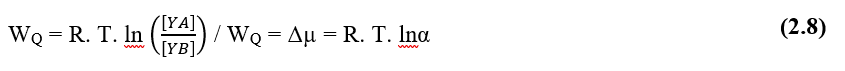
W_Q – Potenziale chimico della soluzione (J)

R – Costante generale del gas (R = 8,31 J Mol^-1 K^-1)

T – Temperatura assoluta (K)

[ Y_A ] – Concentrazione della sostanza Y nel punto A (Mol)

[ Y_B ] – Concentrazione della sostanza Y nel punto B (Mol)

α – Attività chimica

3. RISULTATI E DISCUSSIONI

3.1 SVILUPPO DELL’EQUAZIONE DI NATHAN

Nel tentativo di descrivere matematicamente il processo di diffusione e trasporto degli ioni attraverso i canali ionici nella membrana plasmatica, in funzione del Gradiente di Concentrazione e del Campo Elettrico generati alle estremità extracellulare ed intracellulare della membrana, consideriamo un x, y  e z, il sistema di coordinate in cui ciascun asse rappresenta la rispettiva accelerazione generata dalle forze agenti sul sistema isolato in esame (a_x, a_y e a_z), come mostrato in figura 1.

 Figura 1: Sistema di coordinate (X, Y, Z).

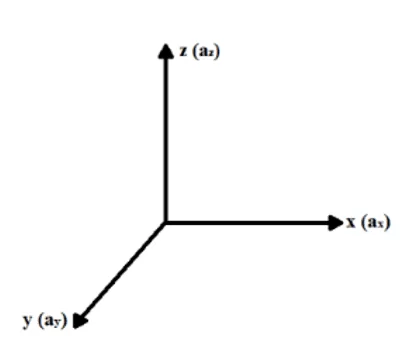
Secondo Halliday (2016), la forza risultante che agisce su una particella come ioni, che attraversano la membrana attraverso canali ionici, può essere decomposta nei suoi componenti in ogni asse x, y e z, essendo direttamente associata ad accelerazioni nei rispettivi assi. Attraverso il principio fondamentale della dinamica o seconda legge di Newton e il principio di sovrapposizione della forza di Newton, l’analisi fisica può essere ottenuta per le forze risultanti su ogni asse che esercitano influenza sullo ione (vedi equazione 3.1):

F_R– Forza risultante totale (N – Kg m s^-2)

F_R(X) – Forza risultante sull’asse X (N – Kg m s^-2)

F_R(Y) – Forza risultante sull’asse Y (N – Kg m s^-2)

F_R(Z) – Forza risultante sull’asse Z (N – Kg m s^-2)

 

Le masse degli ioni si conservano, quindi i fattori direttamente proporzionali alle forze in ciascuna direzione sono le loro accelerazioni nelle rispettive direzioni:

F_R(X) = m . a_x / F_R(Y) = m . a_y / F_R(Z) = m . a_z

Comnando tra le costanti elettrostatiche e gravitazionali (k = 9 x 10⁹ e G = 6,67 x 10^-11), secondo Halliday ³ (2016) questi valori dimostrano che la forza gravitazionale è molto più debole della forza elettrica. Pertanto, in un sistema isolato di particelle in cui considererà attive solo le forze gravitazionali ed elettriche, si può ignorare la forza gravitazionale, poiché la forza elettrica è circa 1,5 x 10²⁰ volte maggiore della forza di peso. Poiché l’accelerazione della gravità nella particella sarà sconsiderata, anche la forza nella componente Z sarà nulla poichél’accelerazione a z sarà esosiderata, riformuleremo l’equazione per il dato studio:

F_R = m . a_x + m . a_y + m . a_z

F_R = m . a_x + m . a_y + m . 0

F_R = m . a_x + m . a_y

Considerando come forze per lo più attive, quelle che esercitano influenza sull’asse X, trascurando gli urti meccanici e qualsiasi altra forza nella componente y, poiché l’insieme dei soluti si muove nel senso di omogeneizzare, dalle regioni ipertoniche a quelle ipotoniche, arriveremo a tale semplificazione della Forza Risultante:

F_R = m . a_x + m . 0

F_R = m . a_x

Un altro punto da notare è che il sistema in esame sarà considerato stazionario o su base permanente, in cui le sue proprietà sono inalterabili rispetto al tempo. Ciò implica che ogni proprietà P del sistema, la derivata parziale in relazione al tempo è zero, considerando un sistema in cui il tempo variabile non è un parametro nello studio del sistema a membrana in questione.

Le membrane cellulari hanno una certa disposizione, analoga al campo elettrico uniforme, in modo che ci sia la concentrazione di cariche positive principalmente sul lato extracellulare e un accumulo di cariche negative sul lato intracellulare. C’è anche una differenza di concentrazione tra le estremità esterna e interna delle cellule (C_{E e} C_I), in cui il sistema esercita una forza trainante per promuovere la traslocazione delle particelle attraverso canali ionici di membrane cellulari, come rappresentato dalla figura 2.

Figura 2: Rappresentazione dello spostamento ioniale tramite canale ionio.

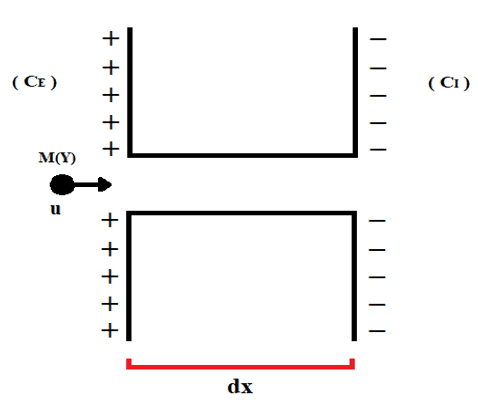
La distanza percorsa dalla molecola rappresentata è equivalente all’elemento di spostamento (dx), che è anche lo spessore della membrana cellulare già citato. La prima legge di Fick può essere descritta come una funzione del gradiente di concentrazione totale (∇D) e della costante di diffusione (D), come espresso di seguito (vedi equazione 3.2):

Tuttavia, considereremo solo l’elemento di lunghezza (?x) già menzionato, al fine di valutare il movimento unidimensionale dei soluti provenienti da regioni ad alta concentrazione, per concentrazioni più basse. Pertanto, i gradienti di concentrazione ( e ) verranno rimossi dall’equazione, di cui torniamo all’equazione 2.1:

Isolando l’elemento (∂x) dalla Prima Legge di Fick, otteniamo:

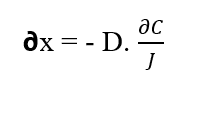
Le particelle di soluto si muovono lungo uno spostamento (∂x) a causa della forza derivata dal potenziale chimico del sistema (W_Q), perché secondo la seconda legge della termodinamica descritta da Tipler (2009), il flusso di materia o energia lascia le regioni con valori più alti di materia o energia per il più piccolo. Se le particelle sono soggette a forze e a causa di questa mossa da parte di un certo elemento di distanza (∂x), si può presumere che tali corpi ingrovano lavoro (W), che è descritto dalla seguente equazione (vedi equazione 2.3):

Il lavoro di una forza costante può anche essere descritto come una funzione della variazione di energia cinetica del sistema (ΔK), come espresso dal teorema dell’energia cinetica (vedi equazione 2.5):

Considerando il movimento unidimensionale delle particelle disciolte in soluzione, in un certo momento iniziale le particelle in relazione a un certo elemento (∂x) non si muovono, quindi la loro velocità iniziale (u₀) può essere considerata nulla, quindi l’Opera è descritta come segue:

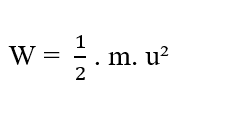
Per un sistema in cui abbiamo un numero n di particelle che si diffondono, ognuna delle quali ha una certa Massa (m(i)) e Accelerazione (a(i)), abbiamo che la Forza Risultante nelle particelle può essere espressa come:

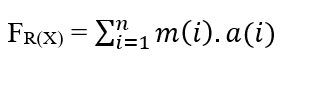
Poiché il sistema ha una Forza Costante, questo movimento è anche descritto con un’accelerazione costante per tutte le particelle secondo un movimento uniformemente vario, che consente di rimuovere l’accelerazione della sommatoria, dalle proprietà dei Somatori:

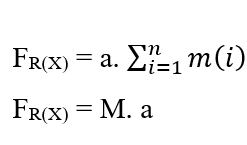
Per raggiungere l’equazione di Nathan, le due equazioni del Lavoro sono equalizzate, e poiché è per trattare il movimento delle molecole come dimostrato, la massa (m) è considerata come la massa totale (M) di una certa quantità di molecole presenti nel sistema in esame, e sostituisce anche l’elemento (dx) con (∂x) della Prima Legge di Fick.

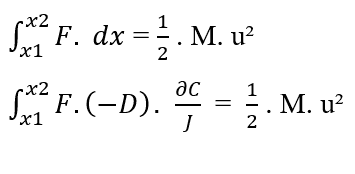
Sapendo che (F, D, J) sono costanti rispetto all’elemento (?C) da integrare, dalla proprietà della costante degli integrali, dall’integrale si possono togliere i termini:

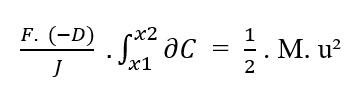
Riscrivendo i limiti di integrazione in relazione al (?C), abbiamo:

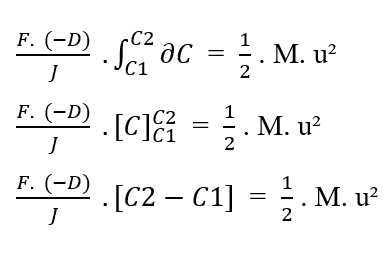
Sapendo [C₂ – C₁ = ΔC] questo, è possibile sostituire il valore nell’equazione:

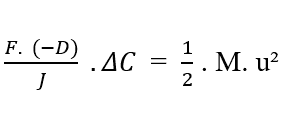
Isolando la densità del flusso variabile (J), otteniamo l’equazione di Nathan (vedi equazione 3.3):

J – Densità di flusso (Mol m^-2 s^-1)

D – Coefficiente di diffusione (m² s^-1)

ΔC – Variazione della concentrazione (Mol m^-3)

F_R – Forza risultante (Kg m s^-2)

M – Massa totale delle particelle diffondenti (Kg)

u – Tasso di diffusione delle particelle (m s^-1)

 

3.2 VALUTAZIONE MATEMATICA E FISICA DELL’EQUAZIONE DI NATHAN

Per confermare la convalida dell’equazione di Nathan in modo matematico, è stato necessario eseguire l’analisi dimensionale descritta da Halliday (2016), in cui controllerà se le unità della Prima Legge Fick sono conservate e le unità dell’equazione di Nathan sono equivalenti. L’analisi dimensionale è uno strumento usato in fisica per determinare l’unità di misura di una certa magnitudine. L’analisi dimensionale è uno strumento che consente la previsione, l’ispezione e l’adattamento delle unità fisiche utilizzate per la risoluzione delle equazioni.

Legge di Fick:

J – (Mol m^-2 s^-1)

Equazione di Nathan:

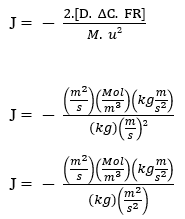
J – (Mol m^-2 s^-1)

 

Generalmente, le grandezze fisiche fondamentali sono espresse come: Lunghezza (L), Massa (M), Tempo (T), Temperatura (θ), Corrente Elettrica (A), Quantità di Materia (Mol) e Intensità della Luce (I). L’analisi dimensionale dell’equazione di Nathan (3.3) può quindi essere eseguita utilizzando tali rappresentazioni di grandezze fisiche fondamentali, secondo l’equivalente di ciascuna variabile nella formulazione esposta, come evidenziato da Marques (2016).

J – Densità di flusso (Mol L^-2 T^-1)

D – Coefficiente di diffusione (L² T^-1)

ΔC – Variazione di concentrazione (Mol L^-3)

F_R – Forza risultante (M L T^-2)

M – Massa totale delle particelle difitating (M)

u – Velocità di diffusione delle particelle (L T^-1)

Ora eseguendo l’analisi dimensionale con le rappresentazioni generali delle quantità fisiche fondamentali, abbiamo:

Legge di Fick:

J – (Mol L^-2 T^-1)

Equazione di Nathan:

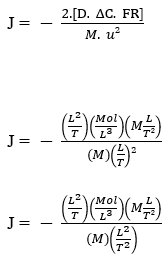
J – (Mol L^-2 T^-1)

 

L’equazione di Nathan dimostra la conservazione delle unità, così come segue alcune affermazioni che la Prima Legge di Fick e la Legge di Graham dimostrano, al fine di correlare alcune variabili in modo diretto o inversamente proporzionale, convalidando fisicamente tale formulazione matematica per il processo di diffusione, indipendentemente dalle unità scelte per le quantità fondamentali, a condizione che abbiano coerenza in generale.

La prima relazione che l’equazione di Nathan mostra è la relazione direttamente proporzionale tra densità di flusso (J) e variazione di concentrazione tra due punti (ΔC). Stabilendo che, un aumento della differenza di concentrazione tra due punti qualsiasi del sistema, sarà direttamente correlato all’aumento della densità di flusso dello stesso, Tale relazione obbedisce alla legge di Fick.

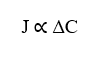
La seconda importante relazione è la diretta proporzionalità tra la Densità di Flusso (J) e la Forza Risultante (F_R) che agisce sulle particelle (γ) che compongono il sistema in esame. Ciò implica che un aumento della variabile Forza risultante che agisce sulle molecole diffondenti aumenterà anche in modo direttamente proporzionale il flusso di particelle.

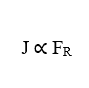
La terza relazione importante è la proporzionalità inversa tra la densità di flusso (J) e la massa totale di qualsiasi elemento gamma (γ), che co formano il sistema in esame. Ciò implica che, considerando per ogni molecola e solo la sua massa molecolare, maggiore è la massa molecolare dell’elemento da diffondere, minore è il suo tasso di trasporto, tale relazione obbedisce alla legge di Fick e alla legge di Graham.

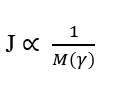
La quarta relazione importante è la proporzionalità inversa tra massa molecolare (M) e quadrato di velocità di diffusione (u). Oppure può essere intesa come la relazione inversa tra la velocità di diffusione e la radice quadrata della massa molecolare dell’elemento (γ). Questa relazione obbedisce alla Legge di Effusione e Diffusione dei Gas di Graham, mostrando la correlazione di Velocity con l’inverso della radice quadrata della massa molecolare.

La densità di flusso (J) è inversamente proporzionale al prodotto tra la massa molecolare (M) – quando per una particella – e il quadrato di velocità di diffusione (u):

Se (J) è costante (K), abbiamo:

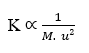
Isolando la variabile Diffusion Rate (u) si arriva a:

 

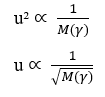
Dal Software Excel versione 2016, è stato inoltre possibile eseguire la modellazione grafica di 20 dati ipotetici per il valore di Massa Molecolare (M), con un intervallo di (0 < M < 21) in ordine crescente, correlato al rispettivo valore di Velocità di diffusione (u), sapendo che la velocità di diffusione di un dato elemento è inversamente proporzionale alla radice quadrata della sua rispettiva massa, come mostrato dalla legge di Graham e dall’equazione di Nathan quando la velocità di trasporto (J) è mantenuta costante e considera solo la massa di una singola particella. Quindi, possiamo vedere la somiglianza dei grafici costruiti in seguito con tali dati (vedi Grafico 1).

Grafico 1: Velocità di diffusione rispetto all’inverso della radice quadrata di massa molecolare.

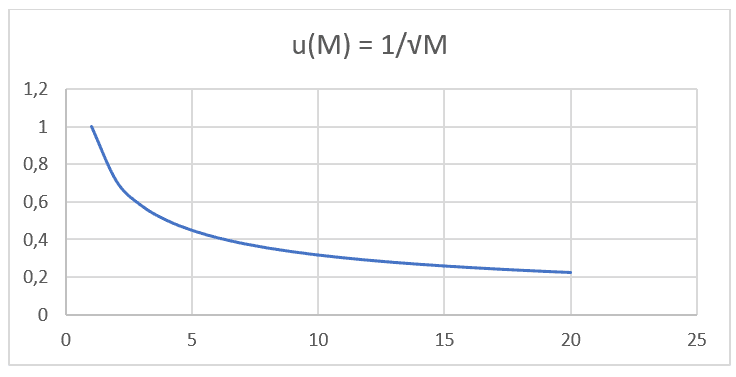
Si nota che entrambe le formulazioni, sia la Legge di Graham che l’Equazione di Nathan, hanno uguale proporzionalità e si basano sullo stesso tipo di funzione: F(x) = . Eseguendo una proiezione grafica con valori di massa molecolare, dati IUPAC e il loro rispettivo tasso di diffusione di 20 diversi gas alle stesse pressioni e temperature elencate nella tabella sottostante (vedi tabella 1), è possibile proiettare un secondo grafico (vedi grafico 2).

Tabella 1: Masse molecolari e rispettive velocità di diffusione.

gas	Massa molecolare (g/mol)	Velocità di diffusione (cm/s)
H2	2	0,7
He	4	0,5
O2	16	0,25
CH4	16	0,25
Ne	20	0,22
H2S	34	0,17
Ar	40	0,15
CO2	44	0,15
NO2	46	0,14
O3	48	0,13
C4H10	58	0,12
NO3	63	0,12
SO2	64	0,12
CS2	76	0,11
SO3	80	0,11
Kr	84	0,10
FeS	88	0,10
Xe	131	0,08
PCl3	137	0,08
Rb	222	0,06

Fonte: L’autore.

Grafico 2: Velocità di diffusione rispetto all’inverso della radice quadrata di massa molecolare.

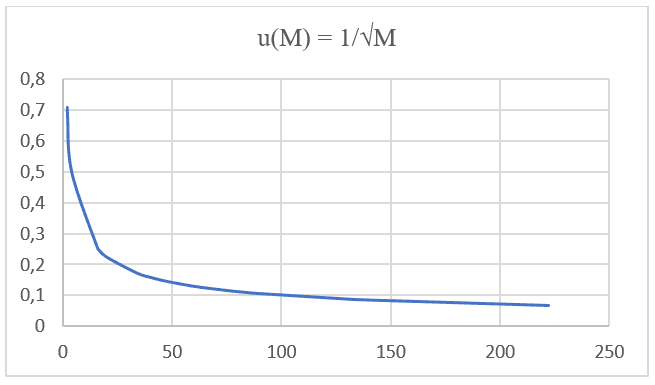
Secondo Zeiger e Taiz (2006), il tempo medio di diffusione può essere definito come il rapporto tra il quadrato della variazione di distanza (ΔX²) e il coefficiente di diffusione dell’elemento (D), espresso dalla seguente formulazione matematica (vedi equazione 3.4):

Dalla definizione di Velocità Scalare Media (u) della cinematica e sostituendo il valore del tempo con la variabile Tempo medio (T_M), otteniamo:

o

 

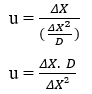
Eseguendo le manipolazioni algebriche si ottiene l’equazione per calcolare il Diffusion Rate (u) di un qualsiasi elemento:

Sostituendo (3,5) nell’equazione di Nathan (3.3), possiamo ottenere la relazione tra il quadrato della variazione di distanza (ΔX) e la variazione di concentrazione (ΔC).

Eseguendo l’analisi dimensionale dell’equazione (3.6) per confermare la conservazione delle unità della Legge di Fick, abbiamo:

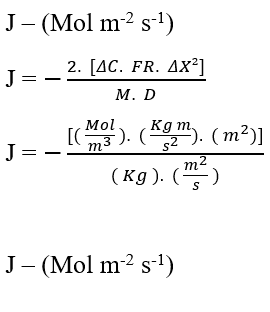
Convalidata la conservazione delle unità dall’analisi dimensionale, si può percepire una relazione importante e comune nell’equazione di Nathan e nella Legge di Fick, è la proporzionalità inversa tra la variazione di concentrazione (ΔC), e il quadrato della variazione di distanza (ΔX²). Affinché questa affermazione sia valida, considereremo costante la velocità di trasporto (J) e analizzeremo solo queste due variabili: Variazione di concentrazione e distanza.

 

Considerando costante la Densità di flusso (J) si ha:

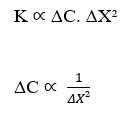
Viene dimostrata la proporzionalità inversa tra la variazione di concentrazione (ΔC) e il quadrato di variazione della distanza (ΔX²). Questa affermazione concorda con la Legge di Fick, perché quando si analizza la correlazione tra queste due variabili, entrambe le formulazioni, Equazione di Nathan e Legge di Fick, descrivono lo stesso grafico che segue la funzione: F(x) = . Di seguito è riportata una dimostrazione del formato grafico (curva gaussiana), variazione di concentrazione rispetto alla variazione quadrata della distanza (vedere figura 3):

Figura 3: Variazione del grafico della concentrazione rispetto al quadrato della variazione di distanza.

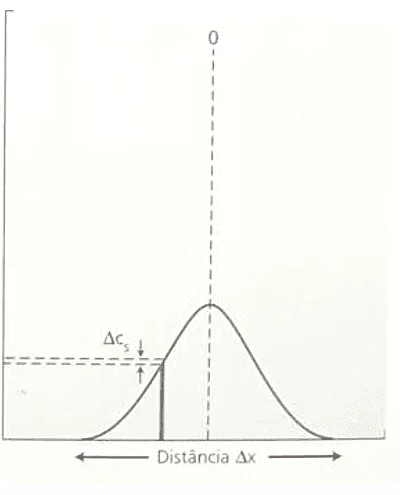
Nel caso di avere solo come variabile determinante nel processo di diffusione di un dato elemento, la variazione di concentrazione (ΔC), supponendo quindi che si tratta di un movimento di particelle la velocità costante e non un movimento uniformemente variato causato da una forza costante, basta sostituire (2.7) in (3.3), l’equazione di Torricelli, che restituirà la descrizione matematica nota come descrizione matematica nota come : 1a legge di Fick.

Sostituendo (2.7) in (3.3) considerando la velocità iniziale (u₀) null, abbiamo:

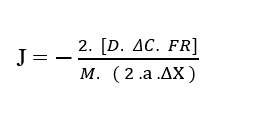
Cancellando i termini Forza risultante (F_R),con i termini nel denominatore Massa totale delle particelle (M) e Accelerazione (a), così come le costanti nel numeratore e denominatore (2), otteniamo di nuovo la formulazione lineare: Prima Legge di Fick (2.1).

 

3.3 SVILUPPO DELL’EQUAZIONE DI NATHAN PER L’ELETTRODIFFUSIONE NELLE MEMBRANE CELLULARI

L’equazione di Nathan può essere estesa per descrivere il processo di diffusione degli ioni attraverso la membrana cellulare, matematicamente, tenendo conto delle seguenti formulazioni matematiche. Secondo Pimentel (2004), la forza trainante dei processi diffusivi nei sistemi biologici è il cosiddetto potenziale chimico del sistema, e nel caso dell’esempio in questione, si verifica il trasferimento di materia da un punto A all’altro B, tale potenziale chimico può essere espresso dalla seguente equazione (2.8):

Ciò implica che un soluto si sposterà da una regione con un maggiore potenziale chimico a una regione più piccola, o nel caso di solventi come l’acqua, dall’osmosi si sposta dalle regioni di concentrazioni più basse di soluto a più grandi. Tuttavia, il flusso di particelle cessa quando i potenziali chimici di entrambe le fasi sono uguali, ottenendo così lo stato finale di equilibrio (HENEINE, 2004).

Tale potenziale di soluzione che produce la forza risultante del sistema, poiché rappresenta la capacità di un dato sistema di eseguire il lavoro, può essere descritto tenendo conto del contributo di altri fattori importanti, come: azione gravitazionale e influenza elettrica sulle particelle a causa dei loro carichi e della differenza nel potenziale elettrico. Pertanto, l’equazione del potenziale massimo può essere espressa dalla formulazione del potenziale elettrochimico, di seguito (vedi equazione 3.7):

Nel caso in cui il contributo del potenziale gravitazionale (m.g.h) venga ignorato, l’equazione sarà ridotta solo al contributo chimico ed elettrico, queste sono le forze che lavorano nell’insieme delle particelle ioniche per muoversi attraverso i canali ionici o molecolari attraverso il bistrato lipidico, entrando nell’ambiente intracellulare (ALBERTS, 2009).

L’equazione di Nathan descrive il processo di diffusione, e il fenomeno naturale del trasporto ionico attraverso la membrana cellulare può essere espresso in modo simile dall’equazione di Nathan, prendendo come Forza risultante (F_R) solo il potenziale chimico della soluzione e contributo elettrico, trascurando il contributo gravitazionale.

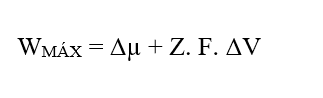
Sapendo che (W = F_R. Δx), sostituendo l’equazione (2.3) otteniamo:

Eseguendo l’analisi dimensionale della Forza Risultante (3.8), dividendola nei suoi appezzamenti chimici ed elettrici, si può percepire l’emergere non più dell’unità di energia Joule (J), ma piuttosto dell’Unità di Forza nel Sistema Internazionale di Misure, Newton (N):

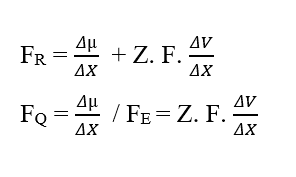
Analizzando la porzione chimica del contributo (F_Q), abbiamo:

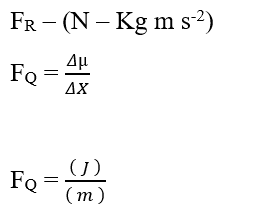
Sapendo che l’unità di energia Joule (J – N.m) può essere sostituita nell’analisi dimensionale, ottenendo:

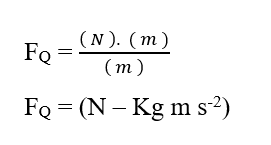
Analizzando la porzione elettrica di contributo (F_E), abbiamo:

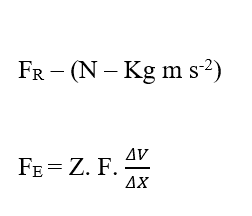
Sapendo che Valencia (Z) è una variabile dimensionale, abbiamo:

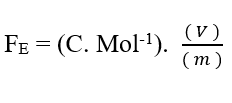
Sapendo che l’unità di tensione Volt (V – J. C^-1), può essere sostituita nell’analisi dimensionale, ottenendo:

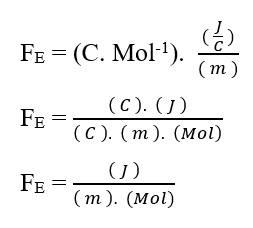
Poiché l’unità Mol è considerata adimensionale, in quanto è relativa solo alle entità che compongono un dato sistema, come: Atomi, molecole, ioni o elettroni; possiamo trascurare questa unità nell’analisi, semplificandola:

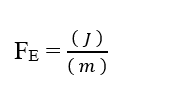
Sapendo che l’unità di energia Joule (J – N.m) può essere sostituita nell’analisi dimensionale, ottenendo:

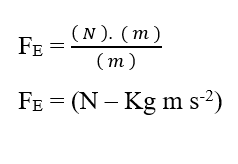
Dall’analisi dimensionale delle due porzioni, chimica ed elettrica, che compongono la Forza Risultante (F_R) del sistema in esame, risulta valida per il calcolo di tale forza. Scrivere i rapporti tra la Variazione del Potenziale Chimico (Δµ) e la Variazione della Distanza (ΔX), la Variazione del Potenziale Elettrico (ΔV) e la Variazione della Distanza (ΔX), sotto forma di limiti di (ΔX 0) e poi nella forma differenziale , avendo la Forza Risultante Istantanea, si ottiene:

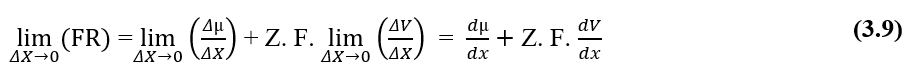
Per una situazione in cui i Potenziali Elettrochimici di due fasi (A) e (B) di un dato sistema sono uguali, cioè in una situazione di equilibrio, si può stabilire il valore di Variazione del Potenziale Elettrico alle estremità delle Membrane Cellulari, che si riferisce all’equazione di Nernst.

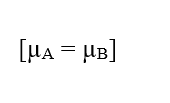
Se i potenziali sono gli stessi, questa affermazione indica che il Lavoro eseguito dalle particelle è nullo, quindi anche la Forza Risultante in esse sarà nulla, poiché non vi è alcun transito di molecole tra le due fasi del sistema:

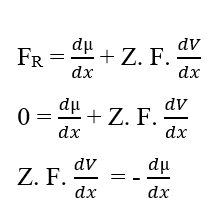
Puoi cancellare gli elementi (dx) che compaiono su entrambi i lati dell’uguaglianza e isolando il termine (dV), quindi lo riscriveremo in base alle variazioni, che risulta:

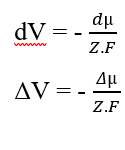
Sostituendo il potenziale chimico (2.3), ristabiliamo il calcolo del potenziale elettrico per una situazione di equilibrio nei sistemi biologici (3.10), noto come equazione di Nernst (HENEINE, 2004).

È possibile sostituire la Forza risultante del sistema (3.9) nell’equazione di Nathan descritta sopra (vedi Equazione 3.3):

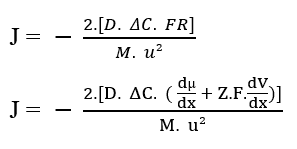
Oltre ai termini tra parentesi, abbiamo l’equazione di Nathan per l’elettrodiffusione nelle membrane cellulari (3.11):

J – Velocità di trasporto o densità del flusso ionico nella membrana (Mol m^-2 s^-1)

D – Coefficiente di diffusione del soluto (m² s^-1)

ΔC – Variazione di concentrazione (Mol m^-3)

M – Massa totale delle particelle difitating (kg)

u² – Velocità di diffusione delle particelle (m s^-1)

Z – Ion Valencia

F – Costante di Faraday (F = 9,648 x 10⁴ C mol^-1)

?µ/?x – Derivato dal potenziale chimico in relazione al dx (Kg m s^-2)

?V/?x – Derivato dal potenziale elettrico in relazione a dx (V m^-1)

Secondo Halliday (2016) per Termodinamica, Energia Interna (U) o Variazione energetica interna (ΔU), è la somma delle energie cinetiche e potenziali di tutte le molecole contenute in un sistema. Questa relazione può essere espressa con la seguente descrizione matematica (vedi equazione 3.12), considerando la velocità media per tutte le particelle costante:

[M – Massa totale delle particelle di sistema]

 

 

Sostituendo l’Equazione (3.13) nell’Equazione di Nathan (3.3), è possibile determinare un termine costante, nominato dall’autore con la lettera greca omega (ω):

Se ora consideriamo il motivo come qualsiasi costante (ω), poiché i valori di tali variabili non cambiano rispetto al tempo, poiché la derivata parziale di qualsiasi termine è nulla . Sapendo che (ω) si presenta come un’unità , un rapporto tra Quantità di Materia Concentrata ed Energia Interna di un sistema, tale relazione è equivalente alla seguente espressione (3.15):

E sapendo che il pacco si riferisce alla Forza risultante del sistema (FR), si può ancora riscrivere questa formulazione come sua forma generale (3.15):

È ora possibile notare che, poiché i termini (D) e (ω) sono costanti, la densità di flusso (J) è direttamente proporzionale alla Forza risultante del sistema (F_R),il che implica che se si verifica un aumento in una di queste variabili, anche l’altra subirà un aumento proporzionale.

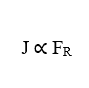
L’equazione di Nathan per l’elettrodiffusione nelle membrane cellulari descrive il flusso di ioni attraverso la membrana, attraverso i canali ionici quando sono aperti, influenzato dal gradiente di concentrazione dei mezzi extracellulari e intracellulari, nonché dal potenziale elettrico o campo elettrico sotto gli ioni, generati dalla membrana cellulare stessa. Questa formulazione tiene conto della Massa Particellare Totale dell’elemento che si diffonderà, delle forze motrici chimiche ed elettriche presenti nel fenomeno del trasporto ionico attraverso la membrana cellulare, tuttavia, se vi sono altri fattori esterni, dovuti all’aumento del Risultato Variabile di forza, l’analisi può essere eseguita in un ambito generalizzato, oltre a concordare con i concetti fisici esistenti e presentati.

4. CONSIDERAZIONI FINALI

In breve, questo articolo proponeva la formulazione della “Equazione di Nathan”, come estensione della 1° Legge di Fick, che descrive il flusso diffusivo delle particelle nelle soluzioni, non solo in funzione della Differenza di Concentrazione (ΔC), ma con l’obiettivo di considerare la Densità del flusso di materia (J) in funzione della forza risultante costante (F_R) che agisce sulle particelle di un dato sistema (vedi equazione 3.3).

Questa formulazione dimostrò la proporzionalità diretta tra la Forza che agisce nelle particelle, e la Densità di Flusso (J), quindi maggiore è la forza esercitata nel sistema, maggiore è il trasporto della materia. La stessa descrizione matematica dei processi naturali di diffusione delle molecole, che consente un’analisi generale di tutte le forze che possono esercitare influenza sotto determinati sistemi in studio, può anche essere estesa per spiegare il trasporto di ioni attraverso la membrana cellulare, quando la Forza risultante sotto le particelle del sistema in questione tiene conto del potenziale chimico e del potenziale elettrico , così come una relazione tra la quantità di materia concentrata e l’energia interna di un sistema (ω), che è stata chiamata dall’autore di “Equazione di Nathan per l’elettrodiffusione nelle membrane cellulari” (vedi equazione 3.11), o anche nella sua formulazione generale (vedi equazione 3.15).

La convalida delle Equazioni è stata valutata dall’analisi dimensionale e dalle relazioni dirette e inversamente proporzionali tra le variabili, in relazione ai postulati proposti dalla prima legge di Fick e dalla legge di Graham, sotto forma di grafici con curve descritte da alcune funzioni che dimostrano le proporzionalità esistenti tra: Velocità di diffusione contro Massa Molecolare di un elemento (vedi grafico 1) , e la variazione di concentrazione rispetto al quadrato della variazione di distanza (vedi grafico 3); mostrandosi come una valida formulazione fisicamente e matematicamente per tale descrizione del fenomeno naturale, perché le unità della Legge di Fick sono conservate nell’Equazione di Nathan, e corrispondono così positivamente riguardo alle proposizioni di tali leggi fisicochimiche già stabilite e alle loro rappresentazioni grafiche, seguendo le proporzionalità descritte da alcune funzioni presentate in precedenza. I prossimi articoli di esperimenti fisici o con specifici software di modellazione, possono valutare la praticità e la coerenza dell’equazione di Nathan con la realtà naturale, riferendosi allo studio del fenomeno di diffusione, al fine di analizzare l’accuratezza e la generalità dei concetti da esso sollevati.

 

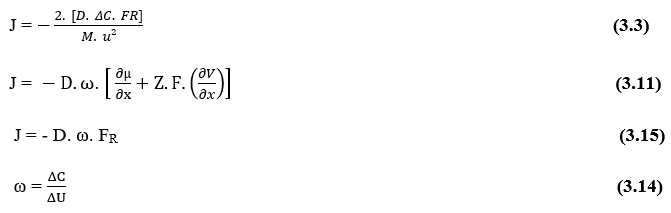
RIFERIMENTI BIBLIOGRAFICI

ALBERTS, Bruce et al. Biologia Molecular da Célula, 5° Edição. Editora: ARTMED, 2010, 1728 p., Vol. 1. ISBN: 978-85-363-2170-7.

BRADY, James; HUMISTON, Gerard. Química Geral, 2° Edição. Editora: LTC, 1995, 404 p., Vol. 1. ISBN: 9788521604495.

DA SILVA, Raissa. Difusão de Gases em Membranas Densas Via Simulação Molecular. Instituto Alberto Luiz Coimbra de Pós-Graduação e Pesquisa na Engenharia (UFRJ), Data da Dissertação de Mestrado: Abril de 2013. Disponível em: http://portal.peq.coppe.ufrj.br/index.php/producao-academica/dissertacoes-de-mestrado/2013-1/47-difusao-de-gases-em-membranas-densas-via-simulacao. Acesso: 25/06/2020.

HENEINE, Ibrahim. Biofísica Básica, 2° Edição. Editora: ATHENEU, 2004, 381 p., Vol. 1. ISBN: 8573791225.

JUNQUEIRA, Luiz C.; CARNEIRO, Jóse. Biologia Celular e Molecular, 9° Edição. Editora: Guanabara Koogan, 2012, 376 p., Vol. 1. ISBN: 9788527720786.

MARQUES, Francisco Das Chagas. Física Mecânica, 1° Edição. Editora: Manole, 2016, 315 p., Vol. 1. ISBN: 9788520427743.

MOREIRA C., Catarina. Difusão Simples. Rev. Ciência Elem., V2(02):144. doi.org/10.24927/rce2014.144. Pulicado: 15 de Setembro de 2010. Disponível em: https://rce.casadasciencias.org/rceapp/art/2014/144/. Acesso: 22/06/2020.

PIMENTEL, Carlos. A Relação da Planta Com a Água, Local: EDUR – Editora Universidade Federal Rural do Rio de Janeiro. 2004, 190 p. ISBN: 85-85720-45-X

TAIZ, Lincoln; ZEIGER, Eduardo. Fisiologia Vegetal, 3° Edição. Editora: ARTMED, 2006, Vol. 1, 722 p. ISBN: 85-363-0291-7.

TIPLER, Paul; MOSCA, Gene. Física para Cientistas e Engenheiros – Mecânica, Ondas, Termodinâmica, 6° Edição. Editora: LTC, 2009, 788 p., Vol. 1. ISBN: 9788521617105.

WALKER, Jearl et al. Halliday & Resnick ¹: Fundamentos de Física – Mecânica, 10° Edição. Editora: LTC, 2016, 372 p., Vol. 1. ISBN-13: 978-8521630357.

WALKER, Jearl et al. Halliday & Resnick ²: Fundamentos de Física – Gravitação, Ondas, Termodinâmica, 10° Edição. Editora: LTC, 2016, 324 p., Vol. 1. ISBN-13: 978-8521630364.

WALKER, Jearl et al. Halliday & Resnick ³: Fundamentos de Física – Eletromagnetismo, 10° Edição. Editora: LTC, 2016, 408 p., Vol. 1. ISBN-13: 978-8521630371.

^[1] Graduazione.

Presentato: Dicembre 2020.

Approvato: Aprile 2021.