ORIGINAL ARTICLE
SOUZA, Nathan Rodrigues Serpa [1]
SOUZA, Nathan Rodrigues Serpa. New Mathematical Formulation of the Molecular Diffusion Process and Electrodiffusion In Cell Membranes. Revista Científica Multidisciplinar Núcleo do Conhecimento. Year 06, Ed. 04, Vol. 15, pp. 34-63. April 2021. ISSN: 2448-0959, Access link: https://www.nucleodoconhecimento.com.br/fisica-en/molecular-diffusion
ABSTRACT
Molecular diffusion is a physical-chemical phenomenon observable in day-to-day life, as simple gases of a perfume expanding through a closed room, as well as microscopically, the absorption of ions by vegetables and animals by cells, via open ionic channels of the plasma membrane. This article of a physical nature proposes the formulation of a new equation called by the author of “Nathan’s Equation”, as an extension of fick’s well-known 1st Law, which aims to describe the natural phenomenon of diffusion, due to the variable Resulting Force of the System, which will allow a general analysis of the forces that will influence this phenomenon , as well as extending this formulation to describe the transport of ions via cell membrane, a formulation called “Nathan’s Equation for Electrodiffusion In Cell Membranes”. Through exploratory method, bibliographic research and mathematical tools were possible to perform such formulations, as well as to interpret them. From the dimensional analysis and postulates proposed by the 1st Fick Law and Graham’s Law for diffusion, in the form of graphs based on experimental and hypothetical data to compare the similarities of the graph curves, it was possible to confirm the mathematical and physical validation for this equation, demonstrating to conserve the units and agree positively with the postulates presented by those other laws already established in the physical-chemical environment.
Keywords: Diffusion, Cell Membrane, Fick’s Law, Nathan’s Equation, Electrodiffusion.
1. INTRODUCTION
Molecular diffusion is a physical-chemical phenomenon observable in day-to-day, as simple gases of a perfume expanding through a closed room, as well as microscopically, the absorption of ions by vegetables and animals by cells, via ionic channels of the plasma membrane. This transport process consists of the spontaneous and irreversible movement of molecules located in regions of high concentration (Hypertonic) to others with lower concentrations (Hypotonic), the driving force for this are the chemical or thermal potentials of the solution, and in the case of cellular membranes electrostatic forces together (DA SILVA, 2013).
According to Alberts (2009), the membrane presents tissue of amphiphilic character, formed by phospholipids with a polar end (Radical Phosphate) and another nonpolar (Fatty Acid Tail). Some polar or charged molecules such as ions have difficulty crossing by simple diffusion to lipid bilayer, displacement made through transporting proteins or channel-making proteins, such as ionic channels. Besides presenting a polarity between the extracellular media with accumulation of positive charges and the intracellular medium with accumulation of negative charges, behaving like a Uniform Electric Field (MOREIRA, 2014).
This exploratory article, with a method of theoretical-mathematical analysis, aims to establish a new mathematical formulation for the description of the process of molecular diffusion and ion transport via ionic channels of cell membranes, which takes into account the Resulting Force of the system (FR), which will allow a general analysis of the actions in the particles. The propositions exposed had as theoretical basis the meeting of diversified bibliographic collection, in the fields of biological, chemical and physical sciences, as well as the analysis of their propositions from physical and mathematical understanding of the results, under the spectrum of other laws that describe a certain aspect of the same phenomenon under study, such as: Fick’s Law and Graham’s Law.
2. DEVELOPMENT
2.1 MATERIAS AND METHODS
This article of exploratory bias aims to establish mathematical formulations to describe the process of molecular diffusion and the flow of ions through open ionic channels of cell membranes, due not only to concentration gradient or electrical potential of the membrane, but to take into account the constant forces operating in general, mathematical formulations these are called by the author of : Nathan’s Equation and Nathan’s Equation For Electrodiffusion In Cell Membranes.
For the mathematical construction, the collection of bibliographic material of various sciences was of great relevance, such as: Cell Biology, Chemistry and Physics. In addition to the material review, after mathematical construction, the dimensional analysis of the equation was performed to verify the conservation of units and their validity, as well as their positive or negative response about the postulates of the Fick and Graham Laws for the description of the diffusion process, based on graphs based on experimental and hypothetical data , in order to compare the graphs created from the mathematical relationships. The knowledge used will be exposed below:
2.2 BIOLOGICAL DEVELOPMENT
The cells are organized into three parts: the plasma membrane, the cytoplasm and the nucleus. One of the focuses of this academic work lies in the understanding of the primary compartment, the cell membrane, with approximately 8 nanometers (nm) or 8 x 10-9 meters (m), observable by electron microscope light. The membrane is not fully permeable, consisting of its main function, being a selective barrea that allows separation, as well as the exchange of substances between extra and intracellular media (JUNQUEIRA and CARNEIRO, 2012).
However, its selective permeability is due to the chemical-structural composition of cell membranes, being composed of a bilayer of phospholipids, proteins and carbohydrates. Phospholipids are ampyphilic tissues, i.e., containing polar and nonpolar parts, the hydrophilic head (Radical Phosphate) is facing the outside of the cell forming electrostatic interaction with the polar molecules of water. Its hydrophobic region consists of its long apolar chains of fatty acids that can easily interact with other liposoluble substances, of which it is more advantageous to have its tail facing the intracellular region. Thus, not all substances are able to cross the cell membrane and enter the cell by simple diffusion, however, such diffusion transport is facilitated by carrying or ionic channel-making proteins when they are opened (ALBERTS, 2009).
2.3 CHEMICAL DEVELOPMENT
According to Taiz and Zeiger (2006), diffusion is a phenomenon of matter transport, in which there is a flow of particles from the regions with higher concentrations to the regions with lower concentrations, with the aim of promoting the equilibrium state or also called homeotase. The mathematical description of such a process is expressed by Fick’s First Law, proposed by physician and physiologist Adolf Eugen Fick (1829 –1901), a differential equation in which the Flow Density (J) is directly proportional to the Concentration Gradient ( 
), and the Diffusion Coefficient (D) that depends on the chemical element under study, as expressed below (see equation 2.1):
This homogenizing flow is a statistical consequence to the random movement of particles, known as the Brownian Movement, spontaneously the molecules move from the hypertonic regions (Higher Concentrations) to the hypotonic regions (Lower Concentrations). The negative sign in Fick’s Law indicates that the flow occurs in the opposite direction to the concentration gradient, being a linear law, no matter how much the difference in concentration between two points is, the flow remains proportional to the gradient.
Other important details about Fick’s Law are as follows: Relationship directly proportional to diffusion area (A) and inversely proportional between particle size and diffusion speed, or its Molecular Mass (M). That is, the larger the area, the higher the transport fee; as well as, the lower the molecular mass of the particle, the higher its transport rate and the faster its diffusion speed will be.
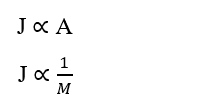
According to Brady and Huminston (1995), Graham’s Law (see equation 2.2), formulated by chemist Thomas Graham (1805 –1869) after his studies on fluid diffusion and effusion, establishes that the Effusion and Diffusion Velocity (u) of two gases (δ1) and (δ2), under the same temperature and pressure conditions, is inversely proportional to the square root of its Densities (d) or Molecular Mass (MM), as expressed below:
or 
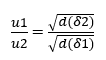
or
2.4 PHYSICAL DEVELOPMENT
One of the fundamental concepts for this article is the well-known “Fundamental Principle of Dynamics” or “Newton’s 2nd Law”, which states: The resulting force that acts under a body, is the product of its mass by acceleration (FR = m. a). Halliday (2016) states that it must first choose the body one wishes to study, and apply the resulting force as the sum of all the forces that act in the body in question.
According to Tipler (2009), Work (W) is the energy transferred to an object through a force that acts on the object itself. To calculate the work that a force performs on an object when it undergoes an offset, we use only the force component parallel to the object offset, the force component perpendicular to the offset does not perform work. The Work (W) of a constant force, as a function of parallel forces (θ = 0°, 180°), can be described through this equation:
W = F. d. cosθ
How; [ Cos(0°, 180°) = 1 ] one can rewrite the equation of work in integral form or as a function of the Variation of a Distance ΔX (see equation 2.3), we have:
According to Halliday (2016), energy is a difficult concept to define. However, we intuitively understand what energy is, from analyzing the effects in the different forms of it, such as: Kinetic Energy and Potential Energies. Conceptually for Tipler (2009), Kinetic Energy is associated with any bodies that have mass and are moving. Be (m) the mass of a material point and (u) its scalar velocity, relative to a given reference. The kinetic energy of the material point is given by (see equation 2.4):
For Uniformly Varied Motion, the work of the resulting force by the body aswells the kinetic energy variation of the body itself. From the Work-Energy Theorem (W = ΔK) we can obtain the expression that equals the Work of a Constant Force (W), with the Kinetic Energy Variation (ΔK), as demonstrated by equations (2.5) and (2.6):
The Uniformly Varied Movement, according to Marques (2016), is one in which a particle changes speed (u0) to another (u) due to a constant force that promotes an acceleration (a) also constant, also producing a displacement (ΔX). This type of movement can be equated without taking into account time, the so-called “Torricelli Equation” (2.7):
According to Pimentel (2004), the driving force of diffusive processes in cellular liquid medium, is the so-called Chemical Potential of any solution, which is configured as the ability of such a solution to perform work under the dissolved particles, in relation to the concentration gradient, a formulation for the Maximum Chemical Potential of water would be (2.8):
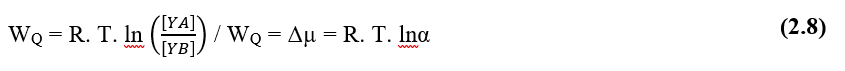
WQ – Chemical Potential of the Solution (J)
R – General Gas Constant (R = 8.31 J Mol-1 K-1)
T – Absolute Temperature (K)
[ YA ] – Concentration of Substance Y at Point A (Mol)
[ YB ] – Concentration of Substance Y at Point B (Mol)
α – Chemical Activity
3. RESULTS AND DISCUSSIONS
3.1 DEVELOPMENT OF NATHAN’S EQUATION
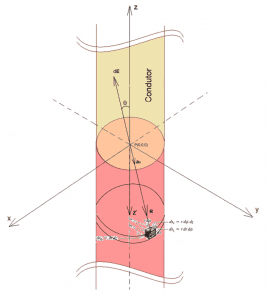
In an attempt to mathematically describe the process of diffusion and transport of ions via ion channels in the plasma membrane, as a function of the Concentration Gradient and Electric Field generated at the extracellular and intracellular ends of the membrane, let us consider an x, y and z coordinate system, in which each axis represents its respective acceleration generated by forces acting on the isolated system under study (ax, ay and az), as shown in figure 1.
Figure 1: Coordinate System (X, Y, Z).
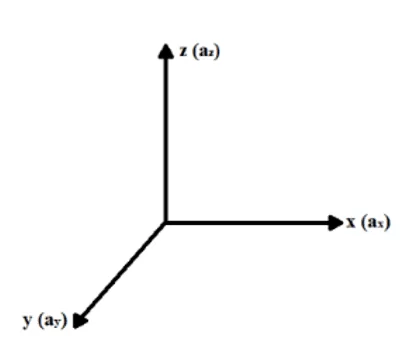
According to Halliday (2016), the resulting force acting on a particle as ions, which are crossing the membrane via ionic channels, can be decomposed into its components in each x, y and z axis, being directly associated with accelerations in the respective axes. Through Newton’s Fundamental Principle of Dynamics or Second Law, and newton’s Principle of Force Overlap, physical analysis can be obtained for the resulting forces on each axis that exert influence over the ion (see equation 3.1):
FR– Total Resulting Force (N – Kg m s-2)
FR(X) – Resulting Force on the X Axis (N – Kg m s-2)
FR(Y) – Resulting Force on the Y Axis (N – Kg m s-2)
FR(Z) – Resulting Force on the Z Axis (N – Kg m s-2)
The masses of the ions are preserved, so the factors directly proportional to the forces in each direction are their accelerations in the respective directions:
FR(X) = m . ax / FR(Y) = m . ay / FR(Z) = m . az
Comparing the electrostatic and gravitational constants (k = 9 x 109 
and G = 6,67 x 10-11 
), according to Halliday ³ (2016) such values demonstrate that the gravitational force is much weaker than the electrical force. Therefore, in an isolated system of particles in which only gravitational and electrical forces are considered to act, the gravitational force can be neglected, since the electrical force is about 1.5 x 1020 times greater than the weight force. As the acceleration of gravity on the particle will be disregarded, the force on the Z component will also be null since the acceleration az will be disregarded, we will reformulate the equation for the given study:
FR = m . ax + m . ay + m . az
FR = m . ax + m . ay + m . 0
FR = m . ax + m . ay
Considering as mostly acting forces those that influence the X axis, ignoring mechanical shocks and any other forces in the y component, since the set of solutes moves in the direction of homogenizing, from hypertonic to hypotonic regions, we will reach such a simplification of the Resulting Force:
FR = m . ax + m . 0
FR = m . ax
Another point to note is that the system under study will be considered stationary or on a permanent basis, in which its properties are unalterable in relation to time. This implies that any P property of the system, the partial derivative in relation to time is zero 
, considering a system in which the variable time is not a parameter in the study of the membrane system in question.
Cell membranes have a certain disposition, as analogous to the Uniform Electric Field, so that there is the concentration of positive charges mostly on the extracellular side, and an accumulation of negative charges on the intracellular side. There is also a difference in concentration between the outer and inner ends of cells (CE and CI), in which the system exerts a driving force to promote the translocation of particles through ionic channels of cell membranes, as represented by Figure 2.
Figure 2: Representation of ion displacement via ionchannel.
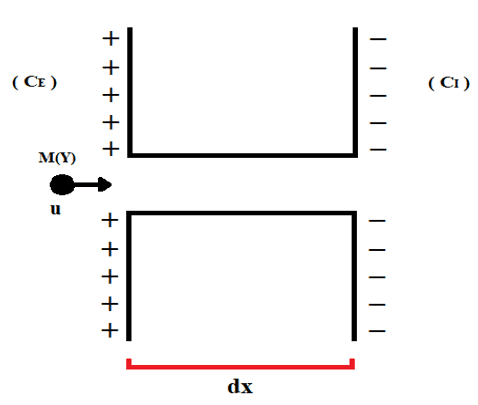
The distance traveled by the molecule represented is equivalent to the displacement element (dx), which is also the thickness of the cell membrane already mentioned. Fick’s First Law can be described as a function of the total concentration gradient (∇D) and the Diffusion Constant (D), as expressed below (see equation 3.2):
However, we will consider only the element of length (?x) already mentioned, in order to evaluate the one-dimensional movement of solutes from high concentration regions, for lower concentrations. Therefore, the Concentration Gradients ( 
and 
) will be removed from the equation, of which we return to equation 2.1:
By isolating the element (?x) from Fick’s First Law, we obtain:
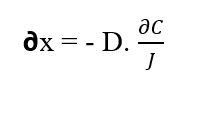
The solute particles move along an displacement (∂x) due to the force derived from the Chemical Potential of the system (WQ), because according to the 2nd Law of Thermodynamics described by Tipler (2009), the flow of matter or energy leaves the regions with higher values of matter or energy for the smallest. If particles are subject to forces and due to this move by certain element of distance (∂x), it can be assumed that such bodies are performing work (W), which is described by the following equation (see equation 2.3):
The Work of a Constant Force can also be described as a function of the Kinetic Energy Variation of the system (ΔK), as expressed by the Kinetic Energy Theorem (see equation 2.5):
Considering the one-dimensional movement of dissolved particles in solution, at a certain initial moment the particles in relation to a certain element (∂x) are not moving, so their Initial Velocity (u0) can be considered null, so the Work is described as follows:
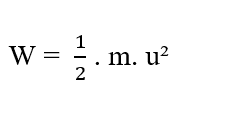
For a system in which we have an n number of particles spreading, each of which has a certain Mass (m(i)) and Acceleration (a(i)), we have that the Resulting Force in the particles can be expressed as being:
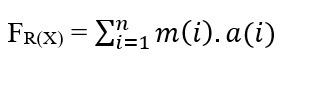
Since the system has a Constant Force, this movement is also described with a Constant Acceleration for all particles according to uniformly varied motion, which allows to remove the Acceleration of the Summation, from the properties of the Somators:
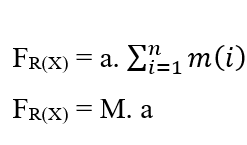
To reach Nathan’s Equation, the two equations of Work are equalised, and because it is to treat the movement of molecules as demonstrated, the mass (m) is considered as the total mass (M) of a certain amount of molecules present in the system under study, and also replaces the element (dx) by (∂x) of Fick’s First Law.
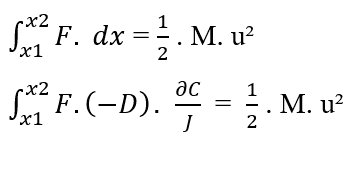
Knowing that (F, D, J) are constants in relation to the element (?C) to be integrated, from the property of the constant of integrals, the terms can be removed from the integral:
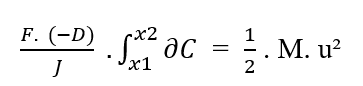
Rewriting the integration boundaries in relation to the (?C), we have:
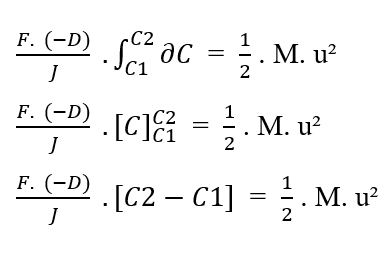
Knowing [C2 – C1 = ΔC] that, you can replace the value in the equation:
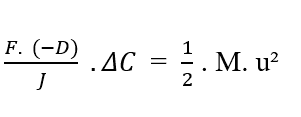
By isolating the Variable Flow Density (J), we get Nathan’s Equation (see equation 3.3):
J – Flux Density (Mol m-2 s-1)
D – Diffusion Coefficient (m² s-1)
ΔC – Concentration Variation (Mol m-3)
FR – Resulting Force (Kg m s-2)
M – Total Mass of Diffusing Particles (Kg)
u – Particle Diffusion Rate (m s-1)
3.2 MATHEMATICAL AND PHYSICAL EVALUATION OF NATHAN’S EQUATION
To confirm the validation of Nathan’s Equation in a mathematical way, it was necessary to perform the Dimensional Analysis described by Halliday (2016), in which he will check whether the units of the First Fick Law are preserved, and the units of the Nathan Equation are equivalent. Dimensional analysis is a tool used in physics to determine the unit of measure of some magnitude. Dimensional analysis is a tool that allows the prediction, inspection and adaptation of the physical units that are used for the resolution of equations.
Fick’s Law:
J – (Mol m-2 s-1)
Nathan’s Equation:
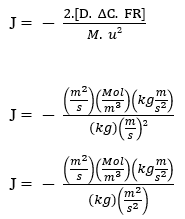
J – (Mol m-2 s-1)
Generally, the fundamental physical quantities are expressed as: Length (L), Mass (M), Time (T), Temperature (θ), Electric Current (A), Amount of Matter (Mol) and Luminous Intensity (I). The dimensional analysis of Nathan’s Equation (3.3) can then be performed using such representations of the fundamental physical quantities, according to the equivalent of each variable of the exposed formulation, as Marques (2016) points out.
J – Flow Density (Mol L-2 T-1)
D – Diffusion Coefficient (L2 T-1)
ΔC – Concentration Variation (Mol L-3)
FR – Resulting Force (M L T-2)
M – Total Mass Of The Difitating Particles (M)
u – Particle Diffusion Speed (L T-1)
Now performing dimensional analysis with the general representations of the fundamental physical quantities, we have:
Fick’s Law:
J – (Mol L-2 T-1)
Nathan’s Equation:
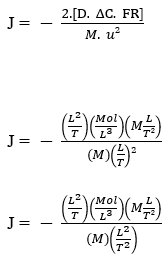
J – (Mol L-2 T-1)
Nathan’s Equation demonstrates the conservation of the units, as well as, follows some statements that The First Law of Fick and Graham’s Law demonstrate, in order to relate certain variables in a direct or inversely proportional manner, physically validating such mathematical formulation for the Diffusion process, regardless of the units chosen for the fundamental quantities, provided that they have coherence in general.
The first relationship that nathan’s equation shows is the directly proportional relationship between flow density (J) and concentration variation between two points (ΔC). By establishing that, an increase in the Difference of Concentration between any two points of the system, will be directly related to the increase of the Flow Density of the same, Such relationship obeys the Law of Fick.
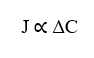
The second important relationship is the direct proportionality between the Flow Density (J) and the Resulting Force (FR) acting on the particles (γ) that make up the system in question. This implies that an increase in the variable Resulting Force that acts under the molecules that diffuse, will also directly proportionally increase the Particle Flow.
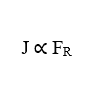
The third important relationship is the inverse proportionality between the Flow Density (J) and the total mass of any gamma element (γ), which make up the system under study. This implies saying that, considering for each molecule and only its Molecular Mass, the higher the Molecular Mass of the element to be diffused, the lower its Transport Rate, Such relationship obeys Fick’s Law and Graham’s Law.
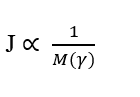
The fourth important relationship is the inverse proportionality between molecular mass (M) and diffusion velocity square (u). Or it can be understood as the inverse relationship between diffusion velocity and the square root of the molecular mass of the element (γ). This relationship obeys Graham’s Law of Effusion and Diffusion of Gases, showing correlation of Velocity to the inverse of the square root of molecular mass.
The Flow Density (J) is inversely proportional to the product between the Molecular Mass (M) – when for a particle – and the diffusion velocity square (u):
If (J) is constant (K), we have:
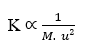
By isolating the Diffusion Rate (u) variable, one arrives at:
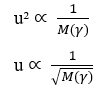
From the Excel Software version 2016, it was also possible to perform the chart modeling of 20 hypothetical data for the value of Molecular Mass (M), with an interval of (0 < M < 21) em ordem crescente, correlacionado ao seu respectivo valor de Velocidade de Difusão (u), sabendo que a velocidade de difusão de um determinado elemento é inversamente proporcional a raiz quadrada de sua respectiva massa, como aponta a Lei de Graham e também a Equação de Nathan quando a Taxa de Transporte (J) se mantém constante e considera-se apenas a massa de uma única partícula. Thus, we can perceive the similarity of the graphs constructed later with such data (see Graph 1).
Graph 1: Diffusion Velocity versus the inverse of the Square Root of molecular mass.
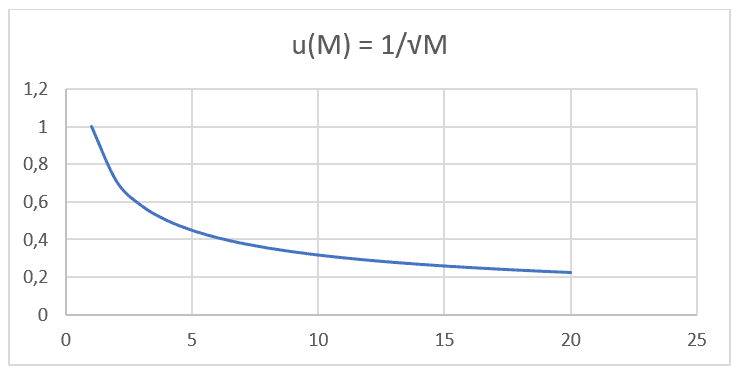
It is noticed that both formulations, both Graham’s Law and Nathan’s Equation, have equal proportionality and are based on the same type of function: F(x) =
. Performing graphical projection with Molecular Mass values, IUPAC data, and its respective Diffusion Speed of 20 different gases at the same pressures and temperatures listed in the following table (see Table 1), you can project a second graph (see Graph 2).
Table 1: Molecular Masses and their respective Diffusion Velocities.
| gas | Molecular Mass (g/mol) | Diffusion Speed (cm/s) |
| H2 | 2 | 0,7 |
| He | 4 | 0,5 |
| O2 | 16 | 0,25 |
| CH4 | 16 | 0,25 |
| Ne | 20 | 0,22 |
| H2S | 34 | 0,17 |
| Ar | 40 | 0,15 |
| CO2 | 44 | 0,15 |
| NO2 | 46 | 0,14 |
| O3 | 48 | 0,13 |
| C4H10 | 58 | 0,12 |
| NO3 | 63 | 0,12 |
| SO2 | 64 | 0,12 |
| CS2 | 76 | 0,11 |
| SO3 | 80 | 0,11 |
| Kr | 84 | 0,10 |
| FeS | 88 | 0,10 |
| Xe | 131 | 0,08 |
| PCl3 | 137 | 0,08 |
| Rb | 222 | 0,06 |
Source: The Author.
Graph 2: Diffusion Velocity versus the inverse of the Square Root of molecular mass.
According to Zeiger and Taiz (2006), the Average Diffusion Time can be defined as the ratio between the square of the Distance Variation (ΔX2) and the Diffusion Coefficient of the element (D), as expressed by the following mathematical formulation (see equation 3.4):
From the definition of Average Scalar Velocity (u) of kinematics and replacing the time value with the variable Mean Time (TM), we obtain:
or 
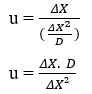
By performing algebraic manipulations, you can obtain the equation to calculate the Diffusion Speed (u) of any element:
By replacing (3.5) in nathan’s equation (3.3), we can obtain the relationship between the square of the Distance Variation (ΔX) and the Concentration Variation (ΔC).
Performing the Dimensional Analysis of the equation (3.6) to confirm the conservation of the units of Fick’s Law, we have:
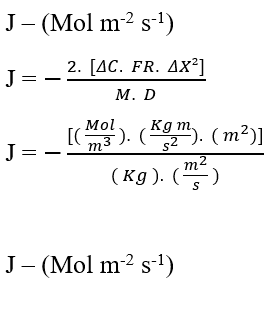
Validated the conservation of units from dimensional analysis, one can perceive an important and common relationship in the Nathan equation and Fick’s Law, it is the inverse proportionality between the Concentration Variation (ΔC), and the square of the Distance Variation (ΔX²). For this statement to be valid we will consider the Transport Rate (J) to be constant, and analyze only these two variables: Variation of Concentration and Distance.
Considering the Flow Density (J) being constant, we have:
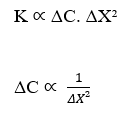
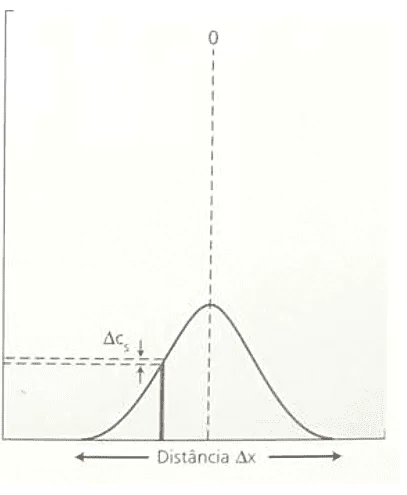
The inverse proportionality between Concentration Variation (ΔC) and the Square of Distance Variation (ΔX²) is demonstrated. This statement agrees with Fick’s Law, because when analyzing the correlation between those two variables, both formulations, Nathan’s Equation and Fick’s Law, describe the same graph that follows the function: F(x) = 
. The following is a graph format demonstration (Gaussian Curve), Concentration Variation versus Distance Square Variation (see Figure 3):
Figure 3: Graph Variation of Concentration versus Square of Distance Variation.
In the case of only having as a determining variable in the diffusion process of a given element, the Concentration Variation (ΔC), assuming then that it is a movement of particles the constant velocity and not a uniformly varied movement caused by a constant force, just replace (2.7) in (3.3), the Torricelli Equation, which will return the mathematical description known as known as a mathematical description known as the : 1st Fick’s Law.
Replacing (2.7) in (3.3) considering the initial velocity (u0) null, we have:
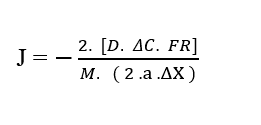
By canceling the terms Resulting Force (FR), with the terms in the denominator Total Particle Mass (M) and Acceleration (a), as well as the constants in the numerator and denominator (2), we obtain again the linear formulation: Fick’s First Law (2.1).
3.3 DEVELOPMENT OF THE NATHAN EQUATION FOR ELECTRODIFFUSION IN CELL MEMBRANES
Nathan’s Equation can be extended to describe the process of diffusion of ions via cell membrane, mathematically, taking into account the following mathematical formulations. According to Pimentel (2004), the driving force of diffusive processes in biological systems is the so-called Chemical Potential of the system, and in the case of the example in question, the transfer of matter from one point A to another B occurs, such Chemical Potential can be expressed from the following equation (2.8):
This implies saying that a solute will move from one region with higher chemical potential to a smaller region, or in the case of solvents such as water, from the osmosis moves from the regions of lower concentrations of solute to larger. However, the particle flow ceases when the chemical potentials of both phases are equal, thus obtaining the final state of equilibrium (HENEINE, 2004).
Such Solution Potential that produces the Resulting Force of the system, because it represents the capacity of a given system to perform work, can be described taking into account the contribution of other important factors, such as: Gravitational Action and Electrical Influence on Particles due to their loads and the difference in electrical potential. Thus, the maximum potential equation can be expressed by the formulation of the Electrochemical Potential, below (see equation 3.7):
In case the contribution of gravitational potential (m.g.h) is disregarded, the equation will be reduced only to the chemical and electrical contribution, these being the forces that work in the set of ionic particles to move through the ionic or molecular channels through the lipid bilayer, entering into the intracellular environment (ALBERTS, 2009).
Nathan’s Equation describes the diffusion process, and the natural phenomenon of ion transport via cell membrane can be similarly expressed by nathan’s equation, taking as Resulting Force (FR) only the Chemical Potential of the solution and electrical contribution, disregarding the gravitational contribution.
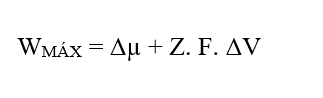
Knowing that (W = FR. Δx), replacing the equation (2.3) we obtain:
By performing the dimensional analysis of the Resulting Force (3.8), dividing it into its chemical and electrical plots, one can perceive the emergence no more of the Joule (J) energy unit, but rather the Unit of Force in the International System of Measurements, newton (N):
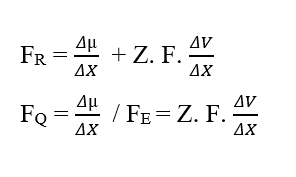
Analyzing the chemical portion of contribution (FQ), we have:
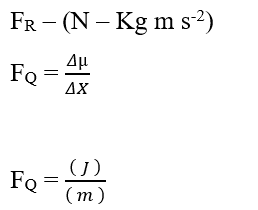
Knowing that the Joule (J – N.m) energy unit can be replaced in dimensional analysis, obtaining:
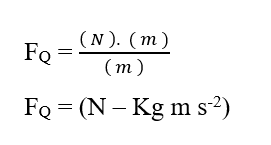
Analyzing the electrical portion of contribution (FE), we have:
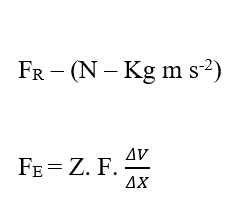
Knowing that Valencia (Z) is a dimensional variable, we have:
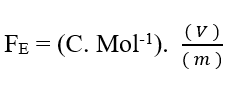
Knowing that the voltage unit Volt (V – J. C-1), can be replaced in dimensional analysis, obtaining:
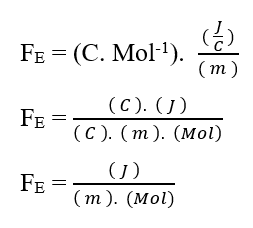
As the Mol unit is considered as adimensional, because it is only related to entities that make up a given system, such as: Atoms, molecules, ions or electrons; we can disregard such a unit in the analysis, simplifying it:
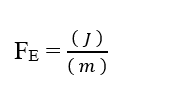
Knowing that the Joule (J – N.m) energy unit can be replaced in dimensional analysis, obtaining:
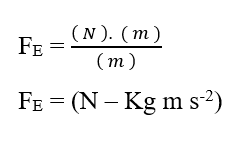
From the dimensional analysis of the two plots, chemical and electrical, which make up the Resulting Force (FR) of the system under study, it is shown to be valid for calculating such force. Writing the ratios between The Variation of Chemical Potential (Δμ) and Distance Variation (ΔX), Variation of Electrical Potential (ΔV) and Distance Variation (ΔX), in the form of limits of (ΔX 0) and then in differential form, having the Resulting Instant Force, we obtain:
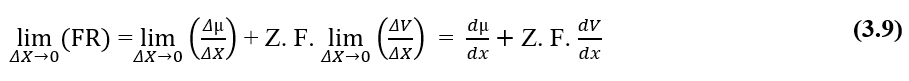
For a situation in which the Electrochemical Potentials of two phases (A) and (B) of a given system are the same, that is, in a equilibrium situation, the value of the Variation of electrical potential at the ends of cell membranes can be established, which refers to The Nernst Equation.
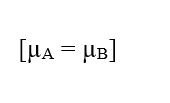
If the potentials are the same, this statement indicates that the Work performed by the particles is null, so the Resulting Force in them will also be null, since there is no transit of molecules between the two phases of the system:
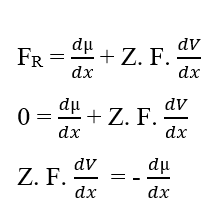
You can cancel the elements (dx) that appear on both sides of the equality and isolate the term (dV), then rewrite according to the variations, which results:
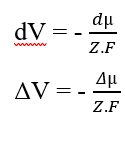
Replacing the Chemical Potential (2.3), we reestablished the calculation of the Electrical Potential for a equilibrium situation in biological systems (3.10), known as the Nernst Equation (HENEINE, 2004).
You can replace the Resulting Force of the System (3.9) in the Nathan Equation described above (see Equation 3.3):
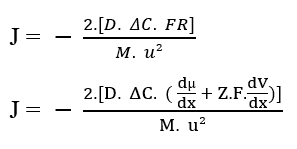
By apart from the terms in the parenthesis, we have nathan’s equation for electrodiffusion in cell membranes (3.11):
J – Transport Rate or Ion Flow Density in membrane (Mol m-2 s-1)
D – Solute Diffusion Coefficient (m2 s-1)
ΔC – Concentration Variation (Mol m-3)
M – Total Mass Of The Difitating Particles (Kg)
u2 – Particle Diffusion Speed (m s-1)
Z – Ion Valencia
F – Faraday constant (F = 9.648 x 104 C mol-1)
?µ/∂x – Derived from Chemical Potential in Relation to dx (Kg m s-2)
?V/∂x – Derived from Electrical Potential in relation to dx (V m-1)
According to Halliday (2016) for Thermodynamics, Internal Energy (U) or Internal Energy Variation (ΔU), it is the sum of the kinetic and potential energies of all molecules that a system contains. This relationship can be expressed, with the following mathematical description (see equation 3.12), considering the average velocity for all constant particles:
[M – Total Mass of System Particles]
Replacing equation (3.13), in Nathan’s Equation (3.3), a constant term can be determined, termed by the author with the Greek letter omega (ω):
If we now consider the reason 
as any constant (ω), since the values of such variables do not change with respect to time, since the partial derivative of any term is null 
. Knowing that (ω) presents as a unit 
, a ratio between Amount of Concentrated Matter and Internal Energy of a system, such relationship is equivalent to the following expression (3.15):
And knowing that the parcel 
refers to the Resulting Strength of the system (FR), one can still rewrite this formulation as its general form (3.15):
It is now possible to notice that, as the terms (D) and (ω) are constant, the Flow Density (J) is directly proportional to the Resulting Force of the system (FR),which implies that if an increase occurs in one of these variables, the other will also suffer a proportional increase.
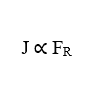
Nathan’s Equation for Electrodiffusion In Cell Membranes describes the flow of ions through the membrane, via ionic channels when they are open, influenced by the concentration gradient of extracellular and intracellular media, as well as Electrical Potential or Electric Field under the ions, generated by the cell membrane itself. This formulation takes into account the Total Mass of particles of the element that will spread, the chemical and electrical driving forces present in the phenomenon of transport of ions via cell membrane, however, if there are other external factors, due to the increase of the variable Resulting Force, the analysis can be done in a generalized scope, in addition to agreeing with the existing and presented physical concepts.
4. FINAL CONSIDERATIONS
In a statement, this article proposed the formulation of the “Nathan’s Equation”, as an extension of Fick’s 1st Law, which describes the diffusive flow of particles in solutions, due not only to the Difference in Concentration (ΔC), but with the objective of considering the Matter Flow Density (J) as a function of the constant Resulting Force (FR) acting on the particles of a given system (see equation 3.3).
This formulation demonstrated the direct proportionality between the Force acting in the particles, and Flow Density (J), so the higher the force exerted in the system, the greater the transport of matter. The same mathematical description of the natural processes of diffusion of molecules, which allows a general analysis of any forces that may exert influence under certain systems under study, can also be extended to explain the transport of ions via cell membrane, when the Resulting Force under the particles of the system in question takes into account the Chemical Potential and Electrical Potential , as well as a relationship between The Amount of Concentrated Matter and the Internal Energy of a System (ω), which was called by the author of “Nathan’s Equation for Electrodiffusion In Cell Membranes” (see equation 3.11), or also in its general formulation (see equation 3.15).
The validation of the Equations were evaluated from dimensional analysis and direct and inversely proportional relationships between the variables, in relation to the postulates proposed by the 1st Fick Law and Graham’s Law, in the form of graphs with curves described by certain functions that demonstrate the proportionalities existing between: Diffusion Speed versus Molecular Mass of an element (see Graph 1) , and the Concentration Variation versus the Square of The Distance Variation (see Graph 3); showing itself as a valid formulation physically and mathematically for such description of the natural phenomenon, because the units of Fick’s Law are preserved in the Nathan Equation, and correspond so positively regarding the propositions of such already established Physicochemical Laws and their graphic representations, following proportionalities described by certain functions presented previously. Next articles from physical experiments or with specific modeling software, can evaluate the practicality and coherence of Nathan’s equation with natural reality, referring to the study of the diffusion phenomenon, in order to analyze the accuracy and generality of the concepts raised by it.
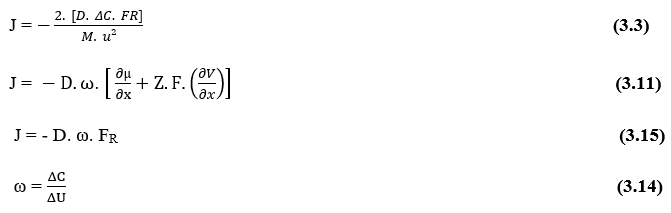
BIBLIOGRAPHIC REFERENCES
ALBERTS, Bruce et al. Biologia Molecular da Célula, 5° Edição. Editora: ARTMED, 2010, 1728 p., Vol. 1. ISBN: 978-85-363-2170-7.
BRADY, James; HUMISTON, Gerard. Química Geral, 2° Edição. Editora: LTC, 1995, 404 p., Vol. 1. ISBN: 9788521604495.
DA SILVA, Raissa. Difusão de Gases em Membranas Densas Via Simulação Molecular. Instituto Alberto Luiz Coimbra de Pós-Graduação e Pesquisa na Engenharia (UFRJ), Data da Dissertação de Mestrado: Abril de 2013. Disponível em: http://portal.peq.coppe.ufrj.br/index.php/producao-academica/dissertacoes-de-mestrado/2013-1/47-difusao-de-gases-em-membranas-densas-via-simulacao. Acesso: 25/06/2020.
HENEINE, Ibrahim. Biofísica Básica, 2° Edição. Editora: ATHENEU, 2004, 381 p., Vol. 1. ISBN: 8573791225.
JUNQUEIRA, Luiz C.; CARNEIRO, Jóse. Biologia Celular e Molecular, 9° Edição. Editora: Guanabara Koogan, 2012, 376 p., Vol. 1. ISBN: 9788527720786.
MARQUES, Francisco Das Chagas. Física Mecânica, 1° Edição. Editora: Manole, 2016, 315 p., Vol. 1. ISBN: 9788520427743.
MOREIRA C., Catarina. Difusão Simples. Rev. Ciência Elem., V2(02):144. doi.org/10.24927/rce2014.144. Pulicado: 15 de Setembro de 2010. Disponível em: https://rce.casadasciencias.org/rceapp/art/2014/144/. Acesso: 22/06/2020.
PIMENTEL, Carlos. A Relação da Planta Com a Água, Local: EDUR – Editora Universidade Federal Rural do Rio de Janeiro. 2004, 190 p. ISBN: 85-85720-45-X
TAIZ, Lincoln; ZEIGER, Eduardo. Fisiologia Vegetal, 3° Edição. Editora: ARTMED, 2006, Vol. 1, 722 p. ISBN: 85-363-0291-7.
TIPLER, Paul; MOSCA, Gene. Física para Cientistas e Engenheiros – Mecânica, Ondas, Termodinâmica, 6° Edição. Editora: LTC, 2009, 788 p., Vol. 1. ISBN: 9788521617105.
WALKER, Jearl et al. Halliday & Resnick ¹: Fundamentos de Física – Mecânica, 10° Edição. Editora: LTC, 2016, 372 p., Vol. 1. ISBN-13: 978-8521630357.
WALKER, Jearl et al. Halliday & Resnick 2: Fundamentos de Física – Gravitação, Ondas, Termodinâmica, 10° Edição. Editora: LTC, 2016, 324 p., Vol. 1. ISBN-13: 978-8521630364.
WALKER, Jearl et al. Halliday & Resnick ³: Fundamentos de Física – Eletromagnetismo, 10° Edição. Editora: LTC, 2016, 408 p., Vol. 1. ISBN-13: 978-8521630371.
[1] Graduation.
Submitted: December, 2020.
Approved: April, 2021.
