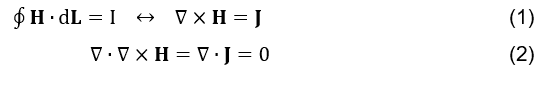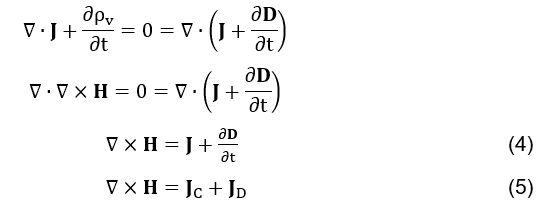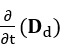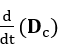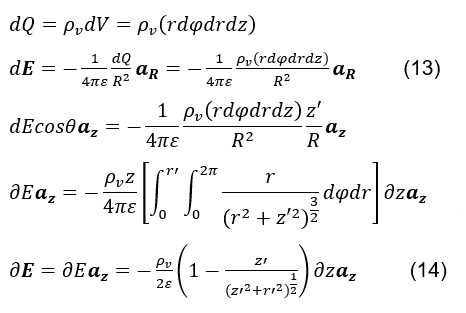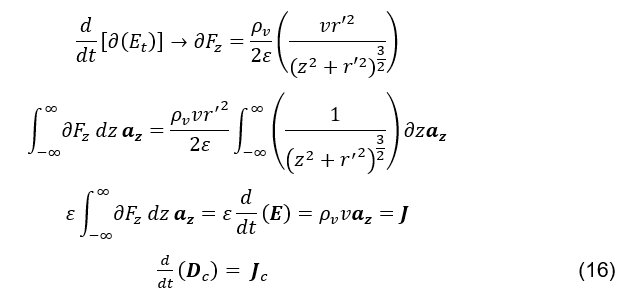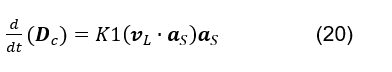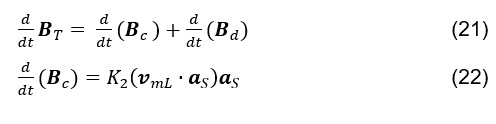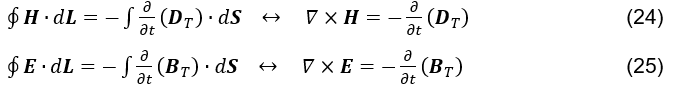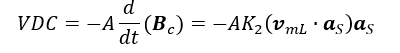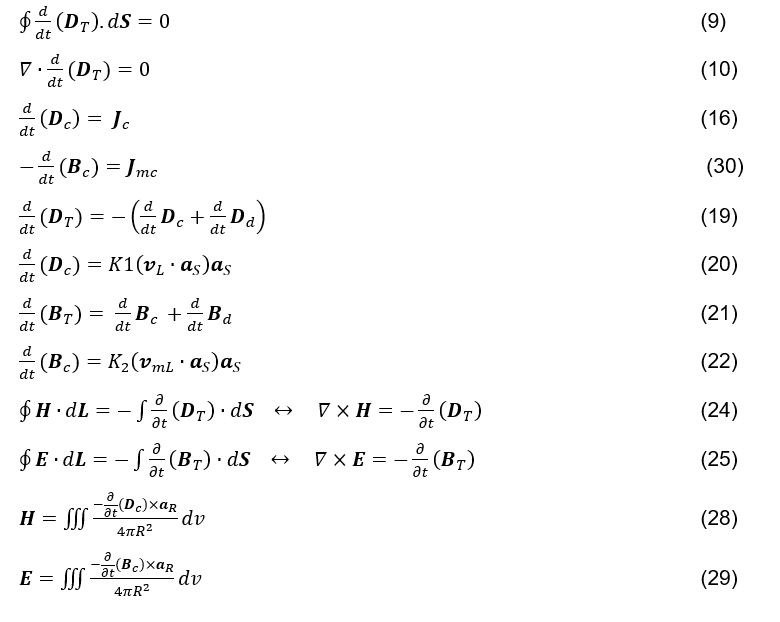Una nuova prospettiva sulla base della densità di corrente

ARTICOLO ORIGINALE

LUCENA, Lucas Ruas de ^[1]

LUCENA, Lucas Ruas de. Una nuova prospettiva sulla guida della densità di corrente. Revista Científica Multidisciplinar Núcleo do Conhecimento. Anno 05, Ed. 08, Vol. 03, pp. 151-167. nell’agosto 2020. ISSN: 2448-0959, collegamento di acesso: https://www.nucleodoconhecimento.com.br/fisica-it/densita-di-corrente, DOI: 10.32749/nucleodoconhecimento.com.br/fisica-it/densita-di-corrente

RIEPILOGO

Questo articolo discute proposte alternative e complementari alle leggi di J.C.Maxwell sull’elettromagnetismo classico, basate su alcune ipotesi, esempi ipotetici e calcoli, con risultati che possono dedurre nuove interpretazioni sulla densità di corrente di conduzione del fenomeno fisico. Queste nuove interpretazioni portano una nuova comprensione alle dinamiche della Legge di Gauss e, essendo vero, rendono la legge Ampère-Maxwell totalmente simmetrica alla legge Faraday-Lenz-Maxwell, senza alcuna incoerenza matematica o fisica. Queste invii portano inevitabilmente implicazioni e punti di vista complementari alla teoria classica dell’elettromagnetismo.

Parole chiave: Elettromagnetismo, densità di corrente, equazione di continuità.

1. INTRODUZIONE

In primo luogo, la soluzione data da J.C.Maxwell è presentata in modo che l’equazione di Ampere (vedi formula 1) diventi matematicamente coerente, rispettando l’identità vettoriale applicata nella formula 2 e coerente con l’equazione di continuità (vedi formula 3).

Di seguito è riportato un esempio dell’applicazione della legge di Gauss (vedere la formula 6) a una superficie chiusa intorno a una delle piastre di un condensatore, Figura 1.

Per ipotesi, si propone che la variazione temporale del flusso elettrico totale, che attraversa la superficie gaussiana totalmente chiusa, sia sempre uguale a zero. Pertanto, la legge di Gauss (vedi formula 6), applicata a situazioni dinamiche, sarebbe diventata l’equazione (vedi formula 9). Affinché questa ipotesi sia basata, sarà necessario che vi sia una variazione temporale della densità del campo elettrico, dello stesso modulo, direzione e direzione della densità di corrente, nell’area di intercessione tra il volume cilindrico del conduttore e la superficie gaussiana, puntando in esso, Figura 1.

Al fine di verificare la coerenza di questa ipotesi, verrà considerato un esempio ideale in cui vi è una corrente continua e omogenea in un filo cilindrico rectilineare infinito lungo l’asse z. Quindi viene calcolata la variazione temporale vettoriale del campo elettrico (vedere la formula 12) al punto P(0,0,0) a causa dello spostamento simultaneo e istantaneo di tutti i carichi, a monte e a valle di P(0,0.0). Questo calcolo comporta l’uguaglianza (vedere la formula 16).

Infine, partendo dalla veridicità fisica dell’uguaglianza (vedi formula 16), ci sono inevitabili implicazioni, formattazione e complementi teorici per le equazioni classiche dell’elettromagnetismo, di Faraday, Lenz, Biot-Savart e Maxwell. Alla fine, è stato suggerito un esperimento di laboratorio per confermare o confutare la teoria sviluppata dall’analisi dell’ipotesi proposta.

2. LE CATENE DI CILINDRATA E DI GUIDA

Il circuito di Ampere, nella sua forma puntuale (vedi formula 1), aveva inadeguatezze matematiche (JACKSON et. al., 1998).

Il risultato dell’equazione (vedere la formula 2) deve essere zero, perché la divergenza del valore rotazionale uguale a zero costituisce un’identità vettoriale. Tuttavia, l’equazione di continuità (HAYT; BUCK et. al., 2013; SHADIKU, 2004),

è incoerente con l’equazione (vedere la formula 2).  Questa correzione è stata fatta brillantemente da J.C.Maxwell, come segue (JACKSON et. al., 1998):

Così l’equazione di Ampere (vedi formula 1) divenne completamente coerente (vedi formula 5). Sia fisicamente, considerando la generazione di campo magnetico dalla variazione temporale della densità del campo elettrico, sia matematicamente, per quanto riguarda l’identità vettoriale citata nell’equazione (vedi formula 2).

Il termine

aggiunto nell’equazione (vedi formula 4) ha la stessa unità di densità di corrente, Amperes per metro quadrato

, che viene definito da J.C.Maxwell della densità della corrente di spostamento, rappresentata da

nell’equazione (vedi formula 5). L’identificazione di questo termine era di fondamentale importanza per comprendere la propagazione delle onde elettromagnetiche. Il termine

nell’equazione (vedere la formula 5) si riferisce alla densità della corrente di conduzione.

3. IPOTESI DI UN’APPLICAZIONE DINAMICA DELLA LEGGE GAUSS

La Legge di Gauss, equazione (vedi formula 6), determina che il flusso totale di densità del campo elettrico che attraversa qualsiasi superficie chiusa è uguale alla carica elettrica totale contenuta all’interno di tale superficie. Maxwell lo osservò nella forma puntica, equazione (vedi formula 7), nota come prima equazione di maxwell (HAYT; BUCK et. al., 2013; SHADIKU, 2004).

Si consideri il primo esempio, essendo una superficie chiusa intorno a una delle piastre di un condensatore che viene caricato da un alimentatore a tensione variabile, come illustrato nella Figura 1.

come illustrato nella Figura 1.  Superficie gaussiana racchiusa su una piastra di condensatore

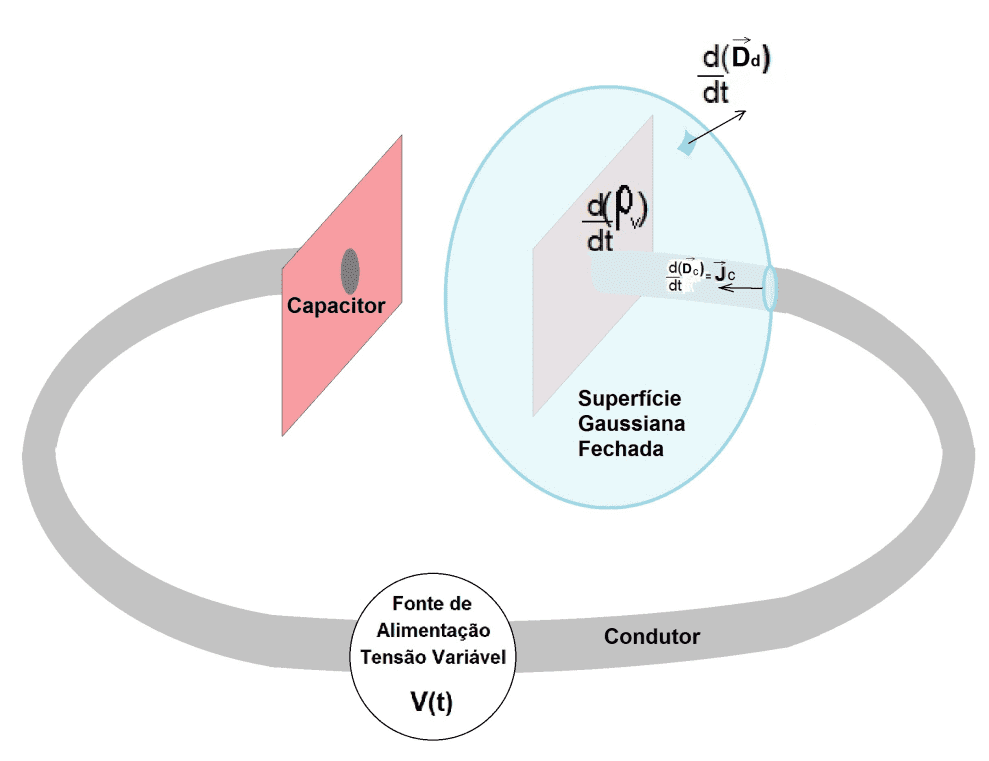
Osservando la figura 1, con una densità di corrente di conduzione nel

driver, le equazioni (vedere la formula 6) e (vedi formula 7), rispettivamente: per una superficie gaussiana completamente chiusa; e per un punto sulla piastra del condensatore, diventano equazioni (vedi formula 8) e (vedi formula 3). (HAYT; BUCK et. al., 2013; SHADIKU, 2004).

L’equazione (vedi formula 8) determina che la variazione temporale del flusso totale di densità del campo elettrico che attraversa la superficie gaussiana è uguale alla variazione temporale della carica elettrica ad essa contenuta internamente.

L’equazione di continuità (c’è la formula 3) applicata a qualsiasi volume infinitesimale della piastra del condensatore, caricata positivamente, determina che la densità della corrente di conduzione

, che lascia quel volume, è uguale alla velocità di tempo alla quale la densità di carico volumetrico ricade su di essa.

L’ipotesi proposta in questo articolo ritiene che le equazioni (vedere la formula 8) e (vedere la formula 3) siano fisicamente complementari. Pertanto, si ritiene che per una superficie Gauss completamente chiusa, intorno a una piastra di condensatore, in condizioni dinamiche, le equazioni (vedi formula 8) e (vedi formula 3) avrebbero il seguente formato.

Dov’è

la variazione temporale della densità del campo elettrico vettoriale generata dalla densità della corrente di conduzione

, dello stesso modulo, della stessa direzione e direzione dello stesso, sulla superficie trasversale di intersezione tra il volume cilindrico del conduttore e il gaussiano, puntando in esso. Ed

è la variazione temporale della densità vettoriale del campo elettrico, nella superficie gaussiana chiusa che lo indica, generata dalla densità di corrente di spostamento

(variazione temporale del numero di linee di campo elettrico che attraversano il Gaussiano chiuso a causa della variazione temporale del carico elettrico totale della piastra dal condensatore interno al Gaussiano); (HAYT; BUCK et. al., 2013; SHADIKU, 2004). come illustrato nella Figura 1.

Le equazioni (vedere la formula 9) e (vedere la formula 10) determinano che la variazione temporale del flusso totale della densità del campo elettrico su qualsiasi superficie gaussiana completamente chiusa è uguale a zero. L’equazione (c’è la formula 10) non contraddice l’equazione della continuità (c’è la formula 3), perché mette in relazione il flusso del carico elettrico, di un volume infinitesimale, con la variazione temporale della densità volumetrica della carica elettrica, in essa; già che, è legato solo alla dinamica del campo elettrico.

Si presume quindi che il fenomeno fisico conduzione densità di corrente

, genera una variazione della densità di campo elettrico

all’intersezione del conduttore cilindrico con la superficie gaussiana, dello stesso modulo, direzione e direzione del vettore

. Uno dei vantaggi della verifica di questa ipotesi sarebbe comprendere l’equazione Ampere-Maxwell (vedere la formula 4) nel seguente formato (vedere la formula 11).

Così, sarebbe intuito che le interazioni tra i campi, elettrici o magnetiche, e particelle cariche, sarebbero, prima di tutto, interazioni tra i soli campi.

Nella ricerca per verificare la veridicità dell’ipotesi proposta, viene creato un esempio di una situazione ipotetica ideale per il calcolo della variazione temporale vettoriale della densità del campo elettrico (vedi formula 12), all’origine, generata da una corrente continua e omogenea in un conduttore cilindrico di lunghezza infinita lungo l’asse z.

4. ESEMPIO DI UNA SITUAZIONE IPOTETICA IDEALE

Supponiamo la seguente configurazione ideale: in un conduttore cilindrico, rectilineare, uniforme, omogeneo, di lunghezza infinita, che attraversa una corrente diretta, di carichi positivi, uniformi e omogenei nella direzione positiva dell’asse z, Figura 2.

Nelle coordinate cilindriche, la variazione temporale del vettore di campo elettrico (vedere la formula 12) generata nel punto P(0,0,0) del piano cartesiano nella Figura 2, a causa dello spostamento volumetrico, simultaneo e istantaneo, di tutti i carichi positivi, a monte e a valle di questo punto, nella direzione positiva dell’asse z.

Anche se, in un vero conduttore con una differenza di potenziale applicata nelle sue estremità, l’elettrone è quello, per modello classico, lo spostamento delle cariche positive nella direzione positiva dell’asse z è stato scelto per il calcolo.

È noto, per simmetria, che il campo elettrico vettoriale risultante E generato dalla somma di tutti i carichi esistenti lungo il conduttore, positivo e negativo, nel punto P(0.0.0), è null.

Tuttavia, consideriamo, in primo luogo, il calcolo del campo elettrico statico (vedi formula 14), generato da un elemento differenziale volumetrico cilindrico, nelle coordinate cilindriche, della densità volumetrica del carico positivo ρ_v, centrato in una posizione iniziale z‘, dove dQ è l’elemento differenziale di carico, r’ è il valore costante assegnato al raggio del conduttore del cilindro R, sono la distanza vettoriale tra il punto P (0,0,0) e l’elemento differenziale dV, a_z è il versor nella direzione positiva di z e la permissività elettrica del conduttore, come mostrato nella Figura 2.a

Si prega di sottolineare che, poiché prendiamo come riferimento il punto di misurazione del campo elettrico fissato in P(0,0,0), la direzione di dE sarà sempre opposta all’ a_R versor. Pertanto, il segno negativo nell’equazione (vedere la formula 13).

come illustrato nella Figura 2. Corrente di guida

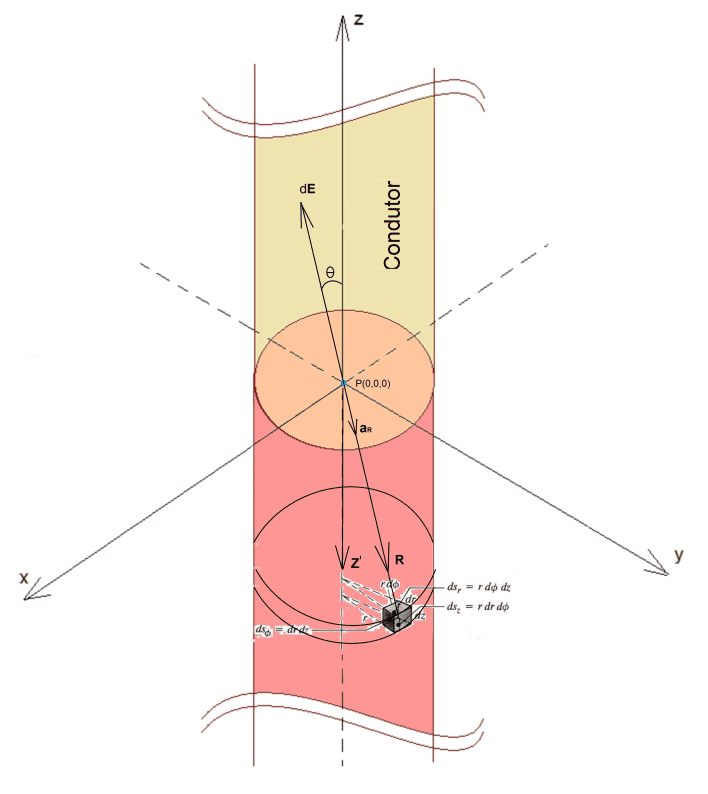
Quindi, considerando che questo disco volumetrico differenziale caricato ha una velocità costante. Il campo elettrico

diventa una funzione solo del tempo variabile t. Considerando la posizione iniziale z’ e la velocità del disco v,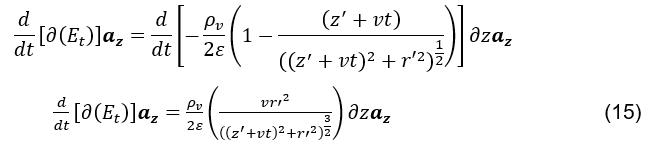

Poiché ciò che si vuole calcolare è la variazione temporale del campo elettrico (vedi formula 12), all’origine, causata dallo spostamento di ogni elemento cilindrico differenziale aggiunto lungo

istantaneamente, sarà considerato esclusivamente per questo calcolo che la funzione dell’equazione (vedi formula 15) dipende solo dalla posizione variabile z,

. Poiché il contributo di ogni elemento differenziale cilindrico, lungo l’intero asse z, passando alla formazione della variazione temporale totale vettoriale del campo elettrico nel punto P(0.0.0), poiché è istantaneo, non dipende dal tempo variabile t. In questo modo, sostituendo z‘ s z, e considerando la variabile  t = t₀ = 0,

L’equazione (vedere la formula 16), quindi, dimostra l’equivalenza vettoriale tra la variazione temporale della densità del campo elettrico nel punto P(0,0,0), generata dallo spostamento istantaneo e simultaneo di tutte le cariche positive lungo il filo cilindrico infinito e la densità della corrente di conduzione in

quello stesso punto.

5. IMPLICAZIONI

Se c’è veridicità fisica nell’ipotesi presentata, si osservano le seguenti implicazioni:

1. Interpretazione dell’applicazione di una dinamica della Legge di Gauss;
2. Nuova concezione delle leggi di Ampere-Maxwell e Faraday-Lenz-Maxwell;
3. Esperimento suggerito per dimostrare la teoria.

5.1 INTERPRETAZIONE DELL’APPLICAZIONE DI UNA DINAMICA DEL DIRITTO GAUSS

L’uguaglianza (vedere la formula 16) è considerata coerente con le equazioni (vedere la formula 9) e (vedere la formula 10). Pertanto, è inteso come ragionevole la seguente interpretazione fisica della legge gauss applicata alla situazione presentata nella Figura 1: la variazione temporale del flusso totale della densità del campo elettrico su qualsiasi superficie gaussiana completamente chiusa è esattamente zero, (vedi formula 17) e (vedi formula 18).

A causa della scelta classica della direzione corrente è quella dello spostamento dei carichi positivi, per rendere le equazioni (vedi formula 24) e (vedi formula 29) simmetriche tra loro, il segno negativo ( – ) è stato inserito in uguaglianza (vedi formula 19).

Qui viene proposta la seguente interpretazione dei fenomeni fisici contemplati in uguaglianza (c’è la formula 19).

La variazione temporale vettoriale della densità del campo elettrico

, risultato della densità della corrente di conduzione

, sembra essere proporzionale alla velocità longitudinale alla quale le linee di campo elettriche attraversano un elemento di area di una superficie gaussiana. La teorizzazione può essere teorizzata:

dove v_L è il vettore di velocità delle linee di campo elettriche che attraversano un elemento di area di una superficie gaussiana, a_S il versor dell’elemento dell’area vettoriale di tale superficie e K₁ una costante, Figura 3.

come illustrato nella figura 3. Variazione temporale della densità del campo elettrico generata da

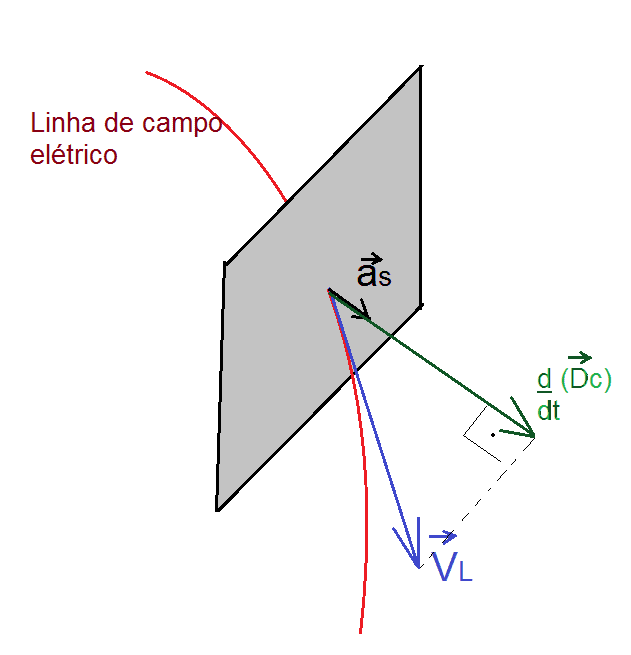
La variazione temporale vettoriale della densità del campo elettrico

, risultante dalla densità della corrente di spostamento

, è correlata alla variazione temporale del numero quantitativo di linee di campo elettriche che attraversano un elemento di area di una superficie gaussiana (HAYT; BUCK et. al., 2013; SHADIKU, 2004).

Essendo vera la teoria proposta, dall’ipotesi iniziale, che la variazione temporale del flusso elettrico totale che attraversa una superficie gaussiana, può essere formata sia dalla variazione temporale del numero di linee di campo elettriche, per unità di area, che la attraversano

, sia dalla velocità longitudinale delle linee di campo elettrico che attraversano un elemento di area,

(vedi formula 20); è intuito, per simmetria (vedi formula 19), che il flusso magnetico che passa attraverso una superficie gaussiana si comporta in modo equivalente (vedi formula 21).

In modo tale che

possa essere generato sia dalla variazione temporale del numero di linee di campo magnetico in un elemento di area (HAYT; BUCK et. al., 2013; SHADIKU, 2004),

; così come la velocità longitudinale con cui le linee del campo magnetico attraversano un elemento di area,

(vedi formula 22). Per simmetria, viene proposta, analogamente all’equazione (vedi formula 20), l’equazione (vedi formula 22). Dove v_mL è il vettore di velocità delle linee di campo magnetico che attraversano un elemento di area di una superficie gaussiana, a_S il versor del vettore dell’elemento area di quella superficie _e K₂ una costante.

5.2 NUOVO DISEGNO DELLE LEGGI AMPERE-MAXWELL E FARADAY-LENZ-MAXWELL

Considerando la possibilità di veridicità nell’ipotesi presentata, si potrebbe concepire la legge Ampere-Maxwell (vedi formula 5) e la legge Faraday-Lenz-Maxwell (vedi formula 23)

rispettivamente, come nella formula 24) e (vedere la formula 25).

5.3 SUGGERITO ESPERIMENTO PER DIMOSTRARE LA TEORIA.

Il presente articolo mira, concisamente, a proporre una teoria, basata su situazioni ipotetiche, senza sperimentazione fisica in laboratorio per la prova, alla fine di esso.

Tuttavia, una proposta per un esperimento di laboratorio sarà presentata di seguito, per quelli di interesse, per dimostrare la veridicità della teoria proposta, o per confutarla.

Per il calcolo di un campo magnetico H, generato esclusivamente da una densità di corrente di conduzione

, utilizzando l’uguaglianza (c’è la formula 16), la legge Biot-Savart (c’è la formula 27) potrebbe essere descritta come nella formula 28.

Poi, si propone di scrivere la legge Biot-Savart modificata (vedi formula 28), simmetricamente per il calcolo del campo elettrico, come in (vedi formula 29).

Al fine di verificare la veridicità della teoria che i campi, elettrici e magnetici, possono essere generati, rispettivamente, dalla velocità di spostamento delle linee dei campi (magnetico ed elettrico), viene proposto il seguente esperimento.

Si tratta di un circuito elettrico formato da un filo conduttivo isolato, arrotolato in modo distribuito e continuo intorno a un materiale ferromagnetico di topologia toroidale, area Una costante della sezione trasversale, alimentata da una sorgente di corrente diretta, con una corrente regolata in modo tale da non saturare magneticamente il materiale ferromagnetico. Ci sarà una densità di campo magnetico B confinata a tutto il materiale ferromagnetico toroidale (HALLIDAY; RESNICK; WALKER et. al., 2013), Figura 4.

Dove è la permeabilità magnetica del materiale ferromagnetico, N il numero di giri, e l il perimetro attraversato dalla sezione trasversale del toroide durante la sua rivoluzione.

Quindi, un filo conduttivo isolato di misurazione turno viene utilizzato intorno alla sezione trasversale del toroide, collegato ad un voltmetro VDC, in modo tale che è possibile spostare la bobina di misurazione lungo il perimetro toroidale, Figura 4.

È noto che il campo magnetico generato da qualsiasi circuito elettrico toroidale ideale, esterno ad esso, è zero (HALLIDAY; RESNICK; WALKER et. al., 2013).

Secondo la teoria presentata, quando la bobina di misurazione si muove con una velocità V lungo il perimetro toroidale, anche se il numero di linee di densità del campo magnetico interne al turno non viene modificato, queste linee passeranno attraverso la superficie gaussiana formata dalla circonferenza della bobina di misurazione, con velocità -V.

Applicando l’equazione proposta (vedi formula 22) alla legge Faraday-Lenz-Maxwell (vedi formula 23), la tensione misurata nel voltmetro dovrebbe essere:

Dov’è l’area della sezione trasversale del toroide.

Così, si propone di sollevare una curva di misure VDC x V, essendo VDC la tensione misurata nel voltmetro, e V il vettore di velocità del turno di misurazione, lungo il perimetro toroidale, Figura 4. Secondo la teoria proposta, questa curva dovrebbe essere una linea retta con una pendenza AK₂, Figura 4.

come illustrato nella Figura 4. Esperimento suggerito per dimostrare la teoria proposta

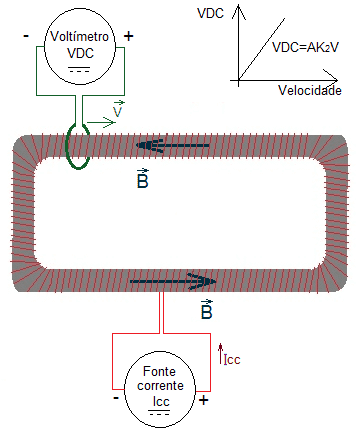
Se l’esperimento viene effettuato con un risultato che corrobora la teoria proposta, si propone anche di considerare l’esistenza della seguente densità di corrente

magnetica di conduzione.

6. CONCLUSIONE

Per comprendere meglio la natura delle correnti di spostamento e di conduzione, è stata sollevata l’ipotesi che, in una superficie gaussiana completamente chiusa, la variazione temporale del flusso totale del campo elettrico, in esso potrebbe sempre essere uguale a zero (vedi formula 9) e (vedi formula 10), non contraddicendo l’equazione di continuità (vedi formula 3).

È stato creato un esempio di una situazione ipotetica ideale, che consentirebbe l’analisi matematica dell’ipotesi creata.

Il risultato di questa analisi, l’uguaglianza (c’è la formula 16), corrobora l’idea che la variazione temporale vettoriale della densità totale del campo elettrico (vedi formula 19) possa esistere dai seguenti due fenomeni fisici distinti.

1 –

→Variazione temporale della densità vettoriale del campo elettrico, in un elemento di area, in funzione della variazione temporale del numero di linee di campo elettriche che lo attraversano. Questa è la comprensione classica del fenomeno della densità della corrente di spostamento, riconosciuto per la prima volta da J.C.Maxwell. (HAYT; BUCK et. al. 2013; SHADIKU, 2004)

2 –

→Variazione temporale della densità vettoriale del campo elettrico, in un elemento di area, in funzione della velocità longitudinale delle linee di campo elettriche che la attraversano (c’è la formula 20), a causa di una densità di corrente di conduzione (vedi formula 16);

Con la premessa della simmetria tra il comportamento dei campi elettrici e magnetici, analogamente le equazioni (vedi formula 19) e (vedi formula 20), sono state prese in considerazione la possibilità che il campo magnetico si comporti allo stesso modo (vedi formula 21) e (vedi formula 22).

Così, si propone una teoria che tutte le interazioni tra i campi, elettrici o magnetiche, e particelle elettricamente caricate, sono, prima di tutto, interazioni tra i soli campi. Ad esempio, quando si applica una potenziale differenza in un circuito elettrico, il campo elettrico generato dalla differenza potenziale interagirà con il campo elettrico dei carichi liberi, costringendoli a muoversi. Lo spostamento dei carichi implica lo spostamento delle loro linee di campo elettrico. La velocità longitudinale alla quale queste linee attraversano un elemento differenziale dell’area sarebbe proporzionale al vettore

in esso contenuto.

Considerando la possibilità della veridicità delle equazioni (vedi formula 9) e (vedi formula 10), derivate dalla dinamica della legge di Gauss, la legge Ampere-Maxwell (vedi formula 5) è scritta, nel formato (vedi formula 24), con maggiore simmetria alla legge Faraday-Lenz-Maxwell (vedi formula 25).

Infine, viene proposto un esperimento di laboratorio per confermare o screditare la teoria proposta e le sue equazioni.

Di seguito sono riportati le equazioni proposte in questo articolo.

RIFERIMENTI

FARADAY, M. Experimental Researches in Electricity. B.Quaritch, Londres, 1939, p.1855.

FARADAY, M. Great Books of the Western World. Vol. 45, encyclopedia Britannica Inc., Chicago, 1952, p. 217-866.

HALLIDAY, D; RESNICK, R; WALKER, J. Fundamentos de Física.  V.3, ED.9ª, LTC, Rio de Janeiro 2013.

HAYT, W.H; BUCK, J.A.  Eletromagnetismo.  ED.8ª, AMGH, Porto Alegre, 2013, p. 48-290.

JACKSON, J.D. Classical Eletrodynamics. ED.3ª, University of California, Berkeley, 1998, p. 237-239.

MAXWELL, J.C. A Treatise on Electricity and Magnetism. Oxford Univ. Press, Oxford, 2002.

MAXWELL, J.C. The Scientific Papers of James Clerk Maxwell. Dover Publ., New York, 1965, v. 1, p. 451.

PLONSEY, R; COLLIN, R.E. Principles and Applications of Electromagnetic Fields. McGraw-Hill, New York, 1961, Topic 2.

SHADIKU, M.N.O. Elementos de Eletromagnetismo. ED.3ª, Bookman, Porto Alegre, 2004, p. 107-350.

^[1] Postgrado in Ingegneria Elettrica (Strumentazione) da PUC-MG (2008), laureato in Ingegneria Industriale Elettrica presso CEFET-MG (2007).

Inviato: Luglio 2020.

Approvato: agosto 2020.