Nueva formulación matemática del proceso de difusión molecular y electrodifusión en membranas celulares

ARTÍCULO ORIGINAL

SOUZA, Nathan Rodrigues Serpa ^[1]

SOUZA, Nathan Rodrigues Serpa. Nueva formulación matemática del proceso de difusión molecular y electrodifusión en membranas celulares. Revista Científica Multidisciplinar Núcleo do Conhecimento. Año 06, Ed. 04, Vol. 15, págs. 34 y 63. Abril de 2021. ISSN: 2448-0959, Enlace de acceso: https://www.nucleodoconhecimento.com.br/fisica-es/difusion-molecular

RESUMEN

A difusão molecular é um fenômeno físico-químico observável no dia a dia, como simples gases de um perfume se expandindo por uma sala fechada, bem como em âmbito microscópico, a absorção de íons por vegetais e animais pelas células, via canais iônicos abertos da Membrana plasmática. Este artículo físico propone la formulación de una nueva ecuación denominada por el autor de “Ecuación de Nathan”, como extensión de la conocida 1ª Ley de Fick, que tiene como objetivo describir el fenómeno natural de difusión, en función de la variable Fuerza resultante. del Sistema, que permitirá un análisis general de las fuerzas actuantes que pueden influir en este fenómeno, así como extender esta formulación para describir el transporte de iones a través de la membrana celular, una formulación denominada “Ecuación de Nathan para la Electrodifusión en Membranas Celulares”. A través de un método exploratorio, investigación bibliográfica y herramientas matemáticas, fue posible realizar tales formulaciones, así como interpretarlas. A partir del análisis dimensional y los postulados propuestos por la 1a Ley de Fick y la Ley de Graham para la difusión, en forma de gráficos basados ​​en datos experimentales e hipotéticos para comparar las similitudes de las curvas de los gráficos, se pudo confirmar la validación matemática y física para tal ecuación, demostrando conservar las unidades y concordar positivamente con los postulados presentados por aquellas otras leyes ya establecidas en el medio físico-químico.

Palabras clave: Difusión, Membrana celular, Ley de Fick, Ecuación de Nathan, Electrodifusión.

1. INTRODUCCIÓN

La difusión molecular es un fenómeno físico-químico observable en el día a día, como simples gases de un perfume que se expanden a través de una habitación cerrada, así como microscópicamente, la absorción de iones por vegetales y animales por las células, a través de canales iónicos de la membrana plasmática. Este proceso de transporte consiste en el movimiento espontáneo e irreversible de moléculas ubicadas en regiones de alta concentración (Hipertónicas) a otras con concentraciones más bajas (Hipotónicas), la fuerza impulsora para esto son los potenciales químicos o térmicos de la solución, y en el caso de las membranas celulares fuerzas electrostáticas juntas (DA SILVA, 2013).

Según Alberts (2009), la membrana presenta tejido de carácter anfifílico, formado por fosfolípidos con un extremo polar (Fosfato Radical) y otro no polar (Cola de Ácidos Grasos). Algunas moléculas polares o cargadas como los iones tienen dificultades para cruzarse por simple difusión a bicapa lipídica, desplazamiento realizado a través del transporte de proteínas o proteínas que hacen canales, como los canales iónicos. Además de presentar una polaridad entre los medios extracelulares con acumulación de cargas positivas y el medio intracelular con acumulación de cargas negativas, comportándose como un Campo Eléctrico Uniforme (MOREIRA, 2014).

Este artículo exploratorio, con un método de análisis teórico-matemático, pretende establecer una nueva formulación matemática para la descripción del proceso de difusión molecular y transporte de iones a través de canales iónicos de membranas celulares, que tenga en cuenta la Fuerza Resultante del sistema (F_R), que permitirá un análisis general de las acciones en las partículas. Las proposiciones expuestas tuvieron como base teórica la reunión de la colección bibliográfica diversificada, en los campos de las ciencias biológicas, químicas y físicas, así como el análisis de sus proposiciones a partir de la comprensión física y matemática de los resultados, bajo el espectro de otras leyes que describen un determinado aspecto del mismo fenómeno en estudio, tales como: La Ley de Fick y la Ley de Graham.

2. DESARROLLO

2.1 MATERIAS Y MÉTODOS

Este artículo de sesgo exploratorio tiene como objetivo establecer formulaciones matemáticas para describir el proceso de difusión molecular y el flujo de iones a través de canales iónicos abiertos de las membranas celulares, debido no sólo al gradiente de concentración o potencial eléctrico de la membrana, sino a tener en cuenta las fuerzas constantes que operan en general, formulaciones matemáticas estas son llamadas por el autor de : Ecuación de Nathan y Ecuación de Nathan para electrodifusión en membranas celulares.

Para la construcción matemática, la colección de material bibliográfico de diversas ciencias fue de gran relevancia, tales como: Biología Celular, Química y Física. Además de la revisión material, después de la construcción matemática, se realizó el análisis dimensional de la ecuación para verificar la conservación de las unidades y su validez, así como su respuesta positiva o negativa sobre los postulados de las Leyes de Fick y Graham para la descripción del proceso de difusión, basado en gráficos basados en datos experimentales e hipotéticos. , con el fin de comparar los gráficos creados a partir de las relaciones matemáticas. El conocimiento utilizado se expondrá a continuación:

2.2 DESARROLLO BIOLÓGICO

Las células se organizan en tres partes: la membrana plasmática, el citoplasma y el núcleo. Uno de los focos de este trabajo académico radica en la comprensión del compartimento primario, la membrana celular, con aproximadamente 8 nanómetros (nm) o 8 x 10^-9 metros (m), observable por luz de microscopio electrónico. La membrana no es totalmente permeable, consistiendo en su función principal, siendo una barrea selectiva que permite la separación, así como el intercambio de sustancias entre medios extra e intracelulares (JUNQUEIRA y CARNEIRO, 2012).

Sin embargo, su permeabilidad selectiva se debe a la composición químico-estructural de las membranas celulares, estando compuesta por una bicapa de fosfolípidos, proteínas y carbohidratos. Los fosfolípidos son tejidos anfílicos, es decir, que contienen partes polares y no polares, la cabeza hidrofílica (Fosfato Radical) está orientada hacia el exterior de la célula formando interacción electrostática con las moléculas polares del agua. Su región hidrofóbica consiste en sus largas cadenas apolares de ácidos grasos que pueden interactuar fácilmente con otras sustancias liposolubles, de las cuales es más ventajoso tener su cola orientada hacia la región intracelular. Por lo tanto, no todas las sustancias son capaces de atravesar la membrana celular y entrar en la célula por simple difusión, sin embargo, tal transporte de difusión se ve facilitado por el transporte o la fabricación de canales iónicos proteínas cuando se abren (ALBERTS, 2009).

2.3 DESARROLLO QUÍMICO

Según Taiz y Zeiger (2006), la difusión es un fenómeno de transporte de materia, en el que hay un flujo de partículas desde las regiones con mayores concentraciones a las regiones con concentraciones más bajas, con el objetivo de promover el estado de equilibrio o también llamado homeotasa. La descripción matemática de tal proceso se expresa por la Primera Ley de Fick, propuesta por el médico y fisiólogo Adolf Eugen Fick (1829 -1901), una ecuación diferencial en la que la Densidad de Flujo (J) es directamente proporcional al Gradiente de Concentración (  ), y  el Coeficiente de Difusión (D) que depende del elemento químico en estudio, como se expresa a continuación (ver ecuación 2.1):

Este flujo homogeneizador es una consecuencia estadística del movimiento aleatorio de las partículas, conocido como movimiento browniano, de forma espontánea las moléculas se mueven desde las regiones hipertónicas (Concentraciones Superiores) a las regiones hipotónicas (Concentraciones Inferiores). El signo negativo en la Ley de Fick indica que el flujo se produce en la dirección opuesta al gradiente de concentración, siendo una ley lineal, por mucho que sea la diferencia de concentración entre dos puntos, el flujo sigue siendo proporcional al gradiente.

Otros detalles importantes sobre la Ley de Fick son los siguientes: Relación directamente proporcional al área de difusión (A) e inversamente proporcional entre el tamaño de partícula y la velocidad de difusión, o su Masa Molecular (M). Es decir, cuanto mayor sea el área, mayor será la tarifa de transporte; así como, cuanto menor sea la masa molecular de la partícula, mayor será su velocidad de transporte y más rápida será su velocidad de difusión.

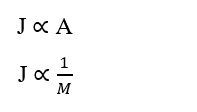
Según Brady y Huminston (1995), la Ley de Graham (véase la ecuación 2.2), formulada por el químico Thomas Graham (1805 -1869) después de sus estudios sobre difusión y derrame de fluidos, establece que la Velocidad de Efusión y Difusión (u) de dos gases (δ1) y (δ2), bajo las mismas condiciones de temperatura y presión, es inversamente proporcional a la raíz cuadrada de sus Densidades (d) o Masa Molecular (MM), como se expresa a continuación:

o

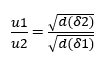
o

 

 

2.4 DESARROLLO FÍSICO

Uno de los conceptos fundamentales para este artículo es el conocido “Principio Fundamental de la Dinámica” o “2ª Ley de Newton”, que establece: La fuerza resultante que actúa bajo un cuerpo, es el producto de su masa por aceleración (F_R = m. a). Halliday (2016) afirma que primero debe elegir el cuerpo que uno desea estudiar, y aplicar la fuerza resultante como la suma de todas las fuerzas que actúan en el cuerpo en cuestión.

Según Tipler (2009), el Trabajo (W) es la energía transferida a un objeto a través de una fuerza que actúa sobre el objeto mismo. Para calcular el trabajo que una fuerza realiza sobre un objeto cuando sufre un desplazamiento, usamos solo el componente de fuerza paralelo al desplazamiento del objeto, el componente de fuerza perpendicular al desplazamiento no realiza el trabajo. El Trabajo (W) de una fuerza constante, en función de fuerzas paralelas (θ = 0°, 180°), se puede describir a través de esta ecuación:

W = F. d. cosθ

Como [Cos (0 °, 180 °) = 1]; puede reescribir la ecuación de trabajo como una Integral o como una función de la Variación de una Distancia ΔX (ver ecuación 2.3), tenemos:

Según Halliday (2016), la energía es un concepto difícil de definir. Sin embargo, entendemos intuitivamente qué es la energía, a partir del análisis de los efectos en las diferentes formas de la misma, tales como: Energía Cinética y Energías Potenciales. Conceptualmente para Tipler (2009), la Energía Cinética está asociada con cualquier cuerpo que tenga masa y se esté moviendo. Sea (m) la masa de un punto material y (u) su velocidad escalar, en relación con una referencia dada. La energía cinética del punto material está dada por (véase la ecuación 2.4):

Para el Movimiento Uniformemente Variado, el trabajo de la fuerza resultante por el cuerpo también la variación de energía cinética del propio cuerpo. A partir del Teorema trabajo-energía (W = ΔK) podemos obtener la expresión que es igual al Trabajo de una Fuerza Constante (W), con la Variación de Energía Cinética (ΔK), como lo demuestran las ecuaciones (2.5) y (2.6):

El Movimiento Uniformemente Variado, según Marques (2016), es aquel en el que una partícula cambia de velocidad (u₀) a otra (u) debido a una fuerza constante que promueve una aceleración (a) también constante, produciendo también un desplazamiento (ΔX). Este tipo de movimiento se puede equiparar sin tener en cuenta el tiempo, la llamada “Ecuación de Torricelli” (2.7):

Según Pimentel (2004), la fuerza impulsora de los procesos difusivos en medio líquido celular, es el llamado Potencial Químico de cualquier solución, que se configura como la capacidad de dicha solución para realizar el trabajo bajo las partículas disueltas, en relación con el gradiente de concentración, una formulación para el Potencial Químico Máximo del agua sería (2.8):

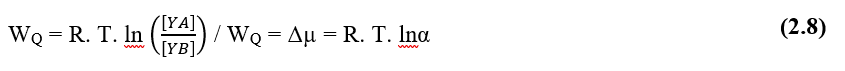
W_Q – Potencial químico de la solución (J)

R – Constante general de gas (R = 8,31 J Mol^-1 K^-1)

T – Temperatura Absoluta (K)

[ Y_A ] – Concentración de la sustancia Y en el punto A (Mol)

[ Y_B ] – Concentración de la sustancia Y en el punto B (Mol)

α – Actividad Química

3. RESULTADOS Y DISCUSIONES

3.1 DESARROLLO DE LA ECUACIÓN DE NATHAN

En un intento de describir matemáticamente el proceso de difusión y transporte de iones a través de canales iónicos en la membrana plasmática, en función del gradiente de concentración y el campo eléctrico generado en los extremos extracelular e intracelular de la membrana, consideremos una x, y y z, sistema de coordenadas en el que cada eje representa su respectiva aceleración generada por las fuerzas que actúan sobre el sistema aislado en estudio (a_x, a_y y a_z), como se muestra en la figura 1.

 Figura 1: Sistema de coordenadas (X, Y, Z).

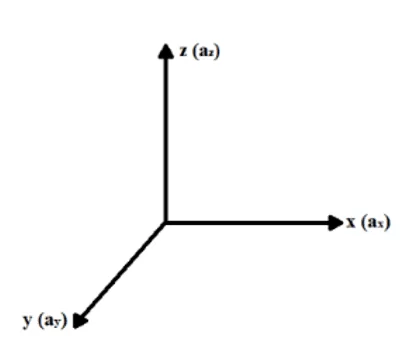
Según Halliday (2016), la fuerza resultante que actúa sobre una partícula como iones, que atraviesan la membrana a través de canales iónicos, puede descomponerse en sus componentes en cada eje x, y y z, estando directamente asociada con aceleraciones en los respectivos ejes. A través del Principio Fundamental de Dinámica o Segunda Ley de Newton, y el Principio de Superposición de Fuerza de Newton, se puede obtener un análisis físico para las fuerzas resultantes en cada eje que ejercen influencia sobre el ion (ver ecuación 3.1):

 

F_R – Fuerza resultante total (N – Kg m s^-2)

F_R(X – Fuerza resultante en el eje X (N – Kg m s^-2)

F_R(Y) – Fuerza resultante en el eje Y (N – Kg m s^-2)

F_R(Z) – Fuerza resultante en el eje Z (N – Kg m s^-2)

Las masas de los iones se conservan, por lo que los factores directamente proporcionales a las fuerzas en cada dirección son sus aceleraciones en las respectivas direcciones:

F_R(X) = m . a_x / F_R(Y) = m . a_y / F_R(Z) = m . a_z

Comparando las constantes electrostática y gravitacional (k = 9 x 10⁹y G = 6,67 x 10-¹¹  ), según Halliday ³ (2016) tales valores demuestran que la fuerza gravitacional es mucho más débil que la fuerza eléctrica. Por tanto, en un sistema aislado de partículas en el que sólo se considera que actúan las fuerzas gravitacionales y eléctricas, la fuerza gravitacional puede despreciarse, ya que la fuerza eléctrica es aproximadamente 1,5 x 1020 veces mayor que la fuerza del peso. Como no se tendrá en cuenta la aceleración de la gravedad sobre la partícula, la fuerza sobre la componente Z también será nula, ya que no se tendrá en cuenta la aceleración az, reformularemos la ecuación para el estudio dado:

F_R = m . a_x + m . a_y + m . a_z

F_R = m . a_x + m . a_y + m . 0

F_R = m . a_x + m . a_y

Considerando como fuerzas mayoritariamente activas, aquellas que ejercen influencia sobre el eje X, sin tener en cuenta los choques mecánicos y cualesquiera otras fuerzas en el componente y, dado que el conjunto de solutos se mueven en el sentido de homogeneización, de regiones hipertónicas a hipotónicas, llegaremos a tal simplificación de la Fuerza Resultante:

F_R = m . a_x + m . 0

F_R = m . a_x

Otro punto a tener en cuenta es que el sistema en estudio se considerará estacionario o de forma permanente, en el que sus propiedades son inalterables en relación con el tiempo. Esto implica que cualquier propiedad P del sistema, la derivada parcial en relación con el tiempo es cero  , considerando un sistema en el que la variable tiempo no es un parámetro en el estudio del sistema de membrana en cuestión.

Las membranas celulares tienen una cierta disposición, como análoga al Campo Eléctrico Uniforme, de modo que existe la concentración de cargas positivas principalmente en el lado extracelular, y una acumulación de cargas negativas en el lado intracelular. También existe una diferencia de concentración entre los extremos externo e interno de las células (C_E y C_I)_, en la que el sistema ejerce una fuerza motriz para promover la translocación de partículas a través de canales iónicos de las membranas celulares, tal y como se representa en la Figura 2.

Figura 2: Representación del desplazamiento iónico a través del canal iónico.

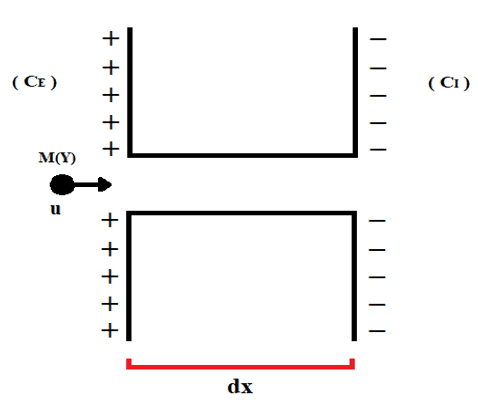
La distancia recorrida por la molécula representada es equivalente al elemento de desplazamiento (dx), que también es el espesor de la membrana celular ya mencionado. La primera ley de Fick se puede describir como una función del gradiente de concentración total (∇D) y la constante de difusión (D), como se expresa a continuación (ver ecuación 3.2):

Sin embargo, solo consideraremos el elemento de longitud (?x) ya mencionado, para evaluar el movimiento unidimensional de solutos desde regiones de altas concentraciones a concentraciones más bajas. Por lo tanto, los gradientes de concentración ( _y ) será eliminado de la ecuación, esta vez volvemos a la ecuación 2.1:

Al aislar el elemento (∂x) de la Primera Ley de Fick, obtenemos:

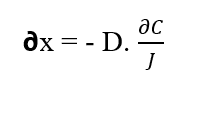Las partículas de soluto se mueven a lo largo de un desplazamiento (∂x) debido a la fuerza derivada del Potencial Químico del sistema (W_Q)_, ya que según la 2ª Ley de Termodinámica descrita por Tipler (2009), el flujo de materia o energía deja las regiones con valores más altos de materia o energía para los más pequeños. Si las partículas están sujetas a fuerzas y debido a este movimiento por cierto elemento de distancia (∂x), se puede suponer que tales cuerpos están realizando trabajo (W), que se describe en la siguiente ecuación (ver ecuación 2.3):

El trabajo de una fuerza constante también se puede describir como una función de la variación de energía cinética del sistema (ΔK), como se expresa en el Teorema de energía cinética (véase la ecuación 2.5):

Considerando el movimiento unidimensional de partículas disueltas en solución, en un momento inicial determinado las partículas en relación con un determinado elemento (∂x) no se están moviendo, por lo que su Velocidad Inicial (u₀) puede considerarse nula, por lo que la Obra se describe de la siguiente manera:

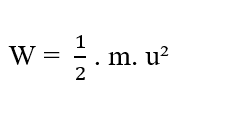
Para un sistema en el que tenemos un número n de partículas que se extienden, cada una de las cuales tiene una cierta Masa (m(i)) y Aceleración (a(i)), tenemos que la Fuerza Resultante en las partículas puede expresarse como:

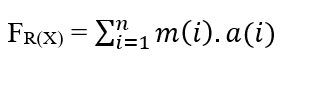
Dado que el sistema tiene una Fuerza Constante, este movimiento también se describe con una Aceleración Constante para todas las partículas según un movimiento uniformemente variado, lo que permite eliminar la Aceleración de la Suma, de las propiedades de los Somadores:

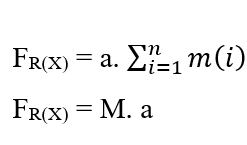
Para llegar a la Ecuación de Nathan, las dos ecuaciones de Trabajo se igualan, y debido a que es tratar el movimiento de las moléculas como se demuestra, la masa (m) se considera como la masa total (M) de una cierta cantidad de moléculas presentes en el sistema en estudio, y también reemplaza el elemento (dx) por (?x) de la Primera Ley de Fick.

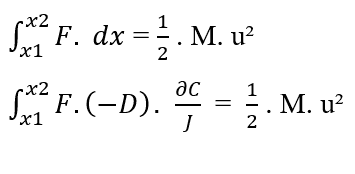
Sabiendo que (F, D, J) son constantes en relación al elemento (?C) a integrar, a partir de la propiedad de la constante de integrales, se pueden quitar los términos de la integral:

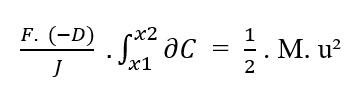
Reescribiendo los límites de integración en relación con el (?C), tenemos:

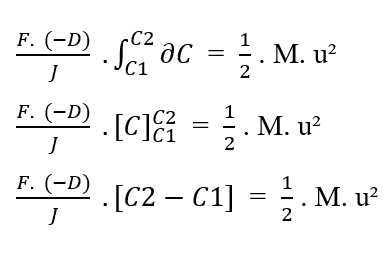
Sabiendo [C₂ – C₁ = ΔC] eso, puede reemplazar el valor en la ecuación:

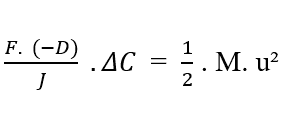
Al aislar la densidad de flujo variable (J), obtenemos la ecuación de Nathan (ver ecuación 3.3):

 

J – Densidad de flujo (Mol m^-2 s^-1)

D – Coeficiente de difusión (m² s^-1)

ΔC – Variación de concentración (Mol m^-3)

F_R – Fuerza resultante (Kg m s^-2)

M – Masa total de partículas difusas (kg)

u – Tasa de difusión de partículas (m s^-1)

3.2 EVALUACIÓN MATEMÁTICA Y FÍSICA DE LA ECUACIÓN DE NATHAN

Para confirmar la validación de la Ecuación de Nathan de forma matemática, fue necesario realizar el Análisis Dimensional descrito por Halliday (2016), en el que comprobará si se conservan las unidades de la Primera Ley de Fick, y las unidades de la Ecuación de Nathan son equivalentes. El análisis dimensional es una herramienta utilizada en física para determinar la unidad de medida de cierta magnitud. El análisis dimensional es una herramienta que permite la predicción, inspección y adaptación de las unidades físicas que se utilizan para la resolución de ecuaciones.

 

Ley de Fick:

J – (Mol m^-2 s^-1)

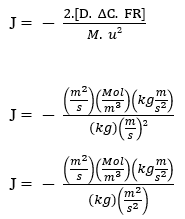
J – (Mol m^-2 s^-1)

Generalmente, las cantidades físicas fundamentales se expresan como: Longitud (L), Masa (M), Tiempo (T), Temperatura (θ), Corriente Eléctrica (A), Cantidad de Materia (Mol) e Intensidad Luminosa (I). El análisis dimensional de la Ecuación de Nathan (3.3) se puede realizar utilizando tales representaciones de las cantidades físicas fundamentales, de acuerdo con el equivalente de cada variable de la formulación expuesta, como señala Marques (2016).

J – Densidad de flujo (Mol L^-2 T^-1)

D – Coeficiente de difusión (L² T^-1)

ΔC – Variación de la concentración (Mol L^-3)

F_R – Fuerza resultante (M L T^-2)

M – Masa Total De Las Partículas Difitantes (M)

u – Velocidad de difusión de partículas (L T^-1)

Ahora realizando análisis dimensionales con las representaciones generales de las cantidades físicas fundamentales, tenemos:

 

Ley de Fick:

J – (Mol L^-2 T^-1)

Ecuación de Nathan:

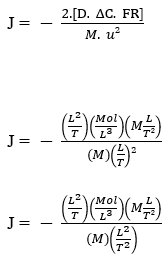
J – (Mol L^-2 T^-1)

La Ecuación de Nathan demuestra la conservación de las unidades, así como, sigue algunas afirmaciones que la Primera Ley de Fick y la Ley de Graham demuestran, con el fin de relacionar ciertas variables de manera directa o inversamente proporcional, validando físicamente dicha formulación matemática para el proceso de Difusión, independientemente de las unidades elegidas para las cantidades fundamentales, siempre que tengan coherencia en general.

La primera relación que muestra la ecuación de Nathan es la relación directamente proporcional entre la densidad de flujo (J) y la variación de concentración entre dos puntos (ΔC). Al establecer que, un aumento en la Diferencia de Concentración entre dos puntos cualesquiera del sistema, estará directamente relacionado con el aumento de la Densidad de Flujo del mismo, Tal relación obedece a la Ley de Fick.

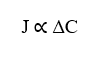
La segunda relación importante es la proporcionalidad directa entre la Densidad de Flujo (J) y la Fuerza Resultante (F_R) que actúan sobre las partículas (γ) que componen el sistema en cuestión. Esto implica que un aumento en la variable Fuerza Resultante que actúa bajo las moléculas que se difunden, también aumentará directamente proporcionalmente el Flujo de Partículas.

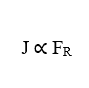
La tercera relación importante es la proporcionalidad inversa entre la Densidad de Flujo (J) y la masa total de cualquier elemento gamma (γ), que conforman el sistema en estudio. Esto implica decir que, considerando para cada molécula y sólo su Masa Molecular, cuanto mayor sea la Masa Molecular del elemento a difundir, menor será su Tasa de Transporte, Tal relación obedece a la Ley de Fick y la Ley de Graham.

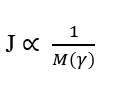
La cuarta relación importante es la proporcionalidad inversa entre la masa molecular (M) y la velocidad de difusión cuadrada (u). O puede entenderse como la relación inversa entre la velocidad de difusión y la raíz cuadrada de la masa molecular del elemento (γ). Esta relación obedece a la Ley de Derrame y Difusión de Gases de Graham, mostrando correlación de la Velocidad con la inversa de la raíz cuadrada de la masa molecular.

La densidad de flujo (J) es inversamente proporcional al producto entre la masa molecular (M) – cuando para una partícula – y el cuadrado de velocidad de difusión (u):

 

Si (J) es constante (K), tenemos:

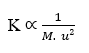
Al aislar la variable Tasa de difusión (u), se llega a:

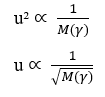
A partir de la versión de Excel Software 2016, también fue posible realizar el modelado gráfico de 20 datos hipotéticos para el valor de Masa Molecular (M), con un intervalo de (0 < M < 21) em ordem crescente, correlacionado ao seu respectivo valor de Velocidade de Difusão (u), sabendo que a velocidade de difusão de um determinado elemento é inversamente proporcional a raiz quadrada de sua respectiva massa, como aponta a Lei de Graham e também a Equação de Nathan quando a Taxa de Transporte (J) se mantém constante e considera-se apenas a massa de uma única partícula. Así, podemos percibir la similitud de los gráficos construidos posteriormente con dichos datos (ver Gráfico 1).

Gráfico 1: Velocidad de difusión versus la inversa de la raíz cuadrada de la masa molecular.

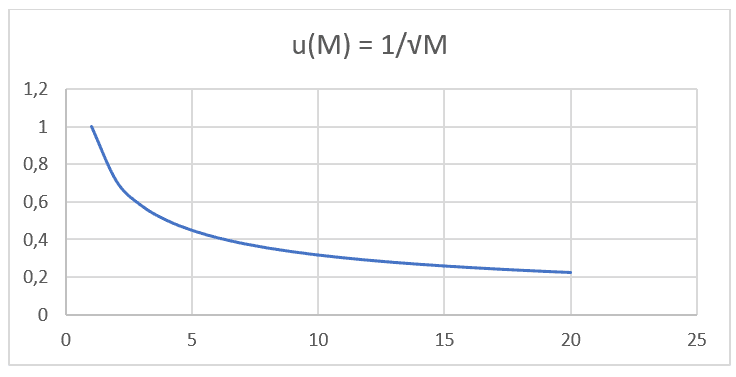
Se observa que ambas formulaciones, tanto la Ley de Graham como la Ecuación de Nathan, tienen la misma proporcionalidad y se basan en el mismo tipo de función: F(x) =. Realizando una proyección gráfica con valores de masa molecular, datos de la IUPAC y su respectiva velocidad de difusión de 20 gases diferentes a las mismas presiones y temperaturas enumeradas en la tabla siguiente (ver Tabla 1), puede proyectar una segunda gráfica (ver Gráfica 2).

Tabla 1: Masas Moleculares y sus respectivas Velocidades de Difusión.

gas	Masa molecular (g/mol)	Velocidad de difusión (cm/s)
H2	2	0,7
He	4	0,5
O2	16	0,25
CH4	16	0,25
Ne	20	0,22
H2S	34	0,17
Ar	40	0,15
CO2	44	0,15
NO2	46	0,14
O3	48	0,13
C4H10	58	0,12
NO3	63	0,12
SO2	64	0,12
CS2	76	0,11
SO3	80	0,11
Kr	84	0,10
FeS	88	0,10
Xe	131	0,08
PCl3	137	0,08
Rb	222	0,06

Fuente: El Autor.

Gráfico 2: Velocidad de difusión versus la inversa de la raíz cuadrada de la masa molecular.

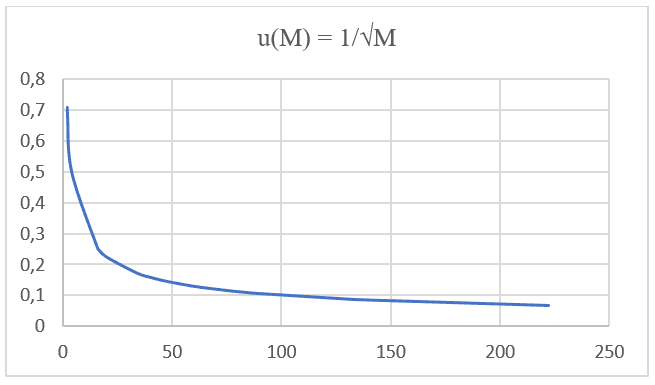
Según Zeiger y Taiz (2006), el Tiempo Medio de Difusión puede definirse como la relación entre el cuadrado de la Variación de Distancia (ΔX²) y el Coeficiente de Difusión del elemento (D), expresado por la siguiente formulación matemática (ver ecuación 3.4):

A partir de la definición de Velocidad Escalar Media (u) de cinemática y sustituyendo el valor de tiempo por la variable Tiempo Medio (T_M), obtenemos:

 

o

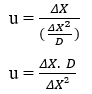
Mediante la realización de manipulaciones algebraicas, se puede obtener la ecuación para calcular la velocidad de difusión (u) de cualquier elemento:

Sustituyendo (3,5) en la ecuación de Nathan (3,3), podemos obtener la relación entre el cuadrado de la Variación de Distancia (ΔX) y la Variación de Concentración (ΔC).

Realizando el Análisis Dimensional de la ecuación (3.6) para confirmar la conservación de las unidades de la Ley de Fick, tenemos:

 

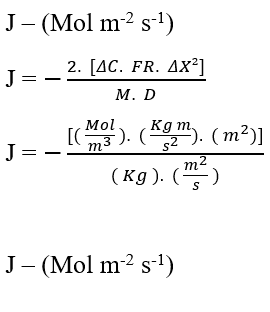
Validada la conservación de unidades a partir del análisis dimensional, se puede percibir una relación importante y común en la ecuación de Nathan y la Ley de Fick, es la proporcionalidad inversa entre la Variación de Concentración (ΔC), y el cuadrado de la Variación de Distancia (ΔX²). Para que esta afirmación sea válida consideraremos que la Tasa de Transporte (J) es constante, y analizaremos solo estas dos variables: Variación de Concentración y Distancia.

 

Considerando que la densidad de flujo (J) es constante, tenemos:

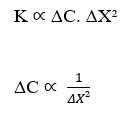
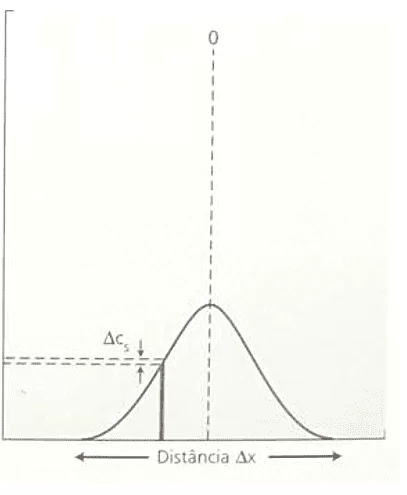
Se demuestra la proporcionalidad inversa entre la Variación de Concentración (ΔC) y el Cuadrado de Variación de Distancia (ΔX²). Esta afirmación concuerda con la Ley de Fick, ya que al analizar la correlación entre esas dos variables, ambas formulaciones, la Ecuación de Nathan y la Ley de Fick, describen la misma gráfica que sigue a la función: F(x) = . La siguiente es una demostración de formato gráfico (Curva gaussiana), Variación de concentración versus Variación de cuadrado de distancia (ver Figura 3):

Figura 3: Variación gráfica de la concentración versus cuadrado de variación de distancia.

En el caso de tener como variable determinante en el proceso de difusión de un elemento dado, la Variación de Concentración (ΔC), suponiendo entonces que se trata de un movimiento de partículas de la velocidad constante y no un movimiento uniformemente variado causado por una fuerza constante, basta con sustituir (2.7) en (3.3), la Ecuación de Torricelli, que devolverá la descripción matemática conocida como una descripción matemática conocida como la : 1st Fick’s Law.

Reemplazando (2.7) en (3.3) considerando la velocidad inicial (u₀) nula, tenemos:

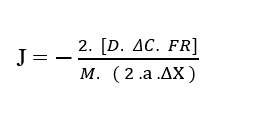
Al cancelar los términos Fuerza Resultante (F_R),con los términos en el denominador Masa Total de Partículas (M) y Aceleración (a), así como las constantes en el numerador y denominador (2), obtenemos de nuevo la formulación lineal: Primera Ley de Fick (2.1).

3.3 DESARROLLO DE LA ECUACIÓN DE NATHAN PARA ELECTRODIFUSIÓN EN MEMBRANAS CELULARES

La Ecuación de Nathan se puede extender para describir el proceso de difusión de iones a través de la membrana celular, matemáticamente, teniendo en cuenta las siguientes formulaciones matemáticas. Según Pimentel (2004), la fuerza motriz de los procesos difusivos en sistemas biológicos es el llamado Potencial Químico del sistema, y en el caso del ejemplo en cuestión, se produce la transferencia de materia de un punto A a otro B, dicho Potencial Químico puede expresarse a partir de la siguiente ecuación (2.8):

Esto implica decir que un soluto se moverá de una región con mayor potencial químico a una región más pequeña, o en el caso de disolventes como el agua, de la ósmosis se mueve de las regiones de concentraciones más bajas de soluto a mayores. Sin embargo, el flujo de partículas cesa cuando los potenciales químicos de ambas fases son iguales, obteniendo así el estado final de equilibrio (HENEINE, 2004).

Dicho Potencial de Solución que produce la Fuerza Resultante del sistema, debido a que representa la capacidad de un sistema dado para realizar trabajos, se puede describir teniendo en cuenta la contribución de otros factores importantes, tales como: Acción Gravitacional e Influencia Eléctrica sobre las Partículas debido a sus cargas y la diferencia en el potencial eléctrico. Así, la ecuación del potencial máximo puede expresarse mediante la formulación del Potencial Electroquímico, a continuación (véase la ecuación 3.7):

En caso de que no se tenga en cuenta la contribución del potencial gravitatorio (m.g.h), la ecuación se reducirá únicamente a la contribución química y eléctrica, siendo estas las fuerzas que trabajan en el conjunto de partículas iónicas para moverse a través de los canales iónicos o moleculares a través de la bicapa lipídica, entrando en el medio intracelular (ALBERTS, 2009).

La Ecuación de Nathan describe el proceso de difusión, y el fenómeno natural del transporte de iones a través de la membrana celular puede expresarse de manera similar por la ecuación de Nathan, tomando como Fuerza Resultante (F_R) sólo el Potencial Químico de la solución y la contribución eléctrica, sin tener en cuenta la contribución gravitacional.

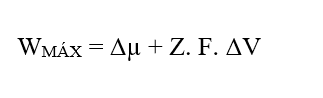
Sabiendo que (W = F_R. Δx), sustituyendo la ecuación (2.3) obtenemos:

Al realizar el análisis dimensional de la Fuerza Resultante (3.8), dividiéndola en sus gráficas químicas y eléctricas, se puede percibir la aparición no más de la unidad de energía Joule (J), sino más bien de la Unidad de Fuerza en el Sistema Internacional de Mediciones, newton (N):

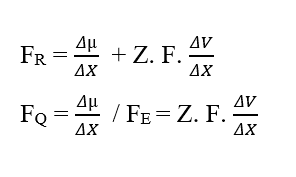
Analizando la porción química de contribución (F_Q)_,tenemos:

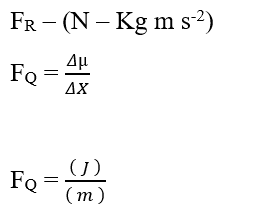
Sabiendo que la unidad de energía Joule (J- N.m) puede ser reemplazada en análisis dimensional, obteniendo:

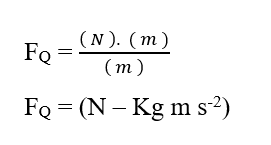
Analizando la porción eléctrica de la contribución (F_E), tenemos:

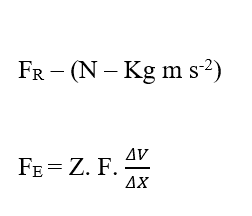
Sabiendo que Valencia (Z) es una variable dimensional, tenemos:

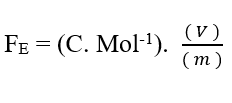
Sabiendo que la unidad de voltaje Voltio (V – J. C^-1), puede ser sustituido en análisis dimensional, obteniendo:

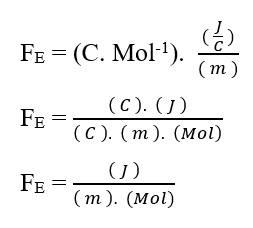
Como la unidad Mol se considera como adimensional, porque sólo está relacionada con entidades que componen un sistema dado, tales como: Átomos, moléculas, iones o electrones; podemos ignorar tal unidad en el análisis, simplificándola:

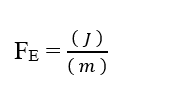
Sabiendo que la unidad de energía Joule (J- N.m) puede ser reemplazada en análisis dimensional, obteniendo:

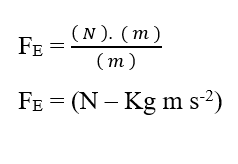
A partir del análisis dimensional de las dos gráficas, química y eléctrica, que conforman la Fuerza Resultante (F_R) del sistema en estudio, se demuestra que es válida para el cálculo de dicha fuerza. Escribiendo las relaciones entre Variación del Potencial Químico (Δμ) y Variación de Distancia (ΔX), Variación del Potencial Eléctrico (ΔV) y Variación de Distancia (ΔX), en forma de límites de (ΔX 0) y luego en forma diferencial, teniendo la Fuerza Instantánea Resultante, obtenemos:

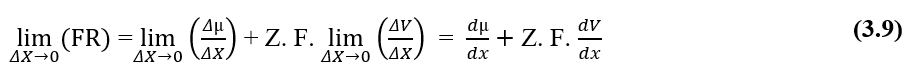
Para una situación en la que los Potenciales Electroquímicos de dos fases (A) y (B) de un sistema dado son los mismos, es decir, en una situación de equilibrio, se puede establecer el valor de la Variación del potencial eléctrico en los extremos de las membranas celulares, que se refiere a la Ecuación de Nernst.

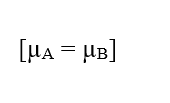
Si los potenciales son los mismos, esta afirmación indica que el Trabajo realizado por las partículas es nulo, por lo que la Fuerza Resultante en ellas también será nula, ya que no hay tránsito de moléculas entre las dos fases del sistema:

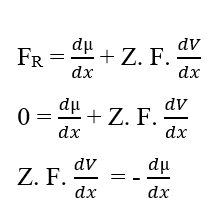
Puede cancelar los elementos (dx) que aparecen a ambos lados de la igualdad y aislar el término (dV), luego reescribir de acuerdo con las variaciones, lo que resulta:

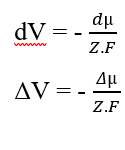
Reemplazando el Potencial Químico (2.3), restablecimos el cálculo del Potencial Eléctrico para una situación de equilibrio en sistemas biológicos (3.10), conocido como la Ecuación de Nernst (HENEINE, 2004).

Puede reemplazar la Fuerza Resultante del Sistema (3.9) en la Ecuación de Nathan descrita anteriormente (ver Ecuación 3.3):

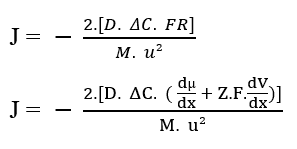
Aparte de los términos en el paréntesis, tenemos la ecuación de Nathan para la electrodifusión en membranas celulares (3.11):

J – Velocidad de transporte o densidad de flujo iónico en membrana (Mol m^-2 s^-1)

D – Coeficiente de difusión del soluto (m² s^-1)

ΔC – Variación de la concentración (Mol m^-3)

M – Masa total de las partículas de diferenciación (Kg)

u² – Velocidad de difusión de partículas (m s^-1)

Z – Ion Valencia

F – Constante de Faraday (F = 9,648 x 10⁴ C mol^-1)

∂μ/∂x – Derivado del Potencial Químico en Relación con dx (Kg m s^-2)

∂V/∂x – Derivado del Potencial Eléctrico en relación con dx (V m^-1)

Según Halliday (2016) para Termodinámica, Energía Interna (U) o Variación de Energía Interna (ΔU), es la suma de las energías cinéticas y potenciales de todas las moléculas que contiene un sistema. Esta relación se puede expresar, con la siguiente descripción matemática (ver ecuación 3.12), considerando la velocidad media para todas las partículas constantes:

[M – Masa total de partículas del sistema]

 

 

Reemplazando la ecuación (3.13), en la Ecuación de Nathan (3.3), se puede determinar un término constante, denominado por el autor con la letra griega omega (ω):

Si ahora consideramos la razón como cualquier constante (ω), ya que los valores de tales variables no cambian con respecto al tiempo, ya que la derivada parcial de cualquier término es nula  . Sabiendo que (ω) se presenta como una unidad , una relación entre la cantidad de materia concentrada y la energía interna de un sistema, dicha relación es equivalente a la siguiente expresión (3.15):

Y sabiendo que el paquete se refiere a la fuerza resultante del sistema (FR), todavía se puede reescribir esta formulación como su forma general (3.15):

 

Ahora es posible notar que, como los términos (D) y (ω) son constantes, la Densidad de Flujo (J) es directamente proporcional a la Fuerza Resultante del sistema (F_R), lo que implica que si se produce un aumento en una de estas variables, la otra también sufrirá un aumento proporcional.

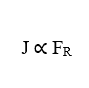
La Ecuación de Nathan para electrodifusión en membranas celulares describe el flujo de iones a través de la membrana, a través de canales iónicos cuando están abiertos, influenciados por el gradiente de concentración de medios extracelulares e intracelulares, así como potencial eléctrico o campo eléctrico bajo los iones, generado por la propia membrana celular. Esta formulación tiene en cuenta la Masa Total de partículas del elemento que se va a diseminar, las fuerzas motrices químicas y eléctricas presentes en el fenómeno de transporte de iones a través de la membrana celular, sin embargo, si existen otros factores externos, debido al aumento de la variable Fuerza Resultante, el análisis se puede realizar en un alcance generalizado, además de coincidir con los conceptos físicos existentes y presentados.

4. CONSIDERACIONES FINALES

En una declaración, este artículo propuso la formulación de la “Ecuación de Nathan”, como una extensión de la 1ª Ley de Fick, que describe el flujo difusivo de partículas en soluciones, debido no solo a la Diferencia de Concentración (ΔC), sino con el objetivo de considerar la Densidad de Flujo de Materia (J) como una función de la Fuerza Resultante constante (F_R) que actúa sobre las partículas de un sistema dado (ver ecuación 3.3).

Esta formulación demostró la proporcionalidad directa entre la Fuerza que actúa en las partículas, y la Densidad de Flujo (J), por lo que cuanto mayor es la fuerza ejercida en el sistema, mayor es el transporte de materia. La misma descripción matemática de los procesos naturales de difusión de moléculas, que permite un análisis general de las fuerzas que puedan ejercer influencia bajo ciertos sistemas en estudio, también puede ampliarse para explicar el transporte de iones a través de la membrana celular, cuando la Fuerza Resultante bajo las partículas del sistema en cuestión tiene en cuenta el Potencial Químico y el Potencial Eléctrico , así como una relación entre La cantidad de materia concentrada y la energía interna de un sistema (ω), que fue llamada por el autor de “Ecuación de Nathan para electrodifusión en membranas celulares” (ver ecuación 3.11), o también en su formulación general (ver ecuación 3.15).

La validación de las Ecuaciones se evaluó a partir del análisis dimensional y de las relaciones directas e inversamente proporcionales entre las variables, en relación con los postulados propuestos por la 1ª Ley de Fick y la Ley de Graham, en forma de grafos con curvas descritas por ciertas funciones que demuestran las proporcionalidades existentes entre: Velocidad de Difusión versus Masa Molecular de un elemento (ver Gráfico 1) , y la Variación de Concentración versus el Cuadrado de La Variación de Distancia (ver Gráfico 3); mostrándose como una formulación válida física y matemáticamente para tal descripción del fenómeno natural, porque las unidades de la Ley de Fick se conservan en la Ecuación de Nathan, y se corresponden tan positivamente con respecto a las proposiciones de tales Leyes Fisicoquímicas ya establecidas y sus representaciones gráficas, siguiendo las proporcionalidades descritas por ciertas funciones presentadas anteriormente. Los siguientes artículos de experimentos físicos o con software de modelado específico, pueden evaluar la practicidad y coherencia de la ecuación de Nathan con la realidad natural, refiriéndose al estudio del fenómeno de difusión, con el fin de analizar la precisión y generalidad de los conceptos planteados por ella.

 

REFERENCIAS BIBLIOGRÁFICAS

ALBERTS, Bruce et al. Biologia Molecular da Célula, 5° Edição. Editora: ARTMED, 2010, 1728 p., Vol. 1. ISBN: 978-85-363-2170-7.

BRADY, James; HUMISTON, Gerard. Química Geral, 2° Edição. Editora: LTC, 1995, 404 p., Vol. 1. ISBN: 9788521604495.

DA SILVA, Raissa. Difusão de Gases em Membranas Densas Via Simulação Molecular. Instituto Alberto Luiz Coimbra de Pós-Graduação e Pesquisa na Engenharia (UFRJ), Data da Dissertação de Mestrado: Abril de 2013. Disponível em: http://portal.peq.coppe.ufrj.br/index.php/producao-academica/dissertacoes-de-mestrado/2013-1/47-difusao-de-gases-em-membranas-densas-via-simulacao. Acesso: 25/06/2020.

HENEINE, Ibrahim. Biofísica Básica, 2° Edição. Editora: ATHENEU, 2004, 381 p., Vol. 1. ISBN: 8573791225.

JUNQUEIRA, Luiz C.; CARNEIRO, Jóse. Biologia Celular e Molecular, 9° Edição. Editora: Guanabara Koogan, 2012, 376 p., Vol. 1. ISBN: 9788527720786.

MARQUES, Francisco Das Chagas. Física Mecânica, 1° Edição. Editora: Manole, 2016, 315 p., Vol. 1. ISBN: 9788520427743.

MOREIRA C., Catarina. Difusão Simples. Rev. Ciência Elem., V2(02):144. doi.org/10.24927/rce2014.144. Pulicado: 15 de Setembro de 2010. Disponível em: https://rce.casadasciencias.org/rceapp/art/2014/144/. Acesso: 22/06/2020.

PIMENTEL, Carlos. A Relação da Planta Com a Água, Local: EDUR – Editora Universidade Federal Rural do Rio de Janeiro. 2004, 190 p. ISBN: 85-85720-45-X

TAIZ, Lincoln; ZEIGER, Eduardo. Fisiologia Vegetal, 3° Edição. Editora: ARTMED, 2006, Vol. 1, 722 p. ISBN: 85-363-0291-7.

TIPLER, Paul; MOSCA, Gene. Física para Cientistas e Engenheiros – Mecânica, Ondas, Termodinâmica, 6° Edição. Editora: LTC, 2009, 788 p., Vol. 1. ISBN: 9788521617105.

WALKER, Jearl et al. Halliday & Resnick ¹: Fundamentos de Física – Mecânica, 10° Edição. Editora: LTC, 2016, 372 p., Vol. 1. ISBN-13: 978-8521630357.

WALKER, Jearl et al. Halliday & Resnick ²: Fundamentos de Física – Gravitação, Ondas, Termodinâmica, 10° Edição. Editora: LTC, 2016, 324 p., Vol. 1. ISBN-13: 978-8521630364.

WALKER, Jearl et al. Halliday & Resnick ³: Fundamentos de Física – Eletromagnetismo, 10° Edição. Editora: LTC, 2016, 408 p., Vol. 1. ISBN-13: 978-8521630371.

^[1] Graduación.

Enviado: Diciembre de 2020.

Aprobado: Abril de 2021.