Nouvelle formulation mathématique du processus de diffusion moléculaire et d’électrodiffusion dans les membranes cellulaires

ARTICLE ORIGINAL

SOUZA, Nathan Rodrigues Serpa ^[1]

SOUZA, Nathan Rodrigues Serpa. Nouvelle formulation mathématique du processus de diffusion moléculaire et d’électrodiffusion dans les membranes cellulaires. Revista Científica Multidisciplinar Núcleo do Conhecimento. An 06, Ed. 04, Vol. 15, p. 34 et 63. avril 2021. ISSN: 2448-0959, Lien d’accès: https://www.nucleodoconhecimento.com.br/fisica-fr/diffusion-moleculaire

RÉSUMÉ

La diffusion moléculaire est un phénomène physico-chimique observable dans la vie quotidienne, comme de simples gaz d’un parfum se développant à travers une pièce fermée, ainsi que microscopiquement, l’absorption d’ions par les légumes et les animaux par les cellules, via des canaux ioniques ouverts de la membrane plasmique. Cet article de nature physique propose la formulation d’une nouvelle équation appelée par l’auteur de « l’équation de Nathan », comme une extension de la 1ère loi bien connue de Fick, qui vise à décrire le phénomène naturel de diffusion, dû à la variable Force résultante du système, ce qui permettra une analyse générale des forces qui influenceront ce phénomène , ainsi que l’extension de cette formulation pour décrire le transport des ions via la membrane cellulaire, une formulation appelée « Équation de Nathan pour l’électrodiffusion dans les membranes cellulaires ». Grâce à une méthode exploratoire, des recherches bibliographiques et des outils mathématiques ont été possibles pour effectuer de telles formulations, ainsi que pour les interpréter. À partir de l’analyse dimensionnelle et des postulats proposés par la 1ère loi de Fick et la loi de Graham pour la diffusion, sous la forme de graphiques basés sur des données expérimentales et hypothétiques pour comparer les similitudes des courbes graphiques, il a été possible de confirmer la validation mathématique et physique de cette équation, démontrant de conserver les unités et d’être d’accord positivement avec les postulats présentés par ces autres lois déjà établies dans l’environnement physico-chimique.

Mots-clés : Diffusion, Membrane cellulaire, Loi de Fick, Équation de Nathan, Électrodiffusion.

1. INTRODUCTION

La diffusion moléculaire est un phénomène physico-chimique observable au jour le jour, comme de simples gaz d’un parfum se développant à travers une pièce fermée, ainsi que microscopiquement, l’absorption d’ions par les légumes et les animaux par les cellules, via les canaux ioniques de la membrane plasmique. Ce processus de transport consiste en le mouvement spontané et irréversible de molécules situées dans des régions de forte concentration (hypertoniques) vers d’autres à des concentrations plus faibles (hypotoniques), la force motrice pour cela sont les potentiels chimiques ou thermiques de la solution, et dans le cas des membranes cellulaires, les forces électrostatiques ensemble (DA SILVA, 2013).

Selon Alberts (2009), la membrane présente des tissus de caractère amphiphile, formés de phospholipides à extrémité polaire (phosphate radicalaire) et un autre non polaire (queue d’acide gras). Certaines molécules polaires ou chargées telles que les ions ont du mal à se croiser par simple diffusion vers la bicouche lipidique, déplacement effectué par le transport de protéines ou protéines de fabrication de canaux, telles que les canaux ioniques. En plus de présenter une polarité entre le milieu extracellulaire avec accumulation de charges positives et le milieu intracellulaire avec accumulation de charges négatives, se comportant comme un champ électrique uniforme (MOREIRA, 2014).

Cet article exploratoire, avec une méthode d’analyse théorique-mathématique, vise à établir une nouvelle formulation mathématique pour la description du processus de diffusion moléculaire et de transport d’ions via des canaux ioniques des membranes cellulaires, qui prend en compte la Force résultante du système (F_R), ce qui permettra une analyse générale des actions dans les particules. Les propositions exposées avaient comme base théorique la rencontre d’une collection bibliographique diversifiée, dans les domaines des sciences biologiques, chimiques et physiques, ainsi que l’analyse de leurs propositions à partir de la compréhension physique et mathématique des résultats, sous l’éventail d’autres lois qui décrivent un certain aspect du même phénomène à l’étude, telles que: la loi de Fick et la loi de Graham.

2. DÉVELOPPEMENT

2.1 MATERIAS ET METHODES

Cet article exploratoire biaisé vise à établir des formulations mathématiques pour décrire le processus de diffusion moléculaire et le flux ionique via les canaux ioniques ouverts des membranes cellulaires, en fonction non seulement du gradient de concentration ou du potentiel électrique de la membrane, mais aussi de prendre en compte la forces constantes agissant en général, ces formulations mathématiques sont appelées par l’auteur : Nathan’s Equation et Nathan’s Equation for Electrodiffusion in Cell Membranes.

Pour la construction mathématique, la collection de matériel bibliographique de diverses sciences était d’une grande pertinence, telles que: biologie cellulaire, chimie et physique. En plus de l’examen des matériaux, après la construction mathématique, l’analyse dimensionnelle de l’équation a été effectuée pour vérifier la conservation des unités et leur validité, ainsi que leur réponse positive ou négative aux postulats des lois de Fick et de Graham pour la description du processus de diffusion, sur la base de graphiques basés sur des données expérimentales et hypothétiques , afin de comparer les graphiques créés à partir des relations mathématiques. Les connaissances utilisées seront exposées ci-dessous :

2.2 DÉVELOPPEMENT BIOLOGIQUE

Les cellules sont organisées en trois parties: la membrane plasmique, le cytoplasme et le noyau. L’un des axes de ce travail académique réside dans la compréhension du compartiment primaire, la membrane cellulaire, avec environ 8 nanomètres (nm) ou 8 x 10^-9 mètres (m), observable par la lumière du microscope électronique. La membrane n’est pas entièrement perméable, constituée de sa fonction principale, étant une barrea sélective qui permet la séparation, ainsi que l’échange de substances entre les milieux extra et intracellulaires (JUNQUEIRA et CARNEIRO, 2012).

Cependant, sa perméabilité sélective est due à la composition chimique-structurelle des membranes cellulaires, étant composée d’une bicouche de phospholipides, de protéines et de glucides. Les phospholipides sont des tissus ampyphiles, c’est-à-dire contenant des parties polaires et non polaires, la tête hydrophile (phosphate radical) fait face à l’extérieur de la cellule formant une interaction électrostatique avec les molécules polaires de l’eau. Sa région hydrophobe est constituée de ses longues chaînes apolaires d’acides gras qui peuvent facilement interagir avec d’autres substances liposolubles, dont il est plus avantageux d’avoir sa queue face à la région intracellulaire. Ainsi, toutes les substances ne sont pas capables de traverser la membrane cellulaire et d’entrer dans la cellule par simple diffusion, cependant, un tel transport de diffusion est facilité par le transport ou la fabrication de protéines ioniques lorsqu’elles sont ouvertes (ALBERTS, 2009).

2.3 DÉVELOPPEMENT CHIMIQUE

Selon Taiz et Zeiger (2006), la diffusion est un phénomène de transport de la matière, dans lequel il y a un flux de particules des régions à concentrations plus élevées vers les régions à plus faibles concentrations, dans le but de promouvoir l’état d’équilibre ou aussi appelé homéomérase. La description mathématique d’un tel processus est exprimée par la première loi de Fick, proposée par le médecin et physiologiste Adolf Eugen Fick (1829 -1901), une équation différentielle dans laquelle la densité d’écoulement (J) est directement proportionnelle au gradient de concentration (  ), et le coefficient de diffusion (D) qui dépend de l’élément chimique à l’étude, tel qu’exprimé ci-dessous (voir équation 2.1):

Ce flux homogénéisant est une conséquence statistique du mouvement aléatoire des particules, connu sous le nom de mouvement brownien, les molécules se déplacent spontanément des régions hypertoniques (Concentrations Plus Élevées) vers les régions hypotoniques (Concentrations Plus Faibles). Le signe négatif dans la loi de Fick indique que l’écoulement se produit dans la direction opposée au gradient de concentration, étant une loi linéaire, peu importe combien la différence de concentration entre deux points est, l’écoulement reste proportionnel au gradient.

D’autres détails importants sur la loi de Fick sont les suivants: Relation directement proportionnelle à l’aire de diffusion (A) et inversement proportionnelle entre la taille des particules et la vitesse de diffusion, ou sa masse moléculaire (M). C’est-à-dire que plus la superficie est grande, plus les frais de transport sont élevés; de plus, plus la masse moléculaire de la particule est faible, plus son taux de transport est élevé et plus sa vitesse de diffusion sera rapide.

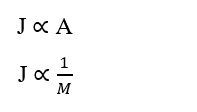
Selon Brady et Huminston (1995), la loi de Graham (voir équation 2.2), formulée par le chimiste Thomas Graham (1805 -1869) après ses études sur la diffusion et l’épanchement des fluides, établit que l’effusion et la vitesse de diffusion (u) de deux gaz (δ1) et (δ2), dans les mêmes conditions de température et de pression, sont inversement proportionnelles à la racine carrée de ses densités (d) ou masse moléculaire (MM), telles qu’exprimées ci-dessous:

ou alors

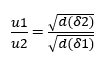
ou alors

 

 

2.4 DÉVELOPPEMENT PHYSIQUE

L’un des concepts fondamentaux de cet article est le célèbre « Principe fondamental de la dynamique » ou « 2ème loi de Newton », qui stipule: La force résultante qui agit sous un corps, est le produit de sa masse par accélération (F_R = m. a). Halliday (2016) déclare qu’il doit d’abord choisir le corps que l’on souhaite étudier, et appliquer la force résultante comme la somme de toutes les forces qui agissent dans le corps en question.

Selon Tipler (2009), le travail (W) est l’énergie transférée à un objet par une force qui agit sur l’objet lui-même. Pour calculer le travail qu’une force effectue sur un objet lorsqu’il subit un décalage, nous utilisons uniquement le composant de force parallèle au décalage de l’objet, le composant de force perpendiculaire au décalage n’effectue pas de travail. Le travail (W) d’une force constante, en fonction des forces parallèles (θ = 0°, 180°), peut être décrit à travers cette équation:

W = F. d. cosθ

Comment; [ Cos(0°, 180°) = 1 ] on peut réécrire l’équation du travail sous forme intégrale ou en fonction de la variation d’une distance ΔX (voir équation 2.3), nous avons:

Selon Halliday (2016), l’énergie est un concept difficile à définir. Cependant, nous comprenons intuitivement ce qu’est l’énergie, en analysant les effets sous les différentes formes de celle-ci, telles que: l’énergie cinétique et les énergies potentielles. Conceptuellement pour Tipler (2009), l’énergie cinétique est associée à tous les corps qui ont de la masse et qui sont en mouvement. Soit (m) la masse d’un point matériau et (u) sa vitesse scalaire, par rapport à une référence donnée. L’énergie cinétique du point de matière est donnée par (voir équation 2.4):

Pour uniformément varié mouvement, le travail de la force résultante par le corps ainsi que la variation d’énergie cinétique du corps lui-même. À partir du théorème travail-énergie (W = ΔK), nous pouvons obtenir l’expression qui est égale au travail d’une force constante (W), avec la variation d’énergie cinétique (ΔK), comme démontré par les équations (2.5) et (2.6):

Le mouvement uniformément varié, selon Marques (2016), est celui dans lequel une particule change de vitesse (u₀₎en une autre (u) en raison d’une force constante qui favorise une accélération (a) également constante, produisant également un déplacement (ΔX). Ce type de mouvement peut être assimilé sans tenir compte du temps, ce que l’on appelle « l’équation de Torricelli » (2.7):

Selon Pimentel (2004), la force motrice des processus diffusifs en milieu liquide cellulaire, est le soi-disant potentiel chimique de toute solution, qui est configuré comme la capacité d’une telle solution à effectuer des travaux sous les particules dissoutes, par rapport au gradient de concentration, une formulation pour le potentiel chimique maximal de l’eau serait (2.8):

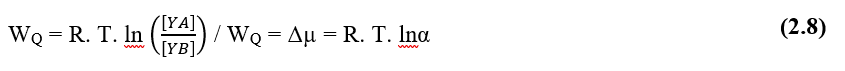
W_Q – Potentiel chimique de la solution (J)

R – Constante générale des gaz (R = 8,31 J Mol^-1 K^-1)

T – Température absolue (K)

[ Y_A ] – Concentration de la substance Y au point A (Mol)

[ Y_B ] – Concentration de la substance Y au point B (Mol)

α – Activité chimique

3. RÉSULTATS ET DISCUSSIONS

3.1 DÉVELOPPEMENT DE L’ÉQUATION DE NATHAN

Pour tenter de décrire mathématiquement le processus de diffusion et de transport des ions via les canaux ioniques dans la membrane plasmique, en fonction du gradient de concentration et du champ électrique générés aux extrémités extracellulaire et intracellulaire de la membrane, considérons un x, y et  z, le système de coordonnées dans lequel chaque axe représente son accélération respective générée par les forces agissant sur le système isolé à l’étude (a_x, a_y et a_z), comme le montre la figure 1.

 Figure 1 : système de coordonnées (X, Y, Z).

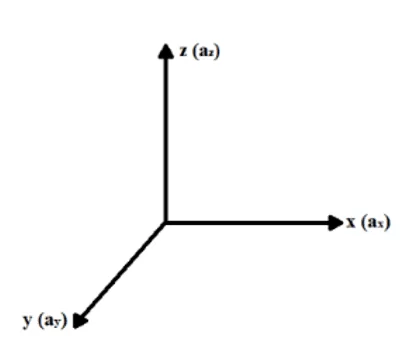
Selon Halliday (2016), la force résultante agissant sur une particule sous forme d’ions, qui traversent la membrane via des canaux ioniques, peut être décomposée en ses composants dans chaque axe x, y et z, étant directement associée aux accélérations dans les axes respectifs. Grâce au principe fondamental de la dynamique ou deuxième loi de Newton et au principe de chevauchement des forces de Newton, on peut obtenir une analyse physique des forces résultantes sur chaque axe qui exercent une influence sur l’ion (voir l’équation 3.1) :

F_R  – Force totale résultante (N – Kg m s^-2)

F_R(X) – Force résultante sur l’axe X (N – Kg m s^-2)

F_R(Y) – Force résultante sur l’axe Y (N – Kg m s^-2)

F_R(Z) – Force résultante sur l’axe Z (N – Kg m s^-2)

 

Les masses des ions sont conservées, de sorte que les facteurs directement proportionnels aux forces dans chaque direction sont leurs accélérations dans les directions respectives :

F_R(X) = m . a_x / F_R(Y) = m . a_y / F_R(Z) = m . a_z

Comparaison des constantes électrostatiques et gravitationnelles (k = 9 x 10⁹  et G = 6,67 x 10^-11 ), selon Halliday ³ (2016) de telles valeurs démontrent que la force gravitationnelle est beaucoup plus faible que la force électrique. Par conséquent, dans un système isolé de particules dans lequel seules les forces gravitationnelles et électriques sont considérées comme agissant, la force gravitationnelle peut être négligée, car la force électrique est environ 1,5 x 10²⁰ fois supérieure à la force pondérale. Comme l’accélération de la pesanteur sur la particule sera ignorée, la force sur la composante Z sera également nulle puisque l’accélération az sera ignorée, nous reformulerons l’équation pour l’étude donnée :

F_R = m . a_x + m . a_y + m . a_z

F_R = m . a_x + m . a_y + m . 0

F_R = m . a_x + m . a_y

En considérant comme forces agissant principalement celles qui influencent l’axe X, en ignorant les chocs mécaniques et toute autre force dans la composante y, puisque l’ensemble des solutés se déplace dans le sens de l’homogénéisation, des régions hypertoniques aux régions hypotoniques, nous atteindrons une telle simplification de la Force résultante :

F_R = m . a_x + m . 0

F_R = m . a_x

Un autre point à noter est que le système à l’étude sera considéré comme stationnaire ou permanent, dans lequel ses propriétés sont inaltérables par rapport au temps. Cela implique que toute propriété P du système, la dérivée partielle par rapport au temps est nulle, en considérant un système dans lequel le temps variable n’est pas un paramètre dans l’étude du système membranaire en question.

Les membranes cellulaires ont une certaine disposition, analogue au champ électrique uniforme, de sorte qu’il y a la concentration de charges positives principalement du côté extracellulaire, et une accumulation de charges négatives du côté intracellulaire. Il existe également une différence de concentration entre les extrémités externe et interne des cellules (C_E et C_I), dans laquelle le système exerce une force motrice pour favoriser la translocation des particules à travers les canaux ioniques des membranes cellulaires, comme représenté par la figure 2.

Figure 2 : Représentation du déplacement des ions via un canal ionique.

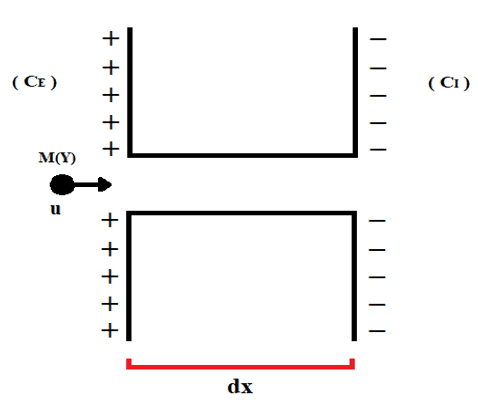
La distance parcourue par la molécule représentée est équivalente à l’élément de déplacement (dx), qui est aussi l’épaisseur de la membrane cellulaire déjà évoquée. La première loi de Fick peut être décrite en fonction du gradient de concentration total (∇D) et de la constante de diffusion (D), comme exprimé ci-dessous (voir équation 3.2) :

Cependant, nous ne considérerons que l’élément de longueur (∂x) déjà mentionné, afin d’évaluer le mouvement unidimensionnel des solutés à partir de régions à forte concentration, pour des concentrations plus faibles. Par conséquent, les gradients de concentration ( et ) seront retirés de l’équation, dont nous revenons à l’équation 2.1:

En isolant l’élément (∂x) de la Première Loi de Fick, on obtient :

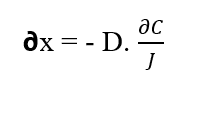
Les particules de soluté se déplacent le long d’un déplacement (?x) dû à la force provenant du Potentiel Chimique du système (W_Q), car selon la 2ème Loi de la Thermodynamique décrite par Tipler (2009), le flux de matière ou d’énergie commence à partir de les régions ayant les valeurs les plus élevées de matière ou d’énergie aux plus faibles. Si les particules sont soumises à des forces et à cause de cela elles se déplacent d’un certain élément de distance (?x), on peut supposer que de tels corps effectuent un travail (W), qui est décrit par l’équation suivante (voir équation 2.3) :

Le travail d’une force constante peut également être décrit comme une fonction de la variation d’énergie cinétique du système (ΔK), telle qu’exprimée par le théorème d’énergie cinétique (voir équation 2.5):

Compte tenu du mouvement unidimensionnel des particules dissoutes en solution, à un certain moment initial, les particules par rapport à un certain élément (∂x) ne se déplacent pas, de sorte que leur vitesse initiale (u₀) peut être considérée comme nulle, de sorte que le travail est décrit comme suit:

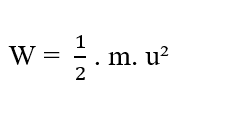
Pour un système dans lequel nous avons un nombre n de particules se propageant, chacune ayant une certaine masse (m(i)) et une certaine accélération (a(i)), nous avons que la force résultante dans les particules peut être exprimée comme étant:

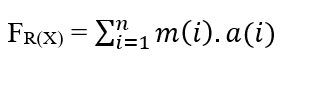
Puisque le système a une Force Constante, ce mouvement est également décrit avec une Accélération Constante pour toutes les particules selon un mouvement uniformément varié, ce qui permet de supprimer l’Accélération de la Sommation, des propriétés des Somators :

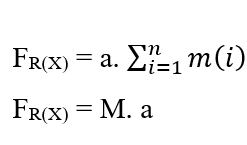
Pour atteindre l’équation de Nathan, les deux équations du Travail sont égalisées, et parce qu’il s’agit de traiter le mouvement des molécules comme démontré, la masse (m) est considérée comme la masse totale (M) d’une certaine quantité de molécules présentes dans le système à l’étude, et remplace également l’élément (dx) par (∂x) de la première loi de Fick.

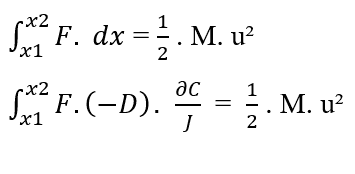
Sachant que (F, D, J) sont des constantes par rapport à l’élément (?C) à intégrer, de la propriété de la constante des intégrales, les termes peuvent être retirés de l’intégrale :

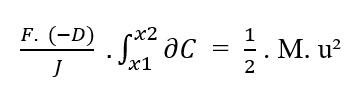
En réécrivant les limites d’intégration par rapport au (?C), nous avons:

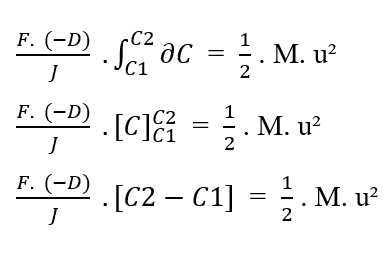
Sachant [C₂ – C₁ = ΔC] cela, vous pouvez remplacer la valeur dans l’équation :

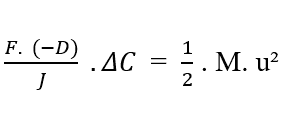
En isolant la densité d’écoulement variable (J), nous obtenons l’équation de Nathan (voir équation 3.3):

J – Densité d’écoulement (Mol m^-2 s^-1)

D – Coefficient de diffusion (m² s^-1)

C – Variation de la concentration (Mol m^-3)

F_R – Force résultante (Kg m s^-2)

M – Masse totale des particules diffusantes (Kg)

u – Taux de diffusion des particules (m s^-1)

 

3.2 ÉVALUATION MATHÉMATIQUE ET PHYSIQUE DE L’ÉQUATION DE NATHAN

Pour confirmer la validation de l’équation de Nathan de manière mathématique, il a été nécessaire d’effectuer l’analyse dimensionnelle décrite par Halliday (2016), dans laquelle il vérifiera si les unités de la première loi de Fick sont préservées et si les unités de l’équation de Nathan sont équivalentes. L’analyse dimensionnelle est un outil utilisé en physique pour déterminer l’unité de mesure d’une certaine ampleur. L’analyse dimensionnelle est un outil qui permet la prédiction, l’inspection et l’adaptation des unités physiques utilisées pour la résolution des équations.

 

La loi de Fick :

J – (Mol m^-2 s^-1)

L’équation de Nathan :

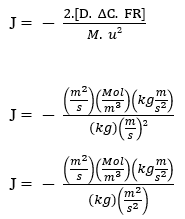
J – (Mol m^-2 s^-1)

Généralement, les grandeurs physiques fondamentales sont exprimées par : Longueur (L), Masse (M), Temps (T), Température (θ), Courant électrique (A), Quantité de matière (Mol) et Intensité lumineuse (I). L’analyse dimensionnelle de l’équation de Nathan (3.3) peut alors être effectuée à l’aide de telles représentations de grandeurs physiques fondamentales, selon l’équivalent de chaque variable dans la formulation exposée, comme le souligne Marques (2016).

J – Densité d’écoulement (Mol L^-2 T^-1)

D – Coefficient de diffusion^{(L2 T-1})

ΔC – Variation de concentration (Mol L^-3)

F_R – Force résultante (M L T^-2)

m – Masse totale des particules difitantes (M)

u – Vitesse de diffusion des particules (L^T-1)

Maintenant, en effectuant une analyse dimensionnelle avec les représentations générales des quantités physiques fondamentales, nous avons:

La loi de Fick :

J – (Mol L^-2 T^-1)

L’équation de Nathan :

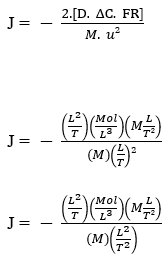
J – (Mol L^-2 T^-1)

 

L’équation de Nathan démontre la conservation des unités, ainsi que suit certaines déclarations que la première loi de Fick et la loi de Graham démontrent, afin de relier certaines variables de manière directe ou inversement proportionnelle, validant physiquement une telle formulation mathématique pour le processus de diffusion, indépendamment des unités choisies pour les quantités fondamentales, à condition qu’elles aient une cohérence en général.

La première relation que montre l’équation de Nathan est la relation directement proportionnelle entre la densité d’écoulement (J) et la variation de concentration entre deux points (ΔC). En établissant que, une augmentation de la différence de concentration entre deux points quelconques du système, sera directement liée à l’augmentation de la densité d’écoulement de la même, Une telle relation obéit à la loi de Fick.

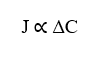
La deuxième relation importante est la proportionnalité directe entre la densité d’écoulement (J) et la force résultante (F_R) agissant sur les particules (γ) qui composent le système en question. Cela implique qu’une augmentation de la variable Force résultante qui agit sous les molécules qui diffusent, augmentera également directement proportionnellement le flux de particules.

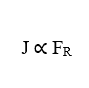
La troisième relation importante est la proportionnalité inverse entre la densité de flux (J) et la masse totale de tout élément gamma (γ), qui constituent le système à l’étude. Ceci implique que, considérant pour chaque molécule et seulement sa Masse Moléculaire, plus la Masse Moléculaire de l’élément à diffuser est importante, plus son Taux de Transport sera faible.Cette relation obéit à la Loi de Fick et à la Loi de Graham.

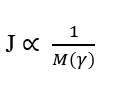
La quatrième relation importante est la proportionnalité inverse entre la masse moléculaire (M) et la vitesse de diffusion carrée (u). Ou il peut être compris comme la relation inverse entre la vitesse de diffusion et la racine carrée de la masse moléculaire de l’élément (γ). Cette relation obéit à la loi d’effusion et de diffusion des gaz de Graham, montrant la corrélation de la vitesse à l’inverse de la racine carrée de la masse moléculaire.

La densité d’écoulement (J) est inversement proportionnelle au produit entre la masse moléculaire (M) – lorsque pour une particule – et la vitesse de diffusion carrée (u) :

 

Si (J) est constant (K), on a :

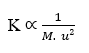
En isolant la variable Taux de diffusion (u), on arrive à :

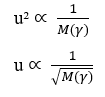
A partir du logiciel Excel version 2016, il a également été possible d’effectuer la modélisation graphique de 20 données hypothétiques pour la valeur de la masse moléculaire (M), avec un intervalle de (0 < M < 21) en ordre croissant, corrélé à sa valeur respective de Vitesse de diffusion (u), sachant que la vitesse de diffusion d’un élément donné est inversement proportionnelle à la racine carrée de sa masse respective, comme le montrent la loi de Graham et l’équation de Nathan lorsque le taux de transport (J) est maintenu constant et ne considère que la masse d’une seule particule. Ainsi, on peut voir la similitude des graphes construits plus tard avec de telles données (voir Graph 1).

Graphique 1 : Vitesse de diffusion par rapport à l’inverse de la racine carrée de la masse moléculaire.

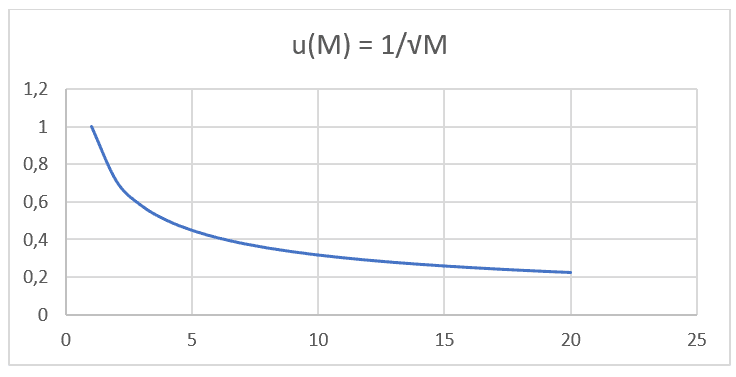
On remarque que les deux formulations, la loi de Graham et l’équation de Nathan, ont une proportionnalité égale et sont basées sur le même type de fonction : F(x) =     . En effectuant une projection graphique avec des valeurs de masse moléculaire, des données IUPAC et sa vitesse de diffusion respective de 20 gaz différents aux mêmes pressions et températures répertoriées dans le tableau suivant (voir tableau 1), vous pouvez projeter un deuxième graphique (voir graphique 2).

Tableau 1 : Masses moléculaires et leurs vitesses de diffusion respectives.

gaz	Masse moléculaire (g/mol)	Vitesse de diffusion (cm/s)
H2	2	0,7
He	4	0,5
O2	16	0,25
CH4	16	0,25
Ne	20	0,22
H2S	34	0,17
Ar	40	0,15
CO2	44	0,15
NO2	46	0,14
O3	48	0,13
C4H10	58	0,12
NO3	63	0,12
SO2	64	0,12
CS2	76	0,11
SO3	80	0,11
Kr	84	0,10
FeS	88	0,10
Xe	131	0,08
PCl3	137	0,08
Rb	222	0,06

Source: L’auteur.

Graphique 2 : Vitesse de diffusion par rapport à l’inverse de la racine carrée de la masse moléculaire.

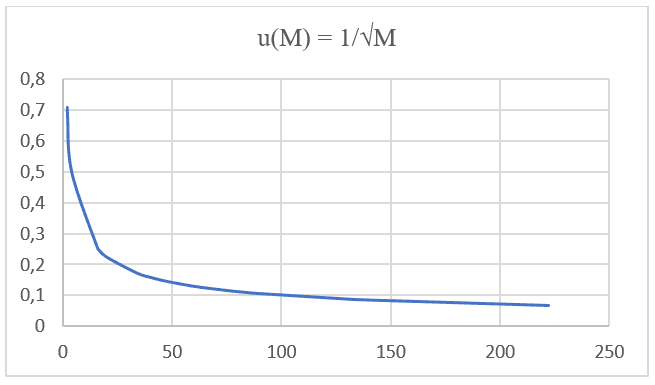
Selon Zeiger et Taiz (2006), le temps de diffusion moyen peut être défini comme le rapportentre le carré de la variation de distance (ΔX²) et le coefficient de diffusion de l’élément (D), tel qu’exprimé par la formulation mathématique suivante (voir équation 3.4):

À partir de la définition de la vitesse scalaire moyenne (u) de la cinématique et en remplaçant la valeur temporelle par la variable Temps moyen (T_M),nous obtenons:

 

ou alors

 

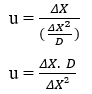
En effectuant les manipulations algébriques, l’équation pour calculer le taux de diffusion (u) de n’importe quel élément peut être obtenue :

En remplaçant (3.5) dans l’équation de Nathan (3.3), on peut obtenir la relation entre le carré de la Variation de Distance (ΔX) et la Variation de Concentration (ΔC).

En effectuant l’analyse dimensionnelle de l’équation (3.6) pour confirmer la conservation des unités de la loi de Fick, nous avons:

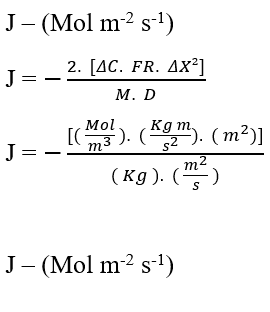
Validé la conservation des unités à partir de l’analyse dimensionnelle, on peut percevoir une relation importante et commune dans l’équation de Nathan et la loi de Fick, c’est la proportionnalité inverse entre la variation de concentration (ΔC), et le carré de la variation de distance (ΔX²). Pour que cette déclaration soit valide, nous considérerons le taux de transport (J) comme constant et n’analyserons que ces deux variables: variation de la concentration et distance.

 

En considérant que la densité d’écoulement (J) est constante, on a :

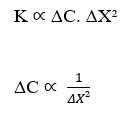
La proportionnalité inverse entre la variation de concentration (ΔC) et le carré de la variation de distance (ΔX²) est démontrée. Cet énoncé est en accord avec la loi de Fick, car lors de l’analyse de la corrélation entre ces deux variables, les deux formulations, l’équation de Nathan et la loi de Fick, décrivent le même graphe qui suit la fonction: F(x) = . Voici une démonstration du format graphique (courbe gaussienne), variation de concentration par rapport à variation carrée de distance (voir figure 3) :

Figure 3 : Variation graphique de la concentration par rapport au carré de la variation de distance.

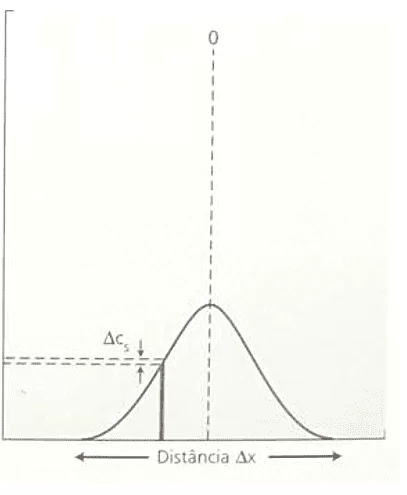
Pour le cas d’avoir seulement comme variable déterminante dans le processus de diffusion d’un élément donné, la variation de concentration (ΔC), en supposant alors qu’il s’agit d’un mouvement de particules à vitesse constante et non d’un mouvement uniformément varié causé par une force constante , il suffit de remplacer (2.7) en (3.3), l’équation de Torricelli, qui renverra la description mathématique connue sous le nom de : 1ère loi de Fick.

En remplaçant (2.7) dans (3.3) compte tenu de la vitesse initiale (u₀₎nulle, nous avons:

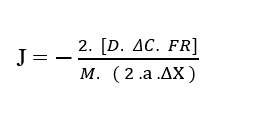
En annulant les termes Force résultante (F_R),avec les termes du dénominateur Masse totale des particules (M) et Accélération (a), ainsi que les constantes dans le numérateur et le dénominateur (2), on obtient à nouveau la formulation linéaire : la première loi de Fick (2.1).

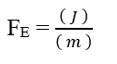
3.3 DEVELOPPEMENT DE L’EQUATION DE NATHAN POUR L’ELECTRODIFFUSION DANS LES MEMBRANES CELLULAIRES

L’équation de Nathan peut être étendue pour décrire le processus de diffusion des ions via la membrane cellulaire, mathématiquement, en tenant compte des formulations mathématiques suivantes. Selon Pimentel (2004), la force motrice des processus diffusifs dans les systèmes biologiques est ce que l’on appelle le potentiel chimique du système, et dans le cas de l’exemple en question, le transfert de matière d’un point A à un autre B se produit, ce potentiel chimique peut être exprimé à partir de l’équation suivante (2.8):

Cela implique de dire qu’un soluté se déplacera d’une région à potentiel chimique plus élevé vers une région plus petite, ou dans le cas de solvants tels que l’eau, de l’osmose se déplacera des régions à plus faibles concentrations de soluté vers des régions plus grandes. Cependant, le flux de particules cesse lorsque les potentiels chimiques des deux phases sont égaux, obtenant ainsi l’état final d’équilibre (HENEINE, 2004).

Un tel potentiel de solution qui produit la force résultante du système, car il représente la capacité d’un système donné à effectuer un travail, peut être décrit en tenant compte de la contribution d’autres facteurs importants, tels que: l’action gravitationnelle et l’influence électrique sur les particules en raison de leurs charges et de la différence de potentiel électrique. Ainsi, l’équation du potentiel maximal peut être exprimée par la formulation du potentiel électrochimique, ci-dessous (voir équation 3.7):

Dans le cas où la contribution du potentiel gravitationnel (m.g.h) est ignorée, l’équation ne sera réduite qu’à la contribution chimique et électrique, ce sont les forces qui travaillent dans l’ensemble des particules ioniques pour se déplacer à travers les canaux ioniques ou moléculaires à travers la bicouche lipidique, entrant dans l’environnement intracellulaire (ALBERTS, 2009).

L’équation de Nathan décrit le processus de diffusion, et le phénomène naturel du transport des ions via la membrane cellulaire peut être exprimé de la même manière par l’équation de Nathan, ne prenant comme force résultante (F_R) que le potentiel chimique de la solution et la contribution électrique, sans tenir compte de la contribution gravitationnelle.

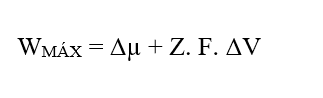
Sachant que (W = F_R. Δx), en remplaçant l’équation (2.3), on obtient :

En effectuant l’analyse dimensionnelle de la Force résultante (3.8), en la divisant en ses parties chimiques et électriques, il est possible de remarquer l’émergence non plus de l’unité d’énergie Joule (J), mais plutôt de l’unité Force dans le Système International de Mesures , le Newton (N) :

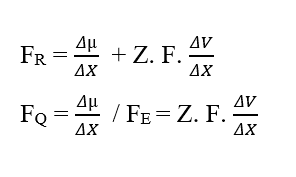
En analysant la portion de contribution chimique (F_Q), nous avons :

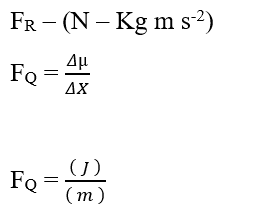
Sachant que l’unité d’énergie Joule (J – N.m) peut être remplacée en analyse dimensionnelle, obtenant :

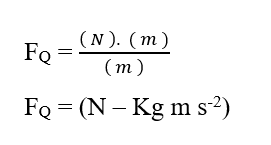
En analysant la portion de contribution électrique (F_E), on a :

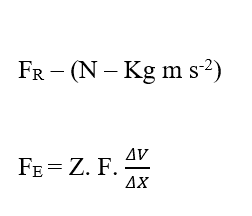
Sachant que Valence (Z) est une variable dimensionnelle, nous avons :

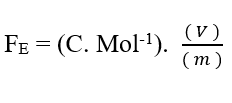
Sachant que l’unité de tension Volt (V – J. C^-1), elle peut être substituée dans l’analyse dimensionnelle, en obtenant :

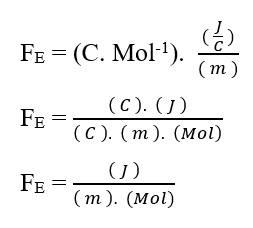
Comme l’unité Mol est considérée comme adimensionnelle, car elle n’est liée qu’aux entités qui composent un système donné, telles que: atomes, molécules, ions ou électrons; nous pouvons ignorer une telle unité dans l’analyse, en la simplifiant:

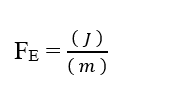
Sachant que l’unité d’énergie Joule (J – N.m) peut être remplacée en analyse dimensionnelle, obtenant :

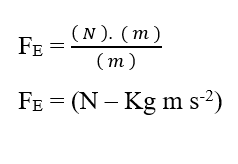
L’analyse dimensionnelle des deux graphiques, chimique et électrique, qui constituent la force résultante (F_R) du système à l’étude, il est démontré qu’elle est valable pour le calcul de cette force. En écrivant les rapports entre la variation du potentiel chimique (Δμ) et la variation de distance (ΔX), la variation du potentiel électrique (ΔV) et la variation de distance (ΔX), sous la forme de limites de (ΔX 0) puis sous forme différentielle, ayant la force instantanée résultante, on obtient:

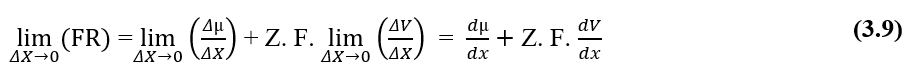
Pour une situation dans laquelle les potentiels électrochimiques de deux phases (A) et (B) d’un système donné sont les mêmes, c’est-à-dire que dans une situation d’équilibre, la valeur de la variation du potentiel électrique aux extrémités des membranes cellulaires peut être établie, ce qui fait référence à l’équation de Nernst.

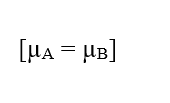
Si les potentiels sont les mêmes, cette déclaration indique que le travail effectué par les particules est nul, de sorte que la force résultante dans celles-ci sera également nulle, car il n’y a pas de transit de molécules entre les deux phases du système:

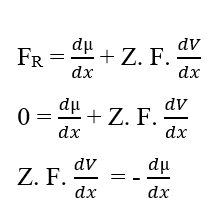
Vous pouvez annuler les éléments (dx) qui apparaissent des deux côtés de l’égalité et isoler le terme (dV), puis réécrire en fonction des variations, ce qui se traduit par :

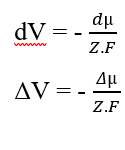
En remplacement du potentiel chimique (2.3), nous avons rétabli le calcul du potentiel électrique pour une situation d’équilibre dans les systèmes biologiques (3.10), connu sous le nom d’équation de Nernst (HENEINE, 2004).

Vous pouvez remplacer la force résultante du système (3.9) dans l’équation de Nathan décrite ci-dessus (voir l’équation 3.3) :

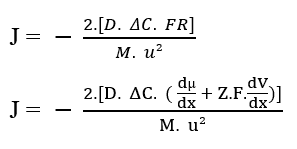
Outre les termes entre parenthèses, nous avons l’équation de Nathan pour l’électrodiffusion dans les membranes cellulaires (3.11):

J – Débit de transport ou densité de débit d’ions dans la membrane (Mol m^-2 s^-1)

D – Coefficient de diffusion soluté (m² s^-1)

ΔC – Variation de concentration (Mol m^-3)

m – Masse totale des particules difitantes (kg)

u² – Vitesse de diffusion des particules (m s^-1)

Z – Ion Valence

F – Constante de Faraday (F = 9,648 x 10⁴ C mol^-1)

?µ/?x- Dérivé du potentiel chimique par rapport à dx (Kg m s^-2)

?V/?x  – Dérivé du potentiel électrique par rapport à dx (V m^-1)

Selon Halliday (2016) pour la thermodynamique, l’énergie interne (U) ou la variation d’énergie interne (ΔU), c’est la somme des énergies cinétiques et potentielles de toutes les molécules qu’un système contient. Cette relation peut être exprimée, avec la description mathématique suivante (voir équation 3.12), en considérant la vitesse moyenne pour toutes les particules constantes:

[M – Masse totale des particules du système]

 

 

En remplaçant l’équation (3.13), dans l’équation de Nathan (3.3), un terme constant peut être déterminé, appelé par l’auteur avec la lettre grecque omega (ω):

Si nous considérons maintenant la raison comme n’importe quelle constante (ω), puisque les valeurs de ces variables ne changent pas par rapport au temps, puisque la dérivée partielle de tout terme est nulle . Sachant que (ω) se présente comme une unité , un rapport entre la quantité de matière concentrée et l’énergie interne d’un système, une telle relation est équivalente à l’expression suivante (3.15) :

Et sachant que le colis  se réfère à la Force résultante du système (FR), on peut encore réécrire cette formulation sous sa forme générale (3.15) :

 

Il est maintenant possible de noter que, comme les termes (D) et (ω) sont constants, la Densité de Flux (J) est directement proportionnelle à la Force résultante du système (F_R), ce qui implique que s’il y a une augmentation de l’une de ces variables, l’autre subira également une augmentation proportionnelle.

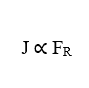
L’équation de Nathan pour l’électrodiffusion dans les membranes cellulaires décrit le flux d’ions à travers la membrane, via les canaux ioniques lorsqu’ils sont ouverts, influencé par le gradient de concentration des milieux extracellulaire et intracellulaire, ainsi que le potentiel électrique ou le champ électrique sous les ions, généré par la membrane cellulaire elle-même. Cette formulation prend en compte la masse particulaire totale de l’élément qui va diffuser, les forces motrices chimiques et électriques présentes dans le phénomène de transport ionique via la membrane cellulaire, cependant, s’il existe d’autres facteurs externes, dus à l’augmentation de la Variable de force, l’analyse peut être effectuée dans un cadre généralisé, en plus d’être en accord avec les concepts physiques existants et présentés.

4. CONSIDÉRATIONS FINALES

Dans une déclaration, cet article proposait la formulation de l’«équation de Nathan », comme une extension de la 1ère loi de Fick, qui décrit le flux diffusif de particules dans les solutions, dû non seulement à la différence de concentration (ΔC), mais dans le but de considérer la densité d’écoulement de matière (J) en fonction de la force résultante constante (F_R) agissant sur les particules d’un système donné (voir équation 3.3).

Une telle formulation a démontré la proportionnalité directe entre la force agissant sur les particules et la densité de flux (J), par conséquent, plus la force exercée sur le système est grande, plus le transport de matière est important. La même description mathématique des processus naturels de diffusion des molécules, qui permet une analyse générale de toutes les forces pouvant influencer certains systèmes à l’étude, peut également être étendue pour expliquer le transport des ions via la membrane cellulaire, lorsque la force résultante sous les particules du système en question prend en compte le potentiel chimique et le potentiel électrique, ainsi qu’une relation entre la quantité de matière concentrée et l’énergie interne d’un système (ω), qui a été appelée par l’auteur « équation de Nathan pour l’électrodiffusion dans le Membranes Cellulars » (voir équation 3.11), ou encore dans sa formulation générale (voir équation 3.15).

La validation des équations a été évaluée à partir d’une analyse dimensionnelle et de relations directes et inversement proportionnelles entre les variables, par rapport aux postulats proposés par la 1ère loi de Fick et la loi de Graham, sous la forme de graphiques avec des courbes décrites par certaines fonctions qui démontrent les proportionnalités existant entre: Vitesse de diffusion par rapport à la masse moléculaire d’un élément (voir graphique 1) et la variation de concentration par rapport au carré de la variation de distance (voir le graphique 3); se montrant comme une formulation valide physiquement et mathématiquement pour une telle description du phénomène naturel, parce que les unités de la loi de Fick sont conservées dans l’équation de Nathan, et correspondent si positivement en ce qui concerne les propositions de ces lois physicochimiques déjà établies et leurs représentations graphiques, suivant les proportionnalités décrites par certaines fonctions présentées précédemment. Les prochains articles d’expériences physiques ou avec des logiciels de modélisation spécifiques, peuvent évaluer la praticité et la cohérence de l’équation de Nathan avec la réalité naturelle, en se référant à l’étude du phénomène de diffusion, afin d’analyser la précision et la généralité des concepts soulevés par celui-ci.

 

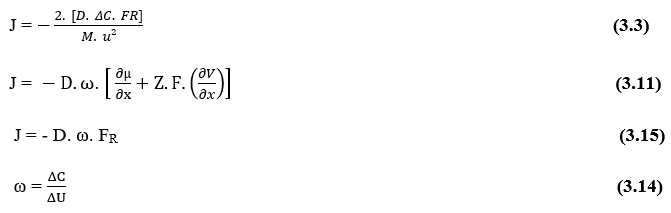
RÉFÉRENCES BIBLIOGRAPHIQUES

ALBERTS, Bruce et al. Biologia Molecular da Célula, 5° Edição. Editora: ARTMED, 2010, 1728 p., Vol. 1. ISBN: 978-85-363-2170-7.

BRADY, James; HUMISTON, Gerard. Química Geral, 2° Edição. Editora: LTC, 1995, 404 p., Vol. 1. ISBN: 9788521604495.

DA SILVA, Raissa. Difusão de Gases em Membranas Densas Via Simulação Molecular. Instituto Alberto Luiz Coimbra de Pós-Graduação e Pesquisa na Engenharia (UFRJ), Data da Dissertação de Mestrado: Abril de 2013. Disponível em: http://portal.peq.coppe.ufrj.br/index.php/producao-academica/dissertacoes-de-mestrado/2013-1/47-difusao-de-gases-em-membranas-densas-via-simulacao. Acesso: 25/06/2020.

HENEINE, Ibrahim. Biofísica Básica, 2° Edição. Editora: ATHENEU, 2004, 381 p., Vol. 1. ISBN: 8573791225.

JUNQUEIRA, Luiz C.; CARNEIRO, Jóse. Biologia Celular e Molecular, 9° Edição. Editora: Guanabara Koogan, 2012, 376 p., Vol. 1. ISBN: 9788527720786.

MARQUES, Francisco Das Chagas. Física Mecânica, 1° Edição. Editora: Manole, 2016, 315 p., Vol. 1. ISBN: 9788520427743.

MOREIRA C., Catarina. Difusão Simples. Rev. Ciência Elem., V2(02):144. doi.org/10.24927/rce2014.144. Pulicado: 15 de Setembro de 2010. Disponível em: https://rce.casadasciencias.org/rceapp/art/2014/144/. Acesso: 22/06/2020.

PIMENTEL, Carlos. A Relação da Planta Com a Água, Local: EDUR – Editora Universidade Federal Rural do Rio de Janeiro. 2004, 190 p. ISBN: 85-85720-45-X

TAIZ, Lincoln; ZEIGER, Eduardo. Fisiologia Vegetal, 3° Edição. Editora: ARTMED, 2006, Vol. 1, 722 p. ISBN: 85-363-0291-7.

TIPLER, Paul; MOSCA, Gene. Física para Cientistas e Engenheiros – Mecânica, Ondas, Termodinâmica, 6° Edição. Editora: LTC, 2009, 788 p., Vol. 1. ISBN: 9788521617105.

WALKER, Jearl et al. Halliday & Resnick ¹: Fundamentos de Física – Mecânica, 10° Edição. Editora: LTC, 2016, 372 p., Vol. 1. ISBN-13: 978-8521630357.

WALKER, Jearl et al. Halliday & Resnick ²: Fundamentos de Física – Gravitação, Ondas, Termodinâmica, 10° Edição. Editora: LTC, 2016, 324 p., Vol. 1. ISBN-13: 978-8521630364.

WALKER, Jearl et al. Halliday & Resnick ³: Fundamentos de Física – Eletromagnetismo, 10° Edição. Editora: LTC, 2016, 408 p., Vol. 1. ISBN-13: 978-8521630371.

^[1] Graduation.

Soumis : Décembre 2020.

Approuvé : Avril 2021.