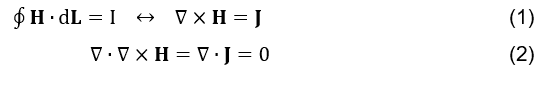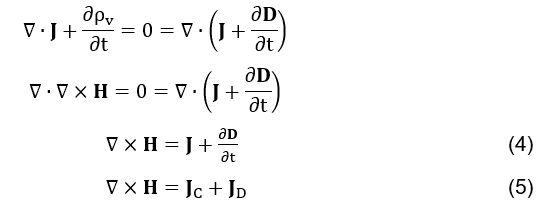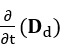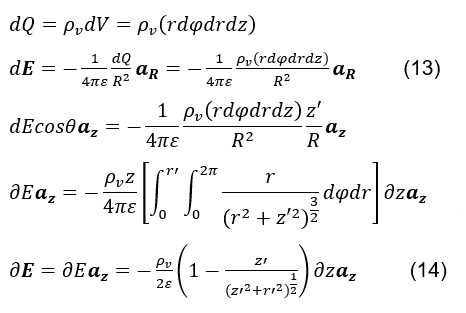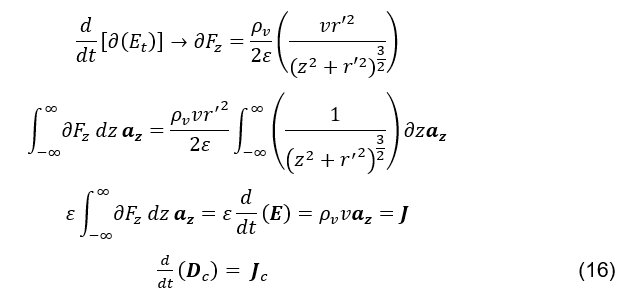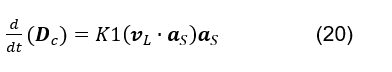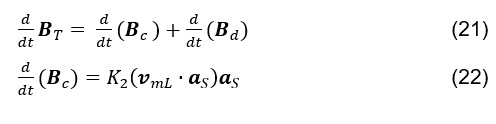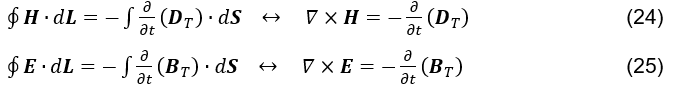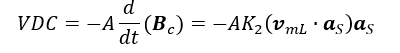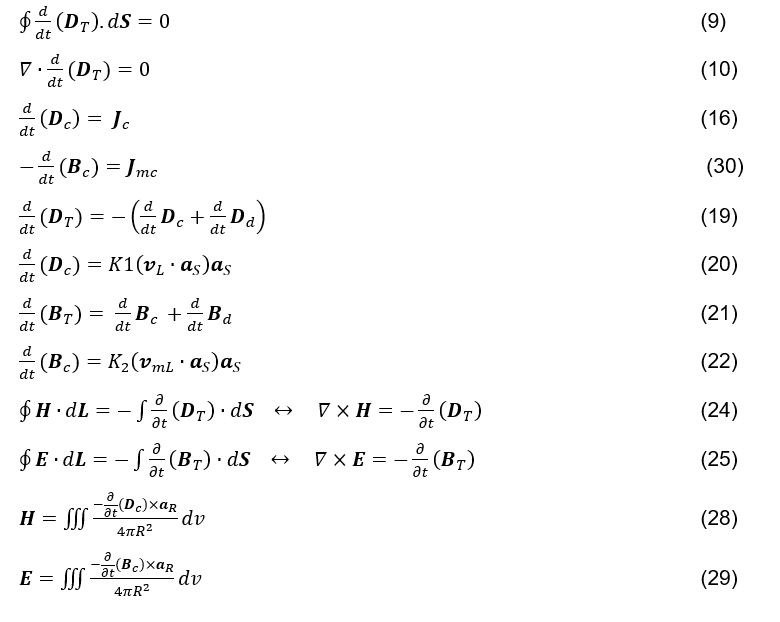ARTICLE ORIGINAL
LUCENA, Lucas Ruas de [1]
LUCENA, Lucas Ruas de. Une nouvelle perspective sur la densité du courant. Revista Científica Multidisciplinar Núcleo do Conhecimento. An 05, Ed. 08, vol. 03, p. 151 à 167. août 2020. ISSN: 2448-0959, Lien d’accès: https://www.nucleodoconhecimento.com.br/fisica-fr/densite-de-chaine, DOI: 10.32749/nucleodoconhecimento.com.br/fisica-fr/densite-de-chaine
RÉSUMÉ
Cet article traite de propositions alternatives et complémentaires aux lois de J.C.Maxwell de l’électromagnétisme classique, basées sur certaines hypothèses, exemples hypothétiques et calculs, avec des résultats qui peuvent déduire de nouvelles interprétations sur le phénomène physique conduction densité actuelle. Ces nouvelles interprétations apportent une nouvelle compréhension de la dynamique de la Loi de Gauss, et, étant vrai, rendent la loi Ampère-Maxwell totalement symétrique à la loi Faraday-Lenz-Maxwell, sans aucune incohérence mathématique ou physique. Ces compréhensions apportent inévitablement des implications et des points de vue complémentaires à la théorie classique de l’électromagnétisme.
Mots clés: Électromagnétisme, densité actuelle, équation de continuité.
1. INTRODUCTION
Premièrement, la solution donnée par J.C.Maxwell est présentée de manière à ce que l’équation d’Ampère (voir formule 1) devienne mathématiquement cohérente, en respectant l’identité vectorielle appliquée dans (voir formule 2) et en cohérence avec l’équation de continuité (voir formule 3).
Vous trouverez ci-dessous un exemple de l’application de la loi de Gauss (voir la formule 6) à une surface fermée autour de l’une des plaques d’un condensateur, figure 1.
Par hypothèse, il est proposé que la variation temporelle du flux électrique total, qui traverse la surface gaussienne totalement fermée, soit toujours égale à zéro. Par conséquent, la loi de Gauss (voir formule 6), appliquée aux situations dynamiques, deviendrait l’équation (voir formule 9). Pour que cette hypothèse soit fondée, il sera nécessaire qu’il y ait une variation temporelle de la densité du champ électrique, du même module, de la même direction et de la même direction de la densité actuelle, dans la zone d’intercession entre le volume cylindrique du conducteur et la surface gaussienne, pointant vers elle, figure 1.
Afin de vérifier la cohérence de cette hypothèse, un exemple idéal sera considéré dans lequel il y a un courant continu et homogène dans un fil cylindrique rectiligne infini le long de l’axe z. Ensuite, la variation temporelle vectorielle du champ électrique est calculée (voir formule 12) au point P(0,0,0) en raison du déplacement simultané et instantané de toutes les charges, en amont et en aval de P(0,0.0). Ce calcul aboutit à l’égalité (voir formule 16).
Enfin, à partir de la véracité physique de l’égalité (voir formule 16), il y a des implications inévitables, la mise en forme et les compléments théoriques pour les équations classiques de l’électromagnétisme, par Faraday, Lenz, Biot-Savart et Maxwell. À la fin, une expérience de laboratoire a été suggérée pour confirmer ou réfuter la théorie développée à partir de l’analyse de l’hypothèse proposée.
2. LES CHAÎNES DE DÉPLACEMENT ET DE CONDUITE
La police de circuit d’Ampère, dans sa forme ponctuelle (voir formule 1), présentait des insuffisances mathématiques (JACKSON et. al., 1998).
Le résultat de l’équation (voir formule 2) doit être nul, car la divergence du fait de rotation étant égal à zéro constitue une identité vectorielle. Cependant, l’équation de continuité (HAYT; BUCK et. al., 2013; SHADIKU, 2004),
est incompatible avec l’équation (voir formule 2). Cette correction a été faite avec brio par J.C.Maxwell, comme suit (JACKSON et. al., 1998):
Ainsi, l’équation d’Ampère (voir formule 1) est devenue complètement cohérente dans (voir formule 5). Tant physiquement, compte tenu de la génération du champ magnétique à partir de la variation temporelle de la densité du champ électrique, et mathématiquement, en ce qui concerne l’identité vectorielle citée dans l’équation (voir formule 2).
Le terme
ajouté dans l’équation (voir formule 4) a la même unité de densité actuelle, Amperes par mètre carré
, étant appelé par J.C.Maxwell de la densité de courant de déplacement, représenté par dans
l’équation (voir formule 5). L’identification de ce terme était d’une importance fondamentale pour comprendre la propagation des ondes électromagnétiques. Le terme
de l’équation (voir formule 5) fait référence à la densité de courant de conduction.
3. HYPOTHÈSE D’UNE APPLICATION DYNAMIQUE DE LA LOI GAUSS
La loi de Gauss, équation (voir formule 6), détermine que le débit total de densité de champ électrique qui traverse toute surface fermée est égal à la charge électrique totale qui est contenue dans cette surface. Maxwell l’a observé sous la forme ponctuelle, équation (voir formule 7), connue sous le nom de première équation de Maxwell (HAYT; BUCK et. al., 2013; SHADIKU, 2004).
Prenons le premier exemple, étant une surface fermée autour d’une des plaques d’un condensateur qui est chargée par une alimentation à tension variable, comme le montre la figure 1.
Figure 1. Surface gaussienne enfermée sur une plaque de condensateur
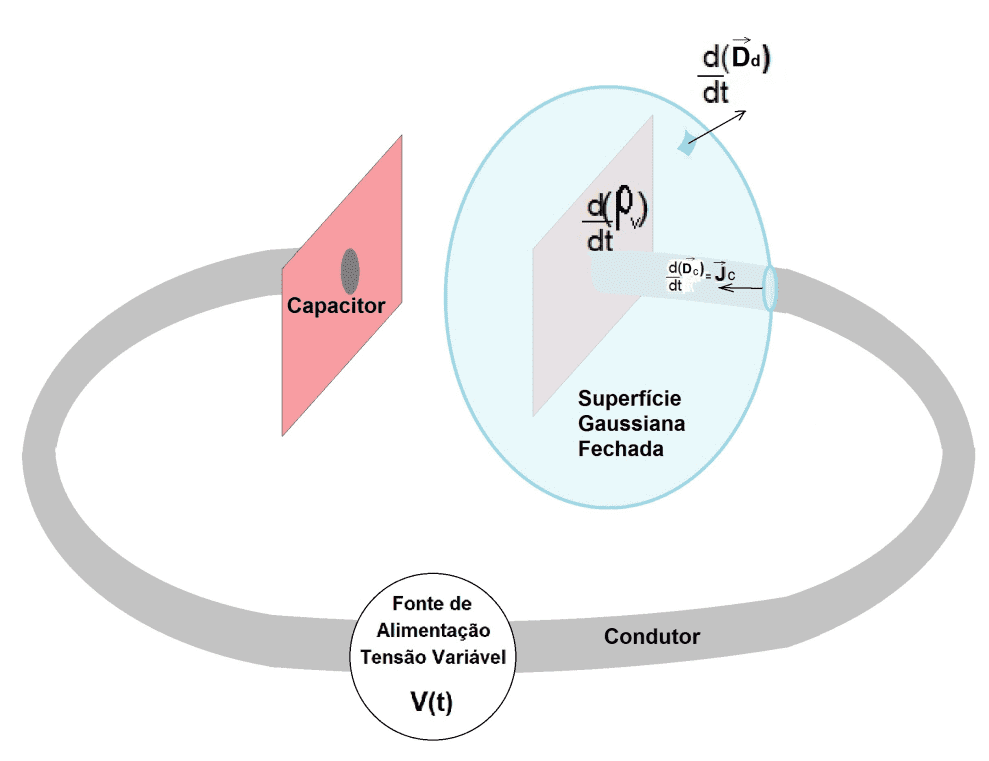
Observation de la figure 1, avec une densité de courant de conduction dans le conducteur,
les équations (voir formule 6) et (voir formule 7), respectivement : pour une surface gaussienne entièrement fermée; et pour un point sur la plaque de condensateur, ils deviennent des équations (voir formule 8) et (voir formule 3). (HAYT; BUCK et. al., 2013; SHADIKU, 2004).
L’équation (voir formule 8) détermine que la variation temporelle du flux total de densité du champ électrique qui traverse la surface gaussienne est égale à la variation temporelle de la charge électrique qui lui est contenue à l’intérieur.
L’équation de continuité (voir formule 3) appliquée à tout volume infinitésimal de la plaque de condensateur, chargée positivement, détermine que la densité de courant de conduction
, qui laisse ce volume donné, est égale à la vitesse de temps à laquelle la densité de charge volumétrique tombe sur elle.
L’hypothèse proposée dans cet article considère que les équations (voir formule 8) et (voir formule 3) sont physiquement complémentaires. Ainsi, on considère que pour une surface gauss entièrement fermée, autour d’une plaque de condensateur, dans des conditions dynamiques, les équations (voir formule 8) et (voir formule 3) auraient le format suivant.
Où
est la variation temporelle de la densité de champ électrique vectorielle générée par la densité du courant de conduction
, du même module, la direction et la direction de la même, sur la surface transversale de l’intersection entre le volume cylindrique du conducteur et le gaussien, pointant en elle. Et
c’est la variation temporelle de la densité vectorielle du champ électrique, dans la surface gaussienne fermée pointant hors de lui, générée par la densité de courant de déplacement
(variation temporelle du nombre de lignes de champ électriques qui traversent le Gaussien fermé en raison de la variation temporelle de la charge électrique totale de la plaque du condensateur interne au gaussien); (HAYT; BUCK et. al., 2013; SHADIKU, 2004). Figure 1.
Les équations (voir formule 9) et (voir formule 10) déterminent que la variation temporelle du flux total de densité de champ électrique sur toute surface gaussienne entièrement fermée est égale à zéro. L’équation (voir formule 10) ne contredit pas l’équation de continuité (voir formule 3), car elle relie le flux de charge électrique, d’un volume infinitésimal, à la variation temporelle de la densité volumétrique de la charge électrique, en elle; déjà cela, n’est lié qu’à la dynamique du champ électrique.
On suppose alors que le phénomène physique conduction densité de courant![]()
, génère une variation de la densité du champ électrique
à l’intersection du conducteur cylindrique avec la surface gaussienne, du même module, la direction et la direction du vecteur
. L’un des avantages de la vérification de cette hypothèse serait de comprendre l’équation d’Ampère-Maxwell (voir formule 4) dans le format suivant (voir formule 11).
Ainsi, il serait intuit que les interactions entre les champs, électriques ou magnétiques, et les particules chargées, seraient, tout d’abord, des interactions entre les champs seulement.
Dans la recherche pour vérifier la véracité de l’hypothèse proposée, un exemple d’une situation hypothétique idéale est créé pour le calcul de la variation temporelle vectorielle de la densité du champ électrique (voir formule 12), à l’origine, générée par un courant continu et homogène dans un conducteur cylindrique d’une longueur infinie le long de l’axe z.
4. EXEMPLE D’UNE SITUATION HYPOTHÉTIQUE IDÉALE
Supposons la configuration idéale suivante : dans un conducteur cylindrique, rectiligne, uniforme, homogène, d’une longueur infinie, qui traverse un courant direct, de charges positives, uniformes et homogènes dans la direction positive de l’axe z, figure 2.
Dans les coordonnées cylindriques, la variation temporelle du vecteur de champ électrique (voir formule 12) générée au point P(0,0,0) du plan cartésien de la figure 2, en raison du déplacement volumétrique, simultané et instantané, de toutes les charges positives, en amont et en aval de ce point, dans la direction positive de l’axe z.
Bien que, dans un vrai conducteur avec une différence de potentiel appliquée dans ses extrémités, l’électron est celui, par modèle classique, le déplacement des charges positives dans la direction positive de l’axe z a été choisi pour le calcul.
On sait, par symétrie, que le champ électrique vectoriel E résultant généré par la somme de toutes les charges existantes le long du conducteur, positif et négatif, au point P(0.0.0), est nul.
Toutefois, considérons, tout d’abord, le calcul du champ électrique statique (voir formule 14), généré par un élément différentiel cylindrique de calcul volumétrique, dans les coordonnées cylindriques, de la densité volumétrique de la charge positive ρv, centrée dans une position initiale z‘, où dQ est l’élément différentiel de charge, r’ est la valeur constante attribuée au rayon du conducteur du cylindre, R sont la distance vectorielle entre le point P (0.0,0) et l’élément différentiel de volume dV , az est le versor dans la direction positive de z, et ε la permissivité électrique du conducteur, comme le montre la figure 2.
S’il vous plaît souligner que, parce que nous prenons comme référence le point de mesure du champ électrique fixé en P(0,0,0), la direction de dE sera toujours opposée à l’aR versor. Par conséquent, le signe négatif dans l’équation (voir formule 13).
Figure 2. Courant de conduite
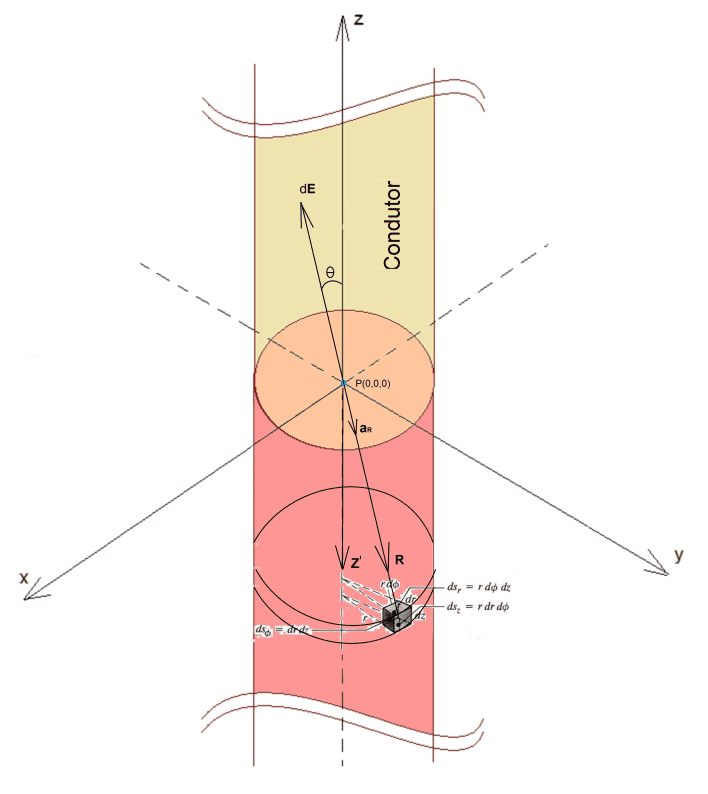
Ensuite, étant donné que ce disque volumétrique différentiel chargé a une vitesse constante. Le champ électrique![]() ne devient une fonction que du temps variable t. Compte tenu de la position initiale z’ et de la vitesse du disque v,
ne devient une fonction que du temps variable t. Compte tenu de la position initiale z’ et de la vitesse du disque v,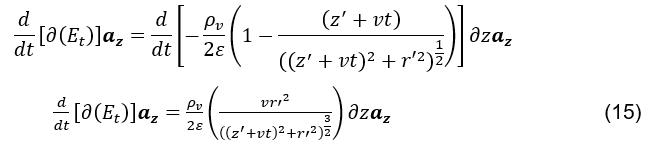
Comme ce que l’on veut calculer est la variation temporelle du champ électrique (voir formule 12), à l’origine, causée par le déplacement de chaque élément cylindrique différentiel ajouté
le long instantanément, il sera considéré exclusivement pour ce calcul que la fonction de l’équation (voir formule 15) ne dépend que de la position variable z,![]()
. Parce que la contribution de chaque élément différentiel cylindrique, le long de l’axe z entier, se déplaçant à la formation de la variation temporelle totale vectorielle du champ électrique au point P(0.0.0), parce qu’il est instantané, ne dépend pas du temps variable t. Ainsi, en remplaçant z’ = z, et compte tenu de la variable t = t0 = 0,
L’équation (voir formule 16), alors, démontre l’équivalence vectorielle entre la variation temporelle de la densité du champ électrique au point P(0,0,0), générée par le déplacement instantané et simultané de toutes les charges positives le long du fil cylindrique infini, et la densité de courant de conduction![]()
à ce même point.
5. IMPLICATIONS
S’il y a véracité physique dans l’hypothèse présentée, les implications suivantes sont observées :
- Interprétation de l’application d’une dynamique de la loi de Gauss;
- Nouvelle conception des lois d’Ampère-Maxwell et faraday-Lenz-Maxwell;
- Expérience suggérée pour prouver la théorie.
5.1 INTERPRÉTATION DE L’APPLICATION D’UNE DYNAMIQUE DE LA LOI GAUSS
L’égalité (voir formule 16) est considérée comme compatible avec les équations (voir formule 9) et (voir formule 10). Ainsi, il est entendu raisonnable que l’interprétation physique suivante de la loi de gauss s’applique à la situation présentée à la figure 1 : la variation temporelle du flux total de densité de champ électrique sur toute surface gaussienne entièrement fermée est exactement nulle (voir formule 17) et (voir formule 18).
En raison du choix classique de la direction actuelle étant celui du déplacement des charges positives, pour rendre les équations (voir formule 24) et (voir formule 29) symétriques les unes avec les autres, le signe négatif ( – ) a été inséré à l’égalité (voir formule 19).
L’interprétation suivante des phénomènes physiques envisagés dans l’égalité est proposée ici (voir formule 19).
La variation temporelle vectorielle de la densité du champ électrique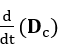 , résultat de la densité du courant de conduction
, résultat de la densité du courant de conduction
, semble être proportionnelle à la vitesse longitudinale à laquelle les lignes de champ électriques traversent un élément de zone d’une surface gaussienne. La théorisation peut être théorisée :
où vL est le vecteur de vitesse des lignes de champ électriques qui traversent un élément de zone d’une surface gaussienne, aS le versor de l’élément de zone vectorielle de cette surface, et K1 une constante, figure 3.
Figure 3. Variation temporelle de la densité du champ électrique générée par
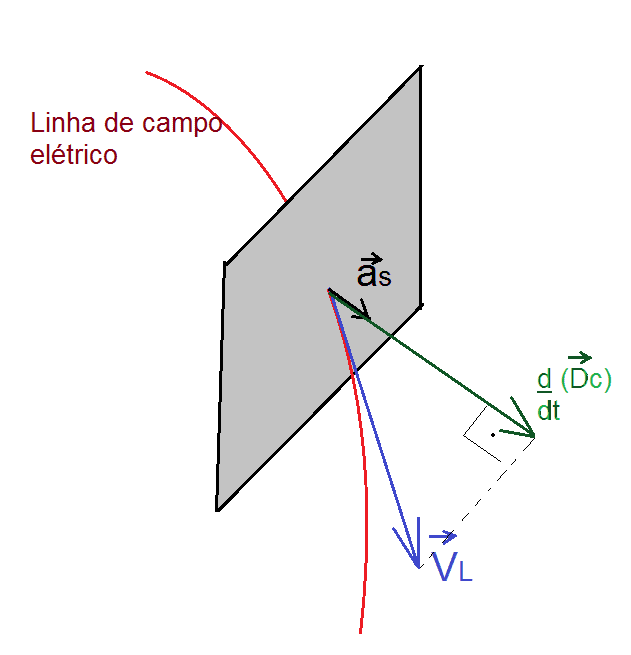
La variation temporelle vectorielle de la densité des champs électriques![]()
, résultant de la densité du courant de déplacement
, est liée à la variation temporelle du nombre quantitatif de lignes de champ électriques qui traversent un élément de zone d’une surface gaussienne (HAYT; BUCK et. al., 2013; SHADIKU, 2004).
Étant vrai, la théorie proposait, à partir de l’hypothèse initiale, que la variation temporelle du flux électrique total qui traverse une surface gaussienne, puisse être formée à la fois par la variation temporelle du nombre de lignes de champ électriques, par unité de surface, qui la traversent
, et par la vitesse longitudinale des lignes de champ électriques qui traversent un élément de zone
(voir la formule 20); il est intuited, par symétrie à (voir formule 19), que le flux magnétique passant par une surface gaussienne se comporte d’une manière équivalente (voir formule 21).
De telle sorte qu’il
puisse être généré à la fois par la variation temporelle du nombre de lignes de champ magnétique dans un élément de zone (HAYT; BUCK et. al., 2013; SHADIKU, 2004),
;ainsi que la vitesse longitudinale avec laquelle les lignes de champ magnétique traversent un élément de zone
(voir la formule 22). Par symétrie, il est proposé, analogue à l’équation (voir formule 20), l’équation (voir formule 22). Où vmL est le vecteur de vitesse des lignes de champ magnétique qui traversent un élément de zone d’une surface gaussienne, aS le versor de l’élément de zone vecteur de cette surface, et K2 une constante.
5.2 NOUVEAU DESIGN DES LOIS AMPÈRE-MAXWELL ET FARADAY-LENZ-MAXWELL
Considérant la possibilité de véracité dans l’hypothèse présentée, on pourrait concevoir la loi Ampère-Maxwell (voir formule 5) et la loi Faraday-Lenz-Maxwell (voir formule 23)
respectivement, comme dans (voir formule 24) et (voir formule 25).
5.3 A SUGGÉRÉ L’EXPÉRIENCE POUR PROUVER LA THÉORIE.
Le présent article vise, succinctement, à proposer une théorie, basée sur des situations hypothétiques, sans expérimentation physique en laboratoire pour la preuve, à la fin de celui-ci.
Toutefois, une proposition d’expérience en laboratoire sera présentée ci-dessous, pour ceux qui sont d’intérêt, afin de prouver la véracité de la théorie proposée, ou de la réfuter.
Pour le calcul d’un champ magnétique H, généré exclusivement à partir d’une densité de courant de conduction
, en utilisant l’égalité (voir formule 16), la loi Biot-Savart (voir formule 27) pourrait être décrite comme étant dans (voir formule 28).
Ensuite, il est proposé d’écrire la loi Biot-Savart modifiée (voir formule 28), symétriquement pour le calcul du champ électrique, comme dans (voir formule 29).
Afin de vérifier la véracité de la théorie selon laquelle les champs, électriques et magnétiques, peuvent être générés, respectivement, par la vitesse de déplacement des lignes des champs (magnétiques et électriques), l’expérience suivante est proposée.
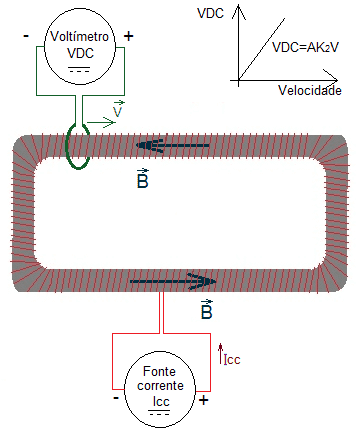
Il s’agit d’un circuit électrique formé par un fil conducteur isolé, enroulé de manière distribuée et continue autour d’un matériau ferromagnétique de topologie toroïdienne, zone Une constante de la section transversale, alimentée par une source de courant direct, avec un courant ajusté de telle sorte qu’il ne sature pas magnétiquement le matériau ferromagnétique. Il y aura une densité de champ magnétique B limitée à tous les matériaux ferromagnétiques toroïdal (HALLIDAY; RESNICK; WALKER et. al., 2013), figure 4.
Où μ est la perméabilité magnétique du matériau ferromagnétique, N le nombre de tours, et l le périmètre traversé par la section transversale du toroide tout au long de sa révolution.
Ensuite, un fil conducteur isolé mesurant le virage est utilisé autour de la section transversale du toroide, relié à un voltmètre VDC, de telle sorte qu’il est possible de déplacer la bobine de mesure le long du périmètre toroidal, figure 4.
On sait que le champ magnétique généré par n’importe quel circuit électrique toroidal idéal, externe à celui-ci, est nul (HALLIDAY; RESNICK; WALKER et. al., 2013).
Selon la théorie présentée, lorsque la bobine de mesure se déplace avec une vitesse V le long du périmètre toroidal, même si le nombre de lignes de densité de champ magnétique internes au virage n’est pas changé, ces lignes passeront à travers la surface gaussienne formée par la circonférence de la bobine de mesure, avec -V vitesse.
Appliquant l’équation proposée (voir formule 22) à la loi Faraday-Lenz-Maxwell (voir formule 23), la tension mesurée dans le voltmètre doit être :
Où est la zone de la section transversale du toroide.
Ainsi, il est proposé d’augmenter une courbe de mesures VDC x V, étant VDC la tension mesurée dans le voltmètre, et V le vecteur de vitesse du tour de mesure, le long du périmètre toroidal, figure 4. Selon la théorie proposée, cette courbe devrait être une ligne droite avec une pente AK2, figure 4.
Figure 4. Expérience suggérée pour prouver la théorie proposée
Si l’expérience est réalisée avec un résultat qui corrobore la théorie proposée, il est également proposé d’examiner l’existence de la densité de courant magnétique
de conduction suivante.
6. CONCLUSION
Afin de mieux comprendre la nature des courants de déplacement et de conduction, on a émis l’hypothèse que, dans une surface gaussienne entièrement fermée, la variation temporelle du flux total du champ électrique, en elle, pourrait toujours être égale à zéro (voir formule 9) et (voir formule 10), ne contredisant pas l’équation de continuité (voir la formule 3).
Un exemple d’une situation hypothétique idéale a été créé, ce qui permettrait l’analyse mathématique de l’hypothèse créée.
Le résultat de cette analyse, l’égalité (voir formule 16), corrobore l’idée que la variation temporelle vectorielle de la densité totale du champ électrique (voir formule 19) peut exister à partir des deux phénomènes physiques suivants.
1 –
→ Variation temporelle de la densité vectorielle du champ électrique, dans un élément de zone, en fonction de la variation temporelle du nombre de lignes de champ électriques qui le traversent. C’est la compréhension classique du phénomène de densité de courant de déplacement, d’abord reconnu par J.C.Maxwell. (HAYT; BUCK et. al. 2013; SHADIKU, 2004)
2 –
→ Variation temporelle de la densité vectorielle du champ électrique, dans un élément de zone, en fonction de la vitesse longitudinale des lignes de champ électriques qui le traversent (voir formule 20), en raison d’une densité de courant de conduction (voir formule 16);
Par la prémisse de la symétrie entre le comportement des champs électriques et magnétiques, de même les équations (voir formule 19) et (voir formule 20), la possibilité que le champ magnétique se comporte de la même manière dans (voir formule 21) et (voir formule 22) ont été considérées.
Ainsi, il est proposé une théorie selon laquelle toutes les interactions entre les champs, électriques ou magnétiques, et les particules chargées électriquement, sont, tout d’abord, des interactions entre les champs seulement. Par exemple, lors de l’application d’une différence potentielle dans un circuit électrique, le champ électrique généré par la différence potentielle interagira avec le champ électrique des charges libres, les forçant à se déplacer. Le déplacement des charges implique le déplacement de leurs lignes de champ électriques. La vitesse longitudinale à laquelle ces lignes traversent un élément différentiel de zone serait proportionnelle au vecteur
qu’il y a.
Considérant la possibilité de la véracité des équations (voir formule 9) et (voir formule 10), dérivée de la dynamique de la loi de Gauss, la loi Ampère-Maxwell (voir formule 5) est écrite, dans le format (voir formule 24), avec une plus grande symétrie à la loi Faraday-Lenz-Maxwell (voir formule 25).
Enfin, une expérience de laboratoire est proposée pour confirmer ou discréditer la théorie proposée et ses équations.
Voici les équations proposées dans cet article.
RÉFÉRENCES
FARADAY, M. Experimental Researches in Electricity. B.Quaritch, Londres, 1939, p.1855.
FARADAY, M. Great Books of the Western World. Vol. 45, encyclopedia Britannica Inc., Chicago, 1952, p. 217-866.
HALLIDAY, D; RESNICK, R; WALKER, J. Fundamentos de Física. V.3, ED.9ª, LTC, Rio de Janeiro 2013.
HAYT, W.H; BUCK, J.A. Eletromagnetismo. ED.8ª, AMGH, Porto Alegre, 2013, p. 48-290.
JACKSON, J.D. Classical Eletrodynamics. ED.3ª, University of California, Berkeley, 1998, p. 237-239.
MAXWELL, J.C. A Treatise on Electricity and Magnetism. Oxford Univ. Press, Oxford, 2002.
MAXWELL, J.C. The Scientific Papers of James Clerk Maxwell. Dover Publ., New York, 1965, v. 1, p. 451.
PLONSEY, R; COLLIN, R.E. Principles and Applications of Electromagnetic Fields. McGraw-Hill, New York, 1961, Topic 2.
SHADIKU, M.N.O. Elementos de Eletromagnetismo. ED.3ª, Bookman, Porto Alegre, 2004, p. 107-350.
[1] Diplômé en génie électrique (instrumentation) de PUC-MG (2008), diplômé en génie électrique industriel de CEFET-MG (2007).
Envoyé : juillet 2020.
Approuvé : août 2020.