Neue mathematische Formulierung des molekularen Diffusionsprozesses und der Elektrodiffusion in Zellmembranen

ARTIGO ORIGINAL

SOUZA, Nathan Rodrigues Serpa ^[1]

SOUZA, Nathan Rodrigues Serpa. Neue mathematische Formulierung des Molekulardiffusionsprozesses und der Elektrodiffusion in Zellmembranen. Revista Científica Multidisciplinar Núcleo do Conhecimento. Jahrgang 06, Ed. 04, Vol. 15, S. 34-63. April 2021. ISSN: 2448-0959, Zugangslink: https://www.nucleodoconhecimento.com.br/fisica/molecular-e-eletrodifusao, DOI: 10.32749/nucleodoconhecimento.com.br/fisica/molecular-e-electrodiffuse

Zusammenfassung

Die molekulare Diffusion ist ein physikalisch-chemisches Phänomen, das im Täglichen Leben beobachtbar ist, als einfache Gase eines Parfüms, das sich durch einen geschlossenen Raum ausdehnt, sowie mikroskopisch die Absorption von Ionen durch Gemüse und Tiere durch Zellen über offene ionische Kanäle der Plasmamembran. Dieser Artikel physikalischer Natur schlägt die Formulierung einer neuen Gleichung vor, die vom Autor von Nathanes Gleichung als Erweiterung des bekannten 1. Gesetzes von genannt wird, das darauf abzielt, das natürliche Phänomen der Diffusion aufgrund der variablen resultierenden Kraft des Systems zu beschreiben, die eine allgemeine Analyse der Kräfte ermöglicht, die dieses Phänomen beeinflussen werden. , sowie die Erweiterung dieser Formulierung, um den Transport von Ionen über Zellmembran zu beschreiben, eine Formulierung namens "Nathanes Gleichung für Elektrodiffusion in Zellmembranen". Durch explorative Methoden, bibliographische Forschung und mathematische Werkzeuge waren möglich, solche Formulierungen durchzuführen, sowie sie zu interpretieren. Aus der dimensionalen Analyse und den Postulaten, die im 1. Fick-Gesetz und Grahams Gesetz zur Verbreitung vorgeschlagen wurden, in Form von Graphen, die auf experimentellen und hypothetischen Daten basieren, um die Ähnlichkeiten der Graphenkurven zu vergleichen, war es möglich, die mathematische und physikalische Validierung für diese Gleichung zu bestätigen, indem sie demonstrierte, um die Einheiten zu konservieren und positiv mit den Postulaten übereinzustimmen, die von den anderen Gesetzen, die bereits in der physikalisch-chemischen Umgebung festgelegt wurden, vorgelegt wurden.

Schlüsselwörter: Diffusion, Cell Membrane, es Law, Nathan es Equation, Electrodiffusion.

1. Einleitung

Die molekulare Diffusion ist ein physikalisch-chemisches Phänomen, das im Alltag beobachtbar ist, als einfache Gase eines Parfüms, das sich durch einen geschlossenen Raum ausdehnt, sowie mikroskopisch die Absorption von Ionen durch Gemüse und Tiere durch Zellen, über ionische Kanäle der Plasmamembran. Dieser Transportprozess besteht aus der spontanen und irreversiblen Bewegung von Molekülen in Regionen mit hoher Konzentration (Hypertonic) zu anderen mit niedrigeren Konzentrationen (Hypotonisch), die treibende Kraft dafür sind die chemischen oder thermischen Potenziale der Lösung und im Falle von Zellmembranen elektrostatische Kräfte zusammen (DA SILVA, 2013).

Laut Alberts (2009) präsentiert die Membran gewebe von amphiphilem Charakter, gebildet durch Phospholipide mit einem polaren Ende (Radical Phosphat) und einem weiteren unpolaren (Fatty Acid Tail). Einige polare oder geladene Moleküle wie Ionen haben Schwierigkeiten, sich durch einfache Diffusion zu Lipid-Bilayerzugeben, Verschiebung durch den Transport von Proteinen oder kanalbildenden Proteinen, wie ionischen Kanälen, zu kreuzen. Neben der Darstellung einer Polarität zwischen den extrazellulären Medien mit Akkumulation positiver Ladungen und dem intrazellulären Medium mit Akkumulation negativer Ladungen, verhalten Sie sich wie ein einheitliches elektrisches Feld (MOREIRA, 2014).

Dieser explorative Artikel mit einer Methode der theoretisch-mathematischen Analyse zielt darauf ab, eine neue mathematische Formulierung für die Beschreibung des Prozesses der molekularen Diffusion und Ionentransport über ionische Kanäle von Zellmembranen zu etablieren, die die resultierende Kraft des Systems (F_{R) berücksichtigt,}die eine allgemeine Analyse der Aktionen in den Teilchen ermöglicht. Die exponierten Sätze hatten als theoretische Grundlage die Begegnung der diversifizierten bibliographischen Sammlung, in den Bereichen der biologischen, chemischen und physikalischen Wissenschaften, sowie die Analyse ihrer Sätze aus dem physikalischen und mathematischen Verständnis der Ergebnisse, unter dem Spektrum anderer Gesetze, die einen bestimmten Aspekt des gleichen Phänomens beschreiben, wie: es Law und Graham es Law.

2. Entwicklung

2.1 MATERIAS UND METHODS

Dieser Artikel der explorativen Voreingenommenheit zielt darauf ab, mathematische Formulierungen zu etablieren, um den Prozess der molekularen Diffusion und den Fluss von Ionen durch offene ionische Kanäle von Zellmembranen zu beschreiben, nicht nur aufgrund des Konzentrationsgradienten oder des elektrischen Potentials der Membran, sondern auch um die konstanten Kräfte zu berücksichtigen, die im Allgemeinen wirken, mathematische Formulierungen, die vom Autor der : Nathan es Equation and Nathan es Equation For Electrodiffusion In Cell Membranes.

Für die mathematische Konstruktion war die Sammlung bibliografischen Materials verschiedener Wissenschaften von großer Bedeutung, wie: Zellbiologie, Chemie und Physik. Zusätzlich zur Materialüberprüfung wurde nach der mathematischen Konstruktion die Maßanalyse der Gleichung durchgeführt, um die Erhaltung der Einheiten und ihre Gültigkeit sowie ihre positive oder negative Reaktion auf die Postulate der Fick- und Graham-Gesetze zur Beschreibung des Diffusionsprozesses zu überprüfen, basierend auf Graphiken, die auf experimentellen und hypothetischen Daten basieren. , um die diagramme zu vergleichen, die aus den mathematischen Beziehungen erstellt wurden. Das verwendete Wissen wird unten verfügbar gemacht:

2.2 BIOLOGISCHE ENTWICKLUNG

Die Zellen sind in drei Teile gegliedert: die Plasmamembran, das Zytoplasma und der Zellkern. Einer der Schwerpunkte dieser wissenschaftlichen Arbeit liegt im Verständnis des Primärfachs, der Zellmembran, mit ca. 8 Nanometern (nm) oder 8 x 10^-9 Metern (m), die durch Elektronenmikroskoplicht beobachtbar sind. Die Membran ist nicht vollständig durchlässig, bestehend aus ihrer Hauptfunktion, da es sich um ein selektives Barrea handelt, das die Trennung ermöglicht, sowie den Austausch von Substanzen zwischen extra- und intrazellulären Medien (JUNQUEIRA und CARNEIRO, 2012).

Seine selektive Durchlässigkeit ist jedoch auf die chemisch-strukturelle Zusammensetzung von Zellmembranen zurückzuführen, die aus einer Doppelschicht von Phospholipiden, Proteinen und Kohlenhydraten besteht. Phospholipide sind ampyphile Gewebe, d.h. mit polaren und unpolaren Teilen, der hydrophile Kopf (Radical Phosphat) ist nach außen gerichtet und bildet eine elektrostatische Wechselwirkung mit den polaren Molekülen des Wassers. Seine hydrophobe Region besteht aus seinen langen apolaren Ketten von Fettsäuren, die leicht mit anderen lipolöslichen Substanzen interagieren können, von denen es vorteilhafter ist, seinen Schwanz mit Blick auf die intrazelluläre Region zu haben. So sind nicht alle Substanzen in der Lage, die Zellmembran zu überqueren und durch einfache Diffusion in die Zelle einzudringen, jedoch wird ein solcher Diffusionstransport durch das Tragen oder ionische Kanalherstellungsproteine erleichtert, wenn sie geöffnet werden (ALBERTS, 2009).

2.3 CHEMISCHE ENTWICKLUNG

Laut Taiz und Zeiger (2006) ist die Diffusion ein Phänomen des Materietransports, bei dem es einen Fluss von Teilchen aus den Regionen mit höheren Konzentrationen zu den Regionen mit niedrigeren Konzentrationen gibt, mit dem Ziel, den Gleichgewichtszustand oder auch Homeotase zu fördern. Die mathematische Beschreibung eines solchen Prozesses wird durch Erstes Gesetz ausgedrückt, das vom Arzt und Physiologen Adolf Eugen (1829 –1901) vorgeschlagen wurde, einer Differentialgleichung, bei der die Strömungsdichte (J) direkt proportional zum Konzentrationsgradienten ( ) ist, und dem Diffusionskoeffizienten (D), der vom untersuchten chemischen Element abhängt, wie unten ausgedrückt (siehe Gleichung 2.1):

Dieser homogenisierende Fluss ist eine statistische Folge der zufälligen Bewegung von Teilchen, bekannt als die Brownian Bewegung, spontan bewegen sich die Moleküle von den hypertonischen Regionen (Höhere Konzentrationen) zu den hypotonischen Regionen (niedrigere Konzentrationen). Das negative Zeichen in es Law weist darauf hin, dass der Fluss in entgegengesetzter Richtung zum Konzentrationsgradienten auftritt, da es sich um ein lineares Gesetz handelt, unabhängig davon, wie groß der Konzentrationsunterschied zwischen zwei Punkten ist, bleibt der Fluss proportional zum Gradienten.

Weitere wichtige Details zum Fick-Gesetz sind folgende: Beziehung direkt proportional zur Diffusionsfläche (A) und umgekehrt proportional zwischen Partikelgröße und Diffusionsgeschwindigkeit oder ihre Molekularmasse (M). Das heißt, je größer die Fläche, desto höher die Transportgebühr; außerdem gilt: Je geringer die Molekularmasse des Teilchens, desto höher seine Transportrate und desto schneller wird seine Diffusionsgeschwindigkeit sein.

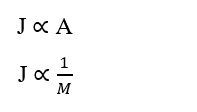
Nach Brady und Huminston (1995), Graham es Law (siehe Gleichung 2.2), formuliert von Chemiker Thomas Graham (1805 –1869) nach seinen Studien über Flüssigkeitsdiffusion und Erguss, stellt fest, dass die Effusions- und Diffusionsgeschwindigkeit (u) von zwei Gasen (1) und (2) unter den gleichen Temperatur- und Druckbedingungen umgekehrt proportional zur Quadratwurzel ihrer Dichten (d) oder der Molekularmasse (MM) ist, wie unten ausgedrückt:

2.4 PHYSISCHE ENTWICKLUNG

Eines der Grundbegriffe für diesen Artikel ist das bekannte "Fundamental Principle of Dynamics" oder "Newton es 2nd Law", das besagt: Die resultierende Kraft, die unter einem Körper wirkt, ist das Produkt seiner Masse durch Beschleunigung (F_R = m. a).

Halliday (2016) erklärt, dass es zuerst die Stelle wählen muss, die man untersuchen möchte, und die resultierende Kraft als Summe aller Kräfte anwenden muss, die in dem betreffenden Körper wirken.

Laut Tipler (2009) ist Labor (W) die Energie, die durch eine Kraft, die auf das Objekt selbst wirkt, auf ein Objekt übertragen wird. Um die Arbeit zu berechnen, die eine Kraft für ein Objekt ausführt, wenn es einen Offset durchläuft, verwenden wir nur die Kraftkomponente parallel zum Objektversatz, die Kraftkomponente senkrecht zum Offset führt keine Arbeit aus. Die Arbeit (W) einer konstanten Kraft, als Funktion von parallelen Kräften (- = 0°, 180°), kann durch diese Gleichung beschrieben werden:

W = F. d. cos

Wie; [ Cos(0°, 180°) = 1 ] man kann die Arbeitsgleichung in integraler Form oder als Funktion der Variation eines Abstands X umschreiben (siehe Gleichung 2.3), haben wir:

Laut Halliday (2016) ist Energie ein schwer zu definierendes Konzept. Wir verstehen jedoch intuitiv, was Energie ist, wenn wir die Effekte in den verschiedenen Formen davon analysieren, wie z. B.: Kinetische Energie und potentielle Energien. Konzeptionell für Tipler (2009) ist Kinetische Energie mit allen Körpern verbunden, die Masse haben und sich bewegen. Seien Sie (m) die Masse eines Materialpunktes und (u) seine Skalargeschwindigkeit relativ zu einem gegebenen Bezug. Die kinetische Energie des Materialpunktes wird durch gegeben (siehe Gleichung 2.4):

Für uniformly Varied Motion, die Arbeit der resultierenden Kraft durch den Körper, die kinetische Energievariation des Körpers selbst anzuschaffen. Aus dem Arbeits-Energie-Theorem (W = K) können wir den Ausdruck erhalten, der dem Werk einer konstanten Kraft (W) entspricht, mit der kinetischen Energievariation (K), wie die Gleichungen (2.5) und (2.6) zeigen:

Die gleichmäßig variierte Bewegung, nach Marques (2016), ist eine, bei der ein Teilchen die Geschwindigkeit (u₀) in ein anderes (u) ändert, aufgrund einer konstanten Kraft, die eine Beschleunigung fördert (a) auch konstant, was auch eine Verschiebung erzeugt .X. Diese Art der Bewegung kann ohne Berücksichtigung der Zeit, der sogenannten "Torricelli-Gleichung" (2.7): gleichgesetzt werden:

Laut Pimentel (2004) ist die treibende Kraft diffusiver Prozesse im zellulären flüssigen Medium das sogenannte chemische Potential jeder Lösung, das als die Fähigkeit einer solchen Lösung konfiguriert ist, unter den gelösten Partikeln Arbeiten durchzuführen, in Bezug auf den Konzentrationsgradienten wäre eine Formulierung für das maximale chemische Potenzial von Wasser (2.8):

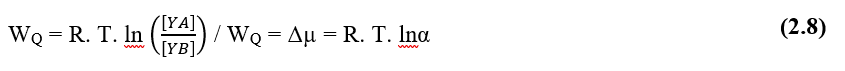
W_Q – Chemisches Potenzial der Lösung (J)

R – Allgemeine Gaskonstante (R = 8,31 J Mol^-1 K^-1)

T – Absolute Temperatur (K)

[ Y_A ] – Konzentration von Stoff Y an Punkt A (Mol)

[ Y_B ] – Konzentration von Stoff Y an Punkt B (Mol)

Lna – ln

α – Chemische Tätigkeit

3. ERGEBNISSE UND DISKUSSIONEN

3.1 ENTWICKLUNG VON NATHAN'S EQUATION

In dem Versuch, den Prozess der Diffusion und des Transports von Ionen über Ionenkanäle in der Plasmamembran in Abhängigkeit von dem Konzentrationsgradienten und dem elektrischen Feld, das in den extrazellulären und intrazellulären Enden der Membran erzeugt wird, mathematisch zu beschreiben, werden wir ein System der Koordinaten x, y und z betrachten, in dem jede Achse ihre jeweilige Beschleunigung darstellt, die durch aktive Kräfte im_{untersuchten isolierten}System (x,_y und_z)erzeugt wird, wie in Abbildung 1 dargestellt.

 Abbildung 1: Koordinatensystem (X, Y, Z).

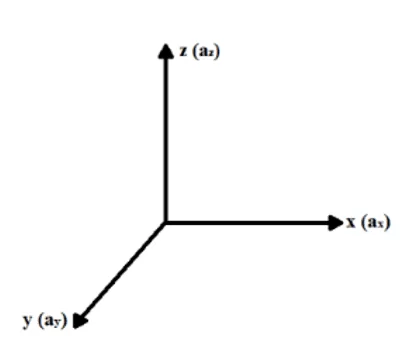
Laut Halliday (2016) kann die resultierende Kraft, die auf ein Teilchen als Ionen einwirkt, die die Membran über ionische Kanäle kreuzen, in jeder x-, y- und z-Achse in ihre Komponenten zerlegt werden, wobei sie direkt mit Beschleunigungen in den jeweiligen Achsen in Verbindung gebracht wird. Durch Newtons Grundprinzip der Dynamik oder des Zweiten Gesetzes und Newtons Prinzip der Kraftüberlappung kann eine physikalische Analyse für die resultierenden Kräfte auf jeder Achse erhalten werden, die Einfluss auf das Ion ausüben (siehe Gleichung 3.1):

Die Massen der Ionen bleiben erhalten, so dass die Faktoren, die direkt proportional zu den Kräften in jeder Richtung sind, ihre Beschleunigungen in den jeweiligen Richtungen sind:

F_R(X) = m . a_x / F_R(Y) = m . a_y / F_R(Z) = m . die_z

Durch die Komnadierung zwischen den elektrostatischen und Gravitationskonstanten (k = 9 x 10⁹ und G = 6,67 x 10^-11) zeigen diese Werte gemäß Halliday 3 (2016), dass die Gravitationskraft viel schwächer ist als die elektrische Kraft. Daher kann man in einem isolierten System von Teilchen, in dem es nur die Gravitations- und elektrischen Kräfte als aktiv betrachtet, die Gravitationskraft ignorieren, da die elektrische Kraft etwa 1,5 x¹⁰ mal größer ist als die Gewichtskraft. Da die Beschleunigung der Schwerkraft im Teilchen entwertet wird, wird die Kraft in der Z-Komponente ebenfalls null sein, da die Beschleunigung auf z überdacht_wird, wir werden die Gleichung für die gegebene Studie neu formulieren:

F_R = m . a_x + m . a_y + m . a_z

F_R = m . a_x + m . a_y + m . 0

F_R = m . a_x + m . a_y

Wenn man die hauptsächlich aktiven Kräfte, diejenigen, die Einfluss auf die X-Achse ausüben, ohne mechanische Schocks und andere Kräfte in Komponente y, da sich die Solutes im Sinne der Homogenisierung bewegen, von hypertonischen zu hypotonischen Regionen, werden wir zu einer solchen Vereinfachung der resultierenden Kraft kommen:

F_R = m . a_x + m . 0

F_R = m . ein_x

Ein weiterer Punkt ist, dass das untersuchte System als stationär oder dauerhaft betrachtet wird, in dem seine Eigenschaften im Verhältnis zur Zeit unveränderlich sind. Dies impliziert, dass jede P-Eigenschaft des Systems, die partielle Ableitung in Bezug auf die Zeit Null ( = 0) ist, wenn man bedenkt, dass die variable Zeit kein Parameter in der Untersuchung des betreffenden Membransystems ist.

Zellmembranen haben eine bestimmte Disposition, analog zum Uniform Electric Field, so dass es die Konzentration positiver Ladungen meist auf der extrazellulären Seite und eine Anhäufung negativer Ladungen auf der intrazellulären Seite gibt. Es gibt auch einen Unterschied in der Konzentration zwischen dem äußeren und inneren Enden von Zellen (C_E und C_I),in dem das System eine treibende Kraft ausübt, um die Translokation von Partikeln durch ionische Kanäle von Zellmembranen zu fördern, wie in Abbildung 2 dargestellt.

Abbildung 2: Darstellung der Ionenverschiebung über Ionenkanal.

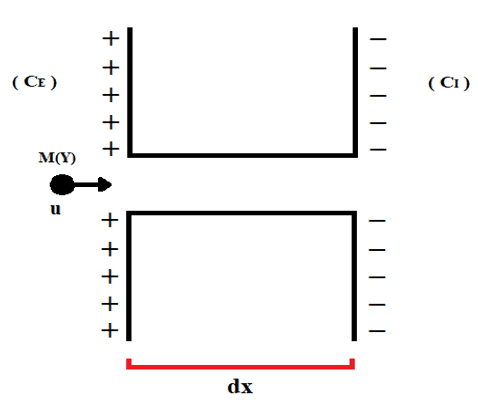
Die entfernung, die das dargestellte Molekül zurückgelegt hat, entspricht dem Verschiebungselement (dx), das auch die Bereitserwähnte Dicke der Zellmembran ist. Erstes Gesetz kann als Funktion des Gesamtkonzentrationsgradienten (und der Diffusionskonstante (D), wie unten ausgedrückt (siehe Gleichung 3.2) beschrieben werden:

Wir werden jedoch nur das bereits erwähnte Längenelement (∂x) berücksichtigen, um die eindimensionale Bewegung von Gelösten aus Regionen mit hoher Konzentration auf niedrigere Konzentrationen zu bewerten. Daher werden die Konzentrationsgradienten ( e ) aus der Gleichung entfernt, von der wir zu Gleichung 2.1 zurückkehren:

Indem wir das Element (∂x) von Erstem Gesetz isolieren, erhalten wir:

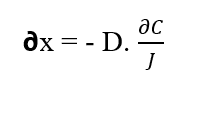
Die gelösten Teilchen bewegen sich entlang einer Verschiebung (∂x) aufgrund der Kraft, die aus dem chemischen Potential des Systems (W Q) abgeleitet_wird,da nach dem 2. Gesetz der Thermodynamik, das von Tipler (2009) beschrieben wurde, der Fluss von Materie oder Energie die Regionen mit höheren Werten der Materie oder Energie für die kleinsten verlässt. Wenn Teilchen Kräften ausgesetzt sind und aufgrund dieser Bewegung durch ein bestimmtes Entfernungselement (∂x), kann davon ausgegangen werden, dass solche Körper Arbeit ausführen (W), die durch die folgende Gleichung beschrieben wird (siehe Gleichung 2.3):

Die Arbeit einer konstanten Kraft kann auch als eine Funktion der kinetischen Energievariation des Systems (K) beschrieben werden, ausgedrückt durch den Kinetischen Energiesatz (siehe Gleichung 2.5):

Unter Berücksichtigung der eindimensionalen Bewegung von gelösten Teilchen in Lösung bewegen sich die Teilchen in einem bestimmten Anfangsmoment in Bezug auf ein bestimmtes Element (∂x) nicht, so dass ihre Anfangsgeschwindigkeit (u₀) als null angesehen werden kann, so dass das Werk wie folgt beschrieben wird:

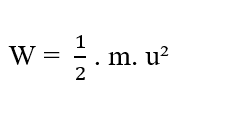
Für ein System, in dem wir eine n Anzahl von Partikeln haben, die sich ausbreiten, von denen jedes eine bestimmte Masse (m(i)) und Beschleunigung (a(i)) hat, haben wir, dass die resultierende Kraft in den Teilchen wie:

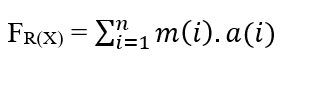
Da das System eine Konstante Kraft hat, wird diese Bewegung auch mit einer Konstantenbeschleunigung für alle Teilchen nach gleichmäßig variierter Bewegung beschrieben, die es ermöglicht, die Beschleunigung der Summation aus den Eigenschaften der Somators zu entfernen:

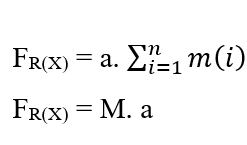
Um Nathans Gleichung zu erreichen, werden die beiden Gleichungen der Arbeit ausgeglichen, und weil es darum geht, die Bewegung von Molekülen wie gezeigt zu behandeln, wird die Masse (m) als Gesamtmasse (M) einer bestimmten Menge von Molekülen betrachtet, die in dem untersuchten System vorhanden sind, und ersetzt auch das Element (dx) durch (∂x) von Erstem Gesetz.

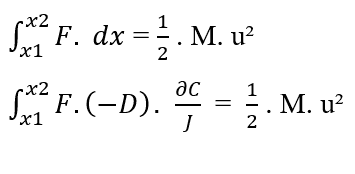
Da sie wissen, dass (F, D, J) in Bezug auf das zu integrierende Element (zu integrieren, aus der Eigenschaft der integralen Konstante die Begriffe aus dem Integral entfernt werden können:

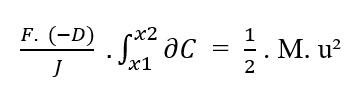
Umschreiben der Integrationsgrenzen in Bezug auf die (∂C), haben wir:

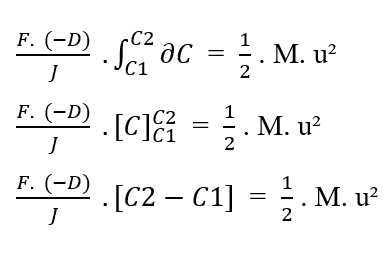
Da [C₂ – C₁ = ΔC] Sie das wissen, können Sie den Wert in der Gleichung ersetzen:

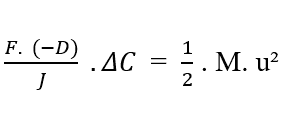
Durch die Isolierung der variablen Strömungsdichte (J) erhalten wir Nathans Gleichung (siehe Gleichung 3.3):

3.2 MATHEMATISCHE UND PHYSISCHE BEWERTUNG VON NATHAN'S EQUATION

Um die Validierung von Nathans Gleichung auf mathematische Weise zu bestätigen, war es notwendig, die von Halliday (2016) beschriebene Dimensionsanalyse durchzuführen, in der er überprüfen wird, ob die Einheiten des Ersten Fickgesetzes erhalten bleiben und die Einheiten der Nathan-Gleichung gleichwertig sind. Die Dimensionsanalyse ist ein Werkzeug, das in der Physik verwendet wird, um die Maßeinheit einer bestimmten Größe zu bestimmen. Die Dimensionsanalyse ist ein Werkzeug, das die Vorhersage, Inspektion und Anpassung der physikalischen Einheiten ermöglicht, die für die Auflösung von Gleichungen verwendet werden.

Im Allgemeinen werden die grundlegenden physikalischen Größen ausgedrückt als: Länge (L), Masse (M), Zeit (T), Temperatur (A), Elektrischer Strom (A), Menge der Materie (Mol) und Lichtstärke (I). Die Dimensionsanalyse von Nathans Gleichung (3.3) kann dann mit solchen Darstellungen der fundamentalen physikalischen Größen durchgeführt werden, entsprechend dem Äquivalent jeder Variablen der exponierten Formulierung, wie Marques (2016) betont.

J – Durchflussdichte (Mol L^-2 T^-1)

D – Diffusionskoeffizient (L² T^-1)

C – Konzentrationsvariation (Mol L^-3)

F_R – resultierende Kraft (M L T^-2)

M – Gesamtmasse der difitierenden Partikel (M)

u – Partikeldiffusionsgeschwindigkeit (L T^-1)

Jetzt, indem wir eine Dimensionsanalyse mit den allgemeinen Darstellungen der grundlegenden physikalischen Größen durchführen, haben wir:

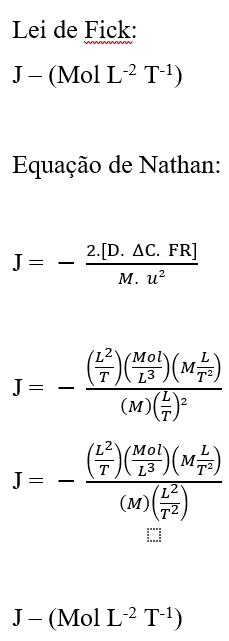
Nathans Gleichung zeigt die Erhaltung der Einheiten, sowie folgt einigen Aussagen, die das Erste Gesetz von und Grahams Gesetz zeigen, um bestimmte Variablen in einer direkten oder umgekehrt proportionalen Weise zu verknüpfen, physisch validieren solche mathematische Formulierung für den Diffusionsprozess, unabhängig von den Einheiten für die grundlegenden Mengen gewählt, vorausgesetzt, dass sie Kohärenz im Allgemeinen haben.

Die erste Beziehung, die nathans Gleichung zeigt, ist die direkt proportionale Beziehung zwischen Strömungsdichte (J) und Konzentrationsvariation zwischen zwei Punkten (C). Indem man feststellt, dass eine Erhöhung der Konzentrationsdifferenz zwischen zwei beliebigen Punkten des Systems in direktem Zusammenhang mit der Erhöhung der Strömungsdichte desselben steht, gehorcht eine solche Beziehung dem Gesetz von.

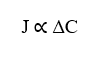
Die zweite wichtige Beziehung ist die direkte Proportionalität zwischen der Strömungsdichte (J) und der resultierenden Kraft (F_R), die auf die Teilchen (γ) einwirkt, aus denen das betreffende System besteht. Dies impliziert, dass eine Erhöhung der variablen resultierenden Kraft, die unter den Molekülen wirkt, die diffundieren, auch den Partikelfluss direkt proportional erhöhen wird.

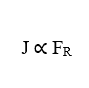
Die dritte wichtige Beziehung ist die umgekehrte Proportionalität zwischen der Strömungsdichte (J) und der Gesamtmasse jedes Gammaelements (γ), aus denen das untersuchte System besteht. Dies impliziert zu sagen, dass, wenn man bedenkt, dass, wenn man für jedes Molekül und nur seine Molekularmasse betrachtet, je höher die Molekularmasse des zu diffundierenden Elements, desto niedriger ist seine Transportrate, eine solche Beziehung gehorcht Gesetz und Grahams Gesetz.

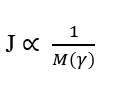
Die vierte wichtige Beziehung ist die umgekehrte Proportionalität zwischen Molekularmasse (M) und Diffusionsgeschwindigkeitsquadrat (u). Oder es kann als die umgekehrte Beziehung zwischen Diffusionsgeschwindigkeit und der Quadratwurzel der Molekülmasse des Elements (γ verstanden werden. Diese Beziehung gehorcht Grahams Gesetz der Effusion und Diffusion von Gasen und zeigt eine Korrelation von Velocity mit der Umkehrung der Quadratwurzel der molekularen Masse.

Die Strömungsdichte (J) ist umgekehrt proportional zum Produkt zwischen der Molekularmasse (M) – wenn für ein Teilchen – und dem Diffusionsgeschwindigkeitsquadrat (u):

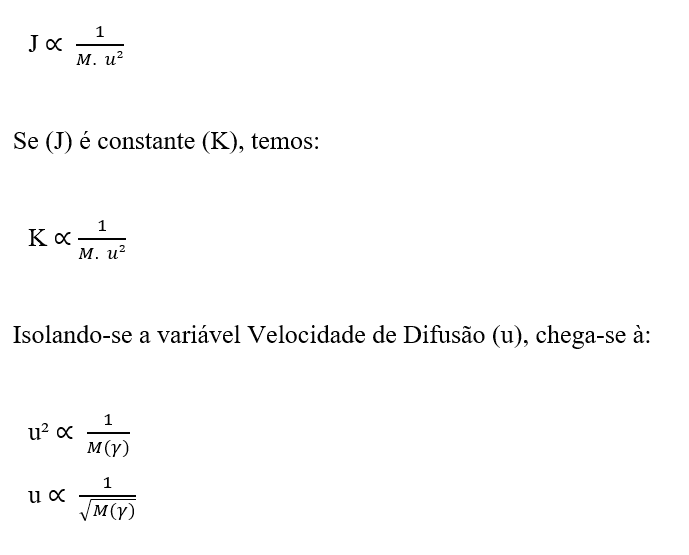
Ab der Excel Software Version 2016 war es auch möglich, die Diagrammmodellierung von 20 hypothetischen Daten für den Wert der Molekularmasse (M) mit einem Intervall von (0 < M < 21) em ordem crescente, correlacionado ao seu respectivo valor de Velocidade de Difusão (u), sabendo que a velocidade de difusão de um determinado elemento é inversamente proporcional a raiz quadrada de sua respectiva massa, como aponta a Lei de Graham e também a Equação de Nathan quando a Taxa de Transporte (J) se mantém constante e considera-se apenas a massa de uma única partícula. So können wir die Ähnlichkeit der später mit solchen Daten erstellten Graphen wahrnehmen (siehe Schaubild 1).

Abbildung 1: Diffusionsgeschwindigkeit versus die Umkehrung der Quadratwurzel der Molekularmasse.

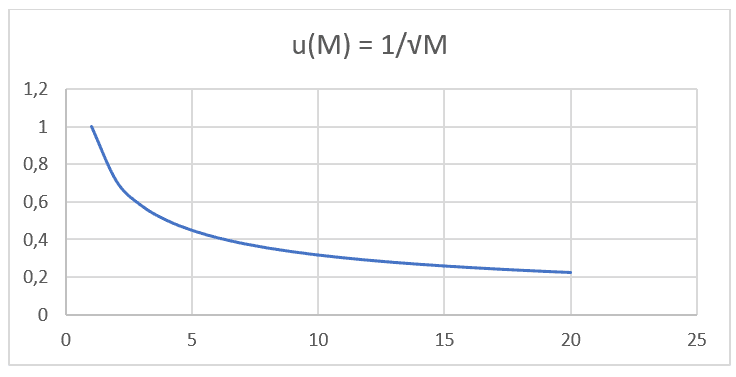
Es wird bemerkt, dass beide Formulierungen, sowohl Grahams Gesetz als auch Nathans Gleichung, die gleiche Proportionalität haben und auf der gleichen Art von Funktion basieren: F(x) = . Durch die grafische Projektion mit Molekularmassenwerten, IUPAC-Daten und der jeweiligen Diffusionsgeschwindigkeit von 20 verschiedenen Gasen bei gleichen Drücken und Temperaturen, die in der folgenden Tabelle aufgeführt sind (siehe Tabelle 1), können Sie ein zweites Diagramm projizieren (siehe Schaubild 2).

Tabelle 1: Molekulare Massen und ihre jeweiligen Diffusionsgeschwindigkeiten.

Gas	Molekularmasse (g/mol)	Diffusionsgeschwindigkeit (cm/s)
H2	2	0,7
He	4	0,5
O2	16	0,25
CH4	16	0,25
Ne	20	0,22
H2S	34	0,17
Ar	40	0,15
CO2	44	0,15
NO2	46	0,14
O3	48	0,13
C4H10	58	0,12
NO3	63	0,12
SO2	64	0,12
CS2	76	0,11
SO3	80	0,11
Kr	84	0,10
FeS	88	0,10
Xe	131	0,08
PCl3	137	0,08
Rb	222	0,06

Quelle: Der Autor.

Abbildung 2: Diffusionsgeschwindigkeit versus die Umkehrung der Quadratwurzel der Molekularmasse.

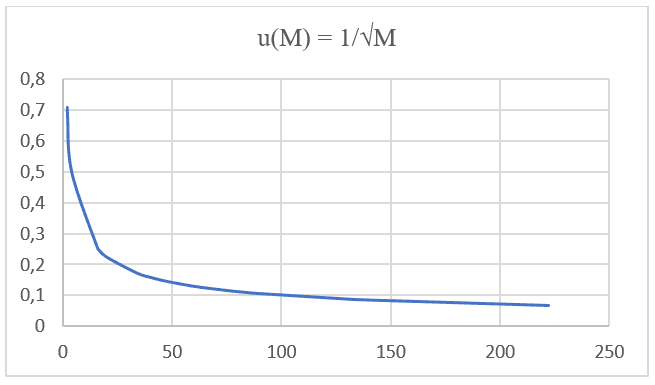
Nach Zeiger und Taiz (2006) kann die durchschnittliche Diffusionszeit als das Verhältnis zwischen dem Quadrat der Entfernungsvariation (X²) und dem Diffusionskoeffizienten des Elements (D) definiert werden, ausgedrückt durch die folgende mathematische Formulierung (siehe Gleichung 3.4):

Aus der Definition der durchschnittlichen Skalargeschwindigkeit (u) der Kinematik und dem Ersetzen des Zeitwerts durch die Variable Mean Time (T_M)erhalten wir:

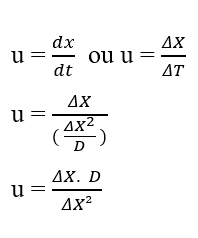
Durch algebraische Manipulationen können Sie die Gleichung zur Berechnung der Diffusionsgeschwindigkeit (u) eines beliebigen Elements erhalten:

Durch Ersetzen (3.5) in nathans Gleichung (3.3) können wir die Beziehung zwischen dem Quadrat der Entfernungsvariation (X) und der Konzentrationsvariation (C) erhalten.

Durch die Dimensionalanalyse der Gleichung (3.6) zur Bestätigung der Erhaltung der Einheiten des Fick-Gesetzes haben wir:

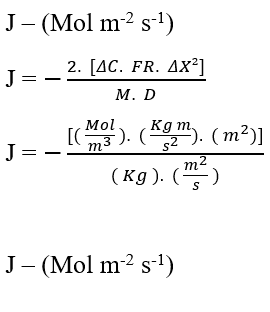
Validiert die Erhaltung von Einheiten aus der Dimensionsanalyse, kann man eine wichtige und gemeinsame Beziehung in der Nathan-Gleichung und Fick-Gesetz wahrnehmen, es ist die umgekehrte Proportionalität zwischen der Konzentrationsvariation (C) und dem Quadrat der Entfernungsvariation (X2). Damit diese Anweisung gültig ist, betrachten wir die Transportrate (J) als konstant und analysieren nur diese beiden Variablen: Variation der Konzentration und Entfernung.

Gezeigt wird die umgekehrte Proportionalität zwischen der Konzentrationsvariation (C) und dem Quadrat der Entfernungsvariation ( X2). Diese Aussage stimmt mit Gesetz überein, denn bei der Analyse der Korrelation zwischen diesen beiden Variablen beschreiben beide Formulierungen, Nathans Gleichung und Fickes Gesetz, dasselbe Diagramm, das der Funktion folgt: F(x) =. Im Folgenden finden Sie eine Graphenformatdemonstration (Gaußsche Kurve), Konzentrationsvariation versus Entfernungsquadratvariation (siehe Abbildung 3):

Abbildung 3: Graphische Variation der Konzentration versus Quadrat der Entfernungsvariation.

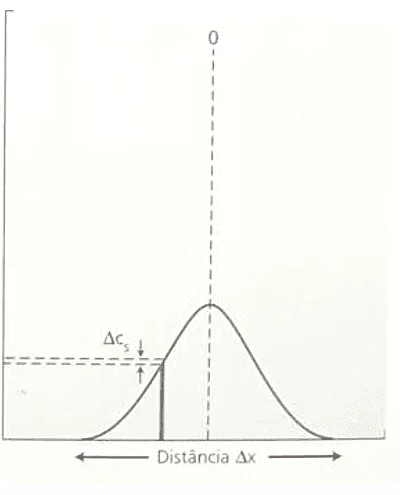
Bei nur als bestimmende Variable im Diffusionsprozess eines bestimmten Elements, der Konzentrationsvariation ,C, wenn man dann davon ausgeht, dass es sich um eine Bewegung von Teilchen handelt, die konstante Geschwindigkeit und nicht eine gleichmäßig variierte Bewegung, die durch eine konstante Kraft verursacht wird, ersetzen Sie einfach (2.7) in (3.3), die Torricelli-Gleichung, die die mathematische Beschreibung zurückgibt, die als mathematische Beschreibung bekannt ist, die als : 1. Fick-Gesetz.

Ersetzen (2.7) in (3.3) unter Berücksichtigung der Anfangsgeschwindigkeit (u₀) null, haben wir:

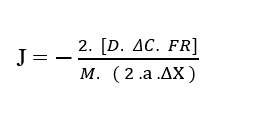
Durch Das Abbrechen der Begriffe Resulting Force (F_R),mit den Begriffen im Nenner Gesamtpartikelmasse (M) und Beschleunigung (a), sowie die Konstanten im Zähler und Nenner (2) erhalten wir wieder die lineare Formulierung: Fickes erstes Gesetz (2.1).

 

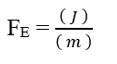Nathans Gleichung kann erweitert werden, um den Prozess der Diffusion von Ionen über Zellmembran zu beschreiben, mathematisch, unter Berücksichtigung der folgenden mathematischen Formulierungen. Laut Pimentel (2004) ist die treibende Kraft diffusiver Prozesse in biologischen Systemen das sogenannte chemische Potential des Systems, und im Falle des betreffenden Beispiels erfolgt die Übertragung von Materie von einem Punkt A auf einen anderen B, ein solches chemisches Potential kann aus der folgenden Gleichung ausgedrückt werden (2.8):

Dies bedeutet zu sagen, dass eine Lösung von einer Region mit höherem chemischen Potenzial in eine kleinere Region oder im Falle von Lösungsmitteln wie Wasser aus der Osmose bewegt sich aus den Regionen mit niedrigeren Konzentrationen von gelösten zu größeren. Der Partikelstrom hört jedoch auf, wenn die chemischen Potenziale beider Phasen gleich sind, wodurch der Endzustand des Gleichgewichts erreicht wird (HENEINE, 2004).

Ein solches Lösungspotential, das die resultierende Kraft des Systems erzeugt, weil es die Fähigkeit eines bestimmten Systems darstellt, Arbeit auszuführen, kann unter Berücksichtigung des Beitrags anderer wichtiger Faktoren beschrieben werden, wie z. B.: Gravitationswirkung und elektrischer Einfluss auf Partikel aufgrund ihrer Lasten und des Unterschieds im elektrischen Potential. So kann die maximale Potentialgleichung durch die Formulierung des elektrochemischen Potentials ausgedrückt werden, unten (siehe Gleichung 3.7):

Wird der Beitrag des Gravitationspotentials (m.g.h) nicht berücksichtigt, so wird die Gleichung nur auf den chemischen und elektrischen Beitrag reduziert, d. h. die Kräfte, die im Satz von ionischen Teilchen wirken, um sich durch die ionischen oder molekularen Kanäle durch die Lipid-Bilayer zu bewegen und in die intrazelluläre Umgebung einzutreten (ALBERTS, 2009).

Nathans Gleichung beschreibt den Diffusionsprozess, und das natürliche Phänomen des Ionentransports über die Zellmembran kann in ähnlicher Weise durch nathans Gleichung ausgedrückt werden, wobei als Resulting Force (F_R) nur das chemische Potential der Lösung und der elektrische Beitrag verwendet wird, wobei der Gravitationsbeitrag außer Acht gelassen wird.

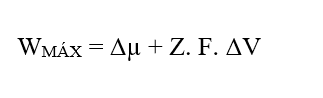
Das wissen (W = F_R. X), ersetzen die Gleichung (2.3) erhalten wir:

Durch die Dimensionalanalyse der resultierenden Kraft (3.8), die sie in ihre chemischen und elektrischen Parzellen aufteilt, kann man die Entstehung der Joule (J) Energieeinheit nicht mehr wahrnehmen, sondern die Einheit der Kraft im Internationalen Messsystem, Newton (N):

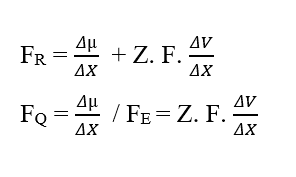
Bei der Analyse des chemischen Beitragsanteils (F_Q)haben wir:

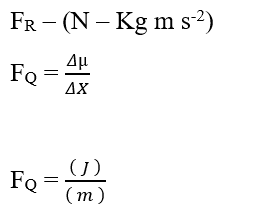
In dem Wissen, dass die Joule (J – N.m) Energieeinheit in der Dimensionsanalyse ersetzt werden kann, erhalten:

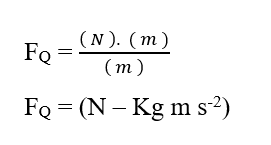
Bei der Analyse des elektrischen Beitragsanteils (F_E)haben wir:

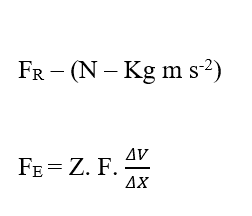
Da wir wissen, dass Valencia (Z) eine Dimensionsvariable ist, haben wir:

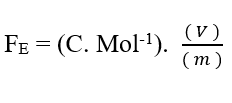
Wohl wissend, dass die Spannungseinheit Volt (V – J. ^C-1),kann in der Dimensionsanalyse ersetzt werden, wodurch:

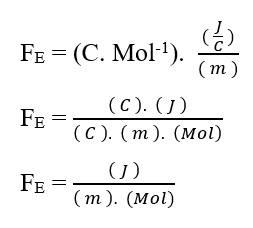
Da die Mol-Einheit als adimensional betrachtet wird, weil sie nur mit Entitäten verwandt ist, die ein bestimmtes System bilden, wie: Atome, Moleküle, Ionen oder Elektronen; wir können eine solche Einheit in der Analyse außer Acht lassen und sie vereinfachen:

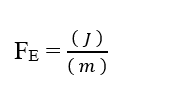
In dem Wissen, dass die Joule (J – N.m) Energieeinheit in der Dimensionsanalyse ersetzt werden kann, erhalten:

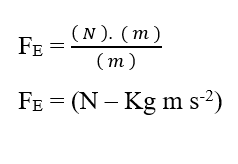
Aus der Dimensionsanalyse der beiden chemischen und elektrischen Parzellen, aus denen die resultierende Kraft (F_R)des untersuchten Systems besteht, wird gezeigt, dass sie für die Berechnung dieser Kraft gültig ist. Schreiben der Verhältnisse zwischen der Variation des chemischen Potentials ()) und der Entfernungsvariation (X), der Variation des elektrischen Potentials (-V) und der Entfernungsvariation (X), in Form von Grenzwerten von (X 0) und dann in Differentialform, mit der resultierenden Sofortkraft, erhalten wir:

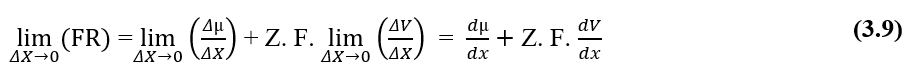
Für eine Situation, in der die elektrochemischen Potentiale zweier Phasen (A) und (B) eines gegebenen Systems gleich sind, d. h. in einer Gleichgewichtssituation kann der Wert der Variation des elektrischen Potentials an den Enden von Zellmembranen ermittelt werden, was sich auf die Nernst-Gleichung bezieht.

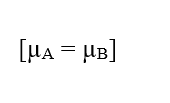
Wenn die Potentiale identisch sind, weist diese Aussage darauf hin, dass die arbeit von den Teilchen ausgeführte Arbeit null ist, so dass die resultierende Kraft in ihnen auch null ist, da es keinen Transit von Molekülen zwischen den beiden Phasen des Systems gibt:

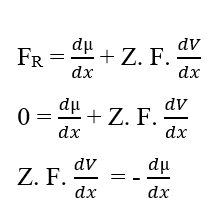
Sie können die Elemente (dx) abbrechen, die auf beiden Seiten der Gleichheit angezeigt werden, und den Begriff (dV) isolieren und dann entsprechend den Variationen neu schreiben, was sich ergibt:

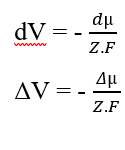
Als Ersatz für das chemische Potential (2.3) haben wir die Berechnung des elektrischen Potentials für eine Gleichgewichtssituation in biologischen Systemen (3.10), bekannt als Nernst-Gleichung (HENEINE, 2004), neu erstellt.

Sie können die resultierende Kraft des Systems (3.9) in der oben beschriebenen Nathan-Gleichung ersetzen (siehe Gleichung 3.3):

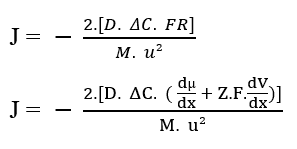
Abgesehen von den Begriffen in der Klammer haben wir nathans Gleichung für Elektrodiffusion in Zellmembranen (3.11):

J – Transportrate oder Ionendurchflussdichte in der Membran (Mol m^-2 s^-1)

D – Solute Diffusionskoeffizient (m² s^-1)

C – Konzentrationsvariation (Mol m^-3)

M – Gesamtmasse der difitierenden Partikel (Kg)

u² – Partikeldiffusionsgeschwindigkeit (m s^-1)

Z – Ion Valencia

F – Faraday konstante (F = 9.648 x 10⁴ C mol^-1)

∂μ/∂x – Abgeleitet vom chemischen Potential in Relation zu dx (Kg m s^-2)

∂V/∂x – Abgeleitet vom elektrischen Potential in Bezug auf dx (V m^-1)

Laut Halliday (2016) für Thermodynamik, Innere Energie (U) oder Interne Energievariation (U) ist es die Summe der kinetischen und potentiellen Energien aller Moleküle, die ein System enthält. Diese Beziehung kann mit der folgenden mathematischen Beschreibung (siehe Gleichung 3.12) unter Berücksichtigung der durchschnittlichen Geschwindigkeit für alle konstanten Teilchen ausgedrückt werden:

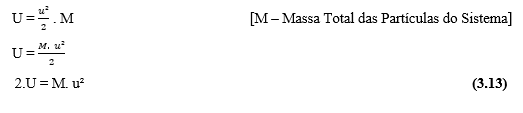
Ersetzen der Gleichung (3.13), in Nathans Gleichung (3.3), kann ein konstanter Begriff bestimmt werden, der vom Autor mit dem griechischen Buchstaben Omega () bezeichnet wird:

Betrachten wir das Verhältnis nun als konstantes (), da sich die Werte solcher Variablen im Verhältnis zur Zeit nicht ändern, da die partielle Ableitung eines Begriffs null ist. In der Kenntnis der Kenntnis, dass ()) als Einheit ein Verhältnis zwischen der Menge der konzentrierten Materie und der inneren Energie eines Systems darstellt, entspricht eine solche Beziehung dem folgenden Ausdruck (3.15):

Und wohl wissend, dass sich die Handlung (bezieht sich auf die resultierende Kraft des Systems (F_R) bezieht, kann man diese Formulierung immer noch als ihre allgemeine Form umschreiben (3.15):

Es ist nun möglich, dass die Strömungsdichte (J), da die Begriffe (D) und ()) konstant sind, direkt proportional zur resultierenden Kraft des Systems (F_{R) ist,}was bedeutet, dass, wenn eine Erhöhung in einer dieser Variablen auftritt, die andere ebenfalls eine proportionale Erhöhung erleiden wird.

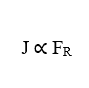
Nathans Gleichung für Elektrodiffusion In Zellmembranen beschreibt den Fluss von Ionen durch die Membran, über ionische Kanäle, wenn sie offen sind, beeinflusst durch den Konzentrationsgradienten von extrazellulären und intrazellulären Medien, sowie elektrisches Potential oder elektrisches Feld unter den Ionen, das von der Zellmembran selbst erzeugt wird. Diese Formulierung berücksichtigt die Gesamtmasse der Teilchen des Elements, das sich ausbreiten wird, die chemischen und elektrischen Antriebskräfte, die im Phänomen des Transports von Ionen über die Zellmembran vorhanden sind, jedoch, wenn es andere externe Faktoren gibt, aufgrund der Zunahme der variablen resultierenden Kraft, kann die Analyse in einem allgemeinen Umfang durchgeführt werden, zusätzlich zur Übereinstimmung mit den bestehenden und vorgestellten physikalischen Konzepten.

4. ENDGÜLTIGE ÜBERLEGUNGEN

In einer Erklärung schlug dieser Artikel die Formulierung der Nathan-Gleichung als Erweiterung von 1. Gesetz vor, das den diffusiven Fluss von Teilchen in Lösungen beschreibt, nicht nur aufgrund der Differenz in der Konzentration (C), sondern mit dem Ziel, die Materieflussdichte (J) als Funktion der konstanten resultierenden Kraft (F_R)zu betrachten, die auf die Teilchen eines gegebenen Systems einwirkt (siehe Gleichung 3.3).

Diese Formulierung zeigte die direkte Proportionalität zwischen der in den Teilchen wirkenden Kraft und der Strömungsdichte (J), so dass je höher die im System ausgeübte Kraft, desto größer der Transport von Materie. Die gleiche mathematische Beschreibung der natürlichen Diffusionsprozesse von Molekülen, die eine allgemeine Analyse aller Kräfte ermöglicht, die unter bestimmten untersuchten Systemen Einfluss ausüben können, kann auch erweitert werden, um den Transport von Ionen über zellmembran zu erklären, wenn die resultierende Kraft unter den Teilchen des betreffenden Systems das chemische Potenzial und das elektrische Potential berücksichtigt. , sowie eine Beziehung zwischen the Amount of Concentrated Matter und der Internal Energy of a System ('), die vom Autor von "Nathan es Equation for Electrodiffusion In Cell Membranes" (siehe Gleichung 3.11) oder auch in seiner allgemeinen Formulierung (siehe Gleichung 3.15) genannt wurde.

Die Validierung der Gleichungen wurde aus der Dimensionsanalyse und den direkten und umgekehrt proportionalen Beziehungen zwischen den Variablen in Bezug auf die im 1. Fick-Gesetz und Grahams Gesetz vorgeschlagenen Postulate in Form von Graphen mit Kurven bewertet, die durch bestimmte Funktionen beschrieben werden, die die Proportionalitäten zwischen: Diffusionsgeschwindigkeit versus Molekularmasse eines Elements demonstrieren (siehe Schaubild 1) und die Konzentrationsvariation im Vergleich zum Quadrat der Entfernungsvariation (siehe Schaubild 3); sich als eine gültige Formulierung physisch und mathematisch für eine solche Beschreibung des Naturphänomens zu zeigen, weil die Einheiten des Fick-Gesetzes in der Nathan-Gleichung erhalten bleiben und so positiv in Bezug auf die Sätze solcher bereits etablierten physikalisch-chemischen Gesetze und ihrer grafischen Darstellungen übereinstimmen, nach Proportionalitäten, die von bestimmten zuvor vorgestellten Funktionen beschrieben werden. Die nächsten Artikel aus physikalischen Experimenten oder mit spezifischer Modellierungssoftware können die Praktikabilität und Kohärenz von Nathans Gleichung mit der natürlichen Realität bewerten und sich auf die Untersuchung des Diffusionsphänomens beziehen, um die Genauigkeit und Allgemeinheit der von ihr aufgeworfenen Konzepte zu analysieren.

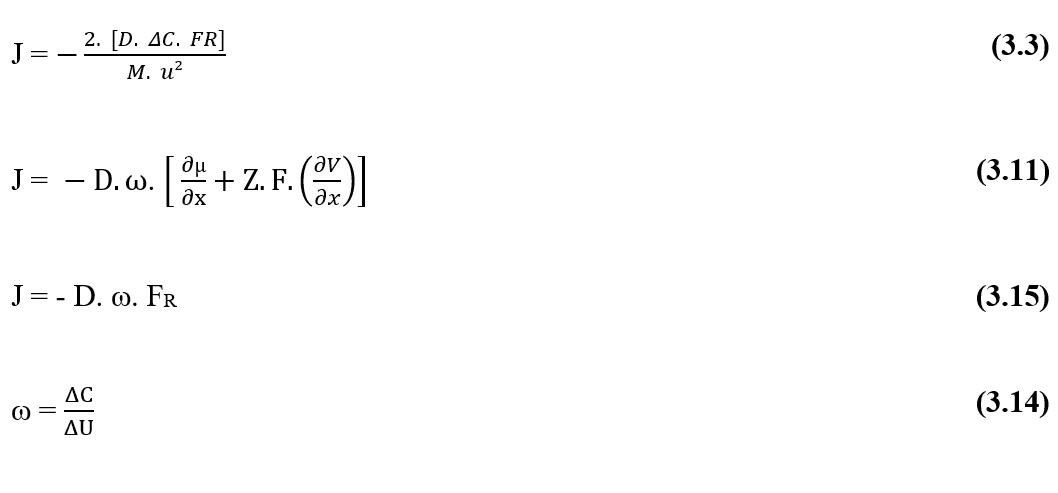
Verweise

ALBERTS, Bruce et al. Biologia Molecular da Célula, 5° Edição. Editora: ARTMED, 2010, 1728 p., Vol. 1. ISBN: 978-85-363-2170-7.

BRADY, James; HUMISTON, Gerard. Química Geral, 2° Edição. Editora: LTC, 1995, 404 p., Vol. 1. ISBN: 9788521604495.

DA SILVA, Raissa. Difusão de Gases em Membranas Densas Via Simulação Molecular. Instituto Alberto Luiz Coimbra de Pós-Graduação e Pesquisa na Engenharia (UFRJ), Data da Dissertação de Mestrado: Abril de 2013. Disponível em: http://portal.peq.coppe.ufrj.br/index.php/producao-academica/dissertacoes-de-mestrado/2013-1/47-difusao-de-gases-em-membranas-densas-via-simulacao. Acesso: 25/06/2020.

HENEINE, Ibrahim. Biofísica Básica, 2° Edição. Editora: ATHENEU, 2004, 381 p., Vol. 1. ISBN: 8573791225.

JUNQUEIRA, Luiz C.; CARNEIRO, Jóse. Biologia Celular e Molecular, 9° Edição. Editora: Guanabara Koogan, 2012, 376 p., Vol. 1. ISBN: 9788527720786.

MARQUES, Francisco Das Chagas. Física Mecânica, 1° Edição. Editora: Manole, 2016, 315 p., Vol. 1. ISBN: 9788520427743.

MOREIRA C., Catarina. Difusão Simples. Rev. Ciência Elem., V2(02):144. doi.org/10.24927/rce2014.144. Pulicado: 15 de Setembro de 2010. Disponível em: https://rce.casadasciencias.org/rceapp/art/2014/144/. Acesso: 22/06/2020.

PIMENTEL, Carlos. A Relação da Planta Com a Água, Local: EDUR – Editora Universidade Federal Rural do Rio de Janeiro. 2004, 190 p. ISBN: 85-85720-45-X

TAIZ, Lincoln; ZEIGER, Eduardo. Fisiologia Vegetal, 3° Edição. Editora: ARTMED, 2006, Vol. 1, 722 p. ISBN: 85-363-0291-7.

TIPLER, Paul; MOSCA, Gene. Física para Cientistas e Engenheiros – Mecânica, Ondas, Termodinâmica, 6° Edição. Editora: LTC, 2009, 788 p., Vol. 1. ISBN: 9788521617105.

WALKER, Jearl et al. Halliday & Resnick ¹: Fundamentos de Física – Mecânica, 10° Edição. Editora: LTC, 2016, 372 p., Vol. 1. ISBN-13: 978-8521630357.

WALKER, Jearl et al. Halliday & Resnick ²: Fundamentos de Física – Gravitação, Ondas, Termodinâmica, 10° Edição. Editora: LTC, 2016, 324 p., Vol. 1. ISBN-13: 978-8521630364.

WALKER, Jearl et al. Halliday & Resnick ³: Fundamentos de Física – Eletromagnetismo, 10° Edição. Editora: LTC, 2016, 408 p., Vol. 1. ISBN-13: 978-8521630371.

^[1] Abschluss.

Eingereicht: Dezember 2020.

Genehmigt: April 2021.