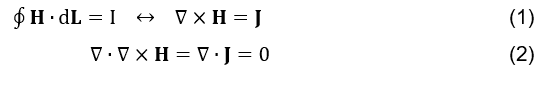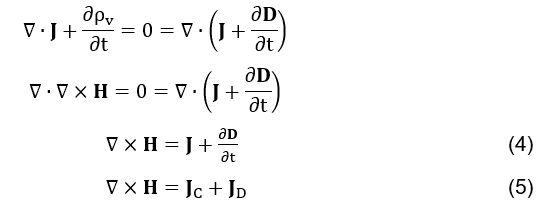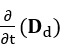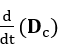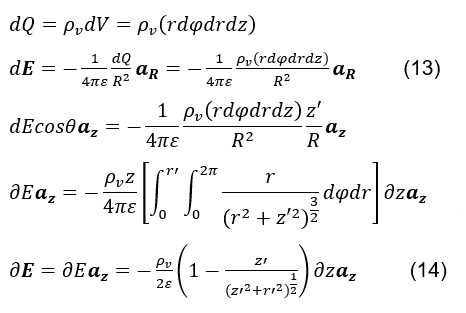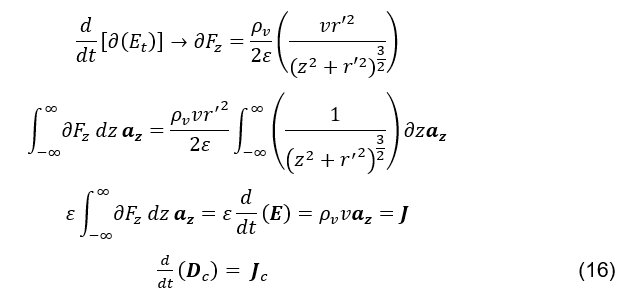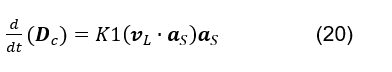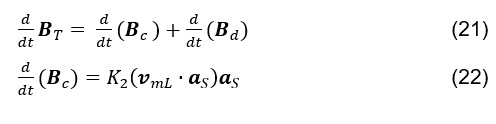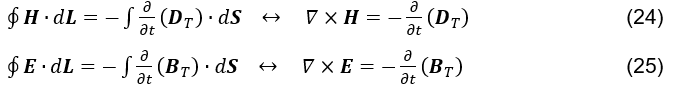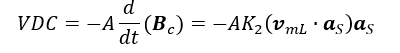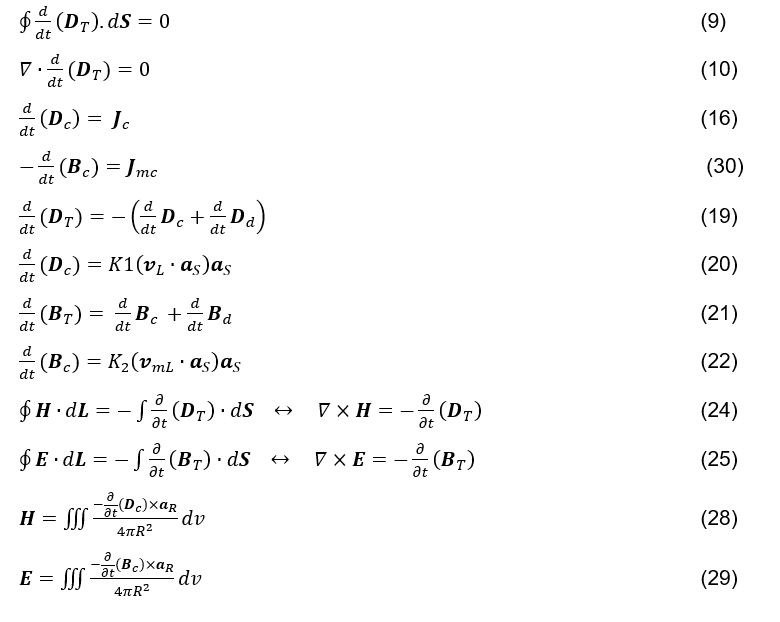Eine neue Perspektive auf die Stromdichte

ORIGINAL-ARTIKEL

LUCENA, Lucas Ruas de ^[1]

LUCENA, Lucas Ruas de. Eine neue Perspektive auf die Stromdichte. Revista Científica Multidisciplinar Núcleo do Conhecimento. Jahrgang 05, Ed. 08, Vol. 03, S. 151-167. August 2020. ISSN: 2448-0959, Zugangslink: https://www.nucleodoconhecimento.com.br/fisica-de/kettendichte, DOI: 10.32749/nucleodoconhecimento.com.br/fisica-de/kettendichte

ZUSAMMENFASSUNG

Dieser Artikel behandelt alternative und ergänzende Vorschläge zu J.C.Maxwell Gesetzen des klassischen Elektromagnetismus, basierend auf bestimmten Hypothesen, hypothetischen Beispielen und Berechnungen, mit Ergebnissen, die neue Interpretationen über die physikalische Phänomenleitungsstromdichte ableiten können. Diese neuen Interpretationen bringen ein neues Verständnis für die Dynamik des Gauss-Gesetzes und machen das Ampère-Maxwell-Gesetz, wahrlich, völlig symmetrisch zum Faraday-Lenz-Maxwell-Gesetz, ohne mathematische oder physische Inkonsistenz. Diese Verständigungen bringen unweigerlich Implikationen und Standpunkte, die die klassische Theorie des Elektromagnetismus ergänzen.

Schlagworte: Elektromagnetismus, Stromdichte, Kontinuitätsgleichung.

1. EINFÜHRUNG

Zunächst wird die von J.C.Maxwell gegebene Lösung so dargestellt, dass die Ampere-Gleichung (siehe Formel 1) mathematisch konsistent wird, wobei die in (siehe Formel 2) angewendete Vektoridentität respektiert und mit der Kontinuitätsgleichung übereinstimmt (siehe Formel 3).

Im Folgenden finden Sie ein Beispiel für die Anwendung des Gauss (siehe Formel 6) auf eine geschlossene Fläche um eine der Platten eines Kondensators, Abbildung 1.

Als Hypothese wird vorgeschlagen, dass die zeitliche Variation des gesamten elektrischen Flusses, der die gaußsche Oberfläche vollständig geschlossen kreuzt, immer gleich Null ist. Daher würde Gauss Gesetz (siehe Formel 6), das auf dynamische Situationen angewendet wird, zur Gleichung werden (siehe Formel 9). Damit diese Hypothese aufbaut, wird es als notwendig erachtet, dass es eine zeitliche Variation der elektrischen Felddichte, des gleichen Moduls, der gleichen Richtung und Richtung der Stromdichte, im Bereich der Fürsprache zwischen dem zylindrischen Volumen des Leiters und der Gaußschen Oberfläche gibt, die darauf zeigt, Abbildung 1.

Um die Konsistenz dieser Hypothese zu überprüfen, wird ein ideales Beispiel in Betracht gezogen, bei dem es einen kontinuierlichen und homogenen Strom in einem unendlichen geradlinigen zylindrischen Draht entlang der z-Achse gibt. Dann wird die vektorzeitliche Variation des elektrischen Feldes (siehe Formel 12) an Punkt P(0,0,0) aufgrund der gleichzeitigen und sofortigen Verschiebung aller Lasten, vor und nach P(0,0,0) berechnet. Diese Berechnung führt zu Gleichheit (siehe Formel 16).

Ausgehend von der physischen Wahrhaftigkeit der Gleichheit (siehe Formel 16) gibt es unvermeidliche Implikationen, Formatierungen und theoretische Ergänzungen für klassische Gleichungen des Elektromagnetismus von Faraday, Lenz, Biot-Savart und Maxwell. Am Ende wurde ein Laborexperiment vorgeschlagen, um die aus der Analyse der vorgeschlagenen Hypothese entwickelte Theorie zu bestätigen oder zu widerlegen.

2. DIE DISPLACEMENT- UND DRIVING CHAINS

Amperes Schaltgesetz in seiner pünktlichen Form (siehe Formel 1) hatte mathematische Unzulänglichkeiten (JACKSON et. al., 1998).

Das Ergebnis der Gleichung (siehe Formel 2) sollte Null sein, da die Divergenz des Rotationswerts gleich Null eine Vektoridentität darstellt. Die Kontinuitätsgleichung (HAYT; BUCK et. al., 2013; SHADIKU, 2004),

mit der Gleichung unvereinbar ist (siehe Formel 2).  Diese Korrektur wurde von J.C.Maxwell brillant wie folgt vorgenommen (JACKSON et. al., 1998):

So wurde die Ampere-Gleichung (siehe Formel 1) völlig konsistent (siehe Formel 5). Sowohl physikalisch, unter Berücksichtigung der Erzeugung von Magnetfeld aus der zeitlichen Variation der Dichte des elektrischen Feldes, als auch mathematisch in Bezug auf die in der Gleichung zitierte Vektoridentität (siehe Formel 2).

Der in

der Gleichung hinzugefügte Begriff (siehe Formel 4) hat die gleiche Einheit der Stromdichte, Ampere pro Quadratme

ter, die von J.C.Maxwell der Verschiebungsstromdichte bezeichnet wird, dargestellt durch die

leichung (siehe Formel 5). Die Identifizierung dieses Begriffs war von grundlegender Bedeutung für das Verständnis der Ausbreitung elektromagnetischer Wellen. Der Begriff

in der Gleichung (siehe Formel 5) bezieht sich auf die Dichte des Leitungsstroms.

3. HYPOTHESIS EINER DYNAMISCHEN ANWENDUNG VON GAUSS LAW

Gauss’ Law, Gleichung (siehe Formel 6), bestimmt, dass der gesamte elektrische Felddichtefluss, der eine geschlossene Oberfläche kreuzt, gleich der gesamten elektrischen Ladung ist, die in dieser Oberfläche enthalten ist. Maxwell beobachtete es in der Punktform, Gleichung (siehe Formel 7), bekannt als maxwells erste Gleichung (HAYT; BUCK et. al., 2013; SHADIKU, 2004).

Betrachten wir das erste Beispiel, das eine geschlossene Fläche um eine der Platten eines Kondensators ist, der von einem Netzteil mit variabler Spannung geladen wird, wie in Abbildung 1 dargestellt.

Abbildung 1.  Gaußsche Oberfläche auf einer Kondensatorplatte eingeschlossen

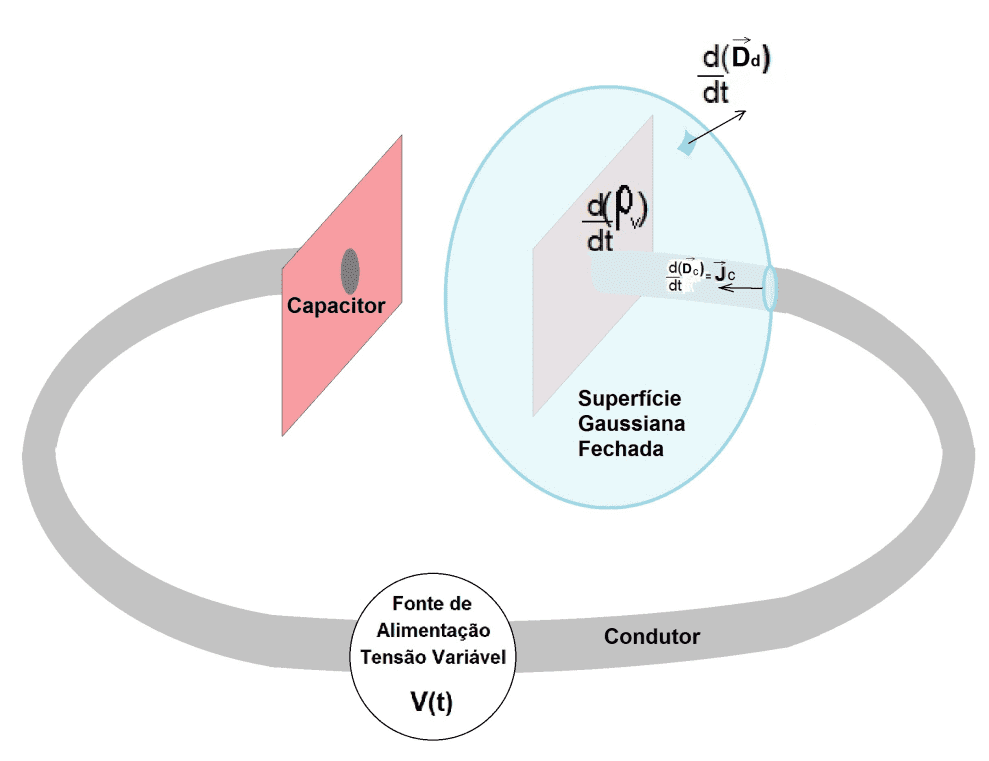
Beobachtung von Abbildung 1, mit einer Leitungsstromdichte im Treiber

, den Gleichungen (siehe Formel 6) bzw. (siehe Formel 7): für eine vollständig geschlossene Gaußsche Oberfläche; und für einen Punkt auf der Kondensatorplatte werden sie zu Gleichungen (siehe Formel 8) und (siehe Formel 3). (HAYT; BUCK et. al., 2013; SHADIKU, 2004).

Die Gleichung (siehe Formel 8) bestimmt, dass die zeitliche Variation des gesamten Dichteflusses des elektrischen Feldes, der die Gaußsche Oberfläche kreuzt, gleich der zeitlichen Variation der darin enthaltenen elektrischen Ladung ist.

Die Kontinuitätsgleichung (siehe Formel 3), die auf jedes unendlich große Volumen der positiv geladenen Kondensatorplatte angewendet wird, bestimmt, dass die Leitungsstromdichte

, die das gegebene Volumen übrig lässt, der Zeitrate entspricht, mit der die volumetrische Lastdichte auf sie fällt.

Die in diesem Artikel vorgeschlagene Hypothese geht davon aus, dass die Gleichungen (siehe Formel 8) und (siehe Formel 3) physisch komplementär sind. Daher wird davon ausgegangen, dass bei einer vollständig geschlossenen Gaußoberfläche um eine Kondensatorplatte unter dynamischen Bedingungen die Gleichungen (siehe Formel 8) und (siehe Formel 3) das folgende Format haben würden.

Wo ist die zeitliche Variation der Vektor-Elektrofelddichte, die durch die Dichte des Leitungsstroms, des gleichen Moduls,

der gleichen Richtung und Richtung desselben erzeugt wird, auf der Querschnittsfläche des Schnittpunkts zwischen dem zylindrischen Volumen des Leiters und dem Gaußschen, der darauf zeigt. Und

es ist die zeitliche Variation der Vektordichte des elektrischen Feldes, in der geschlossenen gaußschen Oberfläche, die darauf zeigt, erzeugt durch die Verschiebungsstromdichte

(zeitliche Variation der Anzahl der elektrischen Feldlinien, die die geschlossene Gaußsche aufgrund der zeitlichen Variation der gesamten elektrischen Last der Platte vom internen Kondensator zum Gaußschen kreuzen); (HAYT; BUCK et. al., 2013; SHADIKU, 2004). Abbildung 1.

Die Gleichungen (siehe Formel 9) und (siehe Formel 10) bestimmen, dass die zeitliche Variation des Gesamtflusses der elektrischen Felddichte auf einer vollständig geschlossenen Gaußschen Oberfläche gleich Null ist. Die Gleichung (siehe Formel 10) widerspricht nicht der Gleichung der Kontinuität (siehe Formel 3), da sie den Fluss der elektrischen Last, eines unendlich simalen Volumens, auf die zeitliche Variation der volumetrischen Dichte der elektrischen Ladung in ihr bezieht; bereits das, hängt nur mit der Dynamik des elektrischen Feldes zusammen.

Es wird dann angenommen, dass das physikalische Phänomen Leitungsstromdichte,

erzeugt eine Variation der elektrischen Felddichte an der

Kreuzung des zylindrischen Leiters mit der Gaußschen Oberfläche, des gleichen Moduls, Richtung und Richtung des Vektors.

Einer der Vorteile der Überprüfung dieser Hypothese wäre, die Ampere-Maxwell-Gleichung (siehe Formel 4) im folgenden Format zu verstehen (siehe Formel 11).

So wäre es intuited, dass die Wechselwirkungen zwischen Feldern, elektrischen oder magnetischen, und geladenen Teilchen, in erster Stelle Wechselwirkungen nur zwischen Feldern sein würden.

Bei der Suche nach der Richtigkeit der vorgeschlagenen Hypothese wird ein Beispiel für eine ideale hypothetische Situation für die Berechnung der vektorzeitlichen Variation der elektrischen Felddichte (siehe Formel 12) am Ursprung erstellt, erzeugt durch einen kontinuierlichen und homogenen Strom in einem zylindrischen Leiter unendlicher Länge entlang der z-Achse.

4. BEISPIEL EINER IDEALEN HYPOTHETISCHEN SITUATION

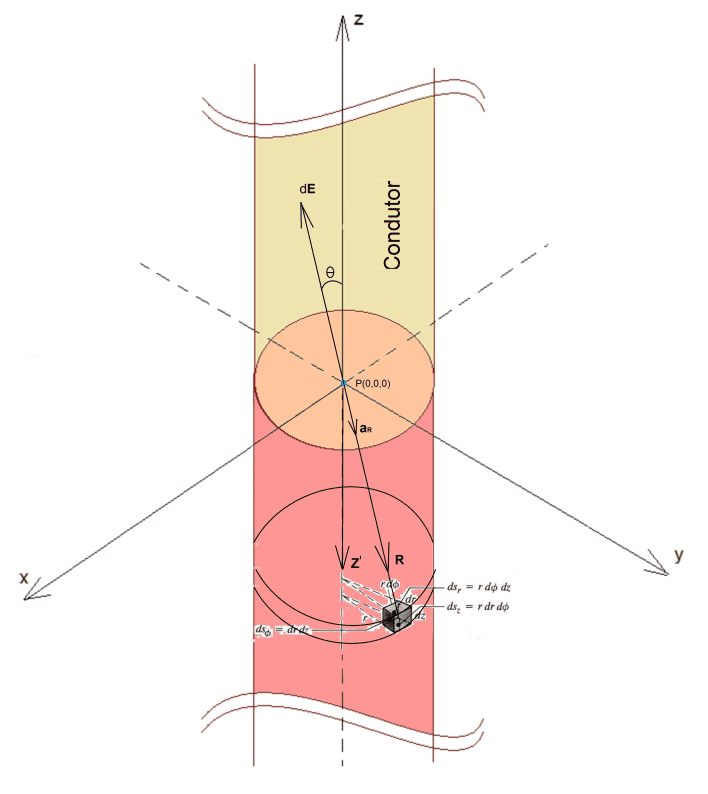
Nehmen wir folgende ideale Konfiguration an: in einem zylindrischen, geradlinigen, gleichmäßigen, homogenen Leiter, von unendlicher Länge, der durch einen Gleichstrom verläuft, von positiven, gleichmäßigen und homogenen Lasten in positiver Richtung der Z-Achse, Abbildung 2.

In zylindrischen Koordinaten wird die zeitliche Variation des elektrischen Feldvektors (siehe Formel 12) am Punkt P(0,0,0) der kartesischen Ebene in Abbildung 2 erzeugt, aufgrund der volumetrischen Verschiebung, simultan und augenblicklich, aller positiven Lasten, vor und nach diesem Punkt, in positiver Richtung der z-Achse.

Obwohl in einem realen Leiter mit einem unterschiedsmöglichen Potential in seinen Extremitäten das Jennisch ist, wurde nach klassischem Muster die Verschiebung positiver Ladungen in positiver Richtung der Z-Achse für die Berechnung gewählt.

Es ist durch Symmetrie bekannt, dass das resultierende Vektor-Elektrofeld E, das durch die Summe aller entlang des Leiters vorhandenen Lasten erzeugt wird, positiv und negativ, an Punkt P(0.0.0), null ist.

Betrachten wir jedoch zunächst die Berechnung des statischen elektrischen Feldes (siehe Formel 14), das von einem zylindrischen volumetrischen Differentialelement in Zylinderkoordinaten mit einer positiven Ladungsvolumendichte ρ_v erzeugt wird, die in einer Anfangsposition z’ zentriert ist, wobei dQ die ist Differenzlastelement, r’ ist der konstante Wert, der dem Radius des Zylinderleiters zugeordnet ist, R der Vektorabstand zwischen dem Punkt P (0,0,0) und dem volumetrischen Differenzelement dV, a_z ist der Versor in der positiven Richtung von z, und ε die elektrische Permittivität des Leiters, wie in Fig. 2 gezeigt.

Bitte beachten Sie, dass, da wir den Messpunkt des in P(0,0,0) fixierten elektrischen Feldes als Referenz nehmen, die Richtung von dE immer dem a_R versor entgegengesetzt sein wird. Daher das negative Vorzeichen in der Gleichung (siehe Formel 13).

Abbildung 2. Fahrstrom

Dann, wenn man bedenkt, dass diese geladene Differentialvolumetdiskette konstante Geschwindigkeit hat. Das elektrische

feld wird nur eine Funktion der variablen Zeit t. Unter Berücksichtigung der Ausgangsposition z’ und der Geschwindigkeit der v-Scheibe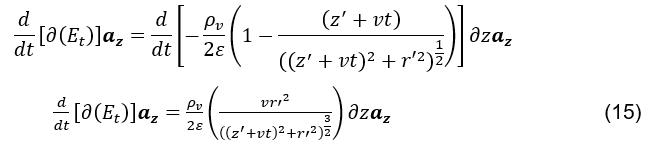

Da man die zeitliche Variation des elektrischen Feldes (siehe Formel 12) am Ursprung berechnen will, verursacht durch die Verschiebung jedes gleich hinzugefügten Differentialzylindrischen

Elements, wird ausschließlich für diese Berechnung berücksichtigt, dass die Funktion der Gleichung (siehe Formel 15) nur von der variablen Position z, abhängt.

Da der Beitrag jedes zylindrischen Differentialelements entlang der gesamten Z-Achse, der sich zur Bildung des Vektors der gesamten zeitlichen Variation des elektrischen Feldes am Punkt P (0.0.0) bewegt, weil es augenblicklich ist, hängt nicht von der variablen Zeit t ab. Ersetzen Sie z’ = z, und berücksichtigen Sie die Variable t = t₀ = 0,

Die Gleichung (siehe Formel 16) zeigt dann die Vektoräquivalenz zwischen der zeitlichen Variation der elektrischen Felddichte am Punkt P(0,0,0), erzeugt durch die sofortige und gleichzeitige Verschiebung aller positiven Ladungen entlang des unendlichen zylindrischen Drahtes, und der Leitungsstromdichte

an demselben Punkt.

5. Auswirkungen

Wenn die dargestellte Hypothese eine physikalische Wahrhaftigkeit aufweist, werden die folgenden Implikationen beobachtet:

1. Auslegung der Anwendung einer Dynamik des Gauss;
2. Neukonzeption der Gesetze von Ampere-Maxwell und Faraday-Lenz-Maxwell;
3. Vorgeschlagenes Experiment, um die Theorie zu beweisen.

5.1 INTERPRETATION DER ANWENDUNG EINES DYNAMICS VON GAUSS LAW

Gleichheit (siehe Formel 16) gilt als konsistent mit Gleichungen (siehe Formel 9) und (siehe Formel 10). Es wird daher als angemessen verstanden, dass die folgende physikalische Auslegung des Gauss, die auf die in Abbildung 1 dargestellte Situation angewendet wird, angemessen ist: Die zeitliche Variation des gesamten Flusses der elektrischen Felddichte auf einer vollständig geschlossenen Gaußschen Oberfläche ist genau Null (siehe Formel 17) und (siehe Formel 18).

Aufgrund der klassischen Wahl der aktuellen Richtung, die der Verschiebung positiver Lasten ist, um die Gleichungen (siehe Formel 24) und (siehe Formel 29) symmetrisch miteinander zu machen, wurde das negative Vorzeichen ( – ) in die Gleichheit eingefügt (siehe Formel 19).

Die folgende Interpretation der in der Gleichheit betrachteten physikalischen Phänomene wird hier vorgeschlagen (siehe Formel 19).

Die vektorzeitliche Variation der elektrischen Felddichte

, ein Ergebnis der Leitungsstromdichte, scheint

proportional zur Längsgeschwindigkeit zu sein, mit der die elektrischen Feldlinien ein Flächenelement einer Gaußschen Oberfläche kreuzen. Theoretisierung kann theoretisiert werden:

wobei v_L der Geschwindigkeitsvektor der elektrischen Feldlinien ist, die ein Flächenelement einer Gaußschen Oberfläche kreuzen, a_S der Versor des Vektorbereichselements dieser Oberfläche und K₁ eine Konstante, Abbildung 3.

Abbildung 3. Zeitliche Variation der Dichte des elektrischen Feldes, die durch

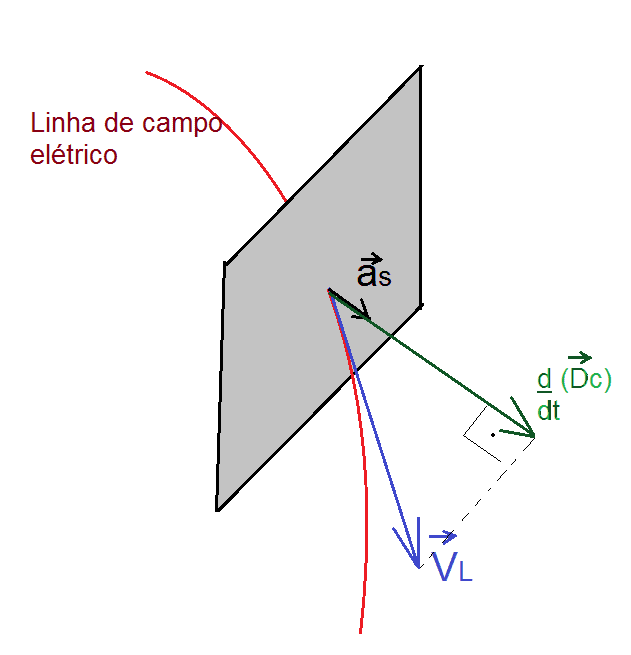
Die vektorzeitliche Variation der elektrischen Felddichte,

die sich aus der Verschiebungsstromdichte ergibt,

hängt mit der zeitlichen Variation der quantitativen Anzahl elektrischer Feldlinien zusammen, die ein Flächenelement einer Gaußschen Oberfläche kreuzen (HAYT; BUCK et. al., 2013; SHADIKU, 2004).

Die Theorie, die von der Ausgangshypothese aus vorgeschlagen wurde, dass die zeitliche Variation des gesamten elektrischen Flusses, der eine Gaußsche Oberfläche kreuzt, sowohl durch die zeitliche Variation der Anzahl der elektrischen Feldlinien, pro Flächeneinheit, die sie kreuzen, als auch

durch die Längsgeschwindigkeit der elektrischen Feldlinien, die ein Flächenelement kreuzen, gebildet werden

kann (siehe Formel 20); es wird durch Symmetrie intuitiert, dass sich der magnetische Fluss, der durch eine Gaußsche Oberfläche fließt, in gleicher Weise verhält (siehe Formel 21).

In einer Weise,

dass es sowohl durch zeitliche Variation der Anzahl der magnetischen Feldlinien in einem Flächenelement erzeugt werden könnte (HAYT; BUCK et. al., 2013; SHADIKU, 2004),

; sowie die Längsgeschwindigkeit, mit der magnetische Feldlinien ein Flächenelement kreuzen

(siehe Formel 22). Durch Symmetrie wird es analog zur Gleichung (siehe Formel 20), der Gleichung (siehe Formel 22) vorgeschlagen. Wobei v_mL der Geschwindigkeitsvektor von Magnetischen Feldlinien ist, die ein Flächenelement einer Gaußschen Oberfläche kreuzen, a_S der Versor des Flächenelementvektors dieser Oberfläche und K₂ eine Konstante.

5.2 NEUES DESIGN VON AMPERE-MAXWELL UND FARADAY-LENZ-MAXWELL LAWS

In Anbetracht der Möglichkeit der Wahrhaftigkeit in der vorgestellten Hypothese könnte man sich das Ampere-Maxwell-Gesetz (siehe Formel 5) und das Faraday-Lenz-Maxwell-Gesetz (siehe Formel 23) vorstellen.

(siehe Formel 24) und (siehe Formel 25).

5.3 VORGESCHLAGENES EXPERIMENT, UM DIE THEORIE ZU BEWEISEN.

Der vorliegende Artikel zielt kurz und bündig darauf ab, am Ende eine Theorie vorzuschlagen, die auf hypothetischen Situationen beruht, ohne physikalische Experimente im Labor zum Beweis.

Im Folgenden wird jedoch ein Vorschlag für ein Laborexperiment vorgelegt, um die Richtigkeit der vorgeschlagenen Theorie zu beweisen oder zu widerlegen.

Für die Berechnung eines Magnetfeldes H, das ausschließlich aus einer Leitungsstromdichte unter Verwendung der

Gleichheit erzeugt wird (siehe Formel 16), könnte das Biot-Savart-Gesetz (siehe Formel 27) wie in (siehe Formel 28) beschrieben werden.

Dann wird vorgeschlagen, das modifizierte Biot-Savart-Gesetz (siehe Formel 28) symmetrisch für die Berechnung des elektrischen Feldes zu schreiben, wie in (siehe Formel 29).

Um die Richtigkeit der Theorie zu überprüfen, dass die elektrischen und magnetischen Felder durch die Verschiebungsgeschwindigkeit der Felder (magnetisch und elektrisch) erzeugt werden können, wird das folgende Experiment vorgeschlagen.

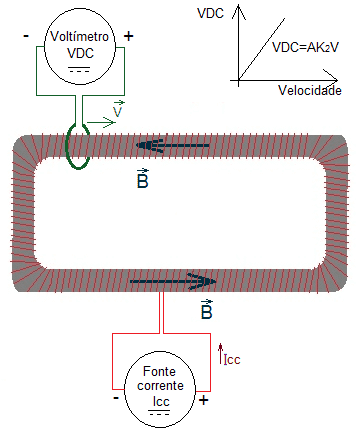
Es ist ein elektrischer Stromkreis, der durch einen isolierten leitfähigen Draht gebildet wird, der in einer verteilten und kontinuierlichen Weise um ein ferromagnetisches Material der toroidalen Topologie gewickelt wird, Bereich A Konstante des Querschnitts, gespeist durch eine Gleichstromquelle, mit einem Strom, der so eingestellt ist, dass er das ferromagnetische Material nicht magnetisch sättigt. Es wird eine magnetische Felddichte B geben, die auf alle toroidalen ferromagnetischen Materialien beschränkt ist (HALLIDAY; RESNICK; WALKER et. al., 2013), Abbildung 4.

Wobei die magnetische Durchlässigkeit des ferromagnetischen Materials, N die Anzahl der Umdrehungen und l der Umfang, der durch den Querschnitt des Toroide während seiner Gesamtenkundung durchquert wird.

Dann wird eine isolierte leitfähige Drahtmessdrehung um den Querschnitt der Toroide verwendet, die mit einem VDC-Voltmeter verbunden ist, so dass es möglich ist, die Messspule entlang des Toroidalumfangs zu verschieben, Abbildung 4.

Es ist bekannt, dass das Magnetfeld, das von einem idealen toroidalen elektrischen Schaltkreis erzeugt wird, außerhalb davon null ist (HALLIDAY; RESNICK; WALKER et. al., 2013).

Nach der vorgestellten Theorie, wenn die Messspule bewegt sich mit einer Geschwindigkeit V entlang der toroidalen Umfang, auch wenn die Anzahl der magnetischen FelddichteLinien internal to the turn nicht geändert wird, werden diese Linien durch die Gaußsche Oberfläche durch den Umfang der Messspule gebildet, mit –V Geschwindigkeit.

Unter Anwendung der vorgeschlagenen Gleichung (siehe Formel 22) auf das Faraday-Lenz-Maxwell-Gesetz (siehe Formel 23) sollte die im Voltmeter gemessene Spannung wie:

Wo ist der Bereich des Querschnitts der Toroide.

Daher wird vorgeschlagen, eine Kurve der Messungen VDC x V zu erhöhen, wobei VDC die im Voltmeter gemessene Spannung und V der Geschwindigkeitsvektor der Messdrehung entlang des Toroidalumfangs ist, Abbildung 4. Nach der vorgeschlagenen Theorie sollte diese Kurve eine gerade Linie mit einer AK₂, Neigung sein, Abbildung 4.

Abbildung 4. Vorgeschlagenes Experiment zum Nachweis der vorgeschlagenen Theorie

Wenn das Experiment mit einem Ergebnis durchgeführt wird, das die vorgeschlagene Theorie bestätigt, wird auch vorgeschlagen, die Existenz der folgenden leitenden magnetischen

Stromdichte zu berücksichtigen.

6. FAZIT

Um die Natur der Verschiebungs- und Leitungsströme besser zu verstehen, wurde die Hypothese aufgestellt, dass in einer vollständig geschlossenen Gaußschen Oberfläche die zeitliche Variation des gesamten elektrischen Feldflusses in ihr immer gleich Null sein könnte (siehe Formel 9) und (siehe Formel 10), was der Kontinuitätsgleichung nicht widerspricht (siehe Formel 3).

Es wurde ein Beispiel für eine ideale hypothetische Situation geschaffen, die eine mathematische Analyse der erstellten Hypothese ermöglichen würde.

Das Ergebnis dieser Analyse, Gleichheit (siehe Formel 16), bestätigt die Vorstellung, dass die vektorzeitliche Variation der Gesamtdichte des elektrischen Feldes (siehe Formel 19) aus den folgenden beiden unterschiedlichen physikalischen Phänomenen bestehen kann.

1 –

–

Zeitliche Variation der Vektordichte des elektrischen Feldes in einem Flächenelement, in Abhängigkeit von der zeitlichen Variation der Anzahl der elektrischen Feldlinien, die es kreuzen. Dies ist das klassische Verständnis des Phänomens der Verschiebungsstromdichte, das zuerst von J.C.Maxwell erkannt wurde. (HAYT; BUCK et. al. 2013; SHADIKU, 2004)

2 –

– Zeitliche Variation der Vektordichte des elektrischen Feldes in einem Flächenelement, in Abhängigkeit von der Längsgeschwindigkeit der elektrischen Feldlinien, die es kreuzen (siehe Formel 20), aufgrund einer Leitungsstromdichte (siehe Formel 16);

Unter der Prämisse der Symmetrie zwischen dem Verhalten der elektrischen und magnetischen Felder, ähnlich wie die Gleichungen (siehe Formel 19) und (siehe Formel 20) wurde die Möglichkeit des Magnetfeldes in der gleichen Weise betrachtet (siehe Formel 21) und (siehe Formel 22) betrachtet.

So wird eine Theorie vorgeschlagen, dass alle Wechselwirkungen zwischen Feldern, elektrischen oder magnetischen, und elektrisch geladenen Teilchen, in erster Stelle Wechselwirkungen nur zwischen Feldern sind. Wenn Sie z. B. einen potenziellen Unterschied in einem elektrischen Stromkreis anwenden, interagiert das elektrische Feld, das durch den potenziellen Unterschied erzeugt wird, mit dem elektrischen Feld der freien Lasten und zwingt sie, sich zu bewegen. Die Verschiebung der Lasten impliziert die Verschiebung ihrer elektrischen Feldlinien. Die Längsgeschwindigkeit, mit der diese Linien ein Flächendifferenzelement durchqueren, wäre proportional zum darin enthaltenen

Vektor.

Unter Berücksichtigung der Möglichkeit der Wahrhaftigkeit von Gleichungen (siehe Formel 9) und (siehe Formel 10), abgeleitet von der Dynamik des Gauß-Gesetzes, wird das Ampere-Maxwell-Gesetz (siehe Formel 5) im Format (siehe Formel 24) mit größerer Symmetrie zum Faraday-Lenz-Maxwell-Gesetz (siehe Formel 25) geschrieben.

Schließlich wird ein Laborexperiment vorgeschlagen, um die vorgeschlagene Theorie und ihre Gleichungen zu bestätigen oder zu diskreditieren.

Im Folgenden finden Sie die in diesem Artikel vorgeschlagenen Gleichungen.

REFERENZEN

FARADAY, M. Experimental Researches in Electricity. B.Quaritch, Londres, 1939, p.1855.

FARADAY, M. Great Books of the Western World. Vol. 45, encyclopedia Britannica Inc., Chicago, 1952, p. 217-866.

HALLIDAY, D; RESNICK, R; WALKER, J. Fundamentos de Física.  V.3, ED.9ª, LTC, Rio de Janeiro 2013.

HAYT, W.H; BUCK, J.A.  Eletromagnetismo.  ED.8ª, AMGH, Porto Alegre, 2013, p. 48-290.

JACKSON, J.D. Classical Eletrodynamics. ED.3ª, University of California, Berkeley, 1998, p. 237-239.

MAXWELL, J.C. A Treatise on Electricity and Magnetism. Oxford Univ. Press, Oxford, 2002.

MAXWELL, J.C. The Scientific Papers of James Clerk Maxwell. Dover Publ., New York, 1965, v. 1, p. 451.

PLONSEY, R; COLLIN, R.E. Principles and Applications of Electromagnetic Fields. McGraw-Hill, New York, 1961, Topic 2.

SHADIKU, M.N.O. Elementos de Eletromagnetismo. ED.3ª, Bookman, Porto Alegre, 2004, p. 107-350.

^[1] Postgraduate in Electrical Engineering (Instrumentation) von PUC-MG (2008), Abschluss in Elektrotechnik am CEFET-MG (2007).

Eingesandt: Juli 2020.

Genehmigt: August 2020.