ARTIGO ORIGINAL
NECO, Diego Correa [1]
NECO, Diego Correa. Inteligência Artificial Em Otimização De Centrais Hidrelétricas. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano 06, Ed. 03, Vol. 15, pp. 70-81. Março de 2021. ISSN: 2448-0959, Link de acesso: https://www.nucleodoconhecimento.com.br/engenharia-eletrica/centrais-hidreletricas, DOI: 10.32749/nucleodoconhecimento.com.br/engenharia-eletrica/centrais-hidreletricas
RESUMO
Este trabalho apresenta a implementação de uma rede neural Multilayer Perceptron para o levantamento do diagrama de colina (diagrama do campo de operação de uma turbina hidráulica) para posteriormente obter o controle do modo operativo do grupo gerador. Esta rede utiliza uma série de dados de ensaios práticos desenvolvidos através do programa Matlab com o algoritmo de Levenberg-Marquadt que é modelado utilizando Inteligência Artificial o comportamento de uma turbina Francis com o intuito de otimizar a central hidrelétrica aumentando a eficiência do grupo gerador. As curvas de colina são usualmente obtidas para a operação tradicional em rotação fixa. Este diagrama determina o campo básico de funcionamento da turbina, entretanto nem sempre é possível fazer o levantamento em campo desse diagrama, ou seja, com a aplicação deste algoritmo otimizamos o tempo e possíveis erros em um levantamento manual de dados.
Palavras Chaves: Geração, Inteligência Artificial, Hidrelétrica.
1. INTRODUÇÃO
Neste tópico será levantado o estado da arte das principais técnicas de otimização. As técnicas de otimização clássicas, apresentam limitações na otimização de plantas geradores com elevado número de grupo geradores.
A otimização está relacionada à melhoria de algo existente, com o objetivo de obter soluções não tradicionais com custo reduzido (SILVA, 2005).
De acordo com Torga (2007), a busca pela solução ótima pode ser realizada pelo uso de algoritmos desenvolvidos para procurar a solução ótima, sem avaliar todas as soluções possíveis.
Há diversos métodos para implementação, dentre as áreas destacam-se: Otimização combinatória, programação não-linear e programação linear (BASTOS, 2004).
A programação não linear (PNL): é aplicável em diversas situações, sendo elas: Programação convexa, programação quadrática; multiplicadores de Lagrange; entre outras. A PNL têm por finalidade solucionar questões que envolvem funções de variáveis não-lineares entre si (desproporcionais). As soluções para problemas não-lineares, apresenta maior dificuldade quando comparado aos lineares (BROOKE; KENDRIK; MEERAUS, 1997). Nos problemas de programação linear a solução encontrada é ótima. Enquanto na PNL não é possível afirmar que a solução é ótima. Sendo necessário analisar a concavidade ou a convexidade da função (WISTON; ALBRIGHT, 2001).
A programação multiobjetiva: é uma técnica de otimização que permite a modelagem para problemas com múltiplas metas a serem otimizadas. A programação por metas busca minimizar os desvios no alcance dos objetivos. Sem a preocupação de maximizar ou minimizar a função-objetivo diretamente, ou seja: buscando solucionar uma condição aceitável e não necessariamente atingir plenamente as metas (MARINS, 2013).
Mas o trabalho de Marins (2013), detalha os tipos de programação por meta, sendo elas:
- Programação por Metas ponderada;
- Programação por Metas com priorização;
- Programação por Metas Minmax;
- Programação por Metas estendida;
- Programação por Metas inteira;
- Programação por Metas binária; e
- Programação por Metas e Análise por Envoltória de dados.
Na otimização combinatória: tem-se os métodos exatos e heurísticos para conduzir a solução ótima no espaço de estados. O método exato busca uma solução ótima, enquanto os métodos heurísticos buscam soluções próximas a um valor ótimo. Enquanto o método heurístico abrange o método o meta-heurístico, podendo citar o algoritmo genético (SANTOS, 2001).
Em Bastos (2004) apresenta a proposta da otimização da operação de plantas hidrelétricas com elevados números de unidades. O método exato é inviável, devido as inúmeras variáveis combinatórias (o que levaria muito tempo de processamento). Esse método constrói múltiplas trajetórias de busca, e suas soluções são combinações das soluções obtidas anteriormente. A otimização combinatória é amplamente usada em problemas de conexão, cobertura e localização. Em geral, a otimização combinatória busca a solução ótima do problema, dentre todos os subconjuntos.
Meta-heurísticas são técnicas de otimização que geram procedimentos de busca baseados em escolhas aleatórias e tendo o conhecimento de resultados iniciais. Sendo aplicadas em problemas de difícil solução, como é apresentado na otimização diária em centrais em cascata utilizando essa técnica de otimização (GOMES, 2018). Em Moreno (2012) faz a otimização em geração hidroelétrica, auxiliando no planejamento diário da operação.
2. INTELIGÊNCIA ARTIFICIAL NA OTIMIZAÇÃO
2.1 ESTADO DA ARTE
Nesse tópico é realizado uma revisão bibliográfica do surgimento e utilização da inteligência artificial (IA). Os algoritmos heurísticos genéricos são conhecidos como meta-heurísticas. Os pesquisadores em Lima; Pinheiro E Santos (2014), trazem o tema IA de maneira profunda e recorrente em seus trabalhos.
As primeiras pesquisas na área de redes neurais artificiais surgiram na década de 40 (1943) (MCCULLOCH; PITTS, 1943). Ainda na mesma década Donald Hebb (1949) descreveu o funcionamento quantitativo da sinapse e do processo de treinamento humano em seu livro. O postulado de aprendizagem de Hebb, é usado atualmente no desenvolvimento de modelos computacionais de sistemas de aprendizagem. Já no final dos anos 50, Rosenblatt motivou diversas pesquisas na área a partir do seu trabalho (ROSENBLATT, 1958, p. 386-408).
De 1969 até 1986, com os trabalhos de Minsky, sobre os Perceptrons (MINSKY, 1961, p. 8-32) e (MINSKY; PAPERT, 1969). Ocorreu um desencorajamento na utilização das redes neurais artificias devido as limitações e incapacidade de solucionar problemas relativamente simples. A partir do surgimento (1986) do algoritmo backpropagation (RUMELHART; HINTON; WILLIAMS, 1986, p.57-65) de treinamento para redes de múltiplas camadas, ocorreu a desestagnação da utilização das redes neurais artificiais. Enquanto Rumelhart publicou na década de 90 uma predição do futuro do algoritmo backpropagation (RUMELHART; WEIGEND, 1990).
2.2 REDES NEURAIS ARTIFICIAIS
Uma rede neural artificial é baseada no modelo do sistema nervoso humano, o qual contém uma coleção de elementos de processamento (neurônios) que se comunicam através da junção entre o dendrito e o axônio (sinapses). O tempo de resposta, para os neurônios artificiais são em torno de um milhão de vezes mais rápidos, quando comparado com os neurônios naturais. Entretanto o grau de conectividade dos neurônios artificiais é 0,1 porcento quando comparado com o cérebro humano (THOMPSON, 1986, p.57-65).
Segundo Haykin (2001), uma rede neural é um processador constituído de unidades de processamento simples, assemelhando-se ao cérebro em dois comportamentos:
- O conhecimento é adquirido pela rede a partir do processo de aprendizagem;
- Os pesos sinápticos, são utilizados no armazenamento do conhecimento adquirido.
Algumas vantagens na utilização das redes neurais artificiais (SILVA, 2005):
- Auto aprendizado;
- Implementação mais rápida;
- Imunidade a falhas e ruídos;
- Capacidade de generalização; e
- Qualidade superior as análises estatísticas convencionais.
Algumas desvantagens na utilização das redes neurais artificiais:
- Treinamento demorado;
- Volume grande de dados;
- Preparação dos dados de entrada; e
- Resultados que contrariam regras e teorias estabelecidas.
Sendo apresentado as funções de ativação e as regras de aprendizagem:
Os três tipos de funções de ativação mais usados para mapear uma rede neural artificial (HAYKIN, 2001):
- Função de limiar: A saída do neurônio assume valor 1 quando seu resultado for positivo, e 0 quando o valor da saída for negativo;
- Função linear por partes: Essa função pode ser considerada uma aproximação de um amplificador não-linear;
- Função sigmóide: É o tipo mais utilizada na construção das redes neurais artificiais. Pode apresentar várias formas, sendo a mais comum a função logística (opção adotada neste trabalho).
Enquanto as principais regras de aprendizagem segundo (HAYKIN, 2001), são:
- Aprendizagem por correção de erro;
- Aprendizagem baseada em memória;
- Aprendizagem Hebbiana;
- Aprendizagem competitiva; e
- Aprendizagem de Boltzmann.
A regra de aprendizagem por correção de erro consiste no ajuste dos pesos sinápticos com o objetivo de minimizar o erro entre a saída da rede e a saída esperada. Quando o erro atinge um valor mínimo pré-estabelecido, os pesos sinápticos não são mais alterados.
Devem ser fornecidos para a rede um conjunto de dados de entrada e um conjunto das saídas esperadas. O erro entre a saída da rede e a saída esperada é utilizado na correção nos pesos sinápticos. Esse algoritmo de treinamento para uma rede neural de múltiplas camadas é chamado de Backpropagation (RUMELHART; HINTON; WILLIAMS, 1986, p. 323:533-536).
3. LEVANTAMENTO DA CURVA DE COLINA
Segundo Saidel (1995), as curvas de colina são usualmente obtidas para a operação tradicional em rotação fixa. Este diagrama determina o campo básico de funcionamento da turbina, entretanto nem sempre é possível fazer o levantamento em campo desse diagrama.
No levantamento da curva de colina é utilizado o algoritmo de Levenberg-Marquardt. O método foi desenvolvido por Levenberg (LEVENBERG, 1944, p. 164–168), e aprimorado por Marquardt (MARQUARDT, 1963, p. 431–441). Este método depende intrinsecamente da escolha do parâmetro damping (NIELSEN, 2005), conhecido como parâmetro Levenberg-Marquardt. Existem diversos trabalhos publicados acerca desse método (NIELSEN, 2003), (MORÉ, 1987, p. 105–116), (MEDEIROS, 2008), e (BENATTI, 2017).
Na região amazônica brasileira, o tipo de turbina mais adequado para o grande fluxo de água e níveis de quedas reduzidas, conforme o valor da rotação específica é a turbina com rotor Kaplan. As usinas de Santo Antônio e Jirau próximas a Porto Velho (capital de Rondônia), apresentam grupos geradores com potência unitária superior a 70MW. Sendo um desafio operar de maneira otimizada. Em Bortoni; Souza e Bastos (2003), mostra a otimização de pequenas centrais. Enquanto Bastos (2004), apresenta em sua dissertação a otimização de 10 unidades geradoras. A equipe de pesquisadores em Bazaraa (1979) faz um estudo sobre a otimização da geração com rotação variável.
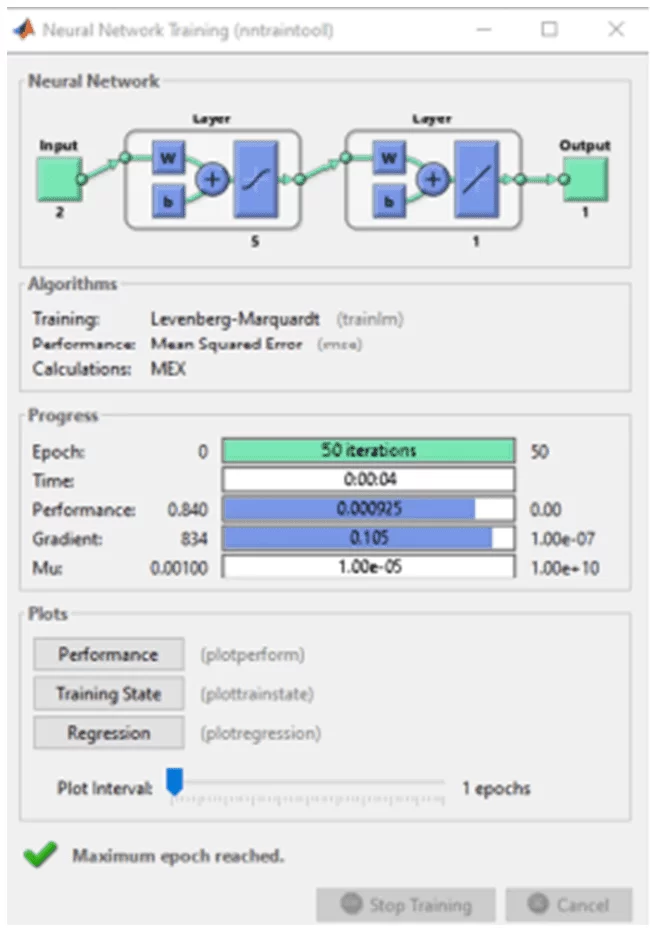
A seguir é apresentado a rede neural de treinamento (figura 1) e o diagrama de colina (figura 2) resultado da simulação do algoritmo desenvolvido neste trabalho, baseado na dissertação Passos (2011).
Fig. 1: Rede neural de treinamento.
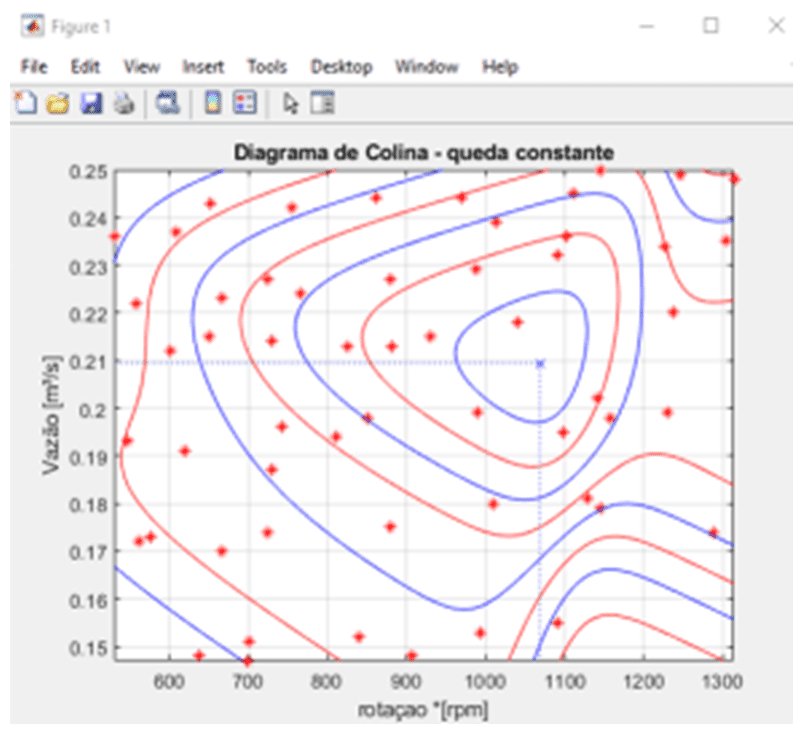
Na figura 2 é apresentado o diagrama de colina operando com queda constante. Sendo de interesse na otimização a operação na região de maior rendimento.
Fig. 2: Diagrama de colina de uma turbina Francis.
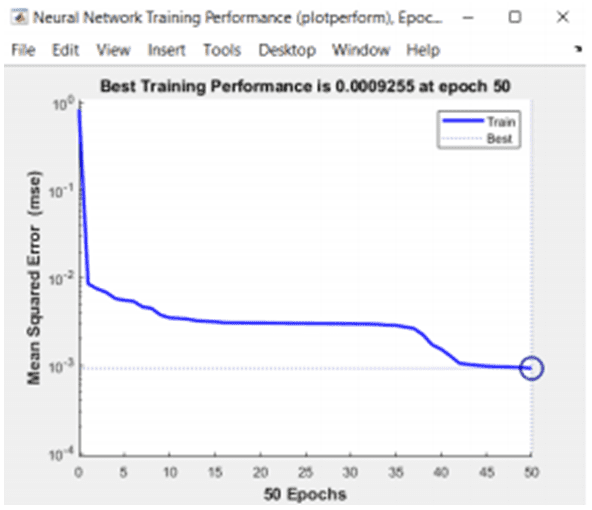
Nas figuras 3, 4 e 5 os parâmetros de treinamento da rede neural, assim como a performance.
Fig. 3: Parâmetros de treinamento.
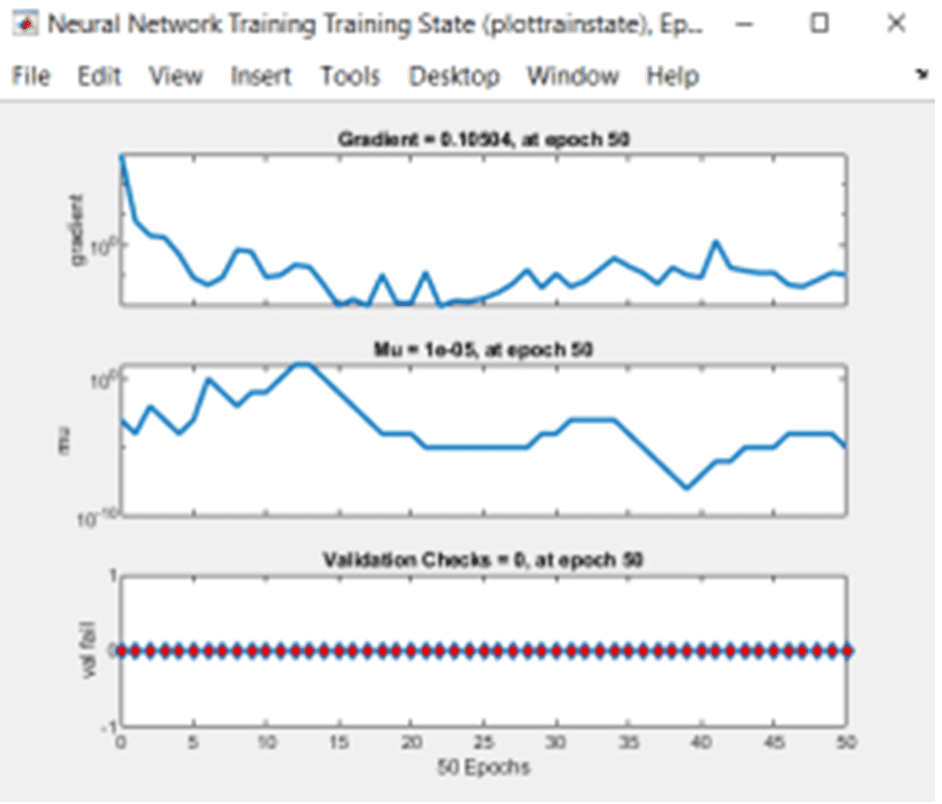
Fig. 4: Regressão linear.
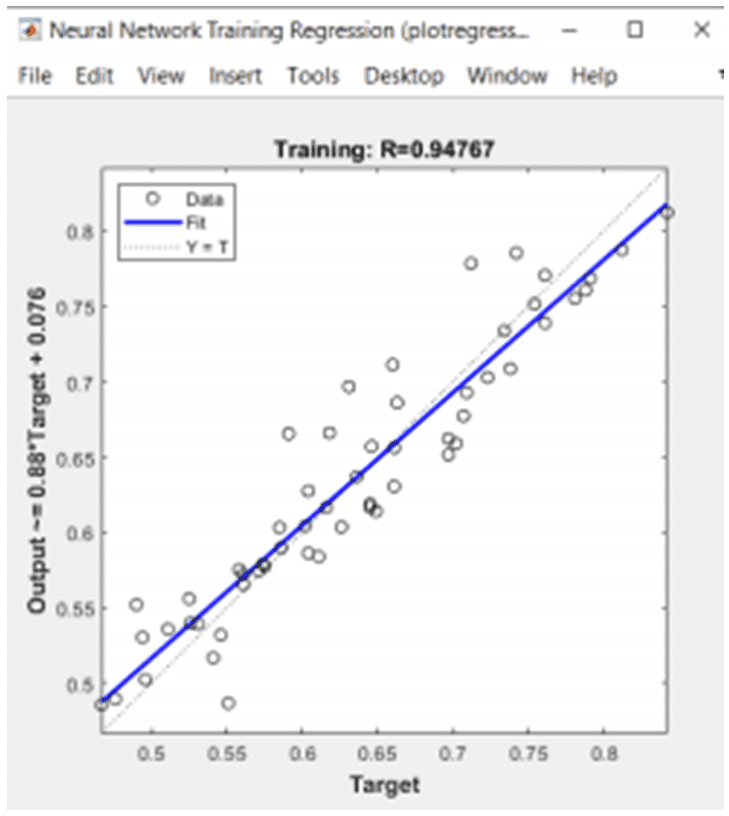
Fig. 5: Treinamento do erro.
4. CONCLUSÃO
A partir da revisão do estado da arte dos métodos de otimização em centrais hidrelétricas é possível constatar a importância do tema na geração de energia hidráulica. A inteligência artificial se mostrou um forte aliado no levantamento dos diagramas de rendimento das turbinas hidráulicas, apresentando elevado rendimento no levantamentos desses gráficos, podendo ser implementado inclusive em tempo real.
REFERÊNCIAS BIBLIOGRÁFICAS
BASTOS, G. S., “Otimização da Operação de Centrais Hidrelétricas pela Distribuição Inteligente de Carga entre Máquinas.”, Dissertação de Mestrado, Universidade Federal de Itajubá, 2004.
BAZARAA, M. S. S. C. M., “NonLinear Programming: Theory and Algorithms”, John Wiley & Sons, 1979.
BENATTI, K. A., “O Método de Levenberg- Marquardt para o Problema de Quadrados Mínimos não Linear,” Dissertação de Mestrado, Universidade Federal do Paraná, 2017.
BORTONI, E. C., L. E. SOUZA E BASTOS G. S., Integração de equipamentos para a operação otimizada de grupos geradores em pequenas centrais hidrelétricas. In: SEMINÁRIO NACIONAL DE CONTROLE E AUTOMAÇÃO, 3. 2003, Salvador. Anais… Salvador:UFBA, 2003.
BORTONI, E. C., SOUZA, Z., VIANA, A., REZEK, A., L. PINTO, SINESCALCHI R., BRAGANÇA R. A. E BERNARDES J. V., “Avaliação da Introdução da Geração com Rotação Variável no Sistema Furnas,” VII Encontro Nacional de Máquinas Elétricas, vol. 1, pp. 1-10, 2018.
BROOKE, A.; KENDRIK, D. e MEERAUS, A., GAMS – Sistema Geral de Modelagem Algébrica. São Paulo, Edgard Blucher Ltda, 1997.
GOMES, C. A., “Otimização da Operação Diária de Usinas Hidrelétricas em Cascata Ulizando Metaheurísticas.”, Dissertação de Mestrado, Universidade Federal do Rio de Janeiro, 2018.
HAYKIN, S., Redes neurais: princípios e práticas. 2 ed. Porto Alegre: Bookmann, 2001.
HEBB, D. O., The Organization of Behaviour: A Neuropsychological Theory, New York: Psychology Press, 1949.
LEVENBERG, K., “A method for the solution of certain problems in least squares”. Quart. Ap. Math. 2, 1944, pp. 164–168.
LIMA, I., C. PINHEIRO, A. M. e SANTOS, F. A. O., Inteligência Artificial. Rio de Janeiro: Elsevier. Julho. 2014.
LOURAKIS, M. I. A., A. Brief Description of the Levenberg Marquardt Algorithm Implemented by levmar. Institute of Computer Science. Foundation for Research and Technology. 2005.
MARINS, A. F. S. e. F. A., “Revisão da literatura sobre modelos de Programação por Metas determinística e sob incerteza.”, FEG/UNESP, 2013.
MARQUARDT, D., “An algorithm for least squares estimation of nonlinear parameters”. J. Soc. Indust. Ap. Math. 11, 1963, pp. 431–441.
MCCULLOCH, W. S. e PITTS, W., “A logical calculus of the ideas immanent in nervous activity.” Bulletin of Mathematical Biophysics. Vol.5, p.115-133, 1943.
MEDEIROS, L. A. d. S., “Acelerando o método de Levenberg- Marquardt para a minimização da soma de quadrados de funções com restrições em caixa,” Tese (Doutorado em Matemática Aplicada) – Programa de Pós-Graduação em Matemática, Campinas: UNICAMP, 2008.
MINSKY, M. L., Steps Towards Artificial Intelligence. In Proc. of the Institute of Radio Engineers 49, p. 8-32, 1961.
MINSKY, M.; PAPERT, S. Perceptrons Cambridge, Mass: MIT Press, 1969.
MORÉ, J. J., “The Levenberg-Marquardt algorithm: implementation and theory”. Em Proceedings of the 1977 Dundee conference on numerical analysis, Lecture Notes in Mathematics 630. G. A. Watson. (Ed.) Berlin, Springer, 1978, pp. 105–116
MORENO, S. R., “Otimização do Planejamento diário de Geração em Usinas Hidrelétricas.”, Dissertação de Mestrado, UFPR, 2012
NIELSEN, H. B., “Damping parameter in Marquardt’s method”. Report IMM-REP1999-05, Technical University of Denmark, Lyngby, Dinamarca, 2005.
O. M. R., “Nonlinear least squares–the Levenberg algorithm revisited”. J. Austral. Math. Soc. (Ser. B) 19, 1976, pp. 343–357.
PASSOS ISMAEL, O., “Metodologia de Obtenção de Curvas de Colina Usando Redes Neurais para Geração Hidroelétrica.” Dissertação de Mestrado, Universidade Federal do Pará, 2011.
ROSENBLATT, F., The perceptron: a probabilistic model for information storage and organization in the brain. Psychological Review. Vol.65, p.386-408, 1958.
RUMELHART, D., G. E. HINTON, and R. J. WILLIAMS. Learning Representations by Back-propagation Error. Nature, p. 323:533-536, 1986.
RUMELHART, D. E.; WEIGEND, S. A., Predicting the Future: A Connectionist Approach. Stanford, 1990.
SAIDEL, M., “Rotação Ajustável em Usinas Hidroelétricas: Novas Premissas para o Planejamento Energético.”, Tese de Doutorado, USP, São Paulo, SP, Brasil,1995.
SANTOS, E. F., “Um Modelo de Pré-Despacho em Usinas Hidrelétricas Usando Algoritmos Genéticos.”, Dissertação de Mestrado, Unicamp, 2001.
SILVA, W. A., Otimização de Parâmetros da Gestão Baseada em Atividades Aplicada em uma Célula de Manufatura. Dissertação (Mestrado em Engenharia de Produção). UNIFEI. Itajubá-MG. 2005.
SOUZA, Z., A. H. M. SANTOS, e BORTONI, E. C., Hidro power plants – Studies for implantation, Third Edition ed., Rio de Janeiro: Interciência, 2018.
THOMPSON, C., “Redes neurais artificiais,” Revista Augustus, Vol.4, nr.6, p.57-65, ago, 1986.
TORGA, B. L. M., Modelagem, Simulação e Otimização em Sistemas Puxados de Manufatura. Dissertação (Mestrado em Engenharia de Produção). UNIFEI. Itajubá-MG. 2007.
WISTON, W. e ALBRIGHT, S. C., Practical Management Science. 2nd, Duxbury Thomson Learning, 2001.
[1] Pós-Graduação. Graduação em Engenharia Elétrica.
Enviado: Fevereiro, 2021.
Aprovado: Março, 2021.
