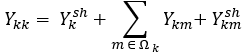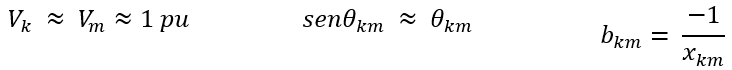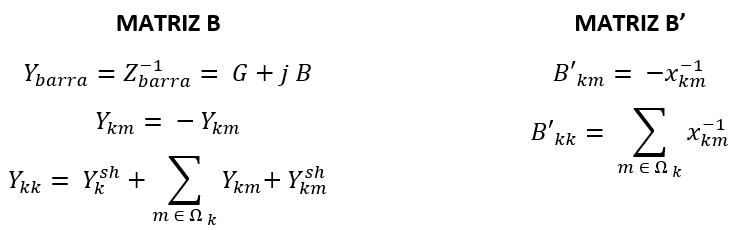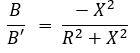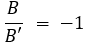Ferramenta Computacional Para Determinação Do Fluxo De Potência Linearizado Em Sistemas Elétricos De Potência

ARTIGO ORIGINAL

SANTOS, Liedson Oliveira dos ^[1]

SANTOS, Liedson Oliveira dos. Ferramenta Computacional Para Determinação Do Fluxo De Potência Linearizado Em Sistemas Elétricos De Potência. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano 06, Ed. 03, Vol. 12, pp. 95-110. Março de 2021. ISSN: 2448-0959, Link de acesso: https://www.nucleodoconhecimento.com.br/engenharia-eletrica/potencia-linearizado, DOI: 10.32749/nucleodoconhecimento.com.br/engenharia-eletrica/potencia-linearizado

RESUMO

O estudo do fluxo de potência possui fundamental importância no planejamento, bem como na determinação das condições de operação, controle e supervisão de sistemas elétricos. A solução clássica do problema de fluxo de potência é obtida por métodos não lineares, entretanto, o método linearizado é comumente utilizado em fases iniciais dos estudos devido à sua ótima precisão e seu baixo custo e esforço computacional. Neste contexto, este trabalho tem como objetivo geral descrever o embasamento teórico do Fluxo de Potência Linearizado e desenvolver uma ferramenta computacional que implemente este modelo, sendo capaz de determinar os ângulos e a distribuição dos fluxos de potência ativa para uma rede elétrica. A apresentação formal dos resultados será feita utilizando o sistema de 14 barras do IEEE, amplamente utilizado pela comunidade acadêmica para validação e teste de programas computacionais. A ferramenta mostrou-se convergente tendo apresentado a solução correta do fluxo de potência ativa para um sistema elétrico teórico utilizado no livro de Alcir Monticelli, bem como para o sistema teste da IEEE quando comparado com a solução do software FLUPOT da Cepel.

Palavras-chave: Fluxo de Potência Linear, Fluxo de Potência Linearizado, Fluxo de Potência CC, Fluxo de Potência DC.

1. INTRODUÇÃO

A função dos sistemas de energia elétrica é fornecer as potências ativas e reativas necessárias às diversas cargas conectadas à rede. Neste contexto, o estudo do fluxo de potência possui fundamental importância no planejamento, bem como na determinação das melhores condições de operação, controle e supervisão de sistemas elétricos (ELGERD, 1981).

O problema do fluxo de potência consiste na determinação do estado da rede, cuja solução é obtida por métodos numéricos de equações não lineares. Entretanto, a distribuição dos fluxos de potência ativa pelos ramos de uma rede pode ser estimada a um baixo custo e esforço computacional por meio do método linearizado, com precisão aceitável para uma série de aplicações desde o planejamento da expansão até a operação de redes elétricas (MONTICELLI, 2003).

O Fluxo de Potência Linearizado, comumente chamado de Fluxo de Potência CC ou DC é baseado no acoplamento da potência ativa (P) e do ângulo de fase (θ) e explora o fato que o fluxo de potência ativa em uma linha de transmissão é aproximadamente proporcional à abertura angular na linha e se desloca no sentido dos ângulos maiores para os ângulos menores (MONTICELLI, 1983).

O modelo linearizado não pode substituir por completo os métodos não lineares, pois ele não considera em sua formulação as magnitudes das tensões nodais e as potências reativas do sistema, porém ressalta-se que este modelo possui grande utilidade em fases iniciais de estudos. Em fases mais avançadas, se for necessário conhecer o valor das tensões, por exemplo, outros métodos clássicos poderão ser utilizados.

Neste contexto, o objetivo desse trabalho é descrever o embasamento teórico do Fluxo de Potência Linearizado e desenvolver uma ferramenta computacional que implemente este modelo, sendo capaz de determinar os ângulos e a distribuição de fluxo de potência ativa para uma rede elétrica. A apresentação formal dos resultados será feita utilizando o sistema de 14 barras do IEEE, amplamente utilizado pela comunidade acadêmica para validação e teste de programas computacionais.

2. FLUXO DE POTÊNCIA LINEAR

Sistemas elétricos fornecem as potências ativas e reativas às diversas cargas conectadas na rede e simultaneamente, a frequência e as várias tensões de barra devem ser mantidas dentro de limites especificados, apesar das variações, por vezes grandes e até certo ponto imprevisíveis, que podem apresentar as demandas das cargas (ELGERD, 1981).

A determinação do fluxo de potência depende, dentre outros fatores, dos elementos da matriz de admitância das barras do sistema, denominada de matriz Y que relaciona as tensões nodais com as correntes injetadas ao sistema através de geradores, Lei de Kirchhoff das Correntes, (MONTICELLI, 1983).

A Figura 01 apresenta a representação do modelo equivalente π para uma linha de transmissão, esquema importante para a determinação do fluxo de potência.

Figura 01: Modelo equivalente π para uma linha de transmissão.

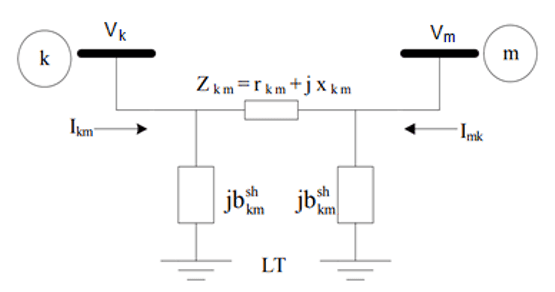
As linhas que possuem a representação dada por um modelo equivalente π podem ser definidas por três parâmetros básicos: a resistência série (r_km), a reatância série (x_km) e a susceptância shunt (?_?^?ℎ). A impedância z_km do elemento série é dada pela soma da resistência e da reatância. A admitância série por sua vez, é dada pelo inverso da impedância. Desta forma:

A condutância g_km e a susceptância b_km são descritas matematicamente por:

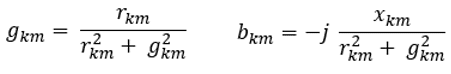Desta forma, chamamos de Y_barra a matriz de admitância nodal ou de admitância de barra, definida como:

Para construção da matriz de admitância de uma rede elétrica é necessário considerar o seguinte procedimento:

• Elementos fora da diagonal principal:

• Elementos da diagonal principal:

Onde:

Ω_k é o conjunto que engloba as barras adjacentes à barra k.

Y_k^sh é a admitância de possíveis elementos ligados na barra k e o nó terra.

Y_km^sh é a admitância de elementos em derivação (susceptância capacitiva da linha).

A matriz Y_barra em sistema elétrico de potência é estruturalmente simétrica e na ausência de transformadores defasadores é também numericamente simétrica. Ela também é complexa, quadrada de dimensão n_b, onde n_b é o número de barras do sistema, além de ser esparsa, isto é, contém muitos zeros (LOURENÇO, 2020).

Por outro lado, no estudo do fluxo de potência em redes elétricas, há outra matriz de susceptância denominada B’ a qual não deve ser confundida com a matriz de susceptância B, componente imaginaria da matriz de admitância Y_barra conforme mostrado na Equação 5. A matriz B’ é utilizada no cálculo da potência ativa que flui pela rede elétrica através do método do Fluxo de Potência Linearizado.

O fluxo de potência ativa P_km e o fluxo no extremo oposto P_mk em uma linha de transmissão são dados pelas expressões (MONTICELLI, 1983):

Onde:

V_k e V_m são as magnitudes das tensões nodais das barras terminais k e m, respectivamente.

θ_km é o ângulo resultante das tensões das barras terminais do ramo km.

P_km e P_mk são os fluxos de potência ativa nos ramos km e mk, respectivamente.

g_km é a condutância no ramo km.

b_km é a susceptância no ramo km.

A definição do método linearizado despreza as perdas e por isso consideramos a resistência série nula, isto é, r_km = 0 e consequentemente g_km = 0. Desta forma:

As seguintes considerações são ainda introduzidas para concretização do método linearizado:

Desta forma, a equação da potência ativa que flui na linha de transmissão é simplificada tal como apresentado abaixo.

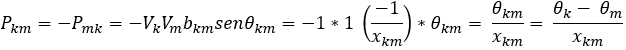Portanto, o fluxo P_km pode então ser aproximado pela seguinte equação (Monticelli, 1983):

Onde θ_km é o vetor dos ângulos das tensões nodais, P_km é o vetor das injeções líquidas de potência ativa e B’ é a matriz de susceptância nodal.

A matriz B’ anteriormente enunciada, é singular, isto é, possui o determinante nulo e por isso não admite inversa. Como no método linearizado há infinitos conjuntos de θ que tornam a Equação 13 verdadeira, faz-se necessário a adoção de uma barra de referência e consequentemente sua eliminação no processo de solução do problema (Lourenço, 2020).

Para construção da matriz de susceptância B’ é necessário considerar o seguinte procedimento:

• Elementos fora da diagonal principal:

• Elementos da diagonal principal:

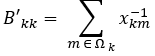Podemos concluir que as matrizes de susceptância B e B’ são diferentes e podem ser obtidas pelos processos anteriormente descritos e abaixo resumidos.

Ao efetuarmos a divisão das matrizes B e B’, obtém-se a seguinte relação:

Por fim, caso a resistência da linha de transmissão seja desprezada, esta relação pode ser simplificada conforme Equação 18.

3. PROGRAMA COMPUTACIONAL PARA O CALCULO DO FLUXO DE POTÊNCIA LINEARIZADO

Para determinação da potência ativa que flui em uma rede elétrica por meio do método linearizado, foi desenvolvido uma ferramenta computacional em linguagem MATLAB®. Para verificar a eficácia e convergência do algoritmo, a rede elétrica teste de três barras visualizada através da Figura 02 e igualmente utilizada no Capítulo 2 do livro “Fluxo de Carga em Redes de Energia Elétrica” de Alcir Monticelli, foi executada no programa computacional.

Figura 02: Rede elétrica exemplo de 3 barras.

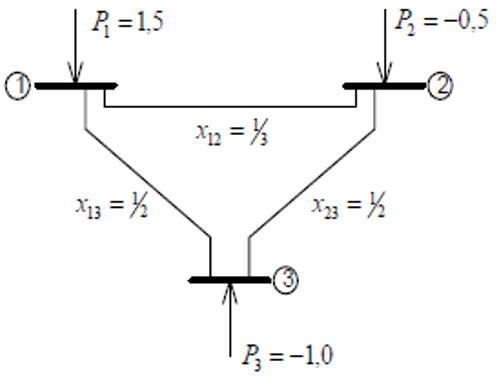
Com base nestes dados, o programa computacional foi executado e o resultado é apresentado na Figura 03.

Figura 03: Resolução do fluxo de potência ativa pelo método linearizado.

Verifica-se a convergência do programa computacional de acordo com a solução obtida por Alcir Monticelli, conforme o conjunto de valores apresentados abaixo.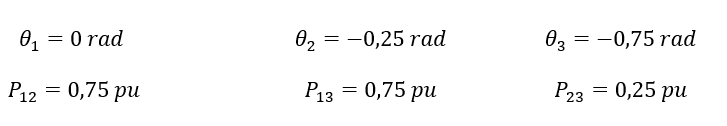

O código do programa computacional implementado pode ser visualizado a seguir.

4. RESULTADOS E DISCUSSÕES

Diante da correta convergência da ferramenta computacional para o problema teórico apresentado por Monticelli em seu livro, o algoritmo foi então executado em um sistema teste do IEEE de 14 barras amplamente utilizado pela comunidade acadêmica para validação e teste de programas computacionais.

Figura 04 – Sistema Elétrico de 14 barras do IEEE.

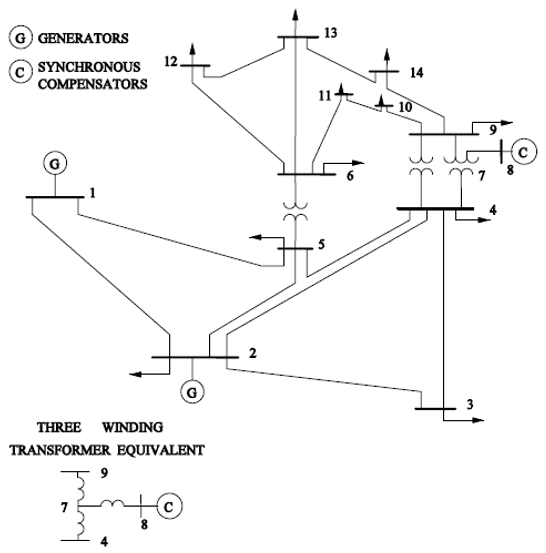
Os dados das linhas e das barras do sistema teste IEEE de 14 barras são apresentados nas Tabelas 01 e 02. Os parâmetros estão normalizados em p.u., para uma potência base de 100 MVA. A referência escolhida para este sistema foi a barra 1 e por isso seu ângulo de fase é zero, isto é, θ₁ = 0°.

Tabela 01 – Dados das linhas do sistema teste de 14 barras do IEEE.

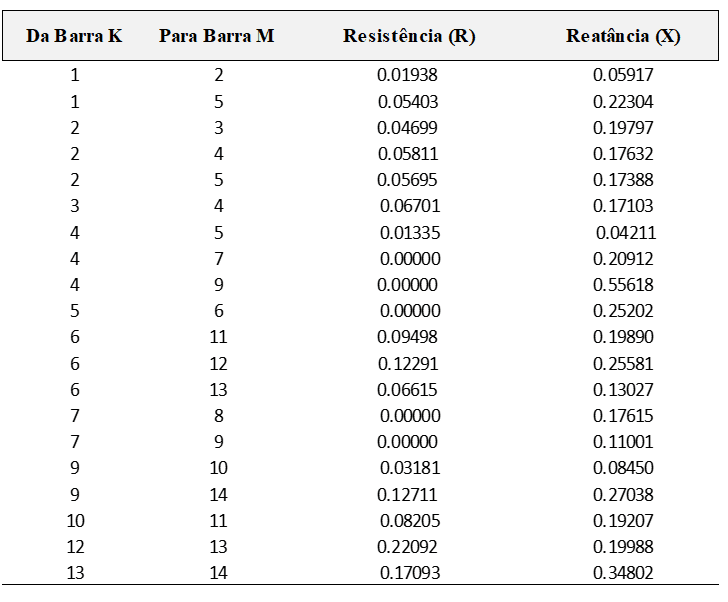
Tabela 02 – Dados das barras do sistema teste de 14 barras do IEEE.

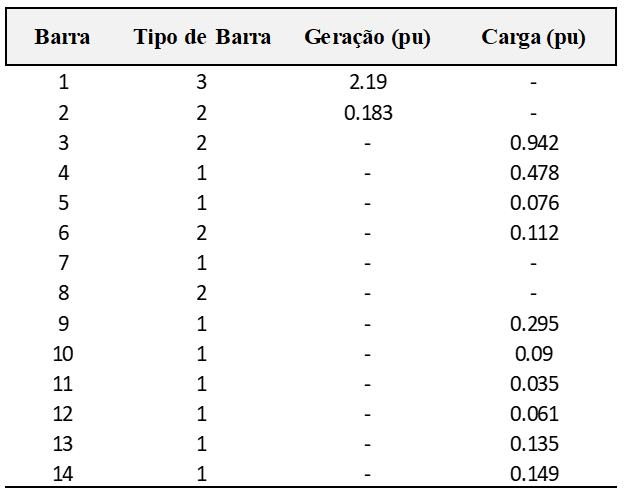
O sistema elétrico foi então executado no programa computacional e o fluxo de potência foi resolvido utilizando o método linearizado cujo embasamento teórico foi apresentado anteriormente. A Figura 05 apresenta os dados da solução para o sistema.

Figura 05: Resolução do fluxo de potência pelo método linearizado.

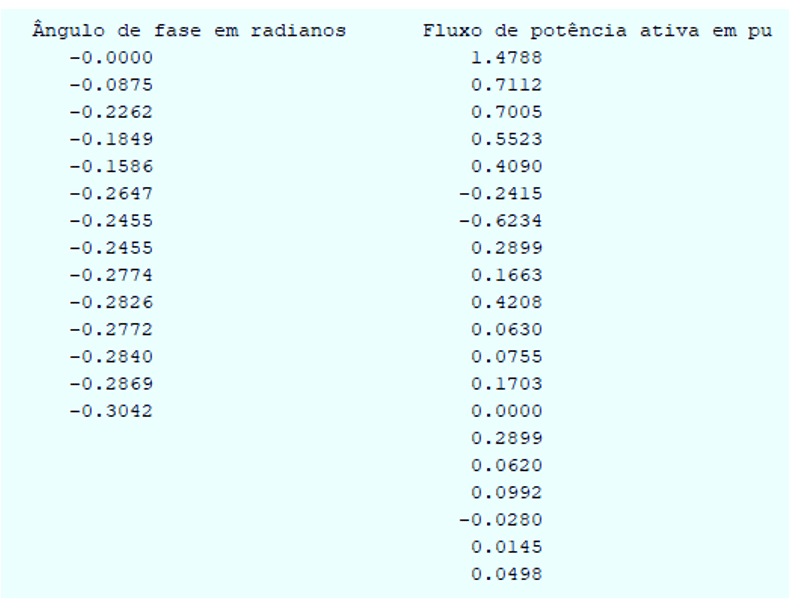
Objetivando verificar a convergência da ferramenta computacional frente ao sistema teste de 14 barras do IEEE, o sistema elétrico foi igualmente executado no Software FLUPOT da Cepel. A comparação das duas soluções para o fluxo de potência ativa que flui na rede elétrica é apresentada na Tabela 03.

Tabela 03: Conferência do fluxo de potência do sistema teste de 14 barras frente ao FLUPOT.

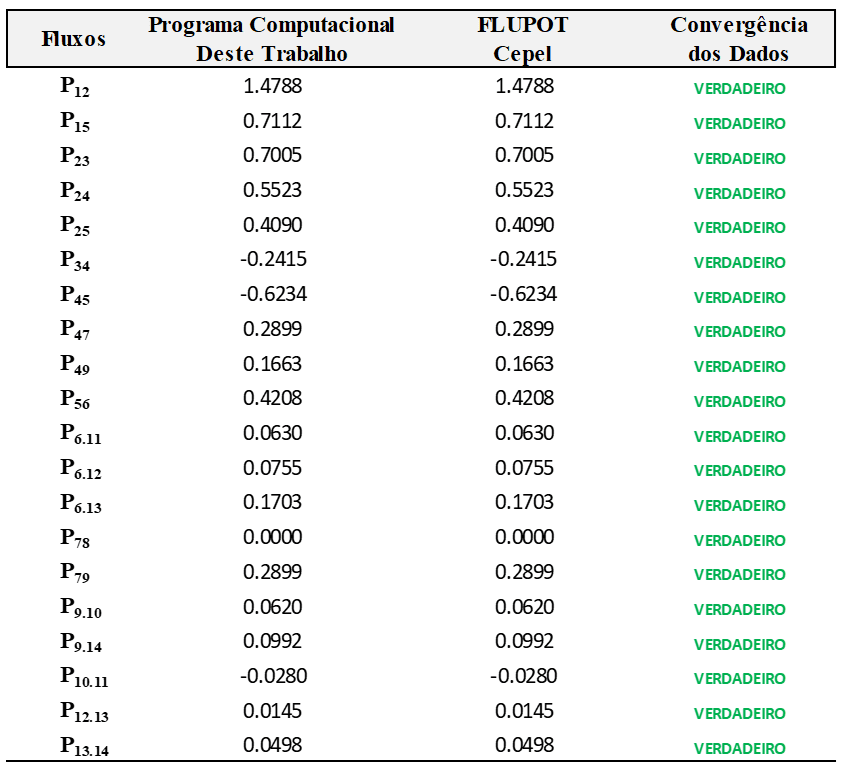
Conforme pode ser visualizado na Tabela 03, o programa computacional obteve 100% de convergência, apresentando os mesmos valores de fluxos de potência quando comparado com o software FLUPOT da Cepel e, portanto, a ferramenta mostrou-se eficaz na solução do problema do Fluxo de Potência Linear de uma rede elétrica.

5. CONCLUSÕES

O estudo do fluxo de potência possui fundamental importância no planejamento, bem como na determinação das condições de operação, controle e supervisão de sistemas elétricos. A determinação do fluxo de potência depende, dentre outros fatores, dos elementos da matriz de admitância das barras do sistema. Neste contexto, este trabalho permitiu aprofundar os conhecimentos sobre a formulação do método do Fluxo de Potência Linear e consequentemente na matriz de admitância Y_barra e suas componentes, a matriz de condutância G_barra e a matriz de susceptância B_barra, além da matriz B’ utilizada no método linearizado de fluxo de potência, tendo sido evidenciada a diferença entre as matrizes B e B’ e seus processos de obtenção.

Para determinação da distribuição dos fluxos de potência ativa pelos ramos de uma rede elétrica, por meio do método do Fluxo de Potência Linear, uma ferramenta computacional foi desenvolvida e inicialmente foi aplicada em um sistema elétrico teste apresentado no livro de Alcir Monticelli, onde foi evidenciada a correta convergência da solução. Posteriormente, o programa foi executado em um sistema teste de 14 barras do IEEE e o resultado foi comparado com a solução obtida pelo software FLUPOT da Cepel, onde foi igualmente verificada total convergência entre as soluções.

Vale salientar que o modelo linearizado não considera as magnitudes das tensões nodais e as potências reativas do sistema e faz aproximações tais como, o seno do ângulo θ_km igual ao próprio ângulo θ_km (senθ_km = θ_km) e as tensões V_k e V_m iguais a 1 pu (V_k = V_m = 1pu), além de desconsiderar as perdas no sistema e os shunts de linha. Entretanto, vale ressaltar que o modelo possui grande utilidade em fases iniciais de estudos, de modo que em fases mais avançadas, caso seja necessário, outros métodos clássicos podem ser utilizados.

REFERÊNCIAS BIBLIOGRÁFICAS

ELGERD, O., I. Introdução à Teoria de Sistemas de Energia Elétrica. Editora McGraw-Hill, São Paulo, 1981.

GÓMEZ-EXPÓSITO, A., CONJETO, A. J., CAÑIZARES, C., Sistemas de Energia Elétrica – Análise e Operação. Editora LTC, Rio de Janeiro, 2011.

HAFFNER, S., Modelagem e Análise de Sistemas Elétricos em Regime Permanente. Apostila, Departamento de Engenharia Elétrica, Universidade do Estado de Santa Catarina, 2007.

IEEE. Sistema Teste de 14 Barras IEEE. Disponível em: https://ieeexplore.ieee.org/. Acesso em: 30/08/2020.

LOURENÇO, E., Análise e Operação de Sistemas Elétricos de Potência. Notas de aula, Departamento de Engenharia Elétrica, Universidade Federal do Paraná, 2020.

MONTICELLI, A. J., Fluxo de Carga em Redes de Energia Elétrica. Editora Edgar Blucher, Centro de Pesquisas de Energia Elétrica, Rio de Janeiro, 1983.

MONTICELLI, A. J.; GARCIA, A., Introdução a Sistemas de Energia Elétrica. Editora UNICAMP, 1ª. Edição, Campinas, 2003.

^[1] Mestrando em Sistemas de Energia pela Universidade Federal do Paraná (UFPR). MBA em Gestão de Projetos pela Universidade de São Paulo (USP). Graduação em Engenharia Elétrica pela Universidade Federal de Uberlândia (UFU).

Enviado: Fevereiro, 2021.

Aprovado: Março, 2021.