ARTIGO ORIGINAL
GOIS, Ben Hur de Oliveira [1], ALVES, Raphael de Sousa Santos [2], ALVES, José Humberto Góes [3]
GOIS, Ben Hur de Oliveira. ALVES, Raphael de Sousa Santos. ALVES, José Humberto Góes. Estudo do combate de momentos das cargas em lajes maciças engastadas. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano 05, Ed. 10, Vol. 17, pp. 88-113. Outubro de 2020. ISSN: 2448-0959, Link de acesso: https://www.nucleodoconhecimento.com.br/engenharia-civil/lajes-macicas
RESUMO
As lajes são os primeiros elementos estruturais a serem calculadas, suas cargas numa edificação e consequentemente, seus respectivos esforços solicitantes, na elaboração de um projeto estrutural. Considerando a extrema necessidade e responsabilidade na precisão destes cálculos para que erros não comprometam a segurança da construção, faz-se necessário um estudo detalhado no cálculo dos momentos fletores positivos e negativos e como estes podem ser combatidos, evitando indesejadas deformações na estrutura. Este trabalho visa demonstrar de forma teórica e prática, como estes momentos fletores produzidos devidos as cargas permanentes e variáveis nas lajes são calculados na engenharia civil e como as armaduras negativas e positivas combatem esses esforços solicitantes.
Palavras-chave: Lajes, momentos fletores, esforços, flecha, armadura.
1. INTRODUÇÃO
As lajes são elementos estruturados por lâminas, solicitados principalmente por cargas normais ao seu plano médio. São elas que compõem os pisos de edifícios correntes de concreto armado. Quando em estruturas laminares planas, o comprimento e a largura predominam sobre a espessura. Assim, as lajes são representadas pelo seu plano médio e diferenciadas pela sua forma, vinculação e proporção dos lados. Comumente, em estruturas correntes, as lajes são retangulares, no entanto podem ter formato trapezoidal ou em L (CAMPOS FILHO, 2014).
Este artigo é uma proposta teórica e prática para um melhor entendimento sobre os momentos fletores em lajes maciças engastadas em duas direções, com explanação teórica sobre o tema proposto, experimento prático para comparação com resultados teóricos, evidenciando como os momentos fletores são combatidos mediante armaduras e a relação entre a deformação da estrutura devido às cargas e seus momentos fletores.
O engenheiro civil ao fazer o projeto estrutural de um edifício e o lançamento das cargas, necessita projetar as lajes, lançar para as vigas, depois para os pilares e finalmente para a fundação, nesta ordem precisamente. Por isso, o dimensionamento preciso das lajes é condição indispensável para um projeto estrutural responsável.
Na graduação em Engenharia Civil, o estudo teórico sobre os momentos fletores que agem nas lajes para o seu consequente dimensionamento de armaduras é bastante abstrato.
Como observar os momentos fletores positivos e negativos em um experimento de forma prática e concreta? Como relacioná-los com a deformação da estrutura? Como agem as armaduras para combater esses momentos fletores? Sendo assim, este artigo:
a) consiste numa pesquisa teórica e prática no assunto, objetivando completar o entendimento deste tipo de laje;
b) elabora um experimento que auxilia o entendimento do comportamento das lajes engastadas no curso de graduação em engenharia civil;
c) comparar os resultados obtidos no experimento com os teóricos, bem como, demonstrar as armaduras de combate aos momentos e as deformações na estrutura.
2. AÇÕES NAS LAJES
2.1 DEFINIÇÃO DO MOMENTO DA FORÇA
Segundo, Borja (2016, p. 2):
Quando uma força é aplicada a um corpo, ela produzirá uma tendência de rotação do corpo em torno de um ponto que não está na linha de ação da força. Essa tendência de rotação algumas vezes é chamada de torque, mas normalmente é denominada momento de uma força, ou simplesmente momento. O momento de uma força em relação a um ponto (situado num corpo) é definido como o produto do módulo da força (F) pela distância do ponto à linha de ação da mesma (d), além da tendência dessa força F fazer girar um corpo rígido em torno de um eixo fixo. O momento depende do módulo de F e da distância d de F em relação ao eixo fixo.
O momento da força M é uma grandeza física medida no Sistema Internacional em (Newton x metro), unidade de força vezes unidade de comprimento. Sua fórmula, M = F x R (produto vetorial) logo, por definição do produto vetorial, o vetor M é perpendicular ao plano que contém os vetores F e R. conforme a figura 1.
FIGURA 1: Momento da Força
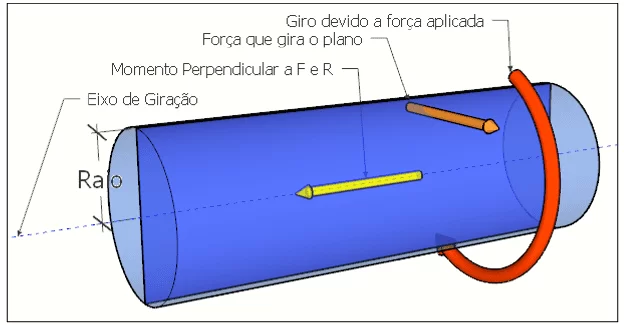
Observa-se que devido a força, o plano gira com seu eixo no centro do plano e o momento da força que surge ao longo do eixo terá sua intensidade proporcional ao produto da força pelo raio de giro.
2.1.2 O MOMENTO DA FORÇA EM LAJES
Com estes conceitos aplicados na Engenharia Civil, são estudados os comportamentos das lajes maciças ao serem solicitadas pelas cargas permanentes e acidentais.
Segundo, Bastos (2015, p. 7):
Para determinação das ações atuantes nas lajes deve-se recorrer às normas NBR 6118, NBR 8681 e NBR 6120, entre outras pertinentes. As ações peculiares das lajes de cada obra também devem ser cuidadosamente avaliadas. Se as normas brasileiras não tratarem de cargas específicas, pode-se recorrer a normas estrangeiras, na bibliografia especializada, com os fabricantes de equipamentos mecânicos, de máquinas, etc.
O cálculo dos Momentos da Força criados nas lajes é condição indispensável para o dimensionamento das barras de aço a serem usadas para suportar a estrutura. As lajes maciças ao serem solicitadas pelos esforços das cargas permanentes e acidentais, tendem ao surgimento de deslocamento no sentido da gravidade do centro da laje, formando uma “barriga” que nos casos de insuficiência de aço podem ser bem perceptíveis a olho nú, ao qual esse fenômeno chama-se flecha.
Conforme, Pereira (2017, p. 32): ‘’O deslocamento transversal máximo de uma barra reta ou placa é chamado de flecha, e o seu cálculo para lajes depende do seu carregamento uniforme e das condições de apoio’’
2.1.3 APLICAÇÃO DO CONCEITO DE MOMENTO DA FORÇA NO ESTUDO DO COMPORTAMENTO DAS LAJES MACIÇAS
As lajes podem ser vistas como um conjunto infinitesimal de placas juntas que somando-se resulta numa unidade monolítica e maciça, como mostra a figura 2.
FIGURA 2: Placas em Lx e Ly na laje e momentos positivos
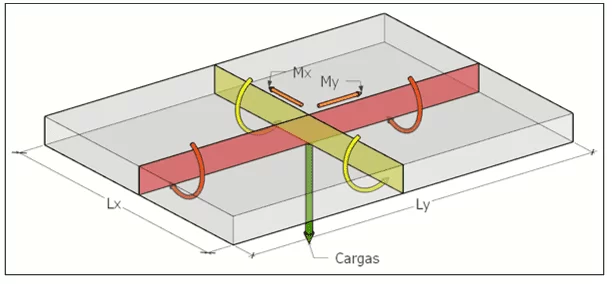
As placas vermelhas estão situadas ao longo do maior vão que, enquanto as placas amarelas estão situadas ao longo do menor vão.
Numa situação hipotética onde a laje não está sujeita a cargas perfeitamente horizontal (sem flecha), deixa esta condição e passa a ser real quando consideramos os efeitos gravitacionais produzidos pelas cargas, como visto na figura 3.
De acordo, Machado (2016):
A determinação dos esforços em lajes isoladas pode ser feita por processos aproximados (MARCUS), pela teoria das placas (BARES), pela teoria das charneiras plásticas (LANGENDONCK), etc. Dentre o conjunto de soluções apresentadas na literatura mundial, destacam-se as tabelas de CZERNY, para determinação dos momentos fletores atuantes em lajes isoladas.
FIGURA 3: Comportamento de esforços em laje.
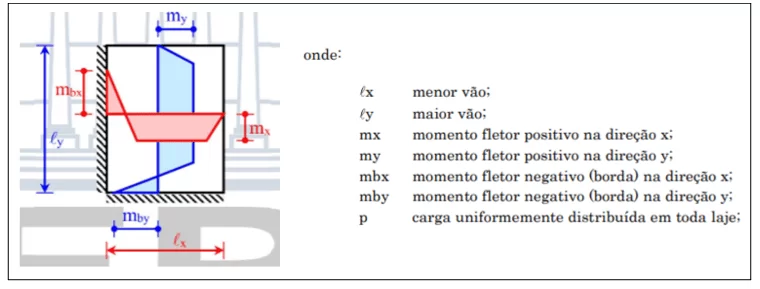
A força peso na região do centro geométrico da laje faz com que as placas tendem a girar surgindo os momentos da força peso que doravante serão denominados de My, que é o momento da força ao longo do maior vão Ly e Mx, que é o momento da força ao longo do menor vão Lx, ambos dependem do raio de giro, que é a espessura da laje, e da intensidade gravitacional das cargas permanentes e acidentais que atuam em cada unidade de área. De forma didática será representado conforme a figura 4.
FIGURA 4: Representação simplificada dos momentos
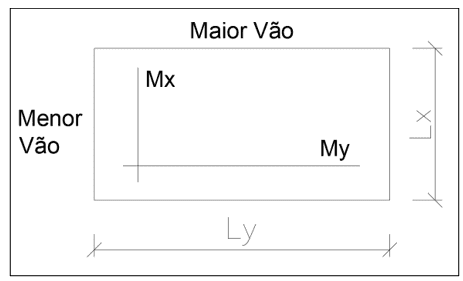
2.1.4 APLICAÇÃO NA ENGENHARIA CIVIL
O experimento proposto neste trabalho visa estudar os momentos da força em sete lajes maciças, organizadas conforme a figura 5.
FIGURA 5: Disposição das lajes e representa
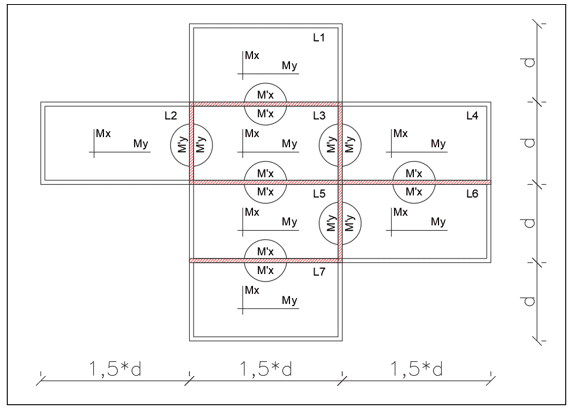
As lajes L1, L2, L3, L4, L5, L6 e L7 possuem as mesmas dimensões (Lx = d), (Ly = 1,5 . d), e área (A=1,5 . d2). Observa-se que L3 possui quatro engastes, união de duas lajes consecutivas, L5 possui três engastes, L4 e L6 possuem dois engastes cada e L1, L2 e L7 possuem apenas um engaste. Nas extremidades que não possuem engates as lajes estão apoiadas sobre as vigas.
Segundo, Bastos (2015, p. 5):
No caso de apoios intermediários de lajes contínuas surgem momentos fletores negativos devido à continuidade das lajes. A ponderação feita entre os diferentes valores dos momentos fletores que surgem nesses apoios conduz ao engastamento elástico. No entanto, para efeito de cálculo inicial dos momentos fletores, as lajes que apresentam continuidade devem ser consideradas perfeitamente engastadas nos apoios intermediários.
O engaste é a união de duas lajes consecutivas, e nessa região as lajes ligadas exercem uma força no sentido da gravidade sobre a viga que as sustentam, e esta reage no sentido contrário com a mesma intensidade, esta força é chamada de força cortante, pois em casos extremos ela pode cortar o engaste e separar as lajes unidas.
Por convenção, os momentos das forças produzidos pelos efeitos das cargas terão sinal positivo e os momentos das forças cortantes que são no sentido contrário terão sinal negativo, pois o momento e a força são grandezas vetoriais que possuem módulo, sentido e direção.
Os momentos Mx e My são positivos devido aos efeitos gravitacionais das cargas permanentes e acidentais sobre a laje e M´x e M´y são os momentos negativos produzidos nos engastes pela força cortante no sentido contrário, vistos na figura 5.
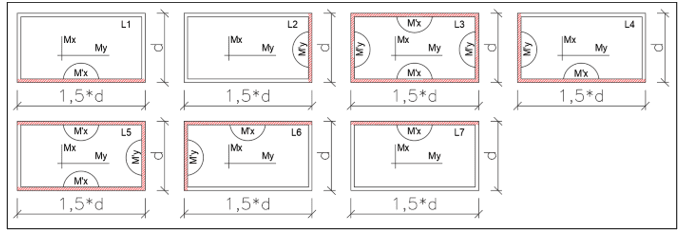
Cada laje será estudada separadamente inicialmente e posteriormente compatibilizados os resultados juntando-as novamente, como mostra a figura 6.
FIGURA 6: Representações individuais das lajes e seus momentos
2.1.5 ARMAÇÃO
De acordo com, Guimarães (2016):
Conjunto de atividades relativas à preparação e posicionamento do aço dentro da estrutura, e a armadura como associação de diversas peças de aço, formando um conjunto para um determinado componente estrutural. Para a colocação das armaduras positivas e negativas: primeiro ocorre o posicionamento das armaduras positivas com seus espaçadores, que evitam o contato entre elas e o fundo da forma, garantindo o recobrimento do aço. Depois são montadas as armaduras negativas, que se apoiam sobre “caranguejos” (pequenos cavaletes confeccionados com aço e que dão apoio à armadura garantindo seu posicionamento em relação à altura da laje)
A armadura na laje de concreto armado em duas direções, correspondem às barras metálicas que combatem os momentos fletores que impedem as deformações verticais. A armadura positiva fica na parte de baixo da laje, acima do cobrimento inferior, trabalhando para que a laje permaneça horizontal mesmo após as ações das cargas permanentes e acidentais. A armadura negativa fica na parte superior da laje, abaixo do cobrimento superior, trabalhando para que as lajes engastadas não se separem devido à força cortante.
Segundo, Pereira (2017): “Já nas lajes armadas em duas direções os esforços solicitantes são importantes para as duas direções principais, calculando então as duas armaduras para suportar os momentos fletores nessas direções.’’
3. O MODELO EXPERIMENTAL
Segundo, Lopes (2012): “As lajes maciças de concreto armado são executadas totalmente na obra, compostas por concreto, contendo armaduras longitudinais e eventualmente transversais, são apoiadas em vigas ou paredes ao longo das bordas.’’
O experimento elaborado neste trabalho visa demonstrar de forma prática o comportamento de cada laje quando submetida aos efeitos de suas cargas permanentes e acidentais com ênfase nas armaduras que combatem os momentos fletores, e para isto foi elaborado um sistema de vigas metálicas de largura 2 cm que servirá de apoio, como ilustrado na figura 7, medidas em metros.
FIGURA 7: Lajes para o experimento
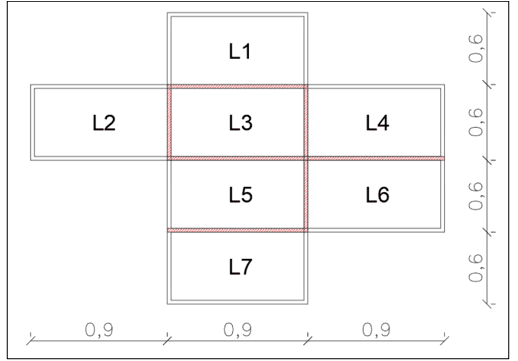
Sobre esta estrutura será colocado uma lona elástica de apoio para as placas de isopor (simulando as lajes de concreto) que serão armadas com barras positivas e negativas, simulando as lajes armadas em duas direções reais. Sobre cada laje será distribuído 1 Kg de areia, assim, como cada laje tem 0,54m2 de área ficando com uma tensão de 1000g por 0,54m2 resultando numa carga de ![]() para cada laje.
para cada laje.
3.1 TEORIA DOS CÁLCULOS DOS MOMENTOS POSITIVOS E NEGATIVOS EM CADA LAJE
Segundo, Bastos (2015, p. 17):
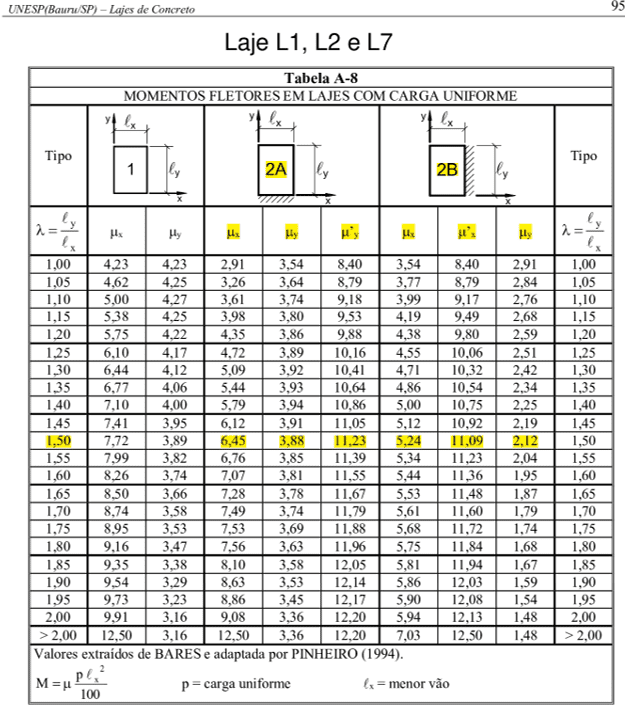
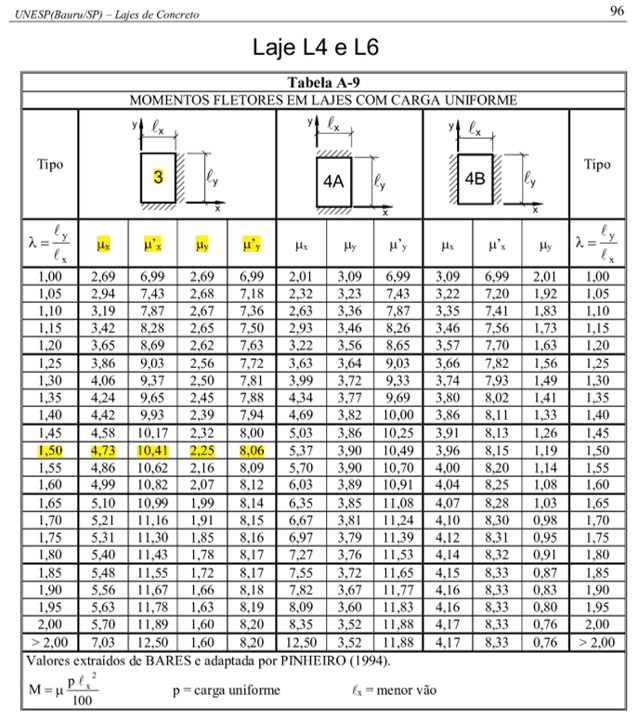
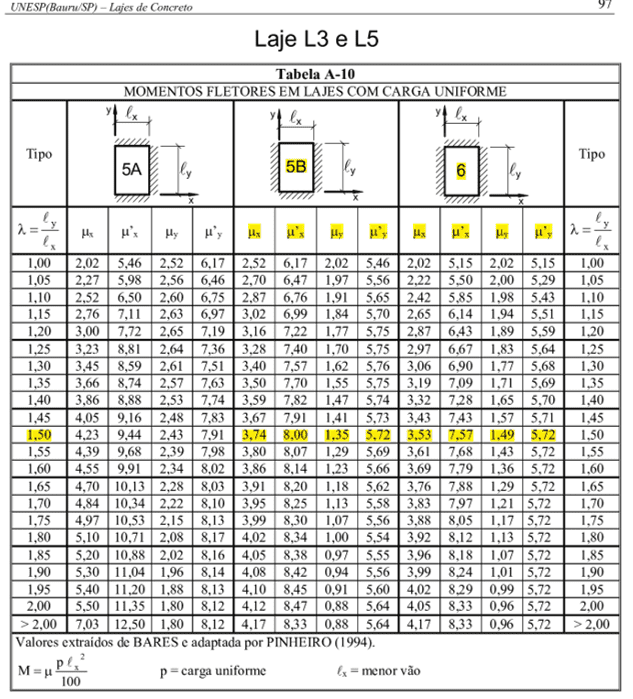
Serão utilizadas as tabelas (Tabela A-8 a Tabela A-17), desenvolvidas por Barés e adaptadas por PINHEIRO (1994). As tabelas servem para o cálculo dos momentos fletores em lajes retangulares com apoios nas quatro bordas. Conforme as tabelas de Barés, os momentos fletores, negativos ou positivos, são calculados pela expressão: ![]()
Para o cálculo dos momentos usaremos a fórmula:
Equação 01:
Onde:
M é o momento da força
p é a carga 1851,85 gf/m2
Lx é comprimento do menor vão, 0,6 m
µ é uma constante de proporcionalidade que depende da razão ![]()
A razão 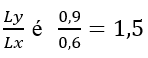 para todas as lajes. A seguir teremos a tabela com todos os coeficientes µx, µy, µ´x e µ´y, disponível nos anexos.
para todas as lajes. A seguir teremos a tabela com todos os coeficientes µx, µy, µ´x e µ´y, disponível nos anexos.
TABELA 1: Valores dos coeficientes µ para o cálculo dos momentos
|
CASO |
LAJE |
Coeficientes µ (adimensional) | |||
| µ x | µ y | µ ´x | µ ´y | ||
| CASO 2B | L1 | 5,24 | 2,12 | 11,09 | – |
| CASO 2A | L2 | 6,45 | 3,88 | – | 11,23 |
| CASO 6 | L3 | 3,53 | 1,49 | 7,57 | 5,72 |
| CASO 3 | L4 | 4,73 | 2,25 | 10,41 | 8,06 |
| CASO 5B | L5 | 3,74 | 1,35 | 8,00 | 5,72 |
| CASO 3 | L6 | 4,73 | 2,25 | 10,41 | 8,06 |
| CASO 2B | L7 | 5,24 | 2,12 | 11,09 | – |
FONTE: Tabela de BARES, adaptada por PINHEIRO (1994), no anexo.
Os valores de p e Lx são constantes, logo a Eq. 01 ficará ![]() , simplificando M = µ . 6,67, assim todos os coeficientes ( µ ) serão multiplicados por 6,67 e obteremos a tabela dos momentos positivos e negativos, tabela 2.
, simplificando M = µ . 6,67, assim todos os coeficientes ( µ ) serão multiplicados por 6,67 e obteremos a tabela dos momentos positivos e negativos, tabela 2.
TABELA 2: Valores calculados dos momentos
Fonte: Autoral
3.2 COMPATIBILIZAÇÃO DOS MOMENTOS NEGATIVOS E CORREÇÃO DOS POSITIVOS
De acordo com, Pinheiro (2010, p. 13): “Em decorrência da compatibilização dos momentos negativos, os momentos positivos na mesma direção devem ser analisados.’’
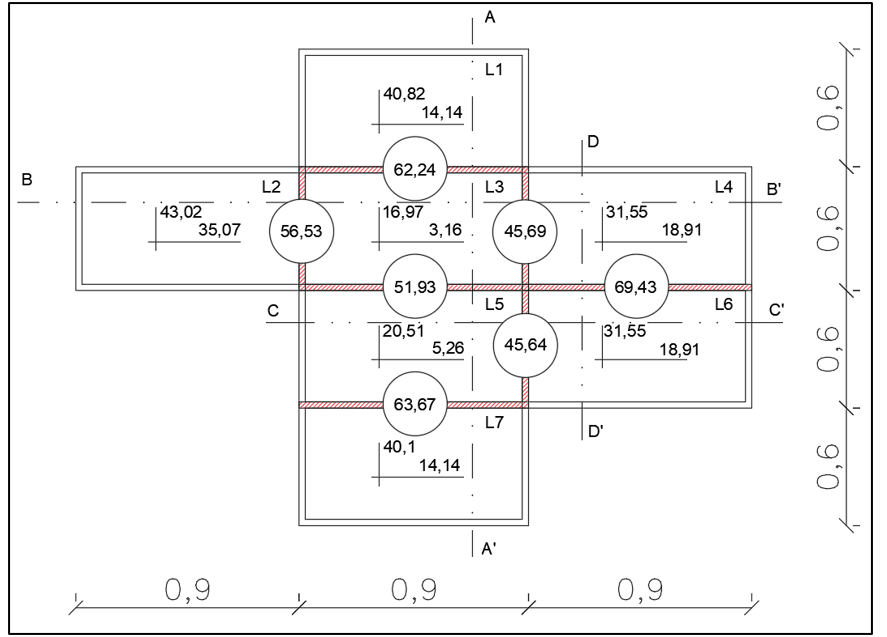
Agora com os valores dos momentos em cada laje, tabela 2, serão necessárias as compatibilizações dos momentos negativos e consequentemente dos positivos, para tanto são feitos quatro cortes A-A´, B-B´,C-C´ e D-D´ para auxílio nos cálculos, segundo a figura 8.
Segundo, Guimarães (2016, p. 32): “Pórticos estruturais sustentados por mais de dois pilares possuem em suas vigas, além do momento positivo gerado pelas cargas permanentes e variáveis da edificação, momentos negativos sobre os apoios’’
FIGURA 8: Momentos a serem compatibilizados com o auxílio dos cortes
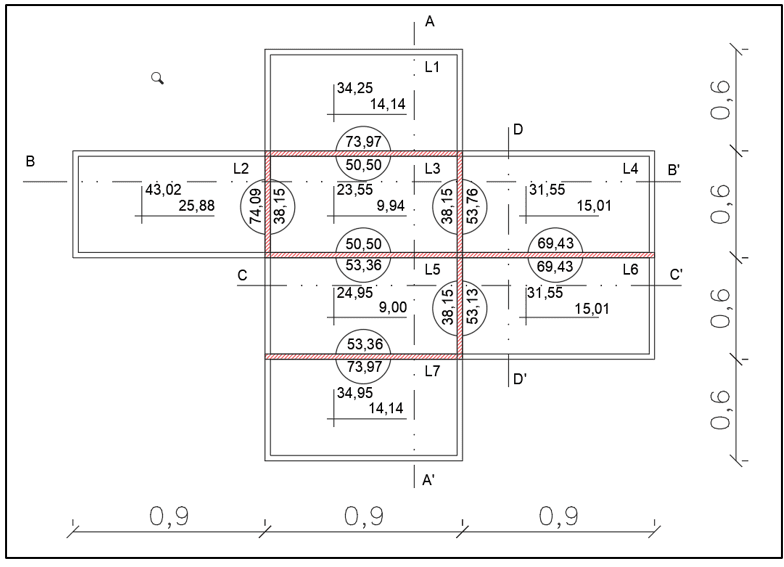
FIGURA 9: Corte A-A´

FIGURA 10: Corte A-A´ compatibilizado

FIGURA 11: Corte B-B´

FIGURA 12: Corte B-B´ compatibilizado

FIGURA 13: Corte C-C´

FIGURA 14: Corte C-C´ compatibilizado
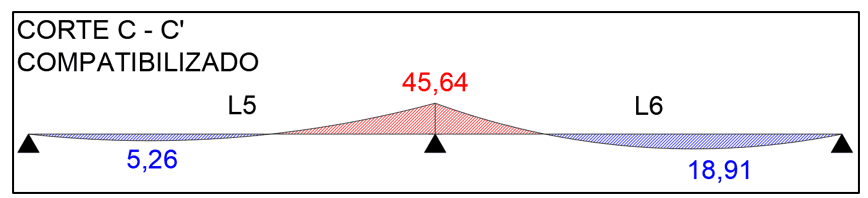
FIGURA 15: Corte D-D´
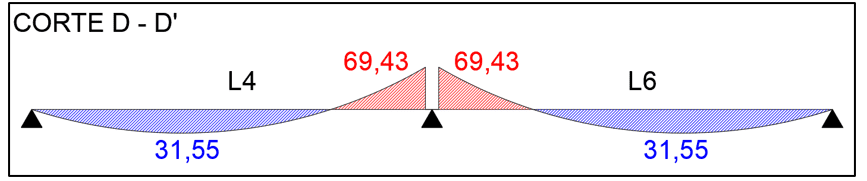
FIGURA 16: Corte D-D´ compatibilizado
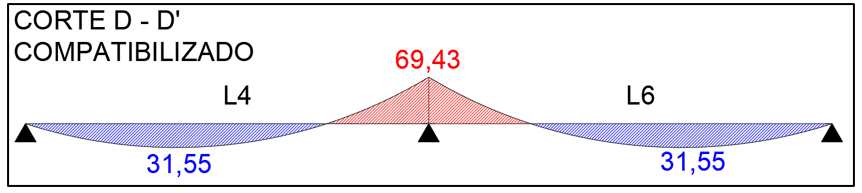
Após os ajustes de todos os momentos positivos e negativos, as lajes compatibilizadas ficam como ilustrado, figura 14.
FIGURA 17: Momentos fletores compatibilizados
3.3 OBSERVAÇÕES SOBRE AS CORREÇÕES
A partir dos dados obtidos com os valores corrigidos de todos os momentos, vistos na figura 17, faz-se as seguintes observações:
TABELA 3: Comparativos das alterações após a compatibilização
FONTE: própria
De maneira geral, com o aumento do momento negativo reduz-se o momento positivo no mesmo sentido e vice-versa, como visto na tabela 3.
A laje L3 possui quatro engastes e a laje L5 três engastes, e são as que ficaram mais evidentes essa afirmativa. Já nas lajes L1, L2, L4 e L6 ocorreu um aumento do momento positivo, ou seja, tendem a uma maior deformação vertical, pois as sete lajes são submetidas à mesma carga.
É esperado que no experimento as lajes com maiores momentos positivos, após serem submetidas às cargas, tenham maiores deslocamentos verticais de deformação e que nos engastes ocorram uma separação das lajes devido aos momentos negativos.
Assim, como proposta deste trabalho, é inserir armaduras positivas para o combate dos momentos positivos e minimizar os deslocamentos verticais de deformação das lajes e inserir armaduras negativas para o combate dos momentos negativos e minimizar a separação das lajes nos engastes devido à força cortante.
3.4 MATERIAIS PARA O EXPERIMENTO E PROCEDIMENTOS
FIGURA 18: Estrutura metálica de vigas para apoio das placas de isopor

Estrutura metálica de vigas com dimensões 0,9m x 0,6m e largura de 2 cm, para o apoio das placas de isopor (lajes).
FIGURA 19: Placas de isopor de 90cm x 60cm e 3cm de espessura

Placas de isopor com dimensões de 0,9m x 0,6m e espessura de 3cm, ao qual funcionará no experimento simulando o concreto
FIGURA 20: Placas de isopor apoiadas na estrutura sem aplicação de cargas

As placas de isopor estão apoiadas na estrutura de vigas, mas sem aplicação de cargas, ficando completamente na horizontal sem a presença de deslocamentos verticais gravitacionais.
FIGURA 21: Placas de isopor apoiadas na estrutura com aplicação de cargas de 1kg de areia em cada laje

As placas de isopor estão apoiadas na estrutura de vigas, com aplicação de cargas, apresentando deslocamentos verticais gravitacionais para baixo devido a ação da carga de 1kg de areia.
FIGURA 22: Armaduras positivas e negativas

Armaduras positivas (ganchos para cima) com 3 barras de 4mm para o vão de 90cm e 4 barras de 4mm para o vão de 60cm. E armaduras negativas (ganchos para baixo) com 3 barras de 4mm de 30cm e 3 barras de 4mm de 25cm para armadura de distribuição, todas amarradas com arame.
FIGURA 23: Placas com armaduras positivas

Armaduras positivas fixadas nas placas de isopor para trabalhar em conjunto simulando o concreto armado.
FIGURA 24: Placas com as armaduras positivas e negativas com carga

As placas de isopor com as armaduras positivas fixadas, armaduras negativas aplicadas nos engastes e aplicação da carga de 1kg de areia em cada laje.
3.5 OBSERVAÇÕES EXPERIMENTAIS RELEVANTES COMPARADAS COM A TEORIA
Ao realizar o experimento, foi possível perceber que as placas de isopor quando foram apoiadas na estrutura de vigas metálicas, quando não submetidas à ação das cargas da areia elas permaneciam perfeitamente na horizontal sem apresentarem deslocamentos verticais que na engenharia são conhecidas como flechas.
Após aplicar 1 kg de areia em cada placa, foi possível notar o surgimento de deslocamentos verticais para baixo na região central de cada placa e medidos com aproximadamente 1 cm de flecha. Todas as placas apresentaram aproximadamente a mesma flecha pois nesse momento ainda sem as armaduras positivas e negativas, todas as placas tinham o mesmo grau de liberdade para se deformarem.
Também foi notado que nos engastes, regiões de encontro de duas placas, surgiram uma separação das mesmas de aproximadamente 1cm, devido ao esforço contrário que a viga exercia sobre elas, esforço esse chamado de força cortante, como apresentado é calculado na tabela 2 e na figura 17.
Após a aplicação das armaduras positivas sob as placas e as armaduras negativas nos engastes, foi aplicado a carga de 1 kg de areia em cada placa e foi observado que nessa configuração de placas e armaduras simulando o concreto armado, não surgiram deslocamentos verticais gravitacionais, ou seja, as flechas foram combatidas pelas as armaduras positivas e as placas permaneceram perfeitamente horizontais. Nos engastes, as placas permaneceram unidas, ou seja, a força cortante foi combatida pelas armaduras negativas.
4. CONSIDERAÇÕES FINAIS
A proposta deste trabalho foi apresentar um experimento original e simples que fosse possível observar resultados calculados teoricamente de forma clara na prática. Não faz parte deste artigo dimensionar as armaduras, mas sim mostrar como elas combatem os deslocamentos das lajes em sua região central, bem como a separação de duas lajes consecutivas nas regiões conhecidas como engastes.
É importante salientar que algumas dificuldades foram enfrentadas, pois ao confeccionar as armaduras, não ficaram todas perfeitamente iguais devido a falta de ferramentas adequadas e a falta de habilidade específica dos autores, por não ter experiência como os armadores experientes empregados nas construções civis, possível de notar na figura 22.
O estudo sobre as lajes, é fundamental e elementar para o engenheiro civil na projeção e execução de residências e prédios, ficando como sugestão, que este experimento reproduzido e aplicado nas aulas de laboratório para os alunos da graduação de engenharia civil com as devidas adaptações que julgar pertinente, a cargo do professor da disciplina de concreto armado.
O objetivo esperado foi alcançado, mesmo com as limitações acima expostas, foi possível notar experimentalmente como trabalha o concreto armado nas lajes. Os momentos fletores positivos, que surgem nas lajes devido às cargas e consequentemente as indesejadas flechas, calculados na parte teórica, vimos de forma experimental que são combatidos com as armaduras positivas e da mesma forma, os momentos fletores negativos que surgem nos engastes, e consequentemente as indesejadas separação das lajes nos engastes, que calculamos na parte teórica, vimos de forma experimental que são combatidos mediantes as armaduras negativas.
REFERÊNCIAS
ARAÚJO, J. M. Curso de Concreto Armado. 4 v., 2. ed., Rio Grande: Editora Dunas, 2003.
ARAÚJO, J. M. de. Lajes maciças de concreto armado: CAPÍTULOS 1 A 4 – Volume 2. 2016. FURG. Disponível em: http://www.editoradunas.com.br/revistatpec/aulas_arquivos/Cap1_V2.pdf. Acesso em: 10 abr. 2020.
ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 6118: Projeto de estruturas de concreto – Procedimento. Rio de Janeiro: ABNT, 2014.
ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 6120: Cargas para o cálculo de estruturas de edificações. Rio de Janeiro: ABNT, 1980.
ASTOS, P. S. dos Santos. Fundamentos do concreto armado. 2006. 98 f. Notas de aulas – Curso de Engenharia Civil, Departamento de Engenharia Civil, Universidade Estadual Paulista, Bauru, 2006. Disponível em: https://s3.amazonaws.com/academia.edu.documents/43189267/FUNDAMENTOS_Concreto.pdf. Acesso em: 17 abr. 2020.
BASTOS, P. S. dos Santos. Lajes de concreto. 2015. 119 f. Notas de aula – Curso de Engenharia Civil, Departamento de Engenharia Civil, Universidade Estadual Paulista, Bauru, 2015. Disponível em: https://s3.amazonaws.com/academia.edu.documents/40136619/Lajes.pdf? Acesso em: 19 abr. 2020.
BORJA, I. Vitorino de. Estabilidade das construções: módulo 02 – momento de uma força. 2016. Disponível em: https://docente.ifrn.edu.br/edilbertoborja/estabilidade-das-construcoes/estabilidade-das-construcoes-subsequente/modulo-02-momento-de-forca/modulo-02-momento-de-forca. Acesso em: 15 abr. 2020
CAMPOS F. A. Projeto de lajes maciças de concreto armado. 2014. 45 f. Notas de aulas – Curso de Engenharia Civil, Universidade Federal do Rio Grande do Sul, Porto Alegre, 2014. Disponível em: https://s3.amazonaws.com/academia.edu.documents/39993840/lajes.pdf. Acesso em: 12 abr. 2020.
GUIMARÃES, Stela R. M. Aplicação de lajes steel deck em edifícios de múltiplos andares. 2016. 79 f. TCC (Graduação) – Curso de Engenharia Civil, Universidade Federal do Rio de Janeiro, Rio de Janeiro, 2016.
LOPES, André F. de O. Estudo técnico comparativo entre lajes maciças e nervuradas com diferentes tipos de enchimento. 2012. 131 f. TCC (Graduação) – Curso de Engenharia Civil, Universidade Federal de Pernambuco, Caruaru, 2012.
MACHADO, Roberto D. Lajes maciças de concreto armado: apostila – capitulo 8. UFPR. Disponível em: http://www.estruturas.ufpr.br/wp-content/uploads/2016/08/ApostilaCA-vMK_cap8.pdf. Acesso em: 21 abr. 2020.
PEREIRA, Rafaela L. R. Análise comparativa entre lajes maciças convencionais e lajes nervuradas. 2017. 103 f. TCC (Graduação) – Curso de Engenharia Civil, Unievangélica, Anápolis-GO, 2017.
PINHEIRO, Libânio M.. Lajes maciças: capítulo 11. Capítulo 11. 2010. Disponível em: http://www.set.eesc.usp.br/mdidatico/concreto/Textos/11%20Lajes%20Macicas.pdf. Acesso em: 20 abr. 2020.
PINHEIRO, Libânio M. Tabelas de lajes. 2007. Disponível em: http://www.set.eesc.usp.br/mdidatico/concreto/Textos/21%20Tabelas%20de%20lajes.pdf. Acesso em: 09 abr.
ANEXO
[1] Bacharelando em Engenharia Civil pela Faculdade Independente do Nordeste, Licenciado em Física pela Universidade Federal da Bahia e Bacharel em Segurança Pública pela Academia de Polícia Militar da Bahia.
[2] Bacharelando em Engenharia Civil pela Faculdade Independente do Nordeste – FAINOR, Técnico em Eletromecânica pelo Instituto Federal Da Bahia – IFBA, Campus Jacobina.
[3] Orientador. Mestrado em Modelagem Computacional. Graduação em Engenharia Civil. Graduação em Sistemas de Informação.
Enviado: Setembro, 2020.
Aprovado: Outubro, 2020.
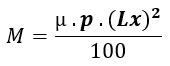

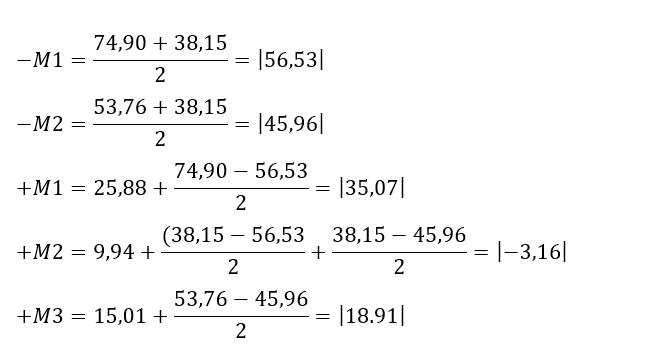
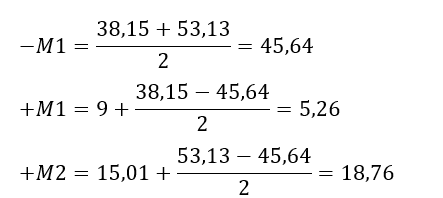


Uma resposta
sou engenheiro civil e estou precisando do material de concreto armado para estudar para concursos públicos e mesmo relembrar os assuntos da área.