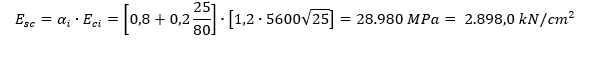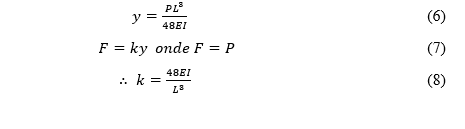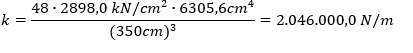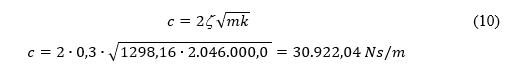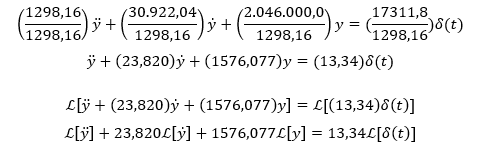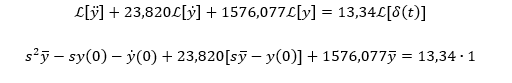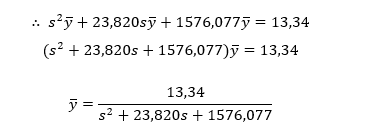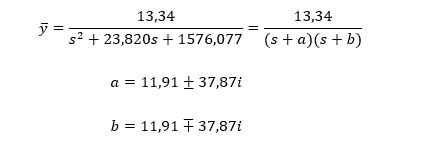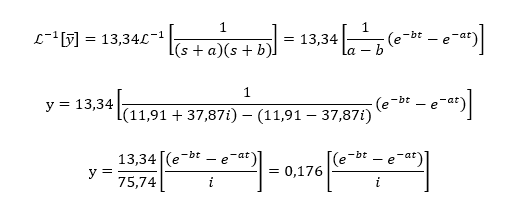Análise de vibração em lajes destinada às academias

ARTIGO ORIGINAL

MOURA, Tiago Rodrigues Coelho de ^[1]

MOURA, Tiago Rodrigues Coelho de. Análise de vibração em lajes destinada às academias. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano 04, Ed. 10, Vol. 10, pp. 116-128. Outubro de 2019. ISSN: 2448-0959, Link de acesso: https://www.nucleodoconhecimento.com.br/engenharia-civil/analise-de-vibracao

RESUMO

Atualmente, as atividades de educação física estão sendo muito praticadas e incentivadas na sociedade. Um dos locais mais usados para essa prática são as academias, pois, elas oferecem uma ampla opção de ferramentas que auxiliam os usuários. Os tipos mais usuais de academias são as comerciais e as de condomínios particulares. Muitos desses ambientes são instalados sobre lajes, principalmente, em condomínios verticais. Como se sabe, os exercícios físicos são executados de forma repetitiva e com uso de objetos pesados. O movimento de qualquer massa significativa provoca um comportamento dinâmico nas estruturas. As análises desses comportamentos são muito importantes e necessárias para o dimensionamento seguro de estruturas destinadas a esse fim. Nesse estudo, de forma analítica, foi feita a análise do comportamento de uma laje. Como método, foi usada a transformada de Laplace e um pulso de Delta de Dirac para solucionar o sistema massa-mola considerado. Os resultados obtidos foram bem satisfatórios para a compreensão teórica do fenômeno da vibração.

Palavras-Chave: Vibração, concreto, estruturas, dinâmica, laje, academia.

1. INTRODUÇÃO

A prática de atividades físicas esportivas está sendo cada vez mais incentivada pelos profissionais da saúde. As academias são ambientes ideais para muitas pessoas que não têm disponibilidade para frequentarem parques ou ambientes semelhantes. Além das academias comerciais, há muitas em condomínios, tanto nos horizontais quanto nos verticais. Na maioria dos condomínios verticais – que são os edifícios – há pouca disponibilidade de espaços apropriados para esse fim, sendo assim, aproveitam-se qualquer local para instalar uma academia. Os equipamentos de academias são compostos por peças pesadas e de movimento repetitivo. Essas repetições feitas pelos usuários, em virtude dos exercícios físicos, provocam diversas oscilações na estrutura. Uma das atividades que mais influencia o comportamento dinâmico de uma laje é o levantamento de peso. Isso porque o impacto de carga sobre uma laje provoca vibrações e descolamentos excessivos. Em estruturas de concreto armado, o fenômeno de vibração deve ser verificado conforme prescrito na NBR 6118 (ABNT, 2014). Esse estudo tem como objetivo mostrar o comportamento dinâmico de uma laje, quando submetida a um impacto de uma carga.

2. DESENVOLVIMENTO

2.1 CONSIDERAÇÕES INICIAIS DE ANÁLISE

Como o objetivo desse estudo é analisar dinamicamente uma laje, para isso, foi adotada a hipótese com medidas definidas, contudo, o modelo poderá ser estendido a outras dimensões. No caso analisado, o comportamento dinâmico é resultado de impactos. O elemento causador do impacto está esquematizado na Figura 1. Esse objeto foi adotado por ser o que contém a maior massa provável em uma academia.

Figura 1 – Esquema de um levantamento de peso

Para esse tipo de exercício, em específico, o impacto acontece de forma rápida e abrupta. Dessa forma, será usado um pulso unitário – o Delta de Dirac – para representar a função desse impacto. A massa do objeto erguida foi adotada com base no recorde mundial de levantamento de peso, na modalidade de Halterofilismo, de acordo com o site de notícia BBC (2004). Esse recorde foi feito pelo iraniano Hossein Rezazadeh, o qual levantou uma massa de 263,5 kg. Esse atleta tem uma altura de 1,86 m e a carga foi levantada acima de sua cabeça. Adotando a hipótese de que a altura total dessa carga foi de 2,20 m, dessa forma, é possível obter a força de impacto na laje com base na conservação de energia.

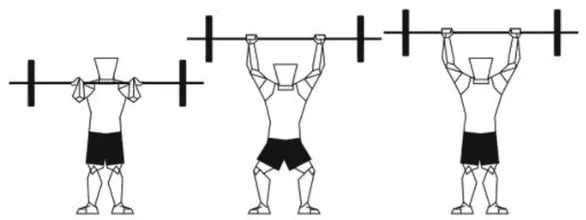
Nas edificações, existem diversos tipos de lajes. Para esse estudo, foi adotada uma do tipo nervurada (conforme Figura 2), tendo em vista que é o modelo mais conveniente para vãos maiores. Foram consideradas medidas hipotéticas: 7 m de comprimento e 3,5 m de largura. No entanto, o modelo apresentado é aplicável a outras dimensões. Nesse caso, a armadura principal é empregada apenas na menor direção.

Figura 2 – Seção transversal tipo da laje

Há várias normas nacionais e internacionais que tratam desse assunto. Em especial, são evidenciadas duas normas brasileiras: a NBR 6118 (ABNT, 2014) e a NBR 8800 (ABNT, 2008). A primeira, em seu item 11.4.2.3 e seção 23, define que devem ser consideradas as ações dinâmicas. A segunda, em seus itens 11.4 e 11.5, trata das observações relacionadas às vibrações nas estruturas que envolvem partes metálicas.

2.2 FERRAMENTAS MATEMÁTICAS

Há várias ferramentas matemáticas para solução do problema proposto nesse artigo. Destacam-se aqui duas que foram usadas: o Delta de Dirac e a Transformada de Laplace. O Delta de Dirac é uma função de pulso unitário e representa, de forma satisfatória, o impacto da carga na laje. A Transformada de Laplace é uma ferramenta matemática importante para solucionar as equações diferenciais ordinárias (EDO). Tais equações governam muitos problemas de engenharia e o tema apresentado aqui é um deles.

2.3 RIGIDEZ E AMORTECIMENTO

Todos os elementos estruturais possuem características próprias que variam em função do tipo de material e da forma geométrica. No caso de vibrações em lajes, é necessária a determinação da rigidez da estrutura e do coeficiente de amortecimento. A rigidez da estrutura é função de dois parâmetros: módulo de elasticidade do concreto e momento de inércia da seção tipo da laje.

O módulo de elasticidade do concreto pode ser determinado com as equações a seguir, em conformidade com a NBR 6118 (ABNT, 2014).

Onde:

e para f_ck menor que 55 MPa;

E_ci: módulo de elasticidade inicial do concreto;

E_cs: módulo de elasticidade inicial do concreto;

α_i: coeficiente função do f_ck;

f_ck: resistência característica do concreto;

α_e: coeficiente dependente do tipo de rocha do agregado, conforme item 8.2.8 da NBR 6118 (ABNT, 2014).

Em função do exposto acima, e adotando as seguintes propriedades para o concreto, pode-se obter o módulo de elasticidade secante:

• Resistência característica do concreto: 25 MPa
• Coeficiente para o basalto: 1,2

O momento de inércia da seção tipo pode ser obtido em função de cada figura geométrica conhecida e aplicando o teorema dos eixos paralelos. Para calcular o centro de gravidade da seção transversal, aplica-se o momento das áreas, assim, chega à seguinte equação, conforme Beer e Johnston (2004).

A equação 3 é usada para calcular o momento de inércia no centroide de uma seção retangular.

Para conhecer o valor do momento de inércia da seção T, é necessário aplicar o teorema dos eixos paralelos.

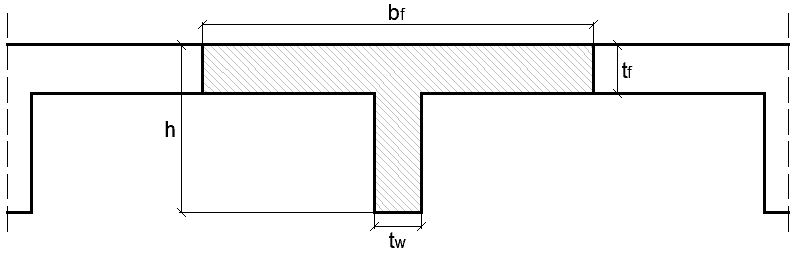
O significado de cada incógnita das equações 2, 3 e 4 podem ser observados na Figura 3 e Tabela 1.

Figura 3 – Centro de gravidade da seção tipo da laje

As dimensões da seção tipo da laje, bem como os cálculos relacionados às equações 2, 3 e 4 estão dispostos na Tabela 1.

Tabela 1 – Dimensões e inércia da seção tipo.

A força de impacto da carga sobre a laje pode ser calculada pela conservação da quantidade de movimento do corpo em queda livre. O tempo de impacto foi obtido, de forma aproximada, pela análise do som emitido quando o objeto colidiu com o piso. O som analisado foi o áudio do vídeo de um atleta de halterofilismo. O tempo aproximado foi de 0,1 segundo, conforme figura 4.

Figura 4 – Análise do som de impacto

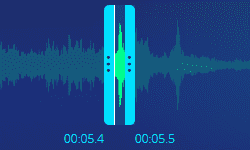
Em função desse tempo encontrado, e dos demais dados do problema, foi calculada a força de impacto, aplicando a equação 5.

Considerando a seção tipo da laje como uma viga bi-apoiada e que o impacto ocorra no centro, ou seja, a situação mais desfavorável, obtém-se o deslocamento máximo. De acordo com Hibbeler (2005), esse deslocamento máximo pode ser calculado aplicando a equação 6. Sabendo que a força elástica é obtida pela equação 7, então, fazendo a manipulação algébrica dessas duas equações, obtemos a rigidez do elemento estudado.

Com os dados das propriedades do concreto e geométricas, foi obtido o coeficiente de rigidez da seção tipo da laje com a equação 8.

Para o dimensionamento de uma laje, devem ser observados os valores de máximos nos esforços e deslocamentos. Todo movimento em um elemento estrutural é amortecido, porém, independente da consideração de cálculo, amortecido ou não, o que é mais importante são as amplitudes máximas desses deslocamentos. Foi adotado para esse estudo um fator de amortecimento () igual a 0,3. Com isso, calcula-se o coeficiente de amortecimento (c), considerando que o peso específico do concreto armado é de 25 kN/m³. A massa total do sistema vibratório (m) é o somatório da massa permanente na laje (peso próprio, usuários, equipamentos, etc.) e da carga de impacto.

• Massa referente ao peso próprio (pp):

• Sobrecarga (sc) mínima de 5 kN/m² para salão de esportes, conforme NBR 6120 (ABNT, 1980), onde a área será apenas a seções tipo da laje.

• Massa do objeto levantado pelo usuário igual 263,50 kg.
• Massa do sistema vibratório.

m= 321,10 + 713,56 + 263,50 =1298,16 kg

O coeficiente de amortecimento do problema, conforme Sartorti (2015), é obtida pela equação 5.

2.4 SISTEMA MASSA-MOLA

Toda estrutura, que por algum motivo entra em vibração, pode ser resolvida como um sistema massa-mola. A massa é concentrada em seu centro de gravidade e se comporta como mostrado na Figura 5.

Figura 5 – Sistema massa mola com amortecimento

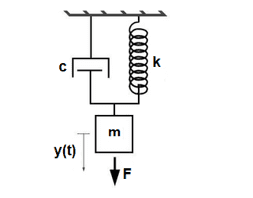
A equação que governa esse problema, conforme Beer e Johnston (2004), é do tipo diferencial ordinária de segunda ordem. Essa EDO é composta por todos os termos da segunda ordem até a ordem zero e está demonstrada na equação a seguir.

Onde

m é a massa do sistema vibratório [kg]

c é o coeficiente de amortecimento [Ns/m]

k é o coeficiente de rigidez [N/m]

F(t) é a função de força do sistema [força em N]

ÿ é a aceleração da massa em função do tempo

ȳ é a velocidade da massa em função do tempo

y é o deslocamento vertical no centro da laje em função do tempo

A função adotada para esse pulso foi o Delta de Dirac δ (t) , com isso, a equação da força em função do tempo ficou conforme o que se segue.

Dessa forma, substituindo F(t) e as constantes na equação 11, obtemos a equação geral que governa o problema.

2.5 RESOLUÇÃO E RESULTADO

Neste estudo, foi adotada a transformada de Laplace () para resolver a EDO que governa o problema proposto. Nesse método, foi usado algumas definições já tabeladas, conforme apresentadas por Hildebrand (1976). A seguir, está apresentado um passo a passo da resolução da equação 13.

• Dividindo toda a equação pelo coeficiente da derivada de mais alta ordem e aplicando a transformada de Laplace para troca de variável.

• Aplicando as definições tabeladas, conforme Hildebrand (1976).

• Aplicando as condições de contorno.

1º – O deslocamento inicial é nulo: y(0) =0

2º – A velocidade inicial é nula: ȳ (0) = 0

• Separando em frações semelhantes às transformadas inversas de Laplace.

• Aplicando a transformada de Laplace inversa e obtendo a solução do problema.

• Aplicando a fórmula de Euler.

• Dessa forma temos a equação 14 que é a solução do problema com relação aos deslocamentos verticais da carga de impacto em função do tempo.

Gráfico 1 – Oscilação da laje em função do tempo

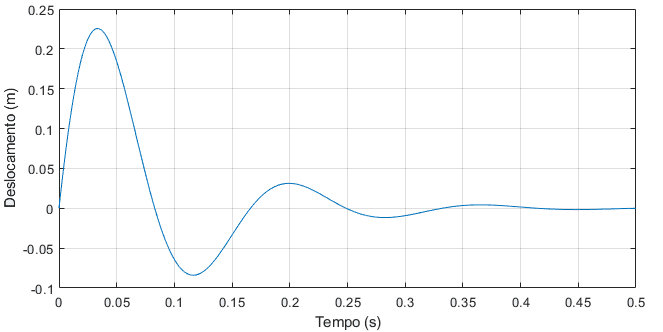
Com base no gráfico 1, ficou notório o quão importante é a consideração desse tipo de carregamento na estrutura. O valor obtido para o deslocamento, nessa situação hipotética, foi superior a 200 mm e isso é inadmissível para lajes com vão de 3,5 m. Além do mais, seria muito provável que a laje sofreria algum tipo de patologia irreversível com um impacto dessa magnitude.

3. CONCLUSÃO

Feita a análise, ficou evidente a importância da consideração dos efeitos dinâmicos em uma laje. Esses efeitos provocam deslocamentos adicionais, além dos causados por cargas estáticas. Desse modo, ao dimensionar um elemento estrutural, deve-se considerar todas as hipóteses mais desfavoráveis à estrutura. Outras considerações importantes, no caso das vibrações, são a fadiga e a ressonância. O gráfico 1 mostrou como a laje se comportou e, nesse caso, há apenas os riscos de fadiga e colapso pelo deslocamento excessivo. Mas, existem outros equipamentos nas academias que podem causar ressonância, é o caso do spinning e da esteira. Dessa forma, todos os efeitos devem ser considerados no dimensionamento, a fim de projetar com segurança e conforto ao usuário.

4. REFERÊNCIAS

ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 6118: projeto de estruturas de concreto: procedimento. Rio de Janeiro, 2014.

______. NBR 8800: projeto de estruturas de aço e de estruturas mistas de aço e concreto de edifícios: procedimento. Rio de Janeiro, 2008.

______. NBR 6120: Cargas para o cálculo de estruturas de edificações: procedimento. Rio de Janeiro, 1980.

BEER, F. P.; JOHNSTON, E. R. et al. Vector Mechanics for Engineers: Statics & Dynamics. 7. ed. McGRAW-HILL, 2004.

HIBBELER, R. C. Mechanics of Materials. 6. ed. New Jersey: Pearson Prentice Hall, 2005.

HILDEBRAND, F. B. Advanced Calculus for Applications. 2. ed. New Jersey: Prentice-Hall, 1976.

Online Voice Recorder. Disponível em: < https://online-voice-recorder.com/pt/>. Acesso em: 13 ago. 2019.

Rezazadeh wins gold. Disponível em: < http://news.bbc.co.uk/sport2/hi/olympics_ 2004/weightlifting/3599690.stm>. Acesso em: 13 ago. 2019.

SARTORTI, A. L. Comportamento Dinâmico de Lajes Maciças de Concreto Leve com Pérolas de EPS. 2015. Tese (Doutorado), USP, São Carlos, 2015.

Toda a verdade sobre o ‘crossfit’ e seus oito exercícios milagrosos. Disponível em: < https://brasil.elpais.com/brasil/2015/11/26/deportes/1448537751_724117.html>. Acesso em: 09 ago. 2019.

^[1] Pós-graduado em Gestão de Obras na Construção Civil pela Faculdade Cidade Verde (FCV), Engenheiro Civil pelo Centro Universitário UNIEURO e técnico em Telecomunicações Aeronáuticas pela Escola de Especialista de Aeronáutica (EEAR).

Enviado: Agosto, 2019.

Aprovado: Outubro, 2019.