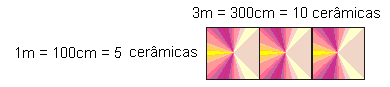ОРИГИНАЛ СТАТЬИ
SCHWANTES, Vilson [1], XAVIER, Márcio Pizzete [2], SCHWANTES, Eloísa Bernardete Finkler [3], SCHWANTES, Daniel [4], JUNIOR, Affonso Celso Gonçalves [5], KRACKE, Elisa [6], JUNIOR, Élio Conradi [7]
SCHWANTES, Vilson. Et al. Этноматематика: Размышления о математике, используемой каменщиками. Revista Científica Multidisciplinar Núcleo do Conhecimento. 04 год, Эд. 07, Vol. 13, стр. 46-66. Июль 2019 года. ISSN: 2448-0959
1. РЕЗЮМЕ
Данная статья является результатом размышлений по этноматематике и анализу учебных сессий, проведенных с Bricklayers в муниципалитете Мерседес – PR. Он находит мотивацию в трудах профессора Убиратана Д. Амброзио, который признает наличие математических знаний в различных культурных пространствах. Основное внимание в исследовании исследует сяокардиат с каждым профессионалом, через проблемные ситуации, которые математика использует для того чтобы сделать бюджет количества керамики обязательно для того чтобы покрыть стены и пола. В исследовании, проведенном с каменщиками, было интересно узнать, являются ли они формальными или неофициальными. Заявления свидетельствуют о понимании того, что математическое знание является динамичным, культурным продуктом, который возникает в различных секторах человеческой деятельности и циркулирует в мире жизни и через него, консолидируется в школе.
Ключевые слова: математическое образование, этноматематика, проблемные ситуации, учебные занятия, керамический бюджет.
2. ВВЕДЕНИЕ
Во всех культурах, на протяжении всей истории, мы находим записи развитой деятельности, которые обозначают существование и необходимость какого-то математического знания. Это эмпирическое знание, используемое в осуществлении нескольких профессий, передаваемых из поколения в поколение и используемых, часто, без людей, не замечающих этого присутствия.
При использовании математических рассуждений для решения проблемной ситуации, иногда можно решить, не обязательно посещая школу. Математические знания могут развиваться естественным путем ежедневной практики, например, в работе каменщиков, профессионалов, которые регулярно используют такие знания.
На протяжении многих десятилетий истории образования знания, вытекающие из социальной практики, игнорировались и не обсуждались в школе. В настоящее время предложение исследовать математические знания, присутствующие в жизни студентов вне школьного контекста, набирает все больше места. Это знание, накопленное человеком в пространстве и временности, представляет собой драгоценное наследие, которое должно быть учтено в школьных программах или в принятой методологии. Есть много педагогов, которые считают, что systate знания могут быть построены из концепций, присутствующих в повседневной жизни профессий, людей.
Для профессора Убиратана Д’Амбрасио, еще до поступления в школу, все дети уже имеют математические знания. Для исследователя это знание является этномамататом[8]. Автор хочет сказать нам, что знания – это не только результат многолетнего изучения, но и плоды опыта, прожитого среди граждан одних и тех же или различных социальных групп.
По словам исследователя, основное предложение этноматематики заключается в том, чтобы попытаться понять математические знания / создание каждой группы интересов, сообщества, людей или нации. В этом смысле его труды считают этномамата:
“… Математика, практикуемые культурными группами, такими как городские и сельские общины, группы работников, профессиональные классы, дети определенной возрастной группы, общества коренных народов и многие другие группы, которые идентифицируют себя по целям и традициям Общие для групп “. (2001, p.9).
Автор видит этноматематику:
“… Стратегия, разработанная человеческим видом на протяжении всей своей истории, чтобы объяснить, понять, управлять и жить с чувствительной реальностью, ощутимой и с ее мнимой, естественно, в естественном естественном и культурном контексте . (Д ЗМБРОСИУС, 1996, стр. 7)
Bricklayers, иногда неграмотным и большую часть времени с небольшим школьным образованием, использовать математические знания, чтобы построить дома, сделать керамические гнездования, строить стены, здания, считается до сих пор, твердые и прочные конструкции. Она, безусловно, существует в этой работе, особенно в расчетах и в организации математических рассуждений используется, знания, которые могут быть использованы в школьном контексте, или в интеграции студентов с тенденцией к этому типу профессии, либо в подходе Более практическая дисциплина математики. Для Карнейро
[…] Преподавание математики в этой концепции позволит студенту связать концепции, работающие в классе, с их ежедневным опытом, в соответствии с их естественной, социальной и культурной средой. Речь идет не об отказе от академической математики, а скорее о включении ценностей, которые имеют опыт в групповом опыте, учитывая историко-культурные связи (CARNEIRO, 2012, стр. 3).
В последние десятилетия число преподавателей, изучающих этноматематику, выросло как исследовательская программа и/или как предложение к педагогической работе. Среди прочего, цель этих учителей заключается в том, чтобы знать процессы генерации, организации и распространения знаний и математических идей, присутствующих в культурных группах, и как разработать действия в области преподавания математики, которые позволяют Контекстуализация формального содержания, охватываемого в классе.
Перспектива этноматематики позволяет нам работать в классе образовательное предложение, которое поощряет студентов и преподавателей в развитии творчества, что приводит как к новым и богатым формам обучения. Это социально-культурное богатство, которое включено в учебный процесс, по словам профессора Убиратана Д’Амброзио, является частью “программы, которая направлена на объяснение процессов генерации, организации и передачи знаний в различных Культурные системы и интерактивные силы, которые действуют в зависимости от трех процессов и между ними». (D’AMBRÓSIO, 1993, p.7).
Еще одна перспектива этноматематики была разработана бразильским исследователем Гельсой Книйником. Для этого автора этноматематика позволяет
Изучение евроцентрических дискурсов, в которые института академической и школьной математики; Анализ влияния истины, производимых дискурсами академической и научной математики; Обсудить вопросы различия в математическом образовании, учитывая центральную роль культуры и силовых отношений, которые ее устанавливают; и изучить языковые игры, которые составляют каждый из различных математики, анализируя их семьи сходства. (KNIJNIK, 2006, p.120).
В исследованиях Книника автор характеризует этноматематику как математику, производимую социальными группами, которые используют свои знания для выполнения своей деятельности. Книйник (2002, стр. 33), делая контрапункт между формальной и неформальной математикой,[9] размышляет о том, […]что если – приобрести знания, полученные в академической математике, используя, когда сталкиваются с реальными ситуациями, то, которые кажутся более уместными.
Согласно Giardinetto (1999), «учитель может и должен использовать ежедневные знания как пункт поддержки для процесса преподавательства-обучения» (p. 68), приносящ студент в поле argumentation, превращая привычку критически чтения, исследования, Вопросы, творчества, необходимые для обучения граждан. Таким образом, они ценятся и свидетельствуют предыдущие знания студентов, формируя из этих, другие знания, всегда из известных.
Важным является установление связей знаний сообщества со знанием школы и знанием школы с знанием сообщества. Через это создание и эти отношения можно отнести значение к обоим знаниям.
Затеянный автором вопрос о том, что школа, больше, чем воспроизвести ежедневные знания, должна быть посредником между этим и школьными знаниями, то есть она должна сделать доступным и новой поколению мудрость, разработанную человечеством, которая проявляется как продукт Историческое и социальное. Эти знания необходимо социализировать, поскольку “это не единственный человек, который строит все знания, а имеет право на доступ к этим знаниям” (GIARDINETTO, 1999, p. 47).
Для Д’амбрезио (2001), в этом контексте, знания представляют собой динамичный характер, всегда открыты для новых подходов. Для этого учитель должен быть в курсе событий, постоянно оценивать свою практику, практиковать новые методики преподавания, а также совершенствовать педагогические действия, которые ранее испытывали, с точки зрения того, что они могут способствовать Педагогических.
Бреда, Лима и Гимарайнш (2011, стр. 15), в своих исследованиях утверждают, что:
Я начал рассматривать предложение этноматематики как возможность дифференциирования работы, которую учитель развивает в школах, то есть контеудистскую и бессмысленную практику можно заменить учителем, ориентированным на новый взгляд, который способствует понимание социально-культурного контекста образования, его процессов мышления и его способов понимания, разъяснений и осуществления своей практики в современном обществе, приглашение[…] вернуться к своей педагогической практике и ее последствиям или даже взглянуть на его роль, Как преподаватель, который занимается различными перспективами предмета в школьном контексте.
Таким образом, в школьном контексте, как учебная программа, которая стремится знать и понимать знания, полученные и используемые в различных культурах, этноматематика может быть изучена, чтобы помочь в преподавательской работе, что делает студентов могут Понять различные “математики”, используемые в других контекстах, оценивая культурное разнообразие и интеллектуальное и творческое развитие каждого народа, каждой культуры или общины.
Мы, учителя математики, в соответствии с D’ambrosius (2001), мы должны быть ясными и быть в полной гармонии с нашей ролью в качестве педагога перед миссией подготовки наших молодых людей к счастливому будущему. Мы должны учить Да математике, но и о гуманности. В этой связи автор подчеркивает:
Педагогическое предложение этноматематики состоит в том, чтобы сделать математику чем-то живым, занимаясь реальными ситуациями во времен[agora]и и пространств[aqui]е. И, через критику, подвергая сомнению здесь и сейчас. При этом мы погружаемся в культурные корни и практикуем культурную динамику. Мы фактически признаем в образовании важность различных культур и традиций в формировании новой цивилизации, межкультурной и междисциплинарной. (D’AMBRÓSIO, 2001, p. 46).
Чтобы сделать это реальностью, учитель должен ежедневно пересматривать свою преподавательскую практику, разрабатывать педагогический проект, который всегда ценит знания и историю каждого студента, стремясь в этой индивидуальности новый и практический контекст для искусства Научить. Важно, чтобы учитель в классе, в дополнение к наслаждению и начиная с знания, что студент приносит из среды, в которой он живет, поощрять его к мысли, что он также играет важную роль в (ре) строительство социальных и культурных знаний, а также знания Математик.
По словам Розы Нету, математику нужно интерпретировать как естественный социокультурный продукт народа, потому что,
Математика была создана и была разработана человеком в соответствии с его потребностями. (…) Культура является одной из форм адаптации, потому что это способ действовать на окружающую среду, которая была построена вместе с ним. (ROSA NETO, 2002, p.7 e 19).
В этом контексте существует значительная взаимосвязь между математикой и культурой, как в результате нашей адаптации в соответствии с потребностями выживания во времени, представляющих культуру, что прошлые поколения оставили нас, эмпирическое наследие , систематический и научный.
3. ОБОСНОВАНИЕ
Математика всегда считалась базовой наукой нескольких областей знаний. Владение его знаниями имеет основополагающее значение для решения проблемных ситуаций в нескольких областях. Учитывая это значение и актуальность необходимо искать новые формы (методы), чтобы научить его, всегда ищет большей эффективности для учебного процесса в школьном контексте.
Многие исследования в этой области также подчеркивают низкий доход студентов в отношении изучения дисциплины, заявив, что существует необходимость в большей контекстуализации содержания происходит лучше ежезнания. Его учение рассматривается, часто студентами, родителями и даже учителями, как абстрактные, далекие от реальности, то есть то, что преподается в классе, представляет себя далеким от повседневных потребностей за пределами школы.
Это отсутствие связи с повседневной жизнью, а также избыток символики преподается в математике в школах, иногда способствует распространению ошибочных идей по отношению к этой дисциплине в школьном контексте. Тесты, которые мы защищаем, находит теоретические основы в трудах профессора Убиратана Д’Амбрасио, с тем чтобы производство математических знаний не может быть отделено от социальных движений и культуры тех, кто производит эти знания.
В этом смысле мы можем утверждать, что существует переплетение между производимой математикой, обществом, которое ее производит, и культурой, которая субсидирует эту продукцию. Это переплетение построено в нескольких руках через когнитивный процесс, опосредованный творческим действием различных субъектов, все мотивированы необходимостью читать, понимать и объяснять реальность, в которой они живут.
Если мы посмотрим на историю человечества и науки, то поймем, что не только математику, но и другие области знаний будут строить и восстанавливать, будучи унесения в отставку в любой исторический момент и в соответствии с требованиями общества. Помпей и Монтейро (2001), в книге Математика и поперечные темы подчеркивают, что учитель должен понимать текущий масштаб своей роли в обществе, потому что, по мнению авторов,
Нынешние учителя сталкиваются с большой проблемой: образованные в разрозненный процесс, они должны будут преодолеть пределы, которые это образование налагает на них и экстраполировать границы содержания видели в частичный и исторический путь (POMPEU и MONTEIRO, 2001, стр. 15).
Учитывая требования такого масштаба, необходимо, чтобы мы стремимся понять эпистемологический процесс математики, то есть генеративный процесс этого знания, причину его организации и систематизации. Минимизация этих рамок в последние десятилетия была предметом озабоченности ряда преподавателей и исследователей.
Для Ролима,
Размышляя об историко-культурном контексте в процессе обучения изучению математики, следует учитывать, что “делать” предполагает нечто большее, чем правила и методы; является признание того, что, как наука, математика сама по себе является зданием человечества (ROLIM, 2010, стр. 43).
Фактом является то, что образовательное предложение, характеризующееся образовательной практикой, способствующей социокультурному воспитанию, позволяющее в классе установить учебные отношения для удовлетворения повседневных потребностей учащихся, растет Все больше и больше как педагогическая альтернатива. По словам Д’амбрезио, это означает построение условий, чтобы студент мог также справиться в классе с различными ситуациями его / ее повседневной жизни.
Это перспектива, которая делает преподавание математики более контекстуализированным, с оценками и проблемами социокультурного характера. Согласно D’ambresio (2001), этноматематика является областью образования, которая стремится отразить на математические знания, которые генерируются от взаимодействия в конкретной культурной группы. Для автора, математические классы, в этой перспективе, основаны на математических знаний извне в классе, и эти знания должны быть разработаны на опыте студента.
Д’амбрусио (2001, стр. 22) В этой связи также делает следующее заявление:
Повседневная жизнь пропитана знаниями и творчеством культуры. В каждый момент люди сравнивают, классифицируют, измеряют, объясняют, обобщают, делают выводы и, каким-то образом, используют материальные и интеллектуальные инструменты, соответствующие их культуре (D’ambresio, 2001, p. 22).
В нашем исследовании, руководящий вопрос был: Какая математика (формальная или неформальная) использовать каменщиков, чтобы сделать бюджет количества керамики, необходимой для покрытия стен и полов. Было очевидно, что профессиональный Мейсон оказывает свои рабочие функции, используя математические навыки, извлеченные из повседневной практики. Для Монтейро (2002, стр. 102) “Культурное ноу-хау имеет другие пути проверки, еще одна логика для его конфигурации. Вопрос в том, почему одно стало универсальным и узаконено, а другое нет». С этой точки зрения автор ссылается на ситуации, аналогичные тем, которые произошли в этом расследовании.
По словам Гердеса:
На протяжении веков, каменщики, иногда неграмотные и, большую часть времени, с очень мало школьного образования, строить дома, стены и другие здания, по-прежнему считается твердых и прочных конструкций сегодня. Таким образом, она существует в их работе, в том, как они делают свои расчеты и организовать их математические рассуждения, мудрость, которая может быть harnated в школьном контексте, или в интеграции некоторых студентов с тенденцией к этому типу профессий или в Более “практический” подход и ближе к повседневной жизни для студентов в целом. Эта ситуация упоминается в работе этого исследования, а именно, в терминологии Гердеса, как “угнетенная математика”, или “скрытая или замороженная математика” (GERDES, 1991, стр. 29).
В исследовании мы исходим из предположения, что каменщики, группа выбрали, чтобы сделать это исследование, составляют группу работников, которые ежедневно используют широкий спектр математических знаний в своей повседневной жизни и без этого знания не будет развивать или осуществлять какую-либо деятельность в гражданском строительстве. Однако, учитывая, что они, как правило, имеют мало школьного образования, было интересно узнать, как они приобрели эти математические знания или же они были предоставлены через повседневную практику.
В этом контексте, эта следственная работа может также способствовать демистификации идея о том, что математика является наукой для немногих, понимая, что существует не один математический язык, но несколько форм мышления Математические, каждый организован и структурирован в своем социальном контексте.
Для обеих школ необходимо разработать образовательные проекты, которые позволяют обмениваться опытом с мероприятиями, где математика используется ежедневно. В этом взаимодействии, помимо того, что позволяет обмен опытом, укрепятся связи и устанавливаются другие педагогические отношения с миром, живущим за пределами школы, и это может быть облегчающим путь в изучении дисциплины.
По словам Д’Амбрасио, уроки математики должны основываться на математических знаниях извне в классе, и эти знания должны развиваться на основе опыта студента. Таким образом, автор утверждает, что этноматическое знание группы/сообщества имеет большое значение, потому что оно служит, является эффективным и подходящим для многих вещей, соответствующих этой культуре, этому этно, и нет необходимости заменять его. Аналогичным образом, математика доминирующей группы служит ему, она полезна, и нет никакого способа игнорировать его (D’ambr’sio, 2001, стр. 80).
Для Карнейро
[…] Преподавание математики в этой концепции позволит студенту связать концепции, работающие в классе, с их ежедневным опытом, в соответствии с их естественной, социальной и культурной средой. Речь идет не об отказе от академической математики, а скорее о включении ценностей, которые имеют опыт в групповом опыте, учитывая историко-культурные связи (CARNEIRO, 2012, стр. 3).
4. PROBLEMATIZING К ЗНАТЬ ДОРОГИ MATEMATIZAR КАМЕНЩИКОВ
В ходе следственной работы, проведенной с группой каменщиков, мы проработали некоторые проблемные ситуации, чтобы убедиться, что математика используется этими специалистами для составления бюджета количества керамики, необходимого для покрытия стен и полов. Это исследование было проведено с точки зрения D’ambr’sio и ROSA, которые рассматривают этноматематику как исследовательскую программу в истории и философии математики, с педагогическими последствиями, когда авторы считают:
Таким образом, эта исследовательская программа представляет собой методологию исследования, которая стремится анализировать местные математические практики, поскольку она стремится ценить, распространять и уважать математические знания (идеи, понятия, процедуры, процессы и практики), которые Происходят в различных культурных контекстах на протяжении всей истории (Д’АМБРЕЗИО и ROSA 2016, стр. 17).
Ситуация-Проблема: Для того чтобы высчитать число прямоугольных плиток [20 por 30]размера cm, необходимо покрыть пол ванной комнаты картинной штольни, размеры 6, 00m 4, 50m (Lezzi, 1996, p. 223), Оскар рассмотрено как «точка отсчета размеры пола пола Ванная комната. Принимая размер керамики, мы выберем 6м, который делится как по керамической стороне 20см, как в 30 см. Уже 4, 50м нет.
Эта мера делится только на 30[medida do outro lado da cerâmica]. Итак, я выбрал то, что было бы проще, взяв 6м ра[600cm]зделены на 30 см, достигнув точного числа 20 керамики в направлении длины. Теперь, взяв керамику в направлении 20см стороны я достиг числа 30 lajotas.
Уже в 4, 50м, делится на 30, я взял 4, 50 м и ра[450cm]зделены на 30 см, достигнув числа 15 плиток, которые вписываются в ширину. Так Есть 15 плитки в смысле 30см. Для достижения расчета я взял 30 плиток, которые идут в длину [600cm]плюс 15, которые идут в ширину, умножается и достиг числа необходимых плиток, которые будут 450 плитки “.
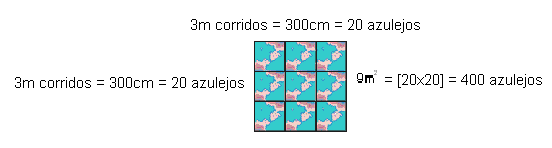
Рассуждения, используемые Мейсон Сержио, чтобы сделать этот же бюджет, демонстрирует, в соответствии с D’ambrosius (2001), что “в различных средах, этноматематика различны” (стр. 35). Таким образом, Мейсон начинает свою речь, подчеркивая, что “сначала вам нужно открыть для себя квадратные метры площади, было бы ра[operação de multiplicação]з. Я нашел 27m2, так что я должен выяснить, сколько плитки вписываются в квадратный метр. Как 30см не[medida do comprimento da placa cerâmica] дают точные в один метр, я увеличивал и использовал 3м, а затем закрыл с 10 lajotas. Этот результат 10 плиток, умноженные на 5 плиток, которые вписываются в ширину. Я нашел число 50 плитки в 3m2 “. Визуализируйте в последовательности дедуктивную мысль, используемую каменщиком, чтобы иметь возможность сделать бюджет.
Продолжая объяснение, Сержио сообщает, что после того, как он обнаружил, что в 3m2 подходят 50 штук, это было только “… Возьмите эти 27m2, разделить на 3, которые привели меня 9 равных частей. Таким образом, 9 раз 50, дает результат количества керамики, которая идет по всей области. Они 450 керамики и до сих пор должны увидеть перерыв “.
Бюджетные расчеты, выполненные Мейсон Альберто, также указал на “450 керамики. Я сделал стороны времени керамической стороны, 0, 20м раз 0, 30м достижения числа 0, 06m2. Этот результат представляет площадь каждой керамики. Теперь я сделал сторону стороны времени пола ванной комнаты, 6m раз 4, 50m и достиг результата 27m2. Затем, ванная комната кадры, 27m2 разделены квадратных метров части 0, 06m2, дал 450 керамики “.
В резолюции излагать: сколько квадратных плиток 15 см в сторону необходимы для внутреннего пальто бассейн с 15 м в длину, 6 м в ширину и 1, 20 м в глубину (ЛЕЗИ,1991, р. 195), Оскар сообщил: “Я решил превратить эти 15 м в 1500 см разделены на 15 см Lajota, в результате чего 100 плитки в длину одной стороны бассейна. Так с другой стороны даст такое же число, т.е. этот ряд, умноженный на 2, дает 200 плиток, которые помещаются по обе стороны длины.
Та же процедура, которую я использовал в ширину, а именно 6м 600см, и эти 600см разделены на 15 дал мне 40 плитки, которые будут идти в ширину. Как у нас есть две ширины здесь, умножение на 2, я нашел 80 плитки. Добавление 200 плитки в длину с 80 шириной, я достиг числа 280 плитки, которые должны быть умножены на глубину, которая составляет 1, 20 м, т.е. 120см. Прежде чем, однако, я разделил эт[medida da profundidade]и 120см, на[medida do azulejo] 15 см и нашел 8 плиток, которые будут идти в глубину бассейна. Теперь, принимая длину и совмещение вверх с шириной, я значу 200 плиток плюс 80 плиток, времена 8 плиток глубины, я достиг числа 2.240 плиток.
Мы все еще должны найти количество плиток со дна бассейна. Это легко вычислить, потому что размеры длины и ширины дна такие же, как стороны, означают 6 м на 15 м. Таким образом, они идут 100 керамики в длину и 40 в ширину дна, в общей сложности 4000 керамики в нижней части бассейна. Добавление числа плитки сторон и нижней я достиг числа 6240 керамики “. Мейсон также подчеркнул, что “вы всегда будете нуждаться в резервации”, чтобы предотвратить возможные поломки, среди других.
Признание существования «других форм мышления», как постулирует Д’амбрезио (2001, стр. 17), проявляется в математических рассуждениях, используемых Сержио для составления этого же бюджета. Сообщая о своем мышлении каменщик подчеркивает, что “сначала мне нужно знать квадратные метры ст[laterais]ены и пола. 15м плюс 6 м, более 15 м и более 6 м, даст боково[42m corridos]й. Это время 1, 20м,[profundidade da piscina] дает 50, 4m2 области.
Тогда я найду кадры снизу[15m vezes 6m = 90m2]. Мы все. Я сделал и дал 140, 4m2. Теперь мне нужно выяснить, сколько плиток помещается в каждом квадратном метре. Только то, что, как плитки 15см на 15 см, в метр не з[corrido]акрывается. Тогда я добавлял, пока я не добрался до 3м. В 3м,[corridos] Есть 20 lajotas. Тогда я взял 3 раза 3, [multiplicado por]буд[cada face da piscina representa uma figura plana – duas dimensões]ет в общей сложности 9m2, что дало 400 Lajotas “. Визуализируйте в представлении, которое следует, рассуждения, используемые каменщиком для выяснения проблемной ситуации.
Продолжая объяснение своих процедур, Сержио следует: “Я взял в общей сложности M2 из бассейна, разделены на 9[9 partes]. Дал 15,6 равных частей по 9м2 кажда[140,4m2 : 9m2 = 15,6]я. Эти 15,6 части в разы превышают количество керамики в 9м2, т.е. 400 керамических. Тогда в каждой части будет 15,6 раза 400, что равно 6240 керамики “.
Отвечая на вопрос, даже если бюджет 6240 керамики даст достаточно, чтобы покрыть бассейн, Сержио легко подчеркивает: потребуется около 5% больше от этого общего из-за поломки.
Для профессора Д’Амброзио, человеческие группы дают знания, которые, хотя и не широко распространены в официальных учебных помещений, является действительным знанием и что школа, а также исследования в области математического образования должны признать и углубить, чтобы обогатить акт Образовательных.
D’ambr’sio (2001, стр. 22-23), отмечает далее, что,
Проводятся многочисленные исследования по этноматематике повседневной жизни. Это этноматематика не в школах, а в семейной среде, в среде игрушек и работы, получаемой от друзей и коллег.
Разрешение этой ситуации-проблемы для Альберто показал знания, которые отождествляются с процедурой, которая будет использоваться учителем математики. Обратите внимание на его объяснение: “Длина бассейна стороны 15м и 15 м, а также добавление ширины 6 м и 6 м дает периметр бассейна, 42м. Теперь 42m раз 1, 20 м от глубины 50, 40 м2 площади по бокам бассейна. Дно бассейна имеет площадь 15м раз 6м и дает 90m2. Добавление боковой области и нижней, я имею в виду 50, 40m2 плюс 90m2 дает 140, 40m2. Это разделено размером плитки, которая составляет 15 см на 15 см и что в M2 дает 0, 0225m2, составляет 6240 плиток. Теперь просто добавьте немного к буферу перерыва ”
Для Демо (1996 год) построение знаний начинается с знаний, включенных каждым человеком в их социально-культурный опыт. Это было очевидно в формах математизза, используемого каждым из каменщиков. Для автора “Нет мелкой доски, абсолютной неграмотности; Все говорят, общаются, используют базовый словарь, управляют понятиями в здравом смысле, имеют отсылки к реальности, в которую они вставлены “(стр. 32).
Поступая в школу, каждый уже накопил некоторые знания, даже если это в рамках здравого смысла. Мы поделились с D’ambrosius (1993), когда мы постулировали, что мы должны понимать, что, когда формальное обучение начинается, ребенок уже имеет этноматематику, которая позволяет ему сталкиваться с интерпретациями систематической математики школы.
Математизар формы каменщиков обозначают в соответствии с Маркес (2000), что “учебные процессы неизбежно вставлены в коммуникативных и общественных общин, в которых люди учатся друг у друга и друг с другом” (стр. 29). Согласно пониманию Помпея и Монтейро (2001), «значимый образовательный процесс начинается с взаимодействия школы и сообщества» (стр. 55), отношения которого могут отказаться от роли школы как привилегированного места для обмена опытом Лучше понять знания, циркулирующие в повседневной жизни.
В проявлениях (вербализации), выраженных каменщиками в учебных сессиях, особенно из математического изготовления этих специалистов, на основе их опыта работы, в обмене знаниями, что они уже участвовали на протяжении всей своей жизни, показывают, Что формальное образование может ценить и подтверждать эти предыдущие знания, свою культуру и социальную среду. Мы считаем, что воспитательная работа, которая оставляет, в диалогически этих знаний, Энрике и контекстуализирует математические знания школы.
По словам Ролима
Размышляя об историко-культурном контексте в процессе обучения изучению математики, следует учитывать, что “делать” предполагает нечто большее, чем правила и методы; является признание того, что, как наука, математика сама по себе является зданием человечества (ROLIM, 2010, P. 43).
В нашем понимании, с этой точки зрения, она устанавливается в законе об образовании отношения широко используется в деловом мире, где выражение “беспроигрышный” говорят и практикуются. В переговорах это выражение имеет характеристику: никто не проигрывает, каждый выигрывает. Оно установлено между компанией и поставщиком идеально отношение.
Для Закона об образовании эти отношения педагогически идеальны, то есть студенты, преподаватели, весь контекст, который является частью образовательного процесса, быть счастливым, успешным. Тогда понятно, что, как и в бизнесе, можно педагогически добиться в классе «беспроигрышных» отношений, просто сделать хорошее и новое планирование, в которое вставляется такая возможность.
Педагогическая перспектива, в которой, как и в деловом мире, где предприниматель и поставщик должен разоблачать свои представления, свои взгляды и свои идеи надлежащим образом и в подходящее время, не оценивая поведение другого, в школе, таким образом, Учитель уважает и ценит предыдущие знания своих учеников.
И когда в школе знание повседневной жизни вступает в «конфронтацию» с формальными знаниями, что мы можем с помощью того, что в деловом мире, часто поставщик думает, отличается от предпринимателя, однако, эти отношения не являются или никогда не должны быть Конфликт или вызвать некоторые износа. Она должна в школе, а также в бизнесе, чтобы представлять собой прекрасную возможность обучения для всех, кто участвует в этом процессе.
Выступления каменщиков, участников исследования, показали, что знания математики, которыми они обладают, были приобретены большую часть времени в развитии и совершенствовании своей профессии, в практике изо дня в день, или даже, видя, что другие выполняют Та же деятельность.
Беседы, которые мы имели с каменщиками на протяжении всего исследования сессий показали, что знания, полученные вне школьной сферы имеет важное значение, и это до учителя, чтобы спасти их и привести их ближе к классу, что делает формальное образование значимым и Сформулировал с реальностью, в которую студент вставляется.
5. ЦЕЛИ
5.1 Покажите, что этноматематика является частью нашей повседневной жизни и размышляют о возможности создания организ[pedreiros]ованных социальных групп в различных формах выражения в рамках их действия, обсуждая в школе способы производства Смыслы повседневной жизни; 5.2 Представить этноматематику как один из путей к обновленному образованию, в рамках большего движения, называемого математическим образованием, стало возможным в этой перспективе, путем отражения между учителем, студентом и сообществом, стремящимся преодолеть Знания, которыми они оба обладают, изменяя их и превращая класс в демократическое пространство обмена знаниями; 5.3 Воспринимать этноматематику как интересную педагогическую альтернативу работе в классе, демистификации математики и приближения к реальным потребностям изо дня в день студентов.
6. МЕТОДОЛОГИЯ
Следственная работа была выполнена через различные моменты, а именно: библиографическое исследование по этноматематике, учебные занятия с каменщиками, в которых предлагались ситуации- проблемы с целью изучения диалогического с каждым Профессионал о математических знаний, которые [formais ou informais]они используют, чтобы сделать бюджет количества керамики, необходимой для покрытия стен и полов. Размышления о возможных связях между математикой и реальностью в возможности установления связей между математическими знаниями каменщика, построенными из их потребностей профессиональных повседневных, с использованием практики Повседневная жизнь и школьная математика.
7. ОЖИДАЕМЫЙ ВКЛАД
Учитывая, что на протяжении всей следственной работы, основанной на дискурсе каменщиков, мы считаем, что эти специалисты для решения предлагаемых проблемных ситуаций не всегда поддерживались знаниями школьной математики.
В то время как было ясно, что каменщики применяли математические знания практически и интуитивно, используя конкретные стратегии, не используя математические формулы, преподаваемые в школе.
Мы надеемся, что преподавание математики в классе с помощью этноматического [10]подхода позволит учителям и студентам узнать о самом культурном разнообразии математики. Что результаты этого исследования помогают в разработке методологии, которая способствует преподаванию математики, в результате чего возможности для изменений в практике преподавания, подход ядерной педагогической практике со знаниями, полученными в ситуациях Из жизни студентов.
Именно из этого отражения педагогическая практика в классе может быть переориентирована на развитие полного гражданства студентов. Это, в соответствии с Pinheiro и Роза (2016),:
[…] Учителя математики погружаются в культурную динамику студентов и используют стратегии преподавания и обучения, которые ценят культурное измерение в классе, с тем чтобы можно было разработать инклюзивное математическое образование, которое могло бы эффективно Внести свой вклад в социальные преобразования (стр. 79).
Таким образом, из учебных сессий и подготовленного текста мы стремимся спровоцировать читателей на возможность педагогического вмешательства, основанного на реальности студента, объединяющей теорию и практику в построении систефированных знаний. Следует также надеяться, что отражения, вытекающие из чтения текста, позволят по-новому взглянуть на реальность и на математическое образование с точки зрения получения знаний из повседневной практики.
Цель состоит в том, чтобы внести свой вклад в Конституцию исследователь профессор своей практики, вызывая его / ее учиться в непрерывном пути, чтобы быть учителем, в соответствии с текущими образовательными потребностями, превращая класс в среду обмена знаниями, Спасение исторических знаний-социально построенных человечеством.
8. БИБЛИОГРАФИЧЕСКИЕ ССЫЛКИ
BREDA, Adriana LIMA, Valderez Marina do Rosário e GUIMARÃES, Gleny Terezinha Duro. A utilização da Etnomatemática nos cursos de formação continuada de professores: implicações das relações de poder saber na produção de subjetividades. Curitiba. Novembro de 2011. Disponível em: http://educere.bruc.com.br/CD2011/pdf/4668 _ 2898.pdf. Acessado em: 20/08/2017.
CARNEIRO, K. T. A. Cultura Surda na aprendizagem matemática da sala de recurso do Instituto Felipe Smaldone: uma abordagem etnomatemática. Anais do 4º Congresso Brasileiro de Etnomatemática. Belém, PA: ICEm4, 2012.
D’Ambrósio Ubiratan. Etnomatemática: Arte ou técnica de explicar e conhecer. Editora Ática, Série Fundamentos, 2. edição, São Paulo, 1993.
——-. Educação matemática: da teoria à prática. 13ª ed. Campinas: Papirus, 1996. (Coleção Perspectivas em Educação Matemática).
————-. Etnomatemática – elo entre as tradições e a modernidade. Coleção Tendências em Educação Matemática, 1. Belo Horizonte: Autêntica, 2001, 112p.
D’AMBROSIO, U.; ROSA, M. Um diálogo com Ubiratan D’Ambrosio: uma conversa brasileira sobre etnomatemática. In BANDEIRA, F. A.; GONÇALVES, P. G. F. (Orgs.). Etnomatemáticas pelo Brasil: aspectos teóricos, ticas de matema e práticas escolares. Curitiba, PR: Editora CRV. 2016. pp. 13-37.
DEMO, Pedro. Pesquisa e construção de conhecimento: Metodologia científica no caminho de Habermas. 3.ed. Rio de Janeiro: Tempo Brasileiro, 1996. 125p.
GERDES, Paulus. Etnomatemática: Cultura, Matemática, Educação. Maputo. Instituto Superior Pedagógico, 1991.
GIARDINETTO, José Roberto Boettger. Matemática escolar e matemática da vida cotidiana. Coleção polêmicas do nosso tempo, autores associados, Campinas – São Paulo, 1999, 128p.
LEZZI, Gelson; Dolce, Osvaldo; Machado, Antonio. Matemática e Realidade. 5ª série, 3. edição reformulada, Atual, São Paulo, 1996, 250p.
————–. Matemática e Realidade. 5ª série, 2. edição, Atual, São Paulo, 1991, 213p.
KNIJNIK, Gelsa. O saber popular e o saber acadêmico na luta pela terra. Revista da Sociedade Brasileira de Educação Matemática. Educação Matemática em Revista. Ano 9, n. 1, p. 27-39, 2002.
————–. Educação matemática, culturas e o conhecimento na luta pela terra. Santa Cruz do Sul, EDUNISC, 2006, 239 p.
MARQUES, Mário Osorio. A aprendizagem na mediação social do aprendido e da docência. Ijuí, Editora UNIJUÍ, 2. edição, 2000, 144 p.
MONTEIRO, A.; Pombeu, G. Jr. A matemática e os temas transversais. Editora Moderna, São Paulo, 2001, 160p.
MONTEIRO, Alexandrina. Reflexão e Ação: Revista do Departamento de Educação/UNISC. Vol. 10, n. 1 (jan./jun.2002) — Santa Cruz do Sul: EDUNISC, 2002.
A Etnomatemática em Cenários de Escolarização: alguns elementos de reflexão. Alexandrina Monteiro, p. 93 – 108.
PINHEIRO, R. C.; ROSA, M. Uma perspectiva etnomatemática para o processo de ensino e aprendizagem de alunos Surdos. RPEM, v. 5, n. 9, p. 56-83, 2016.
ROLIM, Carmem Lucia Artioli. Fórmulas de Silêncio: metodologias no processo de ensino da Matemática. In: SANTOS, Jocyléia Santana. ZAMBONI, Ernesta. Potencialidades Investigativas da Educação. Goiânia: Ed. da PUC Goiás, 2010.
ROSA NETO, R. Didática da matemática, São Paulo: Ática, 2002.
8. Понял с педагогической практикой, которая ценит математику различных культурных групп, принимая во внимание неформальные концепции, построенные предметами через их опыт вне контекста школы.
9. В этом размышлении мы относимся к формальной и неформальной математике в том, что первое считается школой, научной, систематической, узаконной и связанной с классными контекстами, а второе – как ежедневные, спонтанные, знания изо дня в день, Связанные с улицами, опыт омичем и жизнью в общинах, социальными контекстами.
10. В этой работе используется для обозначения исследования концепций, традиций и математических практик социальной группы и педаг[pedreiros]огической работы, которые могут быть разработаны с точки зрения того, что группа интерпретирует и кодифицирует свои знания; Приобретайте знания, полученные в академической математике, используя, когда сталкиваются с контекстуализированными ситуациями, тот, который кажется более подходящим.
[1] Магистр естественных наук Образование – математика, UNIJUI – RS. Степень и специализация в области естественных наук и математики. Профессор Ассистент CCA – Центр сельскохозяйственных наук, кампус маршала Кандидо Рондона, UNIOESTE, PR – Бразилия.
[2] Магистр в области устойчивого развития сельских районов, UNIOESTE, специалист по математике, физика, UNIPAR, управление персоналом и специальное образование с упором на множественную инвалидность, UNIASSELVI, выпускник по математике с упором на физику, UNIPAR.
[3] Специализация в области преподавания точных наук – математика, физика и химия. UNIOESTE – Государственный университет Западной Параны. Выпускной: Наука и математика. UNIJUI, RS. Профессор Государственной школы Парана.
[4] Профессор защиты растений и здоровья человека в Папском католическом университете Чили, факультет наук о растениях, он занимает междисциплинарную должность, разделенную между факультетом агрономии и Ingeniería Forestal (FAIF), факультетом медицины и химическим факультетом. Профессор-исследователь, связанный с Исследовательской группой по почвам и окружающей среде (GESOMA – UNIOESTE). Магистр агрономии от UNIOESTE, кандидат агрономии от UNIOESTE (2013-2016) – сэндвич-период (стипендия CAPES) из Лиссабонского университета, в Высшем институте агрономии (ULisboa).
[5] Уровень производительности исследований 1C от CNPq в области наук об окружающей среде с тремя Postdocs, UEM-PR (Бразилия), Университет Сантьяго-де-Компостела (Испания), UFG-GO (Бразилия). В настоящее время он является адъюнкт-профессором в UNIOESTE-PR и выступает в качестве профессора и исследователя в Центре аграрных наук, преподающего химию. Преподаватель магистерской программы по сельскохозяйственным наукам в УЭМ. В настоящее время он является специальным консультантом CNPq, CAPES и Fundação Araucária. Выступает в качестве добровольного экологического консультанта в MP-SP и CONAMA-DF.
[6] Студент-бакалавр агрономии-УНИОЕСТ-Государственный университет на западе Парана-бакалавриата администрации-Unip-Universidade Паулиста.
[7] Магистрант в области агрономии (растениеводство) из Государственного университета Западной Параны (UNIOESTE). Инженер по сельскому хозяйству окончил UNIOESTE (2014-2018), работает исследователем в Исследовательской группе по почвам и окружающей среде (GESOMA – UNIOESTE).
Представлено: Июнь, 2019.
Утверждено: июль 2019 года.