ОРИГИНАЛЬНАЯ СТАТЬЯ
OLIVEIRA, José Luiz de Jesus Egues de [1], SILVA, Edevaldo Maximo da [2], SANTOS, Cleidison Da Silva [3], PONTES, Dalila Fonseca [4], SILVA, Jandaira Fernandes da [5], QUEIROZ, Jose Pereira de [6], SANTANA, Zenóbia Conceição Castro [7]
OLIVEIRA, José Luiz de Jesus Egues de. Et al. Образовательная конструкция геометрии и использование бетонных материалов в качестве учебного процесса. Revista Científica Multidisciplinar Núcleo do Conhecimento. 05-й год, Эд. 10, Вол. 10, стр. 46-61. Октябрь 2020 года. ISSN: 2448-0959, Ссылка доступа: https://www.nucleodoconhecimento.com.br/образование-ru/образовательная-конструкция, DOI: 10.32749/nucleodoconhecimento.com.br/ru/64432
РЕЗЮМЕ
Исследование выделялось дидактической рефлексией, которая отвечает потребности в экспериментальных конструкциях в классе, с конкретными материалами для оказания помощи в процессе преподавания и изучения геометрии в начальной школе. В этом смысле приписывания анализа этой проблеме, у нас есть как ось, математическое образование, как способ стимулировать студентов к развитию семинаров, в которых они направлены на строительство дидактических материалов как процесс обучения математике. Процесс построения концепции геометрии, которая приписывает навыки и компетенции, которые будут разработаны в студентов на данном этапе, позволило же развивать определенный тип мысли, чтобы понять, описать и представить, организованно, геометрические пространства, информируя о важности, что это содержание имеет в их социальной жизни, как гражданин. Через строительство геометрических фигур с манипулируемыми материалами, мы изучаем все понятия фигуры, с помощью этого инструмента, тем самым стимулируя интерес и мотивацию студентов, предоставляя им геометрические и математические рассуждения. Определения геометрии могут быть построены последовательно, взяв за основу предыдущие знания студентов или нет, в котором мы подчеркиваем, что преподаватели должны создавать мероприятия, в которых студенты делают запросы ситуаций, связанных с геометрическими измерениями, тем самым имея опыт смысла и направления себя и какой-то фигуры, вставленной в пространстве. Однако для усвоения этого учебно-учебного процесса, помимо представления теорий студентам, необходимо было показать геометрические фигуры по их физическим характеристикам, то есть таким образом, чтобы природа обеспечивает нас, а не только своими свойствами и определенными понятиями. Наконец, исследование позволило нам проанализировать интеллектуальные возможности каждого студента, отобранной для этой цели.
Ключевые слова: математическое образование, образовательная конструкция, геометрия.
1. ВВЕДЕНИЕ
Как профессионалы образования и различных областей, мы думаем об этом исследовании, движимом желанием диалога по преподаванию математики обучения, более конкретно наблюдать важность геометрии в образовательном меню студента и, в частности, в начальной школе. Кроме того, как исследователи и знатоки геометрических пространств, мы подчеркиваем аргумент Malba Tahan (1967, стр.31) в своем тексте, который говорит: “Что делает его трудно преподавать математику является неатерируемой латинской привычкой всегда начинать с абстрактным, не переходя через бетон”. Другие авторы также имеют очень важное значение в этой части математики. Мы также будем рассматривать почти отказ от геометрии в базовом образовании, сообщили в некоторых исследованиях, что мы подход в качестве основы для этой работы. Мы также подчеркиваем специфику преподавания содержания геометрии в контексте физического мира для преподавания, а также навыки, которые эта область математики должна обеспечить для студентов, которые будут включены в де-факто образовательное общество.
Тем не менее, процесс обучения математике является предметом большого изучения и обсуждения, потому что новые методологии всегда возникают для удовлетворения спроса, который постоянно меняется в различных условиях обучения.
Учитывая специфику учебного процесса математики в начальной школе, а также перспективу разработки инструментов стимулирования интеллектуальных способностей учащихся и в то же время значение использования математики в повседневной жизни, в которой бесчисленные проблемы могут быть решены, обсуждение важности преподавания содержания с участием геометрии выходит на первый план, потому что это очень интересный путь , чрезвычайно важно, чтобы иметь возможность предоставить студенту более организованный взгляд на мир, в котором он живет. На самом деле, очень важно изучать эту область математики и защищается несколькими преподавателями, в которых они обсуждаются здесь и обсуждаются ниже, в зависимости от важности и специфики этой области.
Мы стараемся с помощью этого исследования внести свой вклад в преподавание математического образования, основанного на развитии навыков и компетенций у студентов.
Развитие семинаров, направленных на строительство дидактических манипулируемых материалов для обучения и учебного процесса, изучение геометрических концепций, которые рассматривают навыки и компетенции, которые будут разработаны студентами на этапе, называемом “образовательное строительство”, позволит студенту развивать определенный тип мысли, чтобы понять, описать и представить, организованным образом, мир, в котором он живет , информируя вас, насколько важен этот контент. Таким образом, в один прекрасный день они могут использовать этот образовательный продукт в своей социальной жизни, или в повседневной жизни, кроме того, что позволяет увеличить представление об использовании геометрических базовых знаний.
2. ПЕДАГОГИЧЕСКИЕ ДИДАКТИЧЕСКИЕ ТЕНДЕНЦИИ В ПРЕПОДАВАНИИ ГЕОМЕТРИИ
Мы считаем, что образовательная конструкция зафиксировала учебный процесс, тем самым храня передаваемый контент, который осуществлялся с помощью манипулируемых бетонных материалов.
По словам Duval (1995), геометрия включает в себя три формы когнитивного процесса: которые заполняют конкретные эпистемологические функции;
Визуализация для гуманистического исследования сложной ситуации; Конструкция конфигураций, которые могут быть отработаны как модель, в которой выполненные действия представлены и наблюдаемые результаты соединены с представленными математическими объектами; Рассуждение, которое является процессом, который приводит к доказательству и объяснению. (DUVAL, 1995).
По словам автора, эти три вида когнитивных процессов переплетаются в их синергии и когнитивно необходимы для владения геометрией. С другой стороны, гевристические проблемы геометрии относится к пространственной записи, которая уступает место формам автономных интерпретаций.
Для Duval (1988) проблемы геометрии представляют большую оригинальность по отношению ко многим математическим задачам, которые могут быть предложены студентам. Кроме того, автор говорит, что в пользу развития когнитивных функций, организуя математически близкие проблемы геометрии, которые требуют тех же знаний, определяет когнитивные категоризации необходимы для обучения.
По словам Machado (2005), большинство проблем преподавания и изучения геометрии имеют дидактическое и лингвистическое происхождение. Для Duval (1995 год) координация различных записей представительства (алгебраическое письмо, геометрические фигуры, дискурс на естественном языке), связанная с обработкой знаний, не осуществляется спонтанно, даже в ходе обучения, которое мобилизует это разнообразие записей.
Тем не менее, предлагаемое исследование должно позволить студенту сделать различные интерпретации геометрии вокруг них, потому что осуществление в его памяти через контакт, то есть “конкретные”, они могут приобрести знания в этом образовательном контексте, и что будет служить в качестве инструмента, который будет включен в их повседневной жизни.
По словам Fiorentini:
Несколько методологических изменений указываются как тенденции обучения, которые стремятся привилегии участия студентов, рассматривая строительство знаний в качестве одной из форм обучения. Математическое знание выходит из физического мира и извлекается человеком через чувства. (FIORENTINI, 1995 год, стр.9).
Национальные параметры учебных программ (PCN, 1998) также признают отсутствие известности, которая была уделена этой области математики, а также подчеркивает, что она развивает основополагающую роль в формировании студента в качестве гражданина.
Для (MACHADO, 2005), большинство проблем преподавания и обучения геометрии дидактической и лингвистического происхождения.
Вышеуказанные авторы ссылаются на эти аспекты в учебных процессах, которые переплетены в их синергии и когнитивно необходимы для владения геометрией. С другой стороны, гевристические проблемы геометрии относится к пространственной записи, которая уступает место формам автономных интерпретаций.
Мы надеемся, что применяемая методология будет педагогическим трендом в нашей повседневной жизни, и что мы действительно можем использовать ее в наших классах, как инструмент обучения в классах геометрии.
3. ИСПОЛЬЗОВАНИЕ БЕТОННЫХ МАТЕРИАЛОВ В ОБУЧЕНИИ ГЕОМЕТРИИ
Препятствия и трудности, с которыми сталкивались студенты во время изучения самой математики, бесчисленны. Есть те, кто не может понять его, и даже учитель не одобряется в заявлении, и те, кто, когда утвержден, по-прежнему не в состоянии применить приобретенные знания. То есть они не понимают его реальной важности.
Таким образом, несколько исследований показывают, что использование манипулируемых материалов дает более высокую производительность у учащихся, чем их использование, в возрасте всех возрастов и во все годы обучения в школе. Это использование является методологическим показателем, которое ценится с момента приобретения до момента строительства концепций, которые могут произойти на всех уровнях образования. Таким образом возникает вопрос: может ли конкретное материал в качестве педагогического использования облегчить преподавание и изучение математики? По словам Carraher и Schilemann (1988), в своих исследованиях они засовыряют, что «нам нужны не предметы в классе, а цели. Нам нужны ситуации, в которых решение проблемы подразумевает использование математических логических принципов, которым нужно учить” (стр.179). Это связано с тем, что материал, «несмотря на то, что он формируется целями, может рассматриваться как набор «абстрактных» объектов, найденных только в школе с целью обучения, и не имеет никакого отношения к миру ребенка» (стр.180). По его мнению, бетон для детей не нужен, потому что манипулятивные объекты могут быть абстрактными в руках в различных ситуациях, с которыми ребенку придется столкнуться в социальном плане. С другой стороны, Fiorentini и Miorim (1990), подтверждают свои слова, сказанные выше, и объясняют, что за каждым используемым материалом скрыто видение математического образования человека и мира. Это означает, что есть педагогическое предложение, которое оправдывает это использование.
Из этого исследования, мы также нашли вопросы для общественности детей с особыми потребностями. Как бы это использование произошло? Как будет выглядеть процесс обучения и обучения для этих детей? Таким образом, итальянский педагог, а также врач Мария Монтессори, реагирует на нас чего результаты после исследования с исключительными детьми, разработанные в начале этого века с различными манипулятивными материалами упором на математику себя. Считалось, что обучение не может быть без действия: «ничто не должно быть дано ребенку, в области математики, без 1-го представления ему конкретной ситуации, которая заставляет его действовать, думать, экспериментировать, открывать, а значит, погружаться в абстракцию». (AZEVEDO, 1979, стр. 27)
После этих размышлений мы воспринимаем, что этот конкретный материал, упомянутый здесь и помещенный в качестве объекта применимости для эффективного обучения, заставляет нас понять, что существует необходимость в осуществлении синтетических и аналитических способностей ребенка, как автор ниже заявляет, что:
Следует заниматься синтетическими и аналитическими способностями ребенка. Синтетические, чтобы студент построить концепцию из бетона. Аналитический, потому что в этом процессе ребенок различает в объекте те элементы, которые составляют глобализацию. Для этого объект должен быть мобильным, который может претерпеть трансформацию, чтобы ребенок можно было определить операцию, лежащую в основе (CASTELUNUOVO, 1970, p.82-91)
Манипулируемые материалы могут иметь основополагающее значение для обучения происходит, и не всегда наиболее подходящим является тот, который уже построен или красивее. Поощряя образовательное строительство детей, мы думаем об облегчении учебного процесса, и именно в этот момент мы понимаем, что конкретное участие в нем делает данный процесс фактически обоснованным. Таким образом, нас сравнивают с национальной учебной программой базового образования, которая устанавливает: Основные компетенции (IDEB, 2001), в отношении использования ресурсов, говорится, что:
Манипулируемые материалы различных типов, на протяжении всего школьного обучения, привилегированный ресурс в качестве отправной точки или поддержки многих школьных задач, в частности, направленных на содействие исследовательской деятельности и математической коммуникации между студентами … […] Все студенты должны научиться пользоваться не только элементарным калькулятором, но и, по мере их продвижения в области базового образования, студенты должны иметь возможность работать с электронной таблицей и с различными образовательными программами, включая функциональные диаграммы и динамическую геометрию (2001, стр.17).
4. МЕТОДОЛОГИЯ
Используемая методология является качественной, библиографической и экспериментальной. Исследование было разработано в ходе педагогических семинаров, организованных модулями, что позволило в то же время развивать деятельность, связанную с “Строительство дидактических материалов, как учебно-учебный процесс”, который мы характеризуем здесь как “образовательное строительство”.
Мы провели семинары с совещаниями, которые были разделены для того, чтобы поставить студента в контакт с темой. Мы применяем понятия фигур, связанных с выбранными текстами математической книги дисциплины геометрии. Другие чтения были отобраны в соответствии с развитием работы. Мы использовали в качестве концепций планирования геометрических фигур в двумерном пространстве и собираем геометрические фигуры трехмерного пространства. На этом этапе изучение геометрии реализуется деятельностью, связанной с действием, должно быть преобладание бетона над символическим, поэтому студент манипулирует и строит объекты различных форм, чтобы затем проанализировать их физические и геометрические характеристики. С этой точки зрения, геометрическая деятельность должна быть проведена, что позволяет исследование концепций, связанных с пространством и формой, способствуя курсу сосредоточены на формировании вставленного студента, потому что они должны понимать геометрический мир, в котором они живут.
4.1 ПРИКЛАДНЫХ СЕМИНАРОВ
Два семинара были проведены в 9м классе начальной школы, в составе 27 учащихся с утра Государственного школьного Vereador Bento Muniz муниципалитета Tangará да Serra-MT. Таким образом, была применена диагностическая оценка, также задуманная как предварительный тест, и с целью получения информации о предыдущих знаниях студентов в контексте евклидовой геометрии, потому что в соответствии с LDB-Законом Руководящих принципов и национальной основы (1961)
Руководящие принципы и предложения, изданные MEC (Министерство образования) выделить и укрепить необходимость признания предыдущих знаний студентов, используя их в качестве инструмента, который облегчает обучение и в качестве мотивирующего фактора, потому что таким образом, студент становится активным субъектов в процессе обучения, больше не просто получатели знаний.
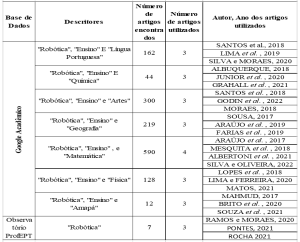
Цифры представляют представленный вопросник, а также ответы некоторых студентов. Первые три вопроса были направлены на проверку понимания учащимися концепции определений полигонов и многоэдр, а также деноминации некоторых элементарных геометрических фигур. Мы заметили, что большинство студентов не задумали определения, которые ставятся под сомнение, что идет вразрез с заявлениями Almouloud (2005), в которых автор утверждает, что несколько исследований указывают на эту дисциплину в качестве одной из проблем обучения. И это становится все более очевидным, когда мы смотрим на другие вопросы, содержащиеся в тесте.
Рисунок 01 – ПРИКЛАДНОЕ ПРЕДЛОЖЕНИЕ.
Рисунок 2 – ПРОДОЛЖИТЕЛЬНОСТЬ ТЕСТА
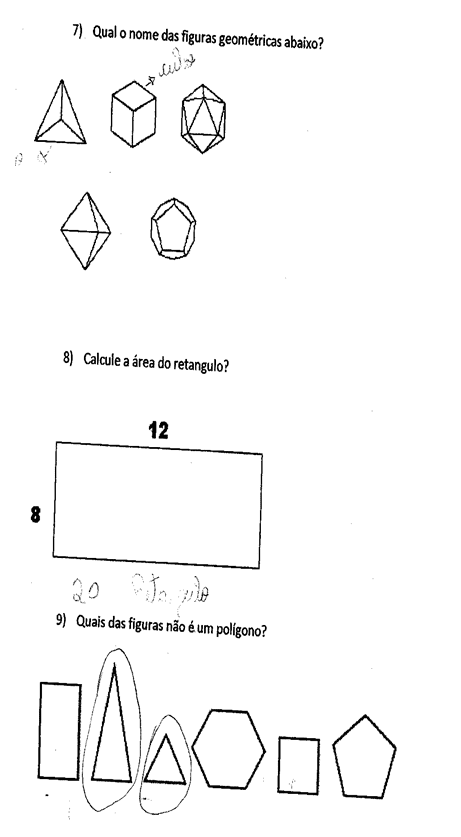
Рисунок – 3. Конструкции

Источник: Own (2011)
Рисунок – 4. Конструкции

Источник: Own (2011)
Рисунок – 5. Конструкции

В этом исследовании было установлено, что подавляющее большинство студентов не признают полигональных и не полигональных форм и не знают, как связать их с количеством их сторон и vertices, и до сих пор показывают сегмент геометрии их повседневной жизни, хотя повседневная жизнь является промоутером изучения геометрии, как указано автором ниже:
Математические знания вытекают из физического мира и извлекаются человеком через чувства” и Miguel и Miorim(1986, стр.66), которые засововыв, что “геометрия настолько важна для человечества, что делает немыслимым вопрос о необходимости ее изучения в школе, потому что мир, в котором мы живем, почти спонтанно геометрический и его использование в повседневной жизни является почти человеческой необходимостью. (FIORENTINI, 1995 год, стр. 9.)
Возможно, эта ситуация усугубится тем, как учителя представляют этот контент, что, по мнению PCN, так же важно, как и в прошлом.
Вопросы, связанные с формами и отношениями между ними, с возможностями космической оккупации, с расположением и перемещением объектов в пространстве, рассматриваются с разных точек зрения, сегодня так же необходимы, как и в прошлом. Повседневные ситуации и осуществление различных профессий, таких как инженерия, биохимия, хореография, архитектура, механика и т.д., требуют способности человека мыслить геометрически (PCNs стр. 122 – 1998).
Во второй момент были предложены конструкции плоских фигур. Во время строительства было установлено, что студенты действительно понимают геометрические фигуры, представленные через конструкции с картоном, то есть бетоном. Были собраны квадратные, прямоугольные, треугольные, круговые, пятиугольные, шестиугольные, гептогональные, антитогональные, энегональные, десятиугольные, додекагональные, тридекагональные, тетрадекагональные, пентадекагональные, все они были вырезаны и, наконец, построены. Мы заметили, что строительство студентами способствовало созданию смыслов самих студентов, с интересом к участию больше, чем если бы эти цифры были представлены на доске учителем. Что подтверждает высказывания Azevedo (2006, стр.27), который считал, что не было обучения без действия: «Ничего не должно быть дано ребенку, в области математики, без 1-го представления ему конкретной ситуации, которая заставляет его действовать, думать, экспериментировать, открывать, а значит, погружаться в абстракцию».
Было также открыто пространство, где студенты имели возможность задать вопрос и спорить о выполняемой деятельности и взаимосвязи форм в нашем сосуществовании. Но после того, как обсуждение было открыто для комментариев, некоторые студенты внесли свой вклад только в том случае, если они были спровоцированы и попросили сделать комментарий. Наиболее частым комментарием студентов было то, что они никогда не участвовали в процессе обучения таким образом, и что они сочли интересным и приятным строить фигуры, а не просто видеть учителя представить их. Таким образом, Machado (2005 год) утверждает, что большинство проблем преподавания и изучения геометрии имеют дидактическое и лингвистическое происхождение; и Pavanello (1993 год), поясняет, что некоторые факторы, связанные с такими трудностями, могут быть связаны с отсутствием интереса студентов, порожденных отсутствием дидактических ресурсов, отсутствием заинтересованных учителей для использования этих различных учебных ресурсов для разработки привлекательного и качественного обучения, которое может использовать новые дидактические концепции, такие, как использование конкретных материалов или педагогических игр для развития их дидактической практики.
С помощью этой деятельности можно было проверить, что образовательный потенциал, предоставляемый конструкциями плоских фигур, очень актуален для педагогических дидактических целей и привлекателен для установления корреляции между содержанием темы, которая должна быть рассмотрена.
На этом этапе студентам также было предложено построить плоские фигуры в группах, где они должны быть окрашены мелками. Этот вид деятельности приводит студента, чтобы сделать предварительное планирование строительства, так как она требует знания геометрических форм или полигонов и требует моторных навыков для обработки материалов.
Мастерская по строительству плоских фигур, помимо динамики, была рекреационной, мотивирующей и педагогически привлекательной, потому что в разное время группы обсуждали, какой полигон будет строить, потому что второй. Fiorentini и Miorim (1990) “говорит, что за каждым используемым материалом скрывается видение образования, математики, человека и мира; то есть, есть, лежащие в основе, педагогическое предложение, которое оправдывает его “.
Примечательно, что семинар как дидактический процесс для деятельности, с помощью визуальных ресурсов и экспериментов, вызывает изменение осанки студентов, с большей мотивацией и участием большинства, что представляет собой более активное участие студентов по отношению к содержанию геометрии, потому что в соответствии с Castelunuovo:
Бетон должен иметь двойную цель: “осуществлять синтетические и аналитические способности ребенка”; чтобы студент мог построить концепцию из бетона; аналитический, потому что в этом процессе ребенку удается различить в объекте те элементы, которые составляют глобализацию. Для этого объект должен быть мобильным, который может претерпеть трансформацию, чтобы ребенок может определить операцию, которая является основной. (CASTELUNUOVO, 1970, стр.82-91).
Геометрические твердые тела были также сделаны, но прежде чем мы представляем некоторые концепции геометрических фигур трех акриловых размеров, таких как пирамиды, призмы, куб, додекаэдрон, icosaedro, тетраэдр, октагедр, сфера, цилиндр для них, чтобы сделать предыдущее планирование и только затем собрать твердые тела, но некоторые студенты уже приобрели концепции плоских форм в предыдущем семинаре, потому что для сборки твердых веществ требуется знание , по словам некоторых студентов никогда не работал с этими твердыми телами конкретно. Картон, палочка барбекю, контактная палка, контактный клей, ножницы и т.д. были использованы для сборки геометрических твердых веществ.
В каждой построенной фигуре использовалось планирование мастерской и применялась связь геометрических твердых веществ с плоскими фигурами, последовательное производство сборок, а также анализировались акриловые формы модели планирования. Этот педагогический потенциал условно взаимодействует со студентами в конструкциях фигур, открывая дискуссию о том, как собраться, был упражнением терпения для заключения этих бетонов.
Мы также можем использовать междисциплинарность в этом педагогическом процессе, потому что, в соответствии с Параметрами национальной учебной программы (1998-MEC):
Учитель должен быть посредником, который поощряет разработку процедур, способствующих развитию у студента интереса к поиску новых горизонтов и обмену знаниями, приобретенными в различных ситуациях. Принимая во внимание эту ориентацию, существует большая потребность в поощрении междисциплинарности и контекстуализации дисциплин и особенно математики
То есть, чтобы облегчить еще более широкий взгляд на объекты и их отношения. Тем не менее, мы подчеркиваем, что, можно увидеть, что не все студенты на самом деле имеют обзор трехмерных фигур, и мы заметили, что некоторые из них были сомнения еще собрать одну из форм твердых. Мы также обнаружили, что этот тип действий готовит студента к поиску решений и в то же время получает этот динамичный процесс педагогического обучения для изучения рассуждений перед конструкциями геометрических форм. Мы убедились, что эта деятельность была сделана с большой приверженностью и участием студентов, однако, в какой-то момент была необходимость сопровождать некоторых студентов в процессе сборки геометрических твердых веществ. Мы записали некоторые замечания, сделанные ими, такие как:
- “Мы считаем, что принимая класс геометрии через геометрические конструкции фигуры узнает гораздо больше и, кроме того, весело”.
- “В дополнение к обучению в теории мы можем лучше учиться на практике, учитель не просто проходит на доске, и это более интересно принимать практические занятия”.
Очевидно, важность этой деятельности, разработанной в образовательной сфере, потому что это дидактическая транспозиция показывает реальность в классе и, работая с этой совместной деятельности мы проверяем важность совместного использования этой важной деятельности в жизни студентов математики и преподавателей.
Этот педагогический потенциал представляет собой действия, которые могут быть реализованы в школьной среде. Эксперимент и приближение геометрической теории в их жизни способствуют образовательной деятельности, в результате что студенты больше заинтересованы в изучении геометрии.
5. ЗАКЛЮЧИТЕЛЬНЫЕ СООБРАЖЕНИЯ
Исследования показывают, что включение мероприятий, которые благоприятствуют социальному взаимодействию, сотрудничеству и экспериментам в классе, может изменить школьную среду, потому что социальный контекст, в который вставляются эти студенты, не изолирован от школы, и одна из задач того же самого заключается в содействии образованию, которое позволяет социальной жизни студентов. Эффективное совместное участие является еще одним моментом, который мы подчеркиваем с семинаров, учитывая, что было показано, что положительный момент, который подкрепляется Lorenzato (2006), когда он заявляет, что: Преподавание отличается от преподавания. Преподавание дает студенту условия для того, чтобы он стройте свои собственные знания.
Мы также подчеркиваем, что использование конкретных материалов в преподавании геометрии в дополнение к содействию взаимодействию студентов с объектом исследования и от этого взаимодействия они могут строить свои знания, а также способствовать дискуссии в смысле выявления таким образом в повседневной жизни студентов, что сокращает расстояние математических концепций и их применимость помимо того, что более интересным и значимым , выступающей в качестве альтернативы для обучения геометрии, которая ускользает от традиционных.
Следует отметить, что разработанные семинары достигли своих целей, которые начались с развития навыков, позволяющих абстракции геометрического содержания, которые могут быть использованы для понимания, описания и представления организованного мира, в котором мы живем.
Считается, что само исследование осуществимо в качестве рабочей методологии, когда подготовлено ранее и предлагает потенциал для простоты, представленной в его развитии, тем самым способствуя процессу обучения геометрии и математике.
Поэтому мы приходим к выводу, что тщательно продуманное «образовательное строительство» имело полезный результат, при большом взаимодействии мы достигли поставленных целей в процессе преподавания и изучения математики, надеемся, что эта работа будет включена в качестве тренда в образовательный процесс студентов и преподавателей.
ССЫЛКИ
ABNT-ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS. NBR 6022: informação e documentação: artigo em publicação periódica científica impressa: apresentação. Rio de Janeiro, 2014. Acesso em 19/03/2012.
ARAÚJO, J.L.; BORBA, M.C. Construindo Pesquisas Coletivamente em Educação Matemática. In: BORBA, M. C.; ARAUJO, J. L. (Org.). Pesquisa Qualitativa em Educação Matemática. Belo Horizonte: Autêntica, 2004.
AZEVEDO, Edith D. M. Apresentação do trabalho matemático pelo sistema montessoriano. In: Revista de Educação e Matemática, n. 3, 1979 (p. 26-27).
BRASIL, Ministério de Educação. PARÂMETROS CURRICULARES NACIONAIS – Matemática – 5ª a 8ª séries, 1998, MEC.
CARRAHER, T. N. Na vida dez, na escola zero. São Paulo: Cortez, 1998.
CASTELNUOVO, E. Didática de La Matemática Moderna. México: Ed Trillas, 1970.
FIORENTINI, Darío. MIORIM, Maria Ângela. Uma reflexão sobre o uso de materiais concretos e jogos no ensino da Matemática. Publicado no Boletim SBEM – SP, ano 4 – n° 7.
FIORENTINI, Dario; LORENZATO, Sérgio. Investigação em Educação Matemática: pressupostos teóricos e metodológicos. Campinas, SP: Autores Associados, 2006 (Coleção Formação de Professores). Artigos da Secretaria de educação do estado de São Paulo
GIMENO SACRISTÁN, J. (2000). O currículo: Uma reflexão sobre a prática (3ª Ed.). Porto Alegre: Artmed.
MACHADO, Silvia Dias Alcântara. Aprendizagem em Matemática – Registro de Representação Semiótica, Campinas-SP; Papirus Educação, 2005, p.11-30, p.125-133.
MATEMÁTICA DIVERTIDA/POLIEDRIS. Disponível em: http://pt.wikipedia.org/wiki/S%C3%B3lidos_geom%C3%A9tricos Acesso em 29/05/2012. jan/julho de 1995.
MINISTÉRIO DA EDUCAÇÃO. Lei nº 4.024 de 20 de dezembro de 1961. Lei de Diretrizes e Bases da Educação Nacional. Diário Oficial [da] República Federativa do Brasil, Brasília, DF, 27 dez. 1961
NCTM (1991). Normas profissionais para o ensino da Matemática. Lisboa: Associação de professores de Matemática e Instituo de Inovação Educacional.
PAVANELLO, Regina Maria, O Abandono do Ensino da Geometria no Brasil: Causa e Consequências. Revista ZETETIKÉ – Editorial – ano1 – n.1 – mar. 1993, p. 7-18.
PAVANELLO, Regina Maria, Por Que Ensinar /Aprender Geometria? Universidade Estadual de Maringá.
PORQUE ENSINAR/APRENDER GEOMETRIA? Disponível em: www.sbempaulista.org.br/epem/anais/mesas_redondas/mr21-regina.doc. Revista – Sociedade Brasileira de Educação Matemática. Rio de Janeiro, n. 4, p.3-13,
TAHAN, Malba. Didática da Matemática 1967, p.31.
[1] Аспирант в области образования в УНР-Аргентина, профессор математики и уголовной полиции МТ.
[2] Кандидат наук в области образования; специалист в области управления школами и управления персоналом; Выпуск по английскому языку португальский / английский язык и его литература, степень бакалавра и степень бакалавра в области физического воспитания.
[3] Аспирант в области образования в Национальном университете Росарио – Унр, Аргентина, имеет степень в области литературы – Английский из Кастело Бранко колледж (2006). Право и философия. Специализация на английском языке.
[4] Аспирант в области образования в Национальном университете Росарио – УНР Аргентина. Окончил в Vernacular Письма из UFBA – Федеральный университет Баия. Он имеет степень магистра и учебную программу, дидактики и оценки из Государственного университета Баия – UNEB, аспирант по методологии преподавания португальского языка и литературы из регионального факультета философии, науки и литературы Candeias-Баия. Обучение испанскому языку сертифицировано DUCLE – ARGENTINA. Преподаватель испанского и португальского языков. Руководитель Государственного колледжа профессор Мария Леал Лопес, Новая Ибия – Баия.
[5] Аспирант в области образования в Национальном университете Росарио – UNR Аргентина, степень бакалавра в области письма. Университет штата Баия, UNEB и педагогика регионального факультета философии, науки и письма Candeias-Баия. Профессиональная степень магистра богословия. Высшая школа образования, EST, Бразилия. Специализация в области лингвистических и литературных исследований. Федеральный университет Баия – UFBA. Специализация в области планирования и управления Sist. Эдук. Расстояние. Баийский государственный университет, UNEB. Специализация в методологии высшего образования. Интегрированные факультеты уток – FIP, специализация в методологии преподавания профессионального образования, UNEB-BAHIA. Бразилия. Обучение испанскому языку сертифицировано DUCLE – ARGENTINA.
[6] Окончил по португальскому и английскому языкам письма из UEG, должность окончил в области высшего образования преподавания, от Ucan Rj; аспирантура по технологиям в области образования из Пук-Рио-де- Посещение докторской диссертации в области образования в UNR argentina.
[7] Окончил Католический университет Сальвадора по специальности «География». 1987 год. Окончила методологию преподавания географии. Кандидат наук в области образования в Национальном университете Росарио-УНР Аргентина.
Отправлено: июль 2020 года.
Утверждено: октябрь 2020 года.