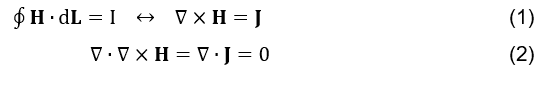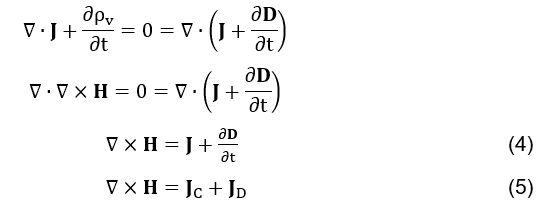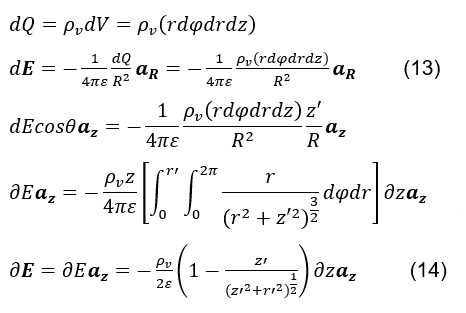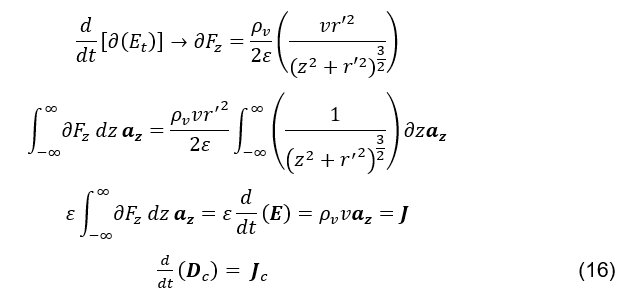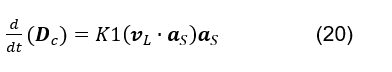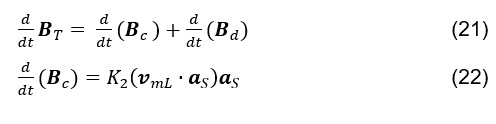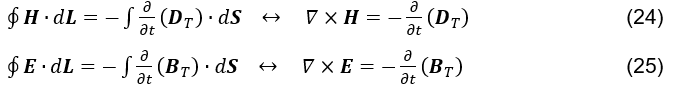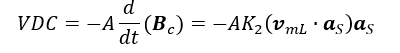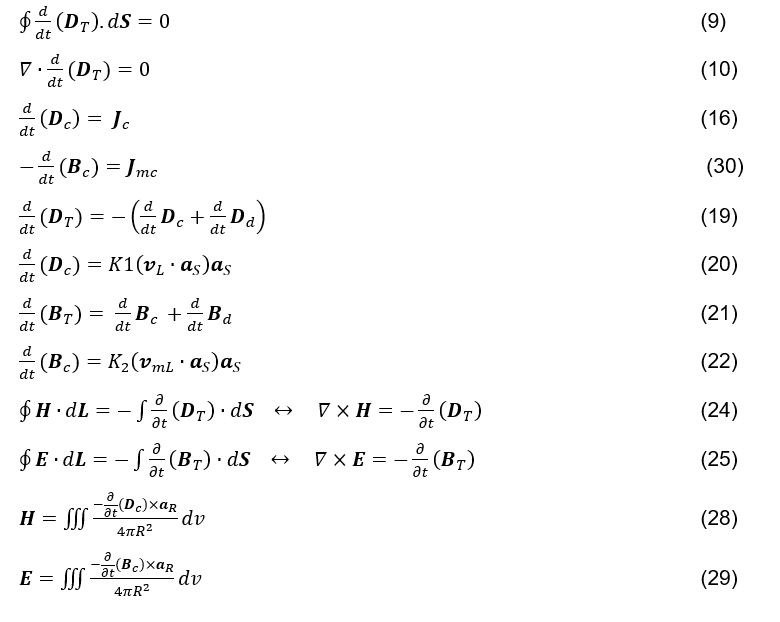ARTIGO ORIGINAL
LUCENA, Lucas Ruas de [1]
LUCENA, Lucas Ruas de. Uma nova perspectiva acerca da densidade de corrente de condução. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano 05, Ed. 08, Vol. 03, pp. 151-167. Agosto de 2020. ISSN: 2448-0959, Link de acesso: https://www.nucleodoconhecimento.com.br/fisica/densidade-de-corrente, DOI: 10.32749/nucleodoconhecimento.com.br/fisica/densidade-de-corrente
RESUMO
Discute-se no presente artigo propostas alternativas e complementares às Leis de J.C.Maxwell, do eletromagnetismo clássico, baseando-se em determinadas hipóteses, exemplos hipotéticos e cálculos, com resultados que possam inferir novas interpretações acerca do fenômeno físico densidade de corrente de condução. Essas novas interpretações trazem um novo entendimento para a dinâmica da Lei de Gauss, e, sendo verdadeiras tornam a Lei de Ampère-Maxwell totalmente simétrica à lei de Faraday-Lenz-Maxwell, sem que haja qualquer inconsistência matemática ou física. Esses entendimentos, inevitavelmente, trazem implicações e pontos de vista complementares à teoria clássica do eletromagnetismo.
Palavras chave: Eletromagnetismo, densidade de corrente, equação da continuidade.
1. INTRODUÇÃO
Primeiramente apresenta-se a solução dada por J.C.Maxwell para que a equação de Ampere (ver fórmula 1) se torne matematicamente consistente, respeitando a identidade vetorial aplicada em (ver fórmula 2), e coerente com a equação da continuidade (ver fórmula 3).
Em seguida apresenta-se um exemplo da aplicação da Lei de Gauss (ver fórmula 6) para uma superfície fechada em torno de uma das placas de um capacitor, Figura 1.
Por hipótese, propõe-se que a variação temporal do fluxo total elétrico, que atravessa a superfície gaussiana totalmente fechada, seja sempre igual à zero. Logo, a Lei de Gauss (ver fórmula 6), aplicada a situações dinâmicas, se tornaria na equação (ver fórmula 9). Para que essa hipótese tenha fundamento, considerar-se-á necessário que haja um vetor variação temporal de densidade de campo elétrico, de mesmo módulo, direção e sentido da densidade de corrente, na área de intercessão entre o volume cilíndrico do condutor e a superfície gaussiana, apontando para dentro da mesma, Figura 1.
A fim de se verificar a consistência dessa hipótese, considerar-se-á um exemplo ideal no qual existe uma corrente contínua e homogênea em um fio cilíndrico retilíneo infinito, ao longo do eixo z. Então se calcula o vetor variação temporal do campo elétrico (ver fórmula 12) no ponto P(0,0,0) devido ao deslocamento simultâneo e instantâneo de todas as cargas, à montante e à jusante de P(0,0,0). Esse cálculo traz como resultado a igualdade (ver fórmula 16).
Por fim, partindo da veracidade física da igualdade (ver fórmula 16), observa-se inevitáveis implicações, formatações e complementações teóricas para clássicas equações do eletromagnetismo, de Faraday, Lenz, Biot-Savart e Maxwell. Sugerindo-se ao final, um experimento em laboratório para confirmar ou desmentir a teoria desenvolvida a partir da análise da hipótese proposta.
2. AS CORRENTES DE DESLOCAMENTO E CONDUÇÃO
A Lei circuital de Ampere, em sua forma pontual (ver fórmula 1), possuía inadequações matemáticas (JACKSON et. al., 1998).
O resultado da equação (ver fórmula 2) deveria ser zero, pois o divergente do rotacional ser igual à zero constitui uma identidade vetorial. Porém a equação da continuidade (HAYT; BUCK et. al., 2013; SHADIKU, 2004),
é inconsistente com a equação (ver fórmula 2). Essa correção foi feita, brilhantemente, por J.C.Maxwell, da seguinte maneira (JACKSON et. al., 1998):
Dessa forma a equação de Ampere (ver fórmula 1) tornou-se completamente consistente em (ver fórmula 5). Tanto fisicamente, por considerar a geração de campo magnético a partir da variação temporal da densidade de campo elétrico, quanto matematicamente, no que diz respeito à identidade vetorial citada na equação (ver fórmula 2).
O termo ![]() adicionado na equação (ver fórmula 4) possui a mesma unidade de densidade de corrente, Amperes por metro quadrado
adicionado na equação (ver fórmula 4) possui a mesma unidade de densidade de corrente, Amperes por metro quadrado ![]() , sendo denominado por J.C.Maxwell de densidade de corrente de deslocamento, representado por
, sendo denominado por J.C.Maxwell de densidade de corrente de deslocamento, representado por ![]() na equação (ver fórmula 5). A identificação desse termo foi de fundamental importância para o entendimento da propagação das ondas eletromagnéticas. O termo
na equação (ver fórmula 5). A identificação desse termo foi de fundamental importância para o entendimento da propagação das ondas eletromagnéticas. O termo ![]() na equação (ver fórmula 5) se refere à densidade de corrente de condução.
na equação (ver fórmula 5) se refere à densidade de corrente de condução.
3. HIPÓTESE DE UMA APLICAÇÃO DINÂMICA DA LEI DE GAUSS
A Lei de Gauss, equação (ver fórmula 6), determina que o fluxo de densidade de campo elétrico total que atravessa qualquer superfície fechada é igual à carga elétrica total que está contida dentro dessa superfície. Maxwell observou-a na forma pontual, equação (ver fórmula 7), conhecida como a primeira equação de Maxwell (HAYT; BUCK et. al., 2013; SHADIKU, 2004).
Consideremos o primeiro exemplo, sendo uma superfície fechada ao redor de uma das placas de um capacitor que está sendo carregado por uma fonte de alimentação de tensão variável, conforme Figura 1.
Figura 1. Superfície gaussiana fechada em uma placa de capacitor
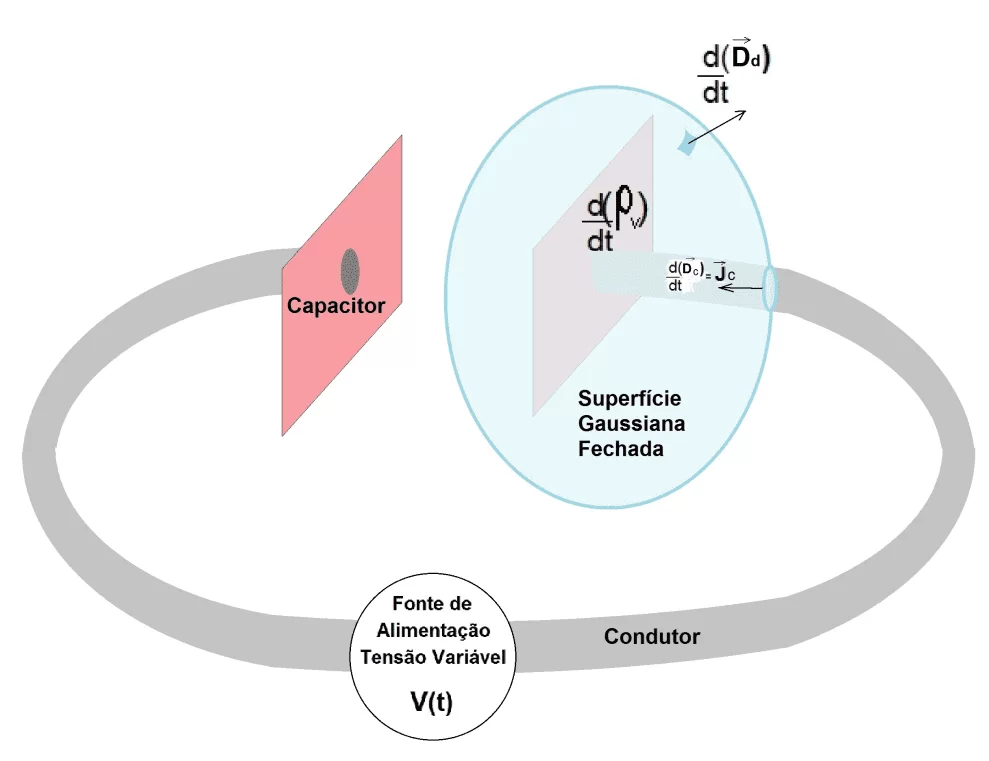
Observando a Figura 1, havendo uma densidade de corrente de condução ![]() no condutor, as equações (ver fórmula 6) e (ver fórmula 7), respectivamente: para a uma superfície gaussiana totalmente fechada; e para um ponto na placa do capacitor, se tornam nas equações (ver fórmula 8) e (ver fórmula 3). (HAYT; BUCK et. al., 2013; SHADIKU, 2004).
no condutor, as equações (ver fórmula 6) e (ver fórmula 7), respectivamente: para a uma superfície gaussiana totalmente fechada; e para um ponto na placa do capacitor, se tornam nas equações (ver fórmula 8) e (ver fórmula 3). (HAYT; BUCK et. al., 2013; SHADIKU, 2004).
A equação (ver fórmula 8) determina que a variação temporal do fluxo total de densidade de campo elétrico que atravessa a superfície gaussiana, é igual à variação temporal da carga elétrica contida internamente à mesma.
A equação da continuidade (ver fórmula 3) aplicada a qualquer volume infinitesimal da placa do capacitor, carregado positivamente, determina que a densidade de corrente de condução ![]() , que deixa esse determinado volume, é igual à taxa temporal com a qual a densidade volumétrica de carga cai, no mesmo.
, que deixa esse determinado volume, é igual à taxa temporal com a qual a densidade volumétrica de carga cai, no mesmo.
A hipótese proposta nesse artigo considera que as equações (ver fórmula 8) e (ver fórmula 3) sejam fisicamente complementares. Dessa forma, considera-se que para uma superfície totalmente fechada de Gauss, em torno de uma placa do capacitor, em condições dinâmicas, as equações (ver fórmula 8) e (ver fórmula 3) teriam o seguinte formato.
Onde ![]() é a variação temporal do vetor densidade de campo elétrico gerada pela densidade de corrente de condução
é a variação temporal do vetor densidade de campo elétrico gerada pela densidade de corrente de condução ![]() , de mesmo módulo, sentido e direção dessa, na superfície transversal de interseção entre o volume cilíndrico do condutor e a gaussiana, apontando para dentro da mesma. E
, de mesmo módulo, sentido e direção dessa, na superfície transversal de interseção entre o volume cilíndrico do condutor e a gaussiana, apontando para dentro da mesma. E 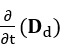 é a variação temporal do vetor densidade de campo elétrico, na superfície gaussiana fechada apontando para fora da mesma, gerada pela densidade de corrente de deslocamento
é a variação temporal do vetor densidade de campo elétrico, na superfície gaussiana fechada apontando para fora da mesma, gerada pela densidade de corrente de deslocamento ![]() (variação temporal do número de linhas de campo elétrico que atravessam a gaussiana fechada em decorrência da variação temporal da carga elétrica total da placa do capacitor interna à gaussiana); (HAYT; BUCK et. al., 2013; SHADIKU, 2004). Figura 1.
(variação temporal do número de linhas de campo elétrico que atravessam a gaussiana fechada em decorrência da variação temporal da carga elétrica total da placa do capacitor interna à gaussiana); (HAYT; BUCK et. al., 2013; SHADIKU, 2004). Figura 1.
As equações (ver fórmula 9) e (ver fórmula 10) determinam que a variação temporal do fluxo total de densidade de campo elétrico, em qualquer superfície gaussiana totalmente fechada, seja igual a zero. A equação (ver fórmula 10) não contradiz a equação da continuidade (ver fórmula 3), pois essa relaciona o escoamento de carga elétrica, de um volume infinitesimal, à variação temporal de densidade volumétrica de carga elétrica, no mesmo; já aquela, está relacionada apenas à dinâmica do campo elétrico.
Supõe-se então que o fenômeno físico densidade de corrente de condução ![]() , gera uma variação de densidade de campo elétrico
, gera uma variação de densidade de campo elétrico 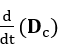 na interseção do condutor cilíndrico com a superfície gaussiana, de mesmo módulo, sentido e direção do vetor
na interseção do condutor cilíndrico com a superfície gaussiana, de mesmo módulo, sentido e direção do vetor ![]() . Uma das vantagens de se averiguar essa hipótese seria entender a equação de Ampere-Maxwell (ver fórmula 4) no seguinte formato (ver fórmula 11).
. Uma das vantagens de se averiguar essa hipótese seria entender a equação de Ampere-Maxwell (ver fórmula 4) no seguinte formato (ver fórmula 11).
Dessa forma, intuir-se-ia que as interações entre campos, elétrico ou magnético, e partículas carregadas, seriam, antes de tudo, interações entre campos apenas.
Na busca por se verificar a veracidade da hipótese proposta, cria-se um exemplo de situação hipotética ideal para o cálculo do vetor variação temporal de densidade de campo elétrico (ver fórmula 12), na origem, gerado por uma corrente continua e homogênea em um condutor cilíndrico de comprimento infinito ao longo do eixo z.
4. EXEMPLO DE UMA SITUAÇÃO HIPOTÉTICA IDEAL
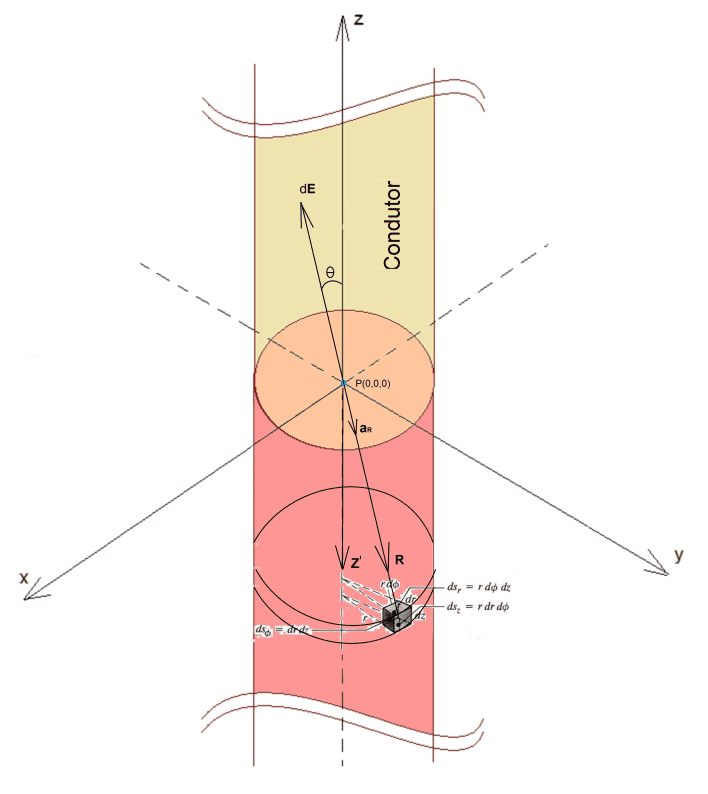
Suponhamos a seguinte configuração ideal: em um condutor cilíndrico, retilíneo, uniforme, homogêneo, de comprimento infinito, o qual percorre uma corrente contínua, de cargas positivas, uniforme e homogênea no sentido positivo do eixo z, Figura 2.
Calcular-se-á, em coordenadas cilíndricas, a variação temporal do vetor campo elétrico (ver fórmula 12) gerada no ponto P(0,0,0) do plano cartesiano da Figura 2, em decorrência do deslocamento volumétrico, simultâneo e instantâneo, de todas as cargas positivas, à montante e à jusante desse ponto, no sentido positivo do eixo z.
Ainda que, em um condutor real com diferença de potencial aplicado em suas extremidades, quem se desloca é o elétron, por padrão clássico, escolheu-se para o cálculo o deslocamento de cargas positivas no sentido positivo do eixo z.
É sabido, por simetria, que o vetor resultante campo elétrico E gerado pelo somatório de todas as cargas existentes ao longo do condutor, positivas e negativas, no ponto P(0,0,0), é nulo.
No entanto consideremos, primeiramente, o cálculo do campo elétrico estático (ver fórmula 14), gerado por um elemento diferencial volumétrico cilíndrico, em coordenadas cilíndricas, de densidade volumétrica de carga positiva ρv, centralizado em uma posição inicial z’, onde dQ é o elemento diferencial de carga, r’ é o valor constante atribuído ao raio do condutor cilindro, R o vetor distancia entre o ponto P(0,0,0) e o elemento diferencial volumétrico dV, az é o versor na direção positiva de z, e ε a permissividade elétrica do condutor, conforme Figura 2.
Notemos que, por tomarmos como referência o ponto de medição do campo elétrico fixado em P(0,0,0), o sentido de dE será sempre oposto ao versor aR. Por isso, o sinal negativo na equação (ver fórmula 13).
Figura 2. Corrente de Condução
Em seguida, considerando-se que esse disco volumétrico diferencial carregado possui velocidade constante. O campo elétrico ![]() passa a ser função apenas da variável tempo t. Considerando-se constantes a posição inicial z’ e a velocidade do disco v,
passa a ser função apenas da variável tempo t. Considerando-se constantes a posição inicial z’ e a velocidade do disco v,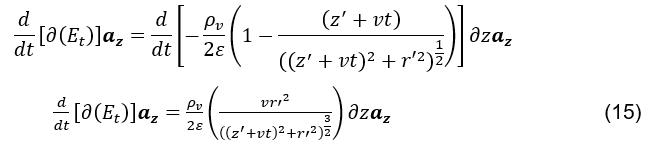
Como o que se quer calcular é a variação temporal do campo elétrico (ver fórmula 12), na origem, causada pelo deslocamento de cada elemento cilíndrico diferencial somado ao longo de ![]() instantaneamente, considerar-se-á exclusivamente para esse cálculo que a função da equação (ver fórmula 15) passa a depender apenas da variável posição z,
instantaneamente, considerar-se-á exclusivamente para esse cálculo que a função da equação (ver fórmula 15) passa a depender apenas da variável posição z, ![]() . Pois a contribuição de cada elemento diferencial cilíndrico, ao longo de todo o eixo z, deslocando-se para a formação do vetor variação temporal total de campo elétrico no ponto P(0,0,0), por ser instantânea, não depende da variável tempo t. Dessa forma, substituindo-se z’ = z, e considerando-se a variável t = t0 = 0,
. Pois a contribuição de cada elemento diferencial cilíndrico, ao longo de todo o eixo z, deslocando-se para a formação do vetor variação temporal total de campo elétrico no ponto P(0,0,0), por ser instantânea, não depende da variável tempo t. Dessa forma, substituindo-se z’ = z, e considerando-se a variável t = t0 = 0,
A equação (ver fórmula 16), então, demonstra a equivalência vetorial entre a variação temporal da densidade de campo elétrico no ponto P(0,0,0), gerada pelo deslocamento instantâneo e simultâneo de todas as cargas positivas ao longo do fio cilíndrico infinito, e a densidade de corrente de condução ![]() nesse mesmo ponto.
nesse mesmo ponto.
5. IMPLICAÇÕES
Havendo veracidade física na hipótese apresentada, observam-se as seguintes implicações:
- Interpretação da aplicação de uma dinâmica da Lei de Gauss;
- Nova concepção das Leis de Ampere-Maxwell e de Faraday-Lenz-Maxwell;
- Experimento sugerido para prova da teoria.
5.1 INTERPRETAÇÃO DA APLICAÇÃO DE UMA DINÂMICA DA LEI DE GAUSS
Considera-se a igualdade (ver fórmula 16) encontrada coerente com as equações (ver fórmula 9) e (ver fórmula 10). Sendo assim, entende-se ser razoável a seguinte interpretação física da Lei de Gauss aplicada à situação apresentada na Figura 1: a variação temporal do fluxo total de densidade de campo elétrico, em qualquer superfície gaussiana totalmente fechada é exatamente zero, (ver fórmula 17) e (ver fórmula 18).
Devido à escolha clássica do sentido da corrente ser o do deslocamento das cargas positivas, para tornar as equações (ver fórmula 24) e (ver fórmula 29) simétricas entre si, inseriu-se o sinal negativo ( – ) à igualdade (ver fórmula 19).
Propõe-se aqui a seguinte interpretação a respeito dos fenômenos físicos contemplados na igualdade (ver fórmula 19).
O vetor variação temporal de densidade de campo elétrico 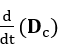 , resultado da densidade de corrente de condução
, resultado da densidade de corrente de condução ![]() , parece ser proporcional à velocidade longitudinal com que as linhas de campo elétrico atravessam um elemento de área de uma superfície gaussiana. Podendo-se teorizar:
, parece ser proporcional à velocidade longitudinal com que as linhas de campo elétrico atravessam um elemento de área de uma superfície gaussiana. Podendo-se teorizar:
onde vL é o vetor velocidade das linhas de campo elétrico que atravessam um elemento de área de uma superfície gaussiana, aS o versor do vetor elemento de área dessa superfície, e K1 uma constante, Figura 3.
Figura 3. Variação temporal da densidade de campo elétrico gerada por
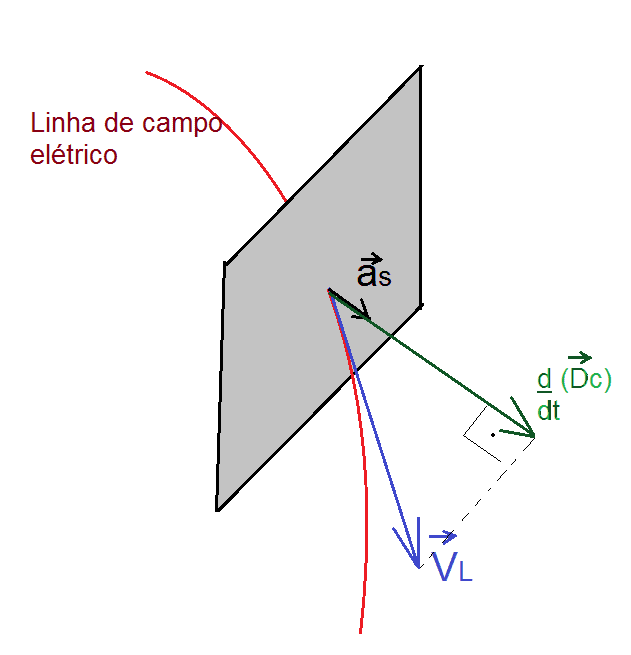
Já o vetor variação temporal de densidade de campo elétrico ![]() , resultado da densidade de corrente de deslocamento
, resultado da densidade de corrente de deslocamento ![]() , está relacionado à variação temporal do número quantitativo de linhas de campo elétrico que atravessam um elemento de área de uma superfície gaussiana (HAYT; BUCK et. al., 2013; SHADIKU, 2004).
, está relacionado à variação temporal do número quantitativo de linhas de campo elétrico que atravessam um elemento de área de uma superfície gaussiana (HAYT; BUCK et. al., 2013; SHADIKU, 2004).
Sendo verdadeira a teoria proposta, a partir da hipótese inicial, de que a variação temporal do fluxo elétrico total que atravessa uma superfície gaussiana, possa ser formada tanto pela variação temporal do numero de linhas de campo elétrico, por unidade de área, que a atravessam ![]() , como pela velocidade longitudinal das linhas de campo elétrico que atravessam um elemento de área,
, como pela velocidade longitudinal das linhas de campo elétrico que atravessam um elemento de área, 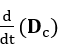 (ver fórmula 20); intui-se, por simetria à (ver fórmula 19), que o fluxo magnético que atravessa uma superfície gaussiana se comporta de forma equivalente (ver fórmula 21).
(ver fórmula 20); intui-se, por simetria à (ver fórmula 19), que o fluxo magnético que atravessa uma superfície gaussiana se comporta de forma equivalente (ver fórmula 21).
De tal forma que ![]() poderia ser gerado tanto pela variação temporal do numero de linhas de campo magnético em um elemento de área (HAYT; BUCK et. al., 2013; SHADIKU, 2004),
poderia ser gerado tanto pela variação temporal do numero de linhas de campo magnético em um elemento de área (HAYT; BUCK et. al., 2013; SHADIKU, 2004), ![]() ; como pela velocidade longitudinal com a qual as linhas de campo magnético atravessam um elemento de área,
; como pela velocidade longitudinal com a qual as linhas de campo magnético atravessam um elemento de área, ![]() (ver fórmula 22). Por simetria, propõe-se, analogamente à equação (ver fórmula 20), a equação (ver fórmula 22). Onde vmL é o vetor velocidade das linhas de campo magnético que atravessam um elemento de área de uma superfície gaussiana, aS o versor do vetor elemento de área dessa superfície, e K2 uma constante.
(ver fórmula 22). Por simetria, propõe-se, analogamente à equação (ver fórmula 20), a equação (ver fórmula 22). Onde vmL é o vetor velocidade das linhas de campo magnético que atravessam um elemento de área de uma superfície gaussiana, aS o versor do vetor elemento de área dessa superfície, e K2 uma constante.
5.2 NOVA CONCEPÇÃO DAS LEIS DE AMPERE-MAXWELL E DE FARADAY-LENZ-MAXWELL
Considerando a possibilidade de veracidade na hipótese apresentada, poder-se-ia conceber a Lei de Ampere-Maxwell (ver fórmula 5) e a Lei de Faraday-Lenz-Maxwell (ver fórmula 23)
respectivamente, como em (ver fórmula 24) e (ver fórmula 25).
5.3 EXPERIMENTO SUGERIDO PARA PROVA DA TEORIA.
O presente artigo tem como objetivo, de forma sucinta, propor uma teoria, baseada em situações hipotéticas, sem experimentação física em laboratório para prova, ao término do mesmo.
No entanto, será apresentada a seguir uma proposta de experimento em laboratório, para quem for de interesse, comprovar a veracidade da teoria proposta, ou desmenti-la.
Para o cálculo de um campo magnético H, gerado exclusivamente a partir de uma densidade de corrente de condução ![]() , utilizando-se da igualdade (ver fórmula 16), a Lei de Biot-Savart (ver fórmula 27) poderia ser descrita como em (ver fórmula 28).
, utilizando-se da igualdade (ver fórmula 16), a Lei de Biot-Savart (ver fórmula 27) poderia ser descrita como em (ver fórmula 28).
Então, propõe-se escrever a Lei de Biot-Savart modificada (ver fórmula 28), simetricamente para o cálculo do campo elétrico, como em (ver fórmula 29).
A fim de se verificar a veracidade da teoria de que os campos, elétrico e magnético, possa ser gerado, respectivamente, pela velocidade de deslocamento das linhas dos campos, (magnéticos e elétrico), propõe-se o seguinte experimento.
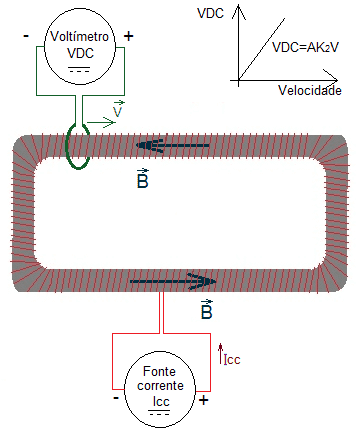
Trata-se de um circuito elétrico formado por fio condutor isolado, enrolado de forma distribuída e contínua ao redor de um material ferromagnético de topologia toroidal, de área A constante da seção transversal, alimentado por uma fonte de corrente contínua, com uma corrente ajustada tal que não sature magneticamente o material ferromagnético. Haverá uma densidade de campo magnético B confinado em todo o material ferromagnético toroidal (HALLIDAY; RESNICK; WALKER et. al., 2013), Figura 4.
Onde μ é a permeabilidade magnética do material ferromagnético, N o número de espiras, e l o perímetro percorrido pela seção transversal do toroide ao longo de sua revolução.
Então utiliza-se uma espira de medição de fio condutor, isolado, ao redor da seção transversal do toroide, interligado à um voltímetro VDC, de tal forma que seja possível o deslocamento da espira de medição ao longo do perímetro toroidal, Figura 4.
É sabido que o campo magnético gerado por qualquer circuito elétrico toroidal ideal, externo ao mesmo, é zero (HALLIDAY; RESNICK; WALKER et. al., 2013).
Pela teoria apresentada, quando a espira de medição desloca-se com uma velocidade V ao longo do perímetro toroidal, ainda que não se altere o número de linhas de densidade de campo magnético internas à espira, essas linhas passarão a atravessar a superfície gaussiana formada pela circunferência da espira de medição, com velocidade -V.
Aplicando a equação proposta (ver fórmula 22) à Lei de Faraday-Lenz-Maxwell (ver fórmula 23), a tensão medida no voltímetro deverá ser:
Onde é a área da secção transversal do toroide.
Sendo assim, propõe-se levantar uma curva de medições VDC x V, sendo VDC a tensão medida no voltímetro, e V o vetor velocidade da espira de medição, ao longo do perímetro toroidal, Figura 4. Pela teoria proposta, essa curva deverá ser uma reta com inclinação AK2, Figura 4.
Figura 4. Experimento sugerido para prova da teoria proposta
Caso seja realizado o experimento com resultado que corrobore a teoria proposta, propõe-se ainda considerar a existência da densidade de corrente magnética ![]() de condução a seguir.
de condução a seguir.
6. CONCLUSÃO
Em busca de se entender melhor a natureza das correntes de deslocamento e condução, levantou-se a hipótese de que, em uma superfície gaussiana totalmente fechada, a variação temporal de fluxo total de campo elétrico, na mesma, poderia ser sempre igual à zero (ver fórmula 9) e (ver fórmula 10), não contradizendo a equação da continuidade (ver fórmula 3).
Foi criado um exemplo de situação hipotética ideal, que possibilitasse analisar matematicamente a hipótese criada.
O resultado dessa análise, igualdade (ver fórmula 16), corrobora com a ideia de que o vetor variação temporal de densidade total de campo elétrico (ver fórmula 19) pode existir a partir dos dois fenômenos físicos distintos a seguir.
1 – 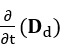 → Variação temporal do vetor densidade de campo elétrico, em um elemento de área, em função da variação temporal do número de linhas de campo elétrico que a atravessam. Esse é o entendimento clássico acerca do fenômeno densidade de corrente de deslocamento, primeiramente reconhecido por J.C.Maxwell. (HAYT; BUCK et. al. 2013; SHADIKU, 2004)
→ Variação temporal do vetor densidade de campo elétrico, em um elemento de área, em função da variação temporal do número de linhas de campo elétrico que a atravessam. Esse é o entendimento clássico acerca do fenômeno densidade de corrente de deslocamento, primeiramente reconhecido por J.C.Maxwell. (HAYT; BUCK et. al. 2013; SHADIKU, 2004)
2 – 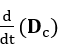 → Variação temporal do vetor densidade de campo elétrico, em um elemento de área, em função da velocidade longitudinal das linhas de campo elétrico que a atravessam (ver fórmula 20), devido a uma densidade de corrente de condução (ver fórmula 16);
→ Variação temporal do vetor densidade de campo elétrico, em um elemento de área, em função da velocidade longitudinal das linhas de campo elétrico que a atravessam (ver fórmula 20), devido a uma densidade de corrente de condução (ver fórmula 16);
Pela premissa de simetria entre o comportamento dos campos elétrico e magnético, analogamente as equações (ver fórmula 19) e (ver fórmula 20), considerou-se a possibilidade do campo magnético se comportar da mesma forma em (ver fórmula 21) e (ver fórmula 22).
Assim, propõe-se uma teoria de que todas as interações entre campos, elétrico ou magnético, e partículas eletricamente carregadas, são, antes de tudo, interações entre campos apenas. Sendo que, por exemplo, ao se aplicar uma diferença de potencial em um circuito elétrico, o campo elétrico gerado pela diferença de potencial irá interagir com o campo elétrico das cargas livres, forçando-as a se movimentarem. O deslocamento das cargas implica no deslocamento de suas linhas de campo elétrico. A velocidade longitudinal com que essas linhas atravessam um elemento diferencial de área seria proporcional ao vetor 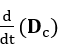 no mesmo.
no mesmo.
Considerando-se a possibilidade da veracidade das equações (ver fórmula 9) e (ver fórmula 10), oriundas da dinâmica da Lei de Gauss, escreve-se a Lei de Ampere-Maxwell (ver fórmula 5), no formato (ver fórmula 24), com maior simetria para com a Lei de Faraday-Lenz-Maxwell (ver fórmula 25).
Por fim, propõe-se um experimento de laboratório para confirmar ou desacreditar a teoria proposta e suas equações.
A seguir, as equações propostas no presente artigo.
REFERÊNCIAS
FARADAY, M. Experimental Researches in Electricity. B.Quaritch, Londres, 1939, p.1855.
FARADAY, M. Great Books of the Western World. Vol. 45, encyclopedia Britannica Inc., Chicago, 1952, p. 217-866.
HALLIDAY, D; RESNICK, R; WALKER, J. Fundamentos de Física. V.3, ED.9ª, LTC, Rio de Janeiro 2013.
HAYT, W.H; BUCK, J.A. Eletromagnetismo. ED.8ª, AMGH, Porto Alegre, 2013, p. 48-290.
JACKSON, J.D. Classical Eletrodynamics. ED.3ª, University of California, Berkeley, 1998, p. 237-239.
MAXWELL, J.C. A Treatise on Electricity and Magnetism. Oxford Univ. Press, Oxford, 2002.
MAXWELL, J.C. The Scientific Papers of James Clerk Maxwell. Dover Publ., New York, 1965, v. 1, p. 451.
PLONSEY, R; COLLIN, R.E. Principles and Applications of Electromagnetic Fields. McGraw-Hill, New York, 1961, Topic 2.
SHADIKU, M.N.O. Elementos de Eletromagnetismo. ED.3ª, Bookman, Porto Alegre, 2004, p. 107-350.
[1] Pós-graduado em Engenharia Elétrica (Instrumentação) pela PUC-MG (2008), graduado em Engenharia Industrial Elétrica pelo CEFET-MG (2007).
Enviado: Julho, 2020.
Aprovado: Agosto, 2020.