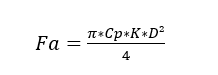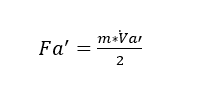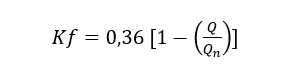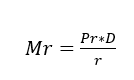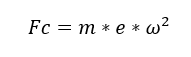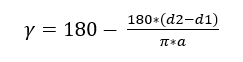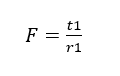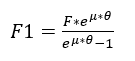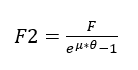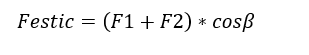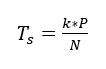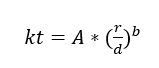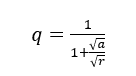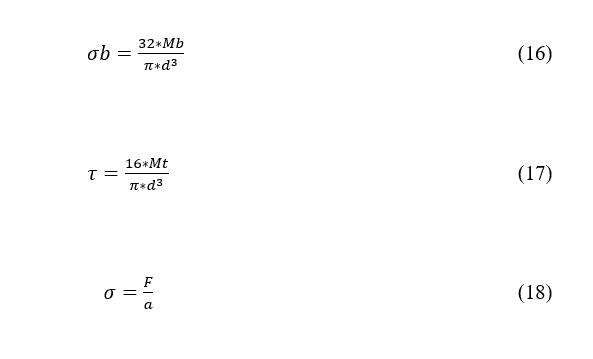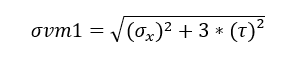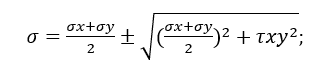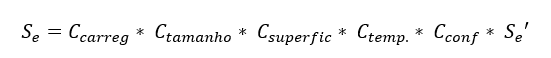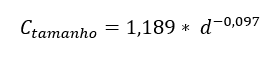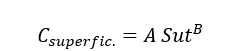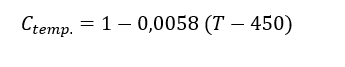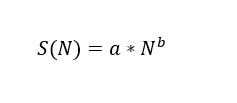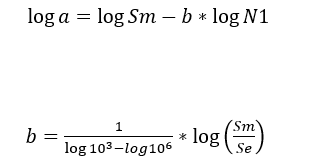ORIGINALER ARTIKEL
PASQUALI, Guilherme [1], NASCIMENTO, Vagner do [2]
PASQUALI, Guilherme. NASCIMENTO, Vagner do. Schadensanalyse und Lebensdauer einer Radialventilator-Antriebswelle. Revista Científica Multidisciplinar Núcleo do Conhecimento. Jahr. 07, Hrsg. 09, Bd. 02, p. 115-139. September 2022. ISSN: 2448-0959, Zugangslink: https://www.nucleodoconhecimento.com.br/engineering-maschinenbau/radialventilator
ZUSAMMENFASSUNG
Dieser Artikel stellt eine numerisch-analytische Studie der Antriebswelle eines industriellen Abluftventilators dar, die aufgrund von Ermüdung im Arbeitsfeld ausgefallen ist und ersetzt werden musste. Das Hauptziel dieser Arbeit bestand darin, den Bereich der Spannungskonzentration zu identifizieren und die Zeit/Anzahl der Zyklen zu quantifizieren, die das Teil bis zum Versagen brauchte. Damit wurden alle mechanischen Belastungen beim Betrieb eines Radialventilators berechnet, um Biegemoment, Schub und Axialkraft im Bauteil zu erhalten. Analytisch zeigte sich der Bereich der größten statischen mechanischen Beanspruchung mit einer großen Kerbempfindlichkeit, die zu mechanischer Ermüdung führt. Anschließend bestätigte die numerische Analyse durch finite Elemente die Berechnungen und bestätigte die Anzahl der Zyklen und den ermüdeten Bereich im Betrieb mit einem relativen Fehler von nur 5 %.
Schlüsselwörter: Radialventilator, Antriebswelle, Ermüdung, Finite Elemente.
EINLEITUNG
Die ständige Weiterentwicklung der technischen Entwicklungstechnologien hat den Zugang zu Werkzeugen und Wissen zur Problemlösung in der Industrie verbessert. Die Verwendung der Finite-Elemente-Methode wurde verwendet, um Schritte zu verkürzen, Berechnungen zu validieren und manchmal Abweichungen und Inkongruenzen in der analytischen Arbeit des Ingenieurs zu identifizieren.
Solche Werkzeuge sind gültig und auch interessant, wenn es um die Auslegung von industriellen Radialventilatoren geht. Maschinen, die einem bestimmten Fluid kontinuierlich Energie zuführen, um den durch Rohrleitungen und Komponenten erzeugten Widerstand zu überwinden und den Fließpunkt zu erreichen, der für den Prozess erforderlich ist, an dem es beteiligt ist.
Für Bleier (1997) eine Kombination der Nutzung der Zentrifugalkraft zur Bewegung der Luft in radialer Richtung mit der Umlenkung des Luftstroms durch die Rotorblätter.
Nach Jorgensen (1999) ein Gerät, das durch die Drehbewegung eines auf einer Achse montierten Flügelrads einen konstanten Luftstrom erzeugt.
Untersuchungsgegenstand dieser Arbeit, für Gujaran und Gholap (2014), werden Übertragungswellen verwendet, um Kraft und/oder Drehmoment durch Zahnräder, Riemenscheiben, Keile, Kupplungen und Kettenräder zu übertragen.
Neben statischen Belastungen wird die Welle einer Reihe dynamischer Belastungen ausgesetzt, zu Ermüdungsbrüchen führen können , nach Roy et al. (2020). Für Zambrano (2014) ist Ermüdung die häufigste Ursache für Probleme mit rotierenden Maschinenwellen, normalerweise an Stellen mit Spannungskonzentration und Keilnuten.
Da der Zweck dieser Arbeit darin besteht, analytisch und numerisch aufzuklären, wie eine Achse auf die mechanischen Anforderungen reagiert, die durch den Betrieb einer Strömungsmaschine auferlegt werden, wurden Spannungen methodisch abgeschätzt und Analysepunkte für die Ermüdungsberechnung ausgewählt.
Trebuna et al. (2009) zeigten, dass Ermüdungsbruch in einer Achse auftreten kann, weil die Betriebsfrequenz der Ausrüstung sehr nahe an der Eigenfrequenz der Maschinenstruktur liegt. Schlecht dimensionierte mechanische Strukturen können mechanische Anregungen verstärken und Ausfälle vorwegnehmen.
Laut Jorgensen (1999) ist die Antriebswelle im Ventilatorbetrieb mechanischen Spannungen, Druck-, Torsions- und Biegemomenten ausgesetzt, die allein oder sogar in Kombination wirken können. Für Norton (2004) kann die Welle damit vollständig wechselnde Belastungen erfahren, wenn man bedenkt, dass Biegemomente auf das Bauteil wirken; und dass die Kombination dieses Biegemoments und eines Drehmoments komplexe mehrachsige Spannungen erzeugt.
Geralmente eixos não possuem diâmetro uniforme, mas sim reduções, chavetas, cantos agudos entre outros. A tensão no eixo em um ponto específico varia de acordo com a rotação levando a fadiga. Mesmo um componente perfeito quando submetido repetidamente a carregamentos de magnitude suficiente, pode eventualmente propagar uma trinca de fadiga em uma região de alta tensão, geralmente iniciando na superfície até que a fratura ocorra. (GUJAR; BHASKAR, 2013, p. 1061).
Ristivojevic (2010) führt aus, dass neben den bekannten Wellenspannungskonzentratoren auch Artikel wie Lager Adapterhülsen aufgrund von Temperaturschwankungen Maßänderungen erfahren und während des Betriebs mechanische Störungen verursachen können.
Callister (2002) erwähnt, dass ein Ermüdungsbruch aufgrund der geringen oder fast nicht vorhandenen plastischen Verformung selbst bei Metallen mit hoher Duktilität brüchig ist. Der Prozess findet durch die Einleitung und Ausbreitung von Rissen statt, und normalerweise verläuft die Oberfläche dieser Risse senkrecht zur Richtung der durch Zug erzeugten Spannung.
Die Studie beschreibt eine Achse, die aufgrund von Ermüdung während ihres Betriebs ausfiel, und versucht, die analytischen Berechnungen und die Theorie zusammen mit den Simulationen zu korrelieren, um zu verstehen, welche kritischen Bereiche es gibt und wie sie unter Berücksichtigung der unten angegebenen Randbedingungen verhindert werden können. Am Ende werden die Ergebnisse zusammen mit den praktischen Auswirkungen und dem, was in der Ausrüstung passiert ist, verglichen.
MATERIALIEN UND METHODEN
Um den Aufwand an einer industriellen Radialventilatorwelle zu verstehen, ist es notwendig, die Ausrüstung und die Betriebsbedingungen zu charakterisieren, um jede der Anforderungen auf kohärente Weise zu quantifizieren und zu identifizieren.
Bei der fraglichen Maschine handelt es sich um einen großen Extraktor mit 400 PS Leistung, mit Durchfluss, statischem Druck und Wellendrehzahl von jeweils 300.798 m³/h, 290 mmCA und 590 U/min.
Abbildung 1: 400 PS Auspuff mit zweiseitiger Welle
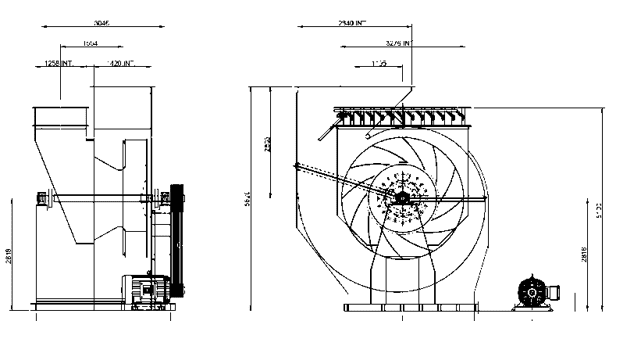
Es ist auch wichtig, die Rotor Einlass- und -auslassdurchmesser und -höhen zu kennen. Ausgestattet mit diesen Informationen ist es möglich, mit der Berechnung der auf der Achse generierten Anfragen zu beginnen.
Jorgensen (1999) weist darauf hin, dass die Berechnung der Axialkraft auf die Welle aufgrund der Druckdifferenz durch Gleichung 1 erfolgt.
Cp ist der Umrechnungsfaktor 9,79 (Pa/mmH20); K die Proportionalitätskonstante, die in diesem Fall 1 ist; p ist der Gesamtdruck des Geräts (mmH20) und D ist der Rotordurchmesser.
Die Richtungsänderung des Luftstroms verursacht auch eine axiale Kraft auf die Achse, die nach Jorgensen (1999) nach Gleichung 2 berechnet wird.
Wobei ?̇ der Massendurchfluss (kg/s) ist; Va’ ist die Axialgeschwindigkeit des Fluids (m/s) und g ist die Erdbeschleunigung (m/s²).
Für Henn (2006) erzeugt der Betrieb eines Ventilators eine Radialkraft auf die Welle, obwohl er nicht genau im Auslegungspunkt arbeitet, in dem er dimensioniert wurde. Gleichung 3 zeigt, wie man sie berechnet.
(3)
Dabei ist Kf der Koeffizient, der je nach angetriebener Strömung variiert und nach Gleichung 4 berechnet wird; ? ist die spezifische Masse der Flüssigkeit (kg/m³); Y ist der Energiesprung (J/kg); D ist der Rotordurchmesser und b5 ist die Rotor Austritts Breite (m).
(4)
Für Gleichung 4 ist Q die von der Maschine angetriebene Durchflussrate und Qn die in der Konstruktion festgelegte nominale Durchflussrate.
Es ist bekannt, dass es laut Jorgensen (1999) keine Möglichkeit gibt, eine perfekt ausgewuchtete rotierende Maschine herzustellen, da es immer Anregungskräfte mit einer Frequenz geben wird, die proportional zur Betriebs Rotation der Ausrüstung ist. Für Shahrooi und Asayesh (2013) kann ein unwuchtiger Rotor in den Begrenzungs Bereichen der Welle bis zu 50 % höhere Spannungen in Bezug auf die Nennbetriebsspannung erzeugen.
Die Norm ISO 1940:2003 legt Grade der Auswucht Qualität entsprechend der Art der Ausrüstung und der Art der Anwendung fest. Nachdem der Qualitätsgrad für Radialventilatoren definiert wurde und die Betriebsdrehzahl vorliegt, ist es möglich, die maximale spezifische Unwuchtmasse für einen Rotor anhand des Diagramms in Abbildung 2 zu bestimmen.
Abbildung 2: Spezifische Unwuchtmassen Tabelle. ISO 1940
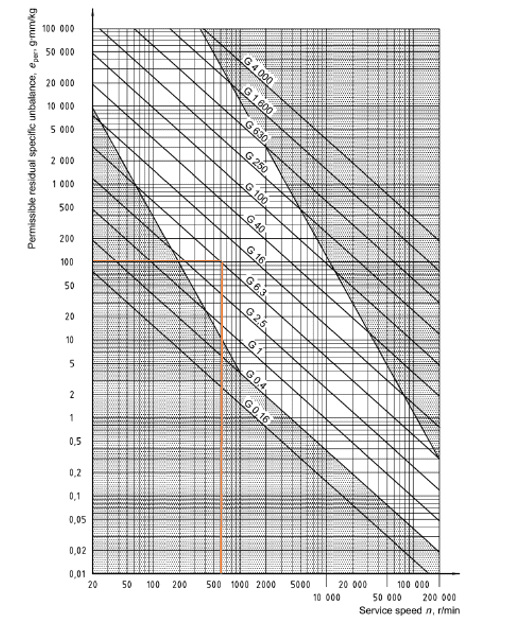
Damit ist es möglich, die Restunwucht Masse zu bestimmen und den höchsten von der Norm zugelassenen Wert zur Berechnung der Fliehkraft anzusetzen.
Nishi (2006) zitiert, dass die Restmasse nach Gleichung 5 berechnet werden kann.
(5)
Dabei ist Mr die Restmasse, Pr das Rotorgewicht (kg), D die spezifische Unwuchtmasse aus der Tabelle (g.mm/kg) und r der Rotorradius (mm).
Unter der Annahme, dass sich diese Unwuchtmasse nahe am Außendurchmesser des Rotors befindet, lässt sich die Zentrifugalkraft nach Gleichung 6 bestimmen.
Dabei ist m die Unwuchtmasse (kg), „e“ die Exzentrizität der Masse (m) und w die Radialgeschwindigkeit (rad/s).
Eine weitere wichtige Überlegung, die sich aus der Maschinenkonstruktion ergibt, ist die Schätzung der Kraft, die durch die Dehnung der Riemen ausgeübt wird, wie in Abbildung 3 gezeigt.
Abbildung 3: Schema von Riemenscheiben und Riemen
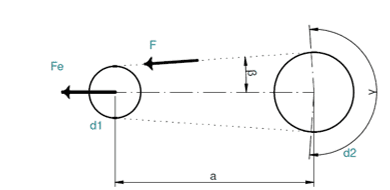
Der erste Schritt zur Berechnung der Riemenspann Spannung besteht darin, den Winkel g durch Gleichung 7 zu bestimmen.
Wobei „a“ der Achsabstand (mm), d2 der Durchmesser der größten Riemenscheibe (mm) und d1 der kleinste (mm) ist.
Während der Winkel b die Hälfte von 180 minus ist![]() . Eine weitere wichtige Gleichung ist Gleichung 8 zur Bestimmung der Tangentialkraft an der kleineren Riemenscheibe.
. Eine weitere wichtige Gleichung ist Gleichung 8 zur Bestimmung der Tangentialkraft an der kleineren Riemenscheibe.
Dabei ist t1 das Drehmoment (Nm) und r1 der Radius der kleinsten Riemenscheibe (mm). Eine weitere notwendige Information ist der Winkel![]() im Bogenmaß, die aufgerufen werden
im Bogenmaß, die aufgerufen werden ![]() .
.
Die Berechnung der Kraft auf die Riemen im gespannten Teil und im lockeren Teil des Riemens wird jeweils durch die Gleichungen 9 und 10 definiert, wobei![]() ist der durchschnittliche Reibungskoeffizient zwischen Riemen und Riemenscheibe.
ist der durchschnittliche Reibungskoeffizient zwischen Riemen und Riemenscheibe.
(9)
Die Gesamt Dehnkraft, der die Welle ausgesetzt ist, wird durch Gleichung 11 abgeschätzt.
Eine weitere wichtige Belastung, der die Welle während des Lüfterbetriebs ausgesetzt ist, ist das Drehmoment, das nach Jorgensen (1999) durch Gleichung 12 definiert ist.
Wobei K ein durch 1000/2 definierter Koeffizient ist![]() , P ist die Motorleistung (kW) und N ist die Wellendrehzahl (U/s).
, P ist die Motorleistung (kW) und N ist die Wellendrehzahl (U/s).
Nachdem alle Belastungen berechnet wurden, können die Querkraft- und Biegemoment Diagramme entlang der Achse gezeichnet werden. Damit werden die kritischen Punkte definiert und die erlittenen Momente bestimmt.
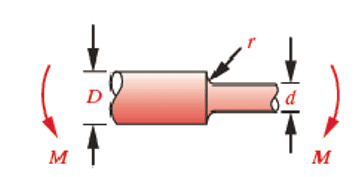
Die Definitionen der Spannungen für die Berechnung der Ermüdung müssen nach Norton (2013), der Kerbempfindlichkeit und dem Spannungskonzentrationsfaktor kf berechnet werden, die die Eigenschaften des Materials berücksichtigen. Zunächst müssen jedoch die geometrischen Konzentrationsfaktoren kt und kts abgeschätzt werden. Bei einer Achse mit Durchmesserreduzierung, wie in Bild 4 dargestellt, muss die Belastungsart berücksichtigt und der Faktor nach Gleichung 13 definiert werden.
Die in Gleichung 13 erforderlichen Daten sind in Tabelle 1 aufgeführt.
Tabelle 1: Daten zur Berechnung von kt
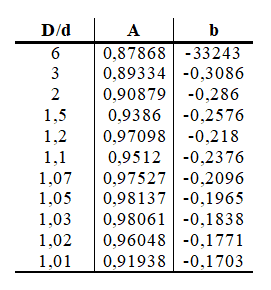
Abbildung 4: Welle mit Reduktion unter Moment
Für Norton (2013) war Neuber einer der ersten, der die Auswirkungen von Diskontinuitäten in Teilen untersuchte, und schlug eine Gleichung vor, um den Spannungskonzentrationsfaktor bei Ermüdung abzuschätzen. Die Kerbempfindlichkeit wird aus Gleichung 14, Kuhn-Hardrath, in Bezug auf die Konstante „a“ und den Kerbradius definiert.
Je höher die Duktilität des Materials, desto geringer die Kerbempfindlichkeit; was auch davon abhängt, wie abrupt die Durchmesserreduzierung ist, unter Berücksichtigung der Rundung der Durchmesserreduzierung.
Tabelle 2: Neubersche Konstante für Stähle

Die Bestimmung des Konzentrationsfaktors kf, angewendet auf die auf Basis der zuvor durchgeführten mechanischen Belastungen errechneten Spannungswerte, erfolgt nach Gleichung 15.
Sobald die interessierenden Punkte definiert sind, wo geschätzt wird, dass es die höchsten Spannungspunkte geben wird und dass die Welle aufgrund von Ermüdung ausfallen sollte, werden die Spannungen gemäß der Art der Anforderung berechnet, siehe Gleichungen 16, 17 und 18.
Dabei ist Mb (N.m) das Biegemoment, Mt (N.m) das Torsionsmoment, F(N) die Axialkraft, „a“ (m²) die Wellen Querschnittsfläche und d (mm) der Durchmesser des ausgewählten Punktes.
Ein guter Parameter, um die numerischen Berechnungen mit den analytischen zu validieren, ist die Schätzung der Von-Mises-Spannung nach Norton (2004), was in Situationen praktisch ist, in denen Normal- und Schubspannungen gemäß Gleichung 19 am selben Punkt kombiniert werden.
Nach Hibbeler (2009) wird der allgemeine Spannungszustand in einer Region durch sechs Komponenten der Normal- und Schubspannung bestimmt. Vereinfachend für einen ebenen Spannungszustand wird die maximale Hauptspannung durch Gleichung 20 bestimmt.
Wie andere mechanische Eigenschaften können auch Ermüdungseigenschaften im Labor getestet werden. Laut Callister (2002) ist die Ausrüstung so konzipiert, dass sie kontrollierte Belastungen, Häufigkeit und Muster von Wiederholungen beschleunigt simuliert, um zu bestimmen, wie viele Zyklen eine Probe eines bestimmten Materials unter vorher festgelegten Bedingungen aushält.
Für Norton (2004) ist die Wöhlerlinie zu einer wichtigen und noch heute verwendeten Methode zur Charakterisierung des Verhaltens von Werkstoffen bei Wechselbeanspruchung geworden. Die ersten Studien zu diesen Eigenschaften in metallischen Werkstoffen wurden 1850 von August Wöhler durchgeführt, und das Hauptergebnis dieser Arbeit war die Erstellung einer Kurve, die die Anzahl der unterstützten Zyklen mit der auf eine Probe ausgeübten Wechselspannung in Beziehung setzt. Rissausbreitung Studien werden bei Belastungsniveaus unterhalb der Festigkeitsgrenze und für eine signifikante Anzahl von Zyklen über 1000 durchgeführt.
Abbildung 5: Wöhlerlinie mit Ausfallwahrscheinlichkeit
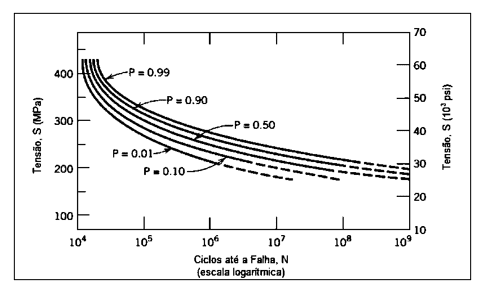
Garcia et al. (2012) weisen darauf hin, dass die Ermüdungsfestigkeit Grenze bei Stählen im Allgemeinen zwischen 35 % und 65 % der Zugfestigkeit Grenze liegt. Die aus Tests mit Proben erhaltenen Werte müssen auch gemäß den tatsächlichen Anwendungsbedingungen des projizierten Teils korrigiert werden, unabhängig davon, ob es sich um Unterschiede in der Temperatur, der Exposition Umgebung und dem Herstellungsverfahren handelt, bis zu dem Punkt, an dem die korrigierte Ermüdungsfestigkeit ermittelt wird, die durch die Gleichung dargestellt wird 21.
Wobei Se’ 54 % des maximalen Spannungswerts für Materialien ist, bei denen Sut kleiner oder gleich 1460 MPa ist. Für Werte darüber wird Se’ gleich 740 Mpa angenommen.
Ccarreg ist nach Norton (2004) der Korrekturfaktor für die Belastungsart, der für Flexion 1,00 und für Normalkraft 0,70 beträgt.
Die Proben haben reduzierte Größen, meistens kleiner als die zu analysierenden Teile, daher wird ein Korrekturfaktor angewendet. Für Durchmesser bis zu 8 mm kann Csize als 1,00 betrachtet werden; für Durchmesser zwischen 8,00 und 250 mm wird Gleichung 22 verwendet.
Die Probe hat eine Oberfläche mit einem polierten Finish. Anders als das konstruierte Teil, das unter anderem an Unvollkommenheiten, Porositäten, Materialfehlern, Kerben und anderen Faktoren leidet, die die Ermüdungsbeständigkeit des Modells verringern.
Tabelle 3: Oberflächenfaktor Koeffizient

Auch nach Norton (2004) ist es zur Definition des Werts dieses Koeffizienten notwendig, die Werte von A und B in Tabelle 3 auszuwählen und in Gleichung 23 anzuwenden.
Für Ctemp ist bekannt, dass die im Labor durchgeführten Tests in einer Umgebung mit kontrollierter Temperatur durchgeführt werden. Laut Shigley (2016) verschwindet die Krümmung der Wöhlerkurve tendenziell bei hohen Temperaturwerten. Es wird empfohlen, folgende Werte anzunehmen: Bis 450°C muss der Wert des Korrekturfaktors 1,00 betragen. Für Temperaturwerte zwischen 450 °C und 550 °C betrachten Sie Gleichung 24.
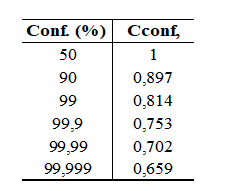
In Bezug auf die Zuverlässigkeit beziehen sich die in Tests erhaltenen Werte auf durchschnittliche Schätzungen für mehrere Tests, bei denen die Abweichung 8% nicht überschreitet. Daher muss ein Zuverlässigkeitsfaktor gemäß Tabelle 4 angenommen werden.
Tabelle 4: Zuverlässigkeit Korrekturfaktor
Erwähnenswert ist auch, dass die Umgebung die Dauerfestigkeit des Teils erheblich beeinflussen kann. Bei Tests mit Vakuum Umgebung, atmosphärischer Luft und Salzwasser Umgebung werden unterschiedliche Ergebnisse gefunden.
Costa (2010) bestätigte durch Experimente, die Wöhlerlinien von metallischen Werkstoffen erhoben, dass tatsächlich eine Unsicherheit für die Realisierung einer Ermüdungskurve besteht, die mit allen bereits erwähnten Variablen zusammen mit den Variationen in den Messmethoden und sogar kombiniert wird in den für den Test verwendeten Maschinen lassen sie den Ingenieur Werte berücksichtigen, die für die Berechnung der Ermüdungslebensdauer oft überschätzt werden.
Laut Shigley (2016) beziehen sich die entwickelten Gleichungen auf die Eigenschaften der Materialien in einem Hochzyklus Bereich, größer als. Norton (2004) erwähnt, dass es mit Low-Cycle-Informationen möglich ist, die Wöhlerlinie des Materials zu bestimmen. Diese Daten sind (Sm), mittlerer Materialwiderstand bei Zyklen, wie in Abbildung 6 gezeigt.
Abbildung 6: Geschätzte Wöhlerkurve
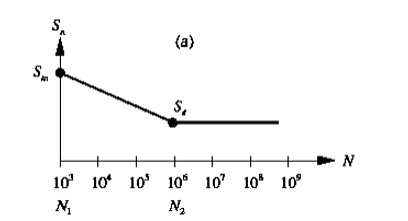
Bei Vorhandensein einer Normalkraft beträgt die angegebene Durchschnittsspannung 75 % der Höchste Widerstandsspannung (Sut). Die Gleichung der Linie, die durch Sm und Se verläuft, kann durch Gleichung 25 bestimmt werden.
Wobei S(N) die Ermüdungsfestigkeit für eine Anzahl von N Zyklen ist, a und b sind Konstanten, die entsprechend den Randbedingungen definiert sind.
Die Koeffizienten a und b sind jeweils durch die Gleichungen 26 und 27 definiert.
(27)
Mit dieser Didaktik ist es möglich, die Anzahl der Zyklen, die die Welle aushalten muss, und den Sicherheitsfaktor für die Ermüdungsfestigkeit analytisch abzuschätzen. Dies bietet einen Ausgangspunkt für numerische Analysen.
Laut Silva et al. besteht die Finite-Elemente-Methode (FEM) aus einer Lösung von Differentialgleichungen durch Integration, die auf eine Menge in kleineren, diskretisierten Teilen angewendet wird. Die Idee, den Untersuchungsbereich in mehrere kleinere Teile aufzuteilen, löst ein Problem hinsichtlich der Schwierigkeit, Interpolationsfunktionen auszuwählen, die das Verhalten der Variablen über den gesamten Satz beschreiben.
Für Silva (2016) ist es möglich, durch die numerische Verwendung der Ansys-Software relative Fehler von 0,4% zu erhalten, indem analytische Spannungswerte in Kraftübertragung Sachsen verglichen werden.
Gujaran und Gholap (2014) erzielten weniger ungefähre Ergebnisse. Ebenfalls über die Ansys-Software, aber für ein komplexeres Ermüdung Problem in einem Wellenmodell mit abrupten Kerben, das beim Vergleich numerischer und analytischer Ergebnisse zu einem Fehler von etwa 28 % führte. Bei Engel und Al-Maeeni (2017) betrug der relative Fehler etwa 7 % bei der maximalen Hauptspannung einer Drehachse einer Biegemaschine.
Für Dejan (2012) deuteten numerische Berechnungen und Simulationen zwar auf eine Lebensdauer einer hydroelektrischen Turbinen Antriebswelle von 2.000.000 Stunden hin, diese versagte jedoch mit etwas mehr als 1.000.000 Stunden an einem bekannten Konzentrationspunkt. Es wird die Hypothese aufgestellt, dass dieser Punkt konstanter Spannung anfälliger für Korrosion wird.
Es wird darauf hingewiesen, dass die Komplexität des Problems die Durchsetzungsrate der in dieser Untersuchung verwendeten Berechnungen direkt beeinflussen kann.
ERGEBNISSE
Alle in dieser Arbeit durchgeführten Berechnungen basieren auf der ingenieurtechnischen Literatur. Die analytisch gewonnenen Daten folgen Protokollen zur Dimensionierung hinsichtlich Dauerfestigkeit mit dem Ziel, den Bruchbereich der untersuchten Abgas Welle zu finden.
Kennen Sie die Betriebseigenschaften dieses Zentrifugalventilators, der Durchfluss beträgt 300.798 m³/h, der statische Druck 290 mm CA und der Durchmesser des Rotors 2,95 m; eine Axialkraft von 19.638 N wird geschätzt, indem die Ergebnisse der Gleichungen 1 und 2 addiert werden.
Unter der Annahme, dass der Lüfter höchstens 10 % außerhalb des optimalen Betriebspunkts arbeitet, wird durch die Gleichungen 3 und 4 die durch die Änderung der Luftströmungsrichtung erzeugte Radialkraft geschätzt, die etwa 35 N beträgt.
In Anbetracht der Tatsache, dass kein rotierender Körper, wie in der Literatur angegeben, eine 100%ige Wucht erreicht, wurde in diesem Fall der höchstmögliche Wert der Restunwucht Masse angenommen. In dem Wissen, dass die Wellendrehzahl 590 U / min beträgt und die für diesen Maschinentyp angenommene Auswuchtgüte Klasse G6.3 ist; eine spezifische Unwucht von 100 g.mm/kg wird durch das Diagramm von Abbildung 3 geschätzt. Betrachtet man den ungünstigsten Fall und wendet diese Masse in den Gleichungen 5 und 6 auf den Außendurchmesser des Rotors an, ergibt sich für die Unwuchtkraft 878 N.
Die Riemenscheiben messen 340 mm und 686 mm und der Achsabstand beträgt ca. 3850 mm. Bei einem Reibwert von 0,25 und einem Motordrehmoment von 2.403 Nm bei den Formeln 7, 8, 9, 10 und 11 ergibt sich eine Spannkraft der Riemen auf der Achse von 38.000 N.
Sobald die Motorleistung und die Wellendrehung bekannt sind, gibt die Literatur an, dass das Nennbetriebsdrehmoment Gleichung 12 folgt, was zu 4.855 Nm führt.
Als Leistung für diese Formel kann der Wert angenommen werden, der durch den Lüfterbetrieb verbraucht wird, berechnet durch Multiplizieren des Volumenstroms in m³/s mit dem statischen Druck in Pa; für diese zweite Hypothese wäre das Nenndrehmoment 4.272 Nm.
Aus diesen technischen Erinnerungsdaten können die Scherkraft- und Biegemoment Diagramme zusammengestellt werden, wie in Abbildung 8 gezeigt.
Basierend darauf und auf den Modell Kerben wurden drei Punkte ausgewählt, um die Spannungen zu berechnen, wie in Abbildung 7 gezeigt; P1, P2 und P3.
Abbildung 7: Achs Berechnungspunkte

Abbildung 8: Scherkraft- und Biegemoment Diagramm
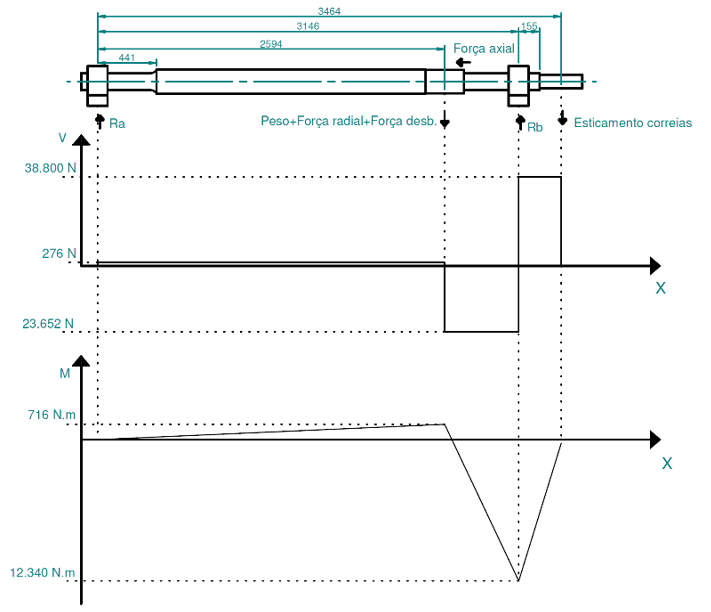
Die an den Analyse Punkten auf der Achse erzeugten Biegemomente sind die folgenden: M1, das 121,4 Nm beträgt; M2 ist 2.655 Nm und M3 6.984 Nm.
Für jeden der ausgewählten Punkte ist es erforderlich, den geometrischen Spannungskonzentrator kt entsprechend der Art der aufgebrachten Belastung zu berechnen, Gleichung 13, Tabelle 1.
Danach wird durch die Neuber-Konstante für Stähle, Tabelle 2 und Gleichung 14 jeder der Kerbempfindlichkeitswerte geschätzt und auf Gleichung 15 angewendet, die die Spannung Konzentrationswerte für dynamische Spannungen kf angibt.
Die Welle ist in axialer Richtung nur am Punkt Ra fixiert, daher wird geschätzt, dass die Axialkraft Spannungen nur am Punkt 1 erzeugt, wenn man bedenkt, dass sie auf die Welle in dem Teil mit einem Durchmesser von 175 mm von rechts aufgebracht wird nach links, siehe Abbildung 8.
An Punkt 1 waren die gefundenen Spannungswerte nach den Gleichungen 16, 17 und 18, wobei bereits Erhöhungen um ihre jeweiligen kf angewendet wurden:
Für Punkt 2, der keine Spannung durch Axialkraft aufweist, ergaben dieselben Berechnungen Spannungen in den folgenden Größenordnungen, außerdem bereits angewendete Kf-Faktoren:
Weiter zu Punkt 3, die gefundenen Werte für die Biege- und Torsionsmomente:![]()
Alle angenommenen Berechnung Hypothese berücksichtigten die ungünstigsten Randbedingungen und konditionierten die Ergebnisse auf den ungünstigsten Fall innerhalb der Toleranzen, die für den Betrieb eines Ventilators und die Dimensionierung einer Achse gelten.
Mit diesen Daten können wir den Spannungszustand an den genannten Punkten bestimmen, indem wir die von Mises-Spannungen abschätzen und damit das numerische Modell kalibrieren. Von Mises-Werte für die Punkte P1, P2 und P3 waren jeweils 24,40 Mpa, 47,50 Mpa und 141,90 Mpa.
Die Berechnung der Anzahl der Zyklen berücksichtigt die maximalen Hauptspannungen Werte, die durch Gleichung 20 Werte von 15,43 Mpa finden; 49,85 MPa und 135,85 MPa für die Punkte 1, 2 und 3.
Da die Materialwelle SAE 1045 ist, musste für die Berechnung der Dauerfestigkeitsgrenze E=206,8 Gpa, Sut= 690 Mpa und Sy= 580 Mpa berücksichtigt werden. Der Ermüdungsanalyse Punkt ist P3.
Um Gleichung 21 anzuwenden, wurden einige Überlegungen angestellt. Cload für Normalkraft Präsenz ist 0,7. Die Größe für eine 100-mm-Welle beträgt 0,7606. Für eine bearbeitete Oberfläche beträgt Csurf 0,958. Die Auslegungstemperatur von 160°C hat keinen Einfluss auf das Modell. Für eine Zuverlässigkeit von 99,99 % beträgt Cconf 0,702.
Unter diesen Bedingungen beträgt die Dauerfestigkeitsgrenze der Achse 124,40 MPa. Bei einem Modell mit normaler Festigkeit betrug die durchschnittliche Festigkeit 517,5 MPa. Somit ist die geschätzte Wöhlerkurve für diese Achse in Abbildung 9 dargestellt.
Abbildung 9: Geschätzte Wöhlerkurve
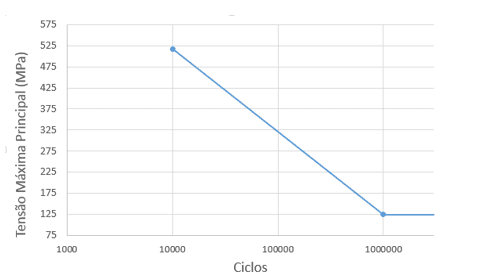
Wenn man weiß, dass die maximale Hauptspannung an Punkt drei zu 135,85 MPa führte und die Gleichungen 25, 26 und 27 anwendet, wird analytisch geschätzt, dass die Welle 653.978 Zyklen aushält.
Die mit der Ansys-Software modellierte numerische Näherung begann mit der Diskretisierung des Modells mit einem Netz aus etwa 160.000 tetraedrischen Elementen zweiter Ordnung, 238.544 Knoten, mit einer Verfeinerung Rate von 1 an den Kerbpunkten, wie in Abbildung 10 dargestellt.
Abbildung 10: Antriebswellennetz
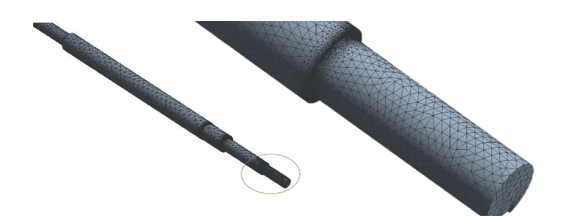
Um zu einem Netz von zufriedenstellender Qualität zu gelangen, ohne übermäßige Ausführungszeit zu verbrauchen und das andererseits keine Verzerrungen und Singularität Spannungen aufweist, wurde die Konvergenz Kurve basierend auf dem Von-Mises-Spannungswert kalibriert, siehe Abbildung 11.
Abbildung 11: Konvergenz Kurve
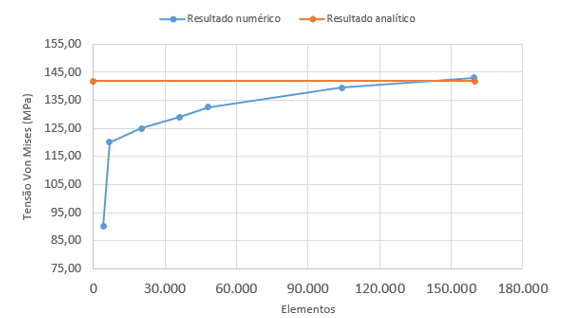
Die baustatische Analyse ergab Spannungswerte im Bereich von 144 Mpa, wie in Bild 12 dargestellt, gegenüber den analytischen 141,90 Mpa. Eine durchaus akzeptable Variante, die eine gute statische Bruchfestigkeit aufweist, da das verwendete Material eine Streckgrenze von 580 MPa aufweist.
Abbildung 12: Von Mises Stress Punkt 3
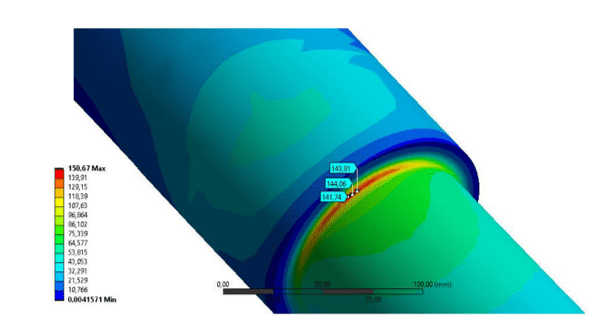
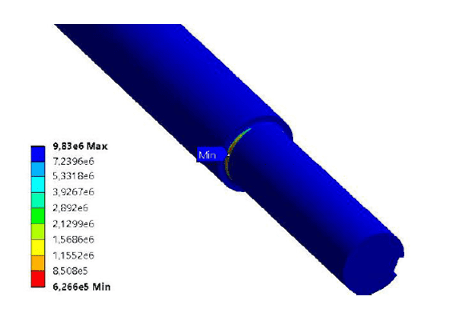
Die Lebensdaueranalyse der Achse berücksichtigte die maximalen Hauptspannungen Werte, die numerisch im Bereich von 149 Mpa liegen, gegenüber den analytischen 135,85 Mpa. Fig. 13 veranschaulicht den P3-Spannung Konzentrationsbereich.
Abbildung 13: Maximale Hauptspannung
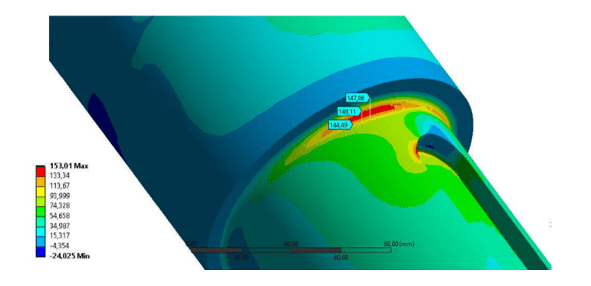
Das Ausführungsmodul für die Ermüdungslebensdauer Analyse wurde unter Verwendung der Ansys Transient structural ausgeführt, wobei die Achse einer vollständig umgekehrten Belastung und der Goodman-Methode ausgesetzt wurde, wie in Abbildung 14 gezeigt.
Abbildung 14: Analyse Ausführungsmodus
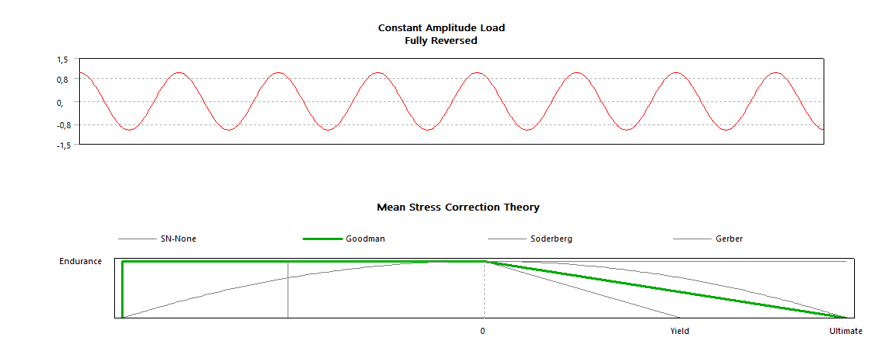
Die Spannungs-Dehnungs-Kurve des für die Ermüdungslebensdauer verwendeten Materials stammte aus der Ansys-Datenbank für SAE 1045-Stahl.
Die angegebene Spindeldrehzahl beträgt 590 U/min, sodass jeder 1-Sekunden-Zyklus 9.833 Wiederholungen entspricht. Die Simulation zeigte eine Lebensdauer von 626.600 Zyklen für den analysierten kritischen Bereich, wie in Abbildung 15 gezeigt.
Abbildung 15: Anzahl der Achsen Lebenszyklen
Analysiert man die Lebensdauer des Teils in Stunden, unter Berücksichtigung der Arbeits Drehung der Achse und dass jede Drehung ein Zyklus ist, hätte das Modell eine Nutzungsdauer von nur 174 Stunden.
Bei Geräten, die 24 Stunden am Tag arbeiten, würde der Ausfall in nur einer Woche auftreten.
Tatsache ist, dass die Achse ermüdet ist und ersetzt werden musste. Aus Gründen des Betriebsgeheimnisses gibt es keine genauen Aufzeichnungen darüber, wie lange es bis zum Ausfall gedauert hat, aber die Studien machen die Anfälligkeit des Teils im Analysebereich deutlich.
Alle Randbedingungen wurden an ihrer oberen Grenze gemessen, wodurch die Ergebnisse zeigen, wie sich die Achse unter extremen Bedingungen verhalten würde. Dasselbe zeigte, dass es bei solchen Parametern in kurzer Zeit katastrophal versagen würde, aber es ist möglich, dass der untersuchte Fall mildere Anfragen durchlaufen hat, bis ein mechanisches Versagen auftritt.
Ein weiterer hervorzuhebender Punkt ist die Möglichkeit von Herstellungsfehlern, wie von Di, Liang und Zhang (2016) hervorgehoben. Ein kleinerer als der spezifizierte Radius des Spannungskonzentrators der Antriebswelle kann die Nennspannung Werte während des Betriebs der Welle verdoppeln und aufgrund der Konstruktion zu einem vorzeitigen und unvorhergesehenen Ausfall führen.
Bei der Auswertung der Vergleichsparameter der Analysen zeigt sich die Konsistenz der Ergebnisse, da die relativen Fehler gering waren. Selbst bei den Ergebnissen der Ermüdungslebensdauer betrug der Fehler zwischen den Studien etwa 4 %, siehe Tabelle 5.
Tabelle 5: Relativer Fehler
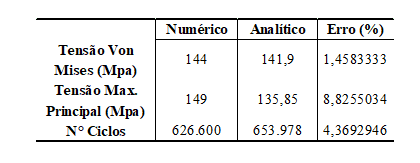
Unter Berücksichtigung aller Faktoren, die bei der Untersuchung und Sammlung von Daten für die Dimensionierung, Berechnung von Anforderungen und Schätzung der Lebensdauer berücksichtigt wurden, war es möglich, das Ziel der Parametrisierung und Gewinnung dieser Informationen auf praktische Weise und auf der Grundlage von Berechnungen und Computersimulationen zu erwägen durch Informationen aus dem zuvor hergestellten und durch Arbeitszeit zusammengebrochenen Stück; was noch mehr Zuverlässigkeit in der bei der Arbeit durchgeführten Methode demonstriert.
FAZIT
Die Antriebswelle eines 400-PS-Abluftventilators fiel aufgrund von Ermüdung während des Betriebs aus, ohne dass genaue Informationen zur Betriebszeit verfügbar waren.
Mit dem Ziel, diese Zeit und den Fehlerbereich abzuschätzen, stellte diese Forschung fest, dass der Fehler sogar analytisch vorhersagbar war. Beim Vergleich der Analysen fielen die Ergebnisse sehr gut aus und hielten Werte in ähnlicher Größenordnung.
Das Hauptziel der Studie war es, Parameter für die Berechnung des Abgasschachts zu erhalten. Dabei geht es um Betriebseigenschaften von Strömungsmaschinen und deren Nuancen. Sobald der Fehler bekannt ist, kann die Gleichung zusammen mit der Simulation mit den Informationen, auf die wir Zugriff hatten, bestätigt werden.
Dies ist eine wichtige Entwicklung, wenn es um die Dimensionierung in der Strömungsmaschinen Industrie geht, sie kann die Grundlage für zukünftige Studien und Wellendimensionierung für zukünftige Projekte sein oder sogar Änderungen am Design dieser Achse testen, die auf eine unbegrenzte Lebensdauer abzielen.
VERWEISE
ANDRESEN, P.; ANTOLOVICH, B. Fatigue and Fracture. ASM Handbook. 1997.
CALLISTER, William. Ciência e Engenharia de Materiais. 5. ed. Rio de Janeiro, RJ: Editora LTC, 2002. 589 p.
COSTA, Leandro Pereira. Avaliação da incerteza de medição no levantamento de curvas de fadiga S-N de materiais metálicos. 2010. Dissertação de Mestrado (Mestrado em Engenharia) – Universidade Federal do Rio Grande do Sul, [S. l.], 2010.
DU, Jinfeng; LIANG, Jun; ZHANG, Lei. Research on the failure of the induced draft fan’s shaft in a power boiler. Engineering Failure analysis, 2016.
ENGEL, B; AL-MAEENI, Sara Salma Hassan. Failure analysis and fatigue life estimation of a shaft of a rotary draw bending machine. International Journal of mechanical and mechatronics engineering, 2017.
GARCIA, A.; SPIM, J. A.; SANTOS, C. A.; Ensaios dos materiais. LTC – Livros técnicos e Científicos Editora Ltda, Rio de Janeiro – RJ, 2012.
GUJARAN, Sandeep; GHOLAP, Shivaji. Fatigue Analysis of Drive Shaft. International Journal Of Research In Aeronautical And Mechanical Engineering, [S. l.], p. 1-8, 10 out. 2014.
GUJAR, R. A.; BHASKAR, S. V. Shaft Design under Fatigue Loading By Using Modified Goodman Method. International Journal of Engineering Research and Applications, [S. l.], p. 1061-1066, 1 ago. 2013.
HENN, Érico Antônio Lopes. Máquinas de Fluido. 2. ed. Santa Maria, RS: Editora da UFSM, 2006. 476 p.
HIBBELER, R. L. Resistência dos materiais. 7. ed. São Paulo: Pearson Prentice Hall, 2009.
INTERNATIONAL ORGANIZATION FOR STANDARDIZATION. ISO 1940:2003. Vibração Mecânica – Requisitos de qualidade de balanceamento para rotores rígidos, [S. l.], 15 ago. 2003.
JORGENSEN, R. Fan Engineering. 9 ed. Buffalo, New York: Howden Buffalo, Inc.: 1999.
MOMČILOVIĆ, Dejan et al. Failure analysis of hydraulic turbine shaft. Engineering Failure Analysis, 2012.
NISHI, E. K. Apostila de balanceamento. Londrina: Nishi eletromecânica, 2006
NORTON, Robert L. Projeto de Máquinas: Uma abordagem integrada. 2. ed. Porto Alegre – RS: Editora Bookman, 2004. 905 p.
ROY, Ankita et al. Investigation of torsional failure of a centrifugal pump shaft. Engineering Failure analysis, Kalinganagar, India, 2020.
SCHIEL, Frederico; Introdução a resistência dos materiais. São Paulo, SP : Editora Harper & Row do Brasil., 1984. 395 p.
SHAHROOI, Shahram; ASAYESH, Masood. Numerical and experimental analysis for fatigue failure investigation on gas recirculation fan shaft. 9th International Conference on Fracture and Strenght of solids, Korea, 2013.
SHIGLEY, J. E. Elementos de máquina. 10. ed. Porto Alegre – RS: Editora AMGH, 2016. 1096 p.
SILVA, J. G.; SOEIRO, F. J.; TRIGUEIRO, G. S.; ROBERTO, A. R.; Análise Estrutural de Chassis de Veículos Pesados com Base no emprego do programa Ansys. Cobenge, Rio de Janeiro, 2001.
SILVA, F. A.; CHAVES, C. A.; GUIDI, E. S.; Análise de falha por fadiga em eixo de transmissão utilizando o método dos elementos finitos. Exacta – EP, São Paulo, v. 14, n. 2, p. 207-219,2016.
TREBUNA, F. et al. Identification of causes of radial fan failure. Engineering Failure Analysis, Kosice, Eslováquia, 2009
ZAMBRANO, O. A.; CORONADO, J. J; RODRIGUEZ, S. A. Failure analysis of a bridge crane shaft. Engineering Failure analysis, 2014.
[1] Spezialist für Predictive Structural Engineering, Maschinenbauingenieur und Techniker für Industrieautomation. ORCID: 0000-0003-4407-3351.
[2] Berater. ORCID: 0000-0001-7965-1620.
Gesendet: Mai 2022.
Genehmigt: September 2022.