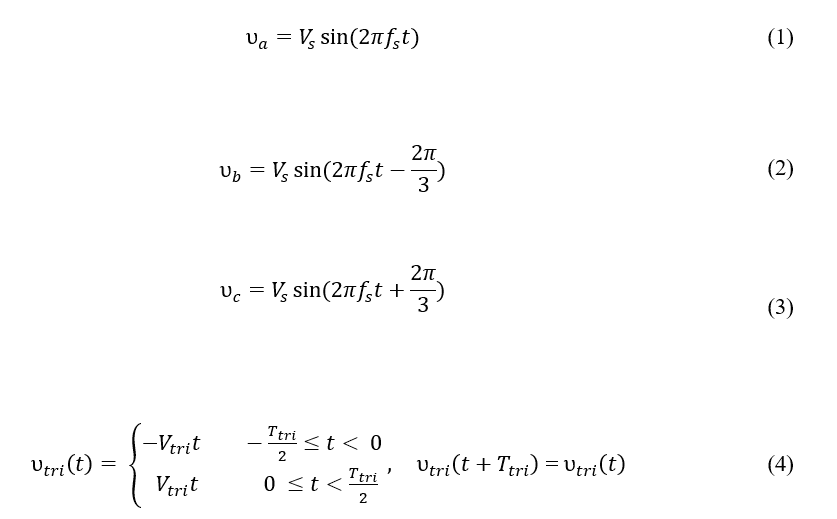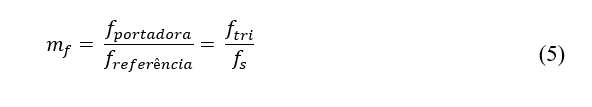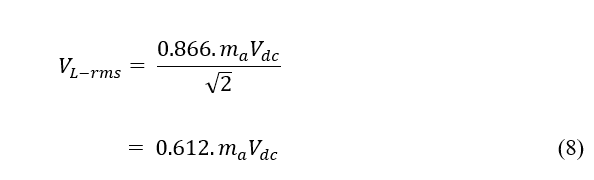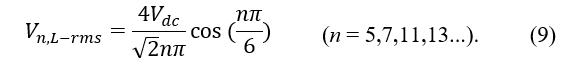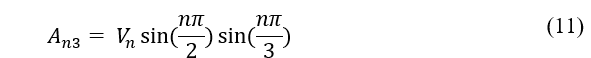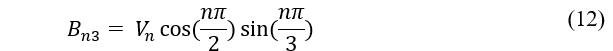Análise comparativa entre as distorções harmônicas totais das técnicas de 6 pulsos e de modulação por largura de pulso senoidal

ARTIGO ORIGINAL

MENDONÇA, Luan Aleixo Canário ^[1]

MENDONÇA, Luan Aleixo Canário. Análise comparativa entre as distorções harmônicas totais das técnicas de 6 pulsos e de modulação por largura de pulso senoidal. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano 06, Ed. 01, Vol. 03, pp. 05-21. Janeiro de 2021. ISSN: 2448-0959, Link de acesso: https://www.nucleodoconhecimento.com.br/engenharia-eletrica/distorcoes-harmonicas

RESUMO

Este trabalho faz uma análise comparativa das distorções harmônicas totais ou do inglês Total Harmonic Distortion (THD) entre duas técnicas de disparos de inversores de frequência: A sequência de 6 pulsos e a Sinusoidal Pulse Width Modulated (SPWM), do português Modulação por Largura de Pulso Senoidal. Inicialmente é feita uma abordagem teórica, mostrando matematicamente as diferenças entre os dois métodos. Em seguida é feita as simulações dos circuitos de ambas as técnicas de disparo. Com as simulações realizadas, este trabalho faz uma análise comparativa das THDs das tensões de saída com o circuito operando em aberto (sem carga conectada na saída). Em seguida é realizada a conexão de uma carga na saída dos inversores (motor) com o intuito de observar o comportamento das correntes em uma carga de característica resistiva-indutiva (RL). O objetivo desta última etapa é avaliar a necessidade ou não da utilização de filtros passa-baixa em casos onde a aplicação não exige um nível extremamente baixo da THD.

Palavras-chave: THD, distorção harmônica, 6 pulsos, SPWM.

1. INTRODUÇÃO

Inversores de frequência em sua grande maioria das vezes, são utilizados para controlar cargas de caráter alternado a partir da manipulação de uma tensão contínua em sua entrada. Dessa forma, a qualidade da tensão alternada na saída dos inversores se torna um fator relevante e deve ser levada em consideração para cada tipo de aplicação. Nesse processo a THD passa a ser uma das grandezas que mensura essa qualidade (HART, 2010).

As formas de onda retangulares das tensões encontradas nas saídas dos inversores servem para algumas aplicações específicas. No entanto, em muitos casos, se faz necessário uma tensão puramente senoidal. Para isso, projetistas de circuitos chaveados muitas vezes se deparam com a necessidade de implementar filtros passa-baixa, e como estes necessitam trafegar uma grande quantidade de potência, precisam ser grandes e robustos, o que consequentemente aumenta os custos finais de produção. Através da aplicação da técnica SPWM, esses filtros podem ser muito reduzidos e as vezes até mesmo omitidos nos circuitos (AHMED, 2000).

Ao final desse trabalho, espera-se ter uma análise comparativa concisa das técnicas de 6 pulsos e a SPWM baseada na simulação dos circuitos, demonstrando as vantagens e desvantagens de cada abordagem.

2. FUNDAMENTAÇÃO TEÓRICA

2.1 INVERSOR ACIONADO POR SEQUÊNCIA DE 6 PULSOS

O funcionamento dos inversores sejam eles monofásicos ou trifásicos, é baseado na comutação das chaves estáticas em uma determinada sequência e por um determinado período. A tensão alternada (AC) do inversor é sintetizada com base na manipulação da tensão contínua (DC) através da abertura e fechamento das chaves fazendo com que na saída seja possível obter valores de tensão positivos e negativos (+V_dc e – V_dc) e defasados por um determinado ângulo (HART, 2010).

Na Figura 1, é apresentado o circuito básico ideal de um inversor trifásico alimentando uma carga conectada em Y.

Figura 1 – Circuito ideal de um inversor trifásico

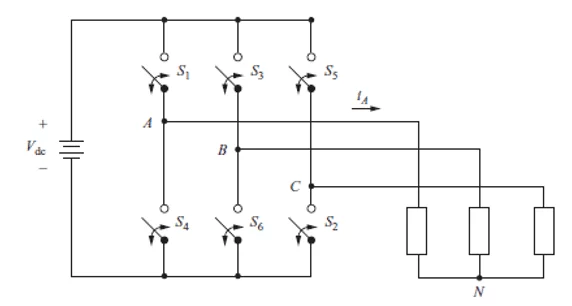
Na técnica de disparo de 6 pulsos, cada chave tem um ciclo de trabalho de 50% e é acionada a cada intervalo de tempo de T/6 (ou 60º), onde T é o período da tensão na saída do inversor. Os pares de chaves (S₁, S₄), (S₃, S₆) e (S₅, S₂) compõem cada um, um braço do inversor trifásico e jamais podem ser acionadas simultaneamente, pois caso o contrário, um curto seria gerado na fonte V_dc (HART, 2010). Na Figura 2, é apresentada a sequência de comutação das chaves do circuito da Figura 1.

Figura 2 – Sequência de comutação de 6 pulsos para um inversor trifásico.

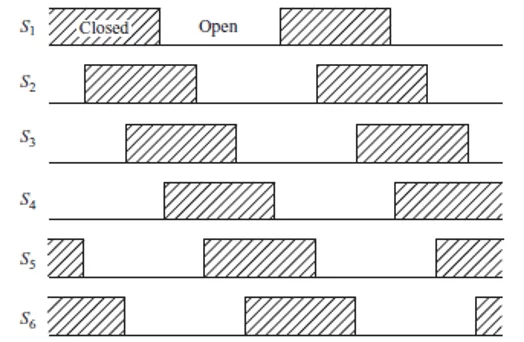
Em seus trabalhos AHMED (2000), apresenta um quadro resumindo o estado de cada chave ao longo de um período e a respectiva tensão de linha na saída do inversor:

Quadro 1 – Sequência de comutação das chaves e as respectivas tensões de linha na saída do inversor.

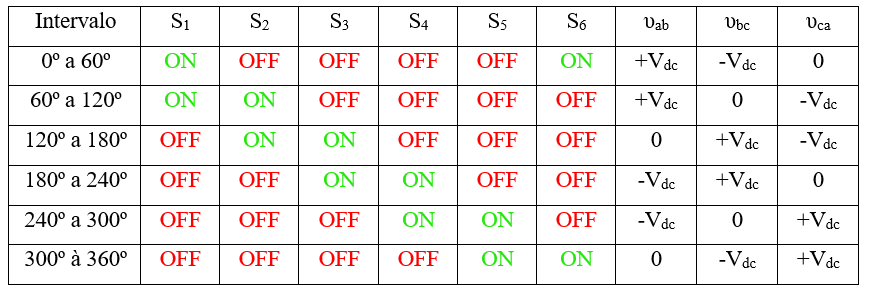
Na Figura 3, é possível ver a forma de onda das tensões de linha e de fase para o inversor da Figura 1 disparado pela técnica de 6 pulsos.

Figura 3 – (a) Tensões de linha na saída do inversor. (b) Tensões de fase na carga conectada em Y.

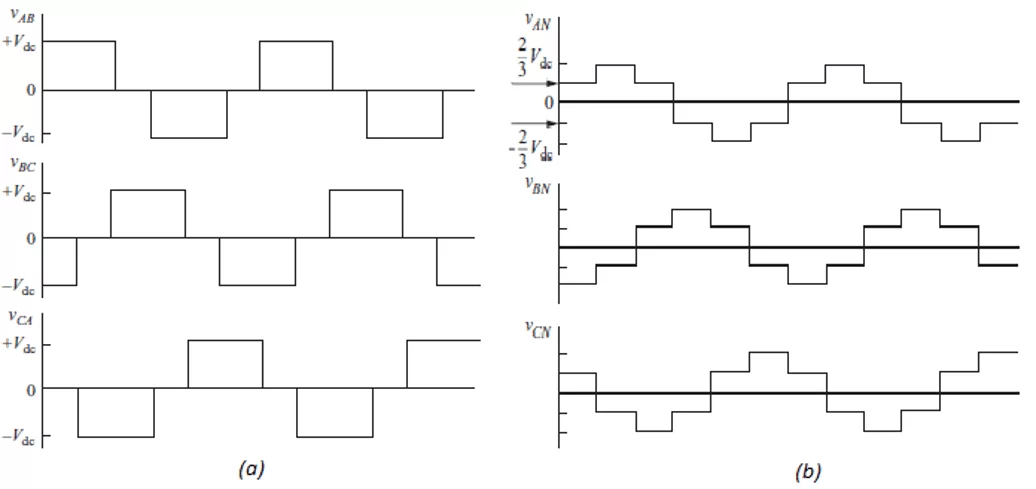
Através da análise da Figura 3 e do Quadro 1, é possível observar que a única forma de alterar os valores rms – root mean square da tensão na saída do inversor é através do controle da tensão V_dc, opção que em muitos casos não está disponível (por exemplo quando a tensão DC é obtida por um retificador não controlado) (HART, 2010).

2.2 INVERSOR ACIONADO POR SPWM

Nesta seção será apresentado o método de acionamento de inversores SPWM.

No acionamento SPWM as chaves estáticas são controladas através da comparação de 3 ondas senoidais defasadas de 120º entre si (ondas de referência) com uma onda triangular de alta frequência (portadora). A frequência fundamental da tensão na saída do inversor é a mesma das ondas de referência e a amplitude da tensão é dada pela relação entre as amplitudes das ondas de referência com a da portadora (HART, 2010).

Como foi visto na seção anterior, o acionamento por 6 pulsos não possibilitava o controle da tensão rms no próprio inversor (dependia da alteração da amplitude da tensão DC). Sendo assim, o SPWM já representa esta enorme vantagem com relação ao acionamento de 6 pulsos. A outra grande vantagem está relacionada com a distorção harmônica presente na tensão de saída do inversor (RASHID, 1999).

Em seus trabalhos, HART (2010) apresenta um quadro contendo a sequência de acionamentos para cada condição de comparação entre as ondas de referência e a triangular. Este quadro pode ser visto a seguir:

Quadro 2 – Sequência de comutação das chaves em função da comparação das ondas senoidais com a onda triangular.

As ondas de referência e a portadora apresentam as seguintes funções:

Onde,

V_s é a amplitude das 3 senóides.

f_s é a frequência das 3 senóides.

V_tri é a amplitude da triangular.

T_tri é o período da triangular (e a frequência é dada por: ).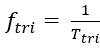                     

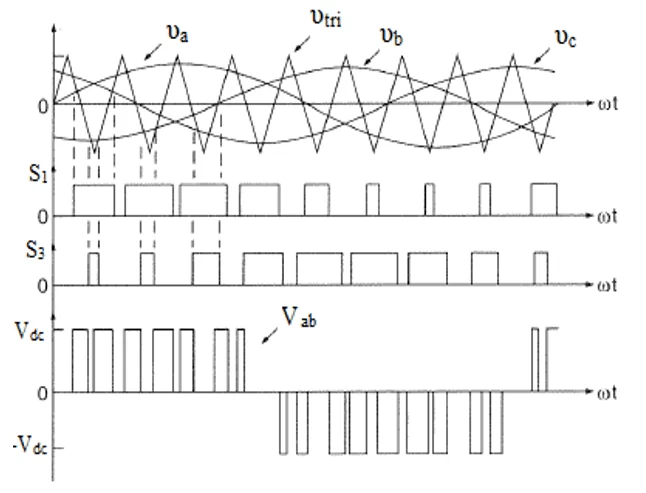
Na Figura 4, são apresentadas graficamente as comparações entre as ondas, bem como as sequências de pulsos geradas para as chaves S₁ e S₃ e a forma de onda da tensão de linha υ_ab, obtida na saída do inversor.

Figura 4 – Formas de onda da modulação por largura de pulso senoidal para o inversor de frequência trifásico.

O controle das grandezas da tensão de saída é realizado através da definição dos índices de modulação de amplitude m_a e frequência m_f (HART, 2010). A definição para esses dois índices é apresentada a seguir:

Índice de modulação de frequência m_f: A frequência fundamental da tensão de saída do inversor é igual a frequência da onda senoidal de referência. As harmônicas presentes na tensão ocorrem em torno da frequência de comutação das chaves estáticas, que por sua vez, é igual a frequência da portadora triangular. Usualmente, a frequência de comutação é muito maior do que a frequência fundamental, e desta forma, com a aplicação de simples filtros passa-baixa é possível reduzir significativamente a distorção harmônica na saída do inversor. Assim, o índice de modulação de frequência é dado pela relação entre a frequência de chaveamento e a frequência da fundamental (HART, 2010).

Índice de modulação de amplitude m_a: Este índice é definido como a relação entre a amplitude da senóide e a amplitude da triangular (HART, 2010).

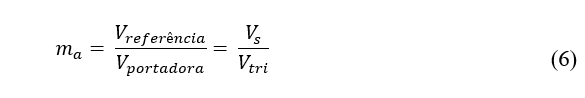Para valores de m_a ≤ 1, a amplitude da tensão de linha da saída é linearmente proporcional a m_a e ao valor da tensão DC que alimenta o inversor (MOHAN; UNDELAND e ROBBINS, 1995). A equação apresentada por Hart (2010), que permite calcular a amplitude da componente fundamental da tensão de linha na saída do inversor trifásico pode ser vista a seguir:

Em seus trabalhos, Mohan; Undeland e Robbins (1995) apresentam uma versão da equação (7) para a obtenção direta do valor rms.

As equações (7) e (8) mostram, que através das amplitudes das ondas de referência e da portadora, é possível controlar a tensão de linha na saída de um inversor trifásico para uma dada tensão DC disponível na entrada.

2.3 THD EM INVERSORES TRIFÁSICOS

Nesta seção será feita uma breve explicação da THD de inversores acionados por sequência de 6 pulsos e por SPWM.

Para o inversor de 6 pulsos, a série de Fourier da tensão de saída é dada pela equação (9), onde as harmônicas ocorrem em n = 6k ± 1 para k = 1,2,3… (n = 5,7,11,13…). Isto é, para este tipo de acionamento, não existem as harmônicas múltiplas de 3 nem as harmônicas pares (RASHID, 1999).

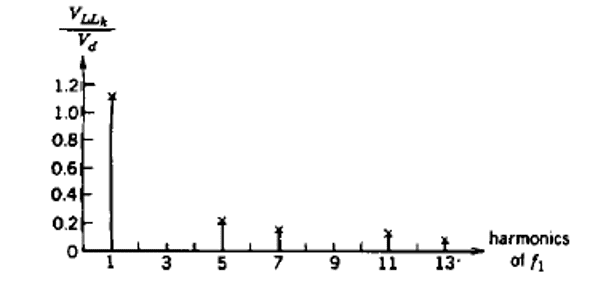
A Figura 5 mostra a representação de Fourier das amplitudes normalizadas em função da ordem das harmônicas de um inversor trifásico de 6 pulsos.

Figura 5 – Amplitudes normalizadas em função da ordem das harmônicas para um inversor trifásico de 6 pulsos.

Para o inversor SPWM, Hart (2010) demonstra que a série de Fourier da tensão de saída é dada pela equação (10).

Onde,

Onde,

A_n3 e B_n3 são os coeficientes da série de Fourier.

V_n é a amplitude da tensão da enésima harmônica de uma das fases.

V_n3 é a amplitude da tensão de linha na saída do inversor.

A Figura 6 mostra a representação de Fourier das amplitudes normalizadas em função da ordem das harmônicas de um inversor trifásico SPWM.

Figura 6 – Amplitudes normalizadas em função da ordem das harmônicas para um inversor trifásico SPWM.

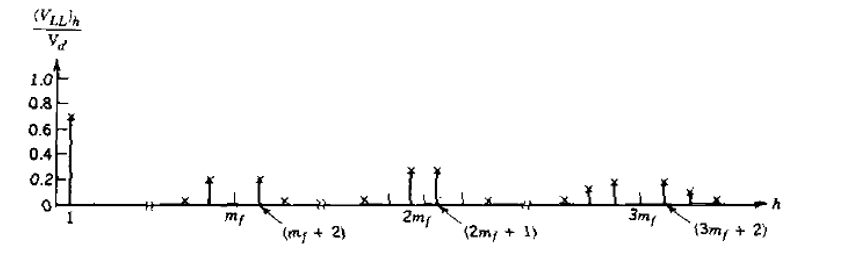
A principal observação a ser feita ao comparar as Figuras 5 e 6 é a localização das primeiras harmônicas após a frequência fundamental. Enquanto que no inversor de 6 pulsos a primeira harmônica ocorre em uma frequência 5 vezes maior que a fundamental, no inversor SPWM a primeira harmônica ocorre em uma frequência m_f – 2 vezes maior que a fundamental. Usualmente, a frequência de comutação é definida de 5 kHz à 20 kHz (MOHAN; UNDELAND e ROBBINS, 1995), o que implica em valores de m_f que vão de 85 até valores maiores que 330. Sendo assim, enquanto no inversor de 6 pulsos o processo de filtragem é muito difícil devido à proximidade da primeira harmônica com a fundamental, no SPWM a primeira harmônica se encontra a pelo menos 2 décadas acima da fundamental, o que permite uma filtragem a partir de simples filtros passa-baixa, que são suficientes para a grande maioria das aplicações (HART, 2010).

3. DESENVOLVIMENTO

3.1 IMPLEMENTAÇÃO DO DISPARO SPWM

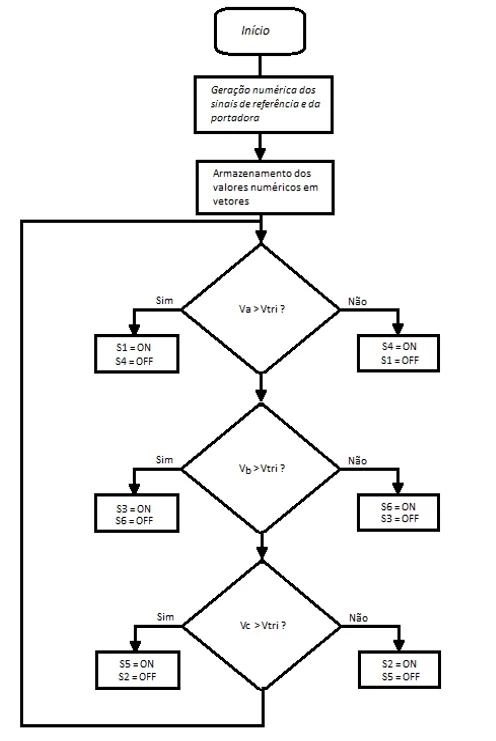
Para a realização das simulações, a primeira etapa consistiu da obtenção de um modelo SPWM em forma de código capaz de ser aplicado a diferentes plataformas de simulação. O software definido para o desenvolvimento do código foi o Matlab. O fluxograma simplificado pode ser visto na Figura 7.

Figura 7 – Fluxograma simplificado para geração do SPWM.

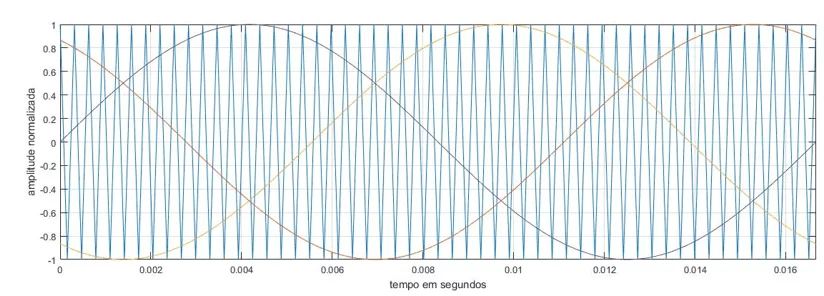
Na Figura 8, é possível observar em um mesmo gráfico o comportamento temporal dos sinais de referência e da portadora plotados através do Matlab. Destaca-se a diferença entre as frequências das ondas de referência e da portadora.

Figura 8 – Plotagem das ondas de referência e da portadora com m_a = 1 e m_f = 53.

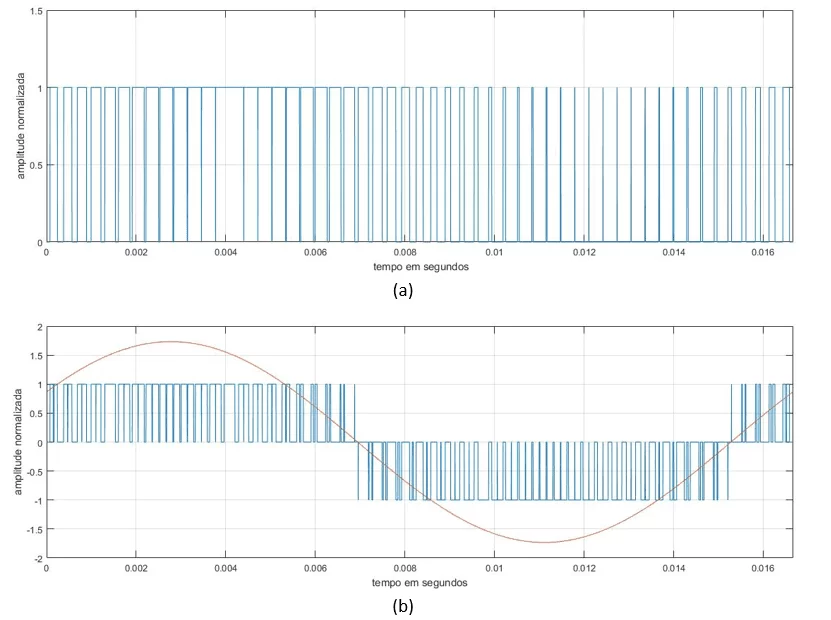
Tomando como exemplo a comparação entre υ_a e υ_tri, é possível obter a sequência de pulsos para as chaves S₁ e S_4. A subtração das sequências de pulsos de duas chaves de braços diferentes nos fornece a forma de onda da tensão de linha na saída de um inversor trifásico. Na Figura 9, é possível ver a sequência de pulsos para a chave S₁ e a forma de onda da tensão de linha V_ab (obtida da subtração das sequências de pulsos de S₁ e S₃).

Figura 9 – (a) Sequência de pulsos para a chave S₁. (b) Forma de onda da tensão V_ab na saída do inversor (em azul), em comparação com uma onda senoidal perfeita (em vermelho).

3.2 SIMULAÇÃO DAS THDs DAS TENSÕES DE SAÍDA DOS INVERSORES

A Figura 10 (a) apresenta o circuito básico de um inversor acionado por sequência de 6 pulsos que foi implementado e simulado no software PSIM. Na Figura 10 (b), podemos ver o seu respectivo espectro de Fourier da tensão de saída com frequência fundamental de 60 Hz, plotado também a partir do software PSIM.

Figura 10 – (a) Inversor de frequência acionado por sequência de 6 pulsos, (b) o espectro de Fourier da tensão de saída.

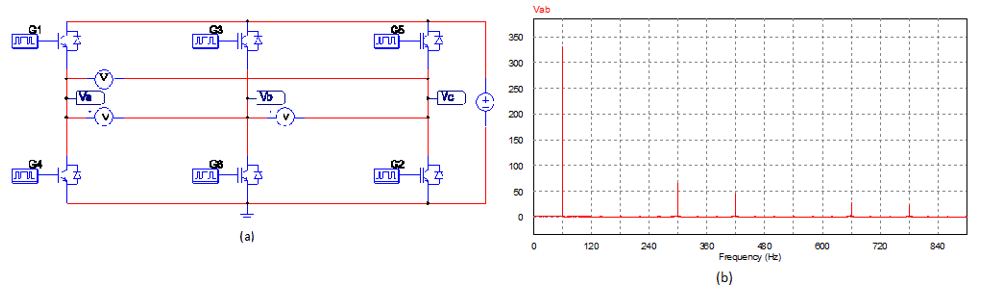
A THD calculada pelo software PSIM para o espectro da Figura 10 (b) foi de: 0.3112.

Na Figura 11, é apresentado o espectro de Fourier da tensão de saída do mesmo circuito inversor, porém acionado pelo SPWM. A frequência fundamental é 60 Hz.

Figura 11 – Espectro de Fourier da tensão de saída do inversor SPWM da Figura 10

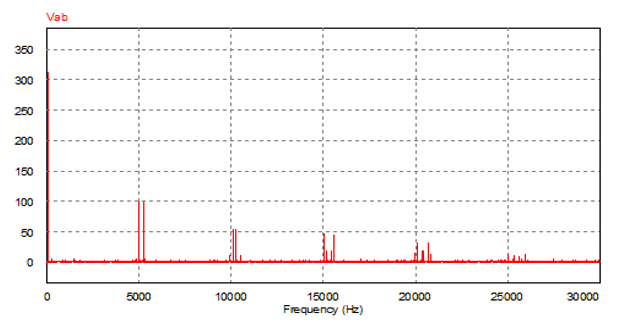
A THD calculada pelo software PSIM para o espectro da Figura 11 foi de: 0.6908.

Comparando as Figuras 10 e 11, é possível observar, que a THD do inversor acionado pelo SPWM, foi maior que o inversor de 6 pulsos, porém a localização da primeira harmônica para o caso do SPWM ocorre em 4980 Hz, enquanto que para o caso de 6 pulsos ocorre em 300 Hz. Isso comprova que é muito mais fácil implementar filtros para o inversor SPWM do que para o inversor de 6 pulsos.

3.3 SIMULAÇÃO DAS THDs DAS CORRENTES DE SAÍDA DOS INVERSORES ALIMENTANDO UMA CARGA RL

Para realizar a análise comparativa das THDs nas correntes de saída dos inversores, foi conectada uma carga de caráter RL (motor) nas saídas dos inversores. Na Figura 12, são apresentadas as formas de onda das correntes em regime permanente nas saídas de um inversor de 6 pulsos e de um inversor SPWM e seus respectivos espectros de Fourier. As simulações foram realizadas com ambos os inversores conectados à mesma carga.

Figura 12 – Forma de onda da corrente na saída de um inversor de 6 pulsos (a), e seu respectivo espectro de Fourier em (b). Forma de onda da corrente de saída de um inversor SPWM (c), e seu respectivo espectro de Fourier (d).

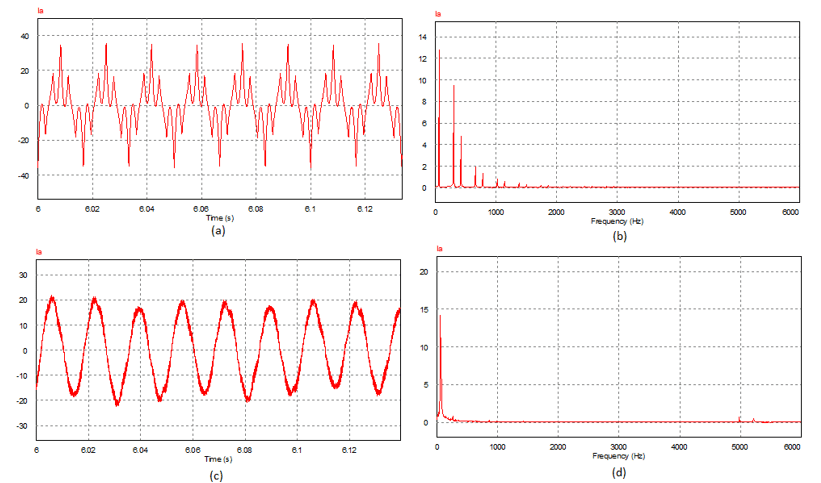
Através da Figura 12, é possível observar, que a distorção harmônica na corrente de saída do inversor SPWM é muito menor do que no inversor de 6 pulsos. Isso é facilmente explicado pela atenuação das harmônicas de alta frequência devido à indutância. Em outras palavras, a impedância de um motor atua como um filtro passa-baixa natural (LISERRE; BLAABJERG e HANSEN, 2005).

4. RESULTADOS DAS SIMULAÇÕES

As simulações das distorções harmônicas na seção anterior demonstraram, que para muitas aplicações, o SPWM pode ser empregado sem a necessidade da implementação de filtros na saída do inversor (Figura 12). Vale ainda ressaltar, que nos casos em que é exigido uma THD extremamente baixa na corrente, o processo de projeto e construção dos filtros é simplificado pelo fato de que, usualmente, a primeira harmônica da tensão de saída de um inversor SPWM ocorre em uma frequência no mínimo 85 vezes maior que a fundamental.

5. CONCLUSÃO

A partir das simulações realizadas e das análises dos resultados, é possível concluir que os inversores disparados pela técnica SPWM apresentam larga vantagem com relação ao valor de frequência onde estão localizadas as primeiras harmônicas presentes no sinal de saída. Em termos quantitativos, enquanto que no inversor disparado pela técnica de 6 pulsos podemos encontrar harmônicas cujo valor é 5 vezes o valor da fundamental, no caso do SPWM esse valor pode variar entre 85 e 330 vezes o valor da fundamental (definido de acordo com as especificações do projeto). Essa distância nas frequências das harmônicas implica que o processo de filtragem afim de obter um sinal puramente senoidal na carga é muito mais simples no SPWM do que na sequência de 6 pulsos. Isso pôde ser facilmente visto a partir dos resultados obtidos nas simulações das correntes de saída ao alimentar uma carga RL.

As correntes do SPWM apresentaram uma THD muito inferior às do disparo de 6 pulsos, mostrando que o próprio circuito RL atua como um filtro passa-baixa, extinguindo-se assim a necessidade de implementação de filtros em casos onde há um nível razoável de tolerância à THD.

O SPWM ainda conta com a vantagem de permitir o controle do valor de tensão da saída do inversor, atributo que não pode ser realizado na técnica do disparo de 6 pulsos.

Como desvantagem da técnica SPWM, temos um custo computacional para implementação prática mais elevado do que o disparo de 6 pulsos, fazendo com que os circuitos digitais de controle necessitem ser ligeiramente mais robustos e velozes.

REFERÊNCIAS

AHMED, ASHFAQ. Eletrônica de Potência. Tradução de Eduardo Vernes Mack. 1ª. ed. São Paulo: Prentice Hall, 2000.

HART, D. W. Power Electronics. 1ª. ed. Valparaiso: McGraw-Hill, 2010.

LISERRE, M.; BLAABJERG, F.; HANSEN,. Design and Control of an LCL-Filter-Based Three-Phase Active Rectifier. IEEE Transactions on Industry Applications, v. 41 Setembro/Outubro 2005. 11.

MOHAN, NED; UNDELAND, TORE M.; ROBBINS, WILLIAM P. Power Electronics Converters, Applications and Design. 2ª. ed. [S.l.]: John Wiley & Sons, Inc, 1995.

RASHID, MUHAMMAD H. Eletrônica de Potência Circuitos, Dispositivos e Aplicações. Tradução de Carlos Alberto Favato. 1ª. ed. São Paulo: Makron Books, 1999.

^[1] Engenheiro Eletricista.

Enviado: Janeiro, 2021.

Aprovado: Janeiro, 2021.