ОРИГИНАЛЬНАЯ СТАТЬЯ
SOUZA JÚNIOR, Elias Pereira De [1]
SOUZA JÚNIOR, Elias Pereira De. «Разница между квадратами» в теореме Пифагора. Revista Científica Multidisciplinar Núcleo do Conhecimento. Год 05, изд.10, том 06, стр. 05-13. Октябрь 2020 г. ISSN: 2448-0959, ссылка для доступа: https://www.nucleodoconhecimento.com.br/математические-олимпиады/теореме-пифагора
АБСТРАКТНЫЕ
Эта статья направлена на то, чтобы показать приложения содержания теоремы Пифагора в построении знаний в классе, уделяя особое внимание алгебраической технике для «разницы между квадратами». Во-первых, в статье исследуется введение и применение теоремы Пифагора в качестве нового содержания в классе в рамках контекстуализированного примера. Таким образом, теорема была продемонстрирована учителем, и учащиеся задавались вопросом и обосновывали альтернативные методы получения результатов в дополнение к продемонстрированной классической теореме Пифагора. Вскоре стали появляться некоторые методы, возможности разрешений для исходного примера, одной из таких форм было геометрическое понятие теоремы, однако студенты продолжили свои исследования. Важнейшей частью класса было рассуждение алгебраической процедуры, которая привлекла внимание по-другому во время исследований студентов, это была «разница между квадратами» как решение теоремы в наборе натуральных чисел, поскольку не все наборы числовые отвечали соотношению. И на этом этапе для учащихся создаются размышления о том, как изучать математику и исследовать ее различными способами, поскольку цель заключалась в том, чтобы исследовать разнообразие математики и обострить чувствительность учащихся, чтобы делать новые открытия. Теорема Пифагора хорошо известна и применяется, ее можно легко найти в различной математической литературе, но научить студентов преодолевать формулы и процедуры – значит научить думать.
Ключевые слова: образование, моделирование, обучение, Пифагор, обучение.
1. ВВЕДЕНИЕ
Тема, представленная в этой статье, была выбрана благодаря опыту, накопленному в классе, который был направлен на изучение способов соотнесения и применения теоремы Пифагора в ее алгебраической и геометрической форме в соответствии с изучением треугольников с акцентом на прямоугольный треугольник, изучением идея теоремы Пифагора с точки зрения студента, таким образом сумев сформировать различные возможности для решения проблем, связанных с теоремой, в том числе «разница между квадратами.
Тем не менее, в этой статье также делается попытка рассказать об опыте, полученном в школе, путем сбора информации и наблюдаемых расчетов, стремясь понять важность конструирования знаний учащимся, таким образом меняя процесс преподавания и обучения. Потому что при формировании знаний студентов становится незаменимым направлять, исследовательскую или даже игровую практику в классе, в которой считается, что из этой практики возникают проблемы, сомнения или уверенность, если это тот путь, по которому студент хочет идти. Следуйте, как делать и чего не делать, чтобы продолжить, таким образом ища идеальное понимание в решении проблем. В этом классе 36 учеников первого класса старшей школы приняли участие в классе «А» Colégio Sagrada Família, Brasília DF.
Таким образом, к теореме Пифагора применяется несколько перспективных исследований. Затем будет показано простое предложение, в котором теорема интерпретируется, связывая ее с разностью квадратов. Таким образом, получается интересный факт, который нужно показать, в том числе с точки зрения образования.
1.1 ПРЕДЛОЖЕНИЕ КЛАССА И ТЕОРЕМА ПИФАГОРА
Подстрекать ученика к поиску решения проблемы или даже поощрять исследования в классе различными способами и возможностями – значит использовать другую методологию, то есть применять математическое моделирование. Следовательно, это скоро делает класс полем исследований и практики, более интересным и привлекательным местом для студентов, и имеет решающее значение.
Математическое образование выходит за рамки традиционного, оно предполагает инновации за счет разнообразия действий, позволяющих использовать бесчисленные методы преподавания и обучения. Поскольку ставить перед учеником задачу находить решения проблем в одиночку, значит открывать возможности для новых открытий, подобно тому, как математика открывается в различных применимых контекстах, D’ambrosio (1998) говорил об упомянутых выше идеях.
Итак, предложение, сделанное студентам, было основано на следующей задаче: лестница длиной 12 метров поддерживается под стеной. Основание лестницы находится на расстоянии 8 метров от стены, как показано на рисунке ниже. Затем учеников попросили определить высоту стены.
Рисунок 1: применение прямоугольного треугольника

Интуитивно ученикам было предложено попытаться найти значение измерения стены, используя фундаментальное определение для любого треугольника, содержание, которое уже изучалось в предыдущие годы, служащее основой для введения другого содержания. В общем, для построения треугольника можно проверить условие существования треугольников, при котором мера любой стороны меньше суммы мер двух других и больше абсолютного значения разницы между ними. мерки, нанося геометрический узор. Наблюдается следующая закономерность:
Рисунок 2: Условие существования треугольника
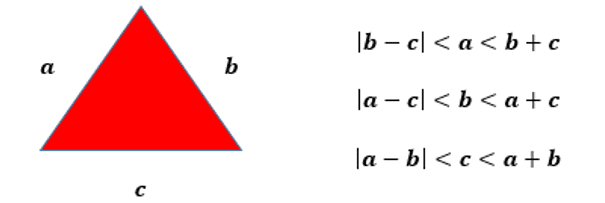
Студенты пришли к некоторым возможным и подходящим значениям для расчета меры лестницы как одной стороны треугольника. Однако для применения теоремы Пифагора необходимо, чтобы треугольник имел хотя бы один из углов, равных 90°. Поэтому следующим шагом было продемонстрировать теорему Пифагора.
1.2 ДЕМОНСТРАЦИЯ ТЕОРЕМЫ ПИФАГОРА
В процессе обучения после первоначального исследования треугольников и их существования следующим шагом было обострить любопытство студентов, чтобы формализовать некоторые курьезы и первоначальные выводы. Итак, в этой части класса ученики соединили несколько квадратов со своими соответствующими областями, пытаясь найти закономерности при посредничестве учителя. Вскоре ученики начали видеть свойства, которые Пифагор использовал для теоремы, основанной на сумме площадей многоугольников, образующих фигуру, построенную из конгруэнтных прямоугольных треугольников, то есть для сравнения площадей, как показано ниже. цифры.
Рис.3.Демонстрация теоремы Пифагора.
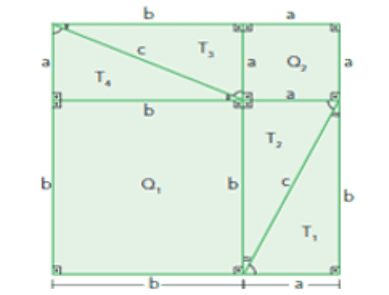
Рис.4.Демонстрация теоремы Пифагора.
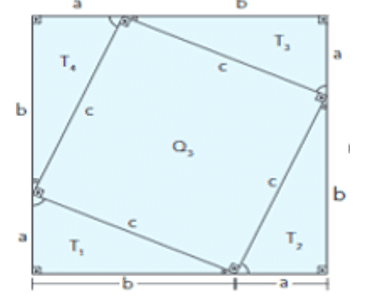
Учтите, что две наименьшие стороны треугольника называются коллекторами, а самая длинная сторона прямоугольного треугольника – гипотенузой. Обратите внимание, что фигуры были построены с использованием четырех совпадающих прямоугольных треугольников, равных «a» и «b», и гипотенузы «c», образующих квадраты большего размера со сторонами, равными (a + b). Если удалить четыре равных прямоугольных треугольника двух фигур, оставшиеся фигуры будут иметь такую же площадь. Следовательно, есть
На рисунке 3:
- Сумма площадей четырех прямоугольных треугольников = (T1 + T2 + T3 + T4)
- Оставшаяся площадь Q1 + Q2 = a2 + b2
На рисунке 4:
- Сумма площадей четырех прямоугольных треугольников = (T1 + T2 + T3 + T4)
- Оставшаяся площадь = Q3 = c2
Итак, c2 = a2 + b2
Это отношение можно применить к любому прямоугольному треугольнику. «C» – это наибольшая сторона треугольника, называемого гипотенузой, «a» и «b» – стороны треугольника, как показано выше.
1.3 ВОЗОБНОВЛЕНИЕ НАЧАЛЬНОГО ПРИМЕРА
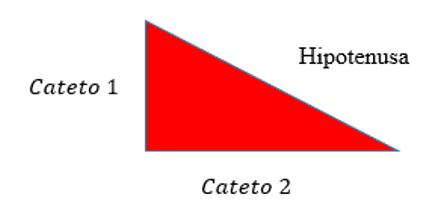
После демонстрации теоремы студентам стало ясно, что речь идет о применении теоремы Пифагора, в которой стороны называются катетерами, а наибольшая сторона треугольника, противоположная углу, называется гипотенузой. Таким образом, отношения Пифагора можно записать так:
(Гипотенуза) ² = (Катето 1) ² + (катето 2) ²
Рисунок 5: прямоугольный треугольник
Следовательно:
Студенты применили приведенный выше список следующим образом:
- Гипотенуза эквивалентна лестнице (12 м).
- Расстояние между лестницей и стеной – ножка (8 м)
- Высота стены – это другая сторона, в данном случае «x».
применяя теорему:
![]()
Вычитая 8² из обеих частей равенства
![]()
![]()
В этот момент ученик задал вопрос о вычитании квадратов: – «Можем ли мы решить это вычитание только после решения квадратов?»
Отсюда и начались исследования других способов вычитания квадратов.
1-е решение:
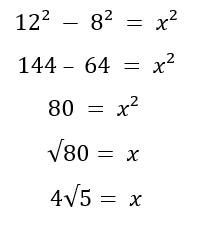
2-е решение:
За закономерностью учитель наблюдал вместе с учениками. Смотри ниже:
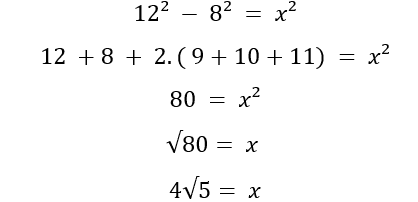
На этом этапе была замечена закономерность разницы между квадратами, в которых числа принадлежат множеству натуральных чисел, в форме
![]() .
.
Пример:
a = 23 и b = 19, применяя …
Сдача теста:
![]()
Равенство верно для чисел
![]()
После тестирования операций с множеством натуральных чисел, он также был применен к некоторым другим наборам, таким как множество целых чисел, которые также работали, и действительные числа, которые в последнем случае некоторые числа не смогли установить истинное равенство, таким образом зафиксировав это приложение для натуральных чисел.
2. ПОДТВЕРЖДЕНИЕ ОТНОШЕНИЙ
Соотношение разницы между квадратами:
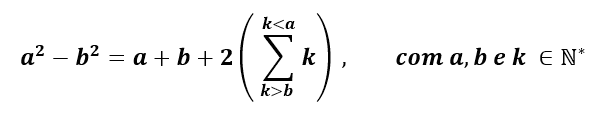
Учитывать
a2 + b2, где a и b принадлежат натуральным числам больше нуля, учитывая, что a > b, мы имеем следующее утверждение для a и b:
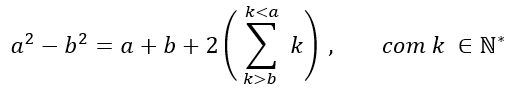
Скоро, если
![]()
потом
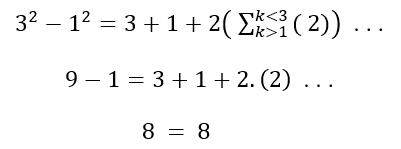
Теперь, рассматривая m как любое натуральное число.
Если a и b истинны, для a и b ∈
![]()
, то a = b + m, также будет истинным при m ∈
![]()
Принимая m = 1, для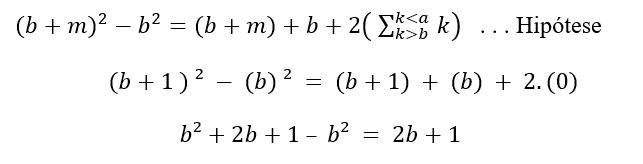
Скоро,
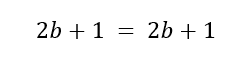
Следовательно, отношения
![]()
, действует для любого
![]()
Как я хотел продемонстрировать!
Эта демонстрация была незамедлительно показана студентам, которые были удивлены тем приложением, которое они придумали, таким образом обнаружив иное отношение к теореме Пифагора в «разнице между квадратами».
3. ЗАКЛЮЧЕНИЕ
Цель побудить студентов находить различные способы решения проблем – накапливать знания, используя уже приобретенные компетенции и навыки, обеспечивая основу для нового обучения и открытий. Эта статья является примером этого, так как основные инструкции были даны учителем, и студенты изучали способы решения проблемы.
Что делает его более интересным, так это то, что в процессе расследования может быть несколько способов достичь результата. Видение этих путей и руководство ими делают математическое образование другим и приятным для студентов, что оправдывает математическое моделирование.
Затем, следуя применению теоремы Пифагора в начальном примере, учитель со студентами обсуждали способы решения разницы между квадратами, всегда давая понять, что построение знаний является фундаментальной частью класса, а учитель – это посредник и студенты делают открытия.
В одном из процессов, в котором ученик поднял вопрос о вычислении разницы между квадратами при решении задачи, класс с учителем смог заявить, что наблюдаемый метод вычитания квадратов действителен в некоторых важных моментах.
Таким образом, учитель продемонстрировал применимость операции, обнаруженной в наборе натуральных чисел, решив вопрос о применимости операции, сделав метод понятным для ученика и класса. Вскоре мы закрыли вопрос и решили другие примеры с помощью обнаруженного метода. Студент вернулся в класс со следующей строкой: «Мы открыли новую формулу, и это круто», для учителя точных слов нет возможности сделать линию более яркой, чем эта.
Студент попросил совета для изучения сумм и демонстраций. То, что мальчик из первого класса средней школы, дальнейшее развитие этого ученика я оставляю в воображении тех, кто читает эту статью.
4. ССЫЛКИ
DANTE, Luiz Roberto. MATEMÁTICA: Contexto e Aplicações volume único / Luiz Roberto Dante, Fernando Viana – – 4. Edição – – São Paulo: Ática, 2018.
HEFEZ, Abramo. Indução Matemática:\induçãofinal”. Estilo OBMEP – Rio de Janeiro – Departamento de Matemática Aplicada Universidade Federal Fluminense, 2009. Disponível em: http://www.obmep.org.br/docs/apostila4.pdf. Acesso em: 04 maio de 2020. D’Ambrósio, U.Etnomatemática. São Paulo: Ática, 1998.
SANTOS. Marconi Coelho dos. Teorema de Pitágoras: suas diversas demonstrações. Campina Grande (PB):UEPB, 2011. 42f. Monografia (Especialização em Educação Matemática para professores do Ensino Médio) {Universidade Estadual da Paraíba, Centro de Ciências e Tecnologia, Campina Grande, 2011.
VIANA, M. C. V.; SILVA, C. M. Concepções de Professores de Matemática sobre a utilização da História da Matemática no processo de Ensino-Aprendizagem. In: ENCONTRO NACIONAL DE HISTÓRIA DA MATEMÁTICA, 9., 2007, Belo Horizonte. Pôsteres… Belo Horizonte, 2007. Disponível: https://www2.unifap.br/matematicaead/_les/2016/03/TCC-REVISADO.pdf Acesso em: 04 maio de 2020.
[1] Аспирантура по математике.
Поступило: сентябрь 2020 г.
Утверждено: октябрь 2020 г.