ОРИГИНАЛЬНАЯ СТАТЬЯ
SOUZA, Nathan Rodrigues Serpa [1]
SOUZA, Nathan Rodrigues Serpa. Новая математическая формулировка процесса молекулярной диффузии и электродиффузии в клеточных мембранах. Revista Científica Multidisciplinar Núcleo do Conhecimento. Год 06, эд. 04, Vol. 15, стр. 34-63. Апрель 2021 года. ISSN: 2448-0959, Ссылка доступа: https://www.nucleodoconhecimento.com.br/fisica-ru/молекулярной-диффузии
СВОДКА
Молекулярная диффузия – это физико-химическое явление, наблюдаемое в повседневной жизни, когда простые парфюмерные газы распространяются через закрытую комнату, а также в микроскоп, поглощение ионов растениями и животными клетками через открытые ионные каналы плазматической мембраны. В этой физической статье предлагается формулировка нового уравнения, названного автором «Уравнения Nathan», как расширения известного 1-го закона Fick, который направлен на описание естественного явления диффузии как функции переменной Результирующей силы. Системы, которая позволит провести общий анализ действующих сил, которые могут влиять на это явление, а также расширить эту формулировку для описания транспорта ионов через клеточную мембрану, формулировку, названную «Уравнение Nathan для электродиффузии в клеточных мембранах». Благодаря исследовательскому методу, библиографическим исследованиям и математическим инструментам стало возможно выполнять такие формулировки, а также интерпретировать их. Из анализа размерностей и постулатов, предложенных 1-м законом Fick и законом Graham для диффузии, в форме графиков, основанных на экспериментальных и гипотетических данных для сравнения сходства графических кривых, можно было подтвердить математическую и физическую валидацию для такое уравнение, демонстрирующее сохранение единиц и положительное согласие с постулатами, представленными этими другими законами, уже установленными в физико-химической среде.
Ключевые слова: Диффузия, Клеточная мембрана, Закон Fick, Уравнение Nathan, Электродиффузия.
1. ВСТУПЛЕНИЕ
Молекулярная диффузия является физико-химическим явлением, наблюдаемым изо дня в день, как простые газы духов, расширяющихся через закрытую комнату, а также микроскопически, поглощение ионов овощами и животными клетками, через ионные каналы плазменной мембраны. Этот транспортный процесс состоит из спонтанного и необратимого движения молекул, расположенных в регионах высокой концентрации (гипертонической) к другим с более низкими концентрациями (гипотоническими), движущей силой для этого являются химические или тепловые потенциалы раствора, а в случае клеточных мембран электростатические силы вместе (DA SILVA, 2013).
По словам Alberts (2009), мембрана представляет ткани амфифилического характера, образованные фосфатипидов с полярным концом (радикальный фосфат) и другой неполярной (жирный кислотный хвост). Некоторые полярные или заряженные молекулы, такие как ионы, испытывают трудности при переходе путем простого диффузии к липидному билейзеру, смещения, сделанного через транспортировку белков или белков для канала, таких как ионные каналы. Помимо представления полярности между внеклеточными носителями с накоплением положительных зарядов и внутриклеточной средой с накоплением отрицательных зарядов, ведя себя как Единое электрическое поле (MOREIRA, 2014).
Эта исследовательская статья, с методом теоретически-математического анализа, направлена на создание новой математической формулировки для описания процесса молекулярной диффузии и ионной транспортировки по ионическим каналам клеточных мембран, которая учитывает результирующую силу системы (FR),которая позволит общий анализ действий частиц. Предложения подвергаются были в качестве теоретической основы заседании диверсифицированной библиографической коллекции, в области биологических, химических и физических наук, а также анализ их предложений из физического и математического понимания результатов, в рамках спектра других законов, которые описывают определенный аспект того же явления в исследовании, таких, как: Закон Fick и закон Graham.
2. РАЗРАБОТКА
2.1 МАТЕРИИ И МЕТОДЫ
Эта статья исследовательской предвзятости направлена на создание математических формулировок для описания процесса молекулярной диффузии и потока ионов через открытые ионные каналы клеточных мембран, благодаря не только градиенту концентрации или электрическому потенциалу мембраны, но и учету постоянных сил, действующих в целом, математические формулировки, которые они называют автором : Уравнение Nathan и уравнение Nathan для электродиффузии в клеточных мембранах.
Для математической конструкции, коллекция библиографического материала различных наук имеет большое значение, таких как: Клеточная биология, химия и физика. В дополнение к материальному обзору, после математической конструкции, был проведен размерный анализ уравнения для проверки сохранения единиц и их действительности, а также их положительный или отрицательный ответ о постулатах законов Fick и Graham для описания процесса диффузии, основанного на графиках, основанных на экспериментальных и гипотетических данных , для того, чтобы сравнить графики, созданные из математических отношений. Используемые знания будут раскрыты ниже:
2.2 БИОЛОГИЧЕСКОЕ РАЗВИТИЕ
Клетки организованы на три части: плазменную мембрану, цитоплазму и ядро. Один из фокусов этой научной работы заключается в понимании первичного отсека, клеточной мембраны, с приблизительно 8 нанометров (нм) или 8 х 10-9 метров (м), наблюдаемых с помощью электронного микроскопа света. Мембрана не полностью проницаема, состоящая из ее основной функции, является селективной барреей, позволяющей разъедино, а также обменом веществами между экстра и внутриклеточными средствами массовой информации (JUNQUEIRA и CARNEIRO, 2012).
Однако его селективная проницаемость обусловлена химико-структурным составом клеточных мембран, состоящим из двуслойного фосфолипида, белков и углеводов. Фосфатипиды являются амфифилическими тканями, т.е. содержащими полярные и неполярные части, гидрофильная головка (радикальный фосфат) сталкивается с внешней стороной клетки, образуя электростатическое взаимодействие с полярными молекулами воды. Его гидрофобная область состоит из длинных аполярных цепей жирных кислот, которые могут легко взаимодействовать с другими липорастворимыми веществами, из которых более выгодно иметь хвост лицом к внутриклеточной области. Таким образом, не все вещества способны пересекать клеточную мембрану и проникать в клетку путем простой диффузии, однако, такой транспорт диффузии облегчается путем переноски или ионных белков, когда они открыты (ALBERTS, 2009).
2.3 ХИМИЧЕСКАЯ РАЗРАБОТКА
По словам Taiz и Zeiger (2006), диффузия является явлением транспорта материи, в котором есть поток частиц из регионов с более высокими концентрациями в регионы с более низкими концентрациями, с целью содействия равновесному государству или также называется гомеотазы. Математическое описание такого процесса выражается в Первом законе Fick, предложенном врачом и физиологом Adolf Eugen Fick (1829 –1901), дифференциальное уравнение, в котором плотность потока (J) прямо пропорциональна Градиенту концентрации ( ![]() ), и Коэффициенту диффузии (D), который зависит от рассматриваемого химического элемента, как уровень ниже (см. уравнение 2.1):
), и Коэффициенту диффузии (D), который зависит от рассматриваемого химического элемента, как уровень ниже (см. уравнение 2.1):

Этот гомогенизирующий поток является статистическим следствием случайного движения частиц, известного как Броуманское движение, спонтанно молекулы перемещаются из гипертонической области (высшие концентрации) в гипотонические области (Нижние концентрации). Отрицательный знак в Законе Fick указывает на то, что поток происходит в противоположном направлении к градиенту концентрации, будучи линейным законом, независимо от того, насколько разница в концентрации между двумя точками, поток остается пропорциональным градиенту.
Другие важные детали о Законе Fick следующие: Отношения, прямо пропорциональные области диффузии (A) и обратно пропорциональные между размером частицы и скоростью диффузии, или ее молекулярной массы (M). То есть чем больше площадь, тем выше транспортный сбор; а также, чем ниже молекулярная масса частицы, тем выше будет ее транспортная скорость и тем быстрее будет ее скорость диффузии.
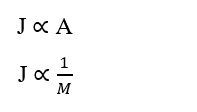
Согласно Brady и Huminston (1995), закон Graham (см. Уравнение 2.2), сформулированный химиком Thomas Graham (1805-1869) после его исследований диффузии и излияния жидкостей, устанавливает, что Скорость (u) излияния и диффузии два газа (δ1) и (δ2) при одинаковых условиях температуры и давления обратно пропорциональны корню квадратному из их плотностей (d) или молекулярной массы (MM), как указано ниже:
![]() или же
или же ![]()
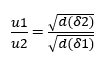
или же

2.4 ФИЗИЧЕСКОЕ РАЗВИТИЕ
Одной из основных концепций этой статьи является известный «Фундаментальный принцип динамики» или «Второй закон Newton», в котором говорится: полученная сила, которая действует под телом, является продуктом его массы путем ускорения (FR = m. a). Halliday (2016) заявляет, что он должен сначала выбрать орган, который хочет изучить, и применить полученную силу в качестве суммы всех сил, которые действуют в этом органе.
Согласно Tipler (2009), Труд (W) — это энергия, передаваемая объекту через силу, которая действует на сам объект. Для расчета работы, выполняемой силой на объекте, когда он подвергается смещению, мы используем только силовой компонент, параллельный смещению объекта, силовой компонент перпендикулярно смещению не выполняет работу. Работа (W) постоянной силы, как функция параллельных сил (θ = 0°, 180°), может быть описана через это уравнение:
W = F. d. cosθ
Нравиться [ Cos(0°, 180°) = 1 ]; можно переписать уравнение работы в интегральной форме или в качестве функции Вариации расстояния ΔX (см. уравнение 2.3), у нас есть:

По словам Halliday (2016), энергию трудно определить. Тем не менее, мы интуитивно понимаем, что такое энергия, анализируя эффекты в различных ее формах, таких как: Кинетическая энергия и потенциальные энергии. Концептуально для Tipler (2009), Кинетическая энергия связана с любыми телами, которые имеют массу и движутся. Быть (м) массой материальной точки и (u) ее масштабной скоростью, по отношению к данной ссылке. Кинетическая энергия материальной точки дается (см. уравнение 2.4):

Для равномерно разнообразного движения, работа полученной силы телом также является кинетической энергетической вариацией самого тела. Из Теоремы Работы-Энергии (W = ΔK) мы можем получить выражение, равное работе постоянной силы (W), с Вариацией Кинетической Энергии (ΔK), о чем свидетельствуют уравнения (2,5) и (2,6):

Равномерно разнообразное движение, согласно Marques (2016), одно в котором частица изменяет скорость (u0) к другому (u) из-за постоянн силы которая способствует ускорению (a) также постоянн, также производящ водоизмещение (ΔX). Этот тип движения можно приравнять без учета времени, так называемого «Уравнения Torricelli» (2,7):

Согласно Pimentel (2004), движущей силой диффузных процессов в клеточной жидкой среде, является так называемый химический потенциал любого раствора, который настроен как способность такого решения выполнять работу под растворенными частицами, по отношению к градиенту концентрации, формулировка для максимального химического потенциала воды будет (2.8):
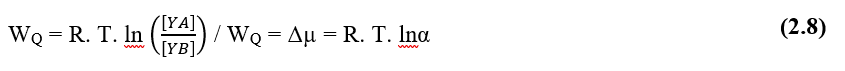
WQ – Химический потенциал решения (J)
R – Общая газовая постоянная (R = 8,31 J Mol-1 K-1)
T – Абсолютная температура (K)
[ YA ] – Концентрация вещества Y в точке А (Mol)
[ YB ] – Концентрация вещества Y в точке B (Mol)
![]()
α – Химическая активность
3. РЕЗУЛЬТАТЫ И ДИСКУССИИ
3.1 РАЗВИТИЕ УРАВНЕНИЯ NATHAN
В попытке математически описать процесс диффузии и транспортировки ионов через ионные каналы в плазменной мембране, как функцию концентрационного градиента и электрического поля, генерируемого во внеклеточных и внутриклеточных концах мембраны, мы рассмотрим систему координат x, y и z, в которой каждая ось представляет свое соответствующее ускорение, генерируемое активными силами в изолированной системе, изучаемой (ax, ay e az), как показано на рисунке 1.
Рисунок 1: Координация системы (X, Y, Z).
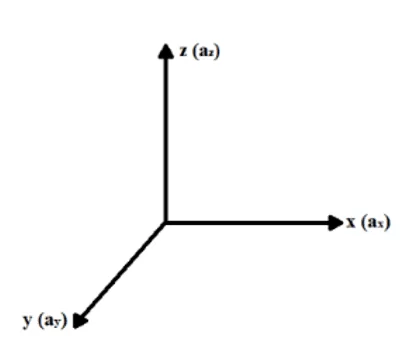
Согласно Halliday (2016), результирующая сила, действующая на такую частицу, как ионы, которые пересекают мембрану через ионные каналы, может быть разложена на ее компоненты по каждой оси x, y и z, которые напрямую связаны с ускорениями в соответствующие оси. С помощью фундаментального принципа динамики или Второго закона Newton и принципа суперпозиции сил можно получить физический анализ результирующих сил на каждой оси, которые влияют на ион (см. Уравнение 3.1):

FR – Общая результирующая сила (N – Kg m s-2)
FR(X) – Результирующая сила по оси X (N – Kg m s-2)
FR(Y) – Результирующая сила по оси Y (N – Kg m s-2)
FR(Z) – Результирующая сила по оси Z (N – Kg m s-2)
Массы ионов сохраняются, поэтому факторы, прямо пропорциональные силам в каждом направлении, являются их ускорениями в соответствующих направлениях:
FR(X) = m . ax / FR(Y) = m . ay / FR(Z) = m . az
Сравнение электростатических и гравитационных постоянных (k = 9 x 109 ![]() и G = 6,67 x 10-11
и G = 6,67 x 10-11 ![]() ), согласно Halliday ³ (2016), такие значения демонстрируют, что гравитационная сила намного слабее, чем электрическая сила. Следовательно, в изолированной системе частиц, в которой действуют только гравитационная и электрическая силы, гравитационной силой можно пренебречь, поскольку электрическая сила примерно в 1,5 x 1020 раз больше, чем сила веса. Поскольку ускорение силы тяжести на частице не будет учитываться, сила на компоненте Z также будет равна нулю, поскольку ускорение az не будет учитываться, мы переформулируем уравнение для данного исследования:
), согласно Halliday ³ (2016), такие значения демонстрируют, что гравитационная сила намного слабее, чем электрическая сила. Следовательно, в изолированной системе частиц, в которой действуют только гравитационная и электрическая силы, гравитационной силой можно пренебречь, поскольку электрическая сила примерно в 1,5 x 1020 раз больше, чем сила веса. Поскольку ускорение силы тяжести на частице не будет учитываться, сила на компоненте Z также будет равна нулю, поскольку ускорение az не будет учитываться, мы переформулируем уравнение для данного исследования:
FR = m . ax + m . ay + m . az
FR = m . ax + m . ay + m . 0
FR = m . ax + m . ay
Считая в основном действующие силы те, которые влияют на ось X, игнорируя механические удары и любые другие силы в компоненте y, поскольку набор растворенных веществ движется в направлении гомогенизации, от гипертонических к гипотоническим областям, мы достигнем такого упрощения Результирующая сила:
FR = m . ax + m . 0
FR = m . ax
Следует также отметить, что изучаемая система будет считаться стационарной или на постоянной основе, в которой ее свойства не могут быть использованы по отношению к времени. Это означает, что любое свойство P системы, частичная производная по отношению к времени равна нулю ![]() , учитывая систему, в которой переменное время не является параметром в изучении мембранной системы в вопросе.
, учитывая систему, в которой переменное время не является параметром в изучении мембранной системы в вопросе.
Клеточные мембраны имеют определенный диспозицию, аналогичную Единому электрическому полю, так что есть концентрация положительных зарядов в основном на внеклеточной стороне, и накопление отрицательных зарядов на внутриклеточной стороне. Существует также разница в концентрации между внешними и внутренними концами клеток (CE и CI), в которойсистема оказывает движущей силой содействовать транслокации частиц через ионные каналы клеточных мембран, как это представлено на рисунке 2.
Рисунок 2: Представление смещения иона через ионный канал.
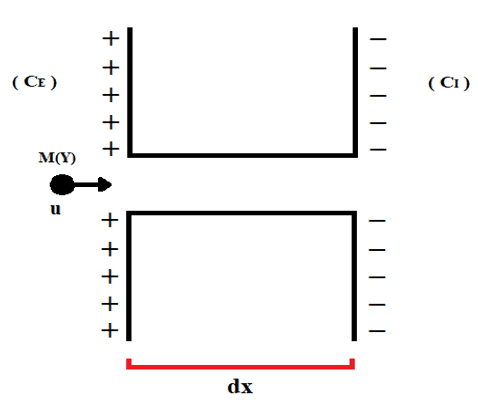
Расстояние, пройденное представленной молекулой, эквивалентно элементу смещения (dx), который также является толщиной уже упомянутой клеточной мембраны. Первый закон Fick можно описать как функцию общего градиента концентрации (∇D) и постоянной диффузии (D), как это выражено ниже (см. Уравнение 3.2):

Однако мы будем рассматривать только уже упомянутый элемент длины (?x), чтобы оценить одномерное движение растворенных веществ из областей с высокими концентрациями в области с более низкими концентрациями. Следовательно, градиенты концентрации (![]() и
и ![]() )
)

Изолируя элемент (?x) от Первого закона Fick, мы получаем:
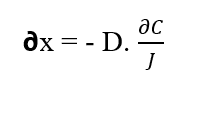 Частицы растворенного вещества движутся вдоль смещения (?x) из-за силы, исходящей от химического потенциала системы (WQ), поскольку согласно 2-му закону термодинамики, описанному Tipler (2009), поток вещества или энергии начинается с регионы с самыми высокими значениями материи или энергии до самых низких. Если на частицы действуют силы и из-за этого они перемещаются на определенный элемент расстояния (?x), можно предположить, что такие тела совершают работу (W), которая описывается следующим уравнением (см. Уравнение 2.3):
Частицы растворенного вещества движутся вдоль смещения (?x) из-за силы, исходящей от химического потенциала системы (WQ), поскольку согласно 2-му закону термодинамики, описанному Tipler (2009), поток вещества или энергии начинается с регионы с самыми высокими значениями материи или энергии до самых низких. Если на частицы действуют силы и из-за этого они перемещаются на определенный элемент расстояния (?x), можно предположить, что такие тела совершают работу (W), которая описывается следующим уравнением (см. Уравнение 2.3):

Работа постоянной силы также может быть описана как функция кинетической энергетической вариации системы (ΔK), выраженной теоремой кинетической энергии (см. уравнение 2.5):

Учитывая одномерное движение растворенных в растворе частиц, в данный начальный момент частицы по отношению к определенному элементу (?x) не движутся, поэтому их начальную скорость (u0) можно считать нулевой, поэтому Работа становится описанной следующим образом:
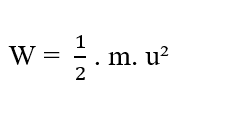
Для системы, в которой у нас есть n количество частиц, каждая из которых имеет определенную массу (m(i)) и ускорение (a(i)), у нас есть, что Результирующая Сила частиц может быть выражена как:
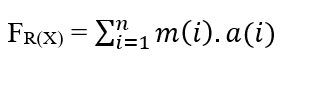
Так как система имеет постоянную Силу, это движение также описывается с постоянным ускорением для всех частиц в соответствии с равномерно разнообразным движением, которое позволяет удалить ускорение суммирования, от свойств Соматоров:
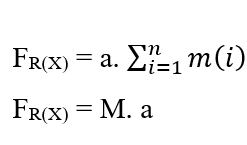
Чтобы достичь уравнения Nathan, два уравнения работы уравняются, и потому, что он предназначен для лечения движения молекул, как попродемонстрировано, масса (м) считается общей массы (M) определенного количества молекул, присутствующих в системе, изучаемой, а также заменяет элемент (dx) на (∂x) первого закона Фика.
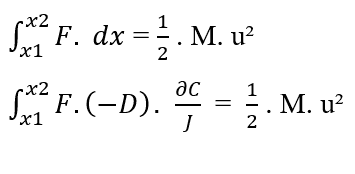
Зная, что (F, D, J) являются константами по отношению к элементу (∂C), который нужно интегрировать, из свойства константы интегралов можно удалить члены из интеграла:
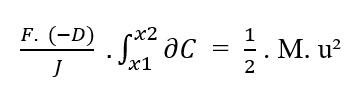
Переписывая границы интеграции по отношению к (∂C), у нас есть:
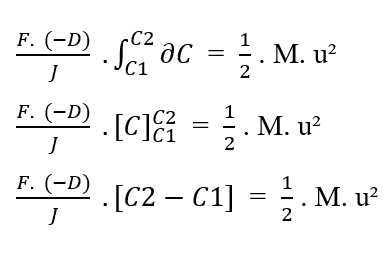
Зная, что [C2 – C1 = ΔC], вы можете подставить значение в уравнение:
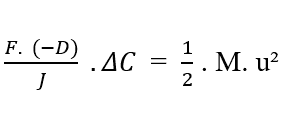
Изолируя переменную плотность потока (J), мы получаем уравнение Натана (см. уравнение 3.3):

J – Плотность потока (Mol m-2 s-1)
D – Коэффициент диффузии (m² s-1)
ΔC – изменение концентрации (Mol m-3)
FR– Результирующая сила (Kg m s-2)
M – Общая масса диффундирующих частиц (Kg)
u – Скорость диффузии частиц (m s-1)
3.2 МАТЕМАТИЧЕСКАЯ И ФИЗИЧЕСКАЯ ОЦЕНКА УРАВНЕНИЯ NATHAN
Чтобы подтвердить проверку уравнения Nathan математическим образом, необходимо было выполнить анализ размеров, описанный Halliday (2016), в котором он проверит, сохранились ли единицы Первого закона Fick, а единицы уравнения Nathan эквивалентны. Размерный анализ является инструментом, используемым в физике для определения единицы измерения некоторой величины. Размерный анализ является инструментом, который позволяет прогнозировать, инспекции и адаптации физических единиц, которые используются для разрешения уравнений.
Закон Fick:
J – (Mol m-2 s-1)
Уравнение Nathan:
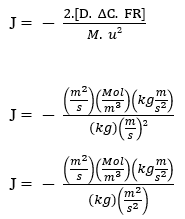
J – (Mol m-2 s-1)
Обычно фундаментальные физические величины выражаются как: длина (L), масса (M), время (T), температура (θ), электрический ток (A), количество вещества (Mol) и интенсивность света (I). Анализ размерности уравнения Nathan (3.3) затем может быть выполнен с использованием таких представлений фундаментальных физических величин в соответствии с эквивалентом каждой переменной в открытой формулировке, как указано Marques (2016).
J – Плотность потока (Mol L-2 T-1)
D – коэффициент диффузии (L2 T-1)
ΔC – изменение концентрации (Mol L-3)
FR – Результирующая сила (M L T-2)
M – Общая масса диффундирующих частиц (M)
u – Скорость диффузии частиц (L T-1)
Теперь, выполняя анализ размерностей с общими представлениями фундаментальных физических величин, мы имеем:
Закон Fick:
J – (Mol L-2 T-1)
Уравнение Nathan:
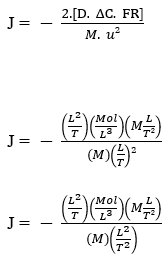
J – (Mol L-2 T-1)
Уравнение Nathan демонстрирует сохранение единиц, а также, следует некоторые заявления, которые Первый закон Fick и Закон Graham продемонстрировать, для того, чтобы связать определенные переменные в прямой или обратно пропорциональной манере, физически проверки такой математической формулировки для процесса диффузии, независимо от единиц, выбранных для основных количеств, при условии, что они имеют согласованность в целом.
Первая связь, которую показывает уравнение Nathan, это прямо пропорциональная связь между плотностью потока (J) и изменением концентрации между двумя точками (ΔC). Устанавливая, что увеличение разницы концентрации между любыми двумя точками системы, будет напрямую связано с увеличением плотности потока же, Такие отношения подчиняется закону Fick.
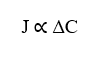
Второе важное соотношение – это прямая пропорциональность между плотностью потока (J) и результирующей силой (FR), действующей на частицы (γ), составляющие рассматриваемую систему. Это означает, что увеличение переменной Результирующей силы, действующей на диффундирующие молекулы, также прямо пропорционально увеличит поток частиц.
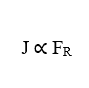
Третьей важной связью является обратная пропорциональность между плотностью потока (J) и общей массой любого гамма-элемента (γ), который составляет систему, на которую ведется исследование. Это означает, что, учитывая каждую молекулу и только ее молекулярную массу, чем выше молекулярная масса элемента, который будет рассеян, тем ниже его скорость транспортировки, такие отношения подчиняются Закону Fick и Закону Graham.
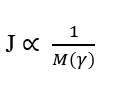
Четвертое важное соотношение – это обратная пропорциональность между молекулярной массой (M) и квадратом скорости диффузии (u). Или это можно понимать как обратную зависимость между скоростью диффузии и квадратным корнем из молекулярной массы элемента (γ). Такое соотношение подчиняется закону истечения и диффузии газа Graham, показывая корреляцию скорости с обратной величиной квадратного корня из молекулярной массы.
Плотность потока (J) обратно пропорциональна продукту между молекулярной массой (M) – когда для частицы – и квадратом скорости диффузии (u):
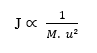
Если (J) постоянна (K), мы имеем:
![]()
Выделяя переменную Скорость диффузии (u), мы получаем:
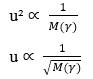
Из программного обеспечения Excel версии 2016 также можно было выполнить графическое моделирование 20 гипотетических данных для значения молекулярной массы (M) с интервалом (0 <M <21) в порядке возрастания, коррелированным с соответствующим значением Скорость диффузии (u), зная, что скорость диффузии данного элемента обратно пропорциональна квадратному корню из его соответствующей массы, как показано законом Graham и уравнением Nathan, когда скорость переноса (J) поддерживается постоянной и учитывает только массу одиночной частицы. Таким образом, мы можем видеть сходство графиков, построенных позже с такими данными (см. График 1).
График 1: Скорость диффузии по сравнению с обратной стороны квадратного корня молекулярной массы.
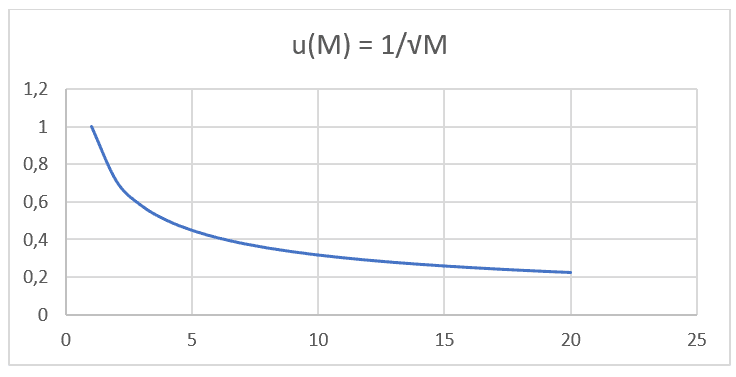
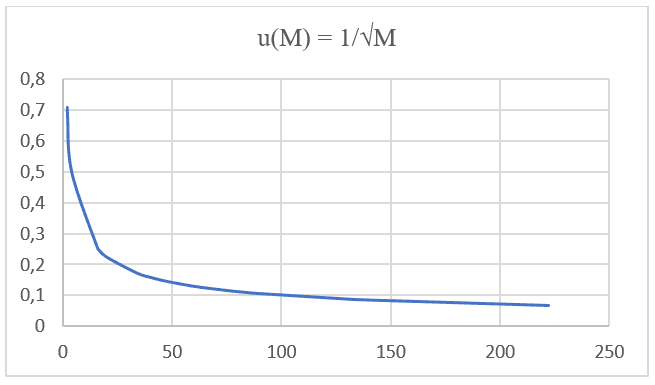
Отмечается, что обе формулировки, как закон Graham, так и уравнение Nathan, имеют равную пропорциональность и основаны на одном и том же типе функции: F(x) = ![]() . Выполняя графическую проекцию со значениями молекулярной массы, данными IUPAC и соответствующей скоростью диффузии 20 различных газов при одинаковом давлении и температурах, перечисленных в следующей таблице (см. таблицу 1), можно проецировать второй график (см. график 2).
. Выполняя графическую проекцию со значениями молекулярной массы, данными IUPAC и соответствующей скоростью диффузии 20 различных газов при одинаковом давлении и температурах, перечисленных в следующей таблице (см. таблицу 1), можно проецировать второй график (см. график 2).
Таблица 1: Молекулярные массы и их соответствующие скорости диффузии.
| газ | Молекулярная масса (г/мол) | Скорость диффузии (см/с) |
| H2 | 2 | 0,7 |
| He | 4 | 0,5 |
| O2 | 16 | 0,25 |
| CH4 | 16 | 0,25 |
| Ne | 20 | 0,22 |
| H2S | 34 | 0,17 |
| Ar | 40 | 0,15 |
| CO2 | 44 | 0,15 |
| NO2 | 46 | 0,14 |
| O3 | 48 | 0,13 |
| C4H10 | 58 | 0,12 |
| NO3 | 63 | 0,12 |
| SO2 | 64 | 0,12 |
| CS2 | 76 | 0,11 |
| SO3 | 80 | 0,11 |
| Kr | 84 | 0,10 |
| FeS | 88 | 0,10 |
| Xe | 131 | 0,08 |
| PCl3 | 137 | 0,08 |
| Rb | 222 | 0,06 |
Источник: Автор.
График 2: Скорость диффузии по сравнению с обратной стороной квадратного корня молекулярной массы.
Согласно Zeiger и Taiz (2006), среднее время диффузии можно определить как отношение между квадратом вариации расстояния (ΔX2) и коэффициентом диффузии элемента (D), как выражено в следующей математической формулировке (см. уравнение 3.4):

Из определения средней скалярной скорости (u) кинематики и замены значения времени переменной Среднее время (TM) мы получаем:
![]()
или же
![]()
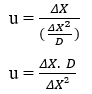
Выполняя алгебраические манипуляции, вы можете получить уравнение для расчета скорости диффузии (u) любого элемента:

Заменив (3,5) в уравнении Nathan (3,3), мы можем получить связь между квадратом вариации расстояния (ΔX) и вариацией концентрации (ΔC).

Выполняя измеримый анализ уравнения (3.6), чтобы подтвердить сохранение единиц закона Fick, у нас есть:
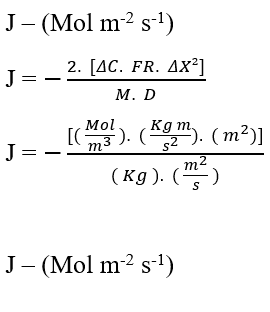
После подтверждения сохранения единиц из размерного анализа, в уравнении Натана и законе Фика можно увидеть важную и общую взаимосвязь, а именно обратную пропорциональность между вариацией концентрации (ΔC) и квадратом вариации расстояния (ΔX²). Чтобы это утверждение было действительным, мы будем считать скорость переноса (J) постоянной и проанализируем только эти две переменные: изменение концентрации и расстояние.
![]()
Учитывая постоянную плотность потока (J), мы имеем:
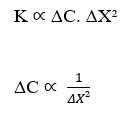
Показана обратная пропорциональность между вариацией концентрации (ΔC) и квадратом вариации расстояния (ΔX²). Это утверждение согласуется с законом Fick, поскольку при анализе корреляции между этими двумя переменными обе формулировки, уравнение Nathan и закон Fick, описывают один и тот же график, который следует за функцией: F (x) = ![]() . Ниже демонстрируется формат графика (кривая Гаусса), зависимость изменения концентрации от вариации квадрата расстояния (см. Рисунок 3):
. Ниже демонстрируется формат графика (кривая Гаусса), зависимость изменения концентрации от вариации квадрата расстояния (см. Рисунок 3):
Рисунок 3: Квадратный график зависимости изменения концентрации от расстояния.
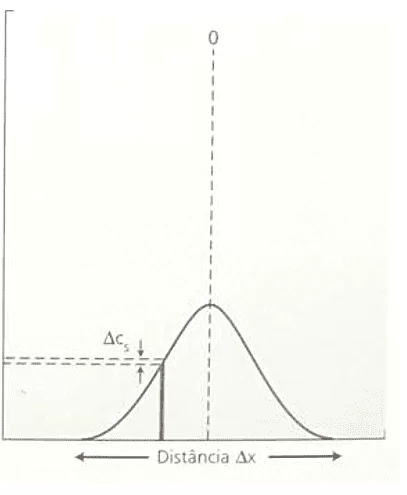
В случае только имея в качестве определяющей переменной в процессе диффузии данного элемента, Вариация концентрации (ΔC), предполагая, что это движение частиц постоянной скорости, а не равномерно разнообразное движение, вызванное постоянной силой, просто заменить (2,7) в (3,3), уравнение Торричелли, который вернет математическое описание, известное как математическое описание, известное как математическое описание : 1-й закон Fick.
Замена (2,7) в (3,3) с учетом начальной скорости (u0) нулевой, у нас есть:
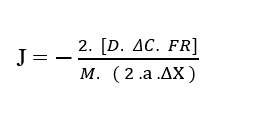
Отменяя термины Результирующая сила (FR) с членами в знаменателе Общая масса частиц (M) и Ускорение (a), а также константы в числителе и знаменателе (2), мы снова получаем линейную формулировку: Первый закон Fick (2.1).

3.3 РАЗРАБОТКА УРАВНЕНИЯ НАТАНА ДЛЯ ЭЛЕКТРОДИФФУЗИИ В МЕМБРАНАХ КЛЕТОК
Уравнение Nathan может быть расширено для математического описания процесса диффузии ионов через клеточную мембрану с учетом следующих математических формулировок. Согласно Pimentel (2004), движущей силой диффузионных процессов в биологических системах является так называемый химический потенциал системы, и в случае рассматриваемого примера происходит перенос вещества из одной точки A в другую B, такой химический потенциал можно выразить из следующего уравнения (2.8):

Это означает, что раствор будет перемещаться из одного региона с более высоким химическим потенциалом в меньший регион, или в случае растворителей, таких как вода, от осмоса перемещается из регионов с более низкими концентрациями растворителя в более крупные. Однако поток частиц прекращается, когда химические потенциалы обеих фаз равны, что обутает окончательное состояние равновесия (HENEINE, 2004).
Такой потенциал решения, который производит результирующую силу системы, поскольку он представляет способность данной системы выполнять работу, может быть описан с учетом вклада других важных факторов, таких как: гравитационное действие и электрическое влияние на частицы из-за их нагрузок и разницы в электрическом потенциале. Таким образом, максимальное потенциальное уравнение может быть выражено формулировкой Электрохимического потенциала ниже (см. уравнение 3.7):

В случае, если вклад гравитационного потенциала (m.g.h) будет проигнорирован, уравнение будет сведено только к химическому и электрическому вкладу, это будут силы, которые работают в наборе ионных частиц, чтобы двигаться через ионные или молекулярные каналы через липидный билейзер, вступая во внутриклеточную среду (ALBERTS, 2009).
Уравнение Nathan описывает процесс диффузии, и природное явление ионого транспорта через клеточную мембрану может быть аналогичным образом выражено уравнением Nathan, принимая в качестве результирующей силы (FR) только химический потенциал раствора и электрический вклад, игнорируя гравитационный вклад.
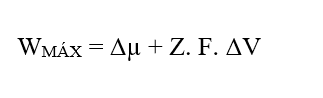
Зная, что (W = FR. Δx), заменив уравнение (2.3) мы получаем:

Выполняя мерный анализ Результирующей Силы (3.8), разделяя ее на свои химические и электрические участки, можно воспринимать появление не более энергетического блока Joule (J), а единицы силы в Международной системе измерений, Newton (N):
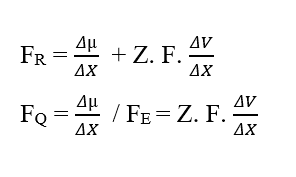
Анализируя долю химического вклада (FQ), мы имеем:
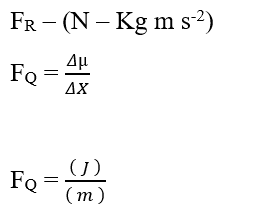
Зная, что блок энергии Joule (J – N.m) может быть заменен в мерном анализе, получении:
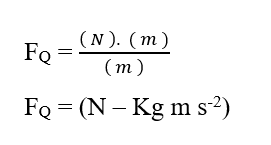
Анализируя долю электрического вклада (FE), мы имеем:
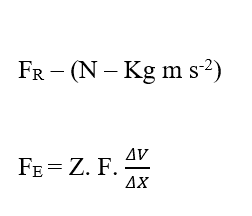
Зная, что Валенсия (Z) является мерной переменной, у нас есть:
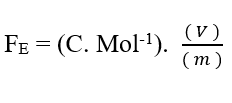
Зная, что единица напряжения Volt (V – J. C-1), ее можно заменить при размерном анализе, получив:
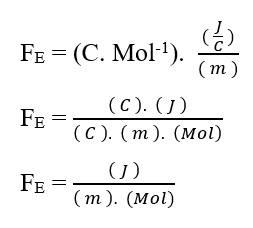
Поскольку единица Моля считается безразмерной, поскольку она связана только с объектами, составляющими данную систему, такими как: атомы, молекулы, ионы или электроны; мы можем не принимать во внимание этот блок при анализе, упрощая его:
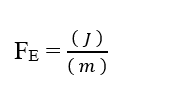
Зная, что блок энергии Joule (J – N.m) может быть заменен в мерном анализе, получении:
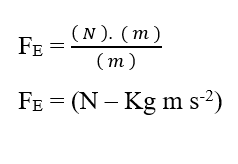
Из анализа размеров двух частей, химической и электрической, которые составляют результирующую силу (FR) исследуемой системы, показано, что она пригодна для расчета такой силы. Запись соотношений между вариацией химического потенциала (Δµ) и вариацией расстояния (∆X), вариацией электрического потенциала (∆V) и вариацией расстояния (ΔX) в форме пределов (∆X 0), а затем в дифференциальной форме , имея Мгновенную результирующую силу, получаем:
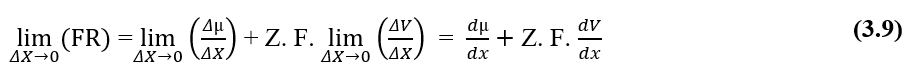
Для ситуации, в которой электрохимические потенциалы двух фаз (A) и (B) данной системы одинаковы, то есть, в равновесной ситуации, значение Вариации электрического потенциала на концах клеточных мембран может быть установлено, что относится к уравнению Нернста.
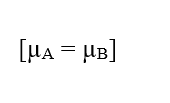
Если потенциалы одинаковы, это утверждение указывает на то, что работа, выполняемая частицами, является недействительной, поэтому результирующая сила в них также будет недействительной, так как между двумя фазами системы нет транзита молекул:
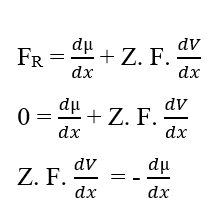
Вы можете отменить элементы (dx), которые появляются по обе стороны равенства и изолировать термин (dV), а затем переписать в соответствии с вариациями, которые результаты:
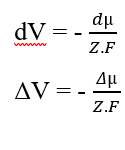
Заменив химический потенциал (2.3), мы восстановили расчет электрического потенциала для равновесной ситуации в биологических системах (3.10), известного как уравнение Nernst (HENEINE, 2004).

Можно подставить результирующую силу системы (3.9) в уравнение Nathan, описанное выше (см. Уравнение 3.3):
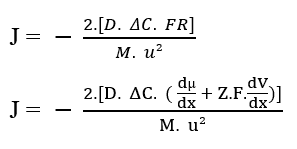
Помимо терминов в скобках, у нас есть уравнение Nathan для электродиффузии в клеточных мембранах (3.11):

J – скорость переноса или плотность ионного потока в мембране (Mol m-2 s-1)
D – Коэффициент диффузии раствора (m2 s-1)
ΔC – Вариация концентрации (Mol m-3)
M – Общая масса дифитирующих частиц (кг)
u2 – Скорость диффузии частиц (m s-1)
В – Ион Валенсия
F – Faraday константа (F = 9,648 x 104 C mol-1)
?µ/?x – Производная химического потенциала по отношению к dx (Kg m s-2)
?V/?x – Получено из электрического потенциала по отношению к dx (V m-1)
Согласно Halliday (2016) для термодинамики, внутренней энергии (U) или изменения внутренней энергии (ΔU), это сумма кинетической и потенциальной энергий всех молекул, содержащихся в системе. Это соотношение может быть выражено следующим математическим описанием (см. Уравнение 3.12), учитывая постоянную среднюю скорость для всех частиц:

[M – Общая масса системных частиц]
Замена уравнения (3,13), в уравнении Nathan (3,3), постоянный термин может быть определен, называют автором с греческой буквы омега (я):

Если мы теперь рассмотрим причину ![]() как любая константа (ω), поскольку значения таких переменных не меняются во времени, поскольку частная производная любого члена равна нулю
как любая константа (ω), поскольку значения таких переменных не меняются во времени, поскольку частная производная любого члена равна нулю ![]() . Зная, что (ω) представляет собой единицу
. Зная, что (ω) представляет собой единицу ![]() , отношение количества концентрированного вещества к внутренней энергии системы, такое соотношение эквивалентно следующему выражению (3.15):
, отношение количества концентрированного вещества к внутренней энергии системы, такое соотношение эквивалентно следующему выражению (3.15): И зная, что посылка
И зная, что посылка ![]() относится к Результирующей прочности системы (FR), эту формулировку все еще можно переписать в ее общей форме (3.15):
относится к Результирующей прочности системы (FR), эту формулировку все еще можно переписать в ее общей форме (3.15):

Теперь можно отметить, что, поскольку члены (D) и (ω) постоянны, плотность потока (J) прямо пропорциональна результирующей силе системы (FR), что означает, что при увеличении одна из этих переменных, другая также будет пропорционально увеличиваться.
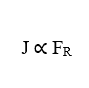
Уравнение Натана для Электродиффузии в клеточных мембранах описывает поток ионов через мембрану, через ионные каналы, когда они открыты, под влиянием градиента концентрации внеклеточных и внутриклеточных средств массовой информации, а также электрический потенциал или электрическое поле под ионами, порожденных самой клеточной мембраны. Эта формулировка учитывает общую массу частиц элемента, который будет распространяться, химических и электрических движущих сил, присутствующих в явлении транспортировки ионов через клеточную мембрану, однако, если Есть другие внешние факторы, в связи с увеличением переменной Результирующая сила, анализ может быть сделано в обобщенном объеме, в дополнение к согласованию с существующими и представленными физическими понятиями.
4. ОКОНЧАТЕЛЬНЫЕ СООБРАЖЕНИЯ
В заявлении, эта статья предложила формулировку «Уравнение Nathan», как расширение 1-го закона Fick, который описывает диффузный поток частиц в решениях, из-за не только разница в концентрации (ΔC), но с целью рассмотрения плотности потока материи (J) в качестве функции постоянной результирующей силы (FR), действующих на частицы данной системы (см. уравнение 3.3).
Эта формулировка продемонстрировала прямую соразмерность между Силой, действующей в частицах, и плотностью потока (J), поэтому чем выше сила, оказываемая в системе, тем больше транспортировка материи. Такое же математическое описание естественных процессов диффузии молекул, которое позволяет общий анализ любых сил, которые могут оказывать влияние в рамках определенных систем, в настоящее время изучается, также может быть расширена, чтобы объяснить транспортировку ионов через клеточную мембрану, когда в результате силы под частицами системы в вопросе принимает во внимание химический потенциал и электрический потенциал , а также связь между количеством концентрированной материи и внутренней энергии системы (ω), которая была названа автором «Уравнение Натана для электродиффузии в клеточных мембранах» (см. уравнение 3.11), или также в его общей формулировке (см. уравнение 3.15).
Проверка уравнений оценивалась на основе мерного анализа и прямых и обратно пропорциональных взаимосвязей между переменными по отношению к постулатам, предложенным 1-м законом Fick и законом Graham, в виде графиков с кривыми, описанными определенными функциями, которые демонстрируют соразмерность, существующую между: скорость диффузии против молекулярной массы элемента (см. график 1) , и вариация концентрации по сравнению с квадратом вариации расстояния (см. график 3); показывая себя в качестве действительной формулировки физически и математически для такого описания природного явления, потому что единицы закона Fick сохраняются в уравнении Nathan, и соответствуют так положительно относительно предложений таких уже установленных физико-химических законов и их графических представлений, следуя пропорциям, описанным определенными функциями, представленными ранее. Следующие статьи из физических экспериментов или с конкретным программным обеспечением моделирования, может оценить практичность и согласованность уравнения Nathan с естественной реальностью, ссылаясь на изучение явления диффузии, с тем чтобы проанализировать точность и общую общую сторону понятий, поднятых им.
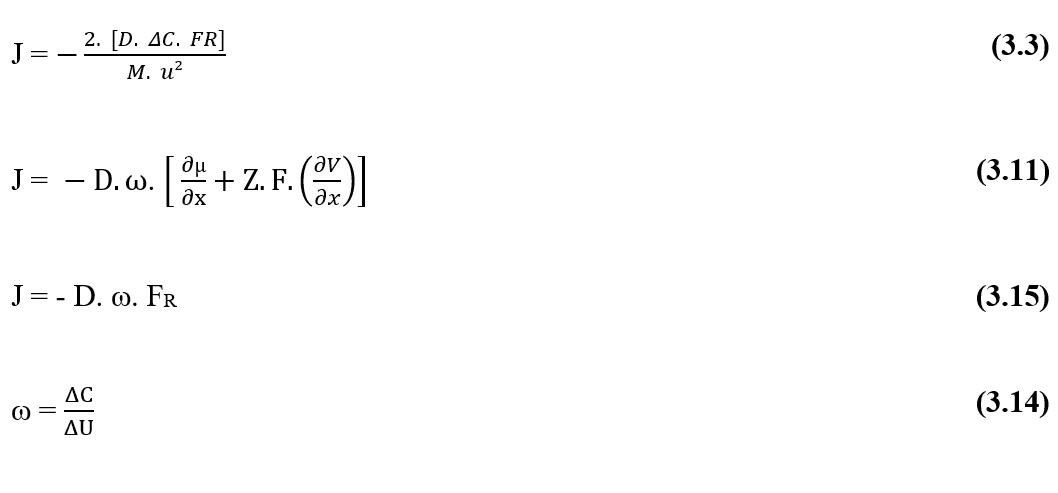
БИБЛИОГРАФИЧЕСКИЕ ССЫЛКИ
ALBERTS, Bruce et al. Biologia Molecular da Célula, 5° Edição. Editora: ARTMED, 2010, 1728 p., Vol. 1. ISBN: 978-85-363-2170-7.
BRADY, James; HUMISTON, Gerard. Química Geral, 2° Edição. Editora: LTC, 1995, 404 p., Vol. 1. ISBN: 9788521604495.
DA SILVA, Raissa. Difusão de Gases em Membranas Densas Via Simulação Molecular. Instituto Alberto Luiz Coimbra de Pós-Graduação e Pesquisa na Engenharia (UFRJ), Data da Dissertação de Mestrado: Abril de 2013. Disponível em: http://portal.peq.coppe.ufrj.br/index.php/producao-academica/dissertacoes-de-mestrado/2013-1/47-difusao-de-gases-em-membranas-densas-via-simulacao. Acesso: 25/06/2020.
HENEINE, Ibrahim. Biofísica Básica, 2° Edição. Editora: ATHENEU, 2004, 381 p., Vol. 1. ISBN: 8573791225.
JUNQUEIRA, Luiz C.; CARNEIRO, Jóse. Biologia Celular e Molecular, 9° Edição. Editora: Guanabara Koogan, 2012, 376 p., Vol. 1. ISBN: 9788527720786.
MARQUES, Francisco Das Chagas. Física Mecânica, 1° Edição. Editora: Manole, 2016, 315 p., Vol. 1. ISBN: 9788520427743.
MOREIRA C., Catarina. Difusão Simples. Rev. Ciência Elem., V2(02):144. doi.org/10.24927/rce2014.144. Pulicado: 15 de Setembro de 2010. Disponível em: https://rce.casadasciencias.org/rceapp/art/2014/144/. Acesso: 22/06/2020.
PIMENTEL, Carlos. A Relação da Planta Com a Água, Local: EDUR – Editora Universidade Federal Rural do Rio de Janeiro. 2004, 190 p. ISBN: 85-85720-45-X
TAIZ, Lincoln; ZEIGER, Eduardo. Fisiologia Vegetal, 3° Edição. Editora: ARTMED, 2006, Vol. 1, 722 p. ISBN: 85-363-0291-7.
TIPLER, Paul; MOSCA, Gene. Física para Cientistas e Engenheiros – Mecânica, Ondas, Termodinâmica, 6° Edição. Editora: LTC, 2009, 788 p., Vol. 1. ISBN: 9788521617105.
WALKER, Jearl et al. Halliday & Resnick ¹: Fundamentos de Física – Mecânica, 10° Edição. Editora: LTC, 2016, 372 p., Vol. 1. ISBN-13: 978-8521630357.
WALKER, Jearl et al. Halliday & Resnick 2: Fundamentos de Física – Gravitação, Ondas, Termodinâmica, 10° Edição. Editora: LTC, 2016, 324 p., Vol. 1. ISBN-13: 978-8521630364.
WALKER, Jearl et al. Halliday & Resnick ³: Fundamentos de Física – Eletromagnetismo, 10° Edição. Editora: LTC, 2016, 408 p., Vol. 1. ISBN-13: 978-8521630371.
[1] градуировка.
Представлено: Декабрь 2020 года.
Утверждено: Aпрель 2021 года.