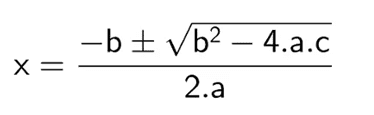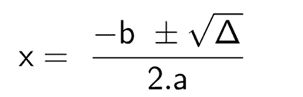ОРИГИНАЛЬНАЯ СТАТЬЯ
PEDREIRA, Sinvaldo Martins [1]
PEDREIRA, Sinvaldo Martins. Неудача Бхаскары. Revista Científica Multidisciplinar Núcleo do Conhecimento. Год. 07, изд. 02, Том. 02, стр. 178-186. Февраль 2022 г. ISSN: 2448-0959, Ссылка для доступа: https://www.nucleodoconhecimento.com.br/математические-олимпиады/неудача-бхаскары
СВОДКА
Эта работа направлена на то, чтобы показать, что из-за недостатков в арифметической системе университетские правила, основанные на неправильном стандарте, могут давать неверные результаты, такие как правило квадратного уравнения, которое может распространять ложную уверенность в точности, для простого факта следования. светских парадигм, без широкого контекстуального наблюдения за вовлеченной реальностью, потому что, имея дело с точными науками, мы всегда должны иметь целостный взгляд, широко рассматривая все вовлеченные факторы, поскольку настоящее действие имеет последствия в будущем и когда мы основываемся на системы несовершенны, у нас появляется ложное ощущение успеха, поскольку мы буквально следуем всем псевдо-предписаниям. Однако возникает новая система, подвергающая испытанию силу арифметического пути, которому необходимо следовать.
Ключевые слова: Неудачи, Точность, Система, Целостный.
1. ВВЕДЕНИЕ
Прежде всего, эта работа предназначена не для того, чтобы принизить гений Бхаскары, а для того, чтобы показать, что из-за концептуального изъяна в арифметической системе даже гении могут ошибаться.
Квадратное уравнение было стандартизировано, представлено в следующей форме: ax² + bx + c = 0, где его решение было неизвестным, поэтому решение задачи пришло с формулой:
Но чтобы упростить решение, сначала найдите дельту;
Δ = b² – 4ac
Затем результат дельты присоединяется к уравнению:
Наконец, поскольку это квадратное уравнение, X имеет два результата:
Х = Х, и Х = Х,,
Пример I:
X² + 10 X – 56 = 0 A = 1, B = 10, C = – 56
Δ = 10² – (4. 1 .- 56)
Δ = 100 – (- 224)
Δ = 324
Х = -10 ± √324
2.1
Х, = -10 + 18 => Х, = 8 => Х, = 4
2 2
Х, = -10 – 18 => Х,, = – 28 => Х,, = – 14
2 2
Итак, ответы: X, = 4 и X,, = -14
Пример 2:
X² – 10 X – 56 = 0 A = 1, B = -10, C = – 56
Δ = -10² – ( 4. 1 .- 56)
Δ = 100 – (- 224)
Δ = 324
Х = -10 ± √324
2.1
Х, = 10 + 18 => Х, = 28 => Х, = 14
2 2
Х, = 10 – 18 => Х,, = – 8 => Х,, = – 4
2 2
Итак, ответы: X, = 14 и X,, = – 4
2. ХОЛИЗМ
2.1 ХОЛИЗМ I
Как упоминалось ранее, давайте использовать немного холизма; каждое квадратное уравнение происходит из дистрибутивного, где:
1-й случай
(а + б)² => (а + б) . (a + b) = a² + 2ab + b² Примечание: по правилу и a, и b строго положительны.
2-й случай
(а – б)² => (а – б) . (a – b) = a² – 2ab + b² Примечание: положительное и b отрицательное по правилу.
2.2 ХОЛИЗМ II
В скрытом термине каждое сложение и каждое вычитание имеют результат, поэтому
a + b = c, следствие (a + b)² = c², тогда; а² + 2ab + b² = с²
a – b = c, следствие (a – b)² = c², тогда; а² – 2аб + б² = с²
2.3 ХОЛИЗМ III
Свидетельствующие термины, давайте поместим термины уравнения в доказательство;
I. а = Х, б = 5, с = 9
Скоро; (a + b)² = c² => (X + 5)² = 9² => X² + 2 . 5X + 25 = 81 => X² + 10X + 25 – 81 = 0 => X² + 10X – 56 = 0
II. а = Х, б = – 5, с = 9
Скоро; (a – b)² = c² => (X – 5)² = 9² => X² – 2 . 5Х + 25 = 81 => Х² – 10Х + 25 – 81 = 0
=>Х² – 10Х – 56 = 0
2.4 ХОЛИЗМ IV
Переписка:
I. Х² + 10Х – 56 = 0
A = X², B = 10X, C = -56, поэтому A = a², B = 2. 5X, C = 25 – 81, подразумевает A = a², B = 2. аб, С = b² – (с²),
II. Х² – 10Х – 56 = 0
A = X², B = -10X, C = -56, поэтому A = a², B = – 2 . 5X, C = 25 – 81, подразумевает A = a², B = – 2 . аб, С = b² – (с²),
3. РАЦИОНАЛИЗАЦИЯ
I. Если в (a + b)² = c² => a² + 2ab + b²- (c²) = 0
A = a², B = 2 ab , C = b² – (c²), Примечание: (B = 2 ab) по правилу a и b строго положительны, In X² + 10X – 56 = 0
A = X² , B = 10X, C = -56, Примечание: (B = 10X) по правилу X строго положителен.
Таким образом, в X² + 10X – 56 = 0 единственный возможный корень равен 4, потому что -14 противоречит математическому правилу.
II. Если в (a – b)² = c² => a² – 2ab + b²- (c²) = 0, (a = X, b = – 5, c = 9)
A = a², B = – 2 ab, C = b² – (c²), Примечание: (B = – 2 ab) как правило, если b отрицательно, a должно быть строго положительным.
В Х² – 10Х – 56 = 0
A = X² , B = -10X, C = -56, Примечание: (B = -10X) по правилу X строго положительно.
Таким образом, в X² – 10X – 56 = 0 единственный возможный корень X равен 14, потому что – 4 противоречит математическому правилу.
4. ЗАКАЗ
4.1 КЕЙС I
Если (X² + 10X – 56 = 0) = (a² – 2ab + b²- (c²)) тогда:
A = X² и A = a², подразумевает (X = a)
B = 10X и B = 2ab, подразумевает (10X = 2ab)
C = -56 и C = + b²- (c²), подразумевает (- 56 = b² – (c²))
Найдя корень, сначала найдите значение b:
если A = X и A + a, B = 10X, где B = 2ab, мы ставим b в качестве доказательства
10X = 10a, подразумевает 10a = 2ab => b = 10a/ 2a => b = 5
Во-вторых, значение c находится;
Если C = -56 и C = + b²- (c²), мы ставим c в качестве доказательства
-56 = b²- (c²) подразумевает -56 = 5²- (c²) => c² = 25 + 56 => c² = 81 => c = 9
Наконец, найдено значение корня;
Таким образом, (a + b)² = c², следует (a + b) = c.
Если ((a + b)² = c²) = ((X + b)² = c²), это подразумевает (X + b) = c, то есть:
Х + 5 = 9 => Х = 9 – 5 => Х = 4
4.2 КЕЙС II
Если (X² – 10X – 56 = 0) = (a² – 2ab + b²- (c²)) тогда:
A = X² и A = a², подразумевает (X = a)
B = – 10X и B = – 2ab, подразумевает (- 10X = 2ab)
C = -56 и C = b²- (c²), подразумевает (- 56 = b² – (c²))
Найдя корень, сначала найдите значение b:
если A = X и A = a, B = -10X, где B = -2ab, мы ставим b в качестве доказательства
– 10X = – 10a, подразумевает – 10a = – 2ab => – b = – 10a/ 2a => – b = – 5
По значению с:
Если C = – 56 и C = – b²- (c²), мы ставим c в качестве доказательства
– 56 = – b²- (c²) подразумевает – 56 = – 5²- (c²) => c² = 25 + 56 => c² = 81 => c = 9
Наконец, значение корня найдено:
Итак, (a – b)² = c², подразумевает (a – b) = c
Если ((a – b)² = c²) = ((X – b)² = c²), это подразумевает (X – b) = c, то есть:
Х – 5 = 9 => Х = 9 + 5 => Х = 14
5. ПАРАДОКС
Как показано в двух примерах, не было необходимости использовать формулу Бхаскары для решения каких-либо квадратных уравнений.
И (X² + 10X – 56 = 0), и (X² – 10X – 56 = 0) решались без использования такого математического ресурса, подчеркивая, что в обоих есть только один возможный корень.
Однако, несмотря на то, что ошибка в формуле Бхаскара была продемонстрирована, все еще существует ошибка большей системной степени, которая заключается в правиле знаков, потому что, как видно и нормализовано Pedreira (2016), квадрат отрицательного числа остается отрицательным, поскольку геометрическое отношения имеют нейтральные характеристики, просто что-то умножают или делят; например: 3 x *3 = *9 (где (*) перед числом указывает на то, что оно отрицательное, чтобы не путать его со знаком (–), указывающим на вычитание), оставляя невозможным изменение знаков при изменении числа. сторона равенства, которая может быть решена с помощью правила Базиса и Компонентов, где Базис (В) равен сумме Компонентов, а Компонент (С) равен разнице Базиса на один или несколько Компонентов,
Пример: B = 15 C = 8 и 7, 15 = 8 + 7 => 15 – 8 = 7 => 8 = 15 – 7 => 8+7 = 15 => 15 – (8 + 7) = 0
6. СРАВНЕНИЕ
Уравнение (a + b)² = c² всегда будет заканчиваться неизвестным в форме: a² + 2ab +b² – (c²) = 0, и это приводит к необходимости второго этапа арифметической обработки для решения проблемы, как видно до. В то время как, если мы используем правило основы и компонентов (BC), решение будет линейным и непрерывным;
Пример: (a + b)² = c², по правилу BC: c (a + b) = c² => ca + cb = c²
7. НА ПРАКТИКЕ:
7.1 ПРИМЕР I
Текущее правило: ( X + 8)² = 144 => ( X + 8) . (Х + 8) = 144 => Х² + 2 . 8 . Х + 64 = 144 =>
X² + 16X + 64 – 144 = 0 => X² + 16X – 80 = 0 (неизвестно)
Базовое правило и компоненты: (X + 8)² = 144 => 12 . Х + 12 . 8 = 144 => 12Х + 96 = 144 =>
12X = 144 – 96 => 12X = 48 => X = 48/12 => X = 4 (прямой результат)
7.2 ПРИМЕР II
Текущее правило: ( X – 5)² = 49 => ( X – 5) . (Х – 5) = 49 => Х² + 2 . – 5 . Х + 25 = 49 =>
X² + 10X + 25 – 49 = 0 => X² + 10X – 14 = 0 (неизвестно)
Базовое правило и компоненты: (X – 5)² = 49 => 7 . Х-7. 5 = 49 => 7X – 35 = 49 =>
7X = 49 +35 => 7X = 84 => X = 84/7 => X = 12 (прямой результат)
7.3 ПРИМЕР III: ДРУГИЕ ВОЗМОЖНОСТИ
Текущее правило: ( X + 6)² = – 121 (нет решения): из-за текущего правила в квадратном уравнении в форме (a + b)² = c², c² всегда будет положительным, потому что каждое положительное или отрицательное число будучи возведенным в четную степень, он становится положительным.
Базовое правило и компоненты: (X + 6)² = *121 => 11X + 11 . 6 = *121 => 11X = *121 – 66 => 11X = *187 => X = *187/11 => X = *17 (имеет решение): из-за правила Базы и Компонентов считать числа либо множители, либо делители, такие как геометрические отношения (RG) и RG, имеют нейтральный характер, независимо от того, возводится ли он в любую степень, четную или нечетную, если он положительный, он будет оставаться положительным, если он отрицательный (*) он будет оставаться отрицательным.
8. ЗАКЛЮЧИТЕЛЬНЫЕ СООБРАЖЕНИЯ
Было доказано, что даже в рамках используемых в настоящее время правил формула квадратного уравнения всегда дает два корня в качестве ответа, вызывая вечную двойственность точности, что само по себе является парадоксом, эта неудача возникает из-за того, что мы не учитываем скрытые члены при его решении, то есть когда рассматриваем дистрибутивный: (a + b)² => (a + b) . (a + b) = a² + 2ab + b² , мы опускаем равенство (c²), и это приводит к неясности в его разрешении, вызывая системную ошибку.
Даже исправляя это упущение, текущая система все же ограничена, потому что, когда мы используем правило Базиса и компонентов, мы бесконечно увеличиваем возможности операций, так как, когда мы рассматриваем геометрические отношения как нейтральные, уравнения, возведенные в любую степень, будут иметь знак их числитель, будь то положительный или отрицательный.
ИСПОЛЬЗОВАННАЯ ЛИТЕРАТУРА
PEDREIRA, S. M. O Valor dos Números. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano 01, Vol. 08. pp. 05-16. setembro de 2016. Disponível em: https://www.nucleodoconhecimento.com.br/matematica/o-valor-dos-numeros.
PEDREIRA, S. M. Reestruturando os Números. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano 04, Ed. 09, Vol. 06, pp. 115-120. Setembro de 2019. Disponível em: https://www.nucleodoconhecimento.com.br/matematica/reestruturando-os-numeros.
SILVA, L. P. M. Fórmula de Bhaskara. Brasil Escola. Disponível em: https://brasilescola.uol.com.br/matematica/formula-bhaskara.htm. Acesso em 15 de dezembro de 2021.
[1] Окончил логистику, 4 семестр по химии, математик-любитель.
Отправлено: Декабрь 2021 г.
Утверждено: Февраль 2022 г.