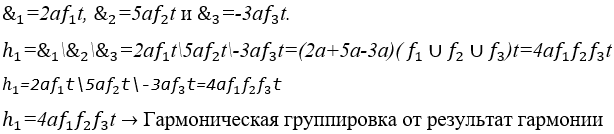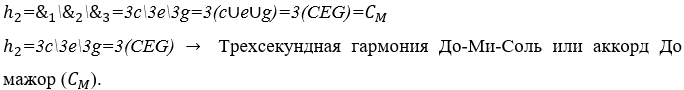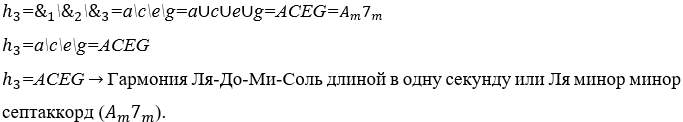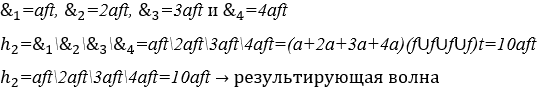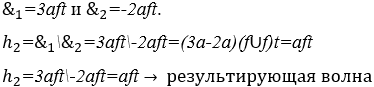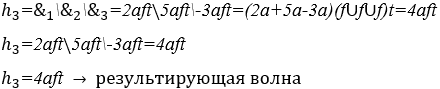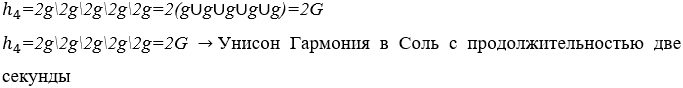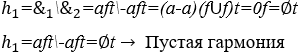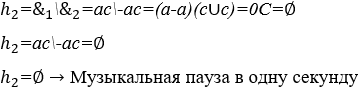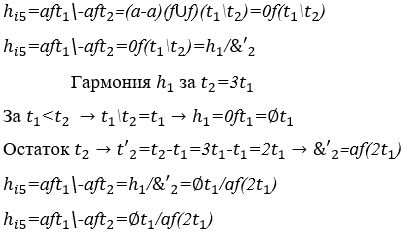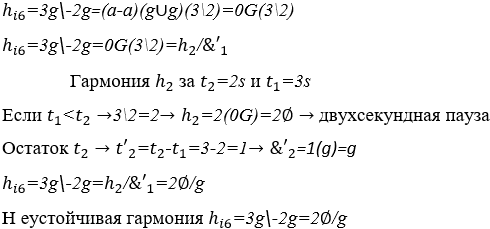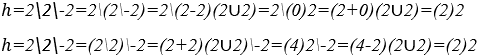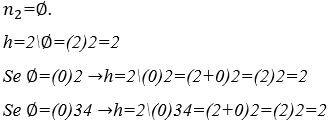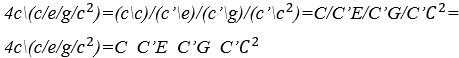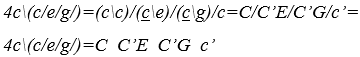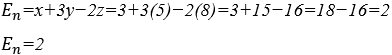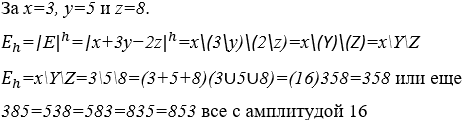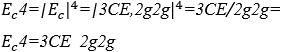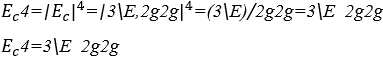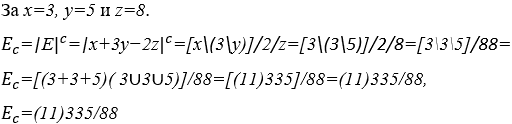ОРИГИНАЛЬНАЯ СТАТЬЯ
VIANA, Arnóbio Araújo [1]
VIANA, Arnóbio Araújo. Гармонизирующая операция (Г) и ее обратная мелодическая операция (М). Revista Científica Multidisciplinar Núcleo do Conhecimento. Год. 07, изд. 03, Том. 03, стр. 144-171. Март 2022 г. ISSN: 2448-0959, Ссылка для доступа: https://www.nucleodoconhecimento.com.br/математические-олимпиады/мелодическая-операция
СВОДКА
Отсутствие математической операции для объяснения взаимодействия волн, особенно между звуковыми волнами музыкальных нот, было проблемой, которая руководила построением этой статьи. В этом контексте целью данного исследования, направленного на лучшую визуализацию простой звуковой волны, была демонстрация операций, разработанных автором этого материала, состоящих из трех наиболее важных характеристик музыки: амплитуды ![]() , частоты
, частоты ![]() и время продолжительности
и время продолжительности ![]() . Таким образом, возникла форма
. Таким образом, возникла форма ![]() и, таким образом, анализируются музыкальные структуры гармонии и мелодии, образованные соответственно их гармоническими и мелодическими группировками, до тех пор, пока не будут получены операциональные свойства этих организаций в их физических явлениях. В группе, где эти музыкальные ноты излучаются одновременно, в пространстве или в одно и то же время, звуковые волны физически находятся в суперпозиции, вызывая интерференцию между ними, создавая таким образом звуковой эффект, называемый музыкантами Гармонией. Оценивая эту структуру в пространстве и времени, была разработана математическая операция, вызывающая это гармоническое явление, приняв базовые операции, возникшие в этой комплексной интерференции, за единую специальную операцию, называемую Гармонизирующая операция или Операция Г. В результате этой операции также была разработана его обратная операция, когда волны музыкальных нот излучаются непрерывно в пространстве или одна за другой во времени, создавая таким образом звуковой эффект, называемый музыкантами мелодией. Анализируя эту структуру в пространстве и времени, была также разработана математическая операция, порождающая это явление, называемая Мелодическая операция или Операция М, которая служит цели этого исследования, целью которого является предоставление Науке математического представления о музыкальных структурах гармоний и мелодий. Музыкальные, обеспечивающие, в общем, новые математические операция, которые могут объяснять явления Природы, упрощая их понимание Наукой.
и, таким образом, анализируются музыкальные структуры гармонии и мелодии, образованные соответственно их гармоническими и мелодическими группировками, до тех пор, пока не будут получены операциональные свойства этих организаций в их физических явлениях. В группе, где эти музыкальные ноты излучаются одновременно, в пространстве или в одно и то же время, звуковые волны физически находятся в суперпозиции, вызывая интерференцию между ними, создавая таким образом звуковой эффект, называемый музыкантами Гармонией. Оценивая эту структуру в пространстве и времени, была разработана математическая операция, вызывающая это гармоническое явление, приняв базовые операции, возникшие в этой комплексной интерференции, за единую специальную операцию, называемую Гармонизирующая операция или Операция Г. В результате этой операции также была разработана его обратная операция, когда волны музыкальных нот излучаются непрерывно в пространстве или одна за другой во времени, создавая таким образом звуковой эффект, называемый музыкантами мелодией. Анализируя эту структуру в пространстве и времени, была также разработана математическая операция, порождающая это явление, называемая Мелодическая операция или Операция М, которая служит цели этого исследования, целью которого является предоставление Науке математического представления о музыкальных структурах гармоний и мелодий. Музыкальные, обеспечивающие, в общем, новые математические операция, которые могут объяснять явления Природы, упрощая их понимание Наукой.
Ключевые слова: Гармонизация, Мелодическая, Гармония, Мелодия.
1. ВВЕДЕНИЕ
В начале 2006 года автор этого материала разработал Гармонизирующая операция для гармонических группировок звуковых волн гармоний музыкальных нот и Мелодическая операция для мелодических группировок звуковых волн своих мелодий.
Проблема, которая мотивировала создание этого материала и разработку этих операций, заключалась в отсутствии математической операции для объяснения взаимодействия волн, особенно между звуковыми волнами музыкальных нот. В этом контексте цель состоит в том, чтобы продемонстрировать операции, разработанные автором этого материала, составленные из трех важнейших характеристик Музыки: амплитуды ![]() , частоты
, частоты ![]() и продолжительности времени
и продолжительности времени ![]() .
.
Для развития этого первоначально считалось, что только для звуковых волн, а позднее вообще для любого другого элемента с вибрацией или без нее имеет место физическое явление «волновой суперпозиция», когда при столкновении двух равных волны, между ними происходит увеличение результирующей амплитуды (SILVA, без даты).
Используя выражение ![]() , сформулированное в этом исследовании для представления звуковой волны с характеристиками: амплитудой
, сформулированное в этом исследовании для представления звуковой волны с характеристиками: амплитудой ![]() , частотой
, частотой ![]() и длительностью
и длительностью ![]() , можно простым способом проанализировать интерференцию между двумя звуковые волны равны
, можно простым способом проанализировать интерференцию между двумя звуковые волны равны ![]() .
.
Когда они встречаются в общей точке ![]() , в этом случае их амплитуды складываются
, в этом случае их амплитуды складываются ![]() , оставаясь одной и той же частотой, с той же длительностью
, оставаясь одной и той же частотой, с той же длительностью ![]()
Оценивая результат этого явления интерференции, было замечено, что в точке встречи p суперпозиции между этими двумя волнами, в дополнение к существующей алгебраической сумме между их амплитудами ![]() , есть также союз между их частотами
, есть также союз между их частотами ![]() за это время, образуя единую звуковую волну, с амплитудой, частотой и временем продолжительности.
за это время, образуя единую звуковую волну, с амплитудой, частотой и временем продолжительности.
В этом первоначальном анализе также был сделан вывод, что эти две операции, сложение между амплитудами и объединение между частотами, в дополнение к формированию результата этого явления также объединяют единую математическую операцию, характеризуемую этой Оперативной Двойственностью. Этим объясняется одновременное испускание волн музыкальных нот, звуковой эффект которых называется Гармонией. Поэтому было принято название операции гармонизации или операции H, приняв левую косую черту (\) в качестве ее математического символа, называемого оператором Г ![]() . Происходя вместе с этим явлением, Принцип Гармонии, где элементы гармоничны, если между ними существует суперпозиция в их пространстве-времени.
. Происходя вместе с этим явлением, Принцип Гармонии, где элементы гармоничны, если между ними существует суперпозиция в их пространстве-времени.
Следовательно, была разработана его обратная работа, при которой звуковые волны выходят из состояния суперпозиции и переходят в непрерывное состояние, где конечное время одной волны равно начальному времени следующей волны![]() , и так далее
, и так далее ![]() , звуковой эффект которого музыканты называют Мелодией. Поэтому было принято название «Мелодия» или М-операция с правой косой чертой (/) в качестве математического символа, называемого М-оператором
, звуковой эффект которого музыканты называют Мелодией. Поэтому было принято название «Мелодия» или М-операция с правой косой чертой (/) в качестве математического символа, называемого М-оператором ![]() , порождая Первый Мелодия, где элементы мелодичны, если между ними существует непрерывность в их пространстве-времени.
, порождая Первый Мелодия, где элементы мелодичны, если между ними существует непрерывность в их пространстве-времени.
2. ОПЕРАЦИЯ ГАРМОНИЗАЦИИ (Г)
Вообще говоря, когда две или более ритмичных периодических волны ![]() , с разными частотами и амплитудами
, с разными частотами и амплитудами ![]() , находятся в эксплуатации Гармонизация или Г
, находятся в эксплуатации Гармонизация или Г ![]() они образуют гармоническую группу, называемую Гармонией
они образуют гармоническую группу, называемую Гармонией![]() , где результирующая частота
, где результирующая частота ![]() определяется операцией объединения между его частотами
определяется операцией объединения между его частотами ![]() и результирующая амплитуда
и результирующая амплитуда ![]() операцией сложения между их амплитудами
операцией сложения между их амплитудами ![]() , которые могут находиться в одной и той же фазе с одинаковыми знаками, в конструктивной интерференции, или в противоположных фазах с противоположными знаками, в деструктивной интерференции.
, которые могут находиться в одной и той же фазе с одинаковыми знаками, в конструктивной интерференции, или в противоположных фазах с противоположными знаками, в деструктивной интерференции.
Чем больше волн этих типов будет в этой операции, тем больше частот будет присоединено ![]() и больше амплитуд добавлено
и больше амплитуд добавлено ![]() в результате этой гармонии
в результате этой гармонии ![]() , как показано в примере ниже.
, как показано в примере ниже.
Операция Гармонизация и ее Гармония между три отчетливыми и ритмичными периодическими волнами:
2.1 СВОЙСТВА ЭКСПЛУАТАЦИИ Г (ГАРМОНИЗАЦИЯ)
2.2 МУЗЫКАЛЬНАЯ ГАРМОНИЯ
В операции гармонизации между звуковыми волнами, особенно ритмическими музыкальными нотами, где обычно гармония основного музыкального аккорда формируется трезвучием или тремя нотами с разными частотами ![]() , результирующее увеличение амплитуды является линейным (MORAIS, 2020).
, результирующее увеличение амплитуды является линейным (MORAIS, 2020).
Предполагая, что эти волны равны ![]() и тот факт, что интенсивность звука человеческого слуха является логарифмической со значением
и тот факт, что интенсивность звука человеческого слуха является логарифмической со значением ![]() (SANTOS, без даты), в этом случае его добавление незначительно, чтобы быть замеченным
(SANTOS, без даты), в этом случае его добавление незначительно, чтобы быть замеченным ![]() . Если эту дробь округлить до единицы
. Если эту дробь округлить до единицы ![]() , математически она как бы не существует в этой гармонии
, математически она как бы не существует в этой гармонии![]() .
.
Из-за этого явления и с учетом этого округления гармония этой операции формировалась только путем вычисления операции объединения между ее частотами![]() . Следовательно, для этого упрощенного результата нет необходимости знать интенсивность звука
. Следовательно, для этого упрощенного результата нет необходимости знать интенсивность звука ![]() , которая должна быть применена в гармонии с музыкальными нотами в операции Г, поскольку она может быть любой, без ущерба для гармонии этой операции.
, которая должна быть применена в гармонии с музыкальными нотами в операции Г, поскольку она может быть любой, без ущерба для гармонии этой операции.
Некоторые H-операции с музыкальными нотами, обозначаемыми их номерами, описаны ниже, где ноты Ля, Си, До, Ре, Ми, Фа и Соль л равны соответственно A, B, C, D, E, F, G,по произведению Guest (2020, стр. 33 до 41):
1) Вычислите гармонию между нотами: Фа ![]() и Си
и Си ![]() , как с двухсекундной продолжительностью, так и с нормальной интенсивностью звука.
, как с двухсекундной продолжительностью, так и с нормальной интенсивностью звука.
2) Вычисление гармонии между музыкальными нотами: До ![]() , Ми
, Ми ![]() и Соль
и Соль ![]() , все три секунды и нормальная интенсивность звука.
, все три секунды и нормальная интенсивность звука.
3) Вычислить гармонию между музыкальными нотами: Ля ![]() , До
, До ![]() , Ми
, Ми![]() и Соль
и Соль ![]() , все с продолжительностью в одну секунду и нормальной интенсивностью звука.
, все с продолжительностью в одну секунду и нормальной интенсивностью звука.
Примечание: в этом исследовании определено, что гармония названа с ее частотами в порядке возрастания и тоническим акцентом на последней частоте. Например,![]() это гармония Ля-До-Ми-Соль длительностью в одну секунду или аккорд Ля минор с септаккордом
это гармония Ля-До-Ми-Соль длительностью в одну секунду или аккорд Ля минор с септаккордом ![]() .
.
2.3 ЕДИНАЯ ГАРМОНИЯ
Унитарная гармония является результатом операции Г между двумя или более равными периодическими волнами ![]() , формирование гармонической группировки одной частоты
, формирование гармонической группировки одной частоты ![]() , с его результирующей амплитудой
, с его результирующей амплитудой ![]() и продолжительность времени
и продолжительность времени ![]()
Этот тип гармонии может выглядеть в этом пространстве-времени так, что в его структуре есть только одна периодическая волна, однако в нем сосуществуют две или более равные периодические волны, занимающие одно и то же пространство-время, составляющие Гармоническое Единое Множество, способное порождая в своей единой структуре две или более непрерывных равных периодических волны в новом пространстве-времени ![]() . В отличие от простого унитарного множества, образованного одной волной, где генерируется только одна волна его структуры
. В отличие от простого унитарного множества, образованного одной волной, где генерируется только одна волна его структуры ![]() .
.
Таким образом, две или более унитарных гармонии будут равны только ![]() , если все его характеристики и величины равны, и когда эта гармония образована только звуковыми волнами музыкальных нот, то она считается гармонией унисона
, если все его характеристики и величины равны, и когда эта гармония образована только звуковыми волнами музыкальных нот, то она считается гармонией унисона ![]() , путем формирования единого звука, с его частотой, амплитудой и временем продолжительности
, путем формирования единого звука, с его частотой, амплитудой и временем продолжительности ![]() , как показано в примерах ниже:
, как показано в примерах ниже:
1) Гармония унисона между четырьмя ритмическими волнами с одинаковыми частотами и разными амплитудами.
График 1: Гармония унисона График 1: Гармония унисона
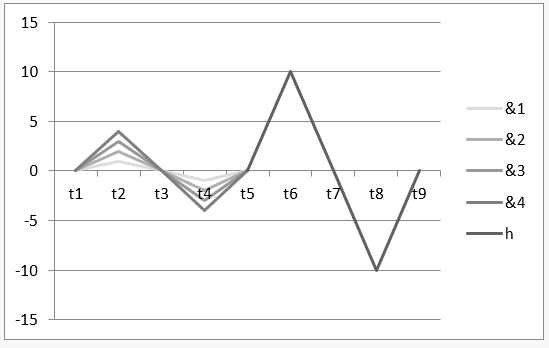
На графике 1 показан временной интервал от t1 до t5, который характеризует работу Г ![]() и, в интервале от t5 до t9 показывается результат операции или ее гармония
и, в интервале от t5 до t9 показывается результат операции или ее гармония ![]() .
.
2) Гармония с деструктивной интерференцией двух ритмических периодических волн:
График 2: Гармония с деструктивным вмешательством ![]()
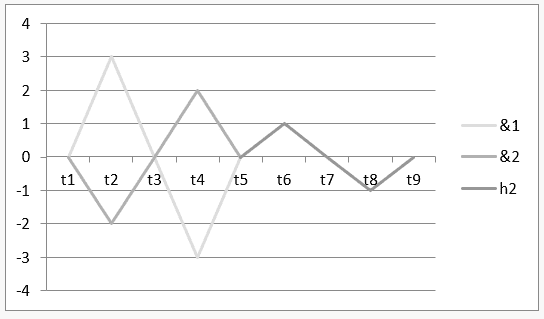
Интервал времени от t1 до t5, показанный на графике выше, представляет собой результат операции Г ![]() и, в интервале от t5 до t9 характеризуют результат этой операции или ее гармоничность
и, в интервале от t5 до t9 характеризуют результат этой операции или ее гармоничность ![]() .
.
3) Созидательная и разрушительная гармония между тремя волнами: ![]()
График 3: Гармония с конструктивным и деструктивным вмешательством ![]()
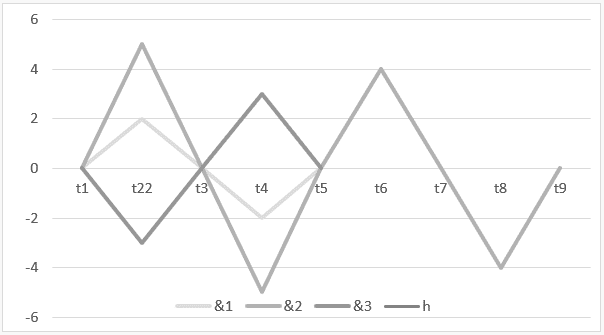
Интервал времени от t1 до t5 демонстрирует операцию Г ![]() и, в интервале от t5 до t9 изображается результат этой операции или ее гармония
и, в интервале от t5 до t9 изображается результат этой операции или ее гармония ![]() .
.
4) Гармония между пятью волнами музыкальных нот, равная ноте Соль, длиной две секунды.
2.4 ПУСТАЯ ГАРМОНИЯ
Пустая гармония является результатом операции Г между волной и ее противоположной волной или операции между несколькими волнами и их противоположными волнами ![]() , формирование гармонической группировки одной частоты
, формирование гармонической группировки одной частоты ![]() , с нулевой амплитудой
, с нулевой амплитудой ![]() и время продолжительности
и время продолжительности ![]()
Такая гармония ![]() , в этом пространстве-времени может показаться, что в его структуре нет периодической волны. Однако он сосуществует с результирующей частотой, с нулевой амплитудой
, в этом пространстве-времени может показаться, что в его структуре нет периодической волны. Однако он сосуществует с результирующей частотой, с нулевой амплитудой ![]() , в состоянии бесконечно мельчайшей вибрации в измерении времени, называемом Гармонической Изначальной Вибрацией (VHP), представленной отрицательным нулем
, в состоянии бесконечно мельчайшей вибрации в измерении времени, называемом Гармонической Изначальной Вибрацией (VHP), представленной отрицательным нулем ![]() , составляющий, таким образом, Гармонический Пустой Набор, называемый Наукой «Квантовым Вакуумом», способный генерировать в своей структуре более одной вибрации в пространстве-времени
, составляющий, таким образом, Гармонический Пустой Набор, называемый Наукой «Квантовым Вакуумом», способный генерировать в своей структуре более одной вибрации в пространстве-времени ![]() , в отличие от простого пустого множества, где ничего не существует и ничего нельзя сгенерировать.
, в отличие от простого пустого множества, где ничего не существует и ничего нельзя сгенерировать.
Таким образом, две пустые гармонии будут равны только в том случае, если их характеристики и количества равны. Какой бы ни была пустая гармония ![]() , считается нейтральным элементом операции гармонизации
, считается нейтральным элементом операции гармонизации ![]() , из-за того, что это только активное время продолжительности, которое скрывает одну или несколько неактивных вибраций или не может взаимодействовать с каким-либо активным элементом.
, из-за того, что это только активное время продолжительности, которое скрывает одну или несколько неактивных вибраций или не может взаимодействовать с каким-либо активным элементом.
Следовательно, результатом гармонии между любым нейтральным элементом и активным элементом является сам активный элемент ![]() , независимо от того, каково происхождение этого нейтрального элемента, если он с одинаковыми частотами
, независимо от того, каково происхождение этого нейтрального элемента, если он с одинаковыми частотами ![]() или с равными частотами
или с равными частотами ![]() , независимо от их продолжительности
, независимо от их продолжительности ![]() , ибо эти вибрации сосуществуют только в Измерении Времени.
, ибо эти вибрации сосуществуют только в Измерении Времени.
Когда эта гармония формируется звуковыми волнами от противоположных музыкальных нот, амплитуда звука полностью исключается из его частоты ![]() , порождая на своем месте тишину во времени, образуя гармонию тишины. В этом случае время его молчания воспринимается человеком, поскольку его продолжительность равна или превышает десятую долю секунды
, порождая на своем месте тишину во времени, образуя гармонию тишины. В этом случае время его молчания воспринимается человеком, поскольку его продолжительность равна или превышает десятую долю секунды ![]() , будучи этой гармонией, известной как музыкальный перерыв
, будучи этой гармонией, известной как музыкальный перерыв ![]() , что будет продемонстрировано на примерах ниже.
, что будет продемонстрировано на примерах ниже.
Когда эта гармония формируется световыми вибрациями, светимость амплитуды ее частоты полностью устраняется ![]() , породив на своем месте тьму во времени, называемую Гармонией Темной Энергия
, породив на своем месте тьму во времени, называемую Гармонией Темной Энергия ![]() и, вероятно, тьма, населяющая Вселенную, порождена этой гармонией, скрытой в ее безмерной Гармонической Пустоте.
и, вероятно, тьма, населяющая Вселенную, порождена этой гармонией, скрытой в ее безмерной Гармонической Пустоте.
1) Гармония между двумя волнами: ![]() , с его графиком в декартовой системе.
, с его графиком в декартовой системе.
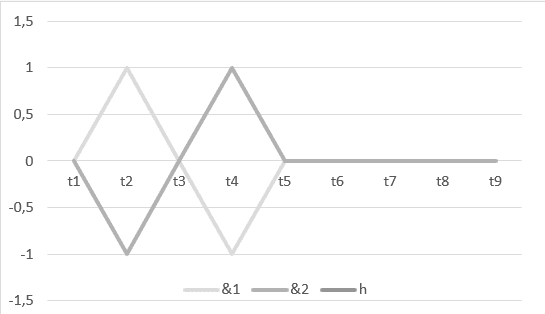
Интервал времени от t1 до t5, показанный на графике выше, представляет операцию Г ![]() и, диапазон от t5 до t9, является результатом этой операции или ее гармонии
и, диапазон от t5 до t9, является результатом этой операции или ее гармонии ![]() .
.
2) Гармония между музыкальными нотами: до, длительностью в одну секунду, с равными и обратными амплитудами ![]() .
.
Примечание: Пустая Гармония – это место в пространстве-времени, где есть мысль, что в нем ничего не существует, однако оно может быть наполнено неощутимыми вибрациями.
2.5 НЕСТАБИЛЬНАЯ ГАРМОНИЯ
Нестабильная гармония является результатом работы Г между двумя или более аритмическими периодическими волнами или с разной продолжительностью ![]() , где более короткая продолжительность образует гармонию этой операции
, где более короткая продолжительность образует гармонию этой операции ![]() , благодаря свойству ритма согласовывать длительности этой волны с наименьшей, оставляя часть длительности наибольшей
, благодаря свойству ритма согласовывать длительности этой волны с наименьшей, оставляя часть длительности наибольшей ![]() , где сохраняется сформированная гармония (/)
, где сохраняется сформированная гармония (/) ![]() .
.
Чем больше число этих аритмических волн при этой операции![]() , большей будет неустойчивость гармонии, образованной
, большей будет неустойчивость гармонии, образованной ![]() , com degradações em harmonias secundárias
, com degradações em harmonias secundárias ![]() , существует ли непрерывный остаток волны большей продолжительности
, существует ли непрерывный остаток волны большей продолжительности ![]() , по приведенным ниже примерам.
, по приведенным ниже примерам.
1) Неустойчивая гармония между двумя аритмическими волнами: ![]() , с его линейным графиком в декартовых координатах.
, с его линейным графиком в декартовых координатах.
График 5: Нестабильная гармония ![]()
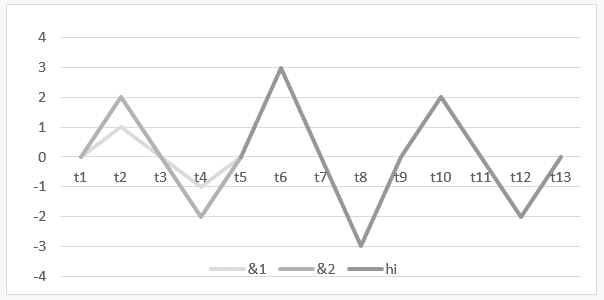
Интервал времени от t1 до t5 показывает график работы Г ![]() и, в интервале от t5 до t13 представлен результат этой операции или ее гармония
и, в интервале от t5 до t13 представлен результат этой операции или ее гармония ![]() .
.
2) Гармония между двумя аритмичными музыкальными нотами: ![]() , соответственно с их длительностью три
, соответственно с их длительностью три ![]() и два
и два ![]() секунды.
секунды.
3) Неустойчивая гармония между тремя аритмичными музыкальными нотами:![]() соответственно длительностью четыре, три и две секунды, с его графиком в системе декартовых осей.
соответственно длительностью четыре, три и две секунды, с его графиком в системе декартовых осей.
График 6: Нестабильная гармония ![]()
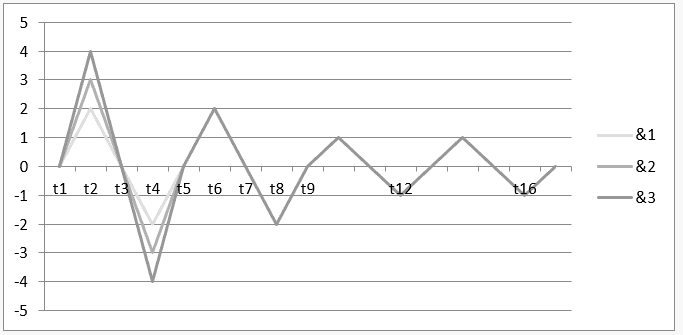
Интервал времени от t1 до t5 представляет собой график операции Г ![]() и, в интервале от t5 до t13 показывается результат этой операции или ее гармония
и, в интервале от t5 до t13 показывается результат этой операции или ее гармония ![]() .
.
4) Неустойчивая гармония между тремя аритмичными музыкальными нотами с одинаковыми частотами:
5) Нестабильная гармония с пустой гармонией между двумя волнами: ![]() один в три раза дольше другого
один в три раза дольше другого ![]()
График 7: Нестабильная гармония с пустой гармонией ![]()
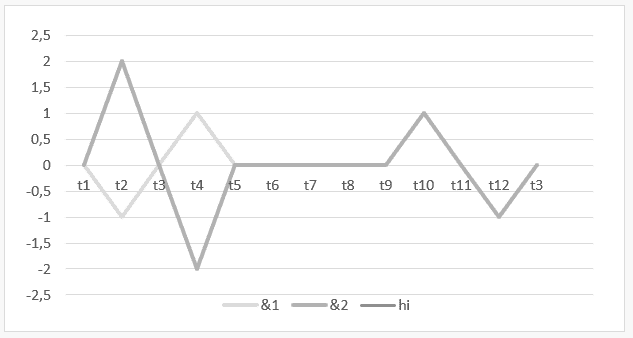
Интервал времени от t1 до t5 изображает операцию Г ![]() а в интервале от t5 до t13 показан результат этой операции или ее гармония
а в интервале от t5 до t13 показан результат этой операции или ее гармония ![]()
6) Гармония между двумя музыкальными нотами Г с одинаковой амплитудой в противоположных фазах, одна из которых длится три секунды, а другая — две секунды ![]()
2.6 ЧИСЛОВАЯ ГАРМОНИЯ
Когда две или более числовые константы ![]() находятся в операции Гармонизации или Г, они считаются ритмическими колебаниями и, поскольку они имеют только один параметр, который может быть либо частотой, либо амплитудой, они одновременно объединяются как частоты
находятся в операции Гармонизации или Г, они считаются ритмическими колебаниями и, поскольку они имеют только один параметр, который может быть либо частотой, либо амплитудой, они одновременно объединяются как частоты ![]() и добавлены как амплитуды
и добавлены как амплитуды ![]() формируя гармонию этой операции
формируя гармонию этой операции ![]()
Любой кластер, образованный комбинацией комбинаторного анализа, считается результатом Г-операции между этими элементами ![]() с результатом их амплитуды, подразумеваемой объединением между ними, как показано в примерах ниже.
с результатом их амплитуды, подразумеваемой объединением между ними, как показано в примерах ниже.
1) Гармония между числовыми константами 1 и 1
![]() Где написано: единица Г равна гармонии единицы с амплитудой два.
Где написано: единица Г равна гармонии единицы с амплитудой два.
2) Гармония между числовыми константами 1 и 1
![]() Где написано: Г минус единица равняется пустой гармонии.
Где написано: Г минус единица равняется пустой гармонии.
3) Гармонии между числовыми константами ![]()
![]() Где читается: три Г четыре равно гармонии три и четыре, с амплитудой семь или, согласно коммутативному свойству этой операции,
Где читается: три Г четыре равно гармонии три и четыре, с амплитудой семь или, согласно коммутативному свойству этой операции, ![]()
4) Гармонии между числовыми константами ![]()
![]() Где написано: Три Г четыре Г минус восемь равняется гармонии три, четыре и восемь с амплитудой минус один или, в соответствии с коммутативным свойством этой операции, любая группировка перестановок между этими тремя элементами с амплитудой минус один
Где написано: Три Г четыре Г минус восемь равняется гармонии три, четыре и восемь с амплитудой минус один или, в соответствии с коммутативным свойством этой операции, любая группировка перестановок между этими тремя элементами с амплитудой минус один ![]()
5) Гармонии между числовыми константами ![]()
![]() Где это читается: Два Г два Г минус два равно гармонии двух с амплитудой два, применяя ассоциативное свойство этой операции.
Где это читается: Два Г два Г минус два равно гармонии двух с амплитудой два, применяя ассоциативное свойство этой операции.
6) Гармонии между числовой константой ![]() и любой нейтральный элемент
и любой нейтральный элемент
Примечание: гармония операции H между любой числовой константой ![]() и любым нейтральным элементом
и любым нейтральным элементом ![]() сама числовая константа с амплитудой, равной ее значению
сама числовая константа с амплитудой, равной ее значению ![]() В этой операции мы знаем, что амплитуда нейтрального элемента равна нулю
В этой операции мы знаем, что амплитуда нейтрального элемента равна нулю ![]() но его частота не определена
но его частота не определена ![]() и даже если бы это было известно
и даже если бы это было известно ![]() она будет находиться во временном измерении, неспособном взаимодействовать ни с одним активным элементом любого измерения.
она будет находиться во временном измерении, неспособном взаимодействовать ни с одним активным элементом любого измерения.
3. ОПЕРАЦИЯ МЕЛОДИЯ ИЛИ ОПЕРАЦИЯ М
Мелодическая операция, или М, есть операция, обратная Гармонизация, потому что по окончании длительности гармонии периодические колебания, находившиеся в суперпозиции, переходят в состояние Непрерывности, то есть образуют непрерывность между своими пространствами. раз, где время окончания одной продолжительности равно времени начала следующей продолжительности ![]() это явление называется принципом мелодия.
это явление называется принципом мелодия.
Поэтому при двух и более периодических колебаниях ![]() остаться в эксплуатации М
остаться в эксплуатации М ![]() результатом является мелодическая группа, которая, если они представляют собой волны музыкальных нот, звуковой эффект приводит к мелодия
результатом является мелодическая группа, которая, если они представляют собой волны музыкальных нот, звуковой эффект приводит к мелодия ![]() и если эти элементы являются числовыми константами в операции М, то они также образуют непрерывную группу между собой, образуя числовую мелодию этой операции
и если эти элементы являются числовыми константами в операции М, то они также образуют непрерывную группу между собой, образуя числовую мелодию этой операции ![]() Таким образом, любая группировка, образованная массивом математики комбинаторного анализа, является результатом операции M, которая не является коммутативным свойством.
Таким образом, любая группировка, образованная массивом математики комбинаторного анализа, является результатом операции M, которая не является коммутативным свойством.
3.1 МЕЛОДИЯ С РАВНЫМИ ЧАСТОТАМИ И ПРОТИВОПОЛОЖНЫМИ АМПЛИТУДАМИ
Обычно музыкальные ноты в М-операции имеют амплитуду в положительной фазе, однако, если есть нота с амплитудой в отрицательной фазе, ее можно модулировать в положительную фазу, поскольку частота остается неизменной, производя тот же звуковой эффект в сформированная мелодия ![]()
Однако этот отрицательный знак может остаться в шифре ноты и в результате мелодии с точкой над ним ![]() Если этот элемент является отрицательной числовой константой в этой операция
Если этот элемент является отрицательной числовой константой в этой операция ![]() Он также может быть смодулирован в положительную сторону
Он также может быть смодулирован в положительную сторону ![]() или определил точку на константе в получившейся мелодия
или определил точку на константе в получившейся мелодия ![]()
3.2 МУЗЫКАЛЬНАЯ ЛОМАТЬ (p)
Музыкальная пауза — это музыкальная нота с нулевой амплитудой звуковой частоты, представленная отрицательным нулем ![]() Музыкальная пауза — это музыкальная нота с нулевой амплитудой звуковой частоты, представленная отрицательным нулем
Музыкальная пауза — это музыкальная нота с нулевой амплитудой звуковой частоты, представленная отрицательным нулем ![]() Он также может подразумеваться только в начале первого такта ритма и в конце последнего такта этого ритма, завершающего его периоды.
Он также может подразумеваться только в начале первого такта ритма и в конце последнего такта этого ритма, завершающего его периоды.
3.3 ПРИМЕРЫ РАБОТЫ M МЕЖДУ ВОЛНАМИ МУЗЫКАЛЬНЫХ НОТ
3.4 ПРИМЕНЕНИЕ РАСПРЕДЕЛИТЕЛЬНОГО СВОЙСТВА ОПЕРАЦИИ Г
Когда музыкальная нота начинается в одном такте и заканчивается в другом, не теряя звуковой непрерывности, ее продолженный шифр получает в следующем такте апостроф, например: ![]()
1) Ритмическое распределение:
2) Основное аритмическое распространение
3) Незначительное аритмическое распространение
3.5 ПРИМЕРЫ ОПЕРАЦИИ M С ЧИСЛОВЫМИ ПОСТОЯННЫМИ
4. АЛГЕБРА КОЛЕБАНИЙ
Алгебра Вибраций есть не что иное, как Алгебра с хотя бы одной из операций Гармонизации или Мелодии в ее выражении.
Даже если он не представляет ни одной из этих операций, его можно модулировать для Алгебры Вибраций с помощью доступных волновых модулей, таких как: Мелодический модуль ![]() , что превращает алгебраическое выражение в мелодию; гармонический модуль
, что превращает алгебраическое выражение в мелодию; гармонический модуль ![]() , который превращает алгебраическое выражение в гармонию; составной модуль
, который превращает алгебраическое выражение в гармонию; составной модуль ![]() , который преобразует алгебраическое выражение в мелодию с гармонией, чьи обычно аритмичные результаты модулируются под любой ритм.
, который преобразует алгебраическое выражение в мелодию с гармонией, чьи обычно аритмичные результаты модулируются под любой ритм.
Через стандартные модули ритма ![]() , которые организуют музыкальные ячейки в ритмические звуковые группы, добавляя их длительности через равные промежутки времени в тактах: Двоичный
, которые организуют музыкальные ячейки в ритмические звуковые группы, добавляя их длительности через равные промежутки времени в тактах: Двоичный ![]() , Тернарный
, Тернарный ![]() или четвертичный
или четвертичный ![]() . В этом случае первый и последний такты любого ритма могут быть неполными музыкальными нотами, как показано в примере ниже.
. В этом случае первый и последний такты любого ритма могут быть неполными музыкальными нотами, как показано в примере ниже.
Учитывая выражене: ![]() и числовые константы
и числовые константы ![]() и звонкий
и звонкий ![]() Значения вычисляются, числовые
Значения вычисляются, числовые ![]() , мелодичный
, мелодичный ![]() , гармонический
, гармонический ![]() это составлено
это составлено ![]()
4.1 РАСЧЕТ ЧИСЛЕННОГО ЗНАЧЕНИЯ E=x+3y−2z
4.2 РАСЧЕТ МЕЛОДИЧЕСКОЙ ЗВУКОВОЙ ЦЕННОСТИ E=x+3y−2z
Мелодический модуль ![]() преобразует числовое алгебраическое выражение в мелодическое алгебраическое выражение, заменяя все существующие операции M (/) операциями.
преобразует числовое алгебраическое выражение в мелодическое алгебраическое выражение, заменяя все существующие операции M (/) операциями.
Обычно аритмичный результат модулируется под любой ритм ![]() организовать музыкальные ноты в одном исполнения.
организовать музыкальные ноты в одном исполнения.
Примечание: операция M между числовой константой ![]() и звуковой константой
и звуковой константой ![]() равна мелодии звуковой константы
равна мелодии звуковой константы ![]() раз
раз ![]()
Модуль мелодического выражения ![]()
Четвертичный ритмический модуль в ![]()
Комментарий: выбор ритма необязателен, и, если был выбран троичный ритмический модуль, последняя нота будет разделена на часть в предпоследнем такте и другую непрерывную часть в последнем такте, обозначенную апострофом в своем шифре ![]()
4.3 ИНТЕРАКТИВНАЯ МЕЛОДИЧЕСКАЯ ЦЕННОСТЬ E=x+3y−2z
Когда в мелодическом модуле происходит замена как звуковых, так и числовых констант, результирующее мелодическое выражение называется интерактивным, поскольку оно включает физическую динамику как функцию числовой константы, как показано в примере ниже.
Данное выражение ![]() и константы
и константы ![]() Вычисляется его мелодическое значение.
Вычисляется его мелодическое значение.
![]() аритмичная интерактивная мелодия
аритмичная интерактивная мелодия
Примечание: числовое значение три (3) в первом такте обозначает любое физическое действие, например: счет от одного до трех тройным тактом и затем воспроизведение указанной мелодии в следующих тактах ![]() Этот счет в бинарном или четверичном ритме затрудняет исполнение этой сложной динамики, поэтому важно выбрать подходящий ритм для интерактивного мелодического выражения.
Этот счет в бинарном или четверичном ритме затрудняет исполнение этой сложной динамики, поэтому важно выбрать подходящий ритм для интерактивного мелодического выражения.
4.4 МЕЛОДИЧЕСКОЕ ЧИСЛОВОЕ ЗНАЧЕНИЕ E=x+3y−2z
Когда в модуле мелодии все константы являются числовыми, результатом является числовая мелодическая группировка, как показано в примере ниже.
![]() мелодическая числовая группировка
мелодическая числовая группировка
4.5 ГАРМОНИЧЕСКОЕ ЗВУКОВОЕ ЗНАЧЕНИЕ E=x+3y−2z
Гармонический звуковой модуль ![]() преобразует числовое алгебраическое выражение в гармоническое звуковое алгебраическое выражение, заменяя все существующие операции Г операциями (\). Результат, как правило, аритмичный, модулированный к любому ритму
преобразует числовое алгебраическое выражение в гармоническое звуковое алгебраическое выражение, заменяя все существующие операции Г операциями (\). Результат, как правило, аритмичный, модулированный к любому ритму ![]() за простоту его исполнения.
за простоту его исполнения.
Примечание: операция Г между числовой константой ![]() и звуковой константой
и звуковой константой ![]() равна гармонии унисона звуковой константы
равна гармонии унисона звуковой константы ![]()
Гармонический модуль ![]() выражения
выражения ![]()
![]()
4.6 ИНТЕРАКТИВНОЕ ГАРМОНИЧЕСКОЕ ЗНАЧЕНИЕ E=x+3y−2z
Когда в гармоническом модуле происходит замена как звуковых, так и числовых констант, результирующее гармоническое выражение называется интерактивным, поскольку оно включает физическую динамику как функцию числовой константы, как показано в примере ниже.
Гармоническое звуковое значение выражения вычисляется ![]() , учитывая константы
, учитывая константы ![]()
![]() гармония в троичном ритме за счет числовой константы
гармония в троичном ритме за счет числовой константы
Примечание: числовое значение три (3) в одиночном такте представляет любое физическое действие, например: счет от одного до трех в тройном размере при исполнении указанной гармония ![]() Этот счет в других ритмах делает исполнение этой динамики сложным и трудновыполнимым, поэтому очень важно выбрать ритм для интерактивного гармонического выражения.
Этот счет в других ритмах делает исполнение этой динамики сложным и трудновыполнимым, поэтому очень важно выбрать ритм для интерактивного гармонического выражения.
4.7 ГАРМОНИЧЕСКОЕ ЧИСЛОВОЕ ЗНАЧЕНИЕ E=x+3y−2z
Когда в гармоническом модуле все константы являются числовыми, результатом является числовая гармоническая группировка, как показано ниже.
4.8 ЦЕННОСТЬ ЗВУКА, СОСТАВЛЯЮЩАЯ ИЗ E=X+3Y−2Z
Композитный модуль ![]() преобразует числовое алгебраическое выражение в звуковые выражения с мелодиями и гармониями, заменяя все существующие операции операциями М и Г. Результат обычно аритмично модулируется под любой ритм
преобразует числовое алгебраическое выражение в звуковые выражения с мелодиями и гармониями, заменяя все существующие операции операциями М и Г. Результат обычно аритмично модулируется под любой ритм ![]() для его простого исполнения. При этом будет вариант, какие операции будут заменены звонкими, и при каждом выборе будет формироваться разное составное звуковое выражение, как показано в примере ниже.
для его простого исполнения. При этом будет вариант, какие операции будут заменены звонкими, и при каждом выборе будет формироваться разное составное звуковое выражение, как показано в примере ниже.
Составное звуковое значение выражения вычисляется ![]() замена первых двух операций
замена первых двух операций ![]() с помощью Г операций и двух последних
с помощью Г операций и двух последних ![]() M операций, для звуковых констант
M операций, для звуковых констант ![]()
![]() аритмическое звуковое составное выражение
аритмическое звуковое составное выражение
Уетверичный ритмический модуль для ![]()
4.9 ИНТЕРАКТИВНОЕ КОМПОНЕНТНОЕ ЗНАЧЕНИЕ E=x+3y−2z
Когда в составном модуле происходит замена как звуковых, так и числовых констант, результирующее составное звуковое выражение является интерактивным, поскольку оно включает физическую динамику через числовую константу, как показано в примере ниже.
Составное звуковое значение выражения вычисляется ![]() замена первых двух операций
замена первых двух операций ![]() с помощью Г операций и двух последних
с помощью Г операций и двух последних ![]() M операций, для числовых констант
M операций, для числовых констант ![]() и звонкий
и звонкий ![]()
![]() аритмическое звуковое составное выражение
аритмическое звуковое составное выражение
Уетверичный ритмический модуль для ![]()
4.10 ЧИСЛОВОЕ ЗНАЧЕНИЕ СОСТОИТ ИЗ E=x+3y−2z
Когда в составном модуле заменяются только числовые константы, результатом является числовая составная группировка, как показано в примере ниже.
5. НАУЧНЫЕ ГИПОТЕЗЫ АВТОРА
С развитием операции «Гармонизация» в данном исследовании возникли некоторые научные гипотезы, выдвинутые автором данного материала, относительно некоторых природных явлений.
5.1 ЧАСТИЧНО-ВОЛНОВАЯ ДВОЙНОСТЬ СВЕТА
Явление корпускулярно-волнового дуализма света, когда свет имеет характеристику либо волны, либо частицы, можно объяснить свойством Операционной Двойственности операции Гармонизации.
Известно, что свет – это гармония, образованная несколькими оттенками световых вибраций в операции Гармонизация или Г ![]() , где результирующая амплитуда имеет функцию сложения между амплитудами этих колебаний.
, где результирующая амплитуда имеет функцию сложения между амплитудами этих колебаний.
Чем больше число вибраций в этой операции, тем больше результирующая световая амплитуда ![]() , воздействуя этим количеством световой энергия на его частичную сторону, в то время как его волновая форма сохраняется в зависимости от работы Союза между частотами этих световых колебаний
, воздействуя этим количеством световой энергия на его частичную сторону, в то время как его волновая форма сохраняется в зависимости от работы Союза между частотами этих световых колебаний![]() , которые образуют гармоническую группировку гармонии этой операции
, которые образуют гармоническую группировку гармонии этой операции ![]() , влияет на его волновую сторону.
, влияет на его волновую сторону.
Из-за длины этих волн сохраняется такое равновесие между этими двумя характеристиками волны и частицы, чего не происходит со звуковой волной из-за ее большой длины волны по отношению к световой волне, при этом преобладает ее сторона. , относительно незначительности его стороны частицы.
5.2 ПРОИСХОЖДЕНИЕ ТЕМНОЙ ЭНЕРГИЯ
Явление Темной Энергия, существующее во Вселенной, может быть следствием Пустой Гармония, результатом операции Гармонизации между вибрациями противоположных светящихся частиц![]() , которые устраняют светимость этих вибраций
, которые устраняют светимость этих вибраций ![]() , порождая на своем месте Тьму, которая составляет Темную Энергию, где результирующая частота этой гармонии сосуществует в состоянии Гармонической Изначальной Вибрации (VPH) в Гармонической Пустоте, также называемой Квантовым Вакуумом.
, порождая на своем месте Тьму, которая составляет Темную Энергию, где результирующая частота этой гармонии сосуществует в состоянии Гармонической Изначальной Вибрации (VPH) в Гармонической Пустоте, также называемой Квантовым Вакуумом.
5.3 СТРУКТУРА ВРЕМЕНИ И СИЛА ЕЕ РАСШИРЕНИЯ
Интервал времени состоит из периода ![]() , формируется в начальный период
, формируется в начальный период ![]() и конец времени
и конец времени ![]() , чья разница между ними измеряет их продолжительность
, чья разница между ними измеряет их продолжительность ![]() Эти периоды неразрывно связаны, где время окончания одного периода равно времени начала следующего периода
Эти периоды неразрывно связаны, где время окончания одного периода равно времени начала следующего периода ![]() и так далее, составляя замкнутый интервал времени от прошедшего периода к настоящему периоду, и открытый в начале будущего периода, образуя его Пространство-Время
и так далее, составляя замкнутый интервал времени от прошедшего периода к настоящему периоду, и открытый в начале будущего периода, образуя его Пространство-Время ![]() , что по Принципу Мелодии равно операции М между этими прошедшими периодами
, что по Принципу Мелодии равно операции М между этими прошедшими периодами ![]() , подарок
, подарок ![]() и будущее
и будущее ![]()
Известно также, что начальный момент ![]() каждого периода характеризуется ритмом
каждого периода характеризуется ритмом ![]() , causado por um impulso intrínseco, dado por uma força com uma duração instantânea
, causado por um impulso intrínseco, dado por uma força com uma duração instantânea ![]() остается время тишины
остается время тишины ![]() до конца этого периода
до конца этого периода ![]() определяемого разницей между временем окончания этого периода и временем
определяемого разницей между временем окончания этого периода и временем ![]() избиение
избиение ![]() этого импульса
этого импульса ![]()
Следовательно, период может быть определен операцией M между ее биением и временем молчания ![]() Замена периодов вашими битами в пространстве-времени
Замена периодов вашими битами в пространстве-времени ![]() ритмическая Каденция Пространства-Времени формируется
ритмическая Каденция Пространства-Времени формируется ![]() чья скорость ударов, называемая ритмическим темпом
чья скорость ударов, называемая ритмическим темпом ![]() обратно пропорциональна его периоду
обратно пропорциональна его периоду ![]() измеряется в сердцебиении в единицу времени.
измеряется в сердцебиении в единицу времени.
Чем короче этот период ![]() чем больше ваш ритмический темп
чем больше ваш ритмический темп ![]() Это явление также способствует своим влиянием на Пространство-Время двум движениям в физических телах, находящихся в его поле действия, одно из которых называется Ритмическим Регентством
Это явление также способствует своим влиянием на Пространство-Время двум движениям в физических телах, находящихся в его поле действия, одно из которых называется Ритмическим Регентством ![]() где тело, не выходя из положения покоя, следует ударам Ритмичный темп
где тело, не выходя из положения покоя, следует ударам Ритмичный темп ![]() и еще один под названием Ритмический танец
и еще один под названием Ритмический танец ![]() когда тело перемещается из положения покоя в другое положение, также в зависимости от Ритмичный темп
когда тело перемещается из положения покоя в другое положение, также в зависимости от Ритмичный темп ![]() этой ритмической каденция.
этой ритмической каденция.
Учитывая период ![]() где время тишины равно нулю
где время тишины равно нулю ![]() мгновенное время импульса
мгновенное время импульса ![]() будет составлять его наименьшую продолжительность
будет составлять его наименьшую продолжительность ![]() следовательно, существует сила отталкивания
следовательно, существует сила отталкивания ![]() неявный в своей структуре, считается слабым в своей ритмической каденции в пространстве-времени
неявный в своей структуре, считается слабым в своей ритмической каденции в пространстве-времени ![]() однако способен отодвинуть любое небесное тело во Вселенной и продвигать своим Ритмическим Темпом, Ритмическим Дирижированием и Ритмическими Танцевальными движениями.
однако способен отодвинуть любое небесное тело во Вселенной и продвигать своим Ритмическим Темпом, Ритмическим Дирижированием и Ритмическими Танцевальными движениями.
Известно, что Вселенная расширяется и ее галактики удаляются друг от друга, что можно объяснить Силой Расширения Времени ее Ритмической Каденции ![]() и, учитывая, что орбиты галактик вокруг центра Вселенной примерно эллиптические, следовательно, их ускоренное расширение еще не объясняется из-за такого приближения к их центру тяжести, где, вероятно, существует гармония черных дыр, с их притяжением сила.
и, учитывая, что орбиты галактик вокруг центра Вселенной примерно эллиптические, следовательно, их ускоренное расширение еще не объясняется из-за такого приближения к их центру тяжести, где, вероятно, существует гармония черных дыр, с их притяжением сила.
Однако это ускорение должно перестать существовать после того, как галактики удалятся от этого центра, с замедлением и, достигнув самых больших орбит, сформируют неустойчивый край Вселенной, подобно неустойчивому жидкому пузырю, так как будут менять форму как функция бесконечностей максимальных афцентров этих галактик во всех направлениях относительно центра Вселенной.
5.4 СИНГУЛЯРНОСТЬ БОЛЬШОГО ВЗРЫВА И МРАЧНОСТЬ РЕЛИГИОЗНОЙ ТЕОРИЯ
Известно, что вся материя образована атомами, находящимися в постоянном колебании, которые, в свою очередь, образованы все более и более мелкими частицами, пока мы не достигнем мельчайшей из всех частиц материи, называемой Элементарной или Первичной Частицой (ANJOS, без даты), представлена в данном исследовании простой вибрацией ![]() с твоей частотой
с твоей частотой ![]() амплитуда
амплитуда ![]() и непрерывное время
и непрерывное время ![]() . Точно так же существует его первичная античастица
. Точно так же существует его первичная античастица ![]() антивещества с той же частотой
антивещества с той же частотой ![]() противоположная амплитуда
противоположная амплитуда ![]() и обратное время
и обратное время ![]() или гармоническое, то есть время идет не из настоящего в будущее в мелодической каденции, а из будущего в настоящее в гармонической каденции.
или гармоническое, то есть время идет не из настоящего в будущее в мелодической каденции, а из будущего в настоящее в гармонической каденции.
Эти светящиеся вибрации в Операция Г ![]() сформирует Первичную Единую Гармонию Тёмной Энергия, способную породить всю энергию материи и антиматерии, содержащуюся в её структуре, в состоянии Изначальной Гармонической Вибрации или в Гармонической Пустоте, также называемой Наукой Квантового Вакуума
сформирует Первичную Единую Гармонию Тёмной Энергия, способную породить всю энергию материи и антиматерии, содержащуюся в её структуре, в состоянии Изначальной Гармонической Вибрации или в Гармонической Пустоте, также называемой Наукой Квантового Вакуума ![]()
Поэтому для любой Теория Происхождения Вселенной всегда допускается существование точки происхождения всего, как, например, Сингулярности Большого Взрыва, Тьмы Религиозной Теория (Библия) или любой другой, что всегда приводит к Изначальная Единая Гармония Темной Энергия ![]() способный генерировать всю энергию для образования как Вселенной Материя
способный генерировать всю энергию для образования как Вселенной Материя ![]() в Ритмической Каденции Непрерывного Времени, с его Силой Расширения
в Ритмической Каденции Непрерывного Времени, с его Силой Расширения ![]() а также вся энергия в формировании Антиматерии или Нематериальной Вселенной
а также вся энергия в формировании Антиматерии или Нематериальной Вселенной ![]() в ритмической каденции
в ритмической каденции ![]() Гармонического Времени, называемого «Время Бога», с его Силой бесконечного притяжения.
Гармонического Времени, называемого «Время Бога», с его Силой бесконечного притяжения.
5.5 НУЛЕВОЕ ВРЕМЯ СОЗДАНИЯ ВСЕЛЕННОЙ
Промежуток времени, какой бы короткой ни была его продолжительность, всегда будет формироваться начальным временем с тактом ![]() , образован силой
, образован силой ![]() и время продолжительности удара больше нуля
и время продолжительности удара больше нуля ![]()
Учитывая это начальное время, можно сказать, что Вселенная зародилась в мгновенном ударе ![]() но до того, как случился этот бит, было нулевое или нулевое время
но до того, как случился этот бит, было нулевое или нулевое время ![]() а чтобы это было правдой, сначала должна быть Пустая Изначальная Гармония
а чтобы это было правдой, сначала должна быть Пустая Изначальная Гармония ![]() , образован бесконечными волнами-частицами материи в гармонии с бесконечными волнами-частицами антиматерии
, образован бесконечными волнами-частицами материи в гармонии с бесконечными волнами-частицами антиматерии ![]()
В этом случае непрерывное время материальной Вселенной ![]() находился также в гармонии со своим противоположным или антипродолжительным временем
находился также в гармонии со своим противоположным или антипродолжительным временем ![]() Вселенной антиматерии, что приводит к Нулевому Времени или Нулевому Времени
Вселенной антиматерии, что приводит к Нулевому Времени или Нулевому Времени ![]() в этой гармонии, полной энергия, накопленной на одной частоте в Гармонической Изначальной Вибрации.
в этой гармонии, полной энергия, накопленной на одной частоте в Гармонической Изначальной Вибрации.
Учитывая кратчайшее возможное время существования гармонии, с ее биением, образованным силой F с определенной интенсивностью ![]() получается, что время — это волна-частица, где
получается, что время — это волна-частица, где ![]() ее амплитуда
ее амплитуда ![]() и обратное время вашего удара – это ваша частота
и обратное время вашего удара – это ваша частота ![]() что в Гармония со своей противоположной волновой частицей, а также со своей противоположной амплитудой
что в Гармония со своей противоположной волновой частицей, а также со своей противоположной амплитудой ![]() и его частота
и его частота ![]() приводит к пустой гармония Нулевое время
приводит к пустой гармония Нулевое время ![]() о Начале Вселенной.
о Начале Вселенной.
5.6 ВСЕМОГУЩАЯ ЕДИНАЯ ГАРМОНИЯ
При формировании Материальной Вселенной непрерывное время с его силой расширения формировало бесчисленные отдельные частицы материи, посредством их комбинаций, с единственной первичной частицей ![]()
В случае формирования Вселенной Антиматерии антиконтинуальное или гармоническое время своей силой притяжения сформировало Первичную Единую Гармонию ![]() притягивая все первичные антивибрации в единую гармонию, способную породить всю свою структуру, формируя Нематериальную или Антиматерическую Вселенную
притягивая все первичные антивибрации в единую гармонию, способную породить всю свою структуру, формируя Нематериальную или Антиматерическую Вселенную ![]() следовательно, называется Всемогущей Унитарной Гармонией (Богом).
следовательно, называется Всемогущей Унитарной Гармонией (Богом).
6. ЗАКЛЮЧИТЕЛЬНЫЕ СООБРАЖЕНИЯ
С развитием операции Гармонизация и обратной ей операция Мелодия стало возможным создать математическую структуру для оценки музыкальных характеристик мелодии, а также гармонию, сделав Музыку не только искусством, но и частью Науки.
Также стало возможным использовать Алгебру не только с числовыми выражениями, но и звуковыми, образующими Алгебру Колебания, с взаимодействием числовых и звуковых величин в результате алгебраического выражения, позволяющим сопровождать физический акт мелодия или гармония, или даже мелодия в сопровождении гармонии
Также был предложен новый взгляд на Вселенную, через макро- и микроперспективу, через концепцию структур гармонических и мелодических вибраций, поскольку все есть вибрация. Таким образом, некоторые гипотезы, выдвинутые автором этого материала, были продемонстрированы для некоторых вопросов, до сих пор остающихся без ответа для Науки, таких как существование Бога.
ИСПОЛЬЗОВАННАЯ ЛИТЕРАТУРА
ANJOS, Talita Alves dos. Partículas elementares. Brasil Escola. Disponível em: https://brasilescola.uol.com.br/fisica/particulas-elementares.htm. Acesso em 21/03/2022.
GUEST, Ian. Harmonia – Método Prático. Editora Luminar. Vol. 1, p. 33 a 41, 2020.
MORAIS, Gustavo. Teoria musical para iniciantes: você sabe o que são os acordes? Terra, julho de 2020. Disponível em: https://www.terra.com.br/diversao/musica/teoria-musical-pra-iniciantes-voce-sabe-o-que-sao-os-acordes,7c62b1fa5e0fe37c8e0180310bc04200tnys05tj.html Acesso em: 20/03/2022.
SILVA, Domiciano Correa Marques da. Interferência de ondas. Brasil Escola. s.d. Disponível em: https://brasilescola.uol.com.br/fisica/interferencia-ondas.htm. Acesso em 17/03/2022.
SANTOS. Marco Aurélio da Silva. A Sensibilidade Auditiva. Mundo da educação. Disponível em: https://mundoeducacao.uol.com.br/fisica/a-sensibilidade-auditiva.htm. Acesso em: 20/03/2022.
[1] Окончил электротехнику. Электроника от Федерального университета Пара-UFPA. ORCID: 0000-0001-7010-9114.
Отправлено: февраль 2022 г.
Утверждено: Март 2022 г.