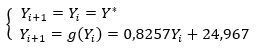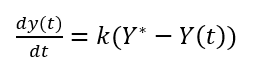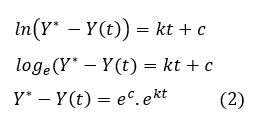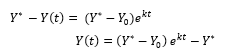ARTIGO ORIGINAL
MACHADO, Carlos Antônio Moraes [1]
MACHADO, Carlos Antônio Moraes Machado. Ajustes Exponencial e Geométrico Para Modelagem do Desmatamento na Amazônia Legal Mato-Grossense, Período de 2005 a 2016. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano 03, Ed. 10, Vol. 09, pp. 107-122 Outubro de 2018. ISSN:2448-0959
RESUMO
O objetivo foi desenvolver modelos, baseado nas séries temporais de crescimento populacional, de modo que, uma das funções tenha melhor desempenho com menor erro possível, no ajuste dos dados de desmatamento, ocorrido na região da Amazônia Legal no Estado de Mato Grosso, período de 2005 a 2016. A evolução do desmatamento depende da capacidade limite ou, quantidade de floresta preservada assim, para o primeiro e segundo modelos, esse limite ou, valor assintótico, será calculado pela equação da reta de regressão linear, obtida por meio da aplicação da técnica de Ford-Walford. O limite de desmatamento para terceiro modelo será o quantitativo de floresta amazônica preservada, registrada pelo INPE no ano de 2016. Independente dos valores assintóticos, o quarto modelo, será desenvolvido por função potência, aplicando a técnica de mudança de variáveis. Todos os ajustes foram avaliados estatisticamente. Os valores obtidos nas medidas do erro quadrático médio e, erro médio percentual para o primeiro e segundo modelos foi muito próximo, resultando em curvas com comportamento similar. Para o terceiro modelo, esses valores foram discrepantes. As melhores medidas estatísticas e, portanto, o melhor ajuste, foi obtido pelo quarto modelo e, com previsões para no máximo até 2018.
Palavras-chave: Ford-Walford, Previsão, Desmatamento.
INTRODUÇÃO
Desde o início da colonização do Brasil florestas vêm sendo destruídas em nome do progresso, da manutenção e expansão das fronteiras agrícolas, da agropecuária, da indústria madeireira, enfim na busca de recursos que possibilitem movimentar a economia e proporcionar lucro.
A Amazônia Legal possui elevada diversidade de espécies de fauna e flora, sendo constituída por nove Estados brasileiros. Tornou-se alvo de intensa exploração tendo taxas de desmatamento elevadas (JUNIOR et al., 2017).
Os resultados mostram que o desflorestamento está associado ao fortalecimento dos sistemas de uso da terra, devido à sua intensificação e, em alguns casos, ao estabelecimento de sistemas de produção voltados para a agricultura intensificada, sugerindo um cenário de expansão da fronteira agrícola semelhante ao que ocorreu no Centro Sul do país (SILVEIRA JUNIOR, 2008). Uma grande parte da floresta amazônica no Estado de Mato Grosso foi e, está sendo convertida em áreas agrícolas e pastoris, acarretando na destruição da fauna e flora desse ecossistema. Segundo FERREIRA et al. (2005), o desmatamento resulta a abertura de estradas pioneiras, o crescimento das cidades, a ampliação de pecuária extensiva, a acelerada exploração madeireira e a crescente agricultura intensiva de monoculturas.
O entendimento do comportamento dos fenômenos ocasionados pelos impactos do homem sobre a natureza, ao longo do tempo, tem instigado pesquisadores na busca de modelos matemáticos que permitam, conforme MEDEIROS E COUTINHO (2013), compreensão e reprodução do mundo real. Fenômenos naturais e antrópicos, não pode ser representado de maneira exata em toda sua complexidade BASSANEZI (TEMAS e MODELOS, P. 61) mas, pretende construir simulações sobre determinada taxa de variação, permitindo elaboração de políticas públicas de controle.
Os modelos matemáticos são utilizados constantemente na solução de problemas da atualidade, explicam de forma quantitativa e qualitativa os fenômenos da vida (BEZERRA et. Al. 2016). A exploração desenfreada da floresta amazônica brasileira, um grande problema, obrigatoriamente deve ser objeto de estudo e controle por parte das autoridades competentes. O uso racional da floresta deve ser entendido como uma saída para reduzir os efeitos das ações que desencadeiam os desmatamentos. Órgãos governamentais como, o Instituto de Pesquisas Espaciais – INPE, disponibilizam, informações relevantes e de caráter científico, obtidos por meio de levantamento rápido de alertas de evidências de alteração da cobertura florestal na Amazônia, além de estimativas anuais de emissões de gases do efeito estufa – GEE. Apesar dos estragos causados à floresta amazônica, as ações de melhoramentos recentes na legislação ambiental e no seu cumprimento, e nas políticas e atitudes públicas, têm reduzido fundamentalmente a ameaça sobre as florestas (LAURENCE et al., 2017).
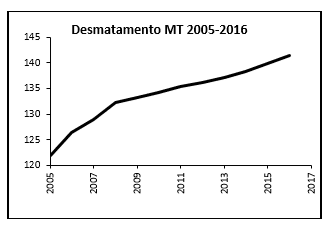
Fig. 1 – Curva do Desmatamento, função discreta Yi = f (xi).
Na figura 1, pode ser observada a curva de evolução do desmatamento para no Estado de Mato Grosso – Amazônia Legal, no período de 2005 a 2016. Esse conjunto de informações pode ser modelado, de tal forma que, permitam interpretação, análise e criação de propostas de controle para manutenção dessa biodiversidade. É bem verdade que, em muitos casos, inclusive para o desmatamento, não se conhece a fórmula da função que seria a solução para o problema estudado (NUNES E MELO, 2017). Complexo ou não, por necessidade, sempre haverá uma alternativa para solução do problema, pois, em qualquer atividade, o planejamento se faz necessário para se obter resultados satisfatórios, auxiliam no estudo da previsão de demanda entre outras estatísticas e assume um papel importante no planejamento operacional (SERRA, 2005). Segundo TAVONI (2013), nas situações do dia-a-dia, como: crescimento populacional, financiamento de um carro ou casa, absorção de um remédio, datação por carbono, resfriamento de um corpo, etc., os ajustes podem ser feitos por logaritmos e exponenciais.
Assim, devido sua importância, modelos matemáticos, tem sido eficiente para o planejamento e avaliação das interferências do homem sobre a natureza e, sobre suas atividades rotineiras, sendo estratégias utilizadas para obtermos alguma explicação ou entendimento de determinadas situações reais (BASSANEZI, 2002, p. 31). Complexo e de natureza relevante, o desmatamento, deve ser objeto de outros estudos que sejam mais abrangentes, levando-se em conta que, essa atividade degradante atinge toda a Amazônia Legal Brasileira.
MÉTODOS
O trabalho foi elaborado a partir das informações sobre desmatamentos fornecidos pelo Instituto de Pesquisas Espaciais – INPE, projeto PRODES, responsável pelo monitoramento da Amazônia Legal brasileira desde 1988. As taxas de desmatamento, período 2005 a 2016, fornecidas pelo PRODES, estão em km2. Os dados reais brutos são anuais e não cumulativos, desde 1988 e, foram modificados para este trabalho, em anuais e cumulativos. Segundo SODRÉ (2007), em seu trabalho, concluiu que as variáveis ambientais não tiveram influência sobre a população estudada. Conforme GRACIAS E LOURENÇO, (2010), o estudo da dinâmica populacional, não se restringe somente a compreensão de variações. Resultados preliminares podem ser obtidos por meio de “dados brutos”, porém, se o objetivo for determinar as causas que deram origem, por exemplo, ao desmatamento então, será necessário considerar todas as variáveis envolvidas no processo.
Para o desenvolvimento dos modelos de ajuste dos dados de desmatamento, foram considerados apenas os valores oficiais registrados, sem a identificação quantitativa das variáveis responsáveis pelo processo. Uma tabela é apresentada ao final da construção dos fundamentos matemáticos, mostrando a evolução de cada modelo e, os valores reais do desmatamento (Yi).
1. AJUSTE DE CURVAS
SÉRIES TEMPORAIS
O registro de (Yi) observações sucessivas, em (xi) instantes distintos, determina uma série temporal; temos então que Yi = f(xi). Dados, cronologicamente organizados permitem compreensão do comportamento passado e projeções para o futuro, por meio de uma reta ou de uma função matemática, utilizando o método de análise de regressão.
Sobre o conjunto de variáveis a ser estudado o pesquisador, intuitivamente, deverá examinar o comportamento (grandeza, média e variação), identificando a existência de uma relação funcional, que permita a elaboração de modelos para interpretação dos dados obtidos, com boa aproximação.
2. CAPACIDADE LIMITE, DEFINIDA PELO MÉTODO FORD-WALFORD E MODELO1
O valor assintótico, do desmatamento (Y*), foi calculado utilizando a método de Ford-Walford. Um ajuste exponencial foi determinado pela diferença entre a capacidade de suporte (Y*) e os valores anuais de desmatamento (Yi). Na hipótese de um crescimento assintótico de Yi, a função que ajusta xi e Yi será:
((Y*) – (Y*-Yi)).
Dado o conjunto de pontos (xi, Yi), i = 1, 2, 3, 4… (tabela 1), e a sequência Yi = f(xi) como sendo de crescimento assintótico, e considerando que Yi é convergente quando xi cresce. Yi tende para o valor assintótico Y*, assim,
O ajuste dos pares (Yi, Yi+1), por uma função g, de modo que Yi+1 = g (Yi), dado que:
nos diz que a sequência de pontos do plano (Yi , Yi+1), converge para (Y*, Y*), sendo Y* o ponto fixo da função g: Y* = g (Yi). Y* é tal que: Yi+1 ≈ Yi. Y* é o limite da sequência Yi, quando:
a função que ajusta os dados de desmatamento (Yi , Yi+1) é dada por: g(Yi) = 0,8257Yi + 24,967. Resolvendo o sistema,
temos,
Yi+1 =Yi = Y* = 143,242.
O valor assintótico Y* = 143,242, deve satisfazer:
A curva dada pelos pontos (xi, Yi), tem a característica de uma exponencial monótona crescente e convergente, estabilizando com valor limite dado por Y* = 143,242. A função que ajusta xi e Yi é dada por:
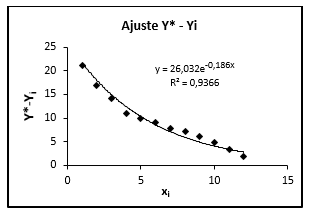
Figura 2 – Curva auxiliar – Função de ajuste de (xi, Yi)
substituindo os valores calculados de Y* e k, obtemos o Modelo1 de crescimento exponencial assintótico:
| Ano | Yi | xi | Y(i+1) | Y* – Yi | Modelo1 |
| 2005 | 122,036 | 1 | 126,369 | 21,20553758 | 121,6278554 |
| 2006 | 126,369 | 2 | 129,047 | 16,87253758 | 125,2962679 |
| 2007 | 129,047 | 3 | 132,305 | 14,19453758 | 128,342054 |
| 2008 | 132,305 | 4 | 133,354 | 10,93653758 | 130,8708898 |
| 2009 | 133,354 | 5 | 134,225 | 9,887537579 | 132,9705154 |
| 2010 | 134,225 | 6 | 135,345 | 9,016537579 | 134,7137791 |
| 2011 | 135,345 | 7 | 136,102 | 7,896537579 | 136,1611649 |
| 2012 | 136,102 | 8 | 137,241 | 7,139537579 | 137,3628911 |
| 2013 | 137,241 | 9 | 138,316 | 6,000537579 | 138,3606526 |
| 2014 | 138,316 | 10 | 139,917 | 4,925537579 | 139,1890677 |
| 2015 | 139,917 | 11 | 141,406 | 3,324537579 | 139,8768788 |
| 2016 | 141,406 | 12 | 1,835537579 | 140,4479503 |
Tabela 1 – Cálculo da capacidade limite e Modelo1.
3. SEGUNDO MODELO MATEMÁTICO, COM ESTABILIDADE EM Y*
O valor limite, calculado para construção do modelo1, e o valor da constante k, obtida no ajuste dos pontos Y* – Yi , foram usados para a elaboração do segundo modelo, desenvolvido a partir das equações diferenciais. Temos que, a taxa de variação do desmatamento em função do tempo, dada por:
Expressão nos diz que: o crescimento do desmatamento em função do tempo é, proporcional quantidade de floresta. Quanto maior for a diferença entre a capacidade de suporte (Y*) e a quantidade inicial de área desmatada (Y0), maior será a taxa de desmatamento.
Desenvolvendo a função (1), aplicando técnicas de integração nos dois membros da expressão, obtemos:
que de ajuste dos dados Yi. Substituindo o valor da constante de desmatamento k = – 0,186, o valor do desmatamento inicial Y0 = 122,036 e, a capacidade limite Y* = 143,2415, obtemos o Modelo 2:![]()
| Yi | xi | (Y*-Y0)*e-kt | Modelo2 | |
| 2005 | 122,036 | 0 | 21,20553758 | 122,036 |
| 2006 | 126,369 | 1 | 17,60639792 | 125,6351397 |
| 2007 | 129,047 | 2 | 14,6181273 | 128,6234103 |
| 2008 | 132,305 | 3 | 12,1370451 | 131,1044925 |
| 2009 | 133,354 | 4 | 10,07706807 | 133,1644695 |
| 2010 | 134,225 | 5 | 8,366723532 | 134,874814 |
| 2011 | 135,345 | 6 | 6,946669625 | 136,294868 |
| 2012 | 136,102 | 7 | 5,767636363 | 137,4739012 |
| 2013 | 137,241 | 8 | 4,788716178 | 138,4528214 |
| 2014 | 138,316 | 9 | 3,975944596 | 139,265593 |
| 2015 | 139,917 | 10 | 3,301121813 | 139,9404158 |
| 2016 | 141,406 | 11 | 2,740834275 | 140,5007033 |
Tabela 2 – Dados Yi e ajuste Modelo 2.
4. MODELO DA ESTIMATIVA DA EVOLUÇÃO DO DESMATAMENTO, USANDO EQUAÇÕES DIFERENCIAIS ORDINÁRIAS – EDO
Também uma expressão matemática, onde não foram aplicados os valores de estabilidade calculados pelo método de Ford-Walford e a constante de desmatamento k.
Foram determinadas as constantes de proporcionalidade e considerado o valor do quantitativo de floresta preservada (valor limite de desmatamento) para o ano de 2016, conforme dados do INPE.
Uma equação diferencial é dita ordinária (EDO) se a função incógnita depender apenas de uma variável. A equação diferencial autônoma dada por:
“A taxa de variação da área de Floresta é proporcional à diferença entre a área de Floresta e o Desmatamento”,
Integrando ambos os lados de (1), obtemos o modelo matemático obtido por meio de equações diferenciais:
a constante c, foi determinada fazendo t = 0 e Fd = 122,036 km2. Para determinação da constante de proporcionalidade k, t = 13, e Fd = 141,406 km2. Foi considerado o valor limite de desmatamento, o quantitativo oficial de floresta de 312,297 km2, no ano de 2016 (INPE).
desenvolvendo a expressão, obtemos as constantes c = -190,261 e k = – 0,0083. A expressão geral fica do Modelo3 fica:
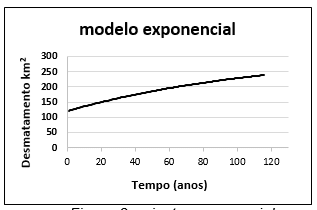
Figura 3 – ajuste exponencial
A curva resultante do ajuste exponencial 3, gráfico 3, cresce lentamente e exponencialmente até a estabilidade
Fp.
| Ano | Yi | xi | Modelo3 |
| 2005 | 122,036 | 0 | 122,036 |
| 2006 | 126,369 | 1 | 123,6086309 |
| 2007 | 129,047 | 2 | 125,1682629 |
| 2008 | 132,305 | 3 | 126,7150036 |
| 2009 | 133,354 | 4 | 128,2489594 |
| 2010 | 134,225 | 5 | 129,7702361 |
| 2011 | 135,345 | 6 | 131,2789385 |
| 2012 | 136,102 | 7 | 132,7751704 |
| 2013 | 137,241 | 8 | 134,2590351 |
| 2014 | 138,316 | 9 | 135,7306346 |
| 2015 | 139,917 | 10 | 137,1900704 |
| 2016 | 141,406 | 11 | 138,637443 |
Tabela 3 – Ajuste exponencial e dados reais (Yi)
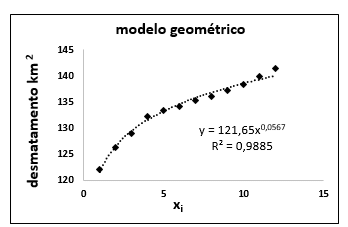
5. AJUSTE LINEAR GEOMÉTRICO
O modelo quatro, não depende dos valores assintóticos e, das constantes calculadas para os ajustes anteriores. Pode ser definido por uma função potência:
com os parâmetros a e b, obtidos por meio de mudança de variável.
obtemos a expressão:
b e a foram determinados por:
obtemos a reta ajustada:
substituindo os valores de a e b em (1), obtemos o Modelo 4:
Figura 4 – Ajuste geométrico de Yi
| Ano | Yi | xi | X = log xi | Y = log yi | X^2 | XY | Modelo4 |
| 2005 | 122,036 | 0 | 0 | 4,804316083 | 0 | 0 | 121,65 |
| 2006 | 126,369 | 1 | 0,693147181 | 4,839206198 | 0,480453014 | 3,354282133 | 126,5262143 |
| 2007 | 129,047 | 2 | 1,098612289 | 4,860176679 | 1,206948961 | 5,339449825 | 129,4687302 |
| 2008 | 132,305 | 3 | 1,386294361 | 4,885109863 | 1,921812056 | 6,772200257 | 131,5978866 |
| 2009 | 133,354 | 4 | 1,609437912 | 4,893007246 | 2,590290394 | 7,874991368 | 133,2734722 |
| 2010 | 134,225 | 5 | 1,791759469 | 4,899517496 | 3,210401996 | 8,778756869 | 134,6583502 |
| 2011 | 135,345 | 6 | 1,945910149 | 4,907827074 | 3,786566308 | 9,550190513 | 135,8404689 |
| 2012 | 136,102 | 7 | 2,079441542 | 4,913404605 | 4,324077125 | 10,21713765 | 136,8728516 |
| 2013 | 137,241 | 8 | 2,197224577 | 4,921738504 | 4,827795843 | 10,81416481 | 137,7899884 |
| 2014 | 138,316 | 9 | 2,302585093 | 4,929540923 | 5,30189811 | 11,35068744 | 138,6156013 |
| 2015 | 139,917 | 10 | 2,397895273 | 4,94104939 | 5,749901739 | 11,84811897 | 139,3667198 |
| 2016 | 141,406 | 11 | 2,48490665 | 4,951635185 | 6,174761058 | 12,3043512 | 140,0559907 |
Tabela 4 – Ajuste Linear Geométrico de Yi
CONCLUSÃO
Foi utilizado o Erro Relativo Percentual – ERP, para medir os desvios quantitativos previstos de desmatamento em torno dos valores reais. Valores de ERP negativos indicam que, os resultados do ajuste foram numericamente inferiores aos valores reais e, nos erros por excesso, os resultados dos ajustes foram superiores aos registros anuais. No primeiro e segundo modelos, a distribuição dos desvios em torno da curva de dados reais obtiveram erro absoluto médio de 0,04% e -0,14% respectivamente. O pior resultado foi do modelo três, 2,7% e, a melhor média foi do quarto ajuste com -0,004%. A distribuição anual dos erros e os valores dos ajustes podem ser vistos nas tabelas 5 e 5.a.
| Ano | Yi | Modelo1 | ERP | Modelo2 | ERP | |||
| 2005 | 122,036 | 121,6278554 | -0,334446103% | 122,036 | 0 | |||
| 2006 | 126,369 | 125,2962679 | -0,848888622% | 125,6351397 | -0,580728138% | |||
| 2007 | 129,047 | 128,342054 | -0,546270707% | 128,6234103 | -0,328244528% | |||
| 2008 | 132,305 | 130,8708898 | -1,083942543% | 131,1044925 | -0,907378801% | |||
| 2009 | 133,354 | 132,9705154 | -0,287568884% | 133,1644695 | -0,142125838% | |||
| 2010 | 134,225 | 134,7137791 | 0,36414905% | 134,874814 | 0,484122963% | |||
| 2011 | 135,345 | 136,1611649 | 0,603025497% | 136,294868 | 0,701812371% | |||
| 2012 | 136,102 | 137,3628911 | 0,926430961% | 137,4739012 | 1,007994898% | |||
| 2013 | 137,241 | 138,3606526 | 0,81582953% | 138,4528214 | 0,882987884% | |||
| 2014 | 138,316 | 139,1890677 | 0,6312123445% | 139,265593 | 0,686538783% | |||
| 2015 | 139,917 | 139,8768788 | -0,0286749895% | 139,9404158 | 0,016735469% | |||
| 2016 | 141,406 | 140,4479503 | -0,677517042% | 140,5007033 | -0,64021095% | |||
Tabela 5 – Erro Percentual Médio dos Modelos 1 e 2.
| Ano | Yi | Modelo3 | ERP | Modelo4 | ERP |
| 2005 | 122,036 | 122,036 | 0 | 121,65 | -0,316300108% |
| 2006 | 126,369 | 123,7406665 | -2,184372074% | 126,5262143 | 0,124408914% |
| 2007 | 129,047 | 125,4300598 | -3,005677861% | 129,4687302 | 0,326803533% |
| 2008 | 132,305 | 127,1043168 | -4,225083288% | 131,5978866 | -0,534457049% |
| 2009 | 133,354 | 128,7635731 | -3,828187078% | 133,2734722 | -0,060386516% |
| 2010 | 134,225 | 130,4079631 | -3,318877922% | 134,6583502 | 0,322853536% |
| 2011 | 135,345 | 132,03762 | -3,004219976% | 135,8404689 | 0,366078493% |
| 2012 | 136,102 | 133,6526758 | -2,444364939% | 136,8728516 | 0,566377891% |
| 2013 | 137,241 | 135,2532612 | -2,172794529% | 137,7899884 | 0,400017773% |
| 2014 | 138,316 | 136,8395061 | -1,869173066% | 138,6156013 | 0,216606403% |
| 2015 | 139,917 | 138,4115388 | -1,948962329% | 139,3667198 | -0,393290425% |
| 2016 | 141,406 | 139,9694866 | -1,957878033% | 140,0559907 | -0,954704393% |
Tabela 5.a – Erro Percentual Médio dos Modelos 3 e 4
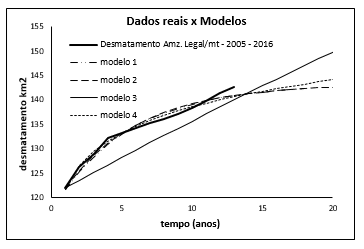
As diferenças entre os valores do EMA e EQM, para os modelos 1 e 2, foram mínimas, mostrando que o ajuste da curva exponencial para os dois modelos, tem comportamento muito similares até a capacidade limite, figura 5.
O terceiro modelo apresentou estimativas discrepantes em todas as análises realizadas. Os melhores resultados foram obtidos pelo modelo quatro, com erros absoluto, médio e quadrático menores. O módulo do erro médio absoluto, do erro quadrático médio e, resíduos podem ser vistos na tabela 6.
| MEDIDAS | Modelo1 | Modelo2 | Modelo3 | Modelo4 |
| |EMA| | 0,797678637 | 0,717433178 | 2,668027683 | 0,516761299 |
| EQM | 0,787352655 | 0,71600734 | 9,173197006 | 0,366836615 |
| RESÍDUOS | Não aleatório | Não aleatório | Não aleatório | Aleatório |
Tabela 6. Medidas Estatísticas
Para os modelos 1, 2 e 3, os resíduos apresentaram comportamento padronizado, ou seja, não há independência nos pontos. A melhor distribuição foi do quarto modelo, com pontos não padronizados no gráfico desmatamento x resíduos padronizados.
Figura 5 – Ajustes e curva de dados reais
Com base nos resultados obtidos, o melhor ajuste para o intervalo 2005-2016, foi o obtido pela função potência (ajuste geométrico), que não usou a capacidade limite dos demais modelos. Nos ajustes 1, 2 e 3, as variações das taxas anuais dos valores previstos de desmatamento, decrescem exponencialmente, tendendo para o valor assintótico, sendo impróprios para previsões, pois, apresentam taxas de crescimento distorcidas da realidade. No modelo quatro, as variações das taxas anuais de desmatamento dos dados ajustados, foram muito próximas das obtidas para os valores reais até, 2012, a partir daí as diferenças aumentam, por conta da diminuição da variação anual do desmatamento previsto pelo modelo. Essa inconsistência na variação da taxa de crescimento produzida pelo modelo é uma indicação de que suas previsões não serão confiáveis, apesar de melhor ajuste. Na figura 5, pode ser observada a dispersão das curvas de ajuste em relação aos dados reais, a partir de 2015, mostrando visualmente o tamanho do erro cometido pelos modelos.
Embora os resultados não tenham sido satisfatórios, pretende esse trabalho servir de motivação para a produção de outros estudos que envolvam não só, o registro puro do quantitativo degradado de floresta, mas, todas as demais variáveis envolvidas no processo.
REFERENCIAS
Medeiros, Rodrigo de Vasconcellos; Coutinho, Eliane dos Santos de Souza, 2013. Ajuste de Curvas e Modelagem Populacional de Petrópolis no Período de 1982 a 1990.
Disponível em: <https://www.researchgate.net/publication/282869792>. Acesso em: 14 de setembro de 2017.
LAURENCE, William F; ALBERNAZ, Ana K. M.; COSTA, Carlos da. O DESMATAMENTO ESTÁ SE ACELERANDO NA AMAZÔNIA BRASILEIRA?. Disponível em: < http://www.biotaneotropica.org.br> Acesso em: 12 de dezembro de 2017.
Serra, C.M.V. et al. Aplicação de séries temporais na análise de demanda turística no estado do Pará usando os modelos de Holt-Winters. Disponível em: <http://www.abepro.org.br/biblioteca/ENEGEP2005_Enegep0606_0932.pdf> Acesso em: 26 de outubro de 2017.
SODRÉ, Ulysses. Crescimento Populacional . Londrina-PR, 27 de Junho de 2007 .
Disponível em: :<http://www.uel.br/projetos/matessencial/superior/pdfs/crescpop.pdf>. Acesso em: 22 novembro de 2017.
Bezerra, S. D. M. et al. Equações Diferenciais aplicadas ao Modelo de Malthus na Dinâmica de Crescimento Populacional de Bataguassu-MS.
Disponível em: <http://www.aems.edu.br/conexao/edicaoanterior/Sumario/2016/downloads>. Acesso em: 15/12/217
Gracias, Antonio Carlos; Lourenço, Sérgio Ricardo. Aplicação de um Modelo Matemático na Simulação da Produção e Importação de Gas Natural no Brasil até 2017. Revista Produção Online, v.10, n. 3, p. 698-717, set., 2010.
Disponível em: <https://www.producaoonline.org.br/rpo/article/viewFile/666/720> Acesso em: 12 de novembro de 2017
INPE – Instituto de Pesquisas Espaciais. PRODES. Base de dados de desmatamento na Amazonia Legal Brasileira.
Disponível em: <http://www.obt.inpe.br/OBT/assuntos/programas/amazonia/prodes>. Acesso em: 12 de agosto de 2017.
BASSANEZI, Rodney Carlos. Temas & Modelos. São Paulo: Contexto, 2002.
Disponível em: <http://gradmat.ufabc.edu.br/livros/Temas%20&%20Modelos-%20o%20livro.pdf>
Acesso em: 03 de junho de 2017.
BASSANEZI, Rodney Carlos. Temas & Modelos. São Paulo: Contexto, 2002. 389 paginas
JUNIOR, Edson Antonio Mengatto; OLIVEIRA, Regina Célia; SILVA, João dos Santos Vila da. O Município de Marabá, PA Frente ao ZEE na Amazônia Legal: Avaliação das Taxas de Crescimento de Desmatamento.
Disponível em : <https://ocs.ige.unicamp.br/ojs/sbgfa/article/view/2206>. Acesso em: 05 de dezembro de 2017.
SILVEIRA JÚNIOR, J. C. Análise da Relação Entre o Desflorestamento e a Atividade Agropecuária no Estado do Mato Grosso. Disponível em: <http://mtc-m12.sid.inpe.br/col/sid.inpe.br/marciana/2003/04.14.11.43/doc/publicacao.pdf >
Acesso em: 20 novembro 2017.
FERREIRA, Leandro Valle; VENTICINQUE, Eduardo; ALMEIDA, Samuel. O desmatamento na Amazônia e a importância das áreas protegidas. Disponível em: <http://www.scielo.br/scielo.php?pid=S0103-40142005000100010&script=sci_arttext&tlng=pt>. Acesso em: 04 de janeiro de 2018.
NUNES,Carla de Azevedo Paes; MELLO, Maria Hermidia de Paula Leite. Método de Ford-Walford Aplicado ao Modelo Generalizado de Von Bertanflay. Disponível em: <www.e-publicacoes.uerj.br/ojs/index.php/cadmat/article/view/30132>. Acesso em: 12 de novembro de 2017
TAVONI, Robson. Os modelos de crescimento populacional de Malthus e Verhulst – uma motivação para o ensino de logaritmos e exponenciais. Biblioteca da UNESP Campus de Rio Claro/SP. Disponível em: <https://repositorio.unesp.br/bitstream/handle/11449/92412/tavoni_r_me_rcla.pdf?sequence=1>. Acessado em: 20 de dezembro de 2017.
[1] Mestre em Física Ambiental pela Universidade Federal de Mato Grosso.
Enviado: Março, 2018
Aprovado: Outubro, 2018