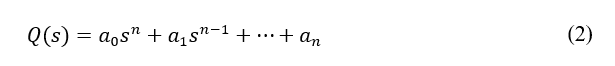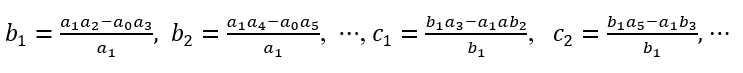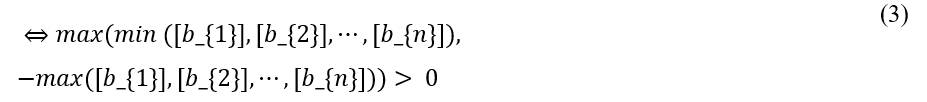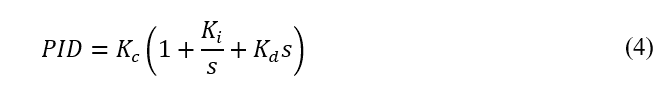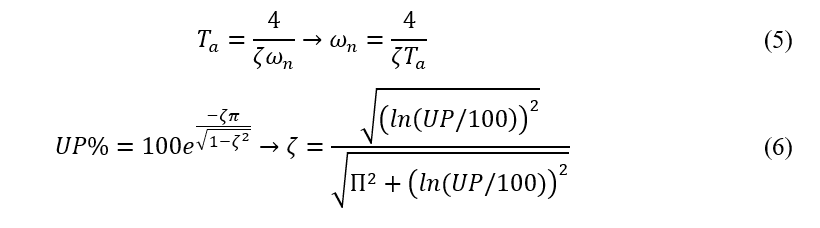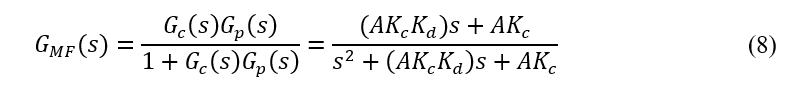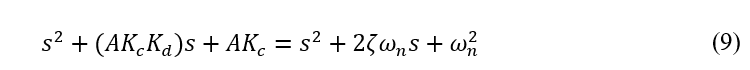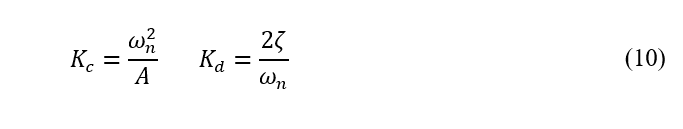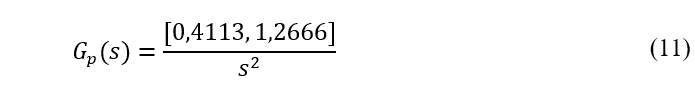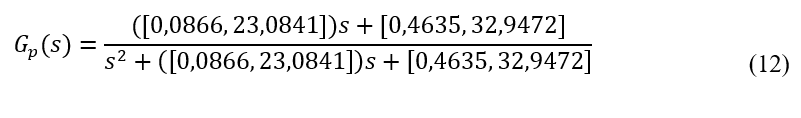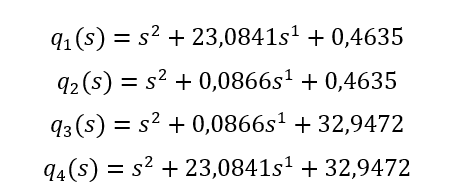ARTIGO ORIGINAL
GOMES, Gabriel Chendes Dias [1], FIGUEIREDO, Letícia Ribeiro [2]
GOMES, Gabriel Chendes Dias. FIGUEIREDO, Letícia Ribeiro. Análise de controle robusto no sistema Ball And Beam. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano 05, Ed. 05, Vol. 02, pp. 153-166. Maio de 2020. ISSN: 2448-0959, Link de acesso: https://www.nucleodoconhecimento.com.br/engenharia-eletrica/ball-and-beam
RESUMO
Este artigo apresenta o projeto de um controlador robusto para o sistema ball and beam. O projeto pode ser dividido em modelagem do sistema, projeto do controlador, em particular o controlador PD, e a análise dos resultados obtidos utilizando os conceitos da teoria de controle robusto. O objetivo é garantir que o sistema atenda aos requisitos do projeto e que se mantenha estável mesmo considerando incertezas nas variáveis do processo.
Palavras-chave: Controle Robusto, Ball and Beam, modelos didáticos, incerteza.
1. INTRODUÇÃO
No cenário dos sistemas dinâmicos, a estabilidade é definida com relação a um dado ponto de equilíbrio. Em muitas aplicações da Biologia, Economia, Física e Engenharia é desejável que todos os estados de um dado sistema tenda a seu estado de equilíbrio. Porém, outros comportamentos podem ocorrer, como o de as soluções oscilarem entre valores próximos ao ponto de equilíbrio ou se afastarem dele (Cipolli, 2012). Levando isso em consideração, a análise da estabilidade de sistemas tornou-se uma importante área de estudo nestes campos e tem desempenhado um papel fundamental em sua evolução.
A análise clássica considera que os sistemas são precisamente conhecidos, mas, em situações reais, seus parâmetros podem ser incertos (de Oliveira, 2016). Umas das abordagens principais que tratam dessas incertezas é a teoria de controle robusto, que é utilizada quando se deseja considerar a existência de incertezas ou erros entre a planta real e o seu modelo matemático no projeto do controlador. Esta teoria leva em consideração que o sistema físico a ser controlado e o ambiente onde irá operar não podem ser modelados com exatidão. Há também a possibilidade de diversos tipos de interferências, sejam elas por meio de ruídos em sensores ou perturbações imprevisíveis (Lordelo e Ferreira, 2005). Isso gera valores inesperados que o controlador deve ser capaz de tratar.
Para o projeto de controladores altamente precisos mesmo na presença de consideráveis incertezas é conveniente recorrer a sistemas de controle robustos (Dorf e Bishop, 2001; Ogata, 2011). Neste contexto, surge o conceito de estabilidade robusta, garantindo a estabilidade não apenas para o sistema nominal, mas também para alguns “vizinhos” (Galdino, 2011), relacionados às incertezas presentes no sistema real.
Aplicar as teorias de controle em plantas reais pode ser complexo, para tornar tangível as pesquisas, a análise e compreensão de modelos didáticos tem apresentado grande aplicabilidade para aprendizado de sistemas de controle (Yu e Ortiz, 2005). Um dos modelos didáticos mais utilizado é o sistema ball and beam, definido, basicamente, como uma tentativa de equilibrar uma esfera em uma determinada posição de uma barra. A ampla aplicabilidade se dá por este sistema apresentar características interessantes, como a instabilidade em malha aberta e forte não-linearidade (Chang et al., 2011), presentes em diversas aplicações de controle real.
Este artigo utiliza deste modelo didático para analisar a estabilidade do sistema utilizando aplicações propostas por Kharitonov (1979) e Jaulin (2001). O restante deste artigo está estruturado da seguinte maneira: a Seção 2 apresenta a modelagem do sistema, a Seção 3 apresenta a fundamentação teórica da análise de estabilidade, a Seção 4 apresenta métodos para projeto de controladores, a Seção 5 apresenta a metodologia da pesquisa, a Seção 6 contém os experimentos e resultados e, por fim, na Seção 7, são apresentadas as conclusões obtidas.
2. MODELAGEM DO SISTEMA
O modelo clássico ball and beam é constituído por uma esfera sobre uma barra, no qual um ponto da barra é fixo por uma junta de rotação, e em outro ponto é fixo o motor, sendo possível levantar e abaixar a barra. O objetivo do sistema é parar a esfera na posição desejada, sendo que o deslocamento atual da esfera é medido com um sensor de posição (Sathiyavathi e Krishnamurthy, 2013). A dinâmica de controle da posição angular, assemelha com a dinâmica de sistemas reais no que tange ao movimento do centro de massa. A Figura (1) ilustra o sistema a ser controlado e as variáveis do processo.
Figura 1: Sistema ball and beam
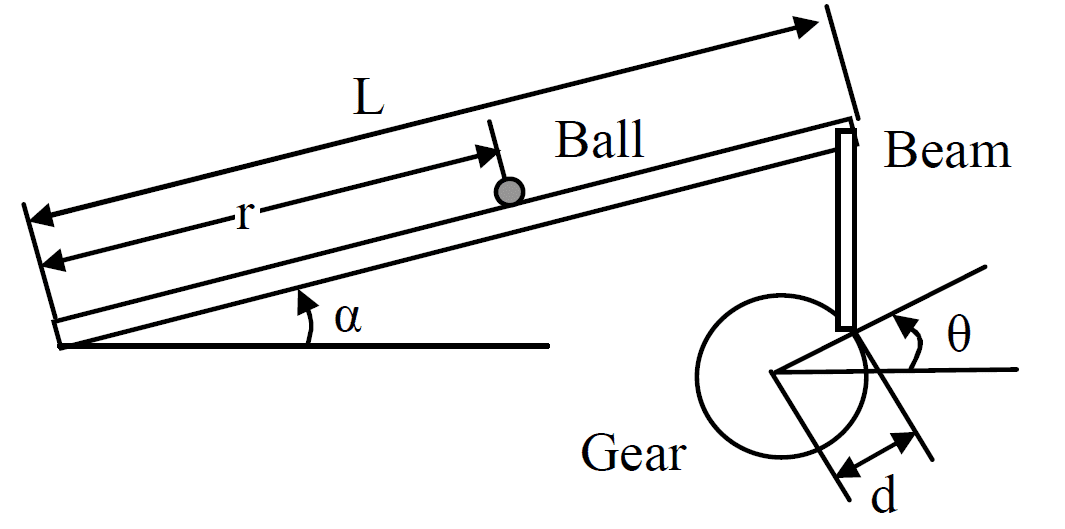
Os parâmetros são definidos por: (m) massa da esfera; (R) raio da esfera; (d) braço de alavanca compensado; (g) aceleração gravitacional; (L) comprimento da barra; (J) momento de inércia da esfera; (r) a posição da esfera; (α) ângulo da barra; (Θ) ângulo de engrenagem do servo.
Existem diferentes métodos para modelagem deste sistema, computacionalmente ou matematicamente. Keshmiri et al. (2012), Bolívar-Vincenty e Beauchamp-Báez (2014), Meenakshipriya e Kalpana (2014) utilizaram do Método de Lagrange para modelar o sistema, Bolívar-Vincenty e Beauchamp-Báez (2014) ainda utilizaram da Mecânica Newtoniana. No modelo proposto por Meenakshipriya e Kalpana (2014), considera-se, para este sistema, que a esfera role sem escorregar e que o atrito entre a barra e esfera é desprezível. A função de transferência da barra, constituída por um integrador duplo, é dada pela equação (1).
O sistema ball and beam é instável em malha aberta e possui forte não-linearidade (Chang et al., 2011), além disso, diversas fontes de incerteza contidas no sistema podem ser consideradas, vinculadas às aproximações do modelo e/ou ao desconhecimento dos valores dos parâmetros. Assim, esse sistema pode ser utilizado para o projeto de um controlador robusto e análise de estabilidade considerando incertezas.
3. FUNDAMENTAÇÃO TEÓRICA DA ANÁLISE DE ESTABILIDADE
Aplicando as operações intervalares às técnicas de análise de estabilidade de sistemas de controle dinâmicos, surge o conceito de estabilidade robusta. Neste contexto, verifica-se a estabilidade não apenas para o sistema nominal, mas para uma família de polinômios provenientes das incertezas do sistema, tratados como intervalos com limitantes inferiores e superiores.
A pesquisa de Kharitonov (1979) é um dos resultados bem conhecidos neste campo. O autor propôs um teorema, denominado Teorema de Kharitonov, que se tornou atraente na análise de estabilidade de sistemas com incerteza do tipo intervalar. Este Teorema reduziu a tarefa de verificar a estabilidade para toda a família de polinômios intervalar investigando apenas a estabilidade de Hurwitz para quatro polinômios especialmente construídos. O exemplo genérico a seguir pode ser utilizado para compreender o Teorema de Kharitonov: Define-se um conjunto Q de polinômios de grau n, equação (2), sendo ![]() para todo l = 0,1,2,…, n-1.
para todo l = 0,1,2,…, n-1.
Os quatro polinômios do Teorema de Kharitonov podem ser vistos na estrutura abaixo.
Para que um sistema com incertezas seja estável, é necessário que todos os polinômios característicos de Kharitonov sejam estáveis. Esta estabilidade é verificada utilizando o critério de Routh e Hurwitz, dado pela Tabela (1). Este critério nos diz que para um sistema ser estável não pode ocorrer troca de sinal na primeira coluna do arranjo, assim todos os pólos do sistema estarão no semiplano esquerdo do domínio de “s” (frequência).
Tabela 1: Critério de Routh e Hurwitz
Outra pesquisa com resultados bem conhecidos neste campo é a de Jaulin (2001). Em sua teoria, o autor considera que o sistema é robustamente estável quando obedece a seguinte condição: [b1], [b2], …, [bn] tem o mesmo sinal
Nesse trabalho utiliza-se do critério de Routh e Hurwitz representado por números intervalares. Assim, [b1], [b2], …, [bn] os valores intervalares da primeira coluna do critério de Routh e Hurwitz.
4. PROJETO DE CONTROLADORES
Diversas análises de controle vêm surgindo para tentar manter a estabilidade ou as características de desempenho do sistema na presença de incertezas (Galdino, 2011). Essas análises e técnicas de controle são denominadas como Teoria de Controle Robusto, que pode ser vista em (Ogata, 2011; Bishop e Dorf, 2001). O termo robusto refere-se que o processo responde satisfatoriamente não apenas para o sistema nominal, mas para sistemas próximos a ele.
Devido a sua facilidade, modelos didáticos têm sido amplamente utilizados para o estudo das teorias de controle. Dentre eles, o sistema ball and beam é um dos mais populares e diversas aplicações de análise de controle foram introduzidas utilizando este modelo, como pode ser visto em (Keshmiri et al., 2012). Este sistema tem ampla gama de aplicações industriais associadas a problemas reais de controle, tais como a estabilização horizontalmente de um avião durante a aterrissagem e em fluxo de ar turbulento (Chang et al., 2012; Shirke e Kulkarni, 2015).
Muitos métodos de controle clássicos e modernos têm sido utilizados para estabilizar o sistema ball and beam (Yu, 2009; Li e Yu, 2010), o que motivou a serem desenvolvidas e aprimoradas técnicas de sintonia (Galdino, 2011; Goncalves et al., 2008; Vigano e Prado, 2017). Apesar da existência de várias técnicas de controle, uma pesquisa feita por Takatsu et al. (1998) constatou que o PID (Proporcional-Integral-Derivativo) é a mais utilizada na prática. A pesquisa foi realizada na década de 1990, entretanto a numerosa utilização desta técnica na indústria continua, onde mais de noventa e cinco por cento das aplicações práticas a exploram (Matušů e Prokop, 2010).
A escolha da ação de controle depende das características da planta a ser controlada, dessa forma tem-se: o controlador Proporcional (P), o Proporcional-Derivativo (PD), o Proporcional-Integral (PI), o PID, entre outras variações. A componente proporcional consiste em um ganho ajustável para tentar eliminar as oscilações do sistema, um ganho muito alto pode levar o sistema a instabilidade, a componente integral , ao adicionar um pólo na origem da função de transferência do controlador, conduz o erro de regime estacionário a zero, mas aumenta o tempo de acomodação e piora a estabilidade relativa, já a componente derivativa permite melhorar o a velocidade de resposta do sistema, mas resulta em um controlador sensível a ruídos e a variações dos parâmetros do sistema (Ogata, 2011). Abaixo é expressa a função de um controlador PID, sendo que as funções do controlador P, PD e PI podem ser extraídas desta.
Umas das técnicas para determinar os valores das componentes do controlador é por Alocação de Polos, seja utilizando diretamente o Lugar das Raízes, técnica gráfica no domínio da frequência que expressa o comportamento do sistema, ou por comparação da equação padrão de mesma ordem da função de transferência em malha fechada do modelo obtido. A equação padrão é escrita em termos do fator de amortecimento (ζ) e da frequência de oscilação (ωn) do sistema, que podem ser descobertos a partir de especificações de desempenho do projeto, como o tempo de amortecimento (Ta), entendido como o tempo que o sistema demora para estabilizar, e o sobressinal (UP%), entendido como a relação entre o valor final e o valor de pico do sistema (Vigano e Prado, 2017), dados pelas equações abaixo.
Com essas informações é possível projetar o controlador. Em seguida, a malha de controle do processo é realimentada e as técnicas de análise de estabilidade são aplicadas, averiguando se o objetivo foi alcançado.
5. METODOLOGIA
Os sistemas de controle necessitam ser projetados de modo que certas propriedades essenciais, como a estabilidade, permaneçam inalteradas sob incertezas existentes (Bhattacharyya e Keel, 1995). Desse modo, este artigo propõe o projeto de um controlador para o modelo didático ball and beam e aplicação de técnicas de análise de estabilidade com incertezas do tipo intervalar para verificar se o sistema é robustamente estável. O modelo adotado para representação do sistema ball and beam foi proposto por Meenakshipriya e Kalpana (2014) sendo este modelo constituído por um integrador duplo, por apresentar dois pólos na origem.
A escolha do PID e suas variações como a técnica de controle deste trabalho foi motivada pela sua aplicabilidade e simplicidade ao resolver os problemas de controle. O controlador foi projetado utilizando a técnica de Alocação de Pólos utilizada por Viagano e Prado (2017). Neste artigo é proposto um controlador PD, visto que a planta possui um integrador duplo. A expressão que representa o controlador PD, utilizada neste trabalho, é apresentada em (7).
Com a função de transferência em malha fechada do sistema, representada em (8), calcula-se os parâmetros do controlador de forma que o sistema atenda aos requisitos do projeto. Isto é alcançado comparando o denominador do sistema desejado com o denominador da equação (8).
O sistema desejado é o sistema padrão com a mesma ordem de (8), escrito em termos do fator de amortecimento (ζ) e da frequência de oscilação (ωn) do sistema. A equação (9) expressa a comparação do sistema modelado com o sistema padrão,
Resultando em:
Os valores do fator de amortecimento (ζ) e da frequência de oscilação (ωn) podem ser descobertos a partir de especificações de desempenho do projeto. Neste artigo, são considerados o tempo de amortecimento (Ta) e o sobressinal (UP%).
Projetado o controlador, a estabilidade do sistema é analisada utilizando as aplicações propostas por Kharitonov (1979) e por Jaulin (2001), que permitirá concluir se o sistema é robustamente estável considerando incertezas do tipo intervalar.
6. EXPERIMENTOS E RESULTADOS
Considera-se que as incertezas do sistema proposto por este artigo estão associadas a massa (m) e o raio (R) da esfera, e consequentemente ao momento de inércia (J), ao comprimento da barra (L) e ao braço de alavanca compensado (d). Os valores intervalares dos dados do sistema são: m=[0,036, 0,040]kg; R=[0,036, 0,040]m; g= [9,81, 9,81]m/s2; d=[0,09, 0,11]m; L= [0,72, 0,88]m; J=10-4[0,311, 0,5679]kgm2.
Empregando a equação (1) é possível construir uma família de funções de transferências da planta dada pela equação (11). Resulta-se, então, nos intervalos A ∈ [A] = [0,4113, 1,2666].
Esse sistema é totalmente instável em malha aberta, pois sua saída aumenta infinitamente para qualquer entrada, além de apresentar forte não-linearidade para grandes inclinações. Para possível alcance da estabilidade deve-se projetar o controlador e realimentar o sistema. Deseja-se que o sistema possua desempenho cujo o tempo de acomodação seja Ta ∈ [Ta] = [4, 8] segundos e o sobressinal seja UP% ∈ [UP%]= [25, 35]. Dado esses parâmetros é possível determinar os valores de ζ e ωn, correspondendo, respectivamente, aos intervalos [0,3057, 0,4185] e [1,1947, 3,2709]. Valores obtidos utilizando equações (5) e (6).
A partir desses parâmetros é possível determinar as variáveis do controlador (Kc e Kd) utilizando a equação (10). Neste instante, todos os valores intervalares das variáveis do sistema foram determinados resultando na seguinte família de função de transferência em malha fechada.
A estabilidade da planta é verificada utilizando duas abordagens, aplicação proposta por Kharitonov (1979) e aplicação proposta por Jaulin (2001). Na primeira abordagem, quatro polinômios são especialmente construídos com base nos limites inferiores e superiores, conforme apresentado em (2) onde Q(s) corresponde ao denominador da função de transferência em malha fechada. Os polinômios deste sistema são expressos abaixo.
O sistema é robustamente estável para todos os valores pertencentes aos intervalos se é comprovada a estabilidade de todos os polinômios característicos de Kharitonov, utilizando o critério de Routh e Hurwitz, conforme Tabela 1. A Tabela 2 apresenta a aplicação do Teorema de Kharitonov para este sistema.
Tabela 2: Análise de Estabilidade: 1ª Abordagem
Observa-se que não ocorre troca de sinal nos valores da primeira coluna do Critério de Routh e Hurwitz para todos os polinômios característicos de Kharitonov, sendo, portanto, estáveis e o sistema é considerado robustamente estável.
Na segunda abordagem, proposta por (Jaulin, 2001), o sistema é considerado robustamente estável quando obedece a condição dada em (3). A Tabela 3 apresenta a aplicação da abordagem proposta, primeiramente apresenta-se o arranjo de Routh e Hurwitz.
Tabela 3: Análise de Estabilidade: 2ª Abordagem
Em seguida é aplicada a condição: max(min([1,1], [0,0866, 23,0841], [0,4635, 32,9472], –max([1,1], [0,0866, 23,0841], [0,4635, 32,9472])) = [0,0866, 1,0000].
Observa-se que a condição é satisfeita uma vez que o valor resultante é maior que zero, portanto, não ocorre troca de sinal na primeira coluna do critério de Routh e Hurwitz, sendo o sistema considerado robustamente estável.
Comprovando a análise realizada, o controle é aplicado em uma planta elaborada pelos autores. Os dados da planta estão contidos nos intervalos acima apresentados e foram utilizadas duas esferas de massa e diâmetro diferentes. No primeiro ensaio, utiliza-se uma esfera de 0,044Kg e 5,3cm (Figura 2), e no segundo ensaio, utiliza-se uma esfera de 0,038Kg e 3,8cm (Figura 3), ambos para uma entrada em degrau de amplitude de 390mm, correspondendo a posição central da barra. Os ensaios foram realizados utilizando o software Matlab/Simulink®.
Figura 2: Resposta do Sistema ao Degrau utilizando a Esfera Grande
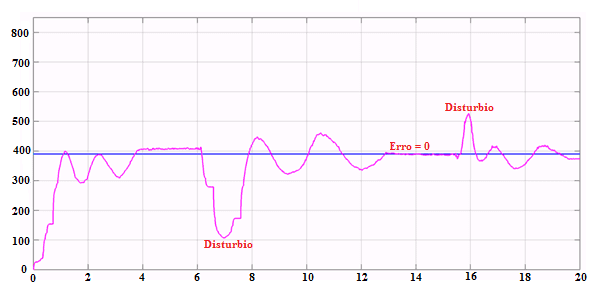
Figura 3: Resposta do Sistema ao Degrau utilizando a Esfera Pequena
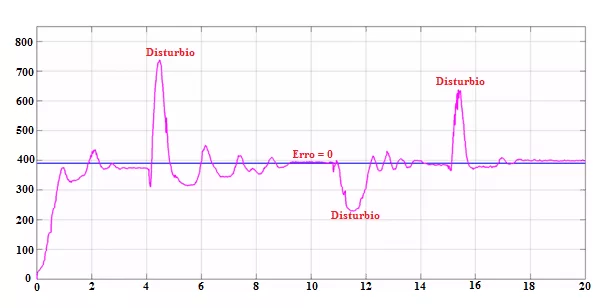
O sistema é estável para os diferentes ensaios com tempo de estabilização dentro da faixa estabelecida nos parâmetros de desempenho. Além disso, o sistema reage rapidamente ao distúrbio devido a ação derivativa que fornece ao sistema uma ação antecipativa evitando previamente que o desvio se torne maior. Em algumas aplicações o sistema apresenta erro de regime permanente que será corrigido com o tempo devido a ação integral da planta, que realiza um somatório do erro até que este se torne significativo para que o sistema atue. Para esses dois sistemas foram realizados numerosos testes sendo verificado que os parâmetros de desempenho estão contidos nos intervalos dados acima.
7. CONSIDERAÇÕES FINAIS
O sistema, ball and beam, além de ser instável em malha aberta apresenta uma não-linearidade forte para inclinações elevadas. Essas características fazem com que o modelo seja amplamente utilizado como planta didática nos estudos de teoria de controle ao aproximar das características de sistemas reais. Neste artigo, foi proposto uma ação de controle capaz de alcançar o desempenho desejado para o sistema, mesmo em condições de incerteza. Além disso, podem ser aplicadas, neste modelo, outras técnicas de controle e análises de incerteza. Com a planta já projetada, existe a possibilidade de modelar o sistema empiricamente, ou seja, com a aquisição de dados utilizando a própria planta.
REFERÊNCIAS
BHATTACHARYYA, S. P.; KEEL, L. H. Robust control: the parametric approach. In: Advances in Control Education 1994. [S.l.]: Elsevier, 1995. p. 49–52.
BISHOP, R. H.; DORF, R. C. Sistemas de controle modernos. Livros Técnicos e Científicos, 2001.
BOLÍVAR-VINCENTY, C. G.; BEAUCHAMP-BÁEZ, G. Modelling the ball-and-beam system from newtonian mechanics and from lagrange methods. In: 12th Latin American and Caribbean Conference for Engineering and Technology (LACCEI’2014), Guayaquil, Ecuador. [S.l.: s.n.], 2014.
CHANG, Y.-H.; CHAN, W.-S.; CHANG, C.-W. Ts fuzzy model-based adaptive dynamic surface control for ball and beam system. IEEE transactions on industrial electronics, IEEE, v. 60, n. 6, p. 2251–2263, 2012.
CHANG, Y.-H. et al. Adaptive fuzzy dynamic surface control for ball and beam system. International Journal of Fuzzy Systems, Chinese Fuzzy Systems Association, Department of Mechanical Engineering National Taiwan University, v. 13, n. 1, p. 1–7, 2011.
CIPOLLI, V. G. Sistemas dinâmicos discretos: análise de estabilidade. Universidade Estadual Paulista (UNESP), 2012.
DORF, R. C.; BISHOP, R. H. Sistemas de controle modernos, 8a edição. Editora LTC, Rio de Janeiro, 2001.
GALDINO, J. C. d. S. Estudo comparativo do desempenho de controladores robustos aplicados a um sistema de tanques acoplados. Dissertação (Mestrado) — Universidade Federal do Rio Grande do Norte, 2011.
GONCALVES, E. N.; PALHARES, R. M.; TAKAHASHI, R. H. A novel approach for H2/H∞ robust pid synthesis for uncertain systems. Journal of Process Control, Elsevier, v. 18, n. 1, p. 19–26, 2008.
JAULIN, L. Applied interval analysis: with examples in parameter and state estimation, robust control and robotics. [S.l.]: Springer Science & Business Media, v. 1, 2001.
KESHMIRI, M. et al. Modeling and control of ball and beam system using model based and non-model based control approaches. International Journal on Smart Sensing & Intelligent Systems, v. 5, n. 1, 2012.
KHARITONOV, V. Asymptotic stability of an equilibrium position of a family systems of linear differential equations. Differential equations, v. 14, p. 1483–1485, 1979.
LI, X.; YU, W. Synchronization of ball and beam systems with neural compensation. International Journal of Control, Automation and Systems, Springer, v. 8, n. 3, 491–496, 2010.
LORDELO, A. D.; FERREIRA, P. A. Análise intervalar e projeto de controladores robustos via programação alvo. Sba: Controle & Automação Sociedade Brasileira de Automatica, SciELO Brasil, v. 16, n. 2, p. 111–123, 2005.
LV, X. H. et al. Design of ball-beam control system based on machine vision. In: TRANS TECH PUBL. Applied mechanics and materials. [S.l.], 2011. v. 71, p. 4219–4225.
MATUŠŮ, R.; PROKOP, R. Experimental verification of design methods for conventional pi/pid controllers. WSEAS Transactions on Systems and Control, World Science and Engineering Academy and Science (WSEAS), 2010.
MEENAKSHIPRIYA, B.; KALPANA, K. Modelling and control of ball and beam system using coefficient diagram method (cdm) based pid controller. IFAC Proceedings Volumes, Elsevier, v. 47, n. 1, p. 620–626, 2014.
OGATA, k. Engenharia de controle moderno. 5o edição. Editora LTC, 2011. OLIVEIRA, F. S. S. de. Controle pi/pid robusto baseado no preditor de smith. Universidade Federal de Minas Gerais, 2016.
SATHIYAVATHI, S.; KRISHNAMURTHY, K. Pid control of ball and beam system–a real time experimentation. NISCAIR-CSIR, India, 2013.
SHIRKE, H.; KULKARNI, N. Mathematical modeling, simulation and control of ball and beam system. International Journal of Engineering Research & Technology, v. 4, n. 3, p. 834–838, 2015.
TAKATSU, H.; ITOH, T.; ARAKI, M. Future needs for the control theory in industries—report and topics of the control technology survey in japanese industry. Journal of Process Control, Elsevier, v. 8, n. 5-6, p. 369–374, 1998.
VIGANO, I. D. S.; PRADO, M. L. M. Projeto de um controlador robusto para um sistema levitador magnético. 2017.
YU, W. Nonlinear pd regulation for ball and beam system. International Journal of Electrical Engineering Education, SAGE Publications Sage UK: London, England, v. 46, n. 1, p. 59–73, 2009.
YU, W.; ORTIZ, F. Stability analysis of pd regulation for ball and beam system. In: IEEE. Control Applications, 2005. CCA 2005. Proceedings of 2005 IEEE Conference on. [S.l.], 2005. p. 517–522.
[1] Pós-graduado em Engenharia de Automação e Eletrônica Industrial e em Engenharia de Desenvolvimento de Projetos Eletrônicos e Graduado em Engenharia de Controle e Automação.
[2] Mestre em Engenharia Elétrica na linha de pesquisa Modelagem, Otimização e Tomada de Decisão, Pós-graduada em Engenharia de Automação e Eletrônica Industrial e em Engenharia de Desenvolvimento de Projetos Eletrônicos e Graduada em Engenharia de Controle e Automação.
Enviado: Abril, 2020.
Aprovado: Maio, 2020.