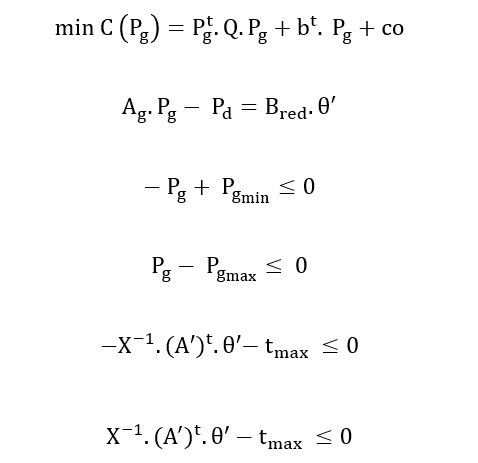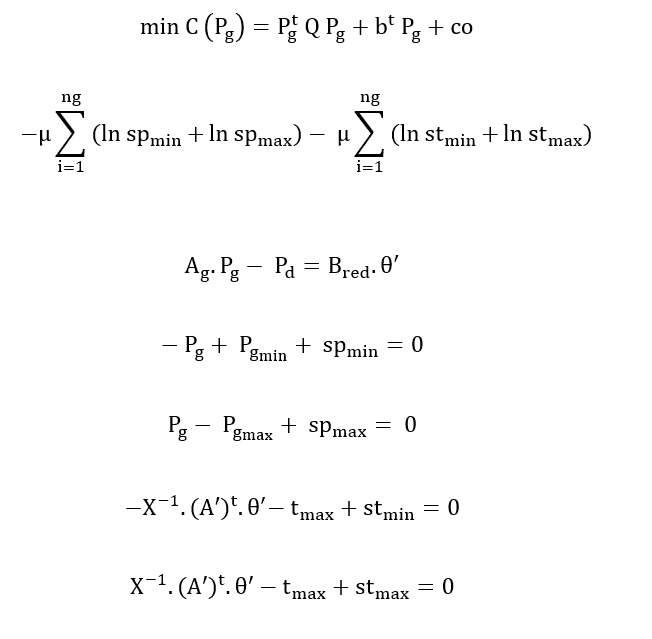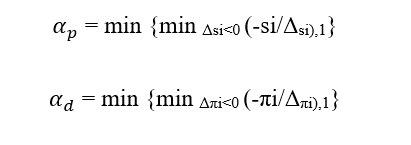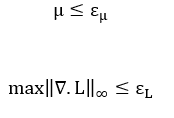Ferramenta computacional para solução do fluxo de potência ótimo linear através do método Primal-Dual de pontos interiores

ARTIGO ORIGINAL

SANTOS, Liedson Oliveira dos ^[1]

SANTOS, Liedson Oliveira dos. Ferramenta computacional para solução do fluxo de potência ótimo linear através do método Primal-Dual de pontos interiores. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano 06, Ed. 04, Vol. 01, pp. 05-27. Abril de 2021. ISSN: 2448-0959, Link de acesso: https://www.nucleodoconhecimento.com.br/engenharia-eletrica/potencia-otimo, DOI: 10.32749/nucleodoconhecimento.com.br/engenharia-eletrica/potencia-otimo

RESUMO

Com o objetivo de encontrar um estado operativo de uma rede elétrica em regime permanente, é desenvolvido o Fluxo de Potência Ótimo (FPO), amplamente utilizado no planejamento, operação e na análise de sistemas elétricos de potência. Neste contexto, este trabalho propõe uma ferramenta computacional desenvolvida no software MATLAB® para solução do problema de otimização do fluxo de potência ótimo que minimiza os custos de produção, utilizando o modelo linearizado e o método primal-dual de pontos interiores. Os resultados obtidos por meio das simulações realizadas com o sistema teste IEEE14, mostram a eficiência e robustez da metodologia e do algoritmo propostos, tendo convergido para a mesma solução do software FLUPOT da Cepel.

Palavras-chave: Fluxo de Potência, Fluxo de Potência Ótimo Linear, FPO Linear, Método Primal-Dual de Pontos Interiores.

1. INTRODUÇÃO

Os sistemas elétricos de potência podem ser definidos como conjunto de equipamentos físicos e elementos de circuitos elétricos conectados, que atuam de modo coordenado com o intuito de gerar, transmitir e distribuir energia elétrica, insumo essencial à sociedade e imprescindíveis ao desenvolvimento socioeconômico dos países (BORGES, 2010).

A indústria de energia elétrica no Brasil tem presenciado consideráveis mudanças ao longo dos últimos anos. A desregulamentação dos sistemas de potência e o crescente aumento de fontes renováveis não despacháveis, como energia eólica e energia solar, acrescenta um grau de complexidade ao desenvolvimento de modelos matemáticos e técnicas de solução para os problemas de despacho econômico e fluxo de potência ótimo [FPO] (ARAÚJO, 2018).

Estes fatores contribuem para a crescente necessidade de métodos, ferramentas e softwares de otimização que sejam rápidos, confiáveis e atendam simultaneamente questões de segurança e de economia em suporte à operação e controle do sistema de potência. Neste contexto, o FPO tem sido um importante método para esse estudo desde a sua introdução por Carpentier em 1962 (ARAÚJO, 2018).

O FPO otimiza uma determinada função objetivo enquanto satisfaz um conjunto de restrições físicas e operacionais, possuindo aplicações em vários problemas de planejamento e operação do sistema, em que as variáveis de controle (ativas, reativas) são ajustadas para minimizar objetivos tais como: custo de geração de potência ativa, perdas no sistema de transmissão, custo de geração de potência reativa, desvio de tensão, maximização de transferência de potência ativa, despacho ótimo de reativos, entre outros. Cada um destes problemas é definido por uma ou mais funções objetivo específicas e por um conjunto de restrições técnicas e operacionais que devem ser respeitadas (FERNANDES, 2004).

Neste trabalho busca-se minimizar a função objetivo que representa os custos de geração de usinas satisfazendo um conjunto de restrições físicas e operacionais do sistema elétrico. A formulação do FPO linear através do método dos pontos interiores é definida como:

• Função Objetivo: Minimizar os custos de geração de usinas térmicas.

Min C (P_g) = P_g^t.Q. P_{g +} b^t . P_g + co

Onde:

P_g: Vetor (ng x 1) de potência geradas, sendo ng o número de barras geradoras.

Q: matriz diagonal com coeficientes quadráticos de custo.

b: vetor de coeficientes lineares de custo.

co: custo constante.

• Restrições de igualdade: Equações de balanço de potência ativa, que colocam a premissa de que a potência gerada total deve ser igual à carga:

A_g. P_g – P_d = B. θ

Onde:

A_g: matriz de incidência gerador-barra (nb x ng).

P_g: vetor das potências geradas.

P_d: vetor (nb x 1) de cargas nas nb barras.

B: matriz de fluxo de carga DC (nb x nb).

θ: vetor de ângulos das barras (nb posições).

nb: número de barras do sistema.

A matriz B é dita singular por possuir determinante nulo e consequentemente não admitir inversa. Desta forma, faz-se necessário a adoção de uma barra de referência e consequentemente sua eliminação no processo de solução do problema de modo que θ_ref = 0º. Com isso, a matriz B é reduzida pela retirada da coluna da barra de referência do processo iterativo, passando a se chamar B_reduzida ou B_red. O novo vetor dos ângulos nas barras θ’ passa a ser representado sem a linha correspondente à barra de referência e a nova matriz de incidência A’ é representada sem a linha correspondente à barra de referência (Fernandes, 2020).

Desta forma, as equações de balanço de potência ativa, tomam a seguinte forma:

A_g. P_g – P_d = B_red . θ’

• Restrições de desigualdade: limites operacionais dos equipamentos. Os limites de geração para cada geradora são:

P_gmin ≤ P_g ≤ P_gmax

Onde:

P_gmin: vetor dos limites mínimos de geração.

P_gmax: vetor dos limites máximos de geração.

ou seja,

P_gmin ≤ P_g

– P_g + P_gmin ≤ 0

P_g ≤ P_gmax

P_g – P_gmax ≤ 0

O fluxo t nas linhas através do modelo linearizado é obtido através da seguinte expressão:

t_ij = θ_i – θ_j

       x_ij

Onde:

t_ij fluxo na linha entre barra i e j.

θ_i – θ_j: diferença angular entre barras.

x_ij: reatância da linha.

Esta expressão pode ser generalizada para todo o sistema por:

t = X^-1. A^t_. θ

Onde:

t: vetor (nl x 1) de fluxo nas linhas.

X: matriz diagonal com reatância xij (nl x nl).

A: matriz de incidência barra-ramo (nb x nl).

θ: vetor de ângulos nas barras.

O fluxo nas linhas é limitado de acordo com:

– t_max ≤ t ≤ t_max

Desta forma, temos que:

– X^-1.A^t. θ – t_max  ≤  0

X^-1. A^t. θ – tmax ≤ 0

Onde t_max é o vetor de limites nas linhas.

2. FLUXO DE POTÊNCIA ÓTIMO LINEAR

Com a função objetivo, as restrições de igualdade e desigualdade, além das modificações submetidas à matriz B transformando-a em matriz B_red, definimos que o problema a ser resolvido é dado por:

O sistema acima pode ser resolvido pelo Método Primal-Dual de Pontos Interiores que consiste em transformar as restrições de desigualdade em restrições de igualdade pela incorporação de variáveis de folga, e associar uma função barreira logarítmica à função objetivo. Com isso, pode-se construir uma função Lagrangeana estendida somente com restrições de igualdade e aplicar as condições de otimalidade de Karush-Kuhn-Tucker [KKT] a esta função. As condições de otimalidade formam um sistema de equações não-lineares, resolvido pelo Método de Newton (ALMEIDA E SALGADO, 1999).

Para se transformar as restrições de desigualdade em igualdade, introduzem-se variáveis de folga ao problema passando assim ser representadas da seguinte forma:

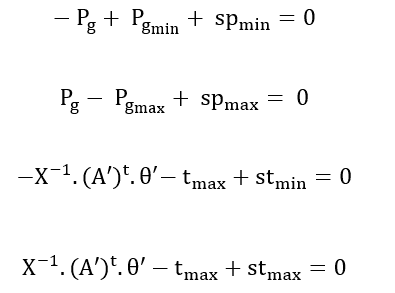As variáveis de folga st_min, st_max, sp_min, sp_max devem ser todas maiores que zero. Além disso, a fim de representar as restrições de não negatividade destas variáveis, o problema é modificado com a introdução de uma barreira logarítmica na função objetivo para penalizá-la quando as variáveis de folga se aproximam da barreira. Assim, o problema é redefinido como:

Onde:

Sp_min: matriz diagonal das variáveis sp_min.

Sp_max: matriz diagonal das variáveis sp_max.

St_min: matriz diagonal das variáveis st_min.

St_max: matriz diagonal das variáveis st_max.

A função Lagrangeana associada a este problema é, portanto:

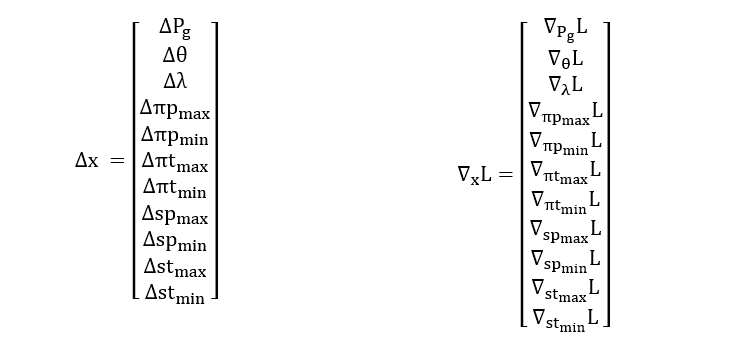
As variáveis do problema primal são: θ, Pg, st_min, st_max, sp_min, sp_max. As variáveis duais são os multiplicadores de Lagrange associados às restrições: λ, πt_min, πt_max, πp_min, πp_max. Desta forma, as condições necessárias de otimalidade de primeira ordem para este problema de otimização são:

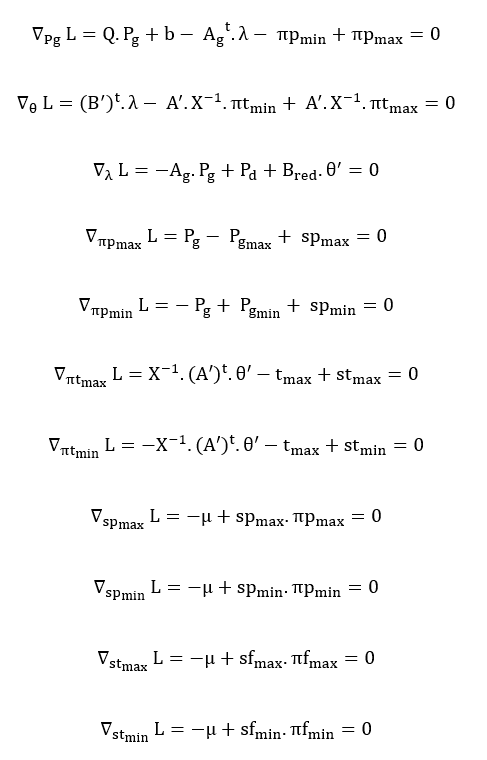Devido ao fato do multiplicador de Lagrange λ estar associado a uma restrição de igualdade, o mesmo não possui restrição de sinal, ou seja, λ pode assumir valores positivos ou negativos. Já as outras restrições implicam nas seguintes restrições de sinal: πf_min ≥ 0, πf_max ≥ 0, πp_min ≥ 0, πp_max ≥ 0 (ALMEIDA E SALGADO, 1999).

Aplicando o Método de Newton às condições de KKT para resolução do sistema por método iterativo, obtém-se o seguinte sistema de equações linearizadas:

H _* Δx = – ∇_xL

Onde a matriz H é obtida por:

Tabela 1.

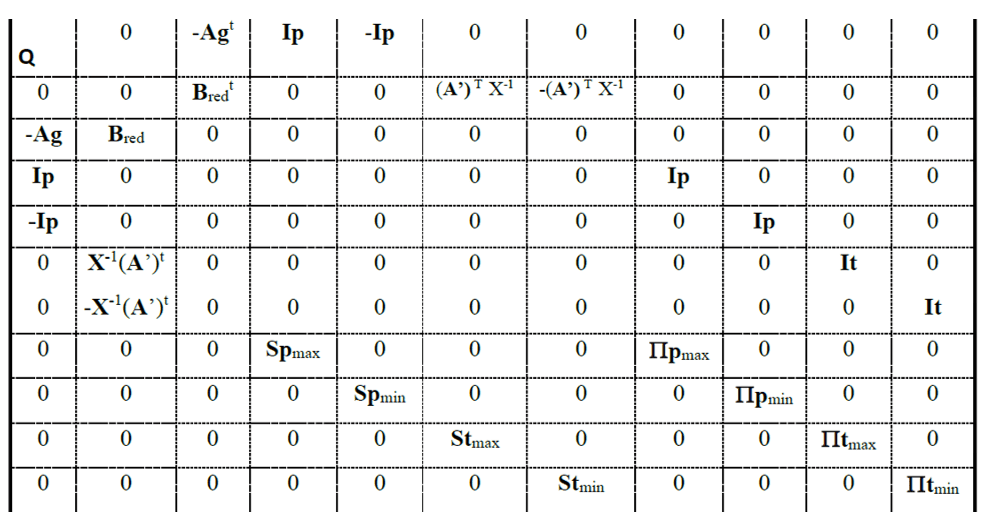
Onde:

Ip: Matriz diagonal do vetor ep.

It: Matriz diagonal do vetor et.

ep: Vetor (ng x 1) unitário

et: Vetor (nl x 1) unitário.

O vetor e são dados por:

Para cada iteração resolve-se o sistema linear:

Δx = – H^-1 _* ∇_xL

Para atualizar os valores de x^k e μ, a cada iteração o sistema linear do item anterior é resolvido, sendo a próxima etapa a determinação do comprimento do passo nos espaços primal e dual, de modo que:

• As variáveis de folga sp_max, sp_min, st_max, st_min, sejam maiores que 0.
• Os multiplicadores de Lagrange πp_max, πp_min, πt_max, πt_min, sejam menores que 0.

Onde:

s: Vetor formado por sp_min, sp_max, sf_min, sf_max.

π: Vetor formado por πp_min, πp_max, πf_min, πf_max.

Após o cálculo dos passos primal e dual, a nova aproximação para a solução ótima pode ser obtida pelas equações:

onde  é uma constante de valor 0,9995 que tem por finalidade garantir a interioridade da nova estimativa de solução.

O último passo dentro de cada iteração é recalcular o valor do parâmetro de barreira , que é baseado no decréscimo do gap de dualida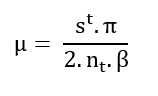de:Onde:

n_t é o número de variáveis primais mais duais,

β é o fator de aceleração (β ≥ 1 )

Para começar o processo de iteração, é necessário definir os valores iniciais das variáveis do problema de modo que satisfaçam as restrições impostas, isto é, estejam dentro da região viável do problema, conforme as seguintes equações:

A solução do problema é encontrada quando as equações que representam as condições de otimalidade são satisfeitas e o gap de dualidade ou parâmetro de barreira é nulo. Portanto, os critérios de convergência são:

Onde:

ε_L  e ε_μ: Tolerâncias para o teste de convergência das iterações.

‖∇.L‖_∞: Norma infinita do gradiente da função Lagrangeana.

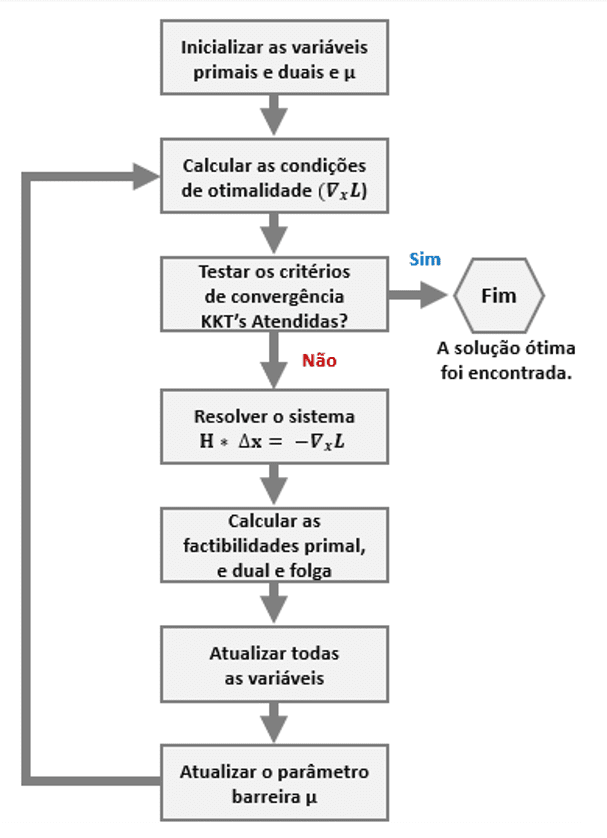
O fluxograma apresentado na Figura 01 representa a lógica do algoritmo para determinação do Fluxo de Potência Ótimo Linear através do Método de Iteração dos Pontos Interiores Primal-Dual. O código do programa computacional implementado pode ser visualizado a seguir.

Figura 01: Fluxograma Método Pontos Interiores Primal Dual.

3. SISTEMA ELÉTRICO PROPOSTO

Para verificação e resolução do Fluxo de Potência Ótimo Linearizado por meio do Método de Pontos Interiores Primal-Dual, foi implementado um programa computacional em linguagem MATLAB® que minimiza os custos de produção. O algoritmo foi então executado em um sistema teste do IEEE de 14 barras amplamente utilizado pela comunidade acadêmica para testes e validação de programas. A Figura 02 ilustra o esquema elétrico do sistema.

Figura 02: Sistema Elétrico de 14 barras do IEEE.

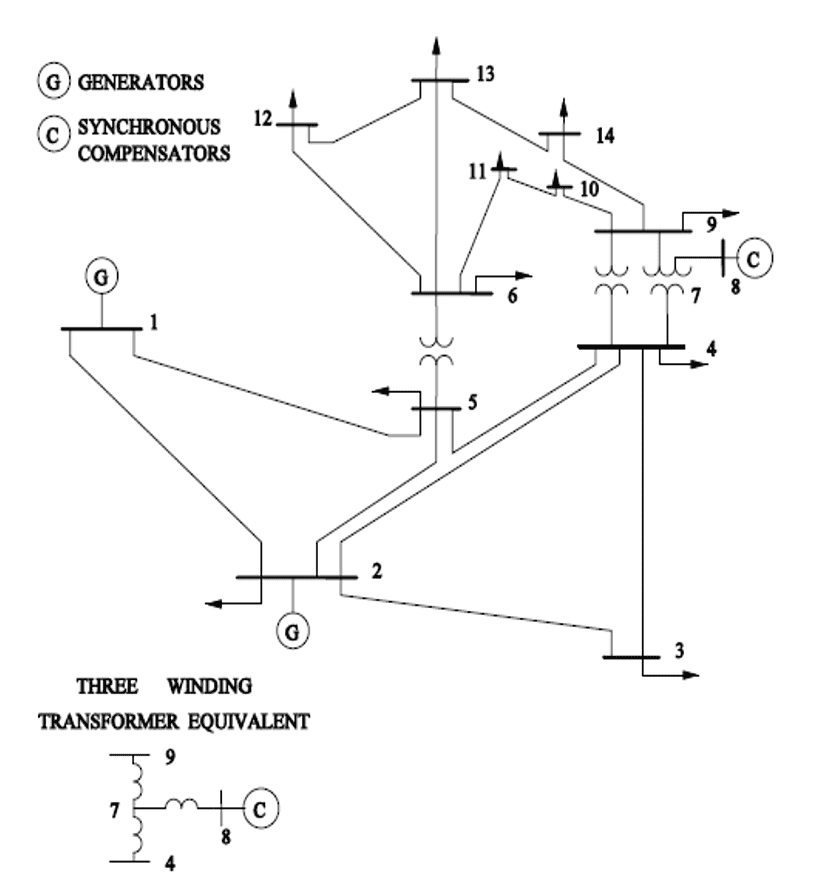
Os dados das linhas e das barras do sistema teste IEEE de 14 barras são apresentados nas Tabelas 01 e 02. Os parâmetros estão normalizados em pu por uma potência base de 100 MVA. A referência escolhida para este sistema foi a barra 1 e por isso seu ângulo de fase é zero, isto é, θ₁ = 0º.

Tabela 01 – Dados das linhas do sistema de 14 barras.

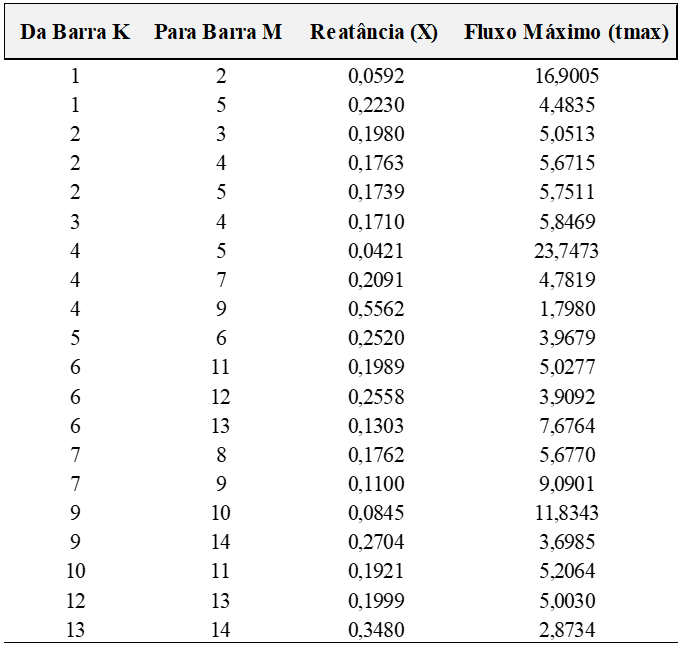
Tabela 02 – Dados das barras do sistema de 14 barras.

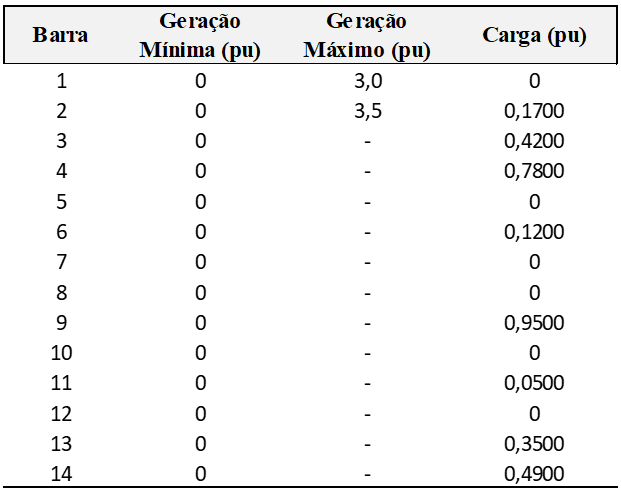
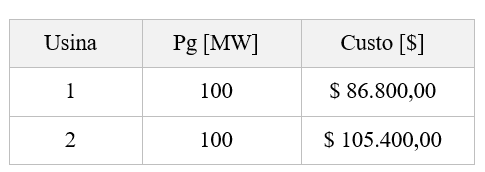
As funções custo das unidades geradoras conectadas às barras 01 e 02 são apresentadas na Tabela 03.

Tabela 03: Custos de geração e capacidades de geração.

4. RESULTADOS E DISCUSSÕES

Avaliando as equações da função custo da Tabela 03, é possível fazer uma pré-análise do sistema. Ao aplicar o mesmo valor de geração para ambas usinas, é possível verificar aquela que possui o maior custo de geração. Desta forma, os custos para geração de 100 MW pelas usinas 01 e 02 são apresentados na Tabela 04.

Tabela 04: Pré-análise dos custos das usinas térmicas.

Da Tabela 04 conclui-se que a usina 02 possui custo de geração mais elevado que a usina 01 e por consequência, é esperado que a usina 01 despache mais energia que a usina 02. Desta forma, respeitando os limites operacionais de geração e considerando uma demanda de 333 MW ou 3,33 pu, é previsto que a unidade 01 despache sua capacidade máxima de 300 MW ou 3 pu e a unidade 02 o saldo remanescente para suprir a carga, isto é, 33 MW ou 0,33 pu. Para confirmar essa pré-análise, o algoritmo foi executado para a condição onde a função objetivo minimiza os custos de produção. Os resultados são apresentados na Figura 03.

Figura 03: Resolução do despacho de geração das usinas.

Conforme esperado, a usina 01 por possuir o menor custo de produção despachou a maior quantia de potência, 300 MW, isto é, sua capacidade máxima de geração. Já a usina 02 despachou o saldo remanescente para atender a carga que era de 333 MW, logo, foram necessários 33 MW. Os custos totais, marginais e incrementais em unidades monetárias ($) são apresentados na Figura 04.

Figura 04: Custos de geração das usinas.

Conforme apresentado na Figura 04, o custo total de geração da usina 01 é de $ 776.400,00 e da usina 02, $ 11.567,00. Já o custo incremental da usina 01 é de 5.168,00 $/h e da usina 02, 697,00 $/h. O custo marginal de operação é de 0,1084 $/MWh. O ângulo de fase de cada barra e o fluxo de potência em cada linha são apresentados na Figura 05.

Figura 05: Solução do Fluxo de Potência Ótimo Linearizado.

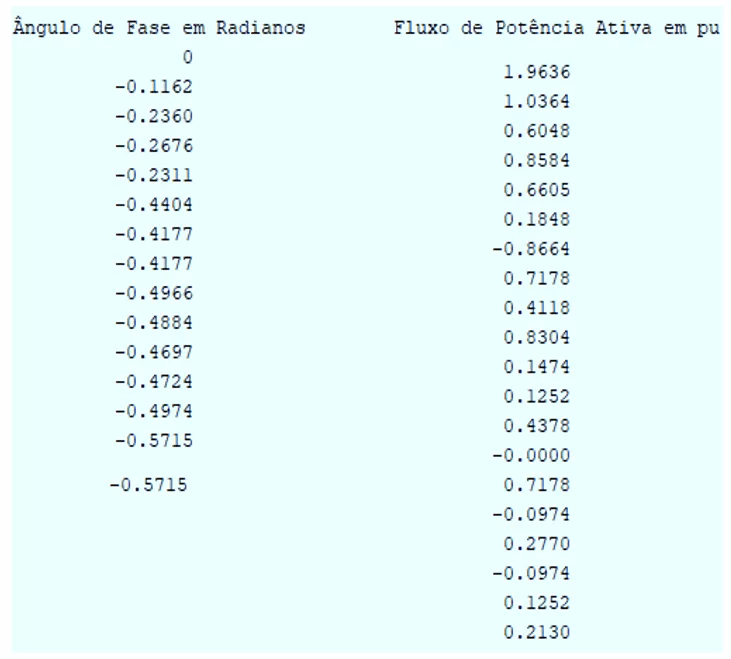
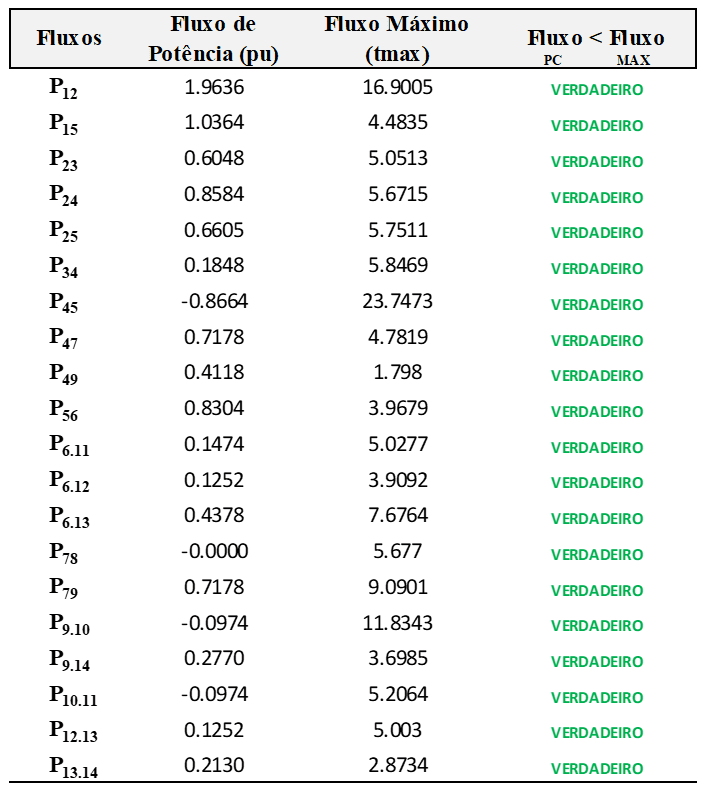
Com o objetivo de verificar a convergência do programa computacional, o sistema teste 14 barras do IEEE foi igualmente executado no Software FLUPOT da Cepel. A comparação das duas soluções para o fluxo de potência ativa que flui na rede elétrica é apresentada na Tabela 05. Conforme pode ser visualizado, o programa computacional convergiu, apresentando os mesmos valores de fluxos de potência em relação à solução obtida pelo software FLUPOT da Cepel. Por fim, na Tabela 06 verifica-se que os fluxos estão dentro dos limites de capacidade das linhas.

Tabela 05: Conferência do fluxo de potência frente ao FLUPOT.

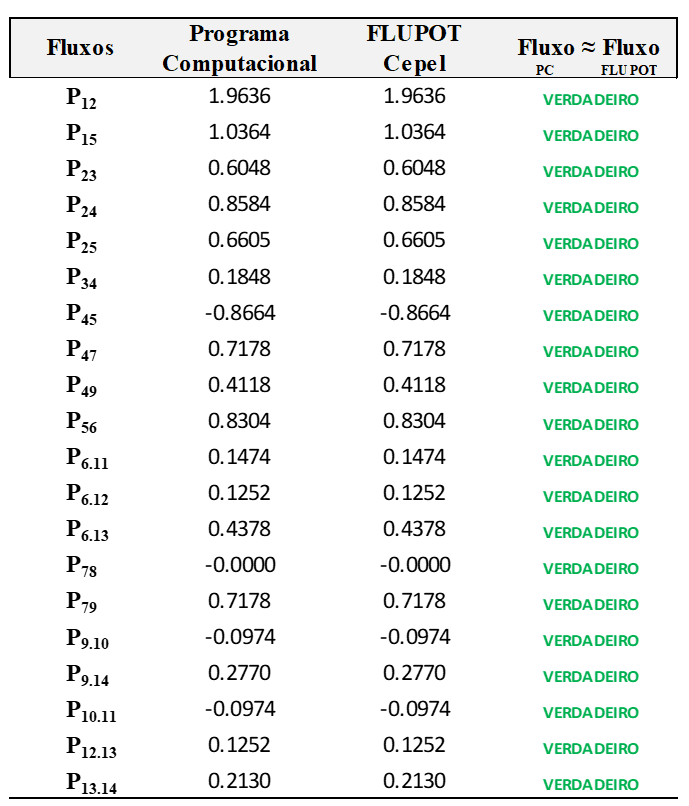
Tabela 06: Conferência das capacidades de fluxo nas linhas.

5. CONCLUSÕES

Este trabalho propôs um programa computacional desenvolvido em ambiente MATLAB® que possibilita a solução do Fluxo de Potência Ótimo Linear através do Método Primal-Dual de Pontos Interiores, comumente utilizado para solucionar problemas de otimização devido sua eficiência e garantia de convergência com esforço computacional razoável, de modo a encontrar um estado operativo de uma rede elétrica em regime permanente, otimizando a geração de cada usina térmica e os fluxos de potência nas linhas por meio da minimização dos custos totais de geração.

O programa computacional foi executado através da utilização de um sistema teste de 14 barras do IEEE, amplamente utilizado no planejamento, operação e na análise de sistemas elétricos de potência, de modo que foi determinado os valores de gerações de cada usina, seus custos totais, marginais e incrementais, além dos ângulos de fase e fluxo de potência ótimo que flui pelas linhas da rede.

Conforme era esperado, a usina 01 despachou sua capacidade máxima de 300MW/3pu por possuir o menor custo de geração. Já a usina 02 despachou o saldo remanescente de 33MW/0,33pu para atender a carga de 333MW/3,33pu em sua integralidade. Com esses valores de geração, os custos totais de produção das usinas 01 e 02 são $ 776.400,00 e $ 11.567,00, respectivamente. Já o custo incremental da usina 01 é de 5.168,00 $/h e da usina 02, 697,00 $/h. O custo marginal de operação é de 0,1084 $/MWh. Os valores das potências ativas que fluem pela rede elétrica foram igualmente determinados e para verificar a convergência do programa computacional, o resultado foi confrontado com a solução obtida pelo software FLUPOT da Cepel, onde foi obtido 100% de igualdade entre as soluções.

Desta forma, os resultados obtidos com as simulações realizadas através da utilização do sistema teste IEEE14 mostram a eficiência do programa computacional frente a metodologia proposta para resolução do Fluxo Potência Ótimo Linear através do Método Primal-Dual de Pontos Interiores, promovendo a minimização dos custos totais de produção de energia elétrica e contribuindo para uma utilização eficiente dos recursos energéticos. Como proposta de trabalhos futuros, o programa pode ser expandido para uma abordagem Não Linear do Fluxo de Potência Ótimo por meio do Método Primal-Dual de Pontos Interiores ou métodos heurísticos com devidas análises e comparações das soluções.

REFERÊNCIAS BIBLIOGRÁFICAS

ALMEIDA, K.C.; SALGADO, R.S. Apostila Técnicas de Otimização Aplicadas à Engenharia. Departamento de Engenharia Elétrica, Universidade Federal de Santa Catarina, Florianópolis, SC, 1999.

ARAUJO, E. Fluxo de potência ótimo em sistemas elétricos de potência através de um algoritmo genético multiobjetivo. Tese de Doutorado, Universidade Estadual Paulista, São Paulo, SP, 2018.

BAPTISTA, C.; BELATI, E.; COSTA, G. Um Método Primal-Dual Aplicado na Resolução do Problema de Fluxo De Potência Ótimo. Revista Brasileira de Pesquisa Operacional, vol. 24 nº 2, Rio de Janeiro, RJ, 2004.

BUENO, B.; MARQUES, J.; SILVA, M. Estudo Comparativo dos Métodos de Despacho Econômico, Fluxo de Potência Ótimo Linear e Não-Linear. Trabalho de Conclusão de Curso, Universidade Tecnológica Federal do Paraná, Curitiba, PR, 2016.

COSTA, R. M. O Método Dual-Newton Aplicado ao Fluxo de Carga Ótimo. Tese de Doutorado, Universidade Estadual de Campinas, Campinas, SP, 1990.

ELGERD, O., I. Introdução à Teoria de Sistemas de Energia Elétrica. Editora McGraw-Hill, São Paulo, 1981.

FERNANDES, T. S. P. Um Modelo de Despacho Ótimo de Potência ara Sistemas Multiusuários. Tese de Doutorado, Universidade Federal de Santa Catarina, Florianópolis, SC, 2004.

FERNANDES, T. S. P. Técnicas de Otimização Aplicadas à Operação de Sistemas Elétricos de Potência. Notas de aula, Departamento de Engenharia Elétrica, Universidade Federal do Paraná, Curitiba, PR, 2020.

IEEE. Sistema Teste de 14 Barras IEEE. Disponível em: https://ieeexplore.ieee.org/. Acesso em 30/09/2020.

SOUZA, M. A. D. S. Investigação e aplicação de métodos primal-dual pontos interiores em problemas de despacho econômico e ambiental. Dissertação de Mestrado, Universidade Estadual Paulista, São Paulo, SP, 2010.

^[1] Mestrando em Sistemas de Energia pela Universidade Federal do Paraná (UFPR). MBA em Gestão de Projetos pela Universidade de São Paulo (USP). Graduação em Engenharia Elétrica pela Universidade Federal de Uberlândia (UFU).

Enviado: Fevereiro, 2021.

Aprovado: Abril, 2021.