Escrita Algébrica A Partir Da Produção De Significados Sobre Situações-Problema

ARTIGO ORIGINAL

SCHWANTES, Vilson ^[1], XAVIER, Márcio Pizzete ^[2], KRACKE, Elisa ^[3], GRAUNKE, Carla Kuhn ^[4], GONÇALVES JUNIOR, Affonso Celso ^[5], SCHWANTES, Eloísa Bernardete Finkler ^[6]

SCHWANTES, Vilson. Et al. Escrita Algébrica A Partir Da Produção De Significados Sobre Situações-Problema. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano 06, Ed. 06, Vol. 09, pp. 34-60. Junho de 2021. ISSN: 2448-0959, Link de acesso: https://www.nucleodoconhecimento.com.br/educacao/situacoes-problema, DOI: 10.32749/nucleodoconhecimento.com.br/educacao/situacoes-problema

RESUMO

Os alunos de modo geral costumam apresentar dificuldades na aprendizagem da matemática algébrica, especialmente em situações-problema que exigem uma tradução da linguagem natural para a linguagem algébrica. Este trabalho investigativo, resultado de sessões de estudo realizadas com alunos do 7º ano do ensino fundamental procurou, antes de iniciar a escrita algébrica com os alunos, entender o que caracteriza e sustenta o pensamento algébrico, fundamentado nos escritos de Lins (1994), e no livro de Vygotsky (2001). Ao trabalhar situações-problema com os alunos distribuídos em grupos, a pesquisa mostrou, através do diálogo estabelecido entre os participantes, dada a relação que existe entre pensamento e linguagem, que são os sentidos produzidos no processo de internalização do pensamento algébrico que permite constituí-lo nos sujeitos, levando-os a escrita algébrica. Ao longo das sessões de estudo também ficou claro que a linguagem age na estruturação do pensamento, constituindo-se em ferramenta básica para uma efetiva elaboração do conhecimento sistematizado e que o pensamento algébrico uma vez desenvolvido e internalizado leva a escrita simbólica.

Palavras-chave: Pensamento Algébrico, Linguagem, Produção de Significado, Generalização, Escrita Algébrica.

1. INTRODUÇÃO

1.1 DA LINGUAGEM AO PENSAMENTO ALGÉBRICO

Desde muito cedo, o ser humano comunica-se através de uma linguagem composta de sons e gestos, cria símbolos, notações e vários tipos de códigos para melhor comunicar suas ideias e as relações por ele estabelecidas para consigo mesmo e com o mundo. No que se refere à matemática, sua história nos remete aos egípcios, babilônios, maias e romanos, como sendo os primeiros povos a criarem uma simbologia para a representação de ideias matemáticas.

O desenvolvimento do pensamento algébrico perpassa pela internalização das estruturas significadas da álgebra pela própria linguagem da álgebra, introduzidas pela posse da linguagem significada. É a produção de significados sobre o contexto de cada situação-problema que possibilita sua representação por meio de uma linguagem simbólica, estritamente algébrica. Segundo Vygotsky (2001), o ponto fulcral se concentra na linguagem que, quando carregada de significados, se transforma em pensamento, o qual pode, nesse momento, ser expresso.

A Figura 1 mostra que o pensamento e a linguagem, expressa pela palavra, têm raízes genéticas distintas, as quais se sintetizam dialeticamente no desenvolvimento cognitivo, num processo em que a linguagem se transforma em pensamento e o pensamento em linguagem. A linguagem atua sobre a organização do pensamento e sobre a maneira de pensar do ser humano e, em dado momento da vida essa organização e estruturação convergem para o surgimento do pensamento verbalizado, conforme ilustrado na Figura 1 e 2.

Figura 1: Relação entre pensamento e linguagem, resultando em dado momento de vida da criança no pensamento verbalizado.

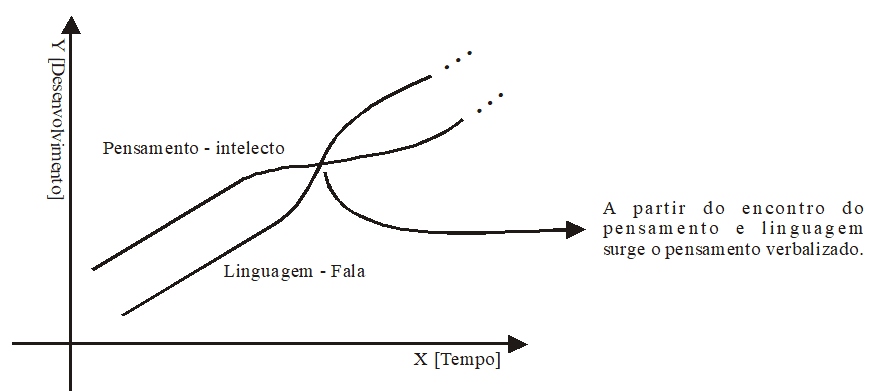
Figura 2: Diagrama da relação entre Pensamento (P) e Linguagem (L).

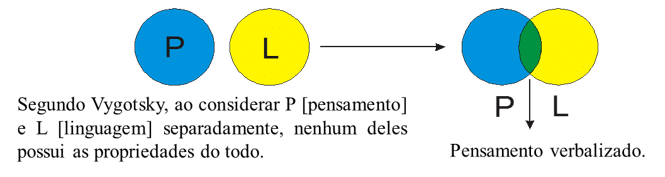
Para Vygotsky (2001), a linguagem estudada [analisada] em separado do pensamento nos leva a teorias inconsistentes. Ele percebeu em suas pesquisas que a relação entre pensamento e palavra é um processo vivo de nascimento do pensamento na palavra. Palavra desprovida de pensamento é palavra morta e um pensamento não expresso por palavras permanece na sombra.

Segundo o autor, toda forma de comunicação gera significados que auxiliam o ser humano a descrever o mundo, interpretá-lo, compreendendo as relações que se estabelecem entre os fenômenos naturais e aqueles provocados pela ação humana. A comunicação das ideias matemáticas presentes em situações-problema, possibilitam aos alunos uma conexão entre a linguagem cotidiana e a linguagem simbólica.

Lorenzato (2008, p. 32) esclarece que a aprendizagem matemática não se dá linearmente, por etapas, mas os conhecimentos matemáticos “(…) interpõem-se e integram-se, num vai e vem contínuo e pleno de inter-relacionamentos e, assim, um vai esclarecendo e apoiando o outro na elaboração dos conceitos.”

Em situações de aprendizagem, o professor usa a linguagem para ensinar e aprender, e o aluno também aprende por meio da linguagem. Assim, em suas modalidades – oral e escrita – a linguagem é o elemento central do desenvolvimento do pensamento e da consciência humana (FARIAS; BORTOLANZA, 2015).

O desafio é significar os signos matemáticos para que a linguagem possa ser lida e compreendida com significação nos contextos onde está inserida. Concordamos plenamente com Vygotsky (2001, p. 10), ao afirmar que “Sem significado a palavra não é palavra, mas som vazio. Privada do significado, ela já não pertence ao reino da linguagem”.

Souza e Diniz (1996) sugerem, como um dos caminhos possíveis à iniciação ao desenvolvimento do pensamento algébrico, a prática de atividades que não exigem a presença, em sua trajetória, de letras. Compartilhamos com as autoras quando propõem a simples observação de sequências repetidas, pelas quais se busca através da correspondência entre a posição do elemento na sequência e a forma que ele ocupa nessa posição, expressar generalidades. A Figura 3 ilustra algumas sequências com essa característica, nas quais aparecem símbolos, números e símbolos, números e figuras geométricas, as quais podem ser desenvolvidas com a finalidade mencionada.

Figura 3: Sequências que apresentam algum tipo de regularidade na repetição de seus elementos.

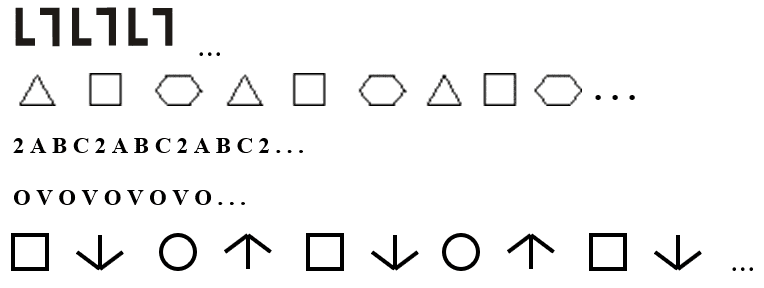
Segundo as autoras, atividades desse tipo permitem ao aluno, além da percepção de regularidades, utilizar a linguagem cotidiana em suas diferentes expressões: Oral, visual e escrita. Tais atividades capacitam o aluno, tanto na comunicação da regra de uma sequência pela linguagem cotidiana quanto para estabelecer uma relação geral que mostre a existência de uma correspondência entre a posição do elemento na sequência e a forma que o elemento apresenta na posição que ocupa.

Situações de caráter numérico e geométrico podem ser problematizadas para explorar aspectos que variam e que não variam, desenvolvendo-se o pensamento algébrico por meio de um processo que vai das palavras utilizadas no cotidiano [linguagem cotidiana] à álgebra [linguagem formal]. A elaboração de conjecturas perpassa o processo de validação do pensamento algébrico, podendo este ser expresso a partir das práticas discursivas.

Compartilhamos com Lins e Gimenez (1997), quando sugerem que esse desenvolvimento é possível em séries anteriores a 6ª série do ensino fundamental. Para isso pode-se explorar situações-problema, nas quais este pensamento se manifesta, podendo ser expresso com ou sem a necessidade de uma linguagem simbólica.

Cabe ressaltar que segundo a Base Nacional Curricular Comum, BNCC (2016), as ideias de regularidade, de generalizações e de equivalências se constituem também em alicerces para o desenvolvimento de outras dimensões da álgebra, como a resolução de problemas de estrutura algébrica e a noção de função. Segundo relata a BNCC:

Os estudantes devem ser motivados a, em seu percurso escolar, questionar, formular, testa e validar hipóteses, buscar contra exemplos, modelar situações, verificar a adequação da resposta a um problema, desenvolver linguagens e, como consequência, construir formas de pensar que o levem a refletir e agir de maneira crítica sobre as questões com as quais ele se depara em seu cotidiano BNCC (2016, p. 131).

A pesquisa realizada mostrou que través do desenvolvimento de sequências repetidas, o aluno pode encontrar um modelo matemático que retrate o pensamento desse contexto sequencial (Figura 4), tendo como suporte a observação e a produção de significados sobre a linguagem. O pensamento algébrico expresso na linguagem simbólica representa uma forma generalizada através da qual lhe seja possível saber, por exemplo, o total de quadradinhos de uma figura numa posição qualquer da referida sequência.

Figura 4: Sequências repetidas que podem ser expressas matematicamente pela linguagem algébrica.

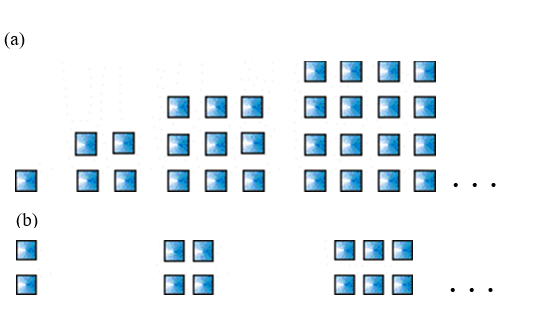
À medida que o aluno produz significados sobre uma situação-problema ele vai desenvolvendo o pensamento algébrico e começa a perceber que a matemática não é uma ciência pronta e acabada, constituída apenas de fórmulas e leis que não se justificam. A observação e a análise de sequências [numéricas, simbólicas, geométricas, …] permitem o reconhecimento de padrões e a produção de significados sobre a linguagem, facilitam a associação de ideias e as generalizações que, por sua vez, também favorecem o surgimento do espírito crítico e o desenvolvimento da capacidade intelectual de pensar.

As autoras Vale e Pimentel, em seu trabalho com padrões ressaltam que:

Muito do insucesso em matemática deve-se ao facto de os alunos recorrerem apenas à memorização e não à compreensão. O primeiro passo para aprender a pensar matematicamente é aprender a descobrir padrões e estabelecer conexões. A procura de padrões deve constituir o núcleo das aulas em todos os temas, já que eles surgem nas fórmulas que descobrimos, nas formas que investigamos e nas experiências que fazemos. (VALE; PIMENTEL, 2011, p.1)

Os pensamentos algébrico e aritmético têm sustentação em suas linguagens específicas, cujos signos foram socialmente construídos e apresentam significados diferentes em contextos distintos. Esses pensamentos, segundo Vygotsky (2001), só poderão ser desenvolvidos quando os significados produzidos nas interlocuções forem internalizados já que, nessa perspectiva, as capacidades intelectuais dos sujeitos são desenvolvidas num processo contínuo pela linguagem significada.

O que se percebe nas escolas não é somente, segundo Lins e Gimenez (1997), o ensino da álgebra tentando se justificar por si só. Há também que se considerar, de acordo com esses autores, que os conceitos propostos são desprovidos de contextualização. Postulam que de todas as formas de linguagem, as palavras possuem um papel fundamental e central para o desencadeamento do desenvolvimento do pensamento humano e algébrico.

O caminho sugerido por Lins e Gimenez (1997) é a produção de significados para a linguagem. Essa produção sobre situações-problema, carregando linguística e matematicamente as palavras de significados permitiria, segundo Vygotsky (2001), a formação dos conceitos. Assim, à medida que os conceitos se formam, inicia-se o desenvolvimento do pensamento algébrico que pode ser expresso simbolicamente por meio da linguagem formal.

Dentro deste contexto, se encaixam uma série de atividades sugeridas por Imenes e Lellis (1997), dentre as quais destaco a que segue:

Figura 5: Sequência de bolinhas em formato de L.

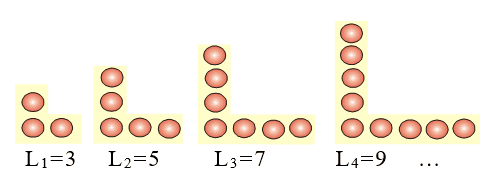
Os autores sugerem que seja observado da esquerda para a direita, o número de bolinhas de cada L da sequência. Perceba, na sequência proposta que cada L representa um número de bolinhas das diferentes posições. Após esta observação inicial, sugere-se uma série de questionamentos, os quais podem ser amadurecidos dialogicamente pelo uso natural da linguagem cotidiana. À medida que os alunos são questionados reflexivamente a respeito do comportamento da sequência, ocorre a elaboração de conjecturas, as quais após serem discutidas e validadas são expressas simbolicamente.

Embora não estejamos analisando esta atividade aqui, destacamos a importância que ela teve quando os alunos observaram atentamente o número de bolinhas em cada L da sequência, quando continuaram desenhando bolinhas para posições subsequentes, descrevendo aos colegas sobre as observações feitas em cada L, no sentido de compreenderem seu comportamento e sua regularidade.

Percebemos que quando esta situação-problema foi entendida pelos alunos, houve na sequência a possibilidade de escrevê-la por meio de uma expressão matemática. Essa ideia geral construída a partir do uso natural da linguagem cotidiana, da introdução e significação dos signos, foi então expressa, em última instância, numa linguagem simbólico-formal.

A pesquisa realizada com o grupo de alunos mostrou a existência de um estreito vínculo entre a linguagem, a produção de significados sobre a mesma e o consequente desenvolvimento de um pensamento que propicia a generalização de acontecimentos presentes em situações do cotidiano que após sua internalização permitem a escrita simbólica. A atividade contribuiu para uma efetiva organização, desenvolvimento e amadurecimento do pensamento algébrico discente na perspectiva da iniciação da escrita simbólica.

2. A FORMAÇÃO DOS CONCEITOS SEGUNDO VYGOTSKY

Nos últimos anos, em educação, têm sido crescentes as investigações que se assumem de natureza sociocultural, inspiradas fundamentalmente em Vygotsky e seus colaboradores.

Os signos, na linguagem matemática, representados pelas palavras e símbolos, constituem-se como elementos fundamentais de construção da relação do homem com o mundo. Segundo Vygotsky (2001), é desde a mais tenra idade que a criança pensa por complexos. Trata-se de um pensamento difuso que é estabelecido através de relações associativas do sujeito para com o objeto. Através dele uma mesma palavra pode apresentar significados distintos e até mesmo opostos. A elaboração de um conceito não ocorre naturalmente pela fala. Passa pela nomeação dos objetos, a qual perpassa pela riqueza do mundo social onde o aluno está inserido. O grau de generalização vai se ampliando pelos contextos vividos.

Assim, a palavra ‘frangueiro’, por exemplo, pode estar para a criança associada à venda de frangos e ao mesmo tempo para um adulto seu significado pode estar relacionado a um jogo de futebol. Em síntese, nesta perspectiva, são as interações com o grupo que orientam a palavra dando-lhe significação. Este tipo de pensamento oriundo de falas sociais, constituídas nas e pelas interações dialógicas, caracteriza um pseudoconceito. Alunos e professores se entendem no ato educativo, pela interlocução, ao expressarem palavras que representam geralmente pensamentos por complexo.

De acordo com Vygotsky (2001), as palavras são construções históricas, cujo significado não é abstrato nem eterno, varia conforme variam as relações que o homem estabelece entre seus semelhantes e com a realidade. Usamos as palavras para designar e representar objetos. Conseguimos abstrair e generalizar suas características. A palavra ‘coelho’, por exemplo, designa qualquer tipo de coelho: Branco, pardo, selvagem, doméstico, grande, pequeno, da índia, etc.

A função de generalização possibilita a comunicação entre os sujeitos. Ao falar com alguém costumamos fazer referência ao objeto, ‘um relógio’, por exemplo, que compramos para a namorada. Nosso interlocutor, mesmo não fazendo a mesma imagem que nós fazemos do relógio em questão, [nós podemos estar imaginando um relógio quadrado e ele um oval, ou ainda, nós um de pulso e ele um de parede], o entendimento ocorre e ele é capaz de imaginá-lo, pois sua característica essencial se mantém preservada.

Essa capacidade extraordinária que o ser humano tem de generalizar e abstrair nos liberta dos limites da experiência concreta. Não precisamos estar em contato direto com o objeto para nos comunicarmos sobre ele. Uma vez que o objeto esteja generalizado, o aluno é capaz de estabelecer relações sobre ele, falar sobre o relógio do exemplo anterior, sem necessariamente precisar estar em contato direto com ele.

O pensamento generalizante acontece quando uma determinada palavra designa um objeto permitindo que sua compreensão aconteça sem a presença física, mas, isso se dá numa relação complexa e aos saltos. A linguagem, neste caso, fornece os conceitos e as formas de compreensão entre o sujeito e o objeto de conhecimento. Segundo Vygotsky (2001, p. 399), “A palavra lembra o seu significado da mesma forma que o casaco de um homem conhecido lembra esse homem ou o aspecto externo de um edifício lembra os seus moradores”.

Para se compreender o desenvolvimento e o apropriamento de um conceito algébrico na perspectiva de Vygotsky, precisa-se compreender que o significado da palavra e dos símbolos evolui e se transforma ao longo do desenvolvimento da vida do aluno. À medida que o aluno convive com novas experiências matemáticas, novos sentidos são incorporados.

Vygotsky (2001) estudou em suas pesquisas os conceitos cotidianos e os conceitos científicos[7]. Compreende por conceitos cotidianos aqueles que durante o processo de desenvolvimento o aluno vai formulando, à medida que utiliza a linguagem para nomear objetos, seres e fatos que fazem parte de sua vivência diária.

No princípio e numa fase anterior à vida escolar da criança, ela pode utilizar o conceito de ‘carro’, por exemplo, sem, no entanto, conseguir definir tal conceito com palavras. Se lhe perguntarmos, o que é um carro, ela não conseguirá chegar a uma definição, porém, nos responderá, na maioria das vezes, a partir do caráter funcional do objeto em questão. A partir dos dados elaborados pela criança em relação a suas experiências vividas, ela nos informa que o carro serve para passear ou que o papai tem um carro.

Segundo Vygotsky (2001), o aluno entra em contato com os conceitos científicos normalmente a partir da fase escolar, quando, de forma planejada e intencional se inicia a aprendizagem sistematizada. Nessa fase esses conceitos representam um corpo articulado de conhecimentos, cujo processo de formação no aluno se inicia pelas interações destes com o professor. Os conceitos científicos representam para o autor “[…] os portões através dos quais a tomada de consciência penetra no reino dos conceitos” (VYGOTSKY, 2001, p. 295). Cabe à escola fazer as interações entre o mundo da vivência do aluno e o mundo científico, possibilitando a aprendizagem através do entrelaçamento destes dois mundos.

Segundo Vygotsky (2001), os conceitos espontâneos e científicos fazem parte de um único processo: O desenvolvimento da formação de conceitos. Inicialmente, esses dois tipos de conceitos encontram-se afastados, são, pela ação reflexiva, distinguidos, e mantêm-se ao longo da vida interligados. Apresentam momentos de convergência e exercem influências mútuas. Através do papel desempenhado pelo outro no estabelecimento de atos colaborativos entre aluno e adulto criam-se, pelo processo dialético, possibilidades de desenvolvimento dos conceitos espontâneos e científicos.

Não há transferências de conclusões obtidas a partir de conceitos espontâneos para conceitos científicos. O conceito espontâneo se caracteriza pelo vínculo de concretude que ele fornece para o aluno. A palavra supermercado, por exemplo, representa apenas o local onde a mãe compra doces e gêneros alimentícios. Com a aquisição do conceito científico, a palavra supermercado passa por um processo de sistematização, generalização. Compreende, um entendimento amplo envolvendo o econômico, o social e o político. Supermercado, nesse estágio, é entre outras coisas, um centro comercial onde se trocam mercadorias por dinheiro, uma atividade comercial que gera empregos e impostos para a nação.

Compartilhamos com Vygotsky (2001, p. 267) quando este postula que:

[…] o domínio da álgebra eleva ao nível superior o pensamento matemático, permitindo entender qualquer operação matemática como caso particular de operação da álgebra, facultando uma visão mais livre, mais abstrata e generalizada… a álgebra liberta o pensamento da criança da prisão das dependências numéricas concretas e o eleva a um nível de pensamento mais generalizado […].

Na perspectiva de Vygotsky (2001), a aprendizagem da álgebra propicia para o aluno um grande leque de relações e, por conseguintes possibilidades de generalização, agora, num grau mais elevado, geral, em relação ao que permite a aritmética. Para o autor, quem compreende álgebra, entende aritmética, pois a álgebra apresenta um grau bem maior de generalização.

O estudo da aritmética se caracteriza por apresentar um caráter mais específico [particular] e a álgebra, um caráter mais generalizante. Isto pode explicar porque a criança compreende primeiramente o que é uma rosa ou uma cadeira e, somente bem mais tarde consegue internalizar os conceitos de flor e mobília. Um estudo que se limita a aritmética, fica no pré-conceito e, portanto, priva o aluno de um nível conceitual mais geral.

Embora Vygotsky não tenha realizado em seus estudos experimentos específicos sobre a formação dos conceitos matemáticos e algébricos, sugeriu que fossem realizados. Referiu-se à relação entre aritmética e álgebra para dizer que a álgebra leva a um desenvolvimento superior das funções psicológicas, servindo, para uma consciência maior da aritmética.

3. DESENVOLVIMENTO

3.1 OS SIGNIFICADOS SÃO PRODUZIDOS, COMUNICADOS, INTERNALIZADOS E ESCRITOS ALGEBRICAMENTE

O trabalho investigativo principal desta pesquisa consistia em levar os alunos a escrita algébrica. Para isso, uma situação-problema e um roteiro pedagógico de questionamentos sobre o problema proposto, foram criteriosamente elaborados. Iniciamos a sessão, com os alunos distribuídos em dois grupos distintos. Ressaltamos desde já a importância que teve a produção de significados sobre o contexto, possibilitando, por meio das diferentes formas de linguagem, a elaboração do pensamento algébrico seguido da escrita simbólica.

A Figura 7 ilustra dois baldes de mesmo tamanho e uma caneca padrão. Cada balde possuía inicialmente quantidade diferente de água em seu interior. Os alunos foram instruídos, após as observações iniciais, conforme descrito no roteiro procedimental, a utilizarem a caneca padrão na transferência da água entre os baldes, no intuito de expressar cada contexto proposto através da linguagem cotidiana e algébrica.

Figura 7: Dois baldes iguais com quantidades de água diferente e uma caneca padrão.

Roteiro procedimental: Ao iniciar o desenvolvimento desta atividade foi solicitado aos alunos que olhassem para os dois baldes contendo água e a caneca padrão[8] que estavam sobre a mesa, ou a representação dos mesmos na folha de atividades. Foi solicitado que após a observação seguissem os procedimentos e questionamentos abaixo. A elaboração dos questionamentos foi elaborada de maneira adaptada ao proposto por Lins e Gimenez (1997, p. 124).

a) Depois de terem lido, observado e conversado sobre esta situação-problema, digam o que viram e o que observaram. O que mais?

b) Comparem os dois baldes: O que se pode dizer com relação aos seus tamanhos?

c) E em relação às quantidades de água contidas nos baldes?

d) O que garante essas falas – relatos/afirmações?

e) Comparem e comentem a respeito:

• da quantidade de água dos baldes;
• do tamanho dos baldes.

f) Como poderíamos representar, usando a linguagem algébrica:

• o balde da esquerda;
• o balde da direita;
• a quantidade de água existente no balde da esquerda;
• a quantidade de água existente no baldes da direita.

g) Escrevam através das linguagens cotidiana e algébrica uma expressão que compare os baldes e as quantidades de água neles existente:

• linguagem cotidiana: [comparando os baldes].
• linguagem cotidiana: [comparando a quantidade de água nos baldes].
• linguagem algébrica: [comparando os baldes].
• linguagem algébrica: [comparando a quantidade de água nos baldes].
• como poderíamos escrever algebricamente 16 canecas?
• para o contexto desta situação, o que representam 16 canecas de água?

h) Representem através das duas formas de linguagem quanta água o balde da esquerda possui a menos que o da direita;

• cotidiana:
• algébrica:
• como poderíamos, em palavras, enunciar essa mesma situação de outra forma?
• agora, usando a linguagem simbólica:

i) Representem através das duas formas de linguagem quanta água o balde da direita possui a mais que o da esquerda:

• cotidiana:
• algébrica:

j) Dos significados produzidos até aqui, existem duas expressões algébricas que representam a mesma ideia? Quais são?

k) O que seria necessário para que o balde da esquerda ficasse com a mesma quantidade de água do balde da direita? Representem essa situação nas duas formas de linguagem:

• cotidiana:
• algébrica:

l) O que acontece se acrescentarmos 2 canecas padrão de água no balde da esquerda? Expressem essa ideia utilizando as linguagens:

• cotidiana:
• algébrica:
• e se acrescentássemos 4 canecas ao invés de duas?

m) Escrevam comparativamente a expressão que representa os dois baldes cheios de água utilizando a linguagem:

• cotidiana:
• algébrica:

n) Criem novas frases sobre a situação dos baldes e justifiquem-nas procurando manter comparativamente inalterada a condição inicial da situação. Vocês podem usar a linguagem cotidiana se quiserem ou então, diretamente, a linguagem simbólica [podem também utilizar o verso da folha de atividades para anotações].

Inicialmente, as questões a até e, pretendiam exercitar as capacidades em visualizar e imaginar situações sobre este contexto, representando-as pelo uso natural da linguagem cotidiana. Após esta etapa buscou-se, elaborar, pelos pensamentos produzidos uma representação simbólica. Para esta atividade e em conformidade com Lins (1994), os alunos foram motivados a gerar, pelo uso natural da linguagem cotidiana, afirmações e justificações para as frases produzidas, elaborando, a partir destas expressões algébricas em relação à situação-problema.

Durante alguns minutos, após terem lido o enunciado da situação-problema, os alunos ficaram observando os baldes transparentes colocados sobre a mesa, suas respectivas quantidades de água e a caneca padrão. Foram na sequência motivados a iniciar a livre conversação a respeito desta situação, falando com seus colegas sobre o que haviam lido e visualizado, anotando, posteriormente, tudo nas folhas que haviam recebido.

Nossa proposição mantinha-se fortemente baseada em Vygotsky (2001) e na perspectiva em que o autor considera a linguagem como um instrumento que age sobre os seres humanos, sendo capaz de modificar-lhes a estrutura das funções psicológicas superiores, da mesma forma como os instrumentos criados pelos seres humanos agem e modificam-lhes as formas humanas de vida no planeta.

Segundo Marques (2001), conversar se tornava imprescindível. Assim os alunos iniciaram seus relatos, socializando suas observações e percepções a respeito do lido e do visualizado. Ao falarem sobre a situação-problema, Daniel relatou que estava vendo “dois baldes iguais” e Felipe acrescentou que a “quantidade de água contida neles é diferente”. Monique percebeu que “os dois baldes têm forma cilíndrica e são iguais, têm o mesmo tamanho”. Talita olhou novamente o texto, voltou-se para os baldes e disse que “em um balde faltam 8 canecas para encher. O tamanho é igual mas o volume [quantidade de água] deles é diferente”. Monique percebeu em sua visualização que “o balde da direita está mais cheio de água que o da esquerda”. Para Luma, “o balde esquerdo precisa de 16 canecas” para que a água atinja o nível já existente no balde da direita.

Neste momento Emerson observou que “com mais 8 canecas se enche o balde da direita”. Caroline comunicou que “os dois baldes são brancos”, ao que Talita acrescentou: “No balde da direita tem mais água do que no da esquerda. Se colocarmos 8 canecas no balde da direita e 24 no da esquerda, o da esquerda alcança o da direita”, ou seja, os dois baldes ficam completamente cheios de água. A partir desta informação, Monique relatou que “no balde da direita faltam 8 canecas para encher. Para ficar igual os dois baldes, faltam 16 canecas de água no balde da esquerda”. Taffarel também havia percebido a diferença de água existente entre os baldes e comunicou que “com 16 canecas de água no balde da esquerda este vai ficar igual a quantidade de água do balde da direita”. Instigados a falar mais sobre o contexto dos baldes, Felipe disse que “para encher o balde da esquerda, precisa três vezes mais água do que o da direita” e Jucilei informou ter percebido que no balde “da esquerda tem menos água que o da direita”.

Após esses relatos, entre outros, pedimos para que dissessem o que, em suas opiniões, daria garantia para que essas falas [item d], essas afirmações pudessem ser consideradas como verdadeiras. Talita prontamente relatou que qualquer pessoa acreditaria, pois “observando os dois baldes, dá para ver, dá para tirar conclusões”. Felipe ponderou que “observando e vendo a pergunta. Já diz no enunciado do problema que precisava de 24 canecas para encher o balde da esquerda e para o da direita são necessárias 8 canecas”. Daniel ainda postulou que “é muito simples, basta observar”, ao que Luma complementou: “Comparando o volume deles [dos baldes] ”, pode-se tirar conclusões.

Foi importante para a continuação dos questionamentos, a percepção de que nesta situação-problema encontramos duas situações distintas. A existência de dois baldes com a mesma capacidade, iguais, porém, contendo cada qual quantidades diferentes de água. Passamos então a pedir que representassem os baldes e a quantidade de água neles contida através de uma linguagem algébrica [item f].

Segundo Vygotsky (2001), cabe ao professor introduzir os signos para desenvolver o pensamento. É a introdução de conceitos próprios da álgebra que possibilita a iniciação do processo de significação dessa linguagem, permitindo a constituição e desenvolvimento do pensamento algébrico buscado.

Nos dois grupos em que esta atividade foi trabalhada, houve uma discussão com a participação de todos os alunos e a busca do consenso para nominar matematicamente, tanto os baldes iguais quanto a quantidade diferente de água neles contida. Em ambos os casos, os alunos decidiram nomear por b₁ e b₂, respectivamente, o balde da esquerda e o da direita e de x e y suas respectivas quantidades de água.

Pedimos, então, para que enunciassem comparativamente, utilizando-se das linguagens cotidiana e algébrica, os baldes e suas respectivas quantidades de água [item g]. Os alunos, sem dificuldades de expressar-se, comunicaram que, pelo fato dos baldes serem iguais, algebricamente, essa situação poderia ser expressa pela expressão: b₁ = b₂. Questionei os alunos sobre o que me garantia poder escrever matematicamente b₁ = b₂. Felipe imediatamente reagiu dizendo: “Porque os baldes são iguais. Só a quantidade de líquido que é diferente”. Para Monique “b₁ e b₂ significa que são dois baldes. É, assim os dois são da mesma forma, do mesmo tamanho, por isso b, só que são dois baldes e nós temos que diferenciá-los”. Talita complementou clarificando que “[…] o da esquerda vai ser o b₁ e o da direita vai ser o b₂^”.

Como já tinham observado que a quantidade de água existente nos baldes era diferente, solicitamos que procurassem analisar comparativamente, por meio de uma expressão algébrica, essas quantidades. Taffarel disse então que “x é menor que y”. Perguntei o que o levava a acreditar que x fosse menor que y, ao que Jucilei respondeu: “Pela quantidade de líquido existente nos baldes”, ao que Emerson complementou: “Pela quantidade de água que observamos nos baldes”. Luma acrescentou “que o balde da esquerda tem 16 canecas de água a menos que o da direita”.

Sobre a possibilidade de enunciar essa situação de outra forma, alguns alunos disseram, simultaneamente, que poderíamos expressar essa mesma situação por y maior que x. Questionamos os alunos sobre o que me garantiria que esta afirmação era verdadeira. Felipe relatou que “a quantidade y de líquido do balde da direita é maior do que a da esquerda [quantidade x]”. Alguns alunos ainda afirmaram que x é diferente de y, pois “os baldes não têm a mesma quantidade de líquido”.

Em seguida o aluno Emerson ressaltou que “o balde da esquerda tem menos água que o balde da direita e que a diferença entre eles é 16 canecas”, ao que Felipe complementou: “Esta quantidade de água é necessária para igualar o nível de água nos dois baldes”. Monique demonstrou uma boa capacidade de generalizar e comunicou matematicamente que estávamos diante de três possibilidades distintas para expressar algebricamente o mesmo fato, ou seja, “ x  y ; x < y ou y > x ”.

Questionados sobre o que mais poderia ser dito sobre o contexto da situação-problema, Monique foi logo dizendo que “esse daqui é y [mostra o balde da direita], menos 16 canecas, fica igual a esse balde [x]. Mostrando desenvoltura, pega papel e escreve dizendo: “daí vai ficar a expressão: y – 16c = x”.

Foi igualmente interessante a observação feita por Talita, ao dizer: “Se eu tirasse 8 canecas daqui [referindo-se ao balde y] e colocasse aqui [no balde x] ia ser igual também”. Neste momento Douglas parabenizou a colega que posteriormente sintetizou essa comunicação expressando-a e explicitando-a como segue: “y-8c = x+8c, se nós tirarmos 8 canecas do balde y, seria o balde da direita, vai ficar igual a quantidade de água do balde x se nele colocarmos essas 8 canecas”. Nesta situação, os dois baldes ficam com a água num mesmo nível, acrescentou Talita.

Embora alguns alunos já houvessem utilizado a expressão 16c para representar 16 canecas de água, perguntei a todos como poderíamos escrever algebricamente 16 canecas. Emerson, Monique e Talita prontamente disseram 16c. Monique procurou justificar sua afirmação esclarecendo que “esse número 16 é o número de canecas de água que a gente tem que colocar no balde da esquerda para deixar os dois baldes com a mesma quantidade de água [sem tirar água do balde da direita] e, esse c significa o volume de água por caneca”. Monique estava correta, pois colocando 16 canecas de água no balde da direita, a diferença nas quantidades originais de água em cada balde será nula.

Pedimos para que explicitassem o que representaria para o contexto dessa situação, 16 canecas de água. Camila iniciou dizendo que “é a diferença”, “que há entre os dois baldes”, complementou Emerson.

A partir desse momento, os alunos foram motivados a representar, através das duas formas de linguagem [cotidiana e algébrica], quanta água o balde da esquerda possuía a menos que o da direita [item h]. Com uma performance de coral, os alunos responderam “16 canecas a menos que o da direita”. O aluno Felipe preferiu enunciar sua frase em separado e relatou que “o balde da esquerda possui 16 canecas de água a menos que o da direita”. Luma enunciou seu pensamento dizendo que: “x mais 16 canecas, igual a y ou, y menos 16 canecas, igual a x”. Questionada a explicitar o que representaria o 16 em sua expressão, Luma disse que “16 é a quantidade, a diferença de água entre os baldes”. Emerson continuou o pensamento de Luma e explicou que para essa mesma frase “o x é a quantidade de água do balde da esquerda, mais 16 canecas, dá igual ao balde da direita [x + 16c = y] ”.

Convidados a enunciar esta mesma situação de forma diferente [item i], os alunos repetiram algumas ideias já abordadas, até que Emerson informou que “y menos 16c é igual a x ; ou ainda, x mais 17c é igual a y mais 1c [y-16c = x, ou então, x+17c = y+c]”. Luma neste momento recordou “que para encher o balde da esquerda precisamos 16 canecas e mais 8 canecas, que é o mesmo que está faltando no outro balde [referindo-se às 8 canecas]. Mostramos e clarificamos aos alunos que a segunda expressão [x+17c = y+c], representava uma expressão transformada da anterior.

Clarificamos que para essa expressão a condição inicial da situação-problema mantinha-se inalterada, ou seja, que a diferença de água entre os baldes continuava sendo de 16 canecas. Luma enunciou ainda que “x+16c+4c é igual a y+4c [x+16c+4c = y+ 4c]”. Em seguida a aluna elaborou outra expressão, enunciando-a como “x + 2c + 14c = y”. Felipe comunicou aos colegas uma outra expressão que elaborou: “x+16 canecas, mais 8 canecas, igual a y+8 canecas [x+16c+8c = y+8c] ”. Solicitamos, então, para que o aluno explicitasse como ficaria o nível de água entre estes dois baldes, nesta expressão, ao que Felipe disse: “Ficam iguais, eles ficam cheios, os dois baldes cheios d’água”.

Pedimos para que refletissem e depois falassem sobre o que aconteceria caso tirássemos, a partir da condição original, uma caneca de água do balde da esquerda e depois uma caneca de água do balde da direita e, novamente uma caneca de cada um dos baldes, até que o balde da esquerda, que tem menos água, se esvaziasse. Talita não titubeou e disse que o balde da direita ficaria com “a mesma quantidade de água que tinha [referindo-se a diferença inicial], 16 canecas”, com o que Monique concordou, repetindo o raciocínio da irmã.

Após todas essas justificações apresentadas os alunos foram questionados sobre a existência de expressões algébricas que poderiam representar a mesma ideia e quais seriam essas expressões [item j]. Monique não titubeou e foi logo dizendo tratar-se das expressões “y-16c = x ; x +16c = y. Poderia também ser y–x = 16c”. Quando solicitamos uma justificação para as expressões, a aluna, em seu relato, mostrou primeiramente o que seria necessário para que o balde da esquerda ficasse com a mesma quantidade de água que o balde da direita. Assim Talita comunicou que “seria necessário tirar 16 canecas de água do balde da direita para ficar igual ao balde da esquerda, ou então, colocar 16 canecas no balde da esquerda para ficar igual ao balde da direita”. Em relação à terceira expressão algébrica, os alunos disseram que ela representava a diferença de água existente entre os baldes.

Para Nobre, Amado e Ponte (2014), que consideram o desenvolvimento do pensamento algébrico uma das grandes finalidades do ensino de matemática, ressaltam que:

[…] as representações escritas produzidas pelos alunos, em particular, na resolução de problemas são poderosas ferramentas que devem ser desenvolvidas por constituírem uma componente essencial da aprendizagem, possibilitando a organização e a comunicação de ideias. Em particular, constituem um meio para a aprendizagem progressiva de métodos formais algébricos, que são umas das componentes importantes do trabalho em Álgebra. (NOBRE; AMADO e PONTE, p.2).

Continuando a reflexão sobre a situação-problema dos baldes e da caneca padrão, questionamos os alunos sobre o que aconteceria caso acrescentássemos duas canecas de água no balde da esquerda, a partir da situação original [item l]. No entendimento de Taffarel “faltam 14 canecas para igualar a água dos dois baldes”. Para Emerson “faltam mais 22 canecas no balde da esquerda para enchê-lo, que é a quantidade de água do balde x. O balde da esquerda aumentou mais 2 canecas, mas continua menor do que o balde da direita [com menos água]”. Emerson ainda representou algebricamente sua última enunciação dizendo que “x mais 2c, menor que y [x+2c < y]”. Pedimos ainda como ficaria a situação, caso acrescentássemos 4 canecas de água no balde da esquerda, ao invés de 2. Emerson logo disse que ficaria “x mais 4 canecas, menor que y  [x + 4c< y]”.

Conduzimos a reflexão no sentido dos participantes relatarem comparativamente de que forma poder-se-ia representar os dois baldes cheios de água [item m]. Felipe expressou seu pensamento falando que “o balde da esquerda com mais 24 canecas fica cheio e o balde da direita, mais 8 canecas também fica cheio. E, algebricamente fica: x+24c = y+8c”. Ao pedir uma justificação para a afirmação de Felipe, o aluno relatou que “[…] ali no enunciado do problema já diz, que faltam 24 canecas para encher o balde da esquerda e o outro pra encher, o da direita, 8 canecas”. Luma ainda acrescentou que agora “os dois, as duas quantidades ficam iguais, são iguais”, ficam “então, os dois baldes cheios”, finaliza Talita.

Como havia uma liberdade de cada aluno se expressar, Monique fez a comunicação de uma outra expressão relativa aos baldes, “y-14c = x+2c”. Talita imediatamente percebeu a possibilidade de enunciar outra expressão a partir desta: “x+2c+14c = y”. Ao solicitar o que mais alguém gostaria de dizer, Monique comunicou que “y-12c = x+4c”, ao que Talita disse “e também: x+4c+12c = y”. Talita insistiu ainda para comunicar outra expressão por ela elaborada “y > x+4c”. Considerando o tempo de discussão decorrido, encerramos o primeiro encontro.

Em outro dia e em momentos distintos continuamos a reflexão sobre esta situação-problema em cada um dos dois grupos em que ela foi trabalhada. A partir desta sessão de estudos, a ideia era que os alunos, em duplas ou trios, criassem frases sobre a situação dos baldes, justificando-as e procurando manter comparativamente inalterada a condição inicial do problema. Como a performance do 1º dia, em termos de produção de significados sobre o contexto, tinha sido muito boa, procuramos deixar os alunos à vontade, no que se refere ao uso ou não da linguagem cotidiana. Ficou a opção de utilizarem, caso quisessem, diretamente a linguagem simbólica. Passamos a relatar as produções mais significativas que ocorreram na exploração do item n, desta situação-problema.

Camila pediu para começar e foi falando “na forma algébrica fiz: 5 canecas mais y, igual a x mais 21 canecas [5c+y = x+21c]. Então, se eu colocar 5 canecas no balde, aquele que é o y [a aluna apontou com o dedo para o balde da direita], será igual ao outro, se naquele [balde x] for colocado 21 canecas”. Questionada sobre como ficaria o nível de água entre os dois baldes nessa nova situação, Camila concluiu seu pensamento dizendo: “Fica igual”, ou seja, os baldes ficam com água num mesmo nível.

Segundo Lins e Gimenez (1997) os alunos, pelas observações e suas produções de significado sobre o contexto, haviam percebido a possibilidade de fazer transformações de expressões partindo da situação-problema. Dentro desta perspectiva, estava claro que tinham percebido que as transformações diretas se constituem numa forma de produzirem sempre outras expressões corretas para o contexto.

Na pesquisa desenvolvida por Carmo (2014), o autor ressalta a importância do uso de padrões e sequências com algum tipo de repetição para introduzir a linguagem algébrica no ensino fundamental, enfatiza o quanto estas atividades podem trazer benefícios na aprendizagem da escrita algébrica, observando, porém, que,

[…] este tipo de atividade está sendo pouco utilizada para a introdução da linguagem algébrica, embora várias pesquisas e documentos oficiais mostrem o potencial desse tipo de atividade para a iniciação do estudo da álgebra (CARMO, 2014, p. 103).

As orientações do roteiro procedimental, utilizadas para elaborarem novas expressões, mantendo sempre os dois baldes de água num mesmo nível, foram bem assimiladas por todos. Jucilei apontou com o dedo e em seguida iniciou a enunciação de outra expressão, “x mais 12c, igual y menos 4c [x+12c = y-4c]. É, se colocarmos 12 canecas no balde x, ali no balde da esquerda e, tirarmos 4 canecas do balde da direita, os baldes ficaram iguais [com a mesma quantidade de água]”. Taffarel, na comunicação de sua expressão, também procurou manter os baldes com a mesma quantidade de água e relatou o que fez “ x-5c = y-21c. Se tirarmos 5 canecas do balde da esquerda e, 21 canecas do balde da direita, ficará com a mesma quantia de água nos baldes”.

Continuando os relatos dos alunos sobre as expressões por eles produzidas em relação à situação-problema em questão, Camila passou a apresentar outra justificação. “Se eu tirar 2 canecas do balde y, vai ficar igual ao balde x se lá for colocado 14 canecas. Em álgebra fica:  y-2c = x+14c”, concluiu a aluna. A expressão “y-26c = x-10c”, elaborada pelo aluno Taffarel, assim como outras expressões elaboradas pelos alunos, em que possuíam valores numéricos elevados, na prática e para o contexto dos dois baldes e da caneca padrão não podia ser realizada, pois estavam limitadas as capacidades físicas destes baldes. No entanto, os alunos as produziram demonstrando estarem numa fase de abstração. Segundo Lins e Gimenez (1997), esta expressão refletia, assim como outras, a possibilidade de se fazer transformações diretas sobre expressões para as quais já se havia produzido, em momentos anteriores, um significado concreto, real.

Em outras expressões produzidas pelos alunos, percebemos que compreenderam que, caso tirássemos ou acrescentássemos a mesma quantidade de água em ambos os baldes, estes manteriam a diferença de 16 canecas de água. Este raciocínio mostrou que os alunos conseguiram generalizar a situação-problema, visualizando uma relação de equilíbrio em relação a expressão inicial [y-16c = x].

Na atividade em que poderiam criar expressões algébricas, mantendo inalterada a condição original da situação-problema [item n], os alunos demonstraram capacidade extraordinária de fazê-lo. Ficou claro que os conceitos próprios da álgebra foram utilizados na execução das situações-problema, não ficando os alunos restritos ao uso natural da linguagem cotidiana.

No desenvolvimento destas atividades, evitamos interferir, deixando liberdade para que o diálogo entre os alunos pudesse fluir ao máximo. Interessante foi a vontade e o engajamento de cada participante, no que se referia ao desejo de mostrar sua capacidade particular de expressar-se e de justificar suas expressões sobre o contexto.

Embora os alunos ainda tivessem dezenas de expressões para enunciar, foi dito a eles que guardaríamos com muito carinho todas essas produções elaboradas. Pedimos então, para que escolhessem as últimas que seriam enunciadas nesta sessão de estudos. Monique foi logo dizendo: “Tenho outra frase. É, eu fiz também: x+8c<y-1c. Se colocar 8 canecas no balde da esquerda, ele ainda fica com menos água que o da direita, caso eu tirar uma caneca só do balde da direita”. Talita não perdeu tempo e continuou falando que “x+13c<y-1c. É, se colocar 13 canecas no balde da esquerda e tirar uma do balde da direita, o balde da esquerda ainda vai ficar com menos água”. Assim que Talita concluiu seu pensamento, Monique retomou a palavra comunicando que “x+2c<y-5c. O balde da esquerda com mais 2 canecas vai continuar sendo menor, com menos água do que o balde y se dele eu tirar só 5 canecas”. Talita reiniciou dizendo que “x+4c<y-11c. Mesmo colocando 4 canecas no balde x e, tirando 11 canecas do balde y, vamos ter ainda no balde x uma quantidade menor de água”. Monique prosseguiu dizendo “eu fiz uma outra assim: x+8c<y+1c. O balde y continua com mais água que o balde x”. Luma disse que elaborou “uma expressão em que o balde x fica com mais água do que o y: x+20c>y+1c”.

Diante das falas dos alunos ficava cada vez mais evidente que os sentidos produzidos no processo de internalização do pensamento algébrico permitem constituí-lo nos sujeitos, levando-os a escrita algébrica. Alguns alunos pareciam estar hipnotizados com a tranquilidade com que Talita e Monique lidavam com as expressões relativas ao contexto dos baldes, outros esforçavam-se para produzir uma nova expressão que pudesse retratar a situação-problema. Esta fase do trabalho foi significativa, pois desafiou alguns alunos a produzirem em função da desenvoltura demonstrada por outros.

Para Mestre e Oliveira (2011), uma generalização “é uma afirmação sobre um conjunto de dados matemáticos” (p. 4). Foi o que constatamos nesta atividade que evidencia o que também foi verificado por Lins e Gimenez (1997), ao explorarem a produção de significados sobre o contexto de dois tanques iguais e um balde padrão. O foco daquela e desta atividade não estava centrado na busca de uma solução única para a situação-problema. Aliás, conforme demonstraram os autores, nas entrelinhas de seus relatos, nem havia um problema para ser resolvido. A atividade tinha sido elaborada com a intenção de fazer com que os alunos, após a leitura reflexiva do texto, enunciassem o que poderia ser falado em relação à situação-problema.

O que os autores propuseram na atividade dos tanques foi muito bem assimilado na atividade similar que realizamos com baldes iguais e uma caneca padrão. O que se pretendia foi compreendido pelos alunos e confirmado pelas enunciações realizadas na forma de expressões diretas e expressões transformadas sobre o contexto dos baldes. Esta atividade se constituiu em uma possibilidade sobre a qual se pode produzir, segundo Lins e Gimenez (1997), significados para a álgebra, perpassando, em sua constituição, um pensamento que pode ser caracterizado como pensamento algébrico e que pode ser escrito simbolicamente.

Voltamos mais uma vez ao enunciado da situação-problema e solicitamos que todos pensassem e falassem sobre o que ela nos havia mostrado. Daniel percebeu que “várias respostas chegam na mesma conclusão. Que para cada expressão, por exemplo, num problema eu posso ter várias e várias respostas, vários caminhos”. Talita postulou que “existem várias formas de se ver as coisas, não existe uma forma só”. Luma também ponderou “que existem vários caminhos para se chegar ao mesmo resultado”.

Estas falas mostraram que não há só um caminho ou uma única maneira de expressar-se a solução para uma situação-problema. O interessante foi que, através destas observações, os alunos desmistificaram a ideia de que há apenas um caminho para a solução de uma situação-problema.

Instigados a falar sobre o que lhes chamou a atenção nesta atividade, Daniel em sua análise considerou-a distinta em relação às atividades normalmente desenvolvidas nas aulas de matemática, o que reforça a observação anterior. “Eu achei diferente”, disse o aluno, ao que seu colega Felipe acrescentou: “Porque lá na escola nós ganhamos”, “a fórmula pronta” completou Daniel, “já feita”, ressaltou novamente Felipe. Fazendo uma rápida analogia entre as aulas de matemática da escola e as sessões de estudo do ensaio empírico, Daniel comunicou que na escola “o professor explica a matéria e te dá a fórmula, te dá o exercício e, você faz o exercício com a fórmula que ele te deu. Você aprende as etapas do cálculo, você não aplica em nada, numa situação-problema ou num problema”. No entanto, ao referir-se especificamente às sessões de estudo, o aluno mencionou “que aqui precisou buscar novos caminhos” que conduzissem o foco da questão para uma solução.

De acordo com Vygotsky (2001), a linguagem age decisivamente na estruturação do pensamento e se constitui em ferramenta básica para uma efetiva construção do conhecimento sistematizado. As significações são produzidas em e sobre situações concretas[9] de interlocução. Nas sessões de estudo, à medida que os alunos perceberam que a linguagem algébrica estava imbricada nas relações estabelecidas entre a linguagem cotidiana e o contexto da produção de significados sobre a situação-problema, expressaram, através da linguagem algébrica, o que Lins e Gimenez (1997) haviam trabalhado na atividade com tanques iguais, ou seja, transformações diretas de expressões, produzindo um novo significado sobre uma expressão já existente.

Nesta perspectiva, produzir significados através da interpretação visual e escrita do texto enunciado na linguagem cotidiana dá sentido ao compreendido. O afloramento do conhecimento perpassava pela enunciação de cada observação percebida. Portanto, falar, dialogar com o outro, torna-se fundamental a fim de se produzir mais e mais significados sobre o texto. constitui-se na chave que possibilita a generalização da situação-problema por meio da linguagem algébrica e por conseguinte sua representação escrita.

4. CONSIDERAÇÕES FINAIS

Na nossa história tradicional de ensino da matemática, a resolução de problemas sempre foi utilizada na sala de aula como uma estratégia para aplicar e fixar um determinado conteúdo matemático. Ensinávamos os algoritmos das operações e por meio deles conduzíamos os alunos a buscar uma resposta final correta, acabada para cada problema proposto.

Na pesquisa com esses alunos de 13 anos de idade, propusemos a elaboração e desenvolvimento do pensamento algébrico, seguido da escrita, numa perspectiva meta-operacional, ou seja, que vai além da postura normalmente adotada nas escolas. Trata-se de um enfoque que compartilha comunicativamente a produção de significados dos participantes, numa dinâmica onde a qualidade da aprendizagem se sobrepõe à quantidade de conceitos.

O percurso investigativo, segundo esta perspectiva, procurou compreender intersubjetivamente o que permite um ser humano pensar algebricamente, buscando clarificar a relação que existe entre pensamento e linguagem para uma efetiva organização e desenvolvimento do pensamento algébrico.

A todo instante os alunos eram instigados a fazer a comunicação das ideias matemáticas presentes na observação e análise de padrões e sequências repetidas. Iniciamos sempre conversando sobre o texto [situação-problema], nas perspectivas de Lins (1994) e Vygotsky (2001). Assim, acreditamos que a produção do pensamento algébrico perpassa pela resolução de situações-problema, que podem, pelo viés da linguagem, ajudar os alunos a comunicar-se matematicamente, tanto pela linguagem cotidiana quanto pela linguagem simbólica.

A discussão crítica e reflexiva do contexto de cada situação-problema, o questionamento das possibilidades interpretativas, a produção de significados e a elaboração dialógica do conhecimento matemático, presente ou oculto, perpassam tanto pela enunciação quanto pelo entendimento do texto, que se torna possível pela internalização dos significados produzidos sobre a linguagem.

Conforme Freire (1987), o desafio consiste em se fazer uma leitura do mundo e na caminhada perceber e compreender as relações que se estabelecem entre o texto e seu contexto, relações estas também imbricadas dinamicamente na linguagem e na realidade. Assim, aos seres humanos, tornar-se-ia mais significativo o desenvolvimento de um pensamento que auxilia a generalização de fatos e acontecimentos do que a costumeira decoreba de centenas de teoremas e fórmulas.

Em síntese, ganha ênfase a construção de modelos e procedimentos. Nas atividades desenvolvidas com os alunos e nas falas correspondentes este aspecto ficou evidente. Segundo Lins (1994), trata-se da possibilidade dialógica de se estabelecer pela problematização um pensar aritmeticamente, um pensar internamente e um pensar analiticamente.

Conversar a respeito de cada situação-problema e, especialmente, o que mais poderia ser verbalizado, criado e produzido para o contexto existencial de cada situação proposta, foi fundamental. Nessa perspectiva, buscou-se de forma continuada, questionar as falas, os significados produzidos no contexto de cada problema, favorecendo o desenvolvimento do espírito crítico, a capacidade de argumentação e generalização.

Os participantes foram levados a reflexões sucessivas sobre as situações-problema propostas e sobre suas falas. Foram instigados a adotar uma postura investigativa e criativa que considero fundamental sempre. Para desenvolver o pensamento algébrico, o sujeito, segundo Lins (1994), precisa enunciar, falar sobre o texto.

Já foi dito que a todo instante os alunos eram instigados a explicitar suas falas e seus procedimentos. Acreditamos que isto contribuiu para realçar e ativar o pensamento algébrico, (re)construindo-o ao longo do diálogo. À medida que a linguagem cotidiana ficou carregada de significados, esse pensamento começou a ficar encorpado, tomar forma e, por conseguinte, sua expressão tornou-se possível.

De fato, à medida que as atividades foram sendo trabalhadas, ficava cada vez mais perceptível a crescente desenvoltura dos alunos, no que diz respeito a conseguirem transitarem entre as diferentes formas de linguagem, culminando com a escrita algébrica do problema proposto.

Em termos de pesquisa, o trabalho não pode ser considerado conclusivo, mas aponta para uma metodologia interessante que possibilita a generalização das ideias matemáticas presentes em situações-problema e que pela linguagem, fundamental para o desenvolvimento do pensamento algébrico, pode conduzir os alunos, aos poucos, a escrever matematicamente, utilizando-se apenas da linguagem simbólica.

REFERÊNCIAS

BRASIL. Ministério da Educação. Base Nacional Curricular Comum. Brasília: 2016.

CARMO, P. F. Um estudo a respeito da generalização de padrões nos livros didáticos de Matemática do Ensino Fundamental. PUC, 2014.

CARVALHO, Maria Cecília Costa e Silva.  Padrões numéricos e sequências.  São Paulo: Moderna, 1997.  79 p.

FARIAS, Sandra Alves; BORTOLANZA, Ana Maria Esteves. O papel da linguagem escrita nos processos de ensino e aprendizagem: um estudo teórico. Educação & Linguagem, v. 18, n. 2, p. 63-85, 2015.

IMENES, L. M.; LELLIS,M.  Matemática. 4 volumes. São Paulo: Scipione, 1997.

LINS, R. C.; GIMENEZ, J.  Perspectivas em aritmética e álgebra para o século XXI.  Campinas: Papirus, 1997.  176 p.

LINS, Rômulo Campos.  O modelo teórico dos campos semânticos: uma análise epistemológica da álgebra e do pensamento algébrico.  Dynamis, Blumenau, v.1, n. 7, p. 29-39, abr./jun, 1994.

LORENZATO, Sérgio. Educação infantil e percepção matemática. 2. ed. Rev. Ampl. Campinas, SP: Autores Associados, 2008.

MARQUES, Mario Osório. Escrever é preciso: o princípio da pesquisa.  4.ed.  Ijuí: Editora UNIJUÍ, 2001.  163 p.

Mestre, C. & Oliveira, H. (2011). O pensamento algébrico e a capacidade de generalização de alunos do 3.º ano de escolaridade do ensino básico. In C. Guimarães & P. Reis (Orgs.) Professores e infâncias: Estudos e experiências (pp. 201-223). São Paulo: Junqueira & Marin Editores.

NOBRE, S.; AMADO, N.; PONTE, J.P. Representações na aprendizagem de sistemas de equações. Disponível em: http://cmup.fc.pt/cmup/eiem/grupos/documents/14.Nobre_Amado_Ponte.pdf. Acesso em: 10 jan. 2014.

SOUZA, Eliane Reame de; DINIZ, Maria Ignez de Souza Vieira.  Álgebra: das variáveis às equações e funções.  2.ed.  São Paulo: IME-USP, 1996.  v. 5

VALE, I.; PIMENTEL, T. Padrões e Conexões Matemáticas no Ensino Básico. Educação Matemática, n. 110, p. 33-38, 2011.

VYGOTSKY, Lev Seminovich. A construção do pensamento e da linguagem.  Trad. De Paulo Bezerra.  São Paulo: Martins Fontes, 2001.  496 p.

APÊNDICE – REFERÊNCIA DE NOTA DE RODAPÉ

7. Conceitos científicos, segundo a perspectiva de Vygotsky (2001), correspondem a um corpo de noções sistematizadas que integram o complexo processo de organização de toda a atividade humana.

8. Caneca utilizada como unidade de medida para acrescentar ou tirar água dos baldes durante a execução da atividade.

9. São entendidas neste trabalho como situações de estudo, através das quais pela investigação estabelece-se uma relação dialógica com a realidade. São, portanto, situações vivenciadas pelos alunos, que fazem parte da atividade humana em diversos setores e que têm a matemática como ferramenta para propiciar o desenvolvimento do pensamento algébrico.

^[1] Mestrado em Educação nas Ciências – Matemática. UNIJUI: Universidade Regional do Noroeste do Estado do Rio Grande do Sul, RS. Início: 2.001. Conclusão: 2.003. Especialização: Ensino de Ciências. FAFIG: Faculdade Estadual de Filosofia, Ciências e Letras de Guarapuava. Início: 1.987. Término: 1.988. Graduação em Matemática. UPF: Universidade de Passo Fundo, RS. Início: 1.984. Conclusão: 1.987. Graduação em Ciências 1º Grau. FACIP: Faculdade de Ciências e Pedagogia de Lages, SC. Início: 1.981. Conclusão: 1.984.

^[2] Mestrando em Desenvolvimento Rural Sustentável, UNIOESTE: Universidade Estadual do Oeste do Paraná, 2020. Especialista em Matemática e Física, UNIPAR, Conclusão em 2010, Graduação em Matemática com ênfase em Física, UNIPAR, conclusão em 2007.

^[3] Graduanda em Agronomia – UNIOESTE – Universidade Estadual do Oeste do Paraná- Graduanda de Administração – Unip – Universidade Paulista.

^[4] Especialista Em Educação Matemática E Especialista Em Física Educacional.

^[5] Pós-Doutor Em Ciências Ambientais.

^[6] Especialização em Ensino de Ciências Exatas – Matemática, Física e Química. UNIOESTE – Universidade Estadual do Oeste do Paraná. Início: 1.997. Término: 1.988. (360h). Graduação: Ciências – Licenciatura Plena – Habilitação Matemática. UNIJUI: Universidade Regional do Noroeste do Estado do Rio Grande do Sul, RS. Início: 1.990. Conclusão: 1.992.  Graduação: Ciências – Licenciatura de 1º. Grau. UNIJUI: Universidade Regional do Noroeste do Estado do Rio Grande do Sul, RS. Início: 1.986. Conclusão: 1.989.

Enviado: Maio, 2021.

Aprovado: Junho, 2021.