Investigação e reflexão no 6° ano: A importância do ensino das frações na percepção dos docentes e discentes

ARTIGO ORIGINAL

SANTOS, Hélio Rodrigues dos ^[1], RECK, Jair ^[2]

SANTOS, Hélio Rodrigues dos. RECK, Jair. Investigação e reflexão no 6° ano: A importância do ensino das frações na percepção dos docentes e discentes. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano 05, Ed. 09, Vol. 08, pp. 175-195. Setembro de 2020. ISSN: 2448-0959, Link de acesso: https://www.nucleodoconhecimento.com.br/educacao/ensino-das-fracoes

RESUMO

O presente artigo apresenta o resultado de uma pesquisa de campo, na qual busca-se compreender a importância da matemática no cotidiano e as dificuldades no processo de ensino-aprendizagem das frações no contexto escolar do ponto de vista dos educadores (as) e educandos (as). A produção das informações foi tecida por meio de pesquisas bibliográficas e entrevistas com professores(as) e alunos(as). A média de idade dos participantes adolescentes está entre 12 e 13 anos. Os aportes teóricos que sustentam a investigação são oriundos da área de aritmética e álgebra. O material de pesquisa é composto por diário de bordo e relatos dos docentes e discentes. Os resultados da prática investigativa indicam que os educandos (as) apresentam compreensão da importância da matemática no cotidiano e na vida. No entanto, demonstraram dificuldade para compreender os conceitos de frações e, também, de conjuntos dos números racionais. Apresentou-se, ainda, em meio ao diálogo, poucas propostas metodológicas baseadas no contexto social do educando (a) e, a partir da interpretação das falas dos educadores (as) que ensinam matemática, verificou-se a dificuldade na socialização da construção de conhecimento, uma vez que a sua formação inicial não é em matemática.

Palavras-chave: Matemática e cotidiano, frações, conjuntos, dificuldade de aprendizagem, generalizações.

1. INTRODUÇÃO

O processo de ensinar e aprender frações na matemática, atualmente, apresenta lacunas/dificuldade de compreensão tanto por parte dos educandos (as) e dos educadores (as). Entendendo que a dificuldade de internalização pode estar tanto no processo de ensino quanto no de aprendizagem, Witt (2018) destaca que a fração, nas escolas públicas, em muitas das vezes, é abordada de forma tradicional, mecânica e operatória, voltada apenas para a resolução de situações problemas propostas no livro didático que, em muitas das vezes, não dialoga com o contexto social do educando (a). Cabe destacar que a matemática da escola é engajada de concepções científicas, ou seja, um jogo de linguagem diferente da matemática usual do dia a dia. Assim sendo, as frações são um dos conteúdos pertinentes à Base Nacional Curricular Comum (BNCC), que, por sua complexidade, gera um grau de incompreensão para os estudantes, referente à sua compreensão e utilização no dia a dia.

De acordo com os Parâmetros Curriculares Nacionais, o uso de símbolos e da linguagem matemática pode ser compreendido do ponto de vista histórico e cultural, tanto a linguagem para georreferenciar-se quanto a simbologia para a sua interpretação da realidade. (BRASIL, 1997). Sob essa ótica, ao pensar de forma prática, o educando (a) interpreta e compreende as múltiplas representações intrínsecas na sociedade.

Visto isso, Freire (1996) realça que o educando (a) interpreta o seu mundo, o seu pequeno mundo carregado de contradições, para que depois possa interpretar a sua volta e a realidade que o precede. Isso nos remete a uma interligação entre o imaginário e o real, manifestando/materializando em aprendizagem. Está percepção nos translada, ao pensar na teoria do desenvolvimento proximal de Vygotsky (1998), na qual a relação do homem com o mundo não é diretiva, ela acontece a partir da intermediação entre homem e cultura, simbologia e manifestação sociocultural, conectados pelo geoespaço em que vive.

Dessa maneira, o presente trabalho tem como objetivo central entender o que os (as) alunos (as) pensam sobre as frações e onde sentem mais dificuldades em resolver os cálculos propostos. Ainda, por parte dos professores (as), como esse sujeito compreende a importância das frações no cotidiano e na sala de aula. Ao professor (a) que leciona o conjunto dos números racionais, é importante ressaltar que eles se configuram como um subconjunto dos números reais. Essa percepção aparenta-se simples, mas para o educando (a), em muitas situações, desencadeia-se de forma complexa. Além de todas essas percepções a respeito das frações, a sua forma de ensinar, sem embasar-se nos matérias concretos, pode dificultar o processo de aprendizagem.

É importante, ainda, salientar que o professor (a), ao explanar o conteúdo das frações, necessita buscar múltiplos meios para tornar a internalização das frações acessíveis e simples, a fim de que o educando (a) possa associar com o seu dia a dia. A aprendizagem baseia na ligação entre conceito, teoria e prática.  Na área da matemática, muitos conteúdos são sequenciais e apresentam níveis de compreensão e abstração. Cada série apresenta níveis e organizações numéricas, cabendo tanto ao professor(a) quanto ao aluno(a) compreendê-la significativamente, para que, nos próximos níveis, seja possível a internalização de forma mais rápida e concreta.

Dessa maneira, a investigação conta com três tópicos, sendo que o primeiro apresenta o ensino de matemática e a sua importância para a sociedade, entendendo que as suas funcionalidades não se deslocam da realidade, ao contrário, é na realidade que tudo se conecta. No segundo tópico, dialogamos para compreender os recursos filosóficos, paradidáticos e dificuldades encontradas no processo de ensino das frações para aguçar a percepção e a compreensão do educando (a) e do professor (a) no que tange aos conhecimentos das frações. No terceiro tópico, refletimos sobre a ideia dos números fracionários e o currículo referência do 6° ano, no qual o presente conjunto apresenta-se com mais intencionalidade e com maior grau de abstração para os educandos(as).

2. O ENSINO DE MATEMÁTICA E A SUA IMPORTÂNCIA PARA A SOCIEDADE

O ato de contar, calcular, representar e enumerar está presente em todas as tomadas de decisões humanas, seja na compra de objetos, produtos, na obtenção de descontos, acréscimos e investimentos financeiros, utilizamos conceitos matemáticos para nos ajudar a interpretar as relações cotidianas.

As compreensões matemáticas carregam consigo valores formativos, generalizações, partições, linguagem, cultura, normas e lógica. Freire, em diálogo com D’Ambrósio (2014), destaca que o letramento matemático é equivalente a literacy, podendo ser compreendida como materacy, demonstrando, assim, que a matemática está em todos os contextos, sejam eles socioeconômicos ou socioculturais.  Nas palavras de Santos (2019), a matemática deve fugir do movimento artístico monolítico da reprodução/memorização e partir para a objetivação prática do objeto, tornando não apenas a sua dinâmica inclinada, mas passando a obter sobre o objeto (conhecimento subjetivo intercultural), a produção livre de conhecimentos colineares.

A matemática está presente em todos os tempos históricos e sociais. No contexto da escola, nos deparamos cotidianamente com a matemática formal/científica, que carrega consonâncias eurocêntricas, abstrações e generalizações transcritas dos objetos presentes na realidade. A matemática, em seu contexto antagônico, está além da família, do trabalho e dos muros da escola. Ela está inserida na sociedade, como produto da própria interpretação da natureza praticada pela própria sociedade. Skovsmose (2001) classifica a matemática como democrática/social e de inclusão, conhecimento que não se desvincula da realidade, que apresenta um papel crítico e de propriocepção do mundo e do entendimento da própria realidade.

Nesse sentido, o autor referência a matemática não como ciência única, mas como papel crítico-formativo, social e político, de significados e significações, que possibilita conviver em sociedade, exercer a cidadania, compreender direitos civis e morais, ou seja, enxergar a matemática em uma vertente interdisciplinar conectada em todos os processos sociais do homem.

Assim sendo, ensinar e aprender matemática consistem em um fenômeno complexo, que parte da teoria para o concreto e vice-versa. Matematizar é algo natural do ser humano, pois aprender matemática já não é visto mais como mera transmissão de conhecimentos ou recepções de informações monolíticas. Essa nova forma deve partir da construção de conhecimentos, coletiva, mediada, participativa e investigativa, com processos dialógicos que envolvem professor (a)-aluno (a) e aluno (a)-professor (a) (BOERI; VIONE, 2019).

Neste viés, a escola e o sistema de ensino necessitam mudar as suas estruturas físicas e pedagógicas, pois a sociedade está em movimento e as formas de aprender matemática também. É preciso pensar o ensino de matemática na atualidade em consonância com a sua totalidade, partindo do real, do sentido e das tomadas de decisões pertinentes ao aluno (a), valorizando os seus conhecimentos, contemplando a sua relação com a natureza e com as várias formas de organizações sociais.

A matemática surgiu na antiguidade por necessidade do homem, converteu-se em um imenso sistema de variadas e extensas disciplinas, ciência que reflete as leis sociais, instrumento pedagógico do mundo (BRASIL, 1997). Por isso, que, ao pensarmos a importância da matemática na vida e na educação, é preciso reconectar-se e entender que a educação básica tem como finalidade desenvolver o educando, possibilitar uma formação comum indispensável, com possibilidades de exercer a sua cidadania, para que o sujeito possa progredir na escola, na vida e nos estudos posteriores, conforme preconizado na Lei de Diretrizes e Bases da Educação, em seu artigo 22 (BRASIL, 1996).

Não há como negar que a matemática faz parte da construção histórica do homem e da sociedade, pois contribui para a formação da capacidade intelectual, estruturação do pensamento, aquisição de lógica e dedução. Não é possível haver cidadania, sem o domínio da matemática, assim, também não é possível exercer complexidades de cidadania sem ela. Por isso, faz-se necessário os conhecimentos para calcular, medir, argumentar, interagir e participar ativamente das tomadas de decisões da própria sociedade (BRANDT; MORRETI, 2016).

O mundo do trabalho requer pessoas preparadas para utilizar diferentes tecnologias e linguagens (que vão além da comunicação oral e escrita), instalando novos ritmos de produção, de assimilação rápida de informações, resolvendo e propondo problemas em equipe (BRASIL, 1997, p. 30).

Nesse sentido, a matemática encontra-se importante no currículo escolar e também para a sociedade, pois, a partir da sua interação com o homem, a matemática permite maior assimilação, raciocínio, psicomotricidade, praticidade e entre outros estímulos. A linguagem matemática está na realidade, por isso é necessário que as suas conexões, entre o sujeito e objeto em seu processo de ensino, aconteçam de forma dinâmica. Assim sendo, as frações que estão no ramo da aritmética assumem um papel dentro do currículo e na vida, uma vez que elas, enquanto significado e significação, encontram-se na realidade.

3. AS FRAÇÕES NO CONTEXTO ESCOLAR: REFLEXÕES SOBRE O ENSINO E AS DIFICULDADES

A sociedade atual tem vivido inúmeras transformações sociais. Entretanto, “apresenta-se um descompasso na lógica interativa e diretiva para a objetividade e a finalidade dos processos socioeducativos envolvendo o currículo escolar e o papel da educação escolar”. (PASSOS; NACARATO, 2016, p. 119).

A educação escolar é fundamental para a transformação social de cunho científico e humanístico, considerando a sua plenitude social de integração-construção e reconstrução social reflexiva. É preciso que o seu papel social seja imbuído de múltiplas determinações capazes de transformar o seu meio e o geoespaço referencial de contato.

No que tange ao conhecimento formal, informada da matemática, as suas determinações/manifestações fazem parte do nosso cotidiano e estão presentes em todas as áreas do conhecimento (MUFFI, 2013). No que se refere ao estudo dos números, operações, frações, funções e, entre outras denominações de conhecimento matemático, que estão inseridos no currículo, constata-se que, no final do ensino médio, os alunos apresentam dificuldades de cálculo (principalmente nas frações), valor numérico, falta de competências e habilidades, ausência de compreensão sobre a importância da sua utilização e da sua representação democrática e social da realidade (BRASIL, 1998).

Dentre os conhecimentos científicos compreendidos na escola e na vida, destacam-se as frações como parte relativa do currículo escolar gerador de discussões (contradições são vistas e revistas), uma vez que a temática é entendida pelos educandos (as) como conteúdo de complexidade. Para centralização da discussão, uma explicação válida para tal situação pode ser encontrada na abordagem e na construção do conhecimento, ou, ainda, em mencionar que a aprendizagem dos números reais/racionais pressupõe rupturas (OKUMA, 2010). Nesse sentido, ao preparar a aula envolvendo os números racionais, é de suma importância a orientação contínua dos educandos (as), pois a generalização e os termos matemáticos podem causar confusões no seu processo de compreensão, visto que:

• • • Cada número racional pode ser representado por diferentes (e infinitas) escritas fracionárias: por exemplo, 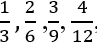….. São diferentes representações de um mesmo número;
    • A comparação entre racionais: acostumados com a relação 3 > 2, terão de compreender uma desigualdade que lhes parece contraditória, ou seja ;
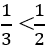    • Se o tamanho da escrita numérica, no caso dos naturais, é um bom indicador da ordem de grandeza (8345 > 83), a comparação entre 2,3 e 2,125 já não obedece ao mesmo critério;
    • Se, ao multiplicar um número natural por outro natural (sendo este diferente de 0 ou 1) a expectativa é a de encontrar um número maior que ambos, ao multiplicar 10 por 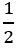se surpreenderão ao ver que o resultado é menor que 10;
    • Se a sequência dos números naturais permite estabelecer sucessor e antecessor, para os racionais isso não faz sentido, uma vez que entre dois números racionais quaisquer é sempre possível encontrar outro racional; assim, o aluno deverá perceber que entre 0,8 e 0,9 estão números como 0,81, 0,815 ou 0,87 (BRASIL, 1998, p. 101).

No que tange ao contexto das frações, são caracterizadas, como expressões matemáticas, àquelas que estão coligadas às ações do homem. Entretanto, a sua compreensão é complexa, pois Makuch (2016) realça que a dificuldade de compreensão pode estar na representação, tais formas são decimais finitas, dízimas periódicas ou, até mesmo, como fração na própria fração. É possível que a mesma fração alcance infinitas possibilidades de representação, pois a equivalência de fração, razão e proporção permite que os números racionais se manifestem em diferentes escalas.

Assim sendo, é possível compreender que o ensino da fração se torna complexo e, em muitas das vezes, o (a) estudante encontra-se desestimulado (a), devido à não compreensão de tantas situações e mudanças. Nessa dimensão, ao lecionar as frações em sala de aula, é necessário o uso dos materiais concretos, como possibilidade de apoio, uma vez que as frações são abstrações de objetos reais da realidade. Assim, a manipulação de objetos facilitará a dedução de valores e a sua representatividade, pois, em sala de aula, é necessário propor situações de investigação e  experimentação, à respeito de diferentes conceitos e propriedades matemáticas, empregando dinamismo, estratégias, recursos e observações, identificando cada vez mais a formal validação das referidas conjecturas (BRASIL, 2017).

Perlin et al. (2015) enfatizam que a aprendizagem baseada em materiais concretos se torna mais significativa, possibilitando maior interpretação da realidade para maior efetuar o grau de abstração, pois apenas desenhar e representar já não são necessários para aprender de forma sistêmica. É preciso ir além das linhas, conectar o imaginário com o concreto.

Nesse sentido, as frações apresentam um grau de complexidade, mas é preciso ir além dos livros didáticos para abordá-la; é preciso propor situações problemas do cotidiano, criar situações problemas que envolvam situações reais da vida do educando (a), pois aprender significa conectar e despertar o sentido.

3.1 A IDEIA DOS NÚMEROS FRACIONÁRIOS

A ideia de fração ou de um número fracionário surge da compreensão de considerar partes de um determinado objeto, ou seja, de compreender o seu todo ou as suas representações em partes. A sua representação nos livros didáticos e acadêmicos é dada pela expressão (a; b ∈ N e Z) / b ≠ 0. Nessa expressão e representação, a letra “a” assume o papel de numerador, que é a parte da fração que indica a quantidade que está sendo considerada, e a função do “b”, que é conhecido por ser denominador, vai indicar o valor do todo.

Para facilitar o entendimento, pensemos em uma pizza inteira inicialmente. Agora, imagine que ela está dividida em quatro pedaços iguais, imaginou né? Se retirarmos um pedaço, significa que ficaremos com duas resoluções: para representar o pedaço que foi retirada; e  para representar a parte que restou da pizza. Toda fração tem uma representação decimal, que pode ser considerada enquanto exata, ou com infinitas casas decimais. Esses números que se repetem após a virgula (consideradas dízimas periódicas) como, por exemplo:  = 1,3333333333333…., dizemos que o seu período é “33”. Com as frações, podemos realizar inúmeras representações e estabelecer cálculos que envolvam adição, subtração, divisão, multiplicação, radiciação e potenciação.

Para os adolescentes, torna-se complexo, em um primeiro estágio, entender que a fração, na verdade, é um número dividido por um outro determinando número, que pertence aos reais e que tem de ser diferente de zero em partes iguais ou diferentes de si, ou, até mesmo, compreender que essa mesma fração pode tornar-se um número natural, inteiro e real e vice-versa.

Assim sendo, a sua compreensão torna-se complexa, devido ao grau de abstração que o educando (a) necessita internalizar mediante a reflexão de que somente os números naturais e inteiros não satisfazem às necessidades humanas. Pois, ao longo da história da humanidade, o fazer matemático auxilia no processo de concretização das necessidades humanas. Necessidades estas impostas pelas evoluções que os próprios seres humanos construíram (POSSAMAI, 2015).

Por isso, fazer uma abordagem sócio histórica é uma importante reflexão, pois na época da agricultura e divisão de terras, os egípcios utilizavam as frações para realizarem cálculos e terem dimensões de suas terras. Para tal dimensão, elencada a história e a cultura, é preciso olhar para trás e conhecer o contexto histórico-cultural, para entendermos que os conhecimentos multiplural vão surgindo de acordo com a necessidade do homem de trabalhar na realidade.

As propostas de ensino e os conteúdos devem promover a construção, coordenação e estruturação de pensamento lógico-dedutivo-matemático, para a implementação e desenvolvimento da criatividade, reflexão, capacidade de análise crítica da realidade e de argumentação para interpretar códigos linguísticos, fatos e fenômenos da realidade (BRASIL, 2001).

Assim, a ideia das frações e da sua inserção no contexto da escola assume um papel significativo, que possibilita ao (à) estudante compreender a sua realidade, partes do todo e interação numérica, apropriação da identidade e de compreensão histórica, que vão estimular a indução e a dedução para os processos interativos e análogos.

4. METODOLOGIA

Na busca em alcançar elementos sociais capazes de proporcionar alcance real dos objetivos traçados, a presente pesquisa optou pela metodologia qualitativa. Descreve Gil (2002), como método de percepção da realidade, no qual necessita de constantes observações, análises e interpretações conexas com o propósito de absorver os processos mais abrangentes e coesos ligados a uma determinada comunidade/contexto social.

O presente trabalho também contou com pequenas entrevistas semiestruturadas, nas quais garantem a liberdade de expressão e a aproximação de conceitos reais sobre determinadas temáticas. Na concepção de Silva (2015), a entrevista é um conjunto de funcionabilidades que tem por proposta/objetivo uma troca de informações entre o pesquisando (a) e o pesquisador (a), onde o pesquisando (a) pode abranger de forma significativa os seus nuances e percepções da realidade. Tais informações são vitais para a certificação real do trabalho, contendo, assim, seguridade e veracidade de informações, nas quais ajudarão o pesquisador a entender tal realidade.

Para possibilitar maior repertório cultural, bibliográfico e social, o presente trabalho contou com um acervo de informações, que, nas palavras de Lakatos e Marconi (2003), a pesquisa bibliográfica é um acervo de pressupostos teóricos que debruçaram sobre a realidade, a fim de estudá-la e de interpretá-la, proporcionando conhecimento para a humanidade. Assim, a pesquisa bibliográfica é um conjunto de múltiplas categorias de texto científicos, que carrega consigo as análises de múltiplas realidades/pesquisas de múltiplos contextos.

A população pesquisada contou com educandos (as) e educadores (as) remanescentes da comunidade Kalunga-Ema. A pesquisa contou com um total de 18 participantes, sendo 2 educadores (as) e 16 educandos (as) que frequentam o ensino fundamental II. Os entrevistados (as) encontram-se divididos em grupos, sendo que um dos grupos são os educadores (as) e, o outro grupo, os educandos (as). Para facilitar a leitura, no grupo de educadores (as), serão avaliados a prática/atuação no processo de ensino-aprendizagem do conteúdo das frações e qual o seu entendimento pelo processo de reflexão mediante ao ensino das frações. No que tange ao grupo dos educandos (as), eles (as) irão participar ativamente de entrevistas simples, para compreendermos o que pensam sobre as frações e o seu processo de ensino-aprendizagem.

Para preservar a identidade dos (as) educadores (as), serão utilizados Ed1 e Ed2, para identificar os (as) educadores (as), e, para os alunos, devido ao número, por meio de gráficos.

4.1 ANÁLISE DE DADOS E PROCEDIMENTOS METODOLÓGICOS

Na primeira faixa de análises, vamos compreender como os (as) professores (as) compreendem os conceitos simples da matemática e, principalmente, o eixo de frações. Em seguida, analisaremos a fala dos (as) alunos (as) por meio de porcentagens, a fim de verificar quais os conceitos dominados pelos educandos e como identificam as relações coexistentes. Segue a análise das falas dos educandos.

4.1.1 TRANSCRIÇÃO DAS QUESTÕES DA ENTREVISTA REALIZADA COM OS PROFESSORES DA COMUNIDADE EMA – ESCOLA ESTADUAL CALUNGA III

Primeira questão: quais são as maiores dificuldades encontradas no ensino de fração? Quais os exemplos você utiliza para abordar as frações em sala de aula?

Eu vejo as frações difíceis, porque elas assumem vários valores e várias formas de serem expressas, por isso ao aluno é difícil, principalmente no 6° ano. Nas minhas aulas, sempre trago algumas abordagens, mas não fujo dos exemplos do livro, busco sempre ensinar a sua forma decimal (Ed1).

As frações historicamente são difíceis de interpretar, mas devido apenas à utilização dos conjuntos dos inteiros com maior frequência para satisfazer às nossas necessidades, ao inserirmos ideia de fração, o sujeito sente-se perdido, devida à não compreensão das suas complexidades e abstração. Por isso, a ludicidade é importante nos espaços escolares (Ed2).

Na fala apresentada pelos (as) educadores (as), retratam as dificuldades encontradas em âmbito educacional para o ensino de frações. Um dos elementos implícitos, que é possível captar, é a transição de séries, pois, em muitas das vezes, os (as) alunos (as) estão acostumados (as) com um tempo mais longo e uma didática menos formalista. Um outro elemento, que foi possível captar, é os métodos pelos quais o conjunto dos números racionais apresentam-se, pois genericamente é mais rígido e necessita de maior domínio por parte do (a) educando(a).

Nascimento (2008) enfatiza que, para a matemática alcançar o seu papel social, é necessário que os conteúdos abordados em sala de aula sejam também utilizados no dia a dia. Assim, é preciso buscar formas de embasar esses conceitos em meio ao processo de ensino-aprendizagem.

Assim sendo, os elementos da discussão apresentaram uma nova reflexão, o que se ensina na escola tem ligação com a realidade? Sob tais concepções, torna-se necessário engajar na historicidade, processualidades e transformações sociais em meio ao processo de ensino, uma vez que o papel social da escola e do professor é possibilitar autonomia para o educando agir perante a sociedade.

Segunda questão: você encontra dificuldade em lecionar o conteúdo das frações? Você utiliza jogos para trabalhar a ludicidade em meio ao ensino de frações?

Encontro no momento de trabalhar em sala de aula, pois baseamos muito no livro didático, e em muitas das vezes os exemplos são confusos para o sujeito que não está naquela realidade apresentada pelo livro. Os jogos são bons para complementar a aula e fazer o conceito de fração ser mais consistente, entretanto, pouco usei jogos, devido a passar mais tempo trabalhando a formalização do conteúdo (Ed1).

As frações como já mencionado, são complexas e para o aluno dominar com propriedade é necessário que o educador tenha muita paciência e didática. Em meio às aulas, sempre busco aproximar o real, pegar a própria família, altura, idade, gênero e entre outras situações. Disponibilizo sempre que posso jogos envolvendo geometria e frações, mas a identificação os alunos conseguem internalizar, porém, ao aumentar o grau, os alunos se perdem em meio aos cálculos e às propriedades (Ed2).

De acordo com as reflexões apresentadas, os (as) educadores (as) enfatizaram que sentem dificuldades ao lecionar o conteúdo das frações, inicialmente, pela complexidade do conteúdo, pois é necessário um entendimento amplo e, em seguida, trazer de forma dinâmica e simples para os (as) educandos (as).

Para Santos (2005), apud Alves e Martens (2011), sem usar materiais concretos, os (as) educadores (as) recorrem a aulas expositivas, onde muitas das vezes a forma de abordagem não satisfaz o processo de aprendizagem. Assim sendo, Alves e Martens (2011) realça que ensinar frações na atualidade é um desafio, por isso, ao serem abordadas, é necessária uma conexão entre o (a) educando (a) e o (a) educador(a), abstração e objeto, conceito e aplicação para melhor internalização dos números racionais. Nesse sentido, é necessário que, por meio da manipulação dos materiais concretos, o professor possibilite a conexão entre o imaginário e o real, para que assim progressivamente o educando consiga abstrair e construir conhecimentos coligados com a realidade.

Terceira questão: na sua opinião, qual a importância do ensino das frações na vida do Educando? Como a matemática pode assumir um papel formativo e social na sociedade?

 As frações são partes da vida, não podemos fugir delas, por isso é importante aprender. A matemática está em tudo, por isso podemos dizer que ela assume um papel social de formação do homem e da própria sociedade (Ed1).

A matemática é social, formativa e inclusiva, com isso não apenas as frações são importantes, mas todo o letramento matemático é necessário. Para mim, a matemática é mais do que números e aplicações, essa matemática deve proporcionar reflexão/ação, historicidade e ser mais acessível (Ed2).

De acordo com os dados apresentados pelos professores, a matemática, em suas percepções, ganha um sentido, uma importância não mais que as outras ciências, mas um olhar social, onde a sua capacidade de processar informações vai além da representação.

Para Skovsmose (2001), a matemática ganha sentido à medida que a consciência da sociedade vai atingindo um novo estágio de interpretação da realidade, por isso, cada vez mais, os modelos de produção de conhecimento em matemática vão ganhando tomada de decisões. Embora limitada, a matemática exerce um poder formatador na vida do sujeito, condicionando procedimentos, comportamentos, ações, transformações, entre outros. Podemos afirmar que essa matemática, defendida pelos professores, é compreendida como crítica da realidade, indo além de fórmulas e de exercícios mecânicos (PESSÔA; JÚNIOR, 2013). Tal percepção enxerga uma realidade, formatada pelos desenvolvimentos sociais e tecnológicos, que reconhece os conhecimentos matemáticos como condições necessárias para exercitar os direitos, deveres e cidadania.

4.1.2 TRANSCRIÇÃO DAS QUESTÕES DA ENTREVISTA REALIZADA COM OS ALUNOS DA COMUNIDADE EMA – ESCOLA ESTADUAL CALUNGA III

Primeira questão: você gosta de estudar matemática escolar?

A matemática na educação básica é entendida por parte dos (as) educandos (as) como excludente e formalista. Devido ao seu grau de abstração/generalização e de processualidades contínuas, muitos (as) estudantes sentem dificuldades, uma vez que, em muitos dos casos, não conseguem compreender os conceitos mais simples nos anos iniciais do ensino fundamental. Muffi (2013) enfatiza que devido aos (às) educandos (as) não conseguirem internalizar com clareza, acabam desistindo e absolutizando a matemática como complexa e de superioridade a outros campos de conhecimento. Nesse sentido, ao serem perguntados (as), os (as) alunos (as) responderam da seguinte maneira:

Figura 1: Respostas dos (as) alunos (as) quanto ao gostar de matemática escolar.

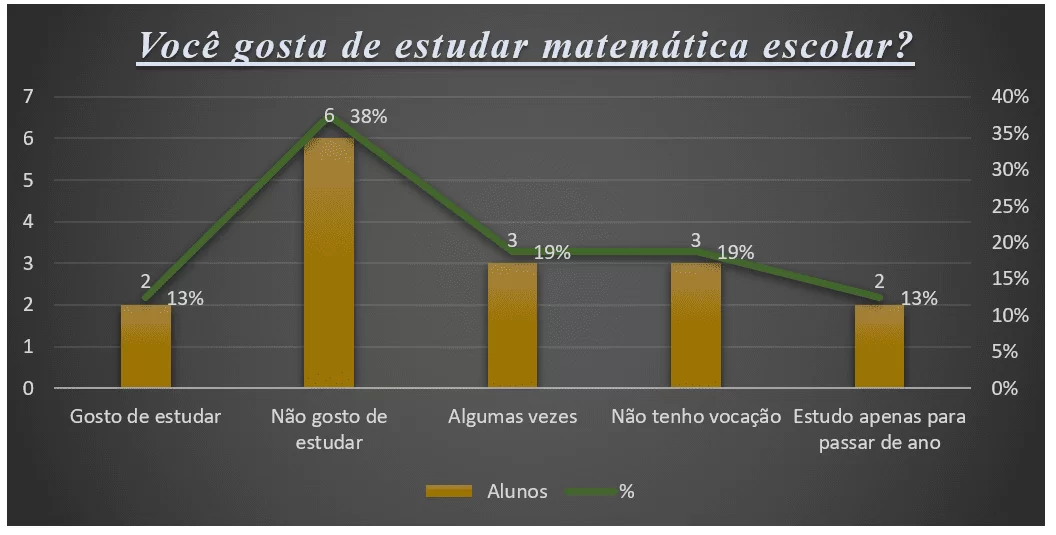
De acordo com os dados apresentados pelos (as) educandos (as), existe uma rejeição no que diz respeito ao estudo da matemática escolar. Para Costa e Prado (2015), um dos fatores, que podem intencionar os (as) educandos (as) a esse entendimento, está na forma pela qual o professor aborda em sala de aula, pois, em muitas das vezes, configura-se como direta, mecânica e científica, dispensando os exemplos da realidade, tornando-a densa e metódica. Muitos alunos a compreendem como monótona, incompreensível e sem estímulo.

Uma outra situação pode estar ligada ao ensino fundamental I, uma vez que o ensino de matemática é ministrado por pedagogos e, em muitas das vezes, os professores que ensinam matemática não apresentam domínio formal do conteúdo. Por isso, ao chegarem em um grau de abstração maior, os (as) educandos(as) por não conseguirem entender de forma delinear e intuitiva, engajam-se do medo e desprezam a matemática, uma vez que ela se encontra de forma processual e cumulativa. As percepções de cada série acabam tornando-se necessárias para a próxima série e assim sucessivamente.

Vendo tais afirmações, cabe aos (às) professores (as) repensarem os métodos e técnicas, ao refletirem sobre o processo de ensino-aprendizagem, pois o (a) educador (a) é o elemento fundamental para transformar o ambiente e torná-lo desafiador e estimulador. Para tais concepções é que o espaço escolar deve mudar a metodologia e inserir as percepções de realidade, aguçando a sua curiosidade para que, assim, a investigação seja o motor de ignição para um novo olhar sobre a matemática.

Segunda questão: qual a importância da matemática para a sua vida?

A matemática não só é um instrumento para ler o mundo, mas também uma forma de compreender as relações explícitas e implícitas de uma determinada sociedade. Devido à sua importância, encontra-se no plano da reflexão/ação de cunho filosófico. Ao perguntar aos (às) educandos(as):

55% responderam que a matemática é importante para todas as tomadas de decisões, para encontrar um emprego, para pagar contas, para comprar e voltar troco, a matemática está em tudo, mas gostam dela quando aprendem.

25% responderam que a matemática está em tudo, mas não é tão importante, estudar língua portuguesa para eles é mais importante. Sabemos que a matemática está em tudo, mas prefiro usar o mínimo dela, pois é repetitiva e cansativa.

20% enfatizaram que os professores(as) dizem que é, mas preferem em sua vida profissional seguir em outra área que não seja matemática, acham que a matemática é desnecessária.

De acordo com as respostas encontradas, percebemos que mais da metade dos (as) estudantes compreendem a importância da matemática. Pelas falas, os (as) educandos (as) compreendem que a matemática está além do currículo e dos muros da escola, compreendem que todas as situações problemas, políticas, sociais e de cidadania estão ligadas à matemática. Ramos (2017) ressalta que não é apenas entender a matemática nas suas fórmulas e generalizações, mas é usá-la de forma consciente para construir cidadania a partir da sua própria consciência.

Cabe ressaltar que, mesmo os alunos citando que a matemática é “cansativa”, “repetitiva”, estão referindo-se à matemática escolar. Para tal relação, Costa e Prado (2015) enfatizam que é contra essas ações de memorização/repetição sem sentido, deslocado da realidade, sendo que, ao ministrar aula em sala de aula, a didática do professor deve mudar. Nesse sentido, deve-se propor um ensino reflexivo e crítico, capaz de transformar a realidade, revestida de aplicabilidade e conceitos fundamentados na realidade.

Terceira questão: o que você acha da ideia de frações? Na sua opinião, são fáceis de serem compreendidas?

As frações são compreendidas como área de conhecimento de difícil internalização, rigorosidade e formalismo. Há de se destacar que, quando o (a) educando (a) não compreende conceitos e, eventualmente, apresenta dificuldades em divisão, as frações tornam-se mais difíceis ainda de compreender. Ao indagar os (as) educandos (as), obtivemos as seguintes afirmações.

Figura 2: Respostas dos (as) educandos (as) quanto ao pensamento sobre as frações.

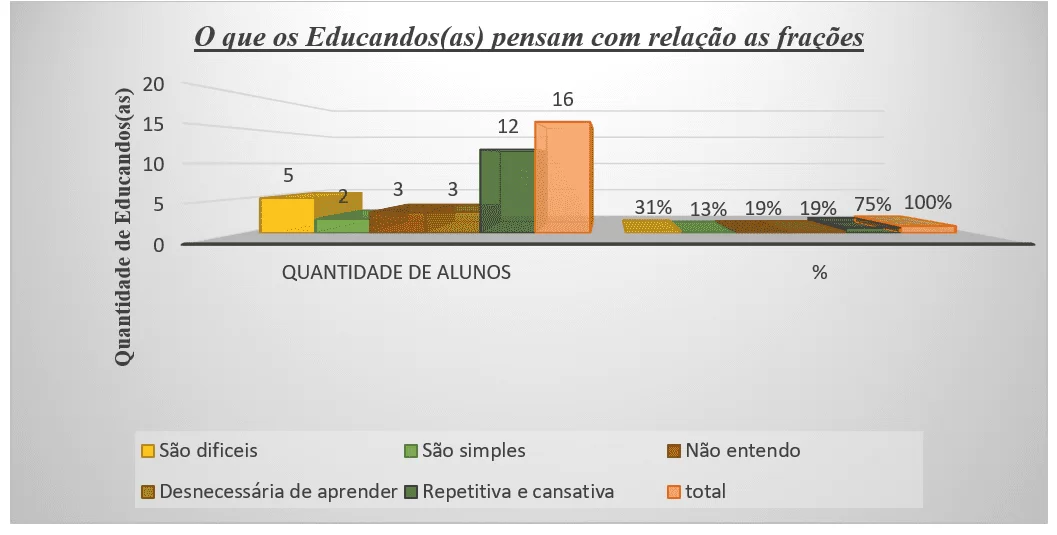
De acordo com o dialogo apresentado pelos (as) educandos (as), constatou-se uma enorme dificuldade em compreender os conceitos e praticidades demandadas das frações, ou seja, o ensino baseado em pizzas e barras de chocolate, que sempre está presente em livros didáticos, necessita ir além. No que tange ao olhar para essa área do conhecimento, são interpretadas, em muitas vezes, como ensino descontextualizado, sem apresentar em ser gradativo.

Nesse sentido, para os atores escolares, o conteúdo repetitivo e cansativo passa a ser apenas um componente escolar, interpretando-o como conhecimento desnecessário para os problemas sociais que poderão vir a enfrentar. Fernandes (2008, p. 20) destaca que é necessário o ensino gradativo e real para que os alunos possam sentir e compreender a sua real importância. Assim, trabalhar as frações deveria ser precedido de outros elementos matemáticos para estruturar e sistematizar pensamentos lógicos. A falta de interesse, constatada na pesquisa, é devido à ausência de pertinência, compreensão lógica e de aprendizagem significativa. Sob tal afirmação, é impossível compreender a significação real, uma vez que a aprendizagem não se consolidou.

Quarta questão: Você tem dificuldades? Se sim, em qual parte do conteúdo?

Como já citado, o conjunto dos números racionais na educação básica é um dos conteúdos mais aclamados pelos (as) educandos (as). A partir de muitas leituras e pesquisas, a fim de verificar, por parte dos estudantes, quais são as suas principais dificuldades e incompreensões, apuraram-se os seguintes dados:

Figura 3: Dificuldades apresentadas pelos (as) educandos (as) na compreensão das frações.

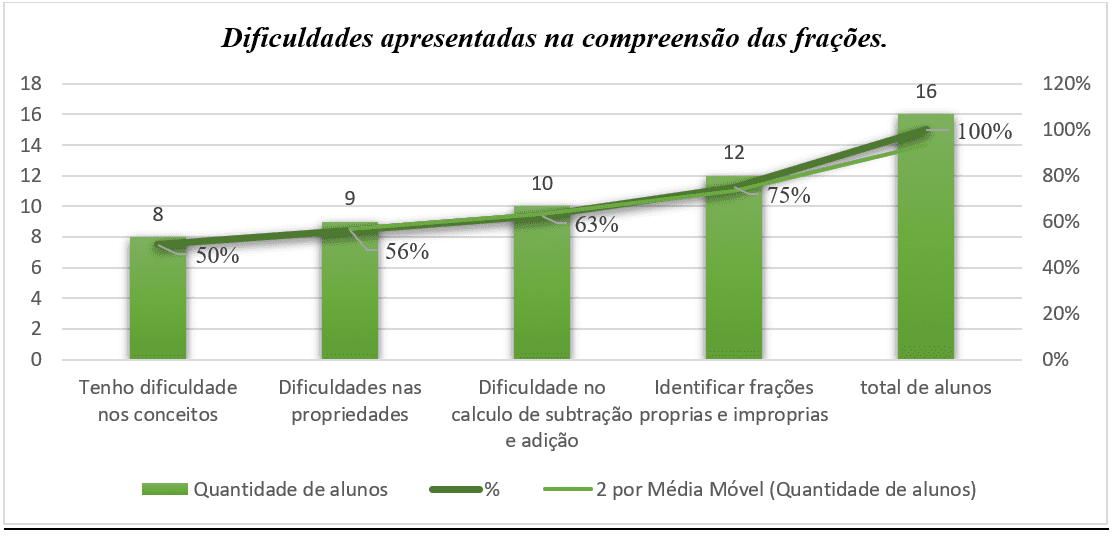
De acordo com as falas apresentadas, a maioria dos alunos explicitaram níveis de dificuldades nas compreensões das frações. Para Azevedo (2019), a confusão ocorre devido à falta de domínio dos conceitos básicos, por ser processual e cumulativa, a não interpretação real dos conceitos pode causar dificuldades em meio à obtenção de compreensão. Ressalta, ainda, que “depois chegam os algoritmos para somar, subtrair, multiplicar e dividir frações, que muitas vezes não fazem sentido para as crianças, por causa do nível de abstração e generalização” (AZEVEDO, 2019, p. 1).

Ainda, de acordo com os dados explicitados, 50% dos (as) educandos (as) não compreendem conceitos, isso significa que, a partir dos próximos níveis e com a inserção da situação problema, este mesmo (a) aluno (a) não conseguirá compreender e executar cálculos. Nesse sentido, faz-se necessário o uso de materiais didáticos para que a maturação desses alunos possa florescer. Pois, Azevedo (2019) explica que, em muitos casos, as crianças não diferem numerador do denominador, ou, ainda mesmo, conhecem os termos, mas não utilizam de forma delinear.

No que tange ao próximo grau de compreensão dos estudantes, 75% não conseguem realizar cálculos mais complexos, remetendo ao problema citado anteriormente, no qual a falta de domínio dos conceitos, divisibilidade e conceitos dos números racionais impossibilita que a aprendizagem ocorra de forma eficaz. Dessa maneira, a partir da fala dos (as) educandos(as), o pressuposto é a conceituação baseada em problemas da realidade, para que a compreensão emerja de forma natural, pois a compreensão de conceitos simples facilitará as tomadas de cálculos complexos.

CONSIDERAÇÕES FINAIS

O presente estudo possibilitou compreender, a partir de entrevistas semiestruturadas, como os (as) educandos (os) e educadores (as) compreendem e interpretam o estudo das frações e suas abordagens no contexto escolar, bem como de identificar/apontar elementos que dificultam ou facilitam o processo de ensino-aprendizagem. A partir da pesquisa, foi possível perceber que a maioria dos alunos não carregam consigo afinidade para desenvolverem e produzirem cálculos matemáticos, entretanto, mediante verificações, demonstrou-se que um dos fatores pode estar relacionado com as frustrações/falta de maturidade e domínio dos conceitos matemáticos, falta de estímulo por parte dos alunos e dos professores e, ainda, a necessidade de aproximação do conteúdo científico com as situações problemas cotidianas.

No que tange às frações e de acordo com as investigações, apresentou-se, em todos os momentos, que os alunos além de não gostarem de matemática, não dominam os conceitos básicos da fração, haja vista que um dos problemas apontados foram o da apropriação dos conceitos, cálculo das propriedades e entre outras situações. Essas dificuldades podem ser um dos fatores em que os alunos utilizam para justificarem o fato de não gostarem de matemática.

No que tange ao professor que leciona matemática, apresentou-se a falta de aporte teórico e de compreensão delinear dos fundamentos dos números racionais. Isso implica em não diferenciar as metodologias, uma vez que, no relato dos educandos, justificava-se em meio ao cansaço e à repetição. Desse modo, tornou-se perceptível que é fundamental propor novas sequências didáticas para o ensino de matemática. Assim sendo, o (a) educador (a) deve propor uma nova forma de ver a matemática e de utilizar práticas pedagógicas que estimulem a investigação e a participação ativa.

Portanto, o presente trabalho buscou evidenciar-apontar e refletir o estudo das frações do ponto de vista dos (as) educadores (as) e educandos (as), bem como identificar os fatores que impossibilitam ou potencializam as compreensões das frações enquanto área do conhecimento. Dessa maneira, de acordo com a investigação, apontou-se que as frações, no olhar dos (as) educandos (as), são complexas e que necessitam de uma nova forma de ser ensinada, haja vista que na percepção dos alunos não representam importância para a sua utilização na vida.

REFERÊNCIAS

ALVES, Denis Rogério Sanches; MARTENS, Adam Santos. Desafios para a construção do conhecimento de frações nas séries intermediários do ensino fundamental. In: CONGRESSO NACIONAL DE EDUCAÇÃO (EDUCERE), 10; SEMINÁRIO INTERNACIONAL DE REPRESENTAÇÕES SOCIAIS, SUBJETIVIDADE E EDUCAÇÃO (SIRSSE), 1, 2011, Paraná. Anais […] Paraná: Pontifica Universidade Católica do Paraná, 2011. Disponível em: <https://educere.bruc.com.br/CD2011/pdf/6413_3640.pdf>. Acesso em: 10/01/2020.

AZEVEDO, Guto. Por que aprender frações é tão difícil? Blog, Frações, Materiais para Professores. Disponível em: < http://gutoazevedo.com.br/aprender-fracoes-e-dificil/>. Acesso em: 27/06/2020.

BOERI, Camila Nicola; VIONE, Marcio Tadeu. Abordagens em educação matemática. [S.l.:s. n.], 2009. Disponível em: <http://www.dominiopublico.gov.br/download/texto/ea000661.pdf>. Acesso em: 02/02/2020.

BRANDT, Celia Finck; MORETTI, Méricles Thadeu (org.). Ensinar e aprender matemática: possibilidades para a prática educativa. Ponta Grossa: Editora UEPG, 2016.

BRASIL. Ministério da Educação. Secretaria de Educação Básica. Secretaria de Educação Continuada, Alfabetização, Diversidade e Inclusão. Conselho Nacional da Educação. Diretrizes Curriculares Nacionais Gerais da Educação Básica. Brasília: MEC, SEB, DICEI, 2013.

BRASIL. Secretaria de Educação Fundamental. Parâmetros curriculares nacionais: introdução aos parâmetros curriculares nacionais. Brasília: MEC/SEF, 1997.

BRASIL. Secretaria de Educação Fundamental. Parâmetros curriculares nacionais: matemática. Brasília: MEC/SEF, 1997.

COSTA, Michel da; PRADO, Maria Elisabette Brisola Brito. Ensino de frações nos anos iniciais do ensino fundamental: dificuldades, entraves e possibilidades. In: CONFERÊNCIA INTERAMERICANA DE EDUCAÇÃO MATEMÁTICA, 14, 2015, México. Anais […].  México, 2015. Disponível em: <http://xiv.ciaem-redumate.org/index.php/xiv_ciaem/xiv_ciaem/paper/viewFile/1035/708>. Acesso em: 15/05/2020.

FERNANDES, Sueli Fátima Homon. “As frações do dia a dia” – operações. 2008. Projeto de Intervenção Pedagógica na Escola.  Ponta Grossa, PR, 2008. Disponível em: <http://www.diaadiaeducacao.pr.gov.br/portals/pde/arquivos/48-2.pdf> Acesso em: 27/06/2020.

FREIRE, Paulo. Pedagogia da autonomia: saberes necessários à pratica educativa. São Paulo: Paz e Terra, 1996.

GIL, Antônio Carlos. Como elaborar projetos de pesquisa. 4. ed. São Paulo: Atlas, 2002.

LAKATOS, Eva Maria; MARCONI, Marina de Andrade. Fundamentos de metodologia científica. 5. ed. São Paulo: Atlas, 2003.

LOPES, Anemari Roesler Luersen; PERLIN, Patricia. Sobre movimento formativo na organização do ensino de frações. In: DIDÁTICA E PRÁTICA DE ENSINO NO CONTEXTO POLÍTICO CONTEMPORÂNEO: CENAS DA EDUCAÇÃO BRASILEIRA, 18, 2016, Mato Grosso. Anais […]. Mato Grosso, 2016.

MACHUCH, Franciele do Belém. O uso de simulações interativas PHET no ensino de frações. 2016. Dissertação (Mestrado em Ensino em Ciências Naturais e Matemática) – Universidade Estadual do Centro-Oeste, Guarapuava, 2016. Disponível em: <http://www2.unicentro.br/ppgen/files/2016/07/Disserta%C3%A7%C3%A3o_Franciele.pdf>. Acesso em: 10/04/2020.

MAFFI, Caroline; MATOS, Diego de Vargas; FRAGA, Francieli Bandeira de; LUPINACCI, Vera Lúcia Martins. Construção e aplicação de materiais didáticos para o ensino de frações nos anos iniciais do ensino fundamental. In: CONGRESSO INTERNACIONAL DE ENSINO DA MATEMÁTICA, 2003, Rio Grande do Sul. Anais […]. Rio Grande do Sul: ULBRA, 2003. Disponível em: <http://www.conferencias.ulbra.br/index.php/ciem/vi/paper/viewFile/607/37>. Acesso em: 03/02/2020.

MONTEIRO, Alexandre Branco; GROENWALD, Claudia Lisete Oliveira. Dificuldades na aprendizagem de frações: reflexões a partir de uma experiência utilizando testes adaptativos. ALEXANDRIA Revista de Educação em Ciência e Tecnologia, Santa Catarina, v. 7, n. 2, p. 103-135, nov. 2014. Disponível em:<https://periodicos.ufsc.br/index.php/alexandria/article/view/38217>. Acesso em: 10/05/2020.

NASCIMENTO, Juliane do. Perspectivas para aprendizagem e Ensino dos números Racionais. Revista de Iniciação Científica da FFC, v. 8, n. 2, p. 196-208, 2008.

OKUMA, Érika Kazue. Ensino e aprendizagem de fração: um estudo comparativo e uma intervenção didática. 2010. Trabalho de Conclusão de Curso (Graduação em Pedagogia) – Centro Universitário Católico Salesiano Auxilium, Lins, 2010. Disponível em: <http://www.unisalesiano.edu.br/biblioteca/monografias/51854.pdf>. Acesso em: 16/04/2020.

PASSOS, CÁRMEN LÚCIA BRANCAGLION; NACARATO, ADAIR MENDES. Trajetória e perspectivas para o ensino de matemática nos anos iniciais. Estud. av., São Paulo, v. 32, n. 94, p. 119-135, dez.  2018. Disponível em: <http://www.scielo.br/scielo.php?script=sci_arttext&pid=S0103-40142018000300119&lng=en&nrm=iso>. Acesso em: 13/06/2020.

PAULO Freire a importância da matemática. Kelly Cristina Baruti. 1 vídeo (2 min.), 2014. Disponível em: <https://www.youtube.com/watch?v=mC4H0itPDP4>. Acesso em: 31/05/2020.

PERLIN, Patricia; FRAGA, Laura Pippi; POZEBON, Simone; LOPÉS, Anemari Roesler Luersen Vieira. O conteúdo de frações nos anos iniciais do ensino fundamental: alguns apontamentos a partir dos documentos oficiais brasileiros. In: CONFERÊNCIA INTERAMERICANA DE EDUCAÇÃO MATEMÁTCA, 14, 2015, México. Anais […] México, 2015. Disponível em: < http://xiv.ciaem-redumate.org/index.php/xiv_ciaem/xiv_ciaem/paper/viewFile/470/579>. Acesso em: 13/03/2020.

PESSÔA, Esther Bahr; JÚNIOR DAMÁZIO, Valdir. Contribuições da educação matemática crítica para o processo de materacia nas séries iniciais do Ensino Fundamental: um olhar através dos Parâmetros Curriculares Nacionais. BoEM, Joinville, v. 1. n. 1, p. 76-98, jul./dez. 2013. Disponível em: < https://www.revistas.udesc.br/index.php/boem/article/view/3953>. Acesso em: 20/02/2020.

PROENCA, Marcelo Carlos de. O ensino de frações via resolução de problemas na formação de futuras professoras de pedagogia. Bolema, Rio Claro, v. 29, n. 52, p. 729-755, ago. 2015. Disponível em: <http://www.scielo.br/scielo.php?script=sci_arttext&pid=S0103-636X2015000200016&lng=en&nrm=iso>. Acesso em: 12/06/2020.

RAMOS, Taurino Costa. A importância da matemática na vida cotidiana dos alunos do ensino fundamental II. Cairu em Revista, ano 06, n. 9, p. 201-218, jan./fev. 2017. Disponível em: <https://www.cairu.br/revista/arquivos/artigos/20171/11_IMPORTANCIA_MATEMATICA.pdf>. Acesso em: 20/06/2020.

SANTOS, Hélio Rodrigues dos. O Programa de Educação Tutorial na Licenciatura em Educação do Campo e a formação de Professores. In: ENCONTRO DE PESQUISADORES, 4, 2019, Arraias, TO. Anais […]. Arraias, TO, 2019.

SILVA, Airton Marques. Metodologia de pesquisa. 2 ed. Fortaleza, CE: 2015.

SKOVSMOSE, Ole. Educação matemática crítica: a questão da democracia. Campinas, SP: Papirus, 2001.

SOUZA, M. J. A. Informática educativa na educação matemática: estudo de geometria no ambiente do software Cabri-Géomètre. 2001. 154 f. Dissertação (Mestrado em Educação Brasileira) – Faculdade de Educação da Universidade Federal do Ceará, Fortaleza, 2001. Disponível em: <http://www.multimeios.ufc.br/arquivos/pc/teses-dissertacoes/DissertacaoMaze.pdf>. Acesso em: 09/06/2020.

TENDÊNCIAS atuais do ensino e aprendizagem de matemática e os PCNs. Anderson Possamai. 1 vídeo (31min.), 2015. Disponível em: < https://www.youtube.com/watch?v=M2WCnUiHjiA>. Acesso em: 14/05/2020.

VIGOTSKY, Lev Semionovitch. A formação social da mente. São Paulo: Martins Fontes, 1998.

WITT, Caroline. O ensino das frações por meio de jogos e aplicativos digitais. 2018. Trabalho de Conclusão de Curso (Especialização) – Universidade Tecnológica Federal do Paraná, Curitiba, 2018. Disponível em: <http://repositorio.roca.utfpr.edu.br/jspui/handle/1/11083>. Acesso em: 17/04/2020.

^[1] Pós-Graduação em Metodologia do Ensino da Matemática e da Física, Pós-Graduação em Metodologia do Ensino da Matemática, Graduação em Pedagogia e Graduando em Educação do Campo.

^[2] Orientador. Doutorado em Educação. Mestrado em Educação Cultura e Sociedade. Especialização em Psicopedagogia. Graduação em Teologia. Graduação em Filosofia.

Enviado: Julho, 2020.

Aprovado: Setembro, 2020.