ARTIGO DE REVISÃO
CRUZ, Evandro Costa [1], SILVA, Francisco Gonçalves Da [2]
CRUZ, Evandro Costa. SILVA, Francisco Gonçalves Da. Função logarítmica – Uma situação didática envolvendo uma classe de estudantes do Ensino Médio. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano 05, Ed. 03, Vol. 05, pp. 42-53. Março de 2020. ISSN: 2448-0959, Link de acesso: https://www.nucleodoconhecimento.com.br/matematica/funcao-logaritmica
RESUMO
Há muito tempo, a Matemática na escola vem sendo responsabilizada pelos percentuais de reprovação e evasão escolar. Diante deste fato, este artigo se inscreve como uma das ações que busca uma mudança significativa desta concepção que diz respeito especificamente aos mecanismos que é empregado no ensino de matemática na escola. Seguindo este plano, foi analisado o potencial metodológico de uma Atividade Orientadora com enfoque nos Ensino de Função logarítmica. A pesquisa ocorreu no âmbito do estágio supervisionado II e III, a mesma envolveu estudantes do primeiro ano do Ensino Médio. A observação ocorreu na Escola Estadual Wanda David Aguiar, localizada na Zona leste, Rua Estrela D’Alva, bairro Raiar do sol no Município de Boa Vista/RR. Na perspectiva metodológica, a pesquisa utilizou o procedimento Estudo de caso, ferramenta de observação não participante. Os participantes da pesquisa são alunos do primeiro ano do ensino médio. Os resultados da pesquisa resultaram numa situação didática orientadora do ensino de função logarítmica no contexto do estágio supervisionado. A conclusão do estudo constatou que a busca por novos métodos é necessária aos docentes, pois, é evidente que atualização os qualificam para novas práticas educacionais.
Palavras chaves: Função Logarítmica, estágio supervisionado, ensino de matemática.
INTRODUÇÃO
Este trabalho objetivou analisar uma forma de organizar o ensino da função logarítmica compreendendo uma das Escolas públicas localizada no município de Boa Vista, capital do Estado de Roraima – RR. Em termos específicos o projeto ocorreu durante a disciplina de estágio, ministrada no curso de Licenciatura em Matemática.
A obra tem como objeto de estudo, o conteúdo matemático – Funções Logarítmicas que reforçam a fundamentação Teórica da pesquisa numa perspectiva do Estágio Supervisionado. O aspecto investigativo do trabalho sugeriu o seguinte problema de pesquisa:
Como organizar o ensino de função logarítmica para estudantes dos anos iniciais do ensino Médio, na escola Estadual Wanda David Aguiar? É a partir desta pergunta que se desenham os outros elementos que constituem o projeto de investigação, conforme postos a seguir.
Tem como objetivo geral analisar como é possível organizar o ensino de função logarítmica na escola Estadual Wanda David Aguiar, para estudantes dos anos iniciais do ensino Médio.
Os objetivos específicos é estabelecer uma organização sumária do conteúdo durante o ensino de matemática para o conteúdo de função logarítmica; Organizar os tópicos de ensino, com base na forma como os conteúdos de ensino se relacionam; Verificar aplicações do conteúdo estudado nas diversas áreas de ensino e conhecimento;
A análise dos aspectos do ensino de matemática nas escolas públicas de Roraima se justifica por se configurar como uma ação que tem objetivo nobre do ponto de vista sócio cultural e econômico, no entanto o uso e aplicação da matemática tanto no aspecto acadêmico, quanto no aspecto sócio econômico e cultural, exige o domínio de conteúdo de forma significativa.
De acordo com Polya (1995), o aluno deve adquirir experiência trabalhando o máximo possível e o papel do professor é auxiliá-lo com as ferramentas certas, sem deixá-lo sozinho, mas também não pode fazer tudo de tal modo que não reste nada para o aluno fazer.
Educar matematicamente para a cidadania envolve estudos dos dados e dos números presentes na vida cotidiana da comunidade. A formação de novos sujeitos sociais que sejam protagonistas de sua própria aprendizagem e, portanto, de sua própria história, passa pela educação e o ensino contextualizado, que valoriza a realidade da comunidade onde se estabelece a escola. É por esta razão que a pesquisa valoriza o ensino de conteúdo matemática, de forma sistemática, ou seja, de modo interativo social.
Por outro lado, esta pesquisa se justifica pela importância da disciplina de estágio para a formação do professor pesquisador de sua própria prática, isto é, do professor pesquisador – reflexivo. A pesquisa ocorre por esta razão, durante a disciplina de estágio II e III, do curso de Licenciatura em Matemática, realizada na Universidade Estadual de Roraima – UERR.
A escolha do tema envolvendo o conteúdo de Função Logarítmica nos anos iniciais do Ensino Médio tem grande relevância para os estudantes, pois seus resultados apontam para impactos de progresso na vida dentro do contexto local, tendo resultados impactantes na formação de novos sujeitos da sociedade que sejam mais justos e dignos de seus pares.
Portanto, a pesquisa ser classificada como relevante, pois buscou fortalecer as discussões de objetos matemáticos em um ambiente com características individuais e culturais, com enfoque na aplicabilidade do conteúdo – função logarítmica na vida cotidiana em geral.
A metodologia utilizada tem base na pedagogia crítica de ensino, que valoriza o processo de instrução usando a Etnomatemática e tem enfoque no domínio conceitual de forma que o resultado da pesquisa se converte em uma proposta elementar de aprendizagem sobre a função logarítmica, e segundo Mussel (2014), ainda hoje se usam ferramentas ultrapassadas, com alunos da era da tecnologia moderna.
Esta obra está organizada em quatro capítulos; o primeiro capítulo, apresentado imediatamente após esta introdução, contém os elementos da pesquisa que são objetivos, justificativa, objeto e problema de pesquisa, local e sujeitos da pesquisa; o segundo capítulo consiste no marco teórico, onde os aportes teóricos D’Ambrósio, Mussel, Polya, foram pessoas que abordaram o tema, didática para o ensino de função logarítmica e aplicações numa visão contextualizada, será explicitados os conceitos de função logarítmica, a fórmula e algumas características de aplicação adaptadas ao cotidiano do aluno; o terceiro capítulo é composto pelo marco metodológico, onde é apresentado ambiente, período e os sujeitos da pesquisa, o planejamento e o desenho do percurso investigativo; o quarto capítulo, apresenta os resultados e discussões sobre como o docente pode atuar visando a aprendizagem significativa do aluno, seguidos da conclusão.
1. FUNÇÃO LOGARÍTMICA
Dentro da logarítmica, o domínio é o conjunto dos números reais maiores e que são zero, o contradomínio é o agrupamento dos elementos que dependem da função, sendo todos números Reais.
A função logarítmica é representada em sua fórmula geral da seguinte maneira:
Consequentemente, temos;
a = base do logaritmo
ƒ (x) = Imagem/ logaritmando
x = Domínio/ logaritmo
De modo particular pode-se exemplificar a representação geométrica da função logarítmica a partir do caso, 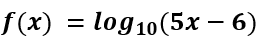 :
:
Figura 01- demonstração gráfica da função 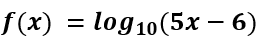 :
:
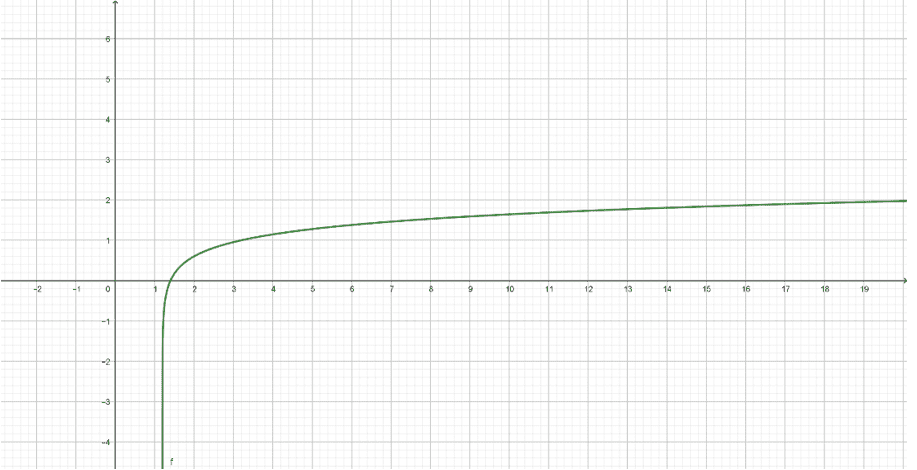
2. O CONCEITO FUNÇÃO LOGARÍTMICA
O conceito de função logarítmica está implícito na definição de Dante (2010, p. 275), como a inversa da função exponencial de base a é a função ![]() , que associa a cada número Real positivo x o número Real
, que associa a cada número Real positivo x o número Real ![]() , chamado logaritmo de x na base a, com a Real positivo e a ≠ 1.
, chamado logaritmo de x na base a, com a Real positivo e a ≠ 1.
2.1 PRINCIPAIS CARACTERÍSTICAS
A partir, da definição de Dante (2010), podemos pontuar que a definição da função logarítmica possui duas características principais que estão representadas no quadro a seguir.
Figura 02- demonstração das características da função logarítmica
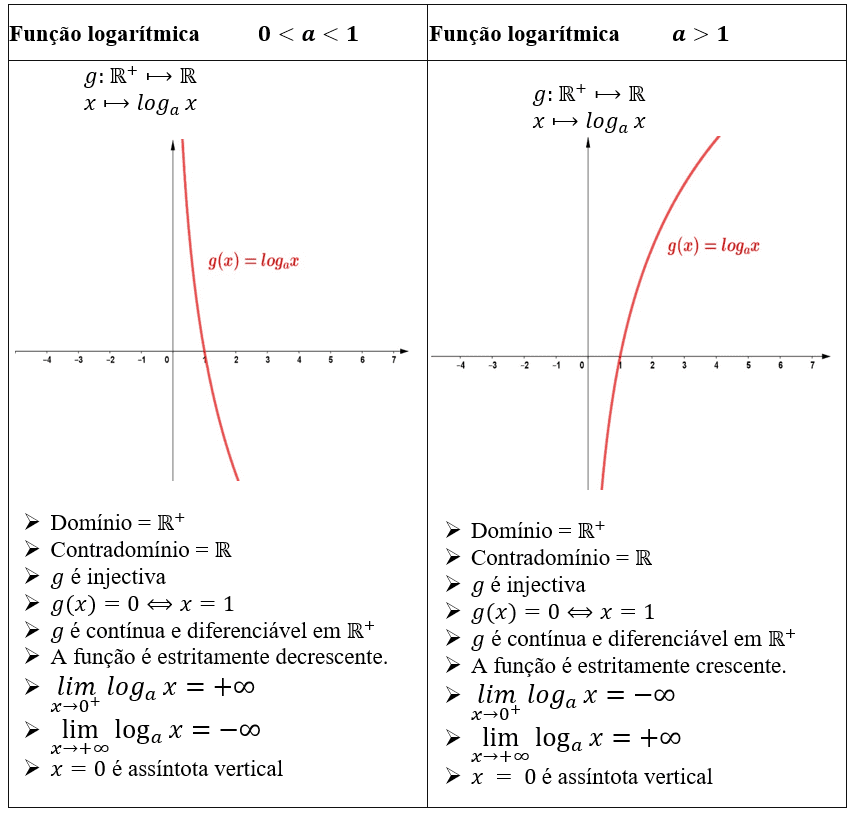
2.2 APLICAÇÕES DA FUNÇÃO LOGARÍTMICA
Diante do contexto exposto acima, ainda é de difícil compreensão, na forma como foi demostrada, para muitos alunos essa forma abstrata dificulta a aprendizagem, por isso, é importante contextualizar o problema usando situação cotidianas vividas pelos discentes.
O cotidiano está impregnado dos saberes e fazeres próprios da cultura. A todo instante, os indivíduos estão comparando, classificando, quantificando, medindo, explicando, generalizando, inferindo e, de algum modo, avaliando, usando os instrumentos materiais e intelectuais que são próprios à sua cultura (CUNHA, 2017).
De acordo com Mussel (2014), a solução de alguns problemas do cotidiano possuem soluções que nada mais são do que uma forma de aplicação do conceito de função logarítmica.
Mas não é qualquer problema, tem que ter sentido para o aluno poder ver de maneira concreto a aplicação do exercício, de acordo com D’Ambrósio “(…) Etnomatemática é a arte ou técnica (techné = tica) de explicar, de entender, de se desempenhar na realidade (matema), dentro de um contexto cultural próprio (etno)” (D’AMBROSIO, 1991, p.9), o docente pode fazer os exercícios de acordo com a realidade cultural do discente.
Nessa perspectiva, acredita-se que um dos caminhos para ajudar na compreensão de problemas envolvendo funções logarítmicas, é fundamentar essa vertente com ações pedagógicas construídas dentro do contexto sociocultural dos alunos, nesse caso a etnomatemática.
Em seguida apresentamos uma adaptação de Mussel (2014), onde esse estudante pesquisador apresenta uma lista de quatro problemas cuja solução são formas de aplicação do conceito de funções Logarítmicas, o uso dessas problemáticas pode facilitar a compreensão do conteúdo por parte dos discentes.
De acordo com Polya (1995, p.5) se o docente “desafia a curiosidade dos alunos, apresentando-lhes problemas compatíveis” que poderá atraí-los com interesse para resolução de problemas, sentindo-se motivado o discente procura buscar soluções além da sala de aula.
O problema do santo sudário de Turim:
Conta a história que 1357, apareceu na França um tecido o qual foi usado para enrolar Jesus Crista após sua morte, tal tecido ficou conhecido como santo sudário. Esses tecidos eram usados para envolver o corpo das pessoas que morram.
Em 1578, um pedaço desse tecido foi encontrado e levado a catedral de Turim, na Itália. Até hoje alguns textos retratam da presença dessa relíquia em Jerusalém no ano 640 d.C. e, no ano 1150 d.C., em Constantinopla.
Em 1988 d.C., o santo sudário foi datado através do teste de C14 constatando-se que o tecido teria cerca de 0,9154800 vezes (aproximadamente) a quantidade de C14 de um tecido feito do mesmo material no ano de 1988. Sendo assim, será mesmo que o tecido teria sido fabricado na época de Jesus Cristo; (MUSSEL 2014).
A apresentação dos conceitos, teoremas, fórmula geral ou específica é de suma importância, no entanto um problema em contexto também pode ajudar, pois pode facilitar a aprendizagem devido o que estar sendo apresentado ser algo do conhecimento do aluno.
Outro problema apresentado por Mussel (2014), é a boca e os germes: aonde diz que a boca dos seres humanos tem aproximadamente 1.000 a 100.000 germes em cada dente, quando saudável. Além de outras 700 espécies de germes são encontrados em nossas bocas. Conjecturando que uma pessoa tenha cerca de 40000 germes por dente, após a sua escovação, e que a taxa de crescimento populacional desses germes seja de 1,3 por hora. Depois de quanto tempo, sem escovar os dentes, esta pessoa estará fora dos padrões de saúde bucal.
Os problemas em contexto cotidiano é uma maneira de atrair a atenção do discente para aquele assunto estudado, fazendo que o professor e aluno consigam alcançar os objetivos com mais facilidade.
Para isso, se faz necessário, que o professor adote um estilo em que o aluno possa se sentir envolvido com a referida disciplina, transmitindo os assuntos em sala de aula e aplicando-os a realidade presente do dia a dia. Demonstrando exemplos práticos e simples, com linguagem compressiva e clara, chamarão mais a atenção dos alunos, despertando sua curiosidade (CUNHA, 2017).
A função logarítmica em sua fase conceitual, pode causar certo desinteresse por parte do aluno devido a abstração que envolve a operação. Mas quando o professor usa exemplos prático o aluno percebe que ele faz aquilo todos os dias, mas de forma natural imperceptível dentro de funções logarítmicas, isso pode despertar a curiosidade de observação quando praticar novas ações.
Portanto, alguns professores preferem organizar o processo de ensino, de forma que as aulas finalizam com a resolução de problemas cuja solução tem o objetivo de aplicar o estudo realizado. Desta forma alguns problemas são selecionados para serem resolvidos posteriormente com o objetivo de consolidar o aprendizado do tema.
Outro percalço encontrado pelos discentes durante os estudos de funções logarítmicas é a construção de gráficos. Dada a complexidade na interpretação e resolução do problema em si, soma-se a isso a construção do gráfico correspondente a função, portanto o docente conseguir um meio que facilite a construção ou até mesmo mostrar opções comparações de erro ou acertos, ajuda na aprendizagem do aluno.
Nesse sentido Mussel (2014, p. 59) sugere alguns recursos educacionais de ordem tecnológica, como é o caso Geogebra, para tornar o estudo mais significante para os estudantes. No entanto, “[…] Os recursos tecnológicos não são obrigatórios para que o aluno possa compreender o conteúdo…, mas é claro que estes recursos podem auxiliá-los para que consigam uma melhor visualização dos gráficos”. Veja o exemplo abaixo:
O anúncio de um time de futebol aparece todos os dias num determinado horário na televisão. Após x dias do início da publicação (x exposições diárias), o número de pessoas (p) que ficam conhecendo o time é dado por p = 3 – 3.(0,95)x, em que p é dado em milhões de pessoas.
a)Verifique se a função é crescente o decrescente e demostre o gráfico.
A função é crescente e o gráfico da função logarítmica p = 3 – 3.(0,95)x é:
Gráfico da função p = 3 – 3.(0,95)x
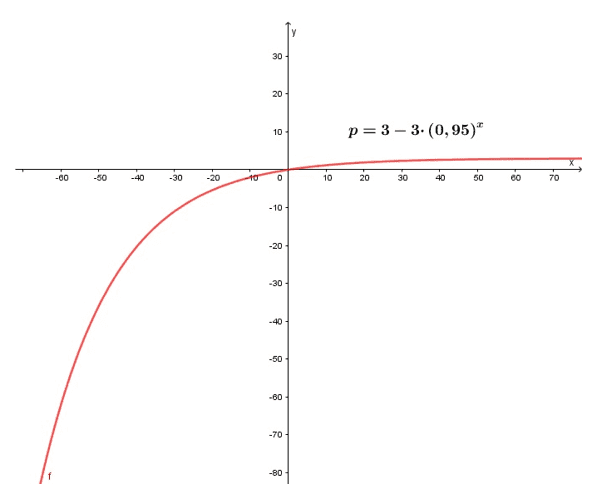
O gráfico supracitado, é possível fazer manualmente, porém o aplicativo Geogebra facilita a construção, sendo uma fonte de verificação de auto aprendizagem além de agilizar a resolução do problema.
De acordo com Barros e Franco:
O software GeoGebra pode substituir satisfatoriamente o caderno de desenho geométrico. Podemos utilizar sua interface gráfica e suas ferramentas para traçar retas, ângulos, circunferências etc. uma das vantagens do uso do GeoGebra é que as construções são dinâmicas, isto é, sem a perda dos vínculos geométricos. Isso permite que o usuário faça grande quantidade de experimentações que lhe possibilite construir proposições geométricas. (BARROS E FRANCO, 2010, p.11)
De acordo com Mussel (2014), a importância dos problemas apresentados nesta sessão, é mostrar que tudo está fundamentado em algumas poucas propriedades envolvendo funções logarítmicas, e que o estudante não deve se preocupar ao lê-los pela primeira vez, caso venha sentir demasiada dificuldade no entendimento dos mesmos, pois uma demonstração matemática, não se absorve instantaneamente.
Nesse sentido, muitos alunos precisam de uma segunda, terceira ou até mesmo uma quarta leitura até que as demonstrações lhe pareçam natural. Por isso é que o professor precisa “(…) ensinar uma matemática viva, uma matemática que vai nascendo com o aluno enquanto ele mesmo vai desenvolvendo seus meios de trabalhar a realidade no qual ele está agindo (D’AMBROSIO, 1991, p. 2)”
3. RESULTADOS E DISCUSSÃO
Do ponto de vista dos resultados, vale lembrar que o objetivo deste estudo foi apontar caminhos que possam ajudar o professor fortalecer a fixação dos conteúdos matemáticos de forma mais significativa.
Nesse sentido, este estudo realiza uma revisão que busca sumarizar e resumir em tópicos o conteúdo de função Logarítmica e por fim acaba apresentando uma seleção de problemas que podem ser utilizados em sala de aula como uma forma de aplicação da matemática no contexto sociocultural dos estudantes.
De acordo com os objetivos da pesquisa, os resultados apresentados podem ser listados da seguinte forma:
– Conceito e definição lógica formal da função logarítmica;
– Fórmula Geral;
– Elementos que compõe o conceito de função Logarítmica;
a = base do logaritmo
ƒ (x) = Imagem/ logaritmando
x = Domínio/ logaritmo
– Gráficos ou representações geométricas;
– Resolução de problemas;
– Aplicações e conjecturas
Relembrando que Mussel (2014) sugere que o estudo passa a ser mais significante para os estudantes, quando o professor consegue utilizar alguns recursos, educacionais de ordem tecnológica como o Geogebra, a proposta aqui posta sugere o uso desse ou outros aplicativos com o mesmo fim conhecido dos professores e pesquisadores matemáticos, no entanto, entendemos que conforme a realidade das escolas estaduais de Roraima, nem sempre esse procedimento irá compor a proposta de ensino dos professores.
É nesse sentido, que Mussel (2014, p. 59) destaca que “os recursos tecnológicos não são obrigatórios para a compreensão do conteúdo”, o uso desses aplicativos somente pode auxiliar o estudante para que o mesmo consiga ampliar a visualização dos gráficos e áreas.
Ainda de acordo com Mussel (2014), a situação proposta tem nos seus apêndices dois problemas que foram selecionados para esta ação docente, numa perspectiva do Estágio Supervisionado.
[…] a importância dos problemas apresentados nesta sessão, é mostrar que tudo está fundamentado em algumas poucas propriedades. Nesse caso o estudante não deve se preocupar se, ao lê-los pela primeira vez, sentir demasiada dificuldade no entendimento dos mesmos. Uma demonstração matemática, por vezes, não se absorve instantaneamente, muitos alunos precisam de uma segunda, terceira ou até mesmo uma quarta leitura para que as demonstrações lhe pareçam naturais. A persistência é a chave do sucesso para o êxito em qualquer área, portanto, não desista. Os exercícios propostos, neste trabalho, dar-te-ão uma base para que você possa aplicar o que foi aprendido durante a leitura do mesmo, então, procure resolver todos os exercícios (MUSSEL, 2014, p. 59).
Corroborando esta citação de Mussel (2014), destaca-se que conforme as orientações contidas nos documentos que normatizam nos termos da lei, o ensino de matemática no Brasil, o ensino de matemática deve ser problematizado. Portanto, a proposta sugere uma avaliação que utiliza 3 instrumentos e que tem como direcionamento a aplicação por meio de resolução de problema. Desta maneira, a proposta acredita que o ensino de matemática se torne mais eficaz, interessante e produtivo.
CONCLUSÃO
O processo investigativo, embora tenha se iniciado com uma pesquisa exploratória no campo da literatura, teve seu objetivo consolidado por meio de uma sequência didática elaborado em quatro etapas (exposição – aplicação – experimentação – avaliação) e, envolveu a o trabalho de grupo com discussões e operações sobre conceitos envolvendo a função logarítmica.
Em particular, a investigação teve como produto final, uma sequência estudada que valorizou a importância do ensino e da pesquisa em Matemática para desenvolvimento de um olhar crítico alcançando os aspectos, econômico e sociocultural da comunidade escolar onde ocorreu a pesquisa.
O objetivo geral proposto nesta pesquisa foi fortalecer o ensino de matemática direcionada para o âmbito do Estágio Supervisionado do Curso de Licenciatura em Matemática da Universidade Estadual de Roraima – UERR.
A pesquisa se construiu e se estruturou mediante nosso acesso à Unidade de ensino – campo de pesquisa que foi a escola Estadual Wanda David Aguiar, primeiramente fazendo observação do professor atuando em sala de aula, e também como os discentes se comportavam disciplinarmente mediantes as aulas.
A escolha do tema decorreu da necessidade de assumirmos que o apelo à definição tradicional dos logaritmos é algo latente e que, o estudo da função logarítmica não deve ser pulado, tanto por suas aplicações, quanto pela necessidade da solução de problemas práticos, e mais ainda, por ser cobrada em exames tradicionais.
Assim sendo, a pesquisa encerra-se aqui, desejando ter deixado sua singela contribuição a caminho de um futuro mais promissor em relação à Matemática empregada nas instituições de ensino do Brasil. Espera-se que este trabalho ajude os estudantes e os professores e estagiários que têm ou que terão contato com esta matéria.
REFERÊNCIAS
BARROS, E. L. (2010). Logaritmos. 4. ed. Rio de Janeiro: Sociedade Brasileira de Matemática, 2010. (Coleção do Professor de Matemática).
CUNHA, Cézar Pessoa. A Importância da Matemática no Cotidiano. Revista Científica Multidisciplinar Núcleo do Conhecimento. Edição 04. Ano 02, Vol. 01. pp 641-650, Julho de 2017.
D’AMBROSIO, Ubiratan. Matemática, ensino e educação: uma proposta global. Temas & Debates: SBEM, São Paulo, ano IV. n.3, p.1-15, 1991.
DANTE, Luiz Roberto, Matemática: contexto e aplicação, São Paulo: Ática, 2010.
GHEDIN, E.; FRANCO, M. A. S. Questões de método na construção da pesquisa em educação. São Paulo: Cortez, 2005.
LIMA, E. L. et al. (1997). A Matemática do Ensino Médio. 9. ed. Rio de Janeiro: Sociedade Brasileira de Matemática, 2006. Volume 1. (Coleção do Professor de Matemática).
MUSSEL, R. (2014). Estudo de Funções Logarítmicas no Ensino Médio. Dissertação de mestrado. Universidade Federal do Paraná. Disponível na web. Acessado em 11/07/2018.
OLIVEIRA, E. L. et al. (2005). Temas e Problemas Elementares. 12. ed. Rio de Janeiro: Sociedade Brasileira de Matemática, 2006. 256 p. (Coleção do Professor de Matemática).
POLYA, G. A arte de resolver problemas. Rio de janeiro: Interciência, 1995.
TAHAN, M. (2001). O Homem que Calculava. 55. ed. Editora Record.
[1] Graduado em pedagogia pela Universidade de Ensino superior- FARES; em licenciatura plena em matemática pela Universidade Estadual de Roraima-UERR; pós-graduado em Metodologia da matemática e física pela Universidade Internacional de Curitiba-UNNTER; Mestre em ciências da educação pela Universidade del Sol- Paraguai.
[2] Bacharel em Teologia pela Faculdade de Ciências, Educação e Teologia do Norte do Brasil- FACETEN, graduado em licenciatura em Física pelo instituto Federal do Pará- IF-PA, licenciado em Pedagogia pela FACETEN e pós-Graduado em Psicopedagogia pela FACETEN.
Enviado: Setembro, 2019.
Aprovado: Março, 2020.
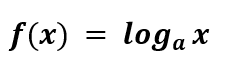
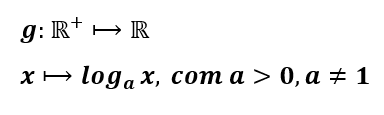


Uma resposta
Olá Evandro, gostei muito do artigo, gratidão.