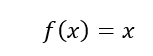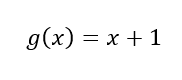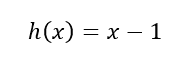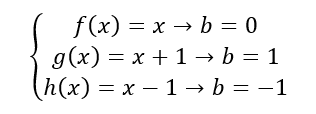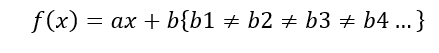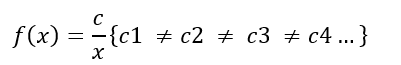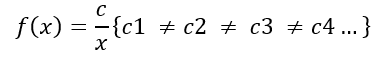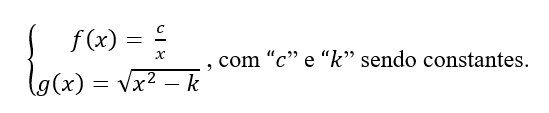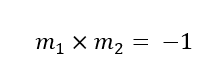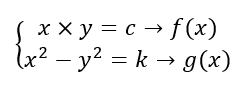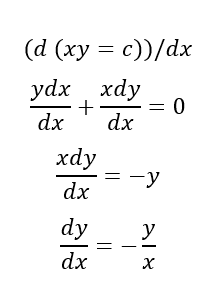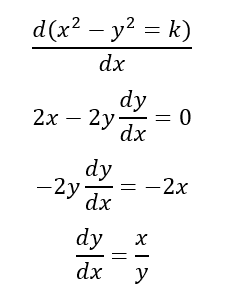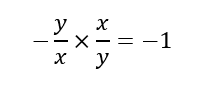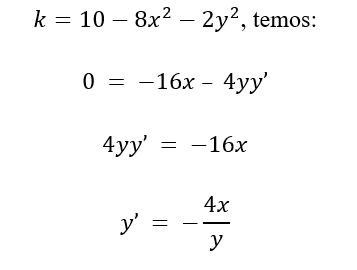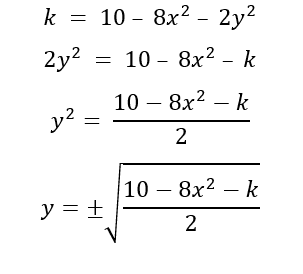ARTIGO ORIGINAL
SILVA, Auriana Kelli Leal [1], BARBOZA, Claudemir Miranda [2], BARROS, Renatto Bambulin Germano [3], KUGER, Evanilda [4], DEUS, Juliano Alves de [5]
SILVA, Auriana Kelli Leal. Et al. Famílias de curvas: Trajetórias ortogonais. Revista Científica Multidisciplinar Núcleo do Conhecimento. Ano 05, Ed. 09, Vol. 01, pp. 05-24. Setembro de 2020. ISSN: 2448-0959, Link de acesso: https://www.nucleodoconhecimento.com.br/matematica/familias-de-curvas, DOI: 10.32749/nucleodoconhecimento.com.br/matematica/familias-de-curvas
RESUMO
O presente artigo tem por objetivo mostrar a definição de trajetórias ortogonais e as suas famílias de curvas. Tendo como principal foco mostrar como encontrar tais trajetórias que constituem diversas curvas que variam conforme sua constante e demonstrar que podemos explorar dentro da física um caso de estudo envolvendo a trajetória que um míssil guiado pela temperatura percorre até atingir um avião. Onde essas trajetórias ortogonais são estabelecidas por meio de uma família de curvas em que intercepta uma outra família dada em um ponto em que o ângulo formado pelas duas retas tangentes de cada família seja reto, ou seja, forma um ângulo de 90º, em resumo essas famílias de curvas são constituídas por diversas curvas em que não se interceptam graficamente. Este artigo tem por objetivo mostrar a definição de trajetórias ortogonais e de encontrar as famílias de curvas: ortogonais, lineares, não lineares e fazer a aplicação dessas famílias de curvas através de ilustrações por meio de exemplificação e esboços.
Palavras-chave: Trajetória, ortogonal, família, curvas.
INTRODUÇÃO
De acordo com Silva (2011) existem frequentemente aplicações de trajetórias ortogonais na física, onde é necessário encontrar famílias ortogonais a outra família de curvas, ou seja, que no ponto onde se interceptam cada membro da família nova, as retas tangentes das curvas da família nova e original formam um ângulo de 90 graus.
Uma aplicação que Silva (2011) apresenta é um problema físico que pode ser resolvido pelas trajetórias ortogonais, que venha ser “uma partícula que se move sob a influência de um campo magnético. Ela descreve sempre uma curva que é perpendicular a cada uma das linhas do campo magnético” (SILVA 2011, p. 31).
Este exemplo pode ser ilustrado pelos mísseis que se movem por influência de temperatura. Considerando um míssil lançado em direção a um avião que se move em que seu motor libera energia aumentando a temperatura ao redor do avião. Esta temperatura que é constante nos dá uma função de uma curva ao redor do avião e também nos dá várias outras curvas pelo motivo de o avião estar se movendo, porém, todas essas curvas fazem parte de uma mesma família de curvas de temperatura constante. O míssil tem que ir a uma trajetória de maior temperatura que se dá na perpendicular a cada curva de temperatura, desta forma a trajetória que o míssil fará será uma trajetória ortogonal a família de curvas da temperatura.
METODOLOGIA
O tema abordado se refere a trajetórias ortogonais, que consiste em uma família de curvas em que se intercepta ortogonalmente a uma outra família de curvas. E que existe várias aplicações na natureza, como no nosso caso de estudo: a trajetória de um míssil guiado pela temperatura constante de uma curva. O artigo foi elaborado por meio da sintetização das ideias, abordando as informações coletadas, como também, dados levantados por meio de pesquisas em sítios virtuais e livros, artigos científicos referentes a trajetórias ortogonais. Foi identificado e selecionado o material bibliográfico pertinente, o segundo passo foi a leitura e fichamento em formato digital do material selecionado com identificação de obras, dos autores e suas ideias centrais. O terceiro passo foi a elaboração de uma lista de palavras-chave referentes a assuntos relevantes para a pesquisa que facilite a localização dos temas no material fichado no momento de construção do relatório final. E, por último, a análise do conteúdo do material para a conclusão da pesquisa.
CURVAS ORTOGONAIS
Segundo Steward (2006, p. 601) por uma curva “c” existe um ponto que passa uma reta tangente “t” a curva “c”, como mostra a imagem abaixo:
Figura 1: reta t tangente a curva c
Se tivermos duas funções f(x) e g(x) que se interceptam em um único ponto A como mostra a imagem abaixo:
Figura 2: função f(x) e g(x)
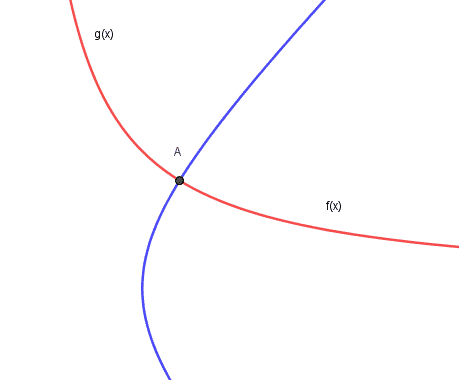
Quando traçamos a reta tangente de f(x) e de g(x) ambas no ponto de intersecção, teremos duas retas tangentes perpendicular como mostra a imagem abaixo:
Figura 3: Retas tangentes perpendiculares
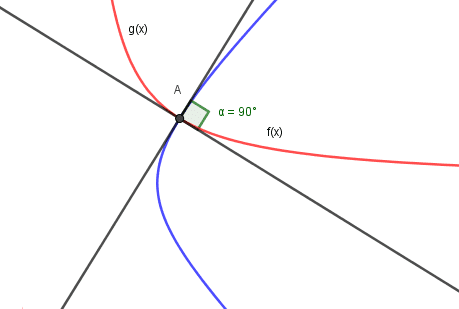
De acordo com Steward (2006) quando duas funções interceptam em um ponto e as tangentes das funções naquele ponto formam um ângulo de 90 graus, temos que as funções são perpendiculares entre si, logo podemos afirmar que:
Bronson; Costa (2008) diz que quando temos uma família de curvas a um parâmetro no plano x-y definida por:
“Onde c representa o parâmetro. O problema consiste em determinar outra família de curvas a um parâmetro, chamadas trajetórias ortogonais da família e dadas automaticamente por: G(x, y, k)” (BRONSON; COSTA, 2008, p. 67).
“Sendo que toda curva da família nova intercepte a família original resultando em uma trajetória ortogonal” (BRONSON; COSTA, 2008, p. 67).
FAMÍLIA DE CURVAS LINEARES
Sendo uma função dada por:
Ela é representada graficamente como mostra a figura:
Figura 4: Função f(x) = x
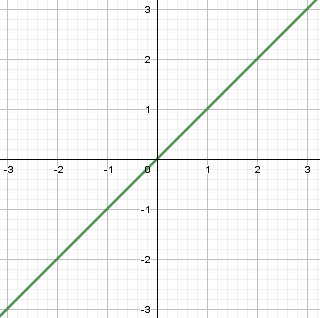
Sendo uma outra função dada por:
Ela é representada graficamente como mostra a figura:
Figura 5: Função g (x)
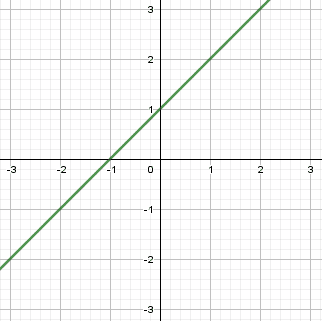
Sendo uma outra função dada por:
Sendo uma outra função dada por:
Figura 6: Função h(x)
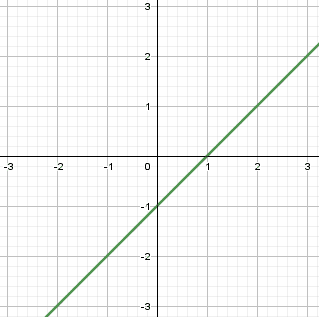
Em resumo temos que f(x), g(x) e h(x) são do tipo linear:
Podemos perceber que no gráfico g(x) a curva translada uma unidade para a esquerda, e a h(x) translada uma unidade para a direita. Em uma função f(x) = ax + b, o “b” tem a função de translada a curva no eixo Y e o “b ” é o ponto onde corta o eixo Y.
Colocando as funções anteriores no gráfico temos:
Figura 7: f(x)=ax+b
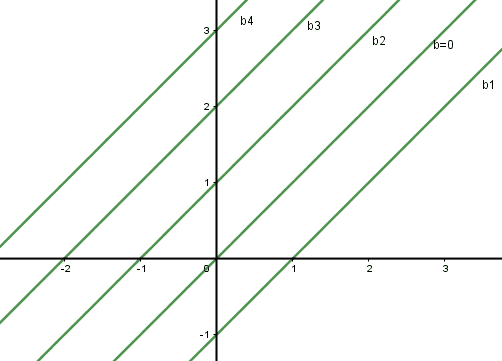
Segundo Steward (2006), temos que:
Todas as retas são paralelas, este conjunto de retas paralelas que são infinitas, pois os valores adotados para “b” pode ser infinito, onde estas infinidades de retas nunca irão se tocar, logo este conjunto de retas é uma família de curvas (STEWARD, 2006, p. 601).
FAMÍLIA DE CURVAS NÃO LINEARES
Sendo uma função dada por:
f(x) = c/x, onde “c” é uma constante.
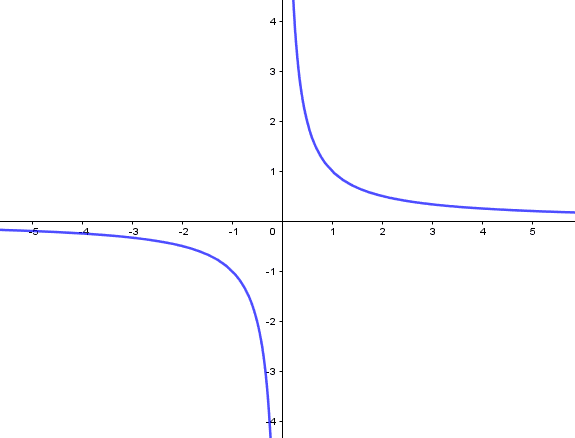
Para c>0, temos a seguinte representação gráfica:
Figura 8: f(x) = c/x
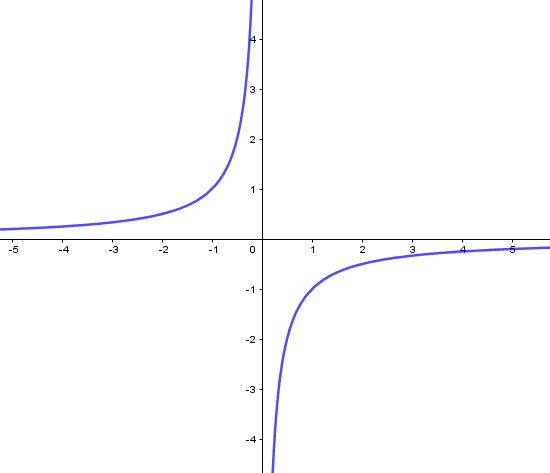
Para c<0, temos a seguinte representação gráfica:
Figura 9: c<0
Atribuindo valores positivos para c temos a seguinte representação gráfica:
Figura 10: Atribuindo valores para c.
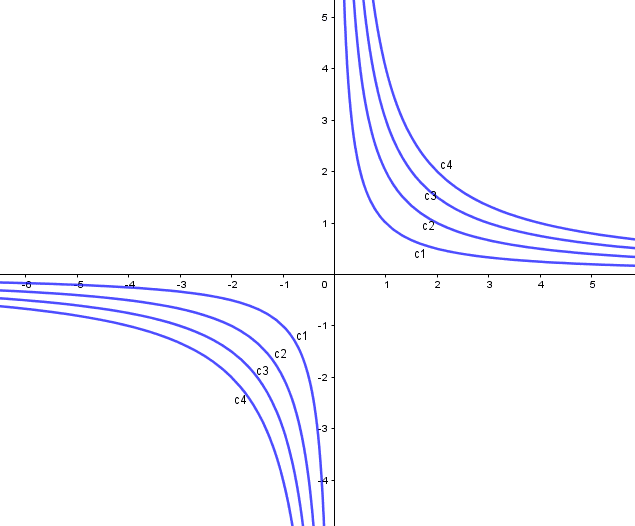
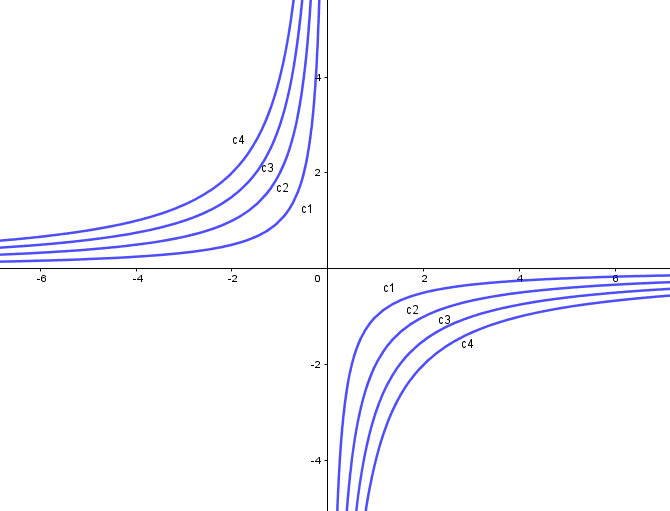
Atribuindo valores negativos para c temos a seguinte representação gráfica:
Figura 11: Atribuindo valores negativos.
Para uma função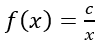 
, atribuindo valores de “c” em positivos e negativos temos a seguinte representação gráfica:
Figura 12: Atribuindo valores negativos e positivos
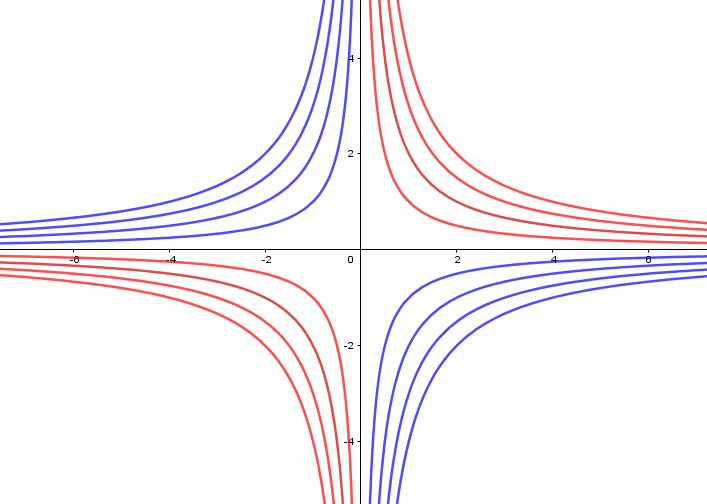
Este conjunto de curvas dada pela função 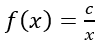, variando o valor de c, não se tocam, logo esta função forma uma família de curvas.
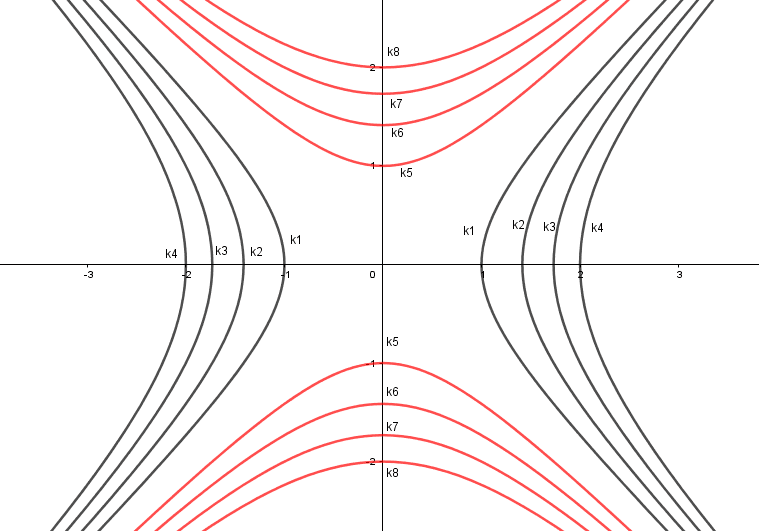
Uma outra família de curva é dada pela função: 
, variando o valor de temos uma família de curvas, onde graficamente é representada da seguinte forma:
Figura 13: Variação de K.
Steward (2006, p. 601) define em resumo que uma família de curvas são: “Todas as curvas de uma função, onde a variação de uma determinada constante irá criar infinitas curvas de modo que elas nunca irão se tocar”.
Como as curvas da figura 13 não se interceptam, então são uma família de curvas.
FAMÍLIAS ORTOGONAIS
Plotando nos gráficos duas famílias de curvas teremos pontos de intersecção destas duas famílias.
“Se a reta tangente no ponto de intersecção das duas famílias formarem um ângulo de noventa graus, então as duas famílias de curvas são ortogonais” (STEWARD, 2006, p. 601).
Em um exemplo de famílias ortogonais temos essas duas funções dadas:
Estas duas funções são representadas graficamente da seguinte forma:
Figura 14: C e K constantes
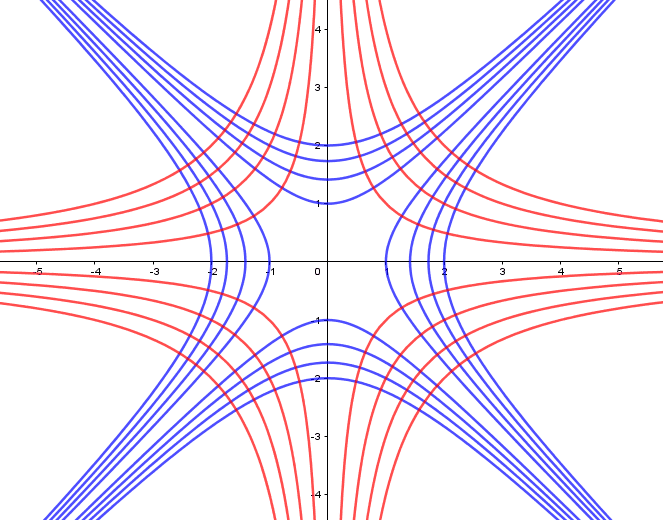
A função f(x) é representado na imagem acima na cor azul e a função g(x) representada pela cor vermelha. Estas famílias se interceptam em vários pontos como mostra a figura:
Figura 15: Famílias de curvas
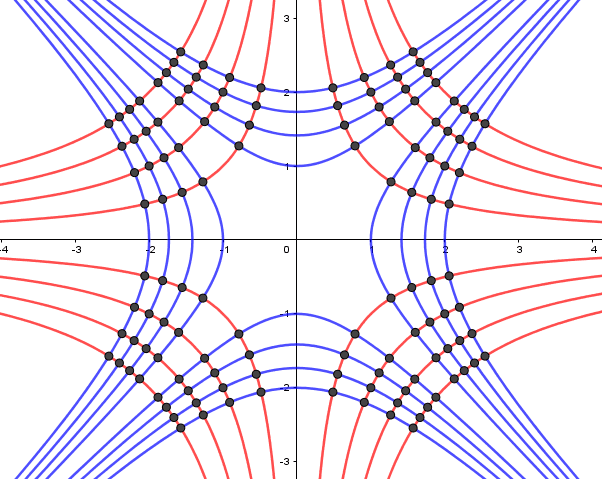
Vamos tomar um único ponto qualquer de intersecção das duas famílias e fazemos a tangente da função f(x) e a tangente da função g(x) no ponto de intersecção. Como mostra a figura:
Figura 16: Intersecção das duas famílias
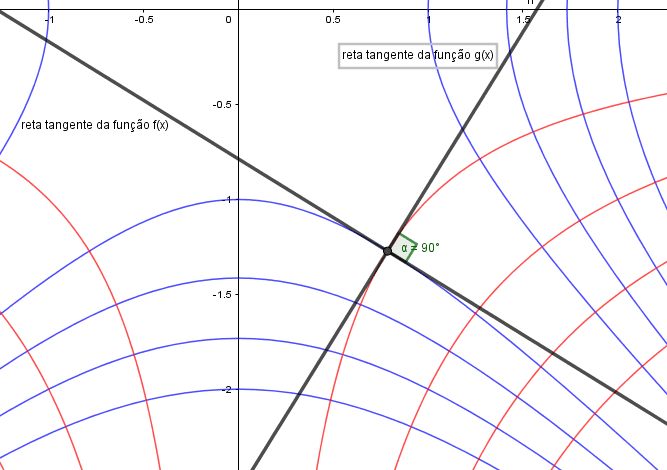
Veja que o ângulo formado pelas duas tangentes é de noventa graus, logo estas duas famílias são ortogonais. Demonstrando matematicamente temos que o produto dos coeficientes angulares de duas retas ortogonais é igual a menos um, da geometria analítica temos que,
Tomando m1 coeficiente angular de f(x) e m2 coeficiente de angular de g(x). E como a derivação de uma função se define pelo coeficiente angular, temos que:
Manipulando f(x) e g(x), temos:
Derivando implicitamente F(x), temos:
Derivando implicitamente G(x), temos:
Fazendo o produto das duas derivadas temos:
Concluindo que as famílias de curvas f(x) e g(x) são ortogonais, pois o produto de seus coeficientes angulares vale menos um.
APLICAÇÃO DE TRAJETÓRIAS ORTOGONAIS
Segue o seguinte problema envolvendo trajetórias ortogonais: “Uma partícula que procura calor está localizada no ponto (1,1) de uma placa lisa de metal, cuja temperatura é uma constante k ao longo da curva k = 10 – 8x2 – 2y2. Determine a trajetória da partícula, caso ela se movimente sempre na direção do aumento da temperatura. ”
Solução: Para encontrar a trajetória da partícula devemos ter a família de curvas ortogonais em relação a curva k. Para isso, primeiramente devemos encontrar a reta tangente a curva k.
Derivando,
Essa solução geral desta equação é a família de trajetórias ortogonais. Já a equação dos círculos com centro na origem é representada como:
Esse parâmetro C podemos colocar qualquer valor desde que seja positivo, onde podemos encontrar uma família de círculos, e obtemos isso pela derivação implícita.
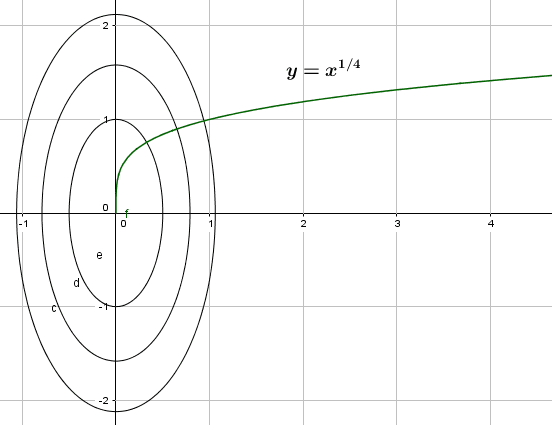
Figura 17: Representação da equação acima
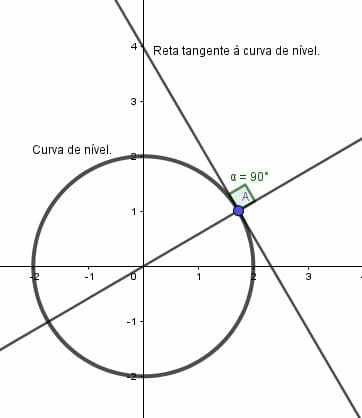
As curvas de níveis e a função 
representando a trajetória da partícula.
Figura 18: Curva de nível
CASO DE ESTUDO: TRAJETÓRIA DE UM MÍSSIL GUIADO POR CALOR
Os mísseis que “seguem” aviões funcionam com um sensor de calor, que o faz seguir o que o sensor apontar como “objeto quente”. Por isso os aviões de guerras podem soltar pequenas bolas de fogo para os lados, para confundir esses mísseis.
Inicialmente, tomemos um ponto A qualquer sendo o míssil teleguiado e um ponto B sendo o avião.
Como o míssil encontra o avião?
De maneira simplificada, o motor do avião gera um aumento de temperatura ao se deslocar, com isso deixa ao seu redor rastro que forma curva onde a temperatura é sempre constante e a temperatura diminuem conforme o avião se afasta. De forma análoga o míssil está ao longo de uma curva que a temperatura também é constante. De acordo com Cordeiro (2014),
Um míssil é um conjunto de explosivos embutidos em um veículo motorizado e controlável. O primeiro modelo usado em larga escala foi o V-1 da Alemanha nazista. Mas foi durante a guerra fria que eles se popularizaram. Chegaram as décadas de 80 e 90 como armas mais importantes, por causa da relativa precisão com que podiam acertar um alvo específico a milhares de quilômetros (CORDEIRO, 2014).
Para descobrirmos a trajetória que esse míssil fará para encontrar o avião, precisamos fazer umas verificações: Primeiro o míssil sempre procura uma região de maior aumento de temperatura, e isso acontece quando ele está perpendicularmente à aquela curva de temperatura constante. O que nos remete a ideia de derivadas parciais. O motor de um avião gera um certo calor ao seu redor, aumentando a temperatura ao seu redor é constante, e vai diminuindo conforme a distância.
Considerando a curva do míssil como sendo uma curva de nível da função temperatura, traçamos a tangente a curva de nível e de maneira perpendicular temos o vetor gradiente (ele é ortogonal a curva de nível) que o contém.
Segundo Fernandes (2011), precisamos encontrar a trajetória do míssil a partir da construção da trajetória ortogonal aquelas curvas de temperatura constante e por isso se chama trajetórias ortogonais, onde se consegue uma família de curvas que procura um caminho que seja todo ortogonal a aquelas curvas dadas no início.
Qual a trajetória o míssil segue para atingir o avião?
O míssil sempre procura a região de maior aumento de temperatura e a região de maior aumento de temperatura acontece quando o míssil está na perpendicular a aquela curva de temperatura constante. Tomamos a curva no qual o míssil se encontra, como sendo uma curva de nível da função temperatura, traçando uma tangente a essa curva de nível e assim perpendicularmente teremos um vetor gradiente, sendo esse ortogonal a curva de nível que o contém e além disso, o gradiente aponta na direção de maior aumento de temperatura.
Assim, o míssil se desloca do ponto B até o ponto C, sendo essa outra curva de nível de temperatura, e repetimos o processo, estando na curva de nível C, o gradiente aponta para a direção de maior aumento de temperatura, traçando uma tangente a curva de nível, formando então um ângulo de 90° e assim repete-se o processo nas curvas D e E até o ponto onde o míssil atinge o avião.
Figura 19. da demonstração acima
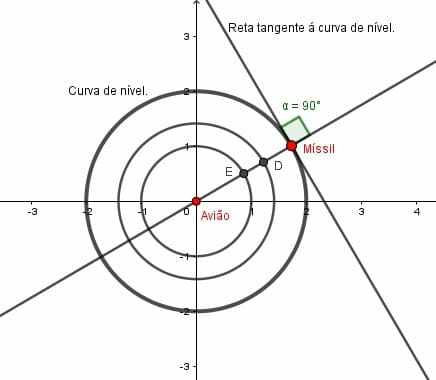
Assim, conseguimos encontrar a trajetória do míssil a partir da construção de toda uma trajetória que seja ortogonal aquelas curvas de temperaturas constantes. Onde temos uma família de curvas e estamos procurando um caminho que seja todo ortogonal aquelas curvas.
CONSIDERAÇÕES FINAIS
Pretende-se com este artigo, ampliar o âmbito de visão relacionado as trajetórias ortogonais por meio de exemplificações, esboços e cálculos; assim a partir do texto abrir possibilidades para novas discussões envolvendo as trajetórias ortogonais.
Como pode-se perceber as trajetórias ortogonais está presente na física quando analisamos um movimento de uma determinada partícula se movimentando em direção ao aumento de temperatura. Torna-se importante encontrar a família ortogonal de curvas para resolver tal problema, uma vez que curvas ortogonais quando se interceptam em um ponto suas retas tangentes formam um ângulo reto, em que o produto dos seus coeficientes angulares resulta em -1.
Após a construção de toda uma trajetória que fosse toda ortogonal as curvas de temperatura liberado pelo avião, encontramos assim, o caminho percorrido pelo míssil para atingir o avião.
REFERÊNCIAS
BRONSON. R; COSTA. G. Equações Diferenciais. 3. Ed. Porto Alegre: Bookman, 2008.
CORDEIRO, Tiago. Como funciona um míssil? ed. Super Interessante, 2014.
FERNANDES, Ronilson. Trajetórias Ortogonais. Rio Grande do Sul: Pontifícia, 2011.
LEITHOLD, Louis. O cálculo com Geometria Analítica. 3. Ed.. São Paulo: harbra, 1994. 2 v.
SILVA. E.C. Equações Diferencias ordinárias em alguns contextos históricos e reais. São Carlos, 2011.
STEWARD. J. Cálculo: Volume I. 5. ed. São Paulo: Pioneira Thomson Learning, 2006.
[1] Graduação em andamento em Matemática.
[2] Mestrado em Mestrado Profissional em Matemática. Especialização em Educação Matemática. Graduação em Matemática.
[3] Especialização em Metodologia de Ensino de Matemática e Física. Graduação em Matemática.
[4] Graduação em Matemática.
[5] Orientador. Doutorado em Física. Mestrado em Física. Graduação em Licenciatura Plena em Física.
Enviado: Março, 2020.
Aprovado: Setembro, 2020.
